| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.1. Алгоритм для ЗН (случай минимизации)
Описанный здесь алгоритм был предложен Кёнигом [22], Эгервари [15] и Куном [23, 24] и известен как венгерский алгоритм.
4.1.1. Описание алгоритма
Присвоение начальных значений
Шаг 1. Вершинам из множеств  графа
графа  присвоить веса
присвоить веса  и соответственно, причем так, чтобы для любого ребра
и соответственно, причем так, чтобы для любого ребра  выполнялось неравенство
выполнялось неравенство 
Формирование графа 
Шаг 2. Построить специальный остовный подграф  графа
графа  с данными текущими весами
с данными текущими весами 
Построение дерева
Шаг 3. Если в  нет никакого альтернирующего дерева
нет никакого альтернирующего дерева  то «выращивать» его, взяв в качестве корня некоторую экспонированную вершину
то «выращивать» его, взяв в качестве корня некоторую экспонированную вершину  графа
графа  принадлежащую множеству
принадлежащую множеству  если экспонированных вершин нет, то перейти к шагу 7. Если альтернирующее дерево уже существует, то продолжать «выращивать» его. Если дерево
если экспонированных вершин нет, то перейти к шагу 7. Если альтернирующее дерево уже существует, то продолжать «выращивать» его. Если дерево  окажется аугментальным, то перейти к шагу 4, а если венгерским — к шагу 5.
окажется аугментальным, то перейти к шагу 4, а если венгерским — к шагу 5.
Аугменталъное дерево
Шаг 4. Улучшить текущее паросочетание, «взаимно поменяв» (вдоль аугментальной цепи) ребра, принадлежащие ему и ему не принадлежащие.
«Отбросить» дерево  и перейти к шагу 3.
и перейти к шагу 3.
Венгерское дерево
Шаг 5. Для ребер  не лежащих в
не лежащих в  одна концевая вершина которых принадлежит текущему дереву
одна концевая вершина которых принадлежит текущему дереву  и помечена
и помечена
как внешняя, а другая концевая вершина не принадлежит  найти
найти

Шаг 6. Для каждой вершины  графа
графа  принадлежащей
принадлежащей  и являющейся внешней вершиной дерева
и являющейся внешней вершиной дерева  поменять
поменять  на
на  а для каждой вершины
а для каждой вершины  графа
графа  принадлежащей
принадлежащей  и являющейся внутренней вершиной дерева
и являющейся внутренней вершиной дерева  заменить
заменить  на
на 
Сохранить дерево  и перейти к шагу 2.
и перейти к шагу 2.
Конец
Шаг 7. Текущее совершенное паросочетание является минимальным.
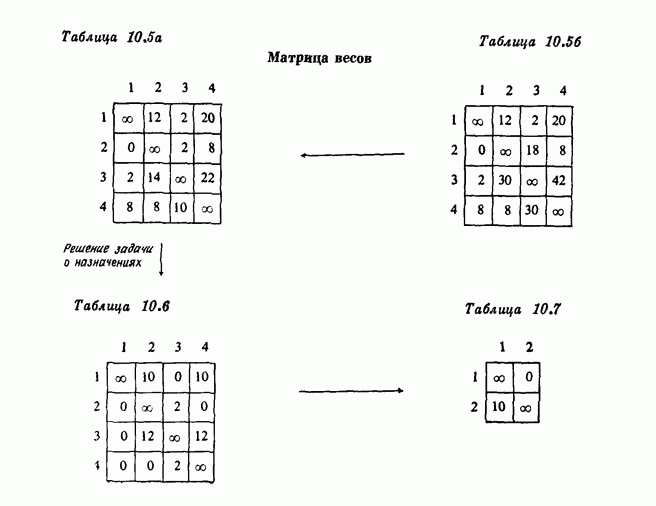
4.1.2. Матричная форма алгоритма
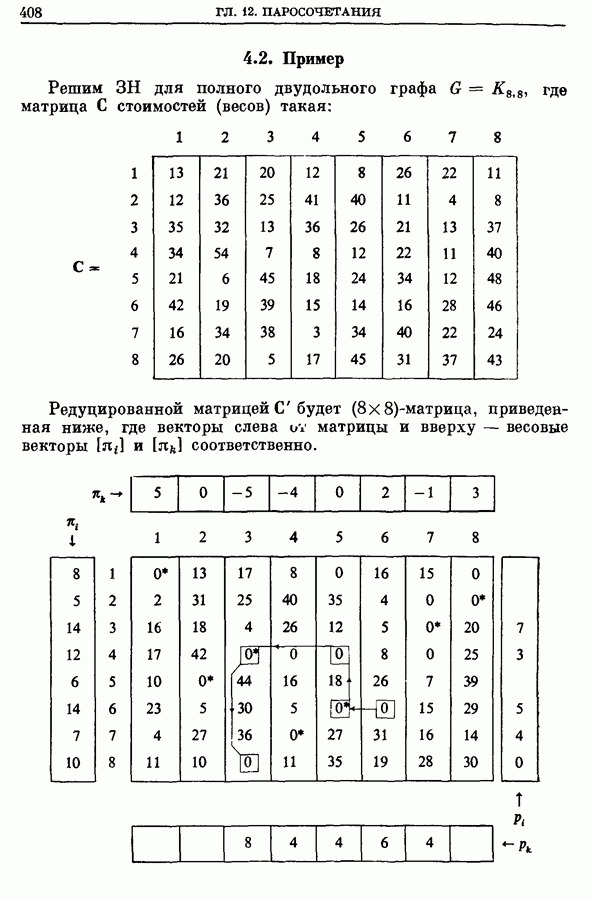
Часто, когда граф является полным, операции вышеприведенного алгоритма реализуются на  -матрице С, строки которой соответствуют вершинам из
-матрице С, строки которой соответствуют вершинам из  а столбцы — вершинам из
а столбцы — вершинам из  Начальные элементы
Начальные элементы  являются стоимостями (весами) ребер
являются стоимостями (весами) ребер 
На шаге 1 алгоритма начальный вес  вершины
вершины  берется равным наименьшему элементу строки i. Вес
берется равным наименьшему элементу строки i. Вес  вычитается из всех элементов строки
вычитается из всех элементов строки  и так делается для всех строк. Вес
и так делается для всех строк. Вес  вершины
вершины  берется равным наименьшему элементу в столбце к получившейся матрицы. Затем
берется равным наименьшему элементу в столбце к получившейся матрицы. Затем  вычитается из всех элементов столбца к, и
вычитается из всех элементов столбца к, и  делается для всех столбцов, в результате чего получается новая матрица
делается для всех столбцов, в результате чего получается новая матрица  . Матрица С называется редуцированной матрицей. Тогда остовным подграфом
. Матрица С называется редуцированной матрицей. Тогда остовным подграфом  будет
будет  гсдвудольный граф с дугами (соединяющими только те вершины
гсдвудольный граф с дугами (соединяющими только те вершины  для которых
для которых  Совершенное паросочетание графа
Совершенное паросочетание графа  будет соответствовать такому выбору нулевых элементов в матрице С, когда в каждой строке и каждом столбце выбрано ровно по одному нулевому элементу С.
будет соответствовать такому выбору нулевых элементов в матрице С, когда в каждой строке и каждом столбце выбрано ровно по одному нулевому элементу С.
Построение альтернирующего дерева в зтом получившемся остовном подграфе  происходит с помощью следующей процедуры расстановки пометок в строках и столбцах матрицы С. Начнем построение произвольного паросочетания в
происходит с помощью следующей процедуры расстановки пометок в строках и столбцах матрицы С. Начнем построение произвольного паросочетания в  отмечая нулевые элементы в С так, чтобы никакие два отмеченные нуля не находились в одном и том же столбце или строке. (Если мы отметили нуль в позиции
отмечая нулевые элементы в С так, чтобы никакие два отмеченные нуля не находились в одном и том же столбце или строке. (Если мы отметили нуль в позиции  то это означает, что ребро
то это означает, что ребро  входит в паросочетание, и наоборот.)
входит в паросочетание, и наоборот.)
Найдем строку  без отмеченных элементов и сделаем пометку
без отмеченных элементов и сделаем пометку  Если такой строки нет, то текущее паросочетание будет минимальным совершенным паросочетанием.
Если такой строки нет, то текущее паросочетание будет минимальным совершенным паросочетанием.  если такая существует — соответствует теперь экспонированной вершине, выбранной в качестве корня альтернирующего дерева,
если такая существует — соответствует теперь экспонированной вершине, выбранной в качестве корня альтернирующего дерева,  являются эквивалентами пометок, используемых для «хранения» этого дерева.) Это надо понимать так: дерево рассматривается как некоторая древовидность с корнем, причем если дуга
являются эквивалентами пометок, используемых для «хранения» этого дерева.) Это надо понимать так: дерево рассматривается как некоторая древовидность с корнем, причем если дуга  входит в эту древовидность, то «хранится равенство»
входит в эту древовидность, то «хранится равенство»  Для корня дерева мы берем
Для корня дерева мы берем  разд. 2.2.1, гл. 7.) Начинаем с такой ситуации, когда есть пометка
разд. 2.2.1, гл. 7.) Начинаем с такой ситуации, когда есть пометка  и когда все другие строки и столбцы не помечены.
и когда все другие строки и столбцы не помечены.
(i) Пометить каждый непомеченный столбец к, содержащий неотмеченный  в помеченной строке
в помеченной строке  меткой
меткой  Если существует несколько возможностей, взять любую.
Если существует несколько возможностей, взять любую.
(ii) Пометить каждую непомеченную строку  содержащую отмеченный
содержащую отмеченный  в помеченном столбце к, меткой
в помеченном столбце к, меткой 
Повторять процесс расстановки пометок (в соответствии с правилами  Эти две операции неявно строят в
Эти две операции неявно строят в  дерево, причем это дерево дается эквивалентами пометок. Стоит заметить, что все «внешние» вершины этого дерева соответствуют строкам из С, а все «внутренние» — столбцам. Применение операций (i) и (ii) продолжается до тех пор, пока не будет помечен столбец
дерево, причем это дерево дается эквивалентами пометок. Стоит заметить, что все «внешние» вершины этого дерева соответствуют строкам из С, а все «внутренние» — столбцам. Применение операций (i) и (ii) продолжается до тех пор, пока не будет помечен столбец  без отмеченных элементов (скажем, меткой
без отмеченных элементов (скажем, меткой  или процесс расстановки пометок нельзя будет продолжать. В первом случае будет найдена аугментальная цепь
или процесс расстановки пометок нельзя будет продолжать. В первом случае будет найдена аугментальная цепь  где
где  Элементы
Элементы  (нули) в позициях
(нули) в позициях  матрицы С попеременно отмечаются или нет для образования лучшего паросочетания. Пометки
матрицы С попеременно отмечаются или нет для образования лучшего паросочетания. Пометки  стираются, и процесс продолжается. Во втором случае обнаруживается венгерское дерево. Если
стираются, и процесс продолжается. Во втором случае обнаруживается венгерское дерево. Если  — множества всех помеченных, а
— множества всех помеченных, а  всех непомеченных строк и столбцов соответственно, то находим
всех непомеченных строк и столбцов соответственно, то находим

(Заметим, что 
Обновление.  для
для  для
для  для
для  А для
А для  в остальных случаях
в остальных случаях  не изменяются. Операции (i) и (ii) теперь снова применяются к новой матрице
не изменяются. Операции (i) и (ii) теперь снова применяются к новой матрице 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
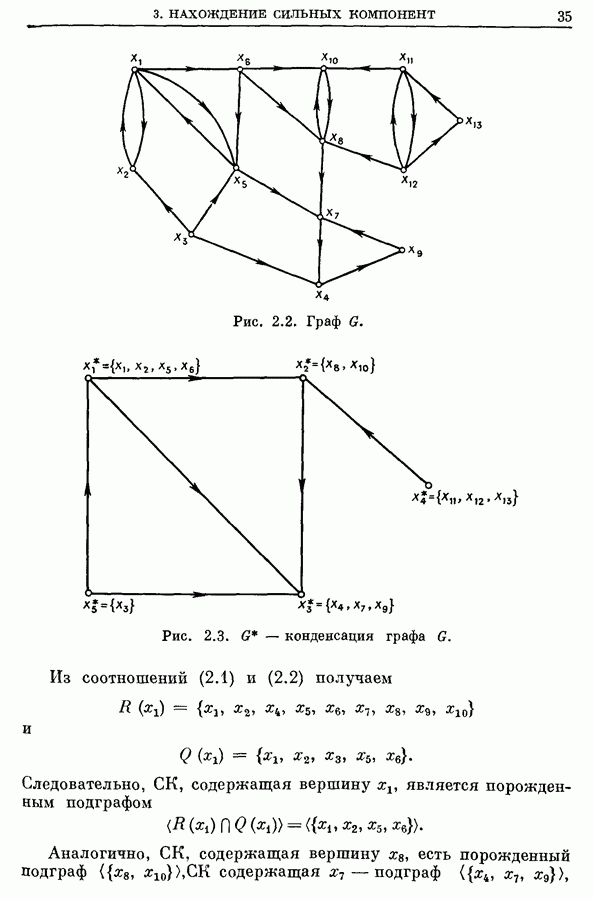
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
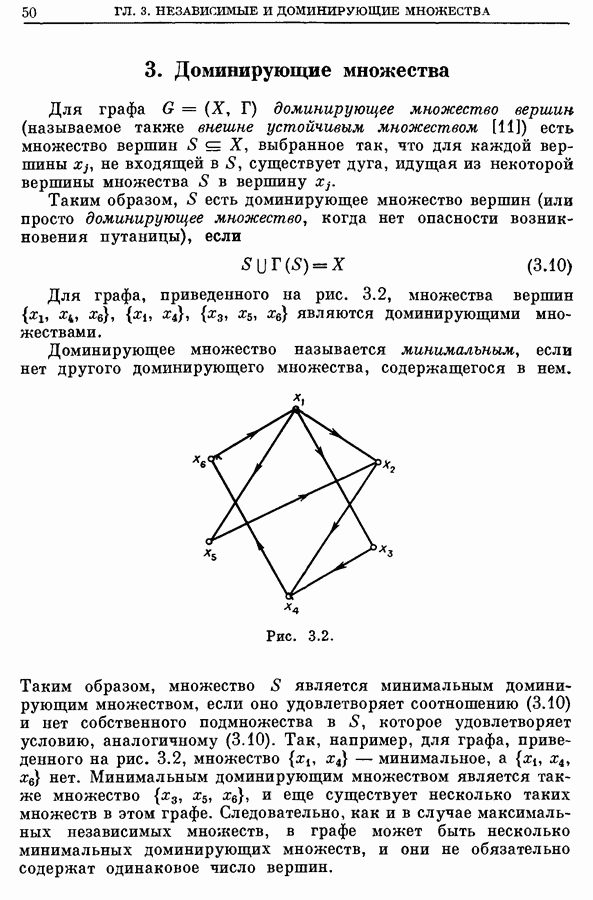
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
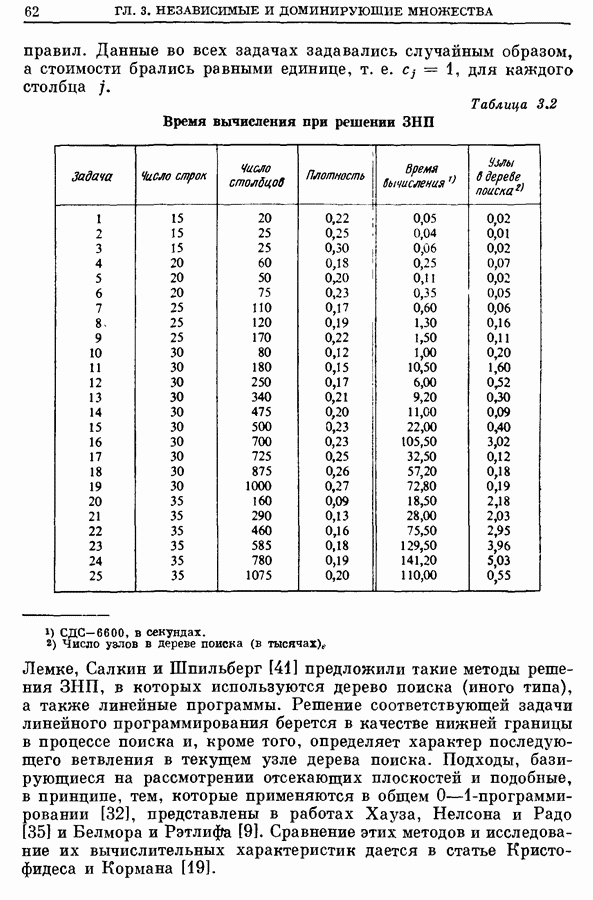
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
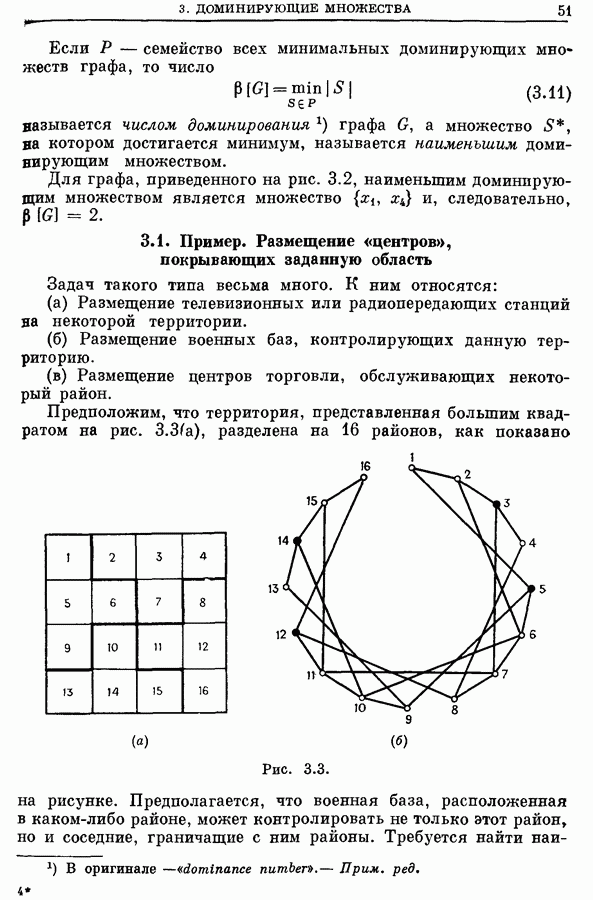
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
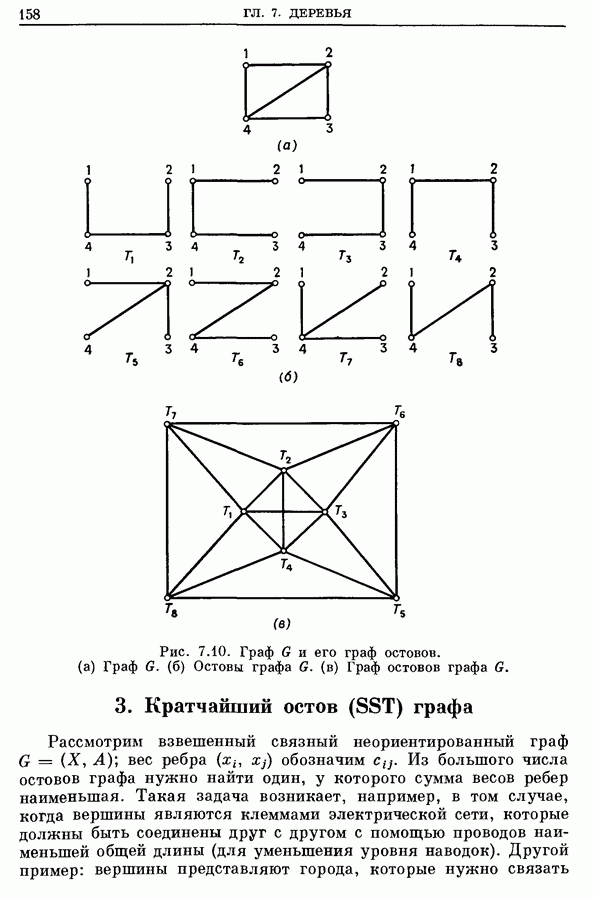
- 2.4. Граф остовов
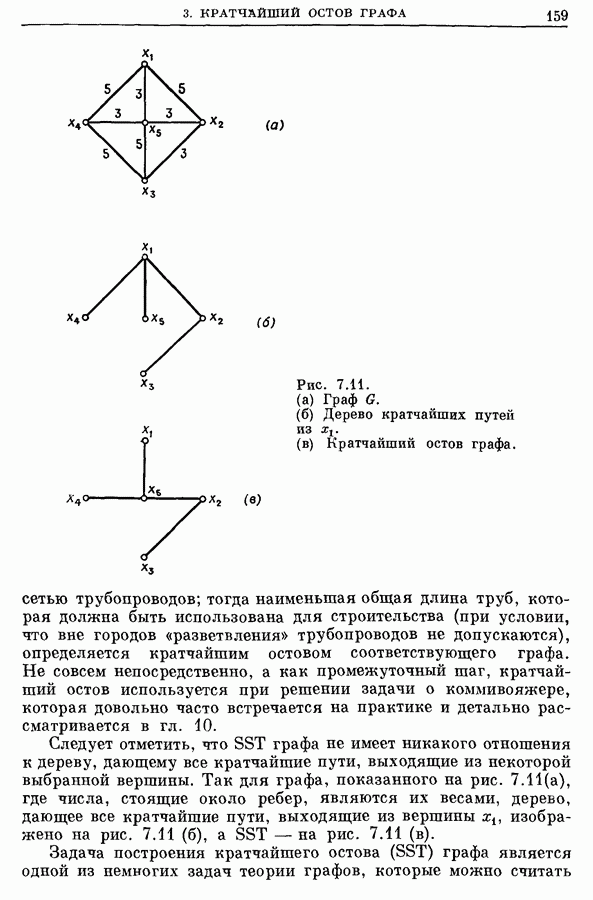
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
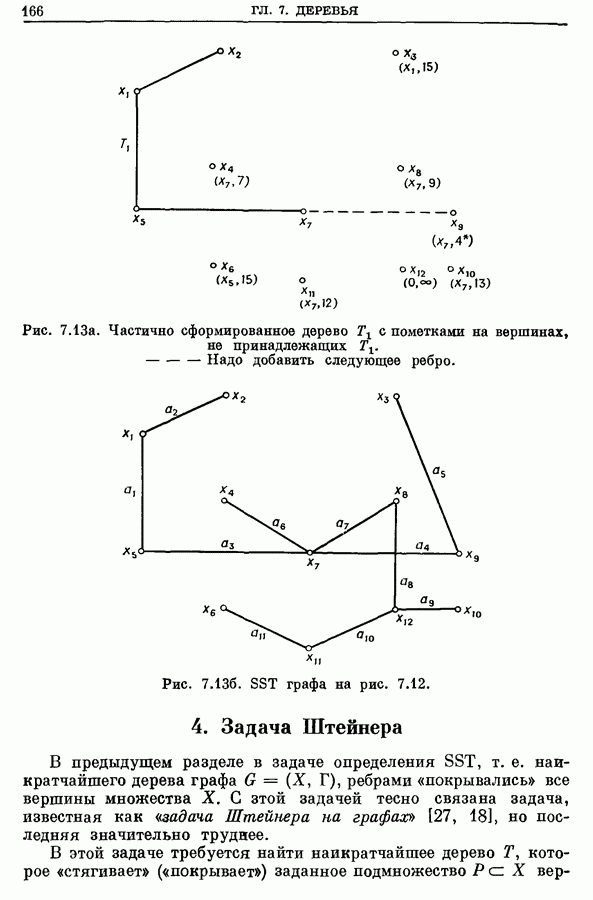
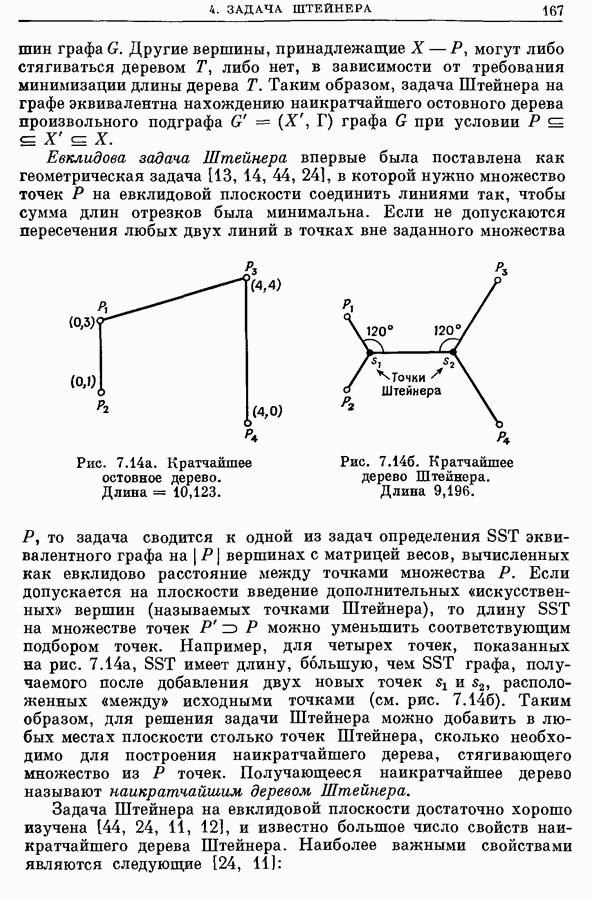
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
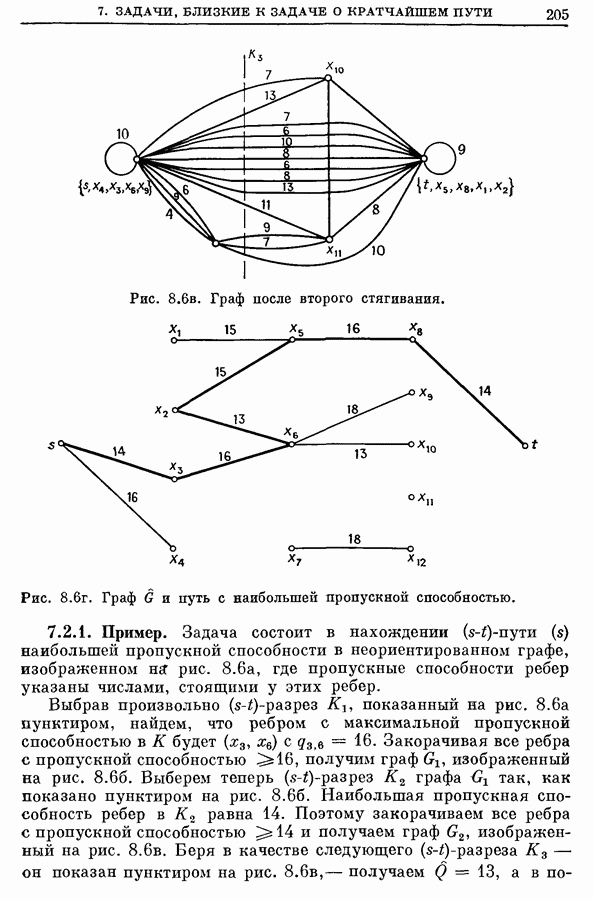
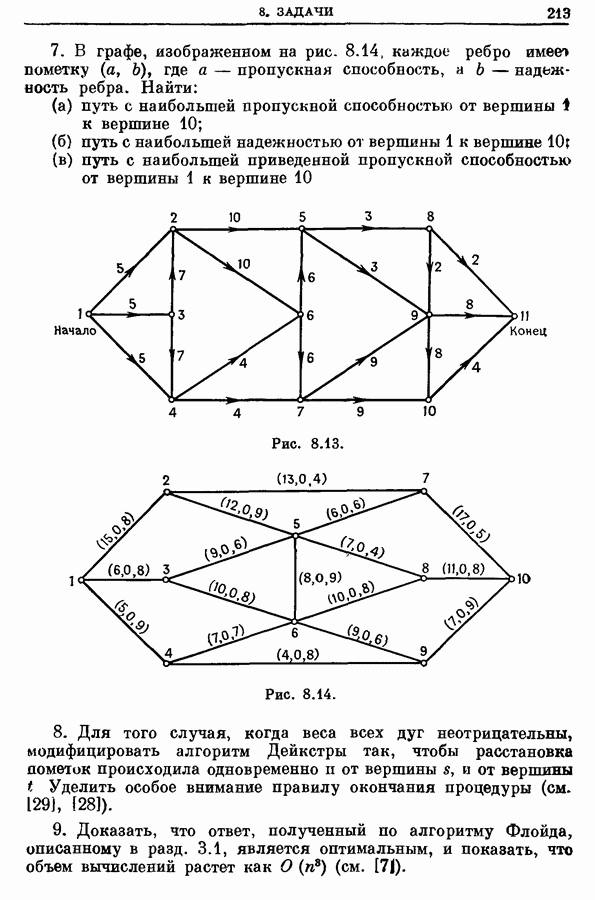
- 7.2. Путь с наибольшей пропускной способностью
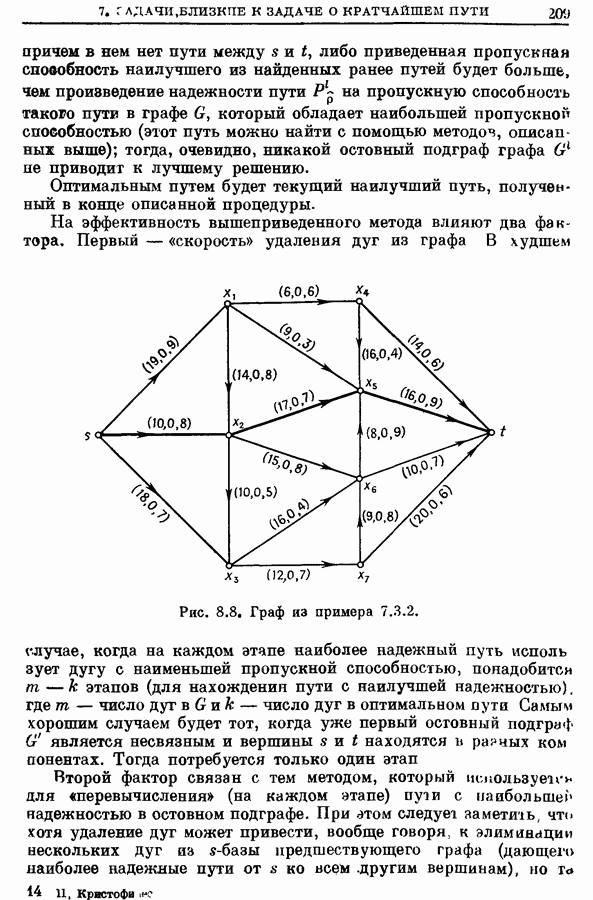
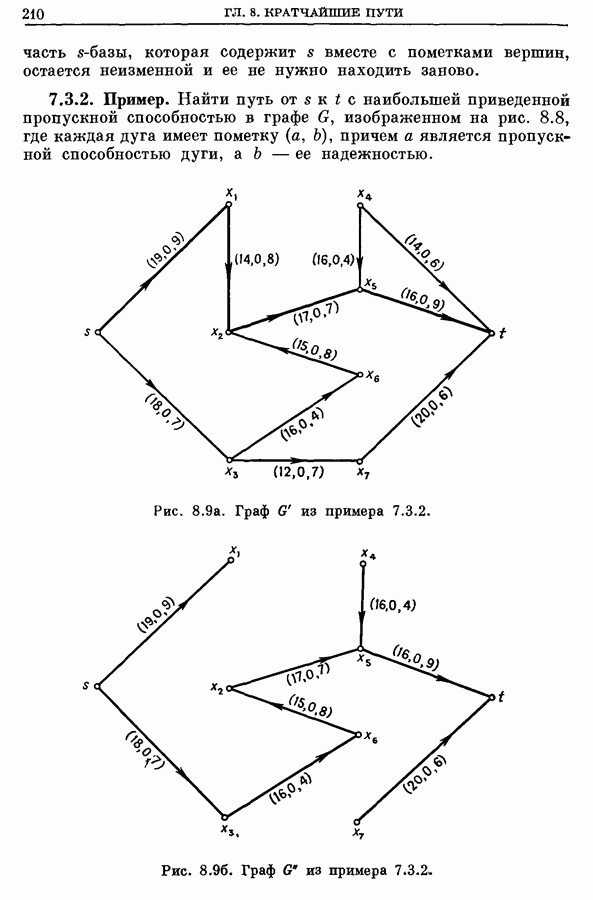
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
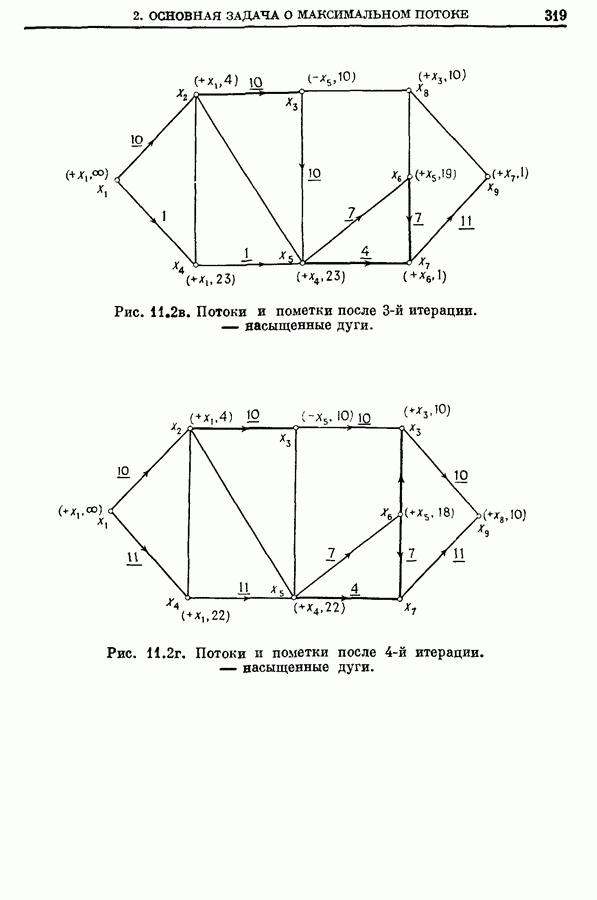
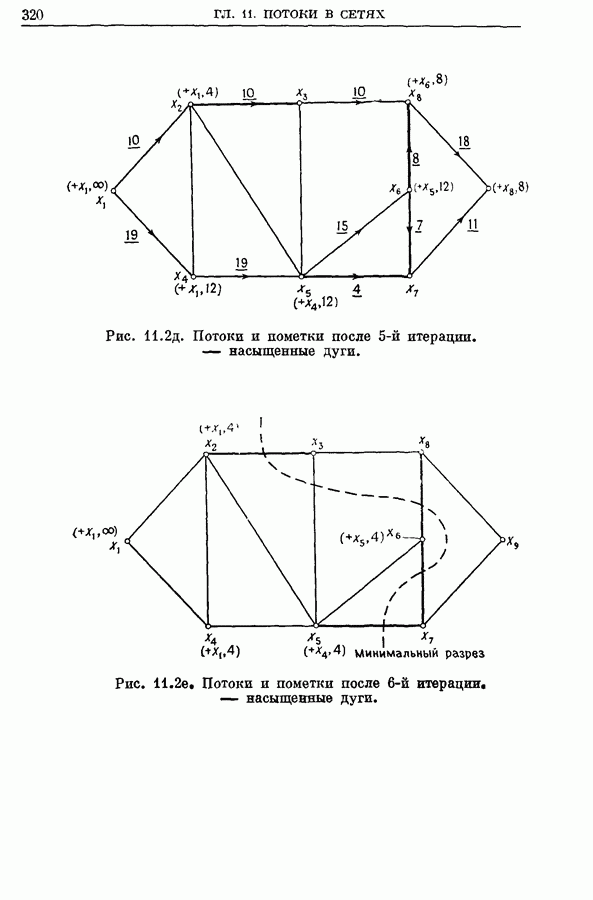
- 2.2. Пример
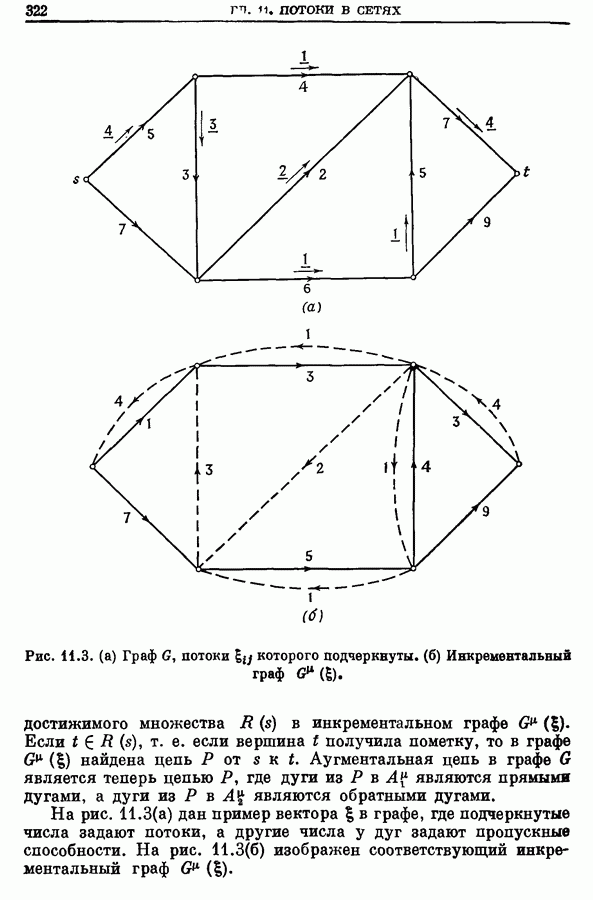
- 2.3. Инкрементальные графы
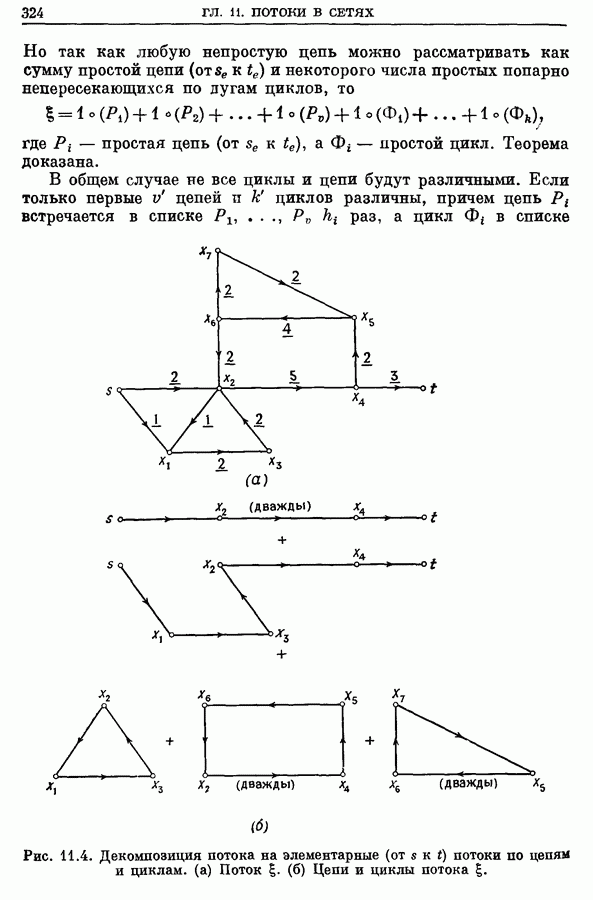
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
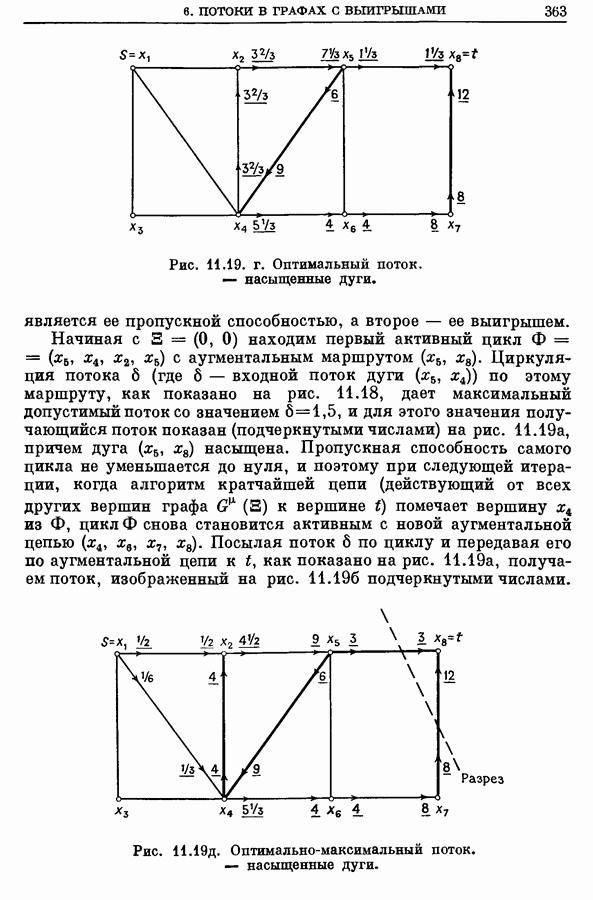
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
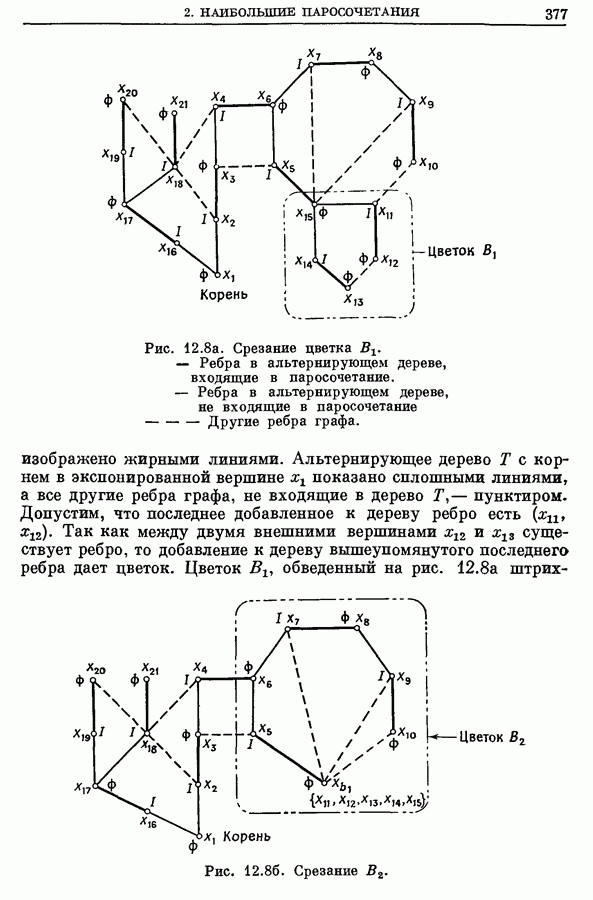
- 2.2. Цветки
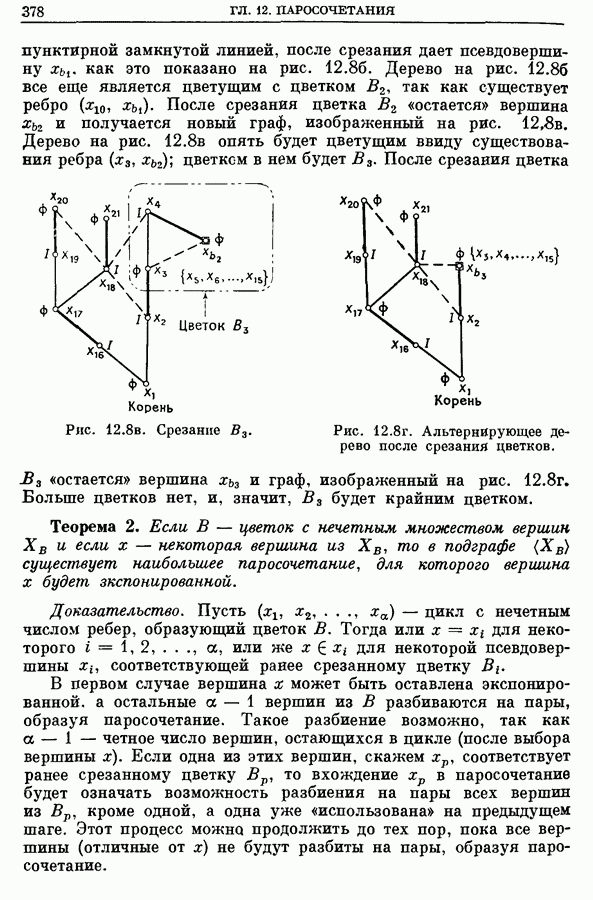
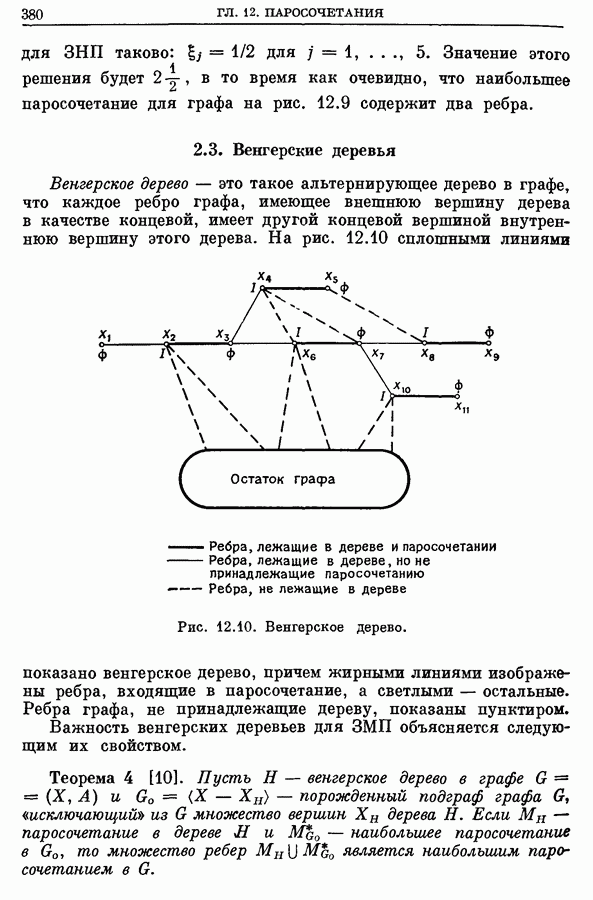
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
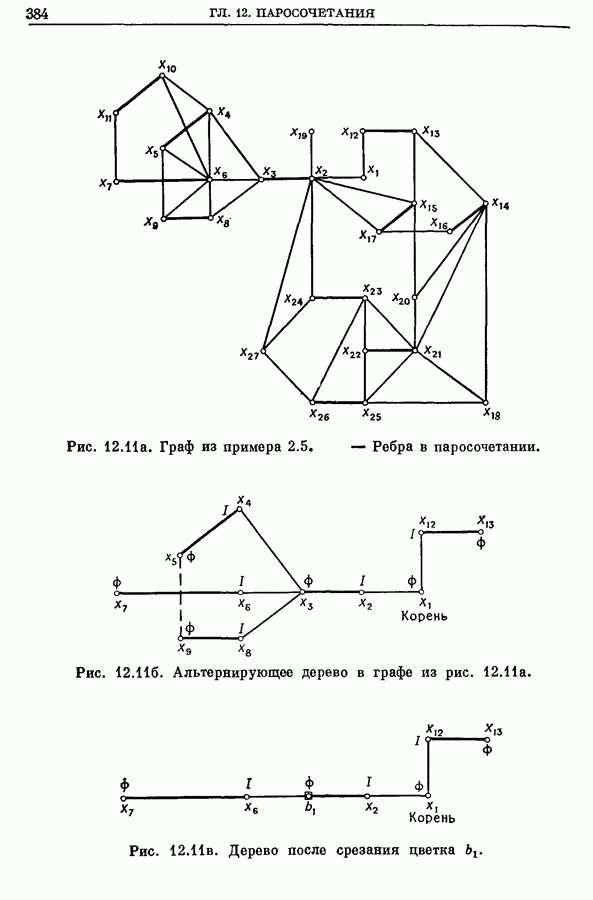
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления