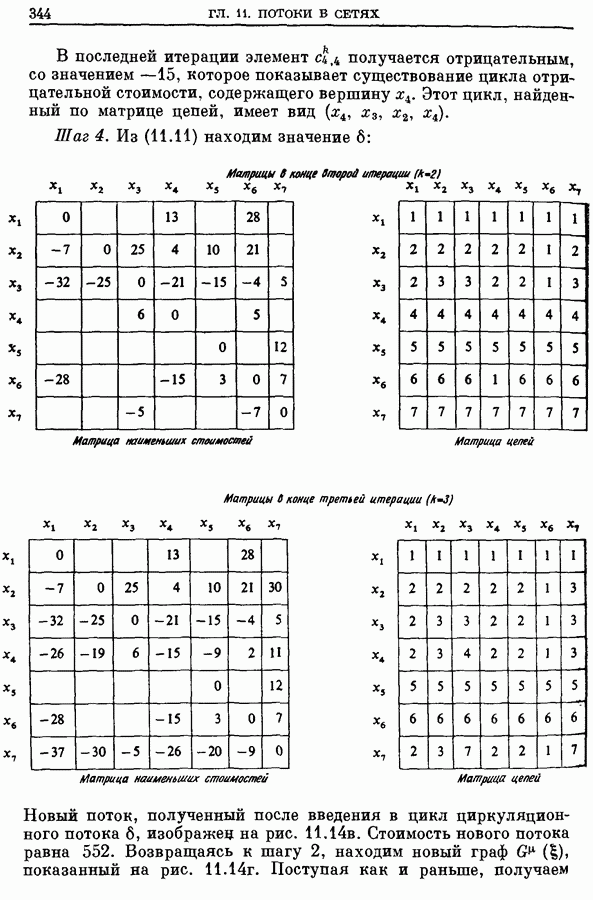
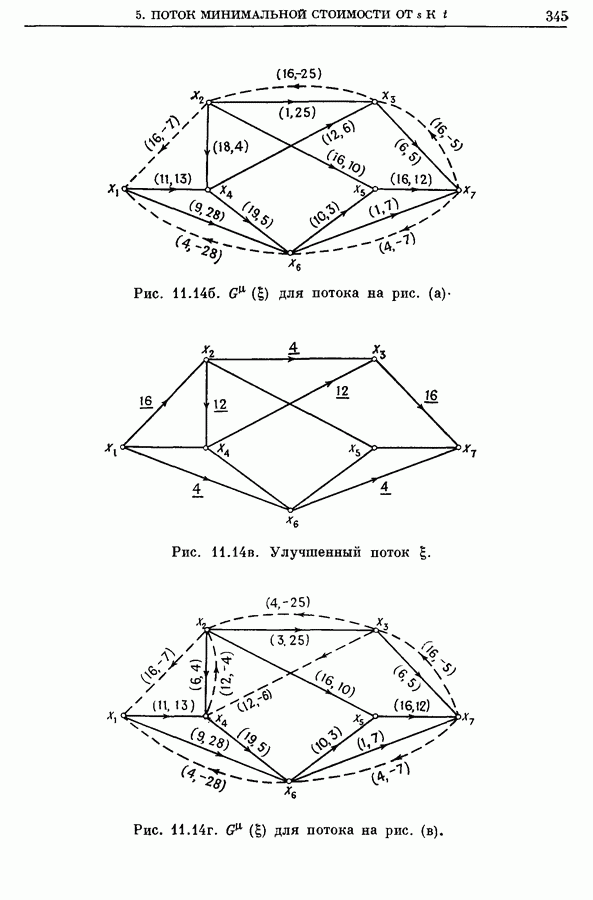
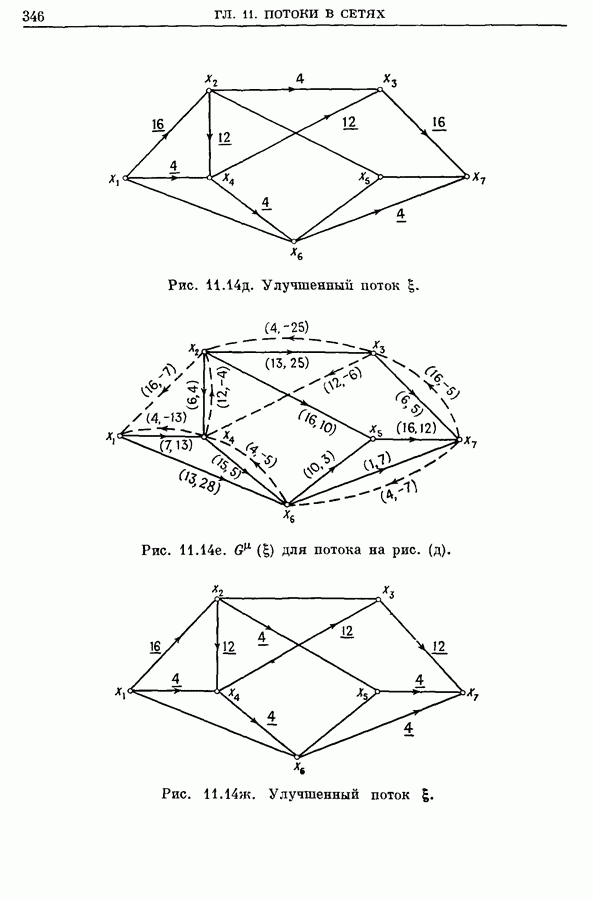
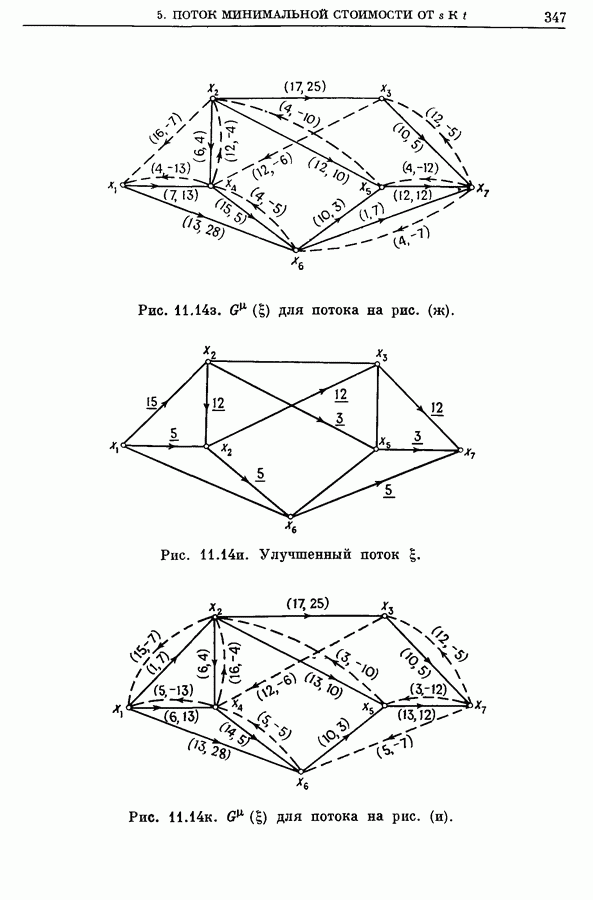
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
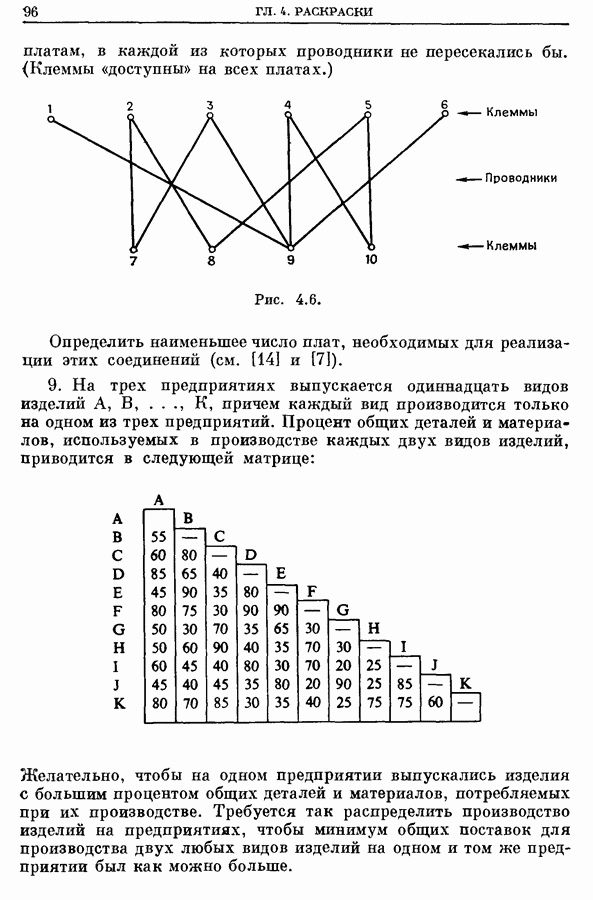
2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
В разд. 4 гл. 3 было введено понятие кликового числа  графа
графа  (как наибольшего числа вершин в полном порожденном подграфе графа
(как наибольшего числа вершин в полном порожденном подграфе графа  и было отмечено, что поскольку между кликами графа
и было отмечено, что поскольку между кликами графа  и максимальными независимыми множествами дополнительного графа
и максимальными независимыми множествами дополнительного графа  существует взаимно однозначное соответствие, то справедливы равенства
существует взаимно однозначное соответствие, то справедливы равенства 
2.1. Нижние оценки для ...
Очевидно, поскольку по крайней мере  цветов требуется для раскраски соответствующей клики графа
цветов требуется для раскраски соответствующей клики графа  (той самой клики, которая «определяет» кликовое число графа
(той самой клики, которая «определяет» кликовое число графа  что
что  является
является

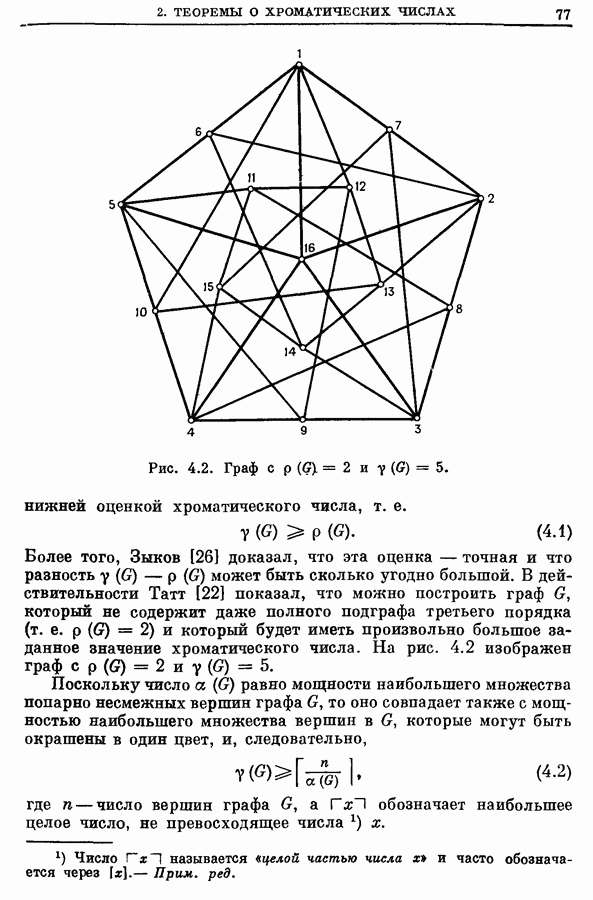
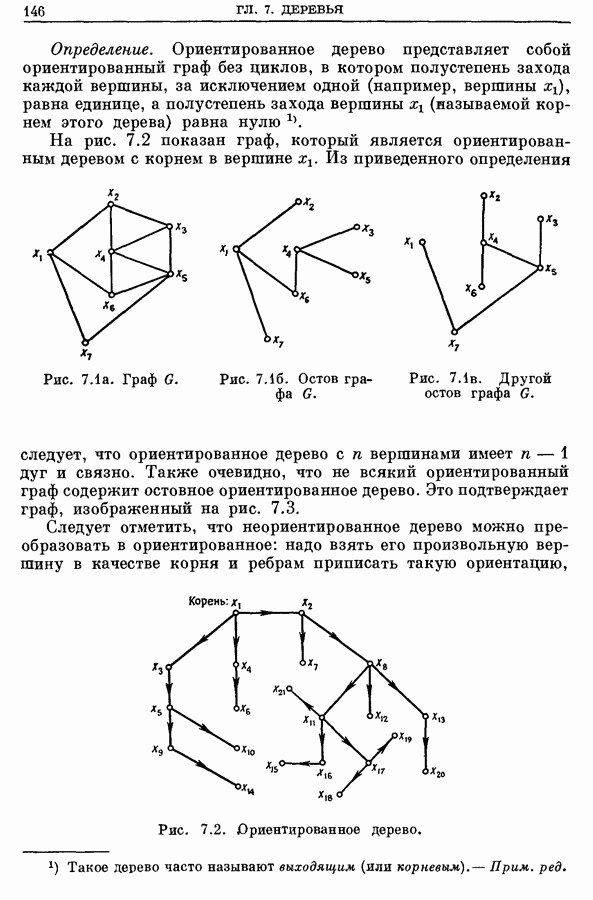
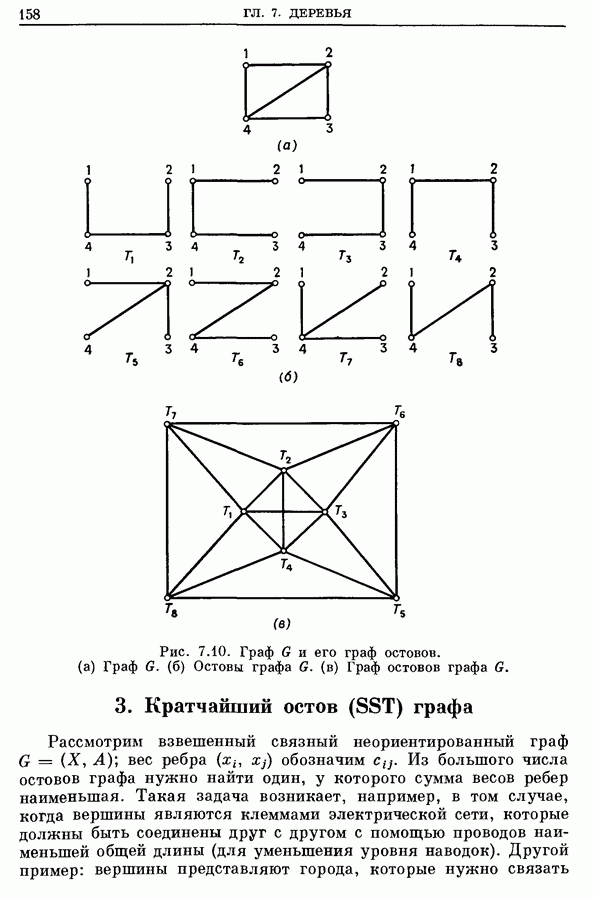
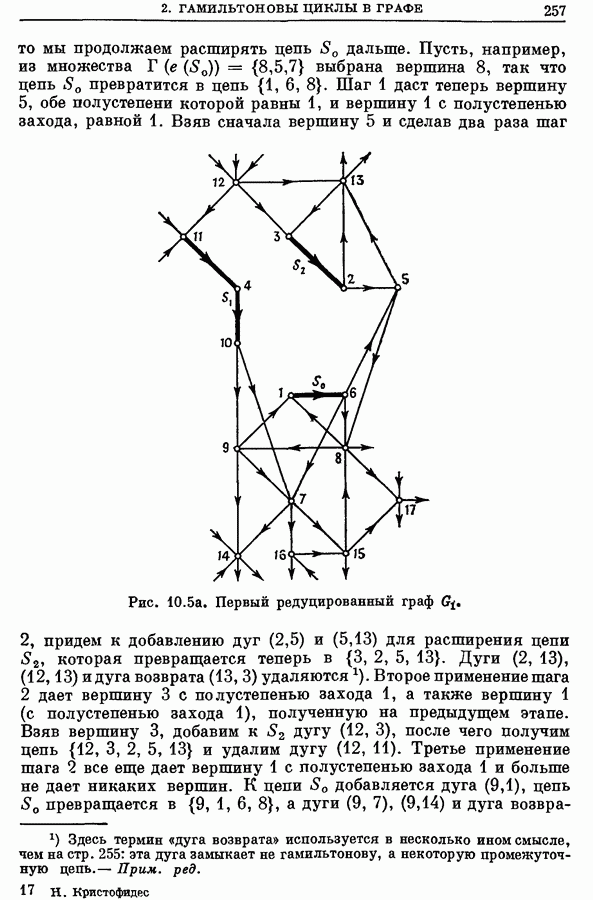
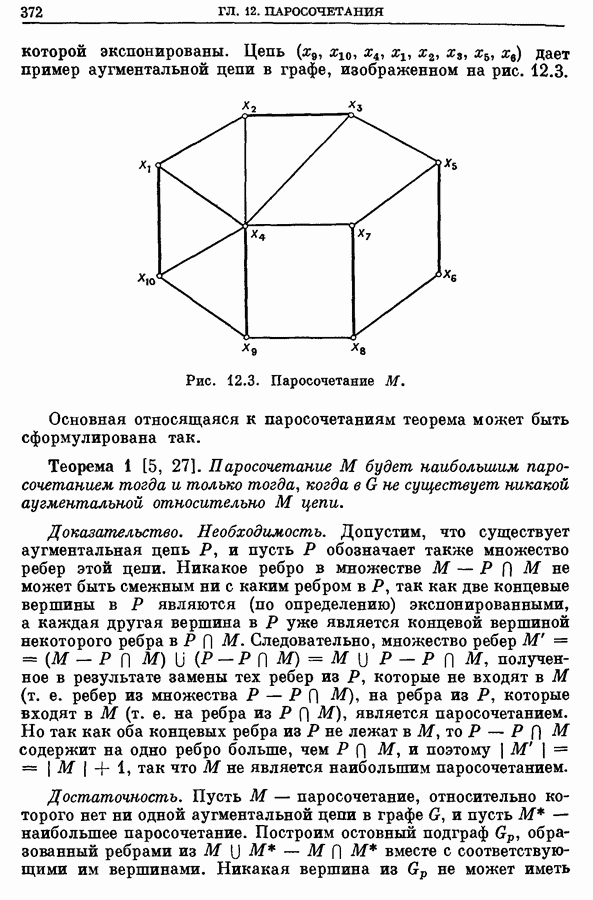
Рис. Граф 
нижней оценкой хроматического числа, т. е.

Более того, Зыков [26] доказал, что эта оценка — точная и что разность  может быть сколько угодно большой. В действительности Татт [22] показал, что можно построить граф
может быть сколько угодно большой. В действительности Татт [22] показал, что можно построить граф  который не содержит даже полного подграфа третьего порядка (т. е.
который не содержит даже полного подграфа третьего порядка (т. е.  и который будет иметь произвольно большое заданное значение хроматического числа. На рис. 4.2 изображен граф с
и который будет иметь произвольно большое заданное значение хроматического числа. На рис. 4.2 изображен граф с  и
и 
Поскольку число  равно мощности наибольшего множества попарно несмежных вершин графа
равно мощности наибольшего множества попарно несмежных вершин графа  то оно совпадает также с мощностью наибольшего множества вершин в
то оно совпадает также с мощностью наибольшего множества вершин в  которые могут быть окрашены в один цвет, и, следовательно,
которые могут быть окрашены в один цвет, и, следовательно,

где  число вершин графа
число вершин графа  обозначает наибольшее целое число, не превосходящее числа х.
обозначает наибольшее целое число, не превосходящее числа х.
Если через  обозначить хроматическое число дополнения графа
обозначить хроматическое число дополнения графа  то можно записать следующие два неравенства, полученные Нордхаузом и Гаддумом [19]:
то можно записать следующие два неравенства, полученные Нордхаузом и Гаддумом [19]:

и

где означает наименьшее целое число, которое не меньше х. Еще одна нижняя оценка для  предложена Геллером [8]:
предложена Геллером [8]:

Майерс и Лин [18] показали, что оценка из (4.1) равномерно мажорирует приведенную выше, и, следовательно, единственное преимущество оценки (4.5) состоит в том, что ее проще вычислять, чем оценку (4.1).
2.2. Верхние оценки для ...
Нижние оценки хроматического числа безусловно более интересны, чем верхние, поскольку (если они достаточно близки к истинному значению) они могут быть использованы в процедуре вычисления  включающей дерево поиска. В то же время верхние оценки хроматического числа подобного применения не находят. Тем не менее в литературе приводятся формулы для вычисления верхних оценок хроматического числа; так Бруксом [3] предложена следующая легко вычисляемая оценка:
включающей дерево поиска. В то же время верхние оценки хроматического числа подобного применения не находят. Тем не менее в литературе приводятся формулы для вычисления верхних оценок хроматического числа; так Бруксом [3] предложена следующая легко вычисляемая оценка:

Другие достаточно точные верхние оценки, также использующие степени вершин графа, можно найти у Уэлша [23] и Вилфа и Секереша [21].
Верхние оценки, связывающие значения  и
и  приводятся у Нордхауза и Гаддума [19]:
приводятся у Нордхауза и Гаддума [19]:

и

Оценки, даваемые формулами (4.3), (4.4), (4.7) и (4.8), являются наилучшими в том смысле, что можно построить графы, на которых эти оценки достигаются. В большинстве случаев, однако, они столь неточны, что не имеют никакой практической значимости.
2.3. Гипотеза четырех красок
Граф, который можно так изобразить на плоскости, что никакие два его ребра не пересекаются между собой, называется планарным. Планарные графы важны как с теоретической, так и с практической точек зрения и обладают рядом таких свойств, связанных с раскраской, о которых следует упомянуть.
Теорема о пяти красках [13]
Каждый планарный граф можно так раскрасить, используя пять цветов, что любые две смежные вершины будут окрашены в разные цвета, т. е. если  планарный граф, то
планарный граф, то 
«Теорема» о четырех красках (недоказанная)
Каждый планарный граф можно так раскрасить, используя 4 цвета, что любые две смежные вершины будут окрашены в разные цвета, т. е.  если
если  планарный граф.
планарный граф.
Впервые примерно в 1850 г. о гипотезе четырех красок речь шла в беседах Августа де Моргана и его ученика  Гутри. Затем о ней говорилось в письме де Моргана сэру Вильяму Рауэну Гамильтону, датированном 23 октября 1852 г. Поскольку тогда довольно быстро нарастал поток «доказательств», «контрдоказательств», гипотез и теорем, относящихся к этой тематике, то накопилась громадная литература по гипотезе четырех красок, и эта «теорема» стала, по-видимому, самой знаменитой нерешенной задачей в математике. Мы не будем здесь подробно обсуждать гипотезу четырех красок и интересующегося ею читателя отсылаем к замечательной работе Оре [2].
Гутри. Затем о ней говорилось в письме де Моргана сэру Вильяму Рауэну Гамильтону, датированном 23 октября 1852 г. Поскольку тогда довольно быстро нарастал поток «доказательств», «контрдоказательств», гипотез и теорем, относящихся к этой тематике, то накопилась громадная литература по гипотезе четырех красок, и эта «теорема» стала, по-видимому, самой знаменитой нерешенной задачей в математике. Мы не будем здесь подробно обсуждать гипотезу четырех красок и интересующегося ею читателя отсылаем к замечательной работе Оре [2].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
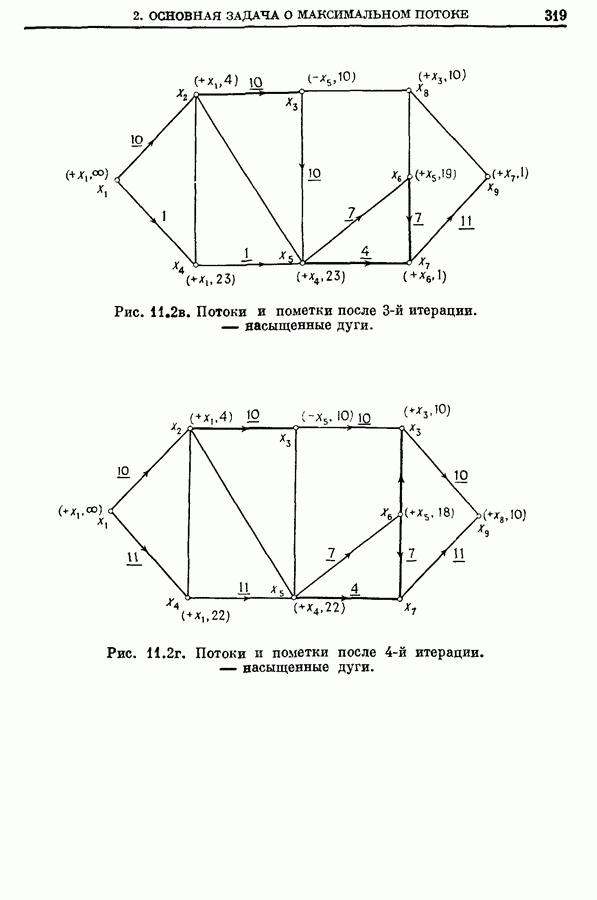
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
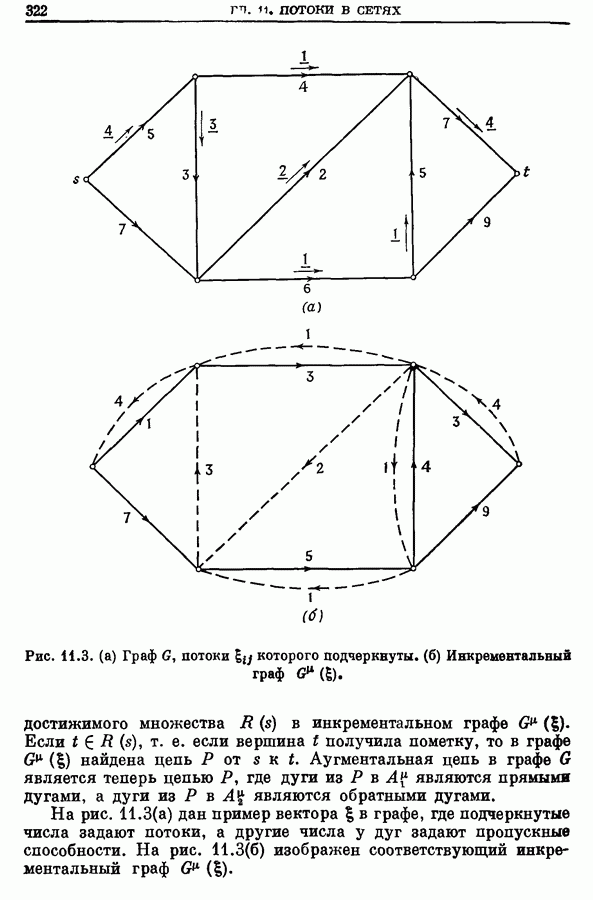
- 2.3. Инкрементальные графы
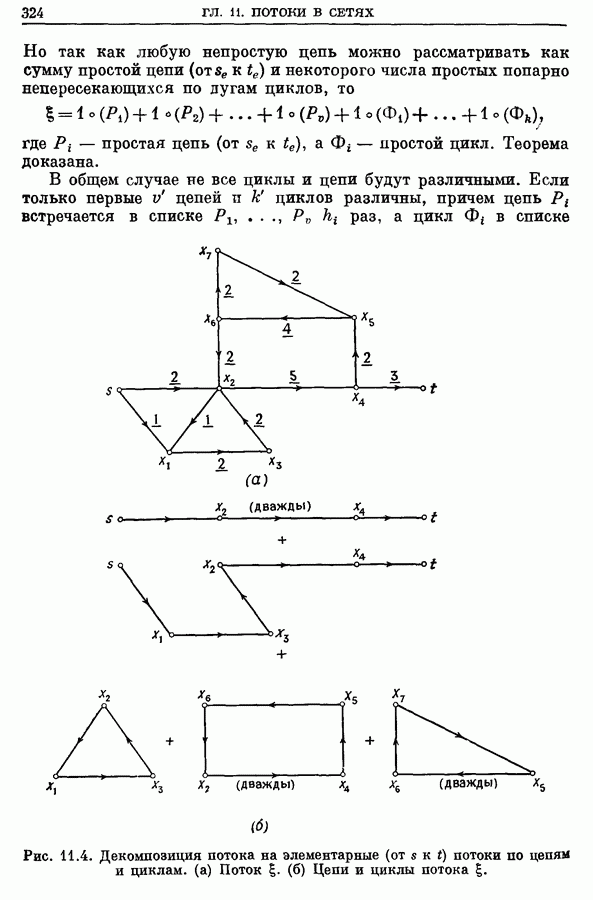
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
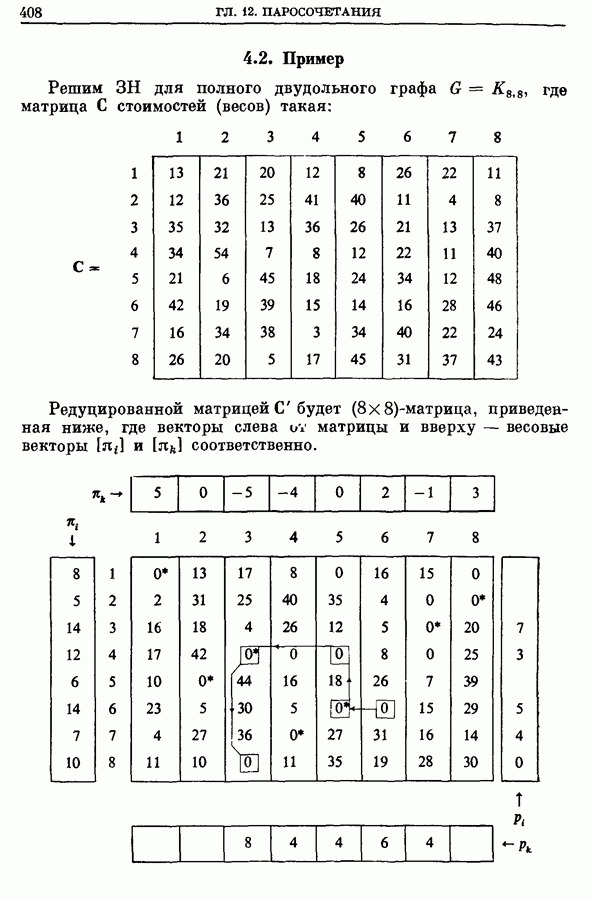
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
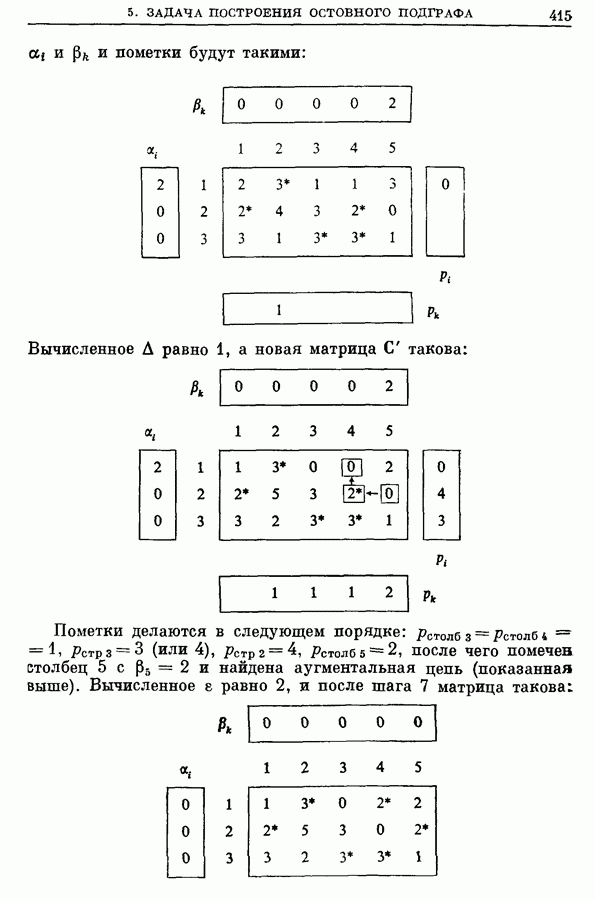
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления