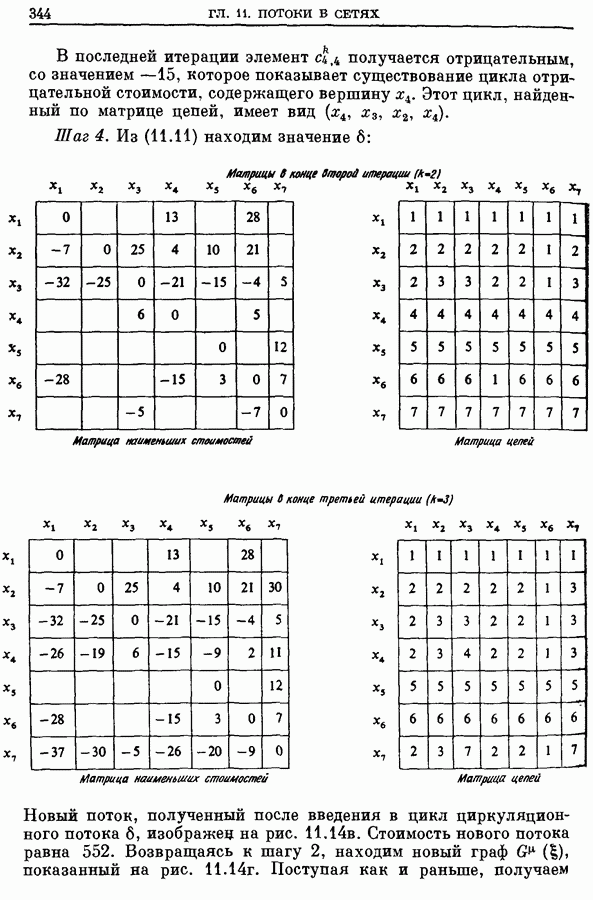
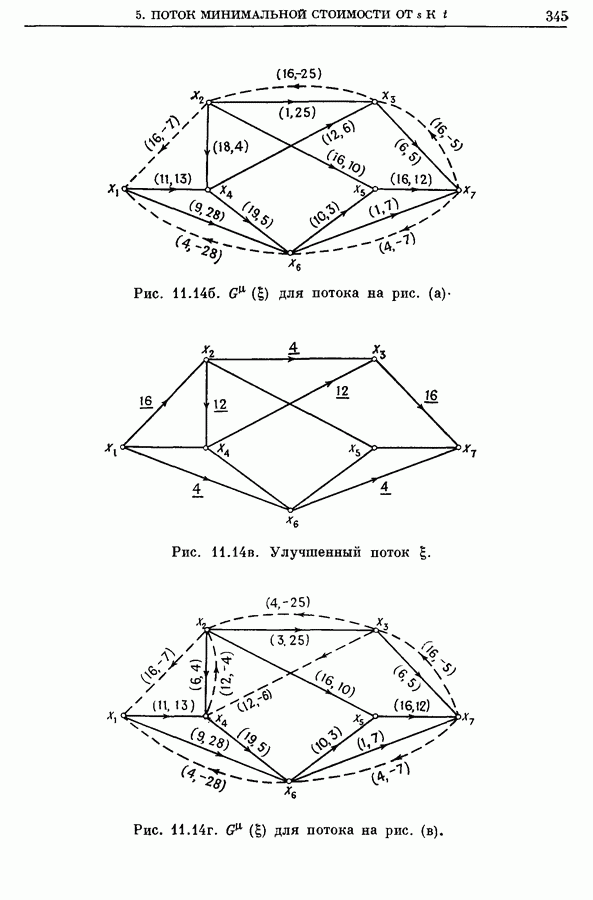
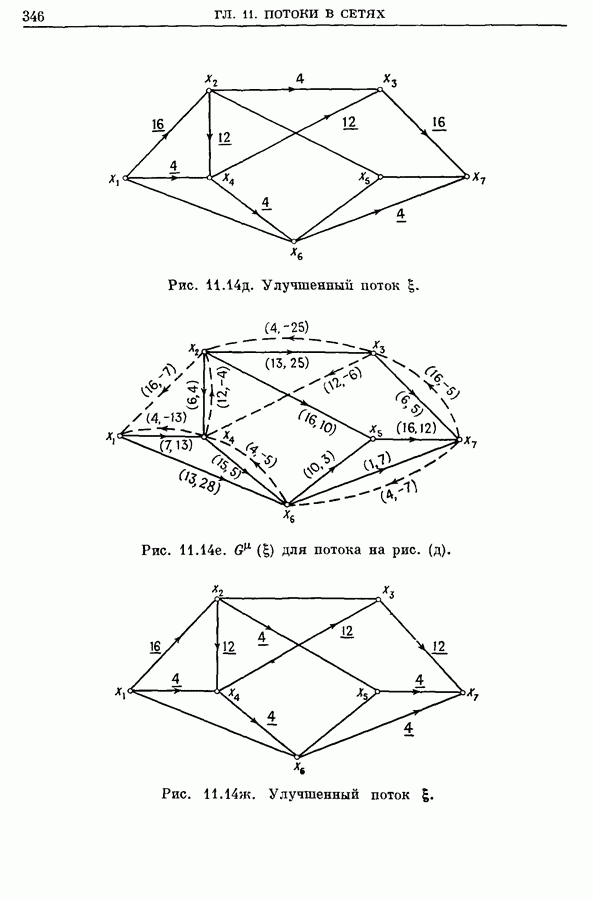
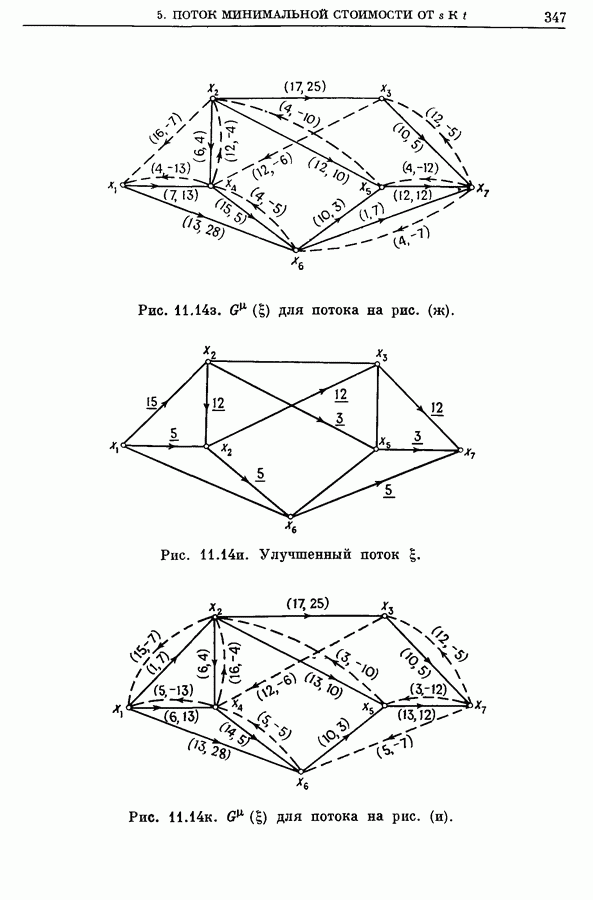
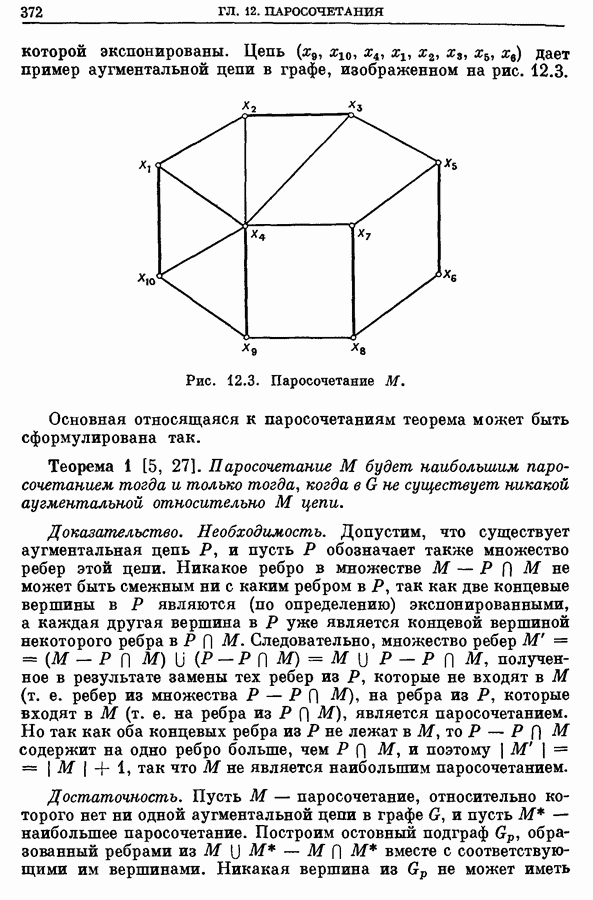
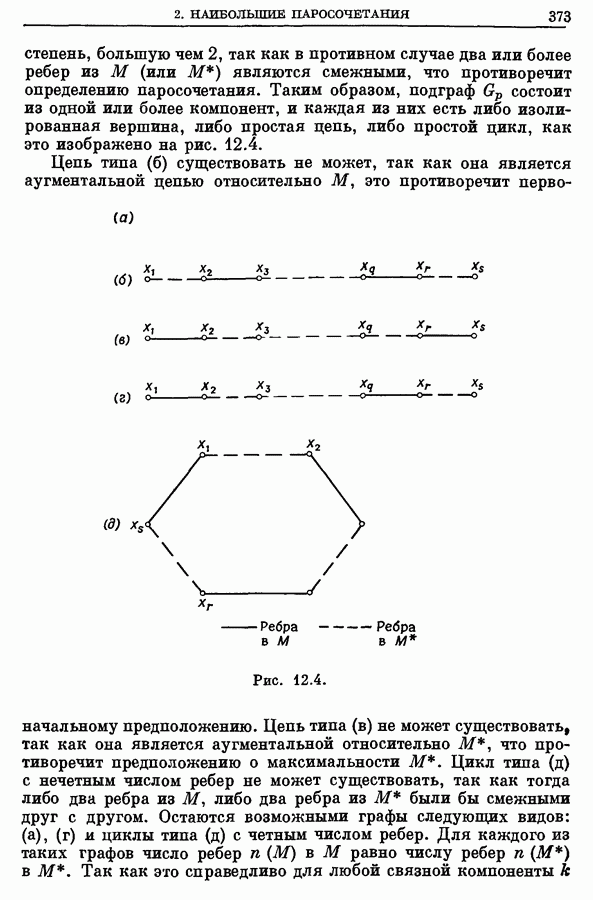
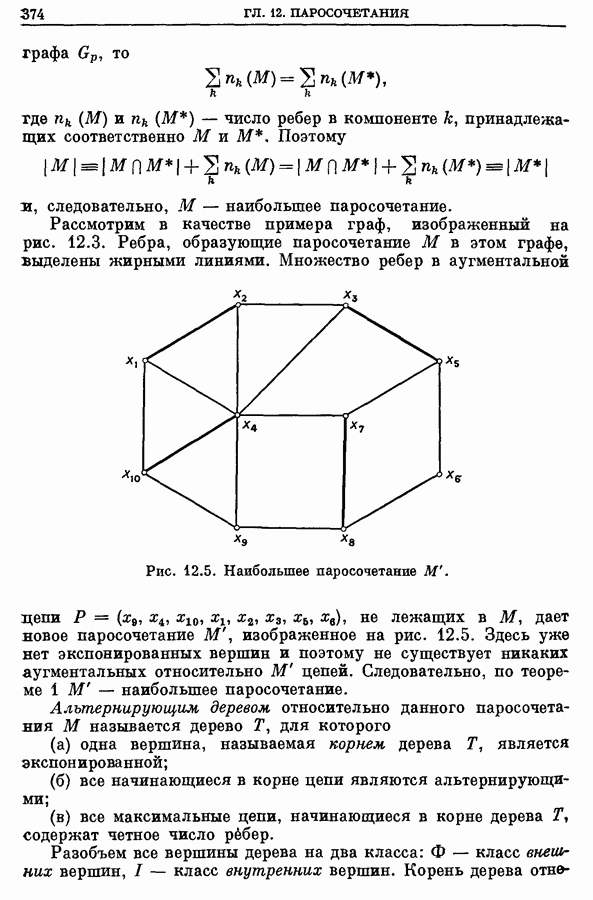
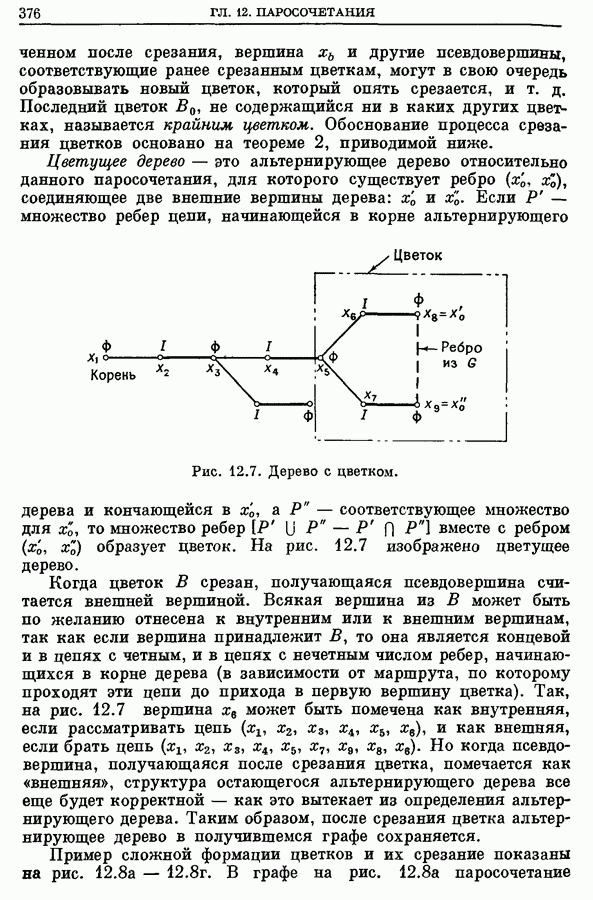
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.3. Алгоритм решения ЗНР, использующий дерево поиска
Как отмечалось ранее, ЗНР тесно связана с ЗНП, являясь по существу ЗНП с дополнительным (неперекрываемость) ограничением. Это ограничение выгодно, если мы пытаемся решить задачу с помощью некоторого метода, использующего дерево поиска: при таком ограничении может рано выясниться, что некоторые возможные ветвления дерева рассматривать не надо. Учитывая вышесказанное, мы сначала займемся алгоритмом решения ЗНР (использующим дерево поиска), а затем покажем, как его можно приспособить к решению ЗНП.
Простые методы решения ЗНР, использующие дерево поиска, были предложены Пирсом [48] и Гарфинкелем и Немхаузером (271.
Сущность этих методов такова. Вначале строятся «блоки» столбцов, по одному на каждый элемент  из
из  т. е. всего
т. е. всего  блоков.
блоков.  блок состоит из таких множеств семейства (представленных столбцами), в которых содержится элемент
блок состоит из таких множеств семейства (представленных столбцами), в которых содержится элемент  но отсутствуют элементы с меньшими индексами —
но отсутствуют элементы с меньшими индексами —  Следовательно, каждое множество (столбец) появляется точно в одном определенном блоке и совокупность блоков может быть представлена в виде таблицы, как показано на рис. 3.1. В конкретных задачах некоторые из блоков могут отсутствовать.
Следовательно, каждое множество (столбец) появляется точно в одном определенном блоке и совокупность блоков может быть представлена в виде таблицы, как показано на рис. 3.1. В конкретных задачах некоторые из блоков могут отсутствовать.
В процессе работы алгоритма блоки отыскиваются последовательно и формирование  блока начинается после того, как каждый элемент
блока начинается после того, как каждый элемент  будет покрыт частным решением. Таким образом, если какое-то множество в блоке к содержит элементы с индексами, меньшими к, то оно должно быть
будет покрыт частным решением. Таким образом, если какое-то множество в блоке к содержит элементы с индексами, меньшими к, то оно должно быть
отброшено (на этом этапе) в соответствии с требованием неперекрываемости.
Множества в пределах каждого блока размещаются в порядке возрастания их стоимостей и перенумеровываются так, что  теперь уже обозначает множество, соответствующее
теперь уже обозначает множество, соответствующее  столбцу таблицы.
столбцу таблицы.
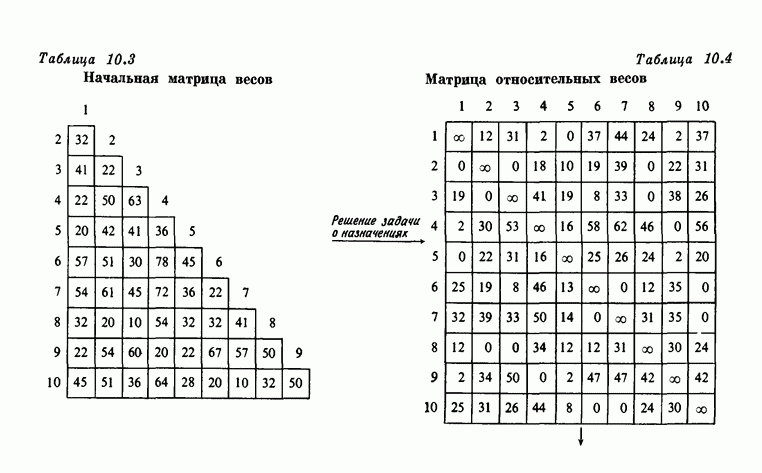
Таблица 3.1 (см. скан) Исходная таблица
Текущее «наилучшее» решение В со стоимостью  известно на любом этапе поиска (В обозначает семейство соответствующих покрывающих множеств). Если
известно на любом этапе поиска (В обозначает семейство соответствующих покрывающих множеств). Если  соответствующие семейство и стоимость на данной стадии поиска,
соответствующие семейство и стоимость на данной стадии поиска,  множество, представляющее те элементы (т. е. строки)
множество, представляющее те элементы (т. е. строки)  которые покрываются множествами из В, то один из простых алгоритмов, использующих дерево поиска, можно описать следующим образом.
которые покрываются множествами из В, то один из простых алгоритмов, использующих дерево поиска, можно описать следующим образом.
Присвоение начальных значений
Шаг 1. Построить исходную таблицу и начать с частного решения: 
Расширение
Шаг 2. Найти  Над блоком
Над блоком  поставить метку (над его первым множеством, которое, как следует из построения таблицы, имеет наименьшую стоимость).
поставить метку (над его первым множеством, которое, как следует из построения таблицы, имеет наименьшую стоимость).
Шаг 3. Начиная с отмеченной позиции в блоке  перебирать его множества
перебирать его множества  скажем, в порядке возрастания индекса
скажем, в порядке возрастания индекса  .
.
(i) Если найдено множество  такое, что
такое, что  стоимость множества
стоимость множества  то перейти к шагу 5.
то перейти к шагу 5.
(ii) В противном случае, т. е. если блок  исчерпан или выбрано множество
исчерпан или выбрано множество  такое, что
такое, что  перейти к шагу 4.
перейти к шагу 4.
Шаг возвращения
Шаг 4. В не может привести к лучшему решению. Если  (т. е. блок 1 исчерпан), то алгоритм заканчивает работу и оптимальным решением является В. В противном случае удалить последнее множество, скажем,
(т. е. блок 1 исчерпан), то алгоритм заканчивает работу и оптимальным решением является В. В противном случае удалить последнее множество, скажем,  добавить его в В, положить
добавить его в В, положить  поставить метку над множеством
поставить метку над множеством  удалить предшествующую метку в блоке I и перейти к шагу 3.
удалить предшествующую метку в блоке I и перейти к шагу 3.
Проверка нового решения
Шаг 5. Обновить данные:  Если найдено лучшее решение
Если найдено лучшее решение  то положить
то положить  и перейти к шагу 4. Иначе перейти к шагу 2.
и перейти к шагу 4. Иначе перейти к шагу 2.
Если поиск оканчивается с исчерпыванием блока 1 (см. выше шаг 4), то целесообразно переставить блоки в порядке возрастания числа столбцов (множеств) в каждом блоке. Это может быть осуществлено (перед построением исходной таблицы) перенумерацией элементов (строк)  в порядке увеличения числа множеств из
в порядке увеличения числа множеств из  содержащих соответствующие элементы.
содержащих соответствующие элементы.
Прежде чем показать, как алгоритм для ЗНР распространяется на ЗНП, кратко упомянем о некоторых других методах, применяемых при решении ЗНР. В [49] Пиро и Ласки дали ряд модификаций приведенного выше основного алгоритма, используя в качестве вспомогательного средства линейное программирование; в [45] Мишо описал другой алгоритм неявного перебора, который основан на задаче линейного программирования, соответствующей ЗНР с «блочной» структурой (рассмотренной выше и игравшей вспомогательную роль).
Предлагались также алгоритмы, включающие итерации симплексного типа, как прямые [4, 5], так и двойственные [58, 37]. В [37] Йенсен успешно применил метод динамического программирования к определенному типу ЗНР.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
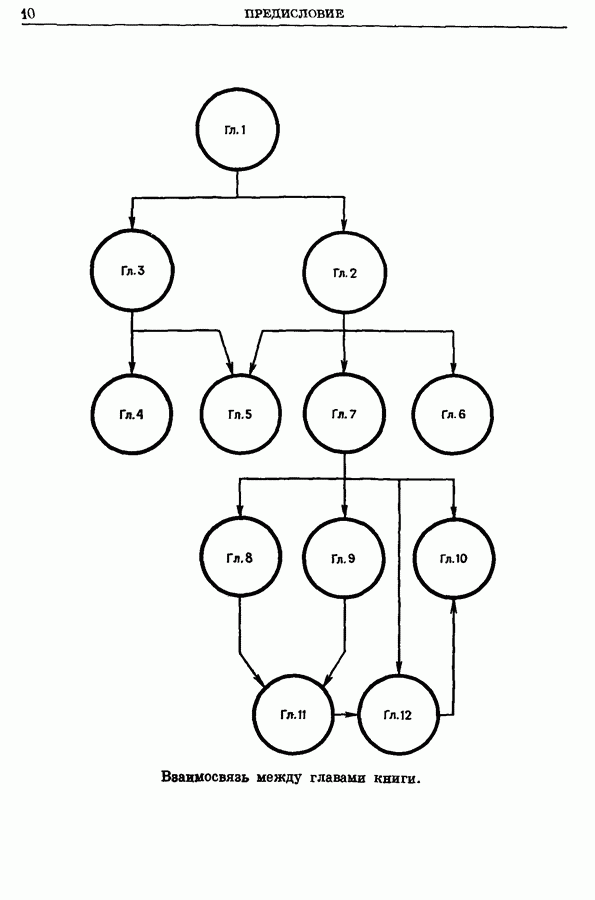
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
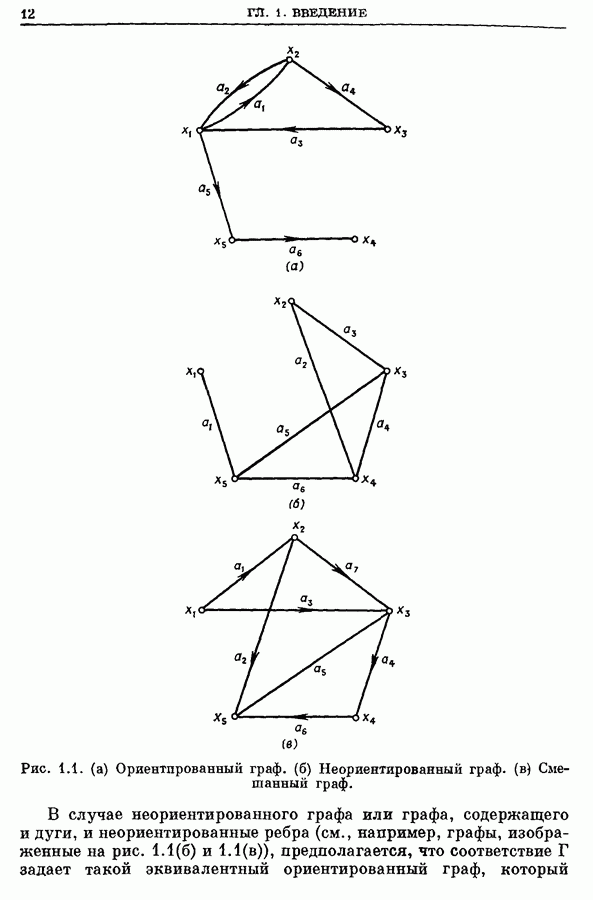
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
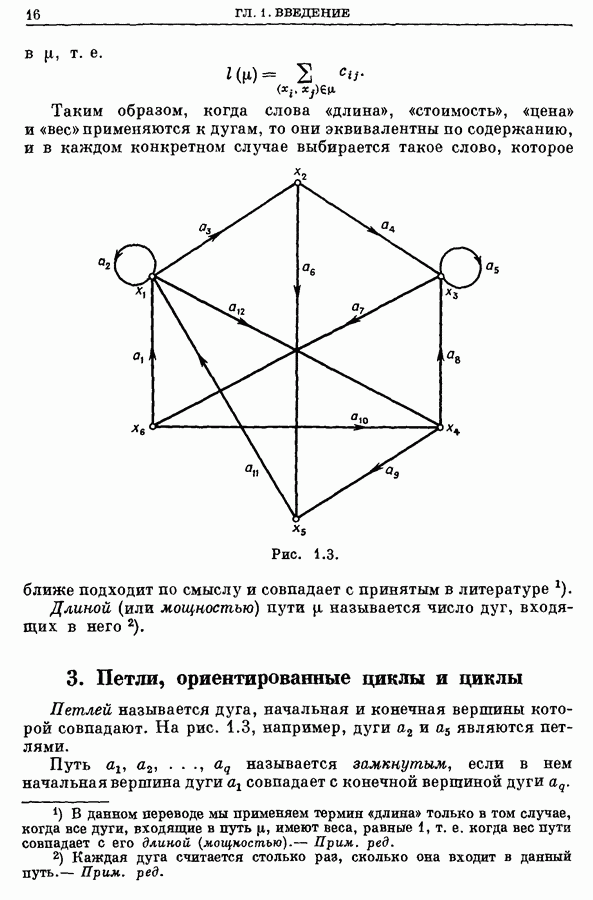
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
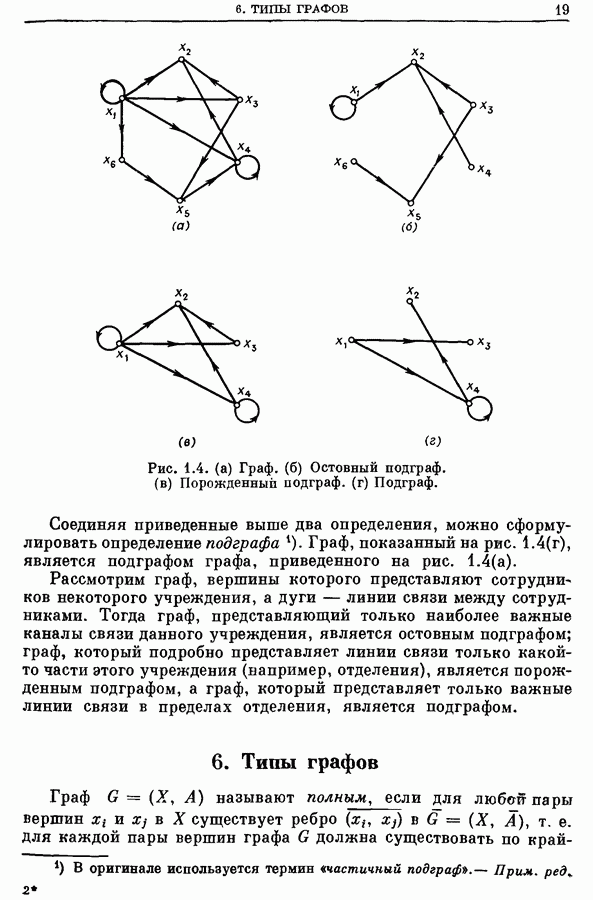
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
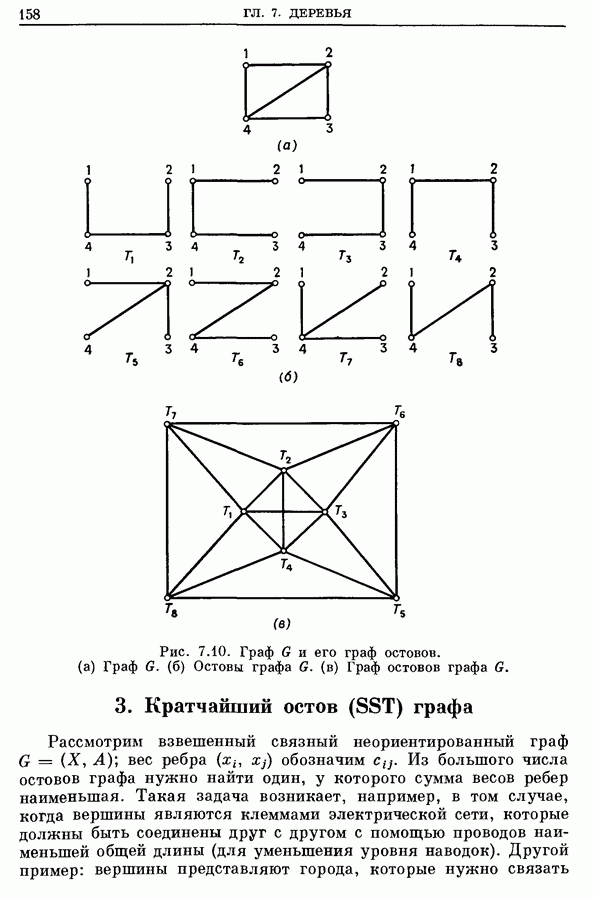
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
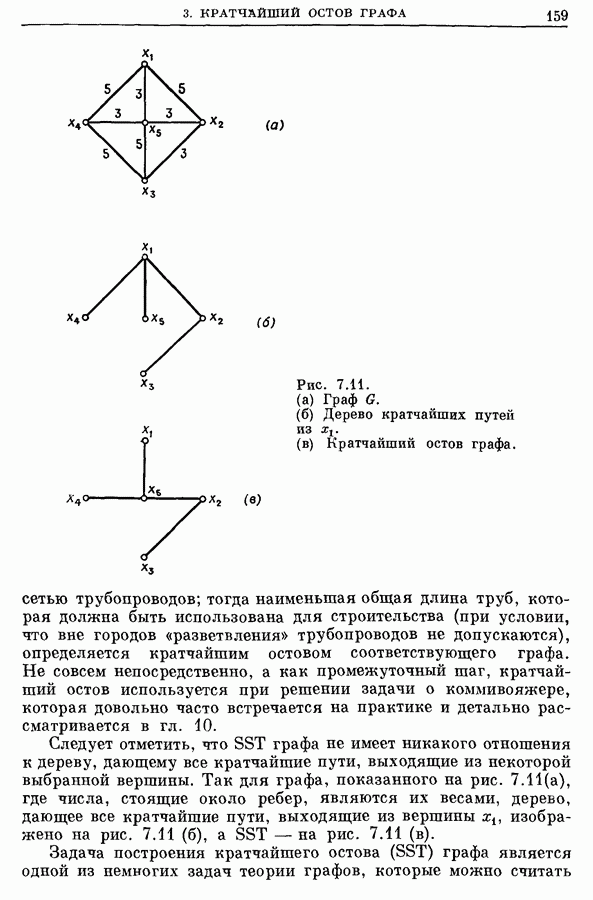
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
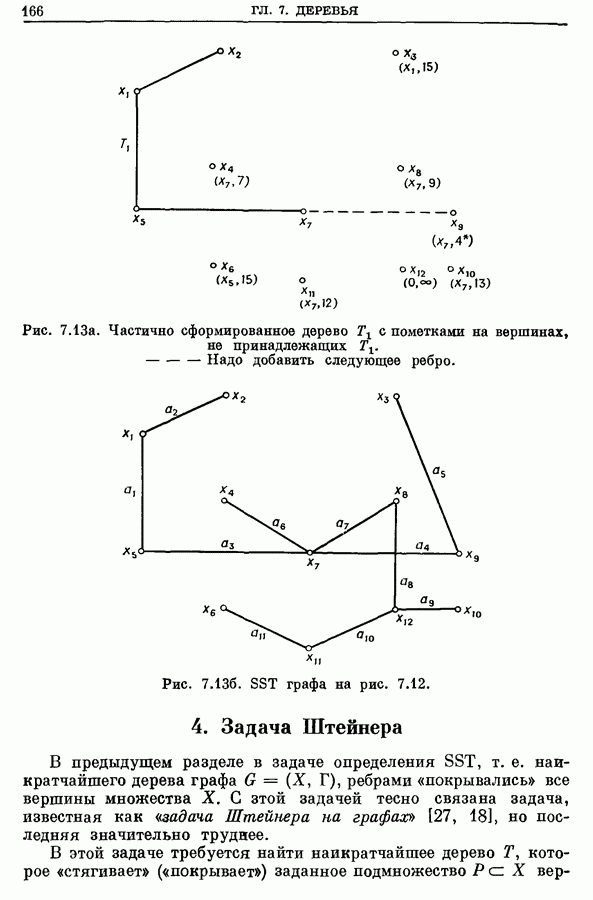
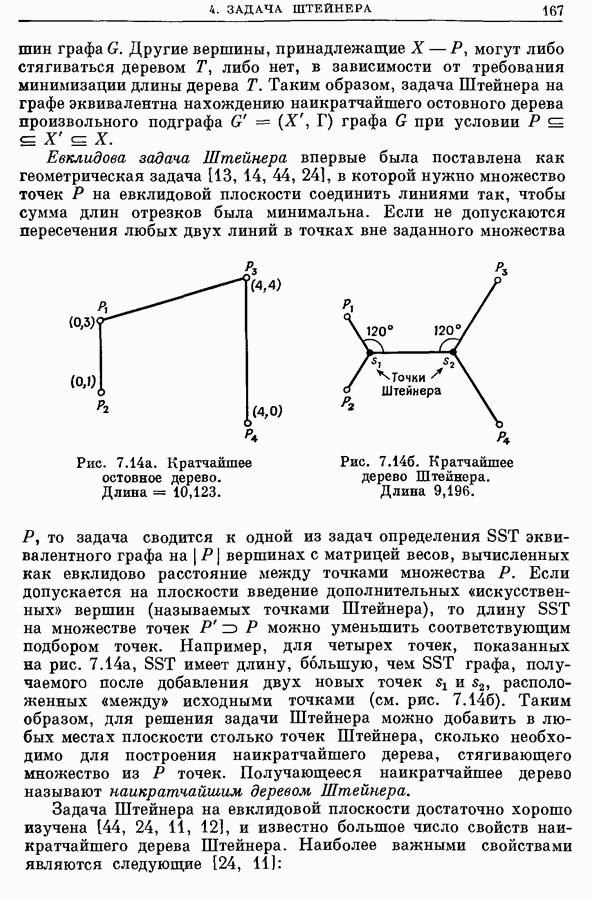
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
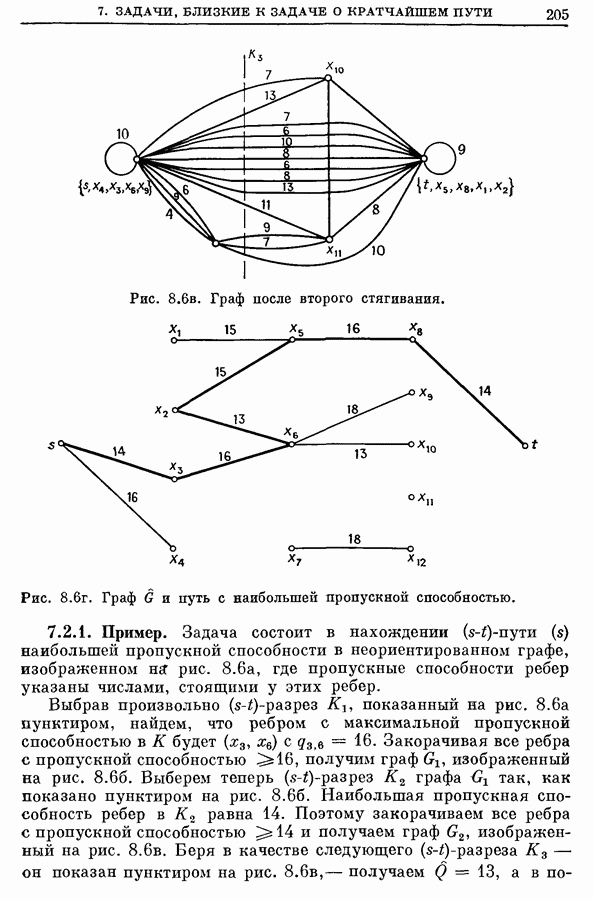
- 7. Задачи, близкие к задаче о кратчайшем пути
- 7.2. Путь с наибольшей пропускной способностью
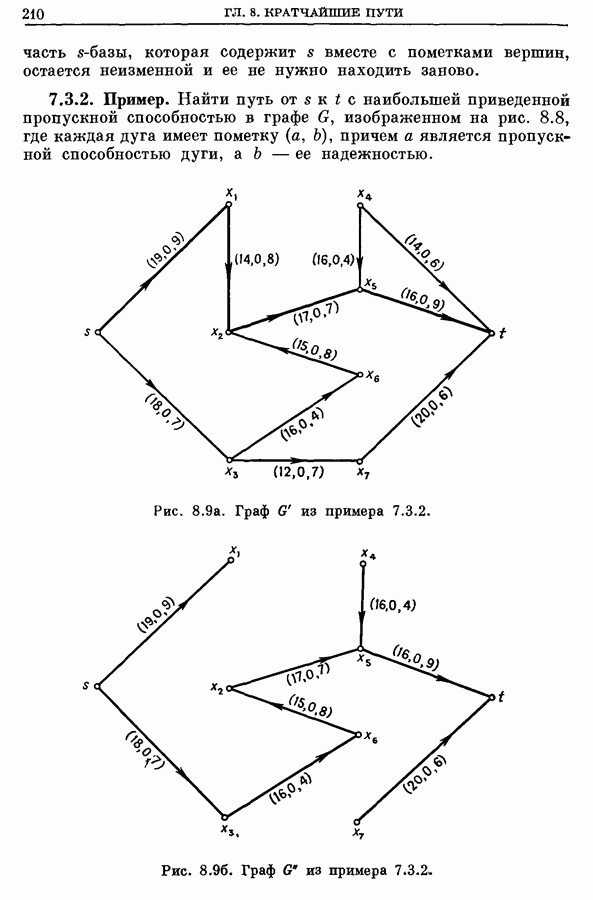
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
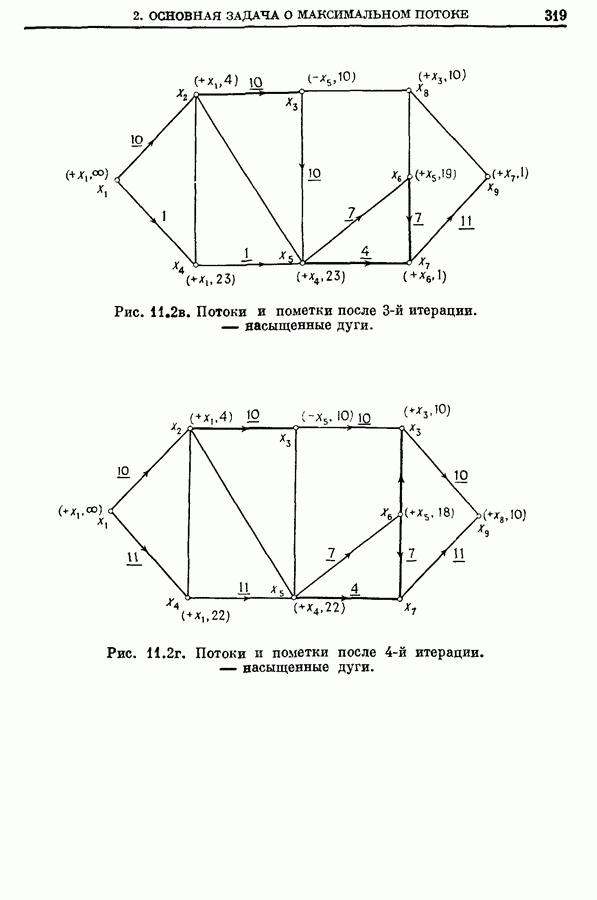
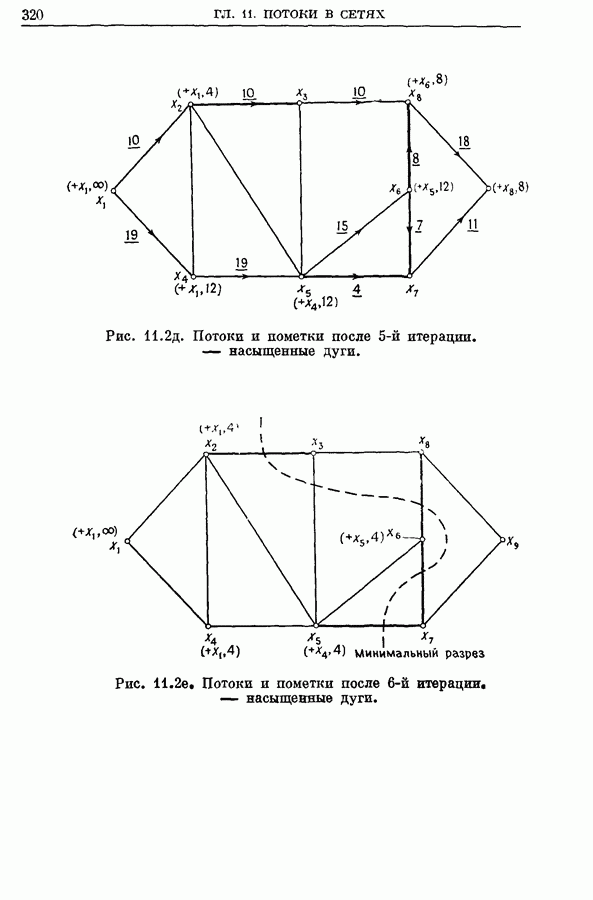
- 2.2. Пример
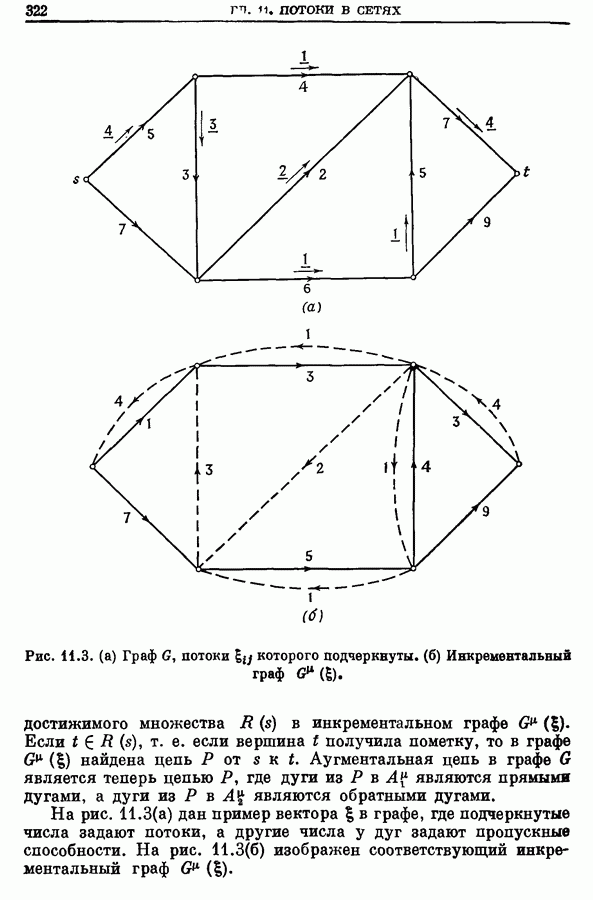
- 2.3. Инкрементальные графы
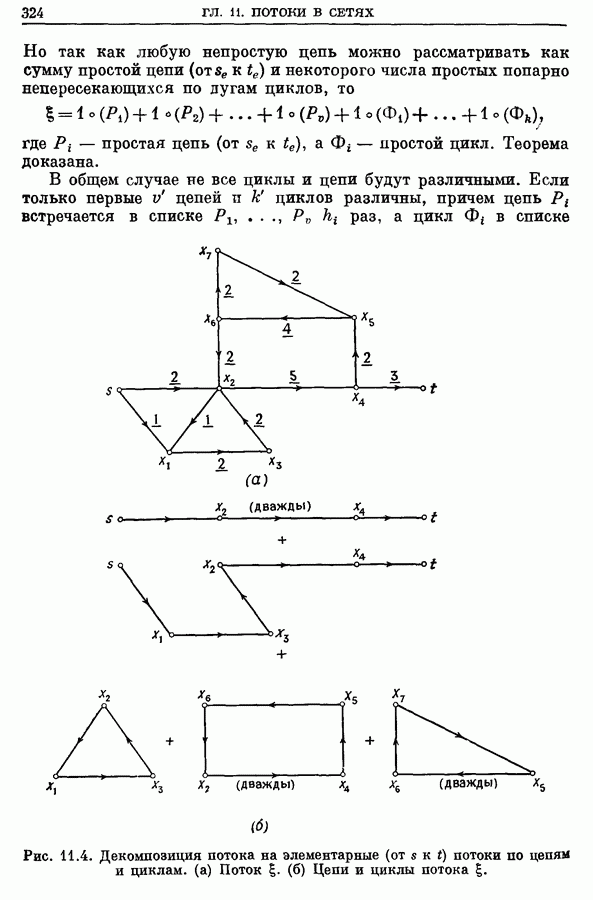
- 2.4. Декомпозиция потока
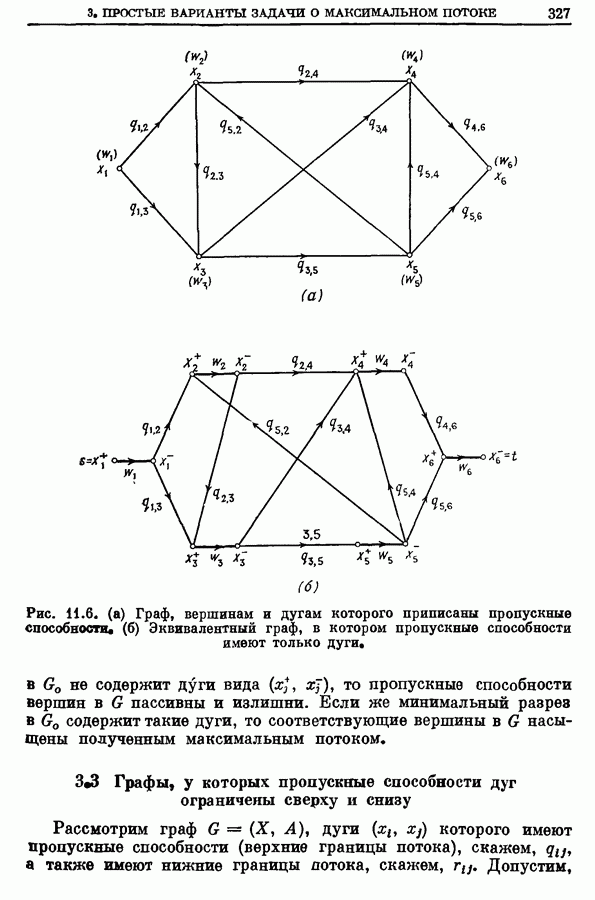
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
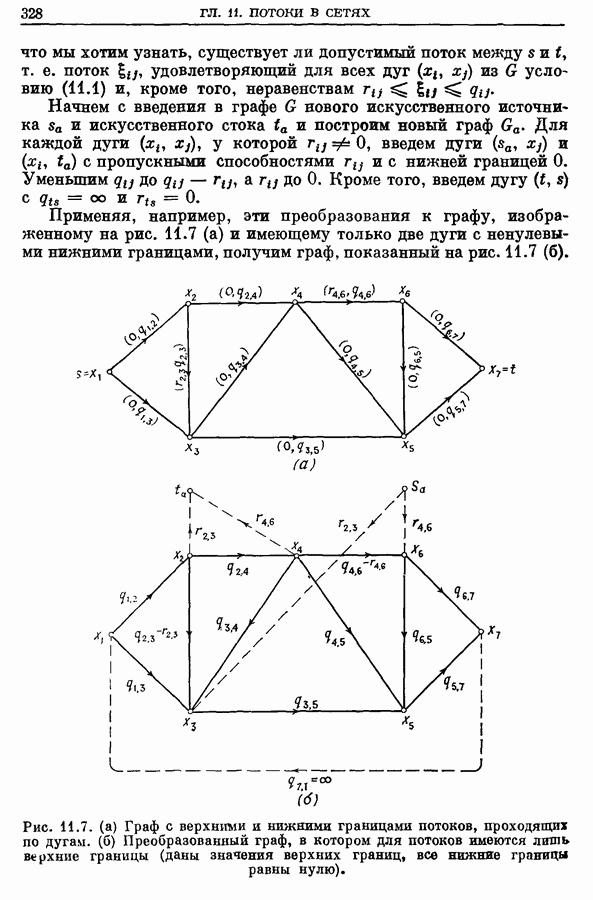
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
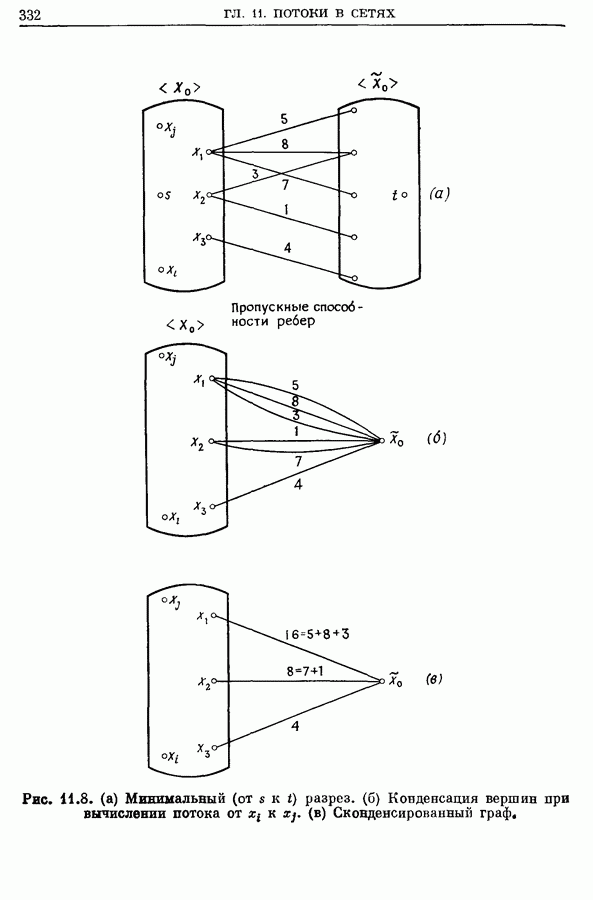
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
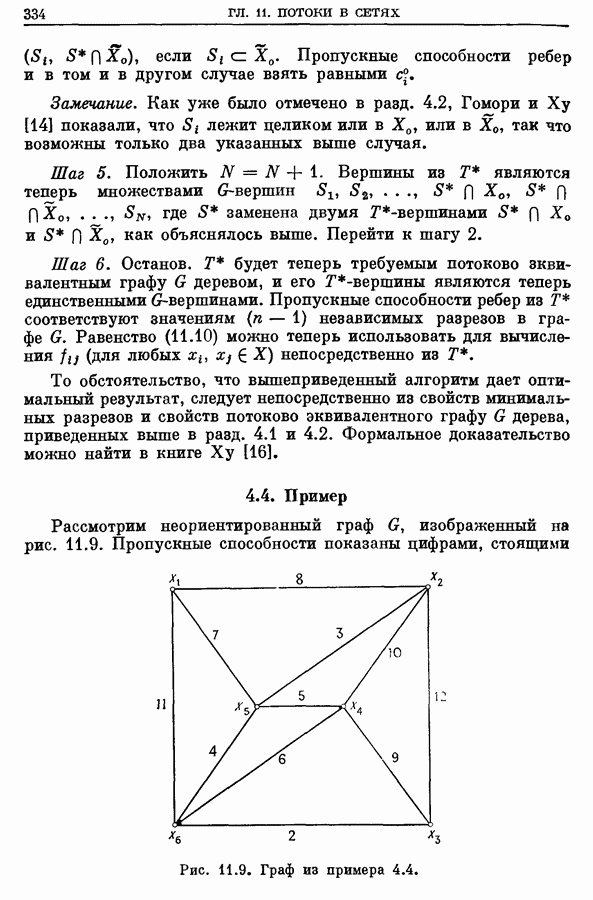
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
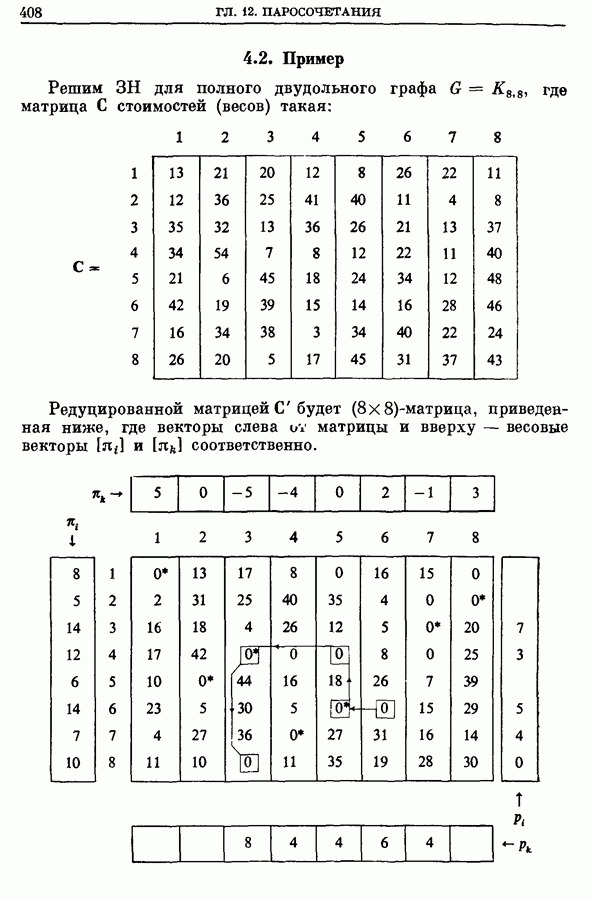
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
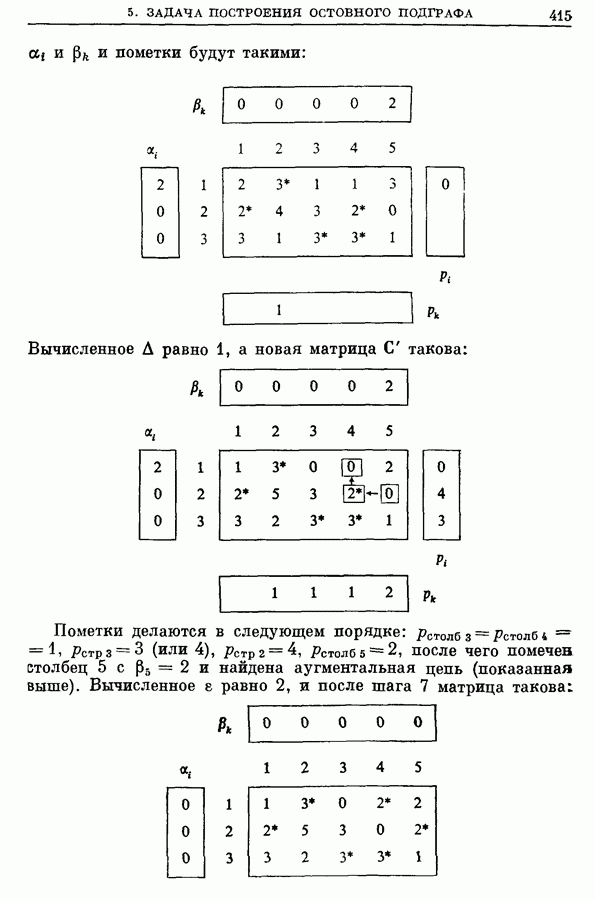
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления