| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Построение всех максимальных независимых множеств
Вследствие упомянутой выше связи между кликами и максимальными независимыми множествами методы, рассматриваемые в данном разделе и описываемые на «языке максимальных независимых множеств», могут быть непосредственно использованы для построения клик. На первый взгляд кажется, что нахождение всех максимальных независимых множеств графа — очень простая задача, которую можно решить последовательным перебором независимых множеств с одновременной проверкой каждого множества на максимальность (последнее осуществляется путем добавления к исследуемому множеству дополнительной, не принадлежащей ему, вершины и выяснения того, сохраняется ли
независимость) и запоминанием максимальных множеств. Представление о простоте задачи действительно справедливо, но только для небольших графов, например с числом вершин, не превосходящим 20. Однако с увеличением числа вершин этот метод поиска становится с вычислительной точки зрения громоздким. Но все же громоздкость здесь не столь велика, как кажется с первого взгляда. Число максимальных независимых множеств увеличивается, но в процессе выполнения процедуры большое число независимых множеств формируется, а затем вычеркивается, так как обнаруживается, что они содержатся в других, ранее полученных множествах и поэтому не являются максимальными.
В этом разделе будет описан систематический метод перебора Брона и Кэрбоша [14], который позволяет обходить указанные выше трудности. В этом методе не нужно запоминать генерируемые независимые множества для проверки их на максимальность путем сравнения с ранее сформированными множествами.
2.3.1. Обоснование алгоритма.
Этот алгоритм является существенно упрощенным перебором, использующим дерево поиска. В процессе поиска — на некотором этапе к — независимое множество вершин  расширяется путем добавления к нему подходящим образом выбранной вершины (чтобы получилось новое независимое множество
расширяется путем добавления к нему подходящим образом выбранной вершины (чтобы получилось новое независимое множество  на этапе к
на этапе к  и так поступают до тех пор, пока добавление вершин станет невозможным, а порождаемое множество не станет максимальным независимым множеством. Пусть
и так поступают до тех пор, пока добавление вершин станет невозможным, а порождаемое множество не станет максимальным независимым множеством. Пусть  будет на этапе к наибольшим множеством вершин, для которого
будет на этапе к наибольшим множеством вершин, для которого  т. е. после добавления любой вершины из
т. е. после добавления любой вершины из  получается независимое множество
получается независимое множество  В некоторый произвольный момент работы алгоритма множество
В некоторый произвольный момент работы алгоритма множество  состоит вообще говоря, из вершин двух типов: подмножества
состоит вообще говоря, из вершин двух типов: подмножества  тех вершин, которые уже использовались в процессе поиска для расширения множеств
тех вершин, которые уже использовались в процессе поиска для расширения множеств  и подмножества
и подмножества  таких вершин, которые еще не использовались. Тогда дальнейшее ветвление в дереве поиска включает процедуру выбора вершины
таких вершин, которые еще не использовались. Тогда дальнейшее ветвление в дереве поиска включает процедуру выбора вершины  добавление ее к
добавление ее к  для построения множества
для построения множества

и порождение новых множеств:

и

Шаг возвращения алгоритма состоит в удалении вершины из  чтобы вернуться к
чтобы вернуться к  изъятии
изъятии  из старого множества
из старого множества
 и добавлении
и добавлении  к старому множеству
к старому множеству  для формирования новых множеств
для формирования новых множеств  и
и 
Легко заметить, что множество  является максимальным независимым множеством только тогда, когда невозможно его дальнейшее расширение, т. е. когда
является максимальным независимым множеством только тогда, когда невозможно его дальнейшее расширение, т. е. когда  Если
Если  то немедленно заключаем, что текущее множество
то немедленно заключаем, что текущее множество  было расширено на некотором предшествующем этапе работы алгоритма путем добавления вершины из
было расширено на некотором предшествующем этапе работы алгоритма путем добавления вершины из  и поэтому оно не является максимальным независимым множеством. Таким образом, необходимым и достаточным условием того, что
и поэтому оно не является максимальным независимым множеством. Таким образом, необходимым и достаточным условием того, что  максимальное независимое множество, является выполнение равенств
максимальное независимое множество, является выполнение равенств

Теперь совершенно очевидно, что если очередной этап работы алгоритма наступает тогда, когда существует некоторая вершина  Для которой
Для которой  то безразлично, какая из вершин, принадлежащих
то безразлично, какая из вершин, принадлежащих  используется для расширения
используется для расширения  и это справедливо при любом числе дальнейших ветвлений; вершина х не может быть удалена из
и это справедливо при любом числе дальнейших ветвлений; вершина х не может быть удалена из  на любом следующем шаге
на любом следующем шаге  Таким образом, условие
Таким образом, условие

является достаточным для осуществления шага возвращения, поскольку из  при всяком дальнейшем ветвлении уже не получится максимальное независимое множество.
при всяком дальнейшем ветвлении уже не получится максимальное независимое множество.
Как и во всяком методе, использующем дерево поиска, здесь выгодно стремиться начать шаги возвращения как можно раньше, поскольку это ограничит «размеры» «ненужной» части дерева поиска. Следовательно, целесообразно сосредоточить усилия на том, чтобы возможно раньше добиться выполнения условия (3.8) с помощью подходящего выбора вершин, используемых при расширении множеств  На каждом следующем шаге процедуры можно выбирать для добавления к
На каждом следующем шаге процедуры можно выбирать для добавления к  любую вершину
любую вершину  на шаге возвращения
на шаге возвращения  будет удалена из
будет удалена из  и включена в
и включена в  Если вершину
Если вершину  выбрать так, чтобы она принадлежала множеству
выбрать так, чтобы она принадлежала множеству  при некоторой вершине х из
при некоторой вершине х из  то на соответствующем шаге возвращения величина
то на соответствующем шаге возвращения величина

уменьшится на единицу (по сравнению с тем значением, которое было до выполнения прямого шага и шага возвращения), так что условие (3.8) теперь станет выполняться раньше.
Таким образом, одйн из возможных способов выбора вершины  для расширения множества
для расширения множества  состоит, во-первых, в нахождении вершины
состоит, во-первых, в нахождении вершины  с возможно меньшим значением величины
с возможно меньшим значением величины
 кроме того, в выборе вершины
кроме того, в выборе вершины  из множества
из множества  Такой выбор вершины
Такой выбор вершины  будет приводить на шаге возвращения к уменьшению величины
будет приводить на шаге возвращения к уменьшению величины  каждый раз на единицу — до тех пор, пока вершина х не станет удовлетворять условию (3.8) при выполнении шага возвращения.
каждый раз на единицу — до тех пор, пока вершина х не станет удовлетворять условию (3.8) при выполнении шага возвращения.
Следует отметить, что поскольку на шаге возвращения вершина  попадает в
попадает в  то может оказаться, что при этом новом входе значение величины
то может оказаться, что при этом новом входе значение величины  меньше, чем для ранее фиксированной вершины х. Значит, надо проверить, не ускорит ли эта новая вершина выполнение условия (3.8). Это особенно важно в начале ветвления, когда
меньше, чем для ранее фиксированной вершины х. Значит, надо проверить, не ускорит ли эта новая вершина выполнение условия (3.8). Это особенно важно в начале ветвления, когда 
2.3.2. Описание алгоритма
Начальная установка
Шаг 1. Пусть 
Прямой шаг
Шаг 2. Выбрать вершину  как упоминалось ранее, и сформировать
как упоминалось ранее, и сформировать  оставляя
оставляя  нетронутыми. Положить
нетронутыми. Положить 
Проверка
Шаг 3. Если удовлетворяется условие (3.8), то перейти к шагу 5, иначе к шагу 4.
Шаг 4. Если  напечатать максимальное независимое множество
напечатать максимальное независимое множество  и перейти к шагу 5. Если
и перейти к шагу 5. Если  то перейти к шагу 5. Иначе перейти к шагу 2.
то перейти к шагу 5. Иначе перейти к шагу 2.
Шаг возвращения
Шаг 5. Положить  Удалить
Удалить  из
из  чтобы получить
чтобы получить  Исправить
Исправить  удалив вершину из
удалив вершину из  и добавив ее к
и добавив ее к  Если
Если  остановиться. (К этому моменту будут уже напечатаны все максимальные независимые множества.) Иначе перейти к шагу 3.
остановиться. (К этому моменту будут уже напечатаны все максимальные независимые множества.) Иначе перейти к шагу 3.
Комментарий по применению описанного выше алгоритма приведен в [14] вместе с программой, написанной на Алголе. Эта программа была опробована для большого числа графов (в частности, для графов Муна-Мозера, см. задачу 10) и было установлено, что время, необходимое для построения максимального независимого множества, почти постоянно и не зависит от размера графа. Все это говорит о том, что данный алгоритм является одним из лучших.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Глава 1. ВВЕДЕНИЕ
- 1. Графы. Определение
- 2. Пути и маршруты
- 2.1. Веса и длина пути
- 3. Петли, ориентированные циклы и циклы
- 4. Степени вершины
- 5. Подграфы
- 6. Типы графов
- 7. Сильно связные графы и компоненты графа
- 8. Матричные представления
- 8.1. Матрица смежности
- 8.2. Матрица инциденций
- Глава 2. ДОСТИЖИМОСТЬ И СВЯЗНОСТЬ
- 2. Матрицы достижимостеи и контрадостижимостей
- 3. Нахождение сильных компонент
- 4. Базы
- 5. Задачи, связанные с ограниченной достижимостью
- Глава 3. НЕЗАВИСИМЫЕ И ДОМИНИРУЮЩИЕ МНОЖЕСТВА. ЗАДАЧА О ПОКРЫВАЮЩИХ МНОЖЕСТВАХ
- 2. Независимые множества
- 2.2. Максимальные полные подграфы (клики)
- 2.3. Построение всех максимальных независимых множеств
- 3. Доминирующие множества
- 4. Задача о наименьшем покрытии
- 4.2. Упрощение задачи
- 4.3. Алгоритм решения ЗНР, использующий дерево поиска
- 4.4. Алгоритм решения ЗНП, использующий дерево поиска
- 4.5. Вычислительная характеристика алгоритма решения ЗНП
- 5. Приложения задачи о покрытии
- 5.2. Информационный поиск [21]
- 5.3. Маршруты полетов самолетов [1, 55, 64, 65]
- 5.4. Упрощение логических (булевских) выражений [30, 50, 51, 67, 44, 43]
- 5.5. Задача о развозке (о доставке) [7, 47, 24]
- 5.6. Другие задачи о покрытии графов
- Глава 4. РАСКРАСКИ
- 2. Некоторые теоремы и оценки, относящиеся к хроматическим числам
- 3. Точные алгоритмы раскраски
- 3.2. Формулировка задачи о раскраске на языке 0-1-программирования
- 3.3. Сведение задачи о раскраске к ЗНП
- 3.4. Алгоритм прямого неявного перебора, использующий дерево поиска
- 4. Приближенные алгоритмы раскрашивания
- 4.1. Последовательные методы, основанные на упорядочивании множества вершин
- 5. Обобщения и приложения
- 5.1. Простая задача размещения (загрузки) [6]
- 5.2. Составление графиков осмотра (проверки)
- 5.3. Распределение ресурсов
- Глава 5. РАЗМЕЩЕНИЕ ЦЕНТРОВ
- 2. Разделения
- 3. Центр и радиус
- 3.1. Размещение аварийных служб и пунктов обслуживания
- 4. Абсолютный центр
- 5. Алгоритмы нахождения абсолютных центров
- 5.2. Размещение аварийных служб (общий случай)
- 5.3. Модифицированный метод Хакими
- 5.4. Итерационный метод
- 6. Кратные центры (р-центры)
- 6.1. Задача размещения нескольких пунктов обслуживания
- 7. Абсолютные p-центры
- 8. Алгоритм нахождения абсолютных p-центров
- Глава 6. РАЗМЕЩЕНИЕ МЕДИАН В ГРАФЕ
- 2. Медиана графа
- 3. Кратные медианы (p-медианы) графа
- 4. Обобщенная p медиана графа
- 5. Методы решения задачи о p-медиане
- 5.2. Алгоритм направленного древовидного поиска
- 5.3. Другой алгоритм направленного поиска
- 5.4. Приближенный алгоритм
- Глава 7. ДЕРЕВЬЯ
- 2. Построение всех остовных деревьев графа
- 2.2. Процедура порождения всех деревьев графа
- 2.3. Пример
- 2.4. Граф остовов
- 3. Кратчайший остов (SST) графа
- 3.1. Алгоритм Краскала
- 3.2. Алгоритм Прима [48]
- 3.3. Родственные задачи
- 3.4. Пример [48]
- 4. Задача Штейнера
- Глава 8. КРАТЧАЙШИЕ ПУТИ
- 2. Кратчайший путь между двумя заданными вершинами s и t
- 2.2. Случай общей матрицы весов
- 3. Кратчайшие пути между всеми парами вершин
- 3.1. Алгоритм Флойда (для произвольной матрицы весов)
- 4. Обнаружение циклов отрицательного веса
- 4.1. Оптимальные циклы в графах с двойными весами [24.9]
- 5. Нахождейие К кратчайших путей между двумя заданными вершинами
- 6. Кратчайший путь между двумя заданными вершинами в ориентированном ациклическом графе
- 6.1. Алгоритм нахождения самого длинного (критического) пути в ориентированном ациклическом графе
- 7. Задачи, близкие к задаче о кратчайшем пути
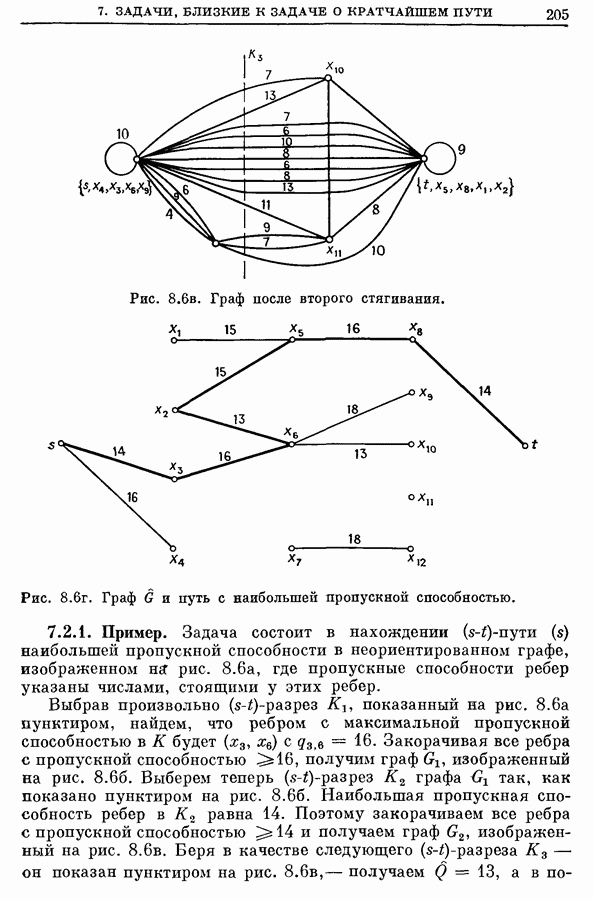
- 7.2. Путь с наибольшей пропускной способностью
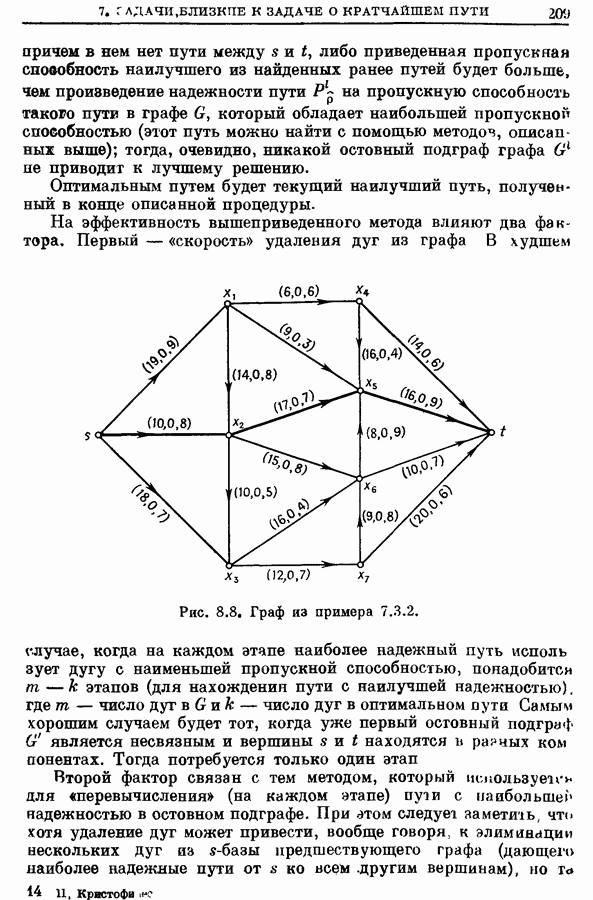
- 7.3. Путь с наибольшей приведенной пропускной способностью
- 7.3.1. Метод нахождения пути наибольшей приведенной пропускной способности
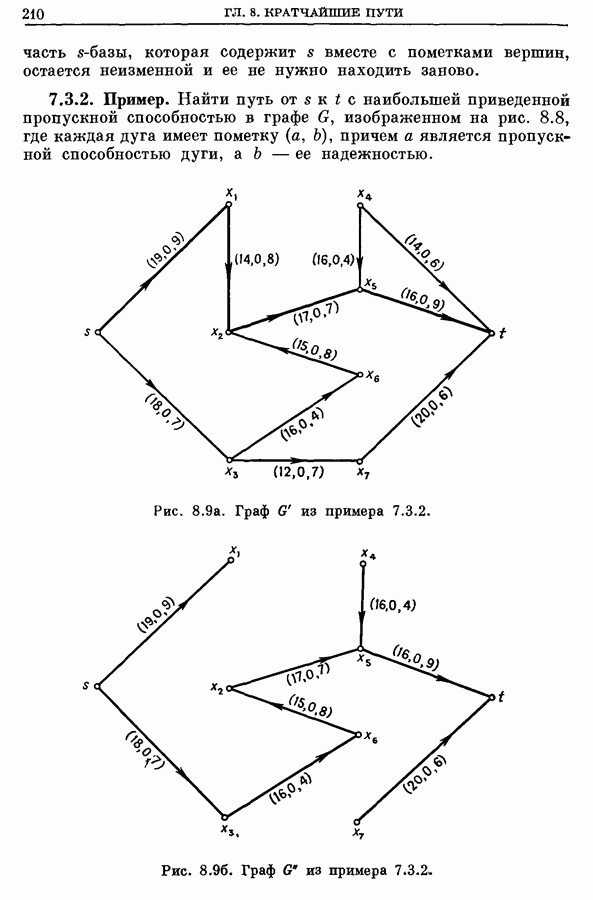
- 7.3.2. Пример.
- Глава 9. ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА
- 2. Цикломатическое число и фундаментальные циклы
- 3. Разрезы
- 4. Матрицы циклов и разрезов
- 5. Эйлеровы циклы и задача китайского почтальона
- 5.1. Некоторые родственные задачи
- 5.2. Алгоритм для задачи китайского почтальона
- 5.3. Связь между эйлеровыми и гамильтоновыми циклами
- Глава 10. ГАМИЛЬТОНОВЫ ЦИКЛЫ, ЦЕПИ И ЗАДАЧА КОММИВОЯЖЕРА
- ЧАСТЬ I
- 2. Гамильтоновы циклы в графе
- 2.2. Метод перебора Робертса и Флореса
- 2.3. Мультицепной метод
- 3. Сравнение методов поиска гамильтоновых циклов
- 4. Простая задача планирования
- ЧАСТЬ II
- 5. Задача коммивояжера
- 5.2. Нижняя граница из задачи о кратчайшем остове
- 5.3. Двойственность
- 6. Задача коммивояжера и задача о кратчайшем остове
- 6.2. Алгоритм поиска, использующий дерево решений
- 6.3. Алгоритм штрафования вершин
- 6.4. Задачи, родственные задаче коммивояжера
- 7. Задача коммивояжера и задача о назначениях
- 7.2. Пример
- 7.3. Вычислительные комментарии и характеристики
- 7.4. Лучшие границы для дерева поиска
- 7.5. Пример из раздела 7.2 с улучшенной границей
- 10. Приложение
- Глава 11. ПОТОКИ В СЕТЯХ
- 2. Основная задача о максимальном потоке (от s к t)
- 2.1. Алгоритм расстановки пометок для задачи о максимальном (от s к t) потоке
- 2.2. Пример
- 2.3. Инкрементальные графы
- 2.4. Декомпозиция потока
- 3. Простые варианты задачи о максимальном потоке (от s к t)
- 3.1. Графы со многими источниками и стоками
- 3.2. Графы с пропускными способностями дуг и вершин
- 3.3. Графы, у которых пропускные способности дуг ограничены сверху и снизу
- 4. Максимальный поток между каждой паров вершин
- 4.2. Конденсация вершин
- 4.3. Алгоритм построения максимального потока между всеми парами вершин
- 4.4. Пример
- 5. Поток минимальной стоимости от s к t
- 5.2. Алгоритм, основанный на цепи наименьшей стоимости
- 6. Потоки в графах с выигрышами
- 6.1. Аугментальные маршруты
- 6.2. Активные циклы
- 6.3. Алгоритм оптимального потока для графов с выигрышами
- 6.4. Пример
- 6.5. Графы с выигрышами в вершинах
- Глава 12. ПАРОСОЧЕТАНИЯ, ТРАНСПОРТНАЯ ЗАДАЧА И ЗАДАЧА О НАЗНАЧЕНИЯХ
- 2. Наибольшие паросочетания
- 2.1. Альтернирующие цепи и деревья
- 2.2. Цветки
- 2.3. Венгерские деревья
- 2.4. Алгоритм для ЗНПС
- 2.5. Пример
- 3. Максимальные паросочетания
- 3.1. Алгоритм для ЗМП
- 3.2. Пример
- 3.3. Некоторые вычислительные результаты
- 4. Задача о назначениях
- 4.1. Алгоритм для ЗН (случай минимизации)
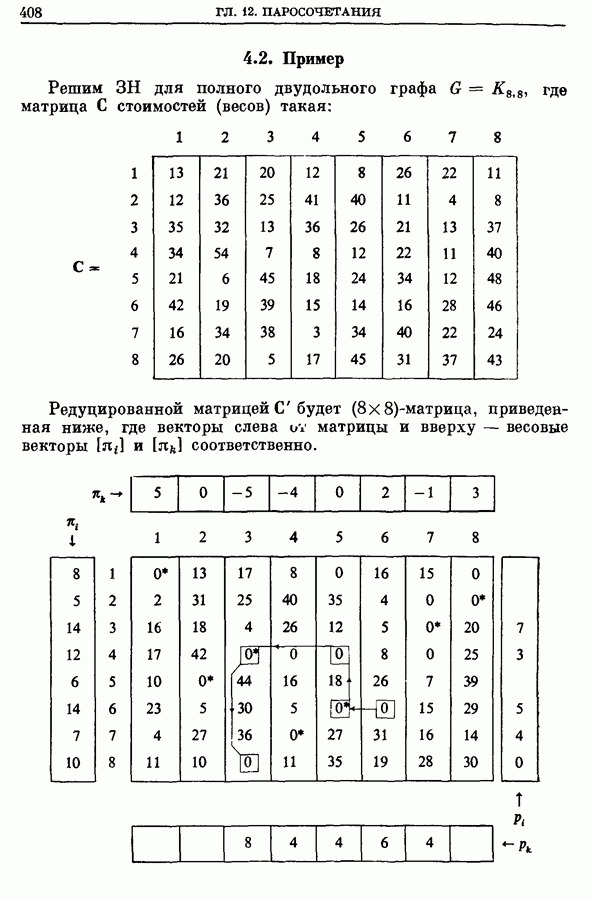
- 4.2. Пример
- 5. Общая задача построения остовного подграфа с предписанными степенями
- 5.1. Транспортная задача
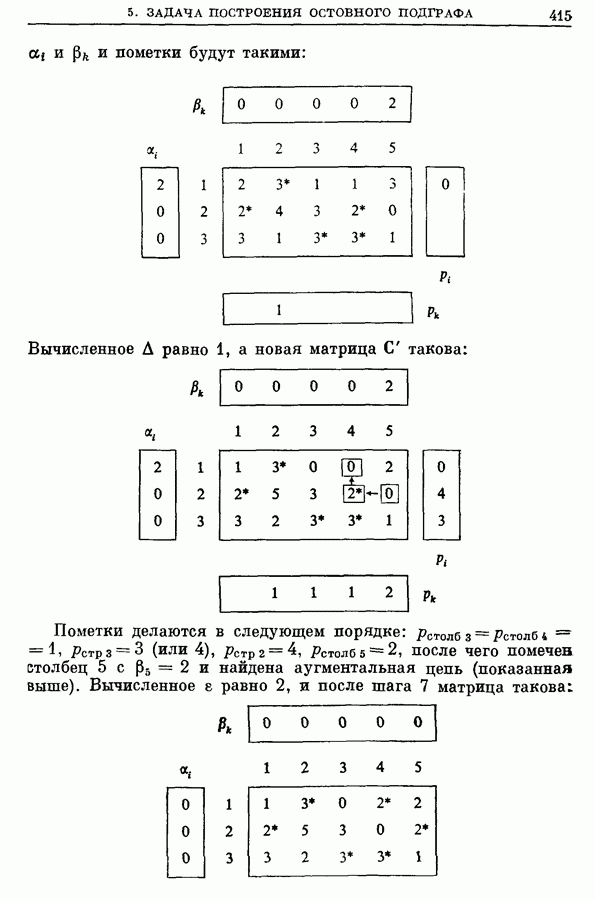
- 5.2. Пример
- 6. Задача о покрытии
- Приложение 1. МЕТОДЫ ПОИСКА, ИСПОЛЬЗУЮЩИЕ ДЕРЕВО РЕШЕНИЙ
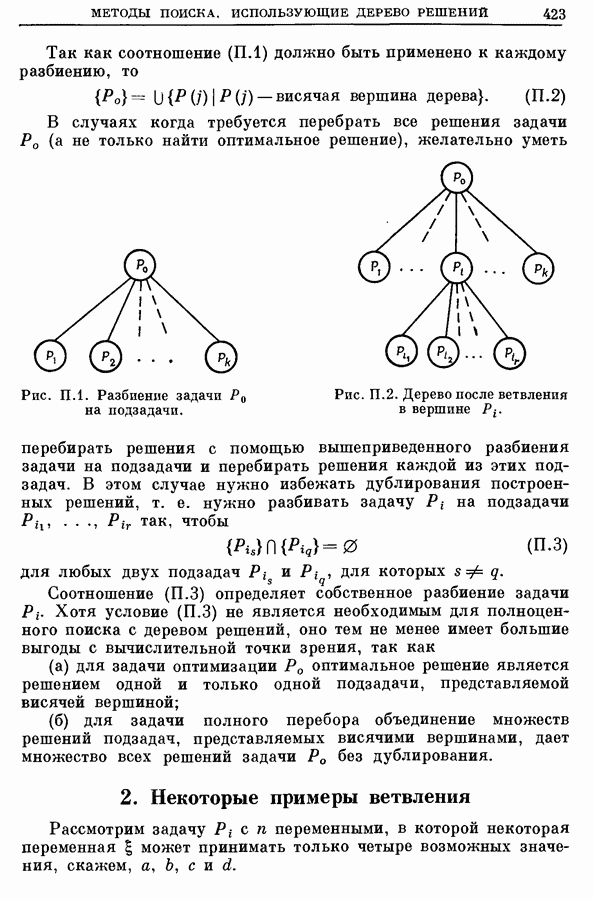
- 1. Принцип поиска, использующий дерево решений
- 2. Некоторые примеры ветвления
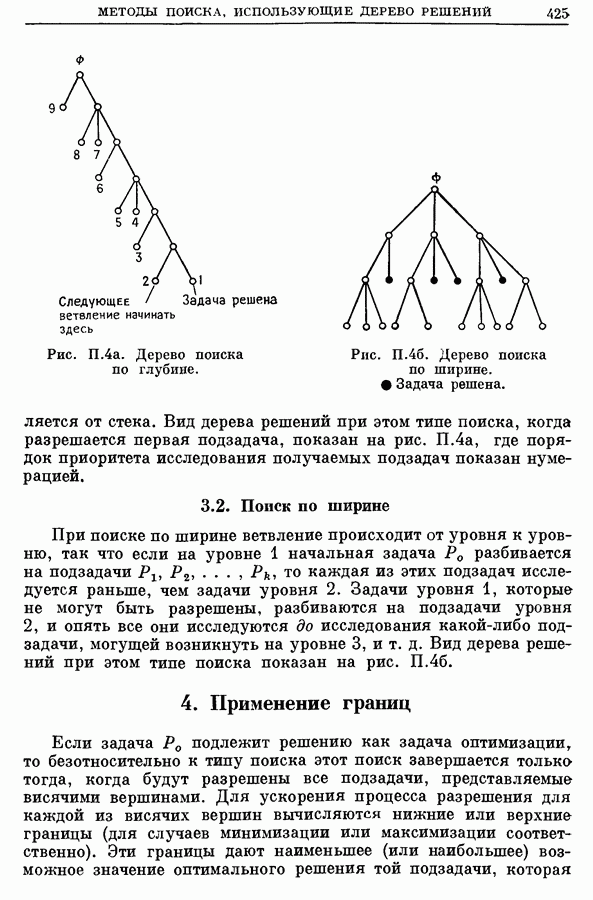
- 3. Типы поиска, использующего дерево решений
- 4. Применение границ
- 5. Функции ветвления