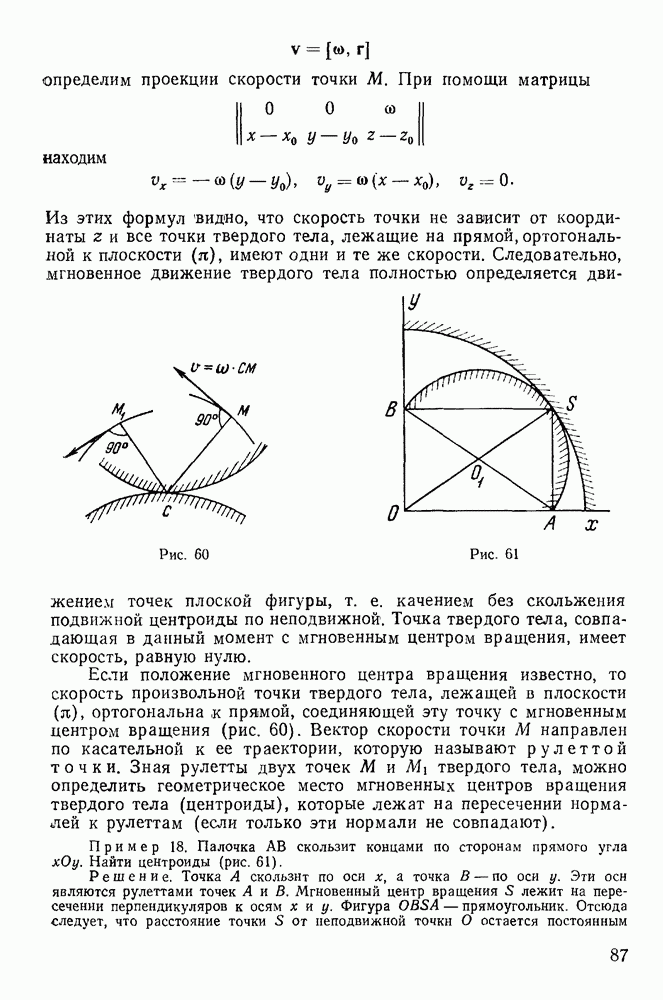
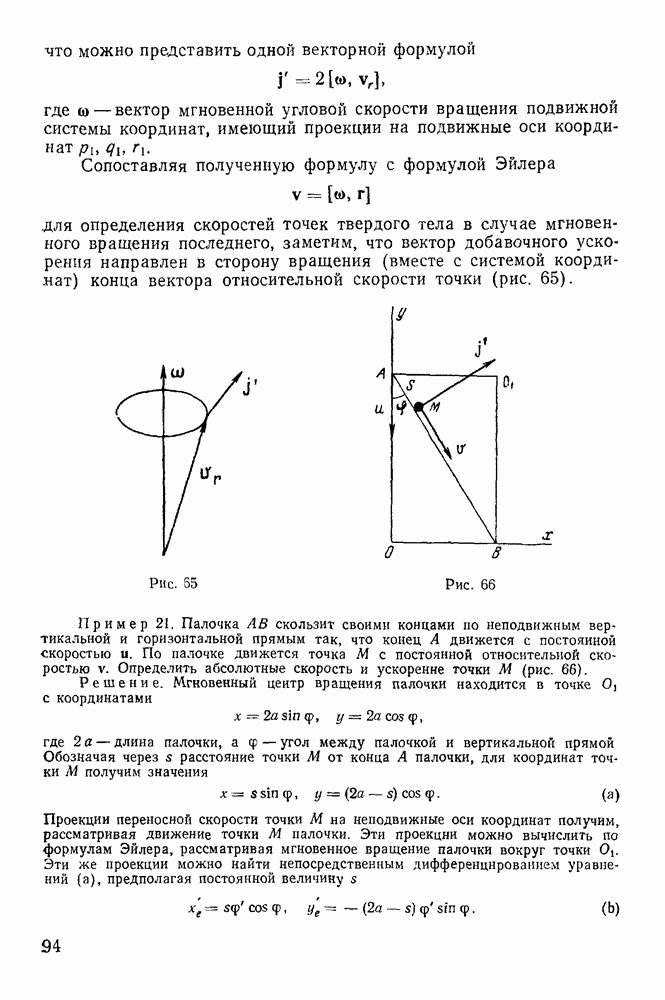
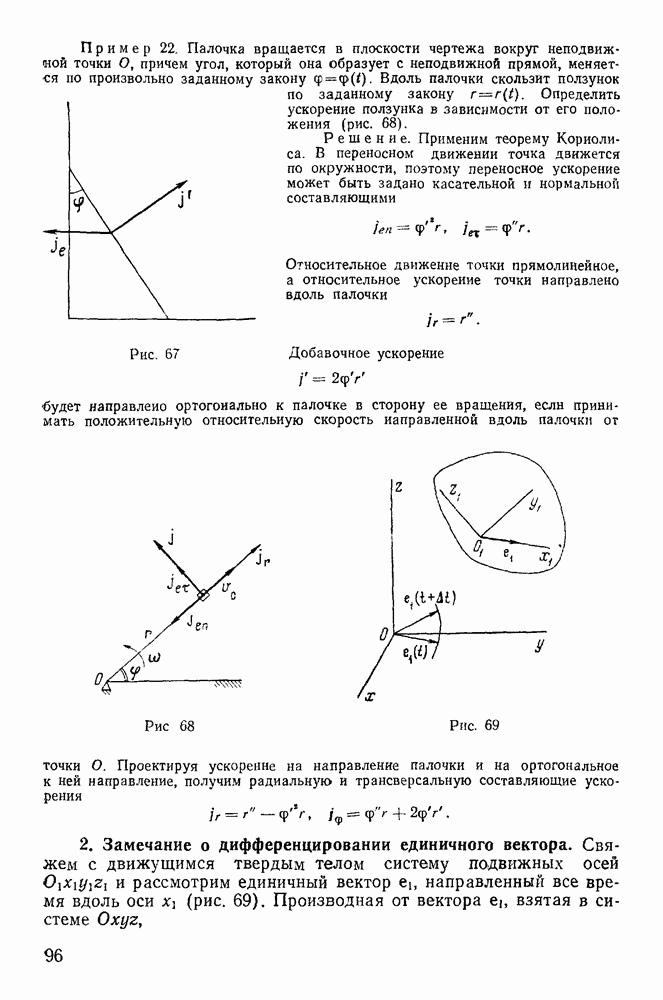
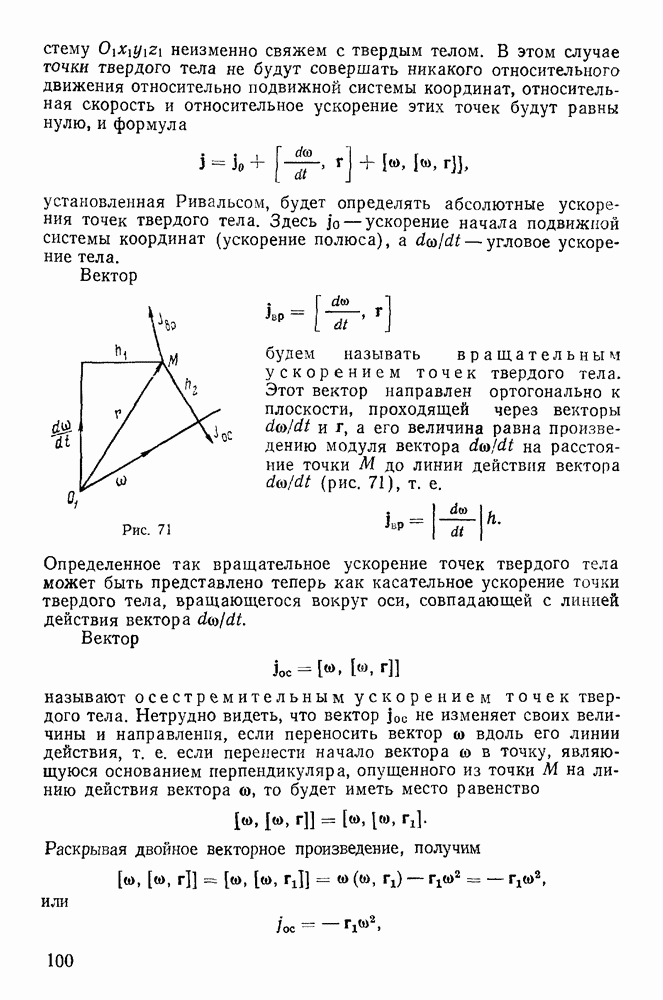
Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.

В 1851 г. Пуансо дал качественную геометрическую картину движения твердого тела в случае Эйлера, основанную на кинематических свойствах этого движения.

За подвижные координатные оси выберем главные оси эллипсоида инерции, построенного для неподвижной точки О. Тогда уравнение эллипсоида инерции запишется в виде

Вектор мгновенной угловой скорости пересечет поверхность эллипсоида инерции в некоторой точке Р, называемой полюсом, координаты которой в дальнейшем будем обозначать через

(рис. 232). Из условия коллинеарности вектора и вектора угловой скорости о) будем иметь

где

Рис. 231

Рис. 232

Нетрудно установить следующие свойства движения такого тела:

1. Отношение остается постоянным во все время движения. В самом деле, из интеграла живых сил имеем

2. Вектор момента количества движения а параллелен вектору нормали к поверхности эллипсоида инерции, построенному в точке Р. Действительно, проекции вектора нормали к поверхности эллипсоида инерции пропорциональны частным производным:

Подставляя сюда в правые части значения получим

Отсюда следует, что вектор а ортогонален к плоскости , касающейся эллипсоида инерции в точке Р. В дальнейшем эту плоскость будем обозначать буквой

3. Расстояние плоскости до центра эллипсоида инерции остается неизменным во все время движения твердого тела. Нетрудно найти (рис. 233), что

Отсюда следует, что плоскость остается неподвижной в пространстве во все время движения.

Рис. 233

4. Конец вектора, все время находится в неподвижной плоскости , параллельной плоскости я. Рассмотрим проекцию вектора на направление вектора момента количества движения

откуда сразу следует утверждение.

Скорость точки Р эллипсоида инерции равна нулю в рассматриваемый момент времени, так как через эту точку проходит вектор мгновенной угловой скорости твердого тела. В результате мы приходим к следующему выводу.

Эллипсоид инерции твердого тела постоянно касается неподвижной плоскости Точка касания Р является полюсом, а прямая — мгновенной осью вращения твердого тела. Кривую, описываемую полюсом на поверхности эллипсоида инерции, Пуансо назвал полодией, а кривую, описываемую полюсом на неподвижной плоскости — герполодией. Подвижный аксоид имеет вершину в точке О, а полодия служит его направляющей. Неподвижный аксоид имеет вершину в той же точке О, а в качестве направляющей — герполодию. Непрерывное движение твердого тела соответствует качению без скольжения подвижного аксоида по неподвижному. Такое движение может быть осуществлено, если заставить эллипсоид инерции катиться и вертеться без скольжения по неподвижной плоскости , положение которой зависит от начальных условий.

В частном случае, когда ось вращения проходит через вершину эллипсоида инерции, твердое тело совершает постоянное вращение около главной оси инерции твердого тела, сохраняющей неизменное положение в пространстве. Такая ось называется постоянной, или перманентной, осью вращения твердого тела.

Если эллипсоид инерции является эллипсоидом вращения, то аксоидом является прямой круговой конус. Ось этого конуса совпадает с наибольшей осью эллипсоида инерции. Полодии и герполодии в этом случае будут окружностями.

Напишем уравнение полодии в общем случае, когда (наименьшая полуось эллипсоида инерции совпадает с осью х). Полодии расположены на поверхности эллипсоида инерции

Кроме того, координаты х, у, z полюса Р удовлетворяют уравнению, которое следует из закона сохранения момента количества движения

после подстановки сюда вместо значений

будем иметь

Полодия представляет геометрическое место точек, удовлетворяющих уравнениям (а) и (b). Умножая уравнение (а) на D и вычитая его из получим уравнение конической поверхности

являющейся подвижным аксоидом.

При или уравнению не удовлетворяет ни одна из точек, расположенных на поверхности эллипсоида инерции. Поэтому в действительном движении величина D должна удовлетворять условиям

Рассмотрим следующие частные случаи:

1. A=D. Уравнение подвижного аксоида получает вид

При этому уравнению удовлетворяет только одна точка с координатами что соответствует вращению вокруг наименьшей оси эллипсоида инерции. Подвижный аксоид вырождается в прямую линию, являющуюся постоянной осью вращения.

Уравнение подвижного аксоида имеет вид

При аксоид вырождается в прямую Этому соответствует постоянное вращение твердого тела вокруг наибольшей оси эллипсоида инерции.

3. D = B. Уравнение эллипсоида инерции записывается в виде

При уравнение аксоида можно преобразовать к виду

Это уравнение определяет две пересекающиеся по оси у плоскости

Если величина D имеет небольшое отклонение от рассмотренных значений, аксоид будет представлять собой коническую поверхность. Так, если D близко по значению к А и удовлетворяет неравенствам

уравнение аксоида сводится к виду

и аксоид будет представлять собой действительный конус, ось которого совпадает с осью х (рис. 234), В пересечении с поверхностью эллипсоида инерции конус образует полодию, являющуюся замкнутой кривой, охватывающей ось х.

Рис. 234

Картина совершенно аналогична той, когда D близко по своему значению к С и удовлетворяет условиям

Если D мало отличается от В, то полодии расположены вблизи кривых, образованных пересечением плоскостей (B = D) с поверхностью эллипсоида инерции.

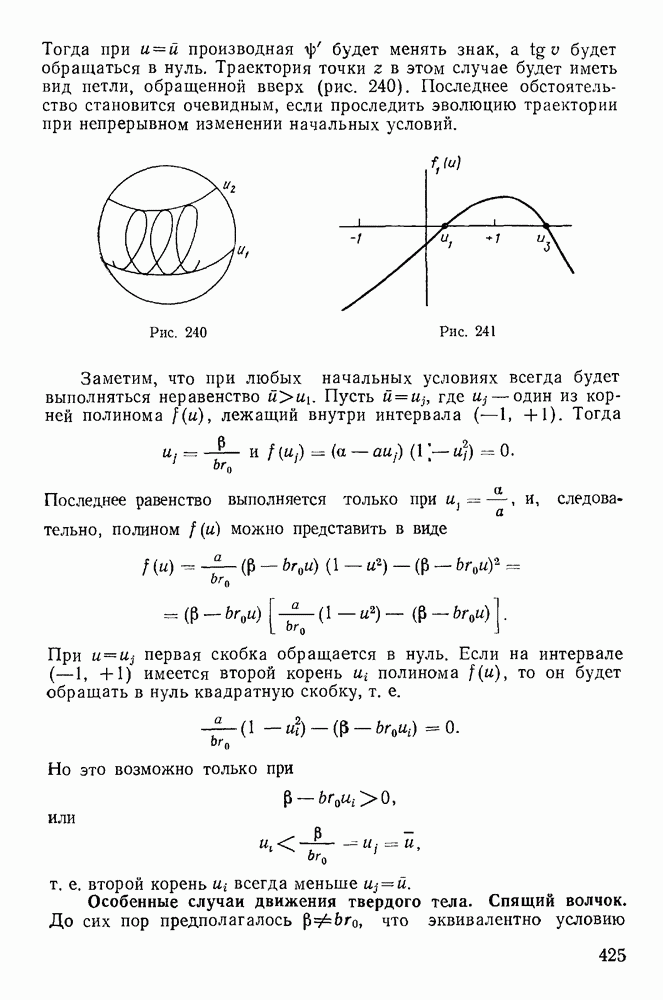
В результате получаем следующую картину: геометрические места полюсов (полодии) при изменении D имеют на эллипсоиде инерции особые точки, совпадающие с точками пересечения главных осей инерции с эллипсоидом инерции. Две из этих точек являются центрами и одна — седлом. Твердое тело совершает постоянные вращения вокруг осей, проходящих через особые точки. Если же телу сообщить начальное движение так, чтобы мгновенная ось вращения пересекла одну из полодий не в особой точке, то при дальнейшем движении твердого тела мгновенная ось вращения будет изменять свое положение в теле, но полюс будет оставаться все время на одной и той же полодии.