| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
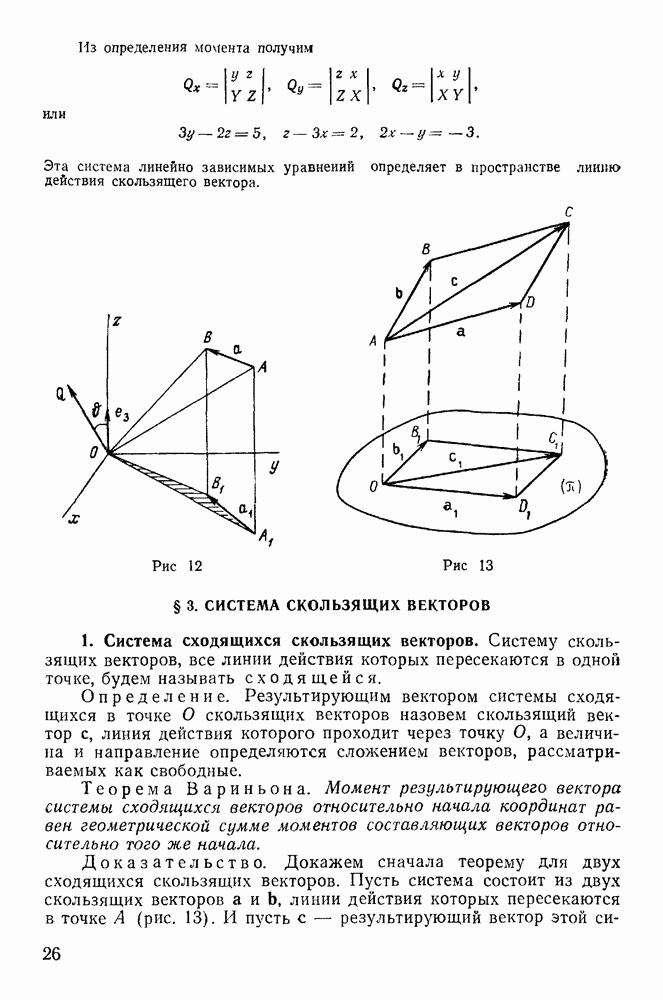
3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
При изучении различных систем векторов особо выделим систему параллельных скользящих векторов.
а) Система параллельных скользящих векторов.
Определение. Векторы, линии действия которых параллельны, называются параллельными скользящими векторами.
Сначала рассмотрим случай двух параллельных векторов, направленных в одну сторону, предполагая, что их линии действия проходят через точки А и В, в которые и перенесем векторы (рис. 14). Проведем через точки А и В прямую и присоединим к системе два равных по величине, противоположно направленных и лежащих на одной прямой АВ, вектора  . Новая система четырех скользящих векторов эквивалентна первоначальной системе. Но последнюю систему векторов
. Новая система четырех скользящих векторов эквивалентна первоначальной системе. Но последнюю систему векторов  можно заменить эквивалентной системой, состоящей из двух скользящих векторов Р и
можно заменить эквивалентной системой, состоящей из двух скользящих векторов Р и  так что
так что

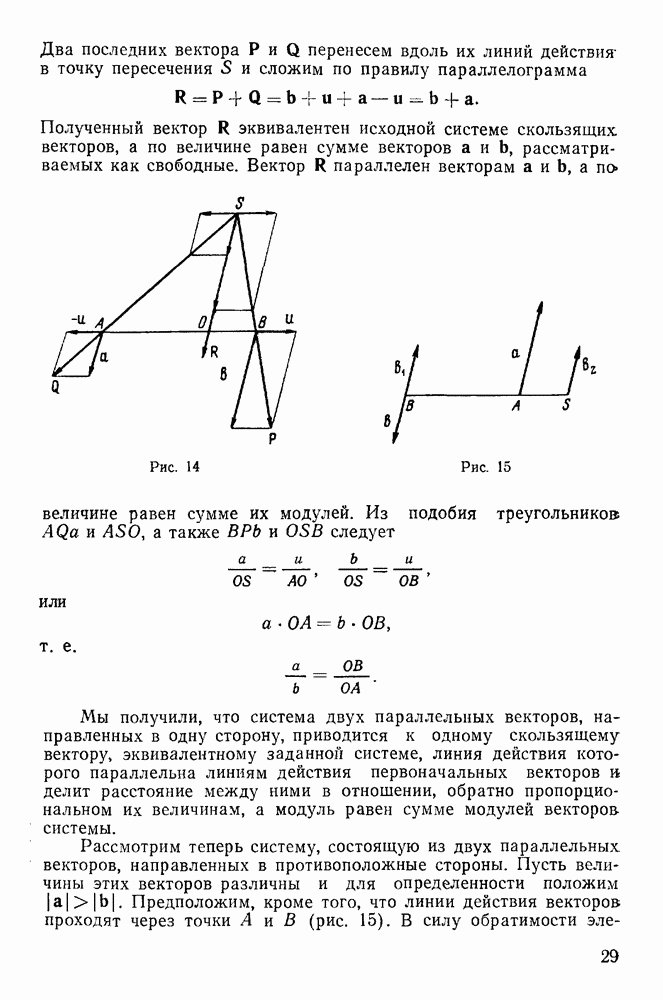
Два последних вектора Р и Q перенесем вдоль их линий действия в точку пересечения  и сложим по правилу параллелограмма
и сложим по правилу параллелограмма

Полученный вектор  эквивалентен исходной системе скользящих векторов, а по величине равен сумме векторов а и
эквивалентен исходной системе скользящих векторов, а по величине равен сумме векторов а и  рассматриваемых как свободные. Вектор
рассматриваемых как свободные. Вектор  параллелен векторам а и
параллелен векторам а и  а по величине равен сумме их модулей.
а по величине равен сумме их модулей.

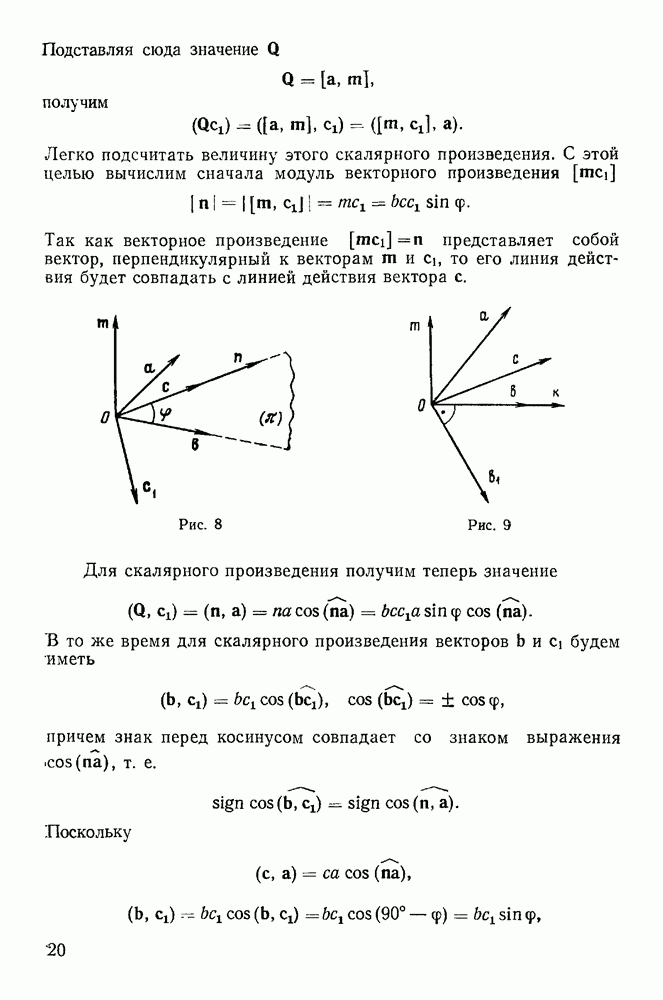
Рис. 14

Рис. 15
Из подобия треугольников  , а также
, а также  следует
следует

или

т. е.

Мы получили, что система двух параллельных векторов, направленных в одну сторону, приводится к одному скользящему вектору, эквивалентному заданной системе, линия действия которого параллельна линиям действия первоначальных векторов и делит расстояние между ними в отношении, обратно пропорциональном их величинам, а модуль равен сумме модулей векторов системы.
Рассмотрим теперь систему, состоящую из двух параллельных векторов, направленных в противоположные стороны. Пусть величины этих векторов различны и для определенности положим  Предположим, кроме того, что линии действия векторов проходят через точки А к В (рис. 15). В силу обратимости
Предположим, кроме того, что линии действия векторов проходят через точки А к В (рис. 15). В силу обратимости
элементарных операций вектор а можно заменить эквивалентной системой из двух векторов  параллельных вектору а, величины которых определяются из равенств
параллельных вектору а, величины которых определяются из равенств

где векторы  рассматриваются как свободные. Отсюда будем иметь
рассматриваются как свободные. Отсюда будем иметь

Линию действия вектора  проведем через точку В, тогда точка
проведем через точку В, тогда точка  на линии действия вектора
на линии действия вектора  определится из условия
определится из условия

или

Система векторов  эквивалентна первоначальной системе. Векторы
эквивалентна первоначальной системе. Векторы  представляют собой нулевую систему скользящих векторов, которую можно отбросить. В результате будем иметь один скользящий вектор
представляют собой нулевую систему скользящих векторов, которую можно отбросить. В результате будем иметь один скользящий вектор  эквивалентный первоначальной системе скользящих векторов, т. е. система двух параллельных скользящих векторов а и
эквивалентный первоначальной системе скользящих векторов, т. е. система двух параллельных скользящих векторов а и  не равных по величине и направленных в противоположные стороны, эквивалентна одному скользящему вектору
не равных по величине и направленных в противоположные стороны, эквивалентна одному скользящему вектору  параллельному первоначальным векторам, линия действия которого делит отрезок, соединяющий точки приложения векторов а и b внешним образом в отношении
параллельному первоначальным векторам, линия действия которого делит отрезок, соединяющий точки приложения векторов а и b внешним образом в отношении

Направления векторов  и а совпадают, а величина
и а совпадают, а величина  равна разности величин векторов а и
равна разности величин векторов а и 
Замечание. Вектор  эквивалентный рассматриваемой системе векторов, называют результирующим вектором системы.
эквивалентный рассматриваемой системе векторов, называют результирующим вектором системы.
б) Пара скользящих векторов и ее свойства.
Рассмотренный выше случай противоположно направленных параллельных векторов исключает равенство  так как при выполнении этого равенства невозможно определить положение линии действия вектора
так как при выполнении этого равенства невозможно определить положение линии действия вектора  Величина вектора
Величина вектора  просто исчезает.
просто исчезает.
Систему двух параллельных векторов, равных по величине, направленных в противоположные стороны и не лежащих на одной прямой, будем называть парой. Пара скользящих векторов обладает целым рядом специфических особенностей и имеет очень большое значение в теории скользящих векторов. Плоскость, определяемую векторами пары, будем называть плоскостью пары, расстояние между линиями действия векторов пары — плечом пары. Векторы пары создают «вращение плеча» в ту
сторону, куда указывают их стрелки. Всегда можно указать ту сторону от плоскости пары, откуда это вращение видно происходящим против хода часовой стрелки. Эту сторону назовем положительной. Введем в рассмотрение вектор  момент пары, направленный перпендикулярно к ее плоскости в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, равный по величине площади параллелограмма, построенного на векторах пары (рис. 16). Будем сначала рассматривать вектор
момент пары, направленный перпендикулярно к ее плоскости в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, равный по величине площади параллелограмма, построенного на векторах пары (рис. 16). Будем сначала рассматривать вектор  как вектор, приложенный к началу вектора —а. По величине и по направлению вектор
как вектор, приложенный к началу вектора —а. По величине и по направлению вектор  совпадает с величиной и направлением вектора момента а относительно точки В
совпадает с величиной и направлением вектора момента а относительно точки В

что дает возможность определить проекции вектора  на оси, координат.
на оси, координат.

Рис. 16

Рис. 17
Заметим, что при помощи элементарных операций пару нельзя привести к одному скользящему вектору, эквивалентному паре. В этом мы уже имели возможность убедиться, рассматривая систему из двух параллельных скользящих векторов, направленных в противоположные стороны. Как было показано, система таких векторов эквивалентна одному результирующему вектору только тогда, когда разность величин векторов отлична от нуля. Если же эта разность стремится к нулю, величина результирующего вектора тоже стремится к нулю, а линия его действия уходит в бесконечность.
Установим следующие свойства пары:
1. При помощи элементарных операций пару можно повернуть в своей плоскости, причем момент пары не изменяет ни величины, ни направления.
В самом деле, пусть имеется пара скользящих векторов  , линии действия которых проходят через точки А и В и пусть плечо пары равно
, линии действия которых проходят через точки А и В и пусть плечо пары равно  (рис. 17). Проведем в плоскости пары две параллельных прямых, расстояние между которыми равно
(рис. 17). Проведем в плоскости пары две параллельных прямых, расстояние между которыми равно  и которые
и которые
образуют угол а с векторами пары. В произвольно выбранных точках С и D этих прямых добавим две нулевые системы скользящих векторов  по величине равных величинам векторов пары, а направленных вдоль этих новых прямых. Полученная новая система шести скользящих векторов эквивалентна первоначальной системе векторов. Перенося теперь нулевые системы векторов вдоль линий их действия в точки А и В пересечения прямых и складывая затем векторы и
по величине равных величинам векторов пары, а направленных вдоль этих новых прямых. Полученная новая система шести скользящих векторов эквивалентна первоначальной системе векторов. Перенося теперь нулевые системы векторов вдоль линий их действия в точки А и В пересечения прямых и складывая затем векторы и  с векторами первоначальной пары, получим новую систему векторов
с векторами первоначальной пары, получим новую систему векторов  эквивалентную первоначальной паре. Векторы
эквивалентную первоначальной паре. Векторы  направлены по общей диагонали ромба в противоположные стороны и равны по величине, т. е. представляют собой нулевую систему, которую можно отбросить. В результате останется система двух скользящих векторов
направлены по общей диагонали ромба в противоположные стороны и равны по величине, т. е. представляют собой нулевую систему, которую можно отбросить. В результате останется система двух скользящих векторов  равных по величине, направленных в противоположные стороны и расположенных на параллельных прямых. Такая система векторов является парой, у которой линии действия векторов повернуты по сравнению с первоначальной на угол а. В рассмотренном преобразовании не изменилось плечо пары, не изменились по величине вектора пары, а следовательно, не изменилась и величина вектора момента пары. Остается неизменным и направление вектора момента пары. Этим доказано, что при помощи элементарных операций пару можно повернуть в своей плоскости, причем величина и направление вектора момента пары остаются инвариантными по отношению к такому преобразованию. Новая пара оказывается эквивалентной первоначальной паре.
равных по величине, направленных в противоположные стороны и расположенных на параллельных прямых. Такая система векторов является парой, у которой линии действия векторов повернуты по сравнению с первоначальной на угол а. В рассмотренном преобразовании не изменилось плечо пары, не изменились по величине вектора пары, а следовательно, не изменилась и величина вектора момента пары. Остается неизменным и направление вектора момента пары. Этим доказано, что при помощи элементарных операций пару можно повернуть в своей плоскости, причем величина и направление вектора момента пары остаются инвариантными по отношению к такому преобразованию. Новая пара оказывается эквивалентной первоначальной паре.
2. При помощи элементарных операций можно изменить плечо пары (изменяя величины векторов обратно пропорционально изменению плеча пары), при этом получаем эквивалентную пару, момент которой по величине и по направлению равен моменту первоначальной пары.
Для доказательства этого предложения предположим, что некоторая прямая А пересекает линии действия векторов пары под прямым углом в точках А и В, так что отрезок АВ равен величине ллеча пары  (рис. 18). Для построения эквивалентной пары, плечо которой
(рис. 18). Для построения эквивалентной пары, плечо которой  на прямой А на расстоянии
на прямой А на расстоянии  по обе стороны от середины О отрезка А В отложим точки С и D и в этих точках добавим две нулевые системы векторов
по обе стороны от середины О отрезка А В отложим точки С и D и в этих точках добавим две нулевые системы векторов  , линии действия которых параллельны векторам пары, а величины определяются из условия
, линии действия которых параллельны векторам пары, а величины определяются из условия

Полученная система шести векторов эквивалентна первоначальной паре. Как нетрудно убедиться, система параллельных векторов а и и (последний проходит через С) эквивалентна одному вектору  с началом в точке О, причем величина вектора
с началом в точке О, причем величина вектора  определяется из равенства
определяется из равенства

С другой стороны, векторы  (последний проходит через точку
(последний проходит через точку  эквивалентны одному вектору
эквивалентны одному вектору  с точкой приложения О, величина которого определяется из равенства
с точкой приложения О, величина которого определяется из равенства

Векторы  и
и  представляют нулевую систему, отбросив которую, получим пару векторов
представляют нулевую систему, отбросив которую, получим пару векторов  с плечом
с плечом  эквивалентную первоначальной паре. Момент новой пары
эквивалентную первоначальной паре. Момент новой пары

т. е. равен по величине и по направлению моменту первоначальной пары.

Рис. 18

Рис. 19
3. При помощи элементарных операций пару можно переносить в параллельную плоскость. При этом величина и направление вектора момента пары остаются неизменными.
В самом деле, пусть заданная пара скользящих векторов а и —а расположена в плоскости  а линии действия векторов пары проходят через точки А и В (рис. 19). Перпендикуляры, восстановленные к плоскости
а линии действия векторов пары проходят через точки А и В (рис. 19). Перпендикуляры, восстановленные к плоскости  в точках А и В, пересекают параллельную плоскость
в точках А и В, пересекают параллельную плоскость  в точках
в точках  Добавим в этих точках две пулевые системы скользящих векторов
Добавим в этих точках две пулевые системы скользящих векторов  по величине равных вектору а, линии действия которых параллельны линиям действия вектора а. Новая система шести векторов эквивалентна первоначальной паре. Система параллельных векторов а и
по величине равных вектору а, линии действия которых параллельны линиям действия вектора а. Новая система шести векторов эквивалентна первоначальной паре. Система параллельных векторов а и  эквивалентна одному скользящему вектору
эквивалентна одному скользящему вектору  а линия действия его проходит через точку пересечения диагоналей параллелограмма
а линия действия его проходит через точку пересечения диагоналей параллелограмма  Аналогично, система векторов
Аналогично, система векторов  эквивалентна одному скользящему вектору
эквивалентна одному скользящему вектору  линия действия которого тоже проходит через точку пересечения диагоналей. Векторы
линия действия которого тоже проходит через точку пересечения диагоналей. Векторы  представляют собой нулевую систему скользящих векторов, отбросив которую, получим систему,
представляют собой нулевую систему скользящих векторов, отбросив которую, получим систему,
состоящую из двух скользящих векторов  расположенных в плоскости
расположенных в плоскости  и представляющих собой пару с моментом, равным моменту первоначальной пары.
и представляющих собой пару с моментом, равным моменту первоначальной пары.
Замечание. Плоскость пары нельзя повернуть вокруг прямой, не являющейся ортогональной к плоскости пары. В самом деле, если предположить, что существуют две эквивалентные нары, лежащие соответственно в плоскостях  пересекающихся по прямой А (рис. 20), то каждую из этих пар можно реализовать некоторым заданным вектором а, расположенным на прямой А, и двумя параллельными векторами
пересекающихся по прямой А (рис. 20), то каждую из этих пар можно реализовать некоторым заданным вектором а, расположенным на прямой А, и двумя параллельными векторами  равными по величине и расположенными соответственно в плоскостях
равными по величине и расположенными соответственно в плоскостях 

Рис. 20

Рис. 21
Утверждение об эквивалентности пар сводится теперь к условию эквивалентности двух параллельных скользящих векторов  равных по величине, но не лежащих на одной линии действия. Последнее противоречит определению скользящих векторов.
равных по величине, но не лежащих на одной линии действия. Последнее противоречит определению скользящих векторов.
Рассмотренные свойства пары скользящих векторов говорят о том, что элементарными операциями можно изменять положение пары в пространстве, но при этом остается неизменным вектор момента пары, обладающий свойствами свободного вектора. По отношению к элементарным операциям вектор момента пары инвариантен.
Следствие. Две пары эквивалентны, если их векторы моментов пар равны по величине, параллельны и одинаково направлены. Пары определяются своими моментами, которые являются свободными векторами.
Теорема о сложении пар. Две произвольные пары эквивалентны одной паре, момент которой равен геометрической сумме моментов заданных пар.
Доказательство. Рассмотрим две произвольные пары, плоскости которых пересекаются по некоторой прямой I, проходящей через точку О, с моментами соответственно  (рис. 21). На прямой I отложим произвольный отрезок
(рис. 21). На прямой I отложим произвольный отрезок  и заданные пары преобразуем так, чтобы плечо каждой из них было равно величине
и заданные пары преобразуем так, чтобы плечо каждой из них было равно величине
отрезка ОА. Представленные пары можно теперь реализовать векторами  проходящими соответственно через точки О и А, а моменты этих пар будут соответственно равны
проходящими соответственно через точки О и А, а моменты этих пар будут соответственно равны

Складывая векторы  получим два скользящих вектора
получим два скользящих вектора

линии действия которых проходят соответственно через точки А и О. Векторы а и —а равны по величине, параллельны и направлены в противоположные стороны, т. е. представляют собой пару, эквивалентную двум первоначальным парам. Применяя алгебру свободных векторов для определения величины и направления момента результирующей пары, будем иметь

или


Рис. 22
в) Приведение произвольной системы скользящих векторов.
Рассмотрим произвольную систему скользящих векторов  линии действия которых проходят соответственно через точки
линии действия которых проходят соответственно через точки  При помощи элементарных операций можно построить простейшую эквивалентную систему скользящих векторов. В самом деле, добавим в точке О нулевую систему скользящих векторов а и — а, линия действия которых параллельна линии действия вектора
При помощи элементарных операций можно построить простейшую эквивалентную систему скользящих векторов. В самом деле, добавим в точке О нулевую систему скользящих векторов а и — а, линия действия которых параллельна линии действия вектора  а величины равны величине вектора
а величины равны величине вектора  (рис. 22). Система векторов
(рис. 22). Система векторов  будет представлять пару, момент которой
будет представлять пару, момент которой

является вектором свободным. Проводя такие же преобразования для каждого вектора системы, в результате получим систему сходящихся скользящих векторов  и систему пар с моментами
и систему пар с моментами  Новая система скользящих векторов эквивалентна первоначальной системе векторов
Новая система скользящих векторов эквивалентна первоначальной системе векторов  Систему сходящихся скользящих векторов
Систему сходящихся скользящих векторов  можно заменить одним результирующим вектором
можно заменить одним результирующим вектором

линия действия которого проходит через точку О. Складывая пары скользящих векторов  получим результирующую пару с моментом
получим результирующую пару с моментом

В результате приходим к следующей теореме.
Теорема. Для произвольной системы скользящих векторов всегда можно построить эквивалентную систему, состоящую из трех скользящих векторов, причем линия действия одного из этих векторов (результирующего вектора) проходит через наперед заданную точку, а два других представляют пару с моментом, равным сумме моментов векторов системы относительно той же точки.
Процесс построения результирующего вектора и результирующей пары носит название приведения системы скользящих векторов кпроизвольной точке.
Теорема об эквивалентности двух систем скользящих векторов. Две системы скользящих векторов  эквивалентны тогда и только тогда, когда при приведении к произвольной точке каждой из этих систем их результирующие векторы и моменты результирующих пар совпадают.
эквивалентны тогда и только тогда, когда при приведении к произвольной точке каждой из этих систем их результирующие векторы и моменты результирующих пар совпадают.
Доказательство. (Необходимость). Предположим сначала, что система скользящих векторов  эквивалентна системе скользящих векторов
эквивалентна системе скользящих векторов  Приводя систему скользящих векторов
Приводя систему скользящих векторов  к произвольной точке О, получим результирующий вектор
к произвольной точке О, получим результирующий вектор  и результирующую пару скользящих векторов
и результирующую пару скользящих векторов  с моментом
с моментом  Эта система трех скользящих векторов эквивалентна системе
Эта система трех скользящих векторов эквивалентна системе  , а значит и системе
, а значит и системе  т. е. последнюю можно получить из векторов
т. е. последнюю можно получить из векторов  при помощи элементарных операций. В силу обратимости элементарных операций векторы
при помощи элементарных операций. В силу обратимости элементарных операций векторы  получаются из системы
получаются из системы  при помощи элементарных операций и представляют собой результирующий вектор и результирующую пару этой системы.
при помощи элементарных операций и представляют собой результирующий вектор и результирующую пару этой системы.
(Достаточность). Если предположить, что две системы скользящих векторов  приводятся к одному и тому же результирующему вектору и к одной и той же паре, то такие системы эквивалентны. Это утверждение непосредственно следует из обратимости элементарных операций.
приводятся к одному и тому же результирующему вектору и к одной и той же паре, то такие системы эквивалентны. Это утверждение непосредственно следует из обратимости элементарных операций.
г) Изменение точки приведения системы скользящих векторов. Инварианты.
Предположим, что система скользящих векторов уже приведена к началу координат и что результирующий вектор равен  а момент результирующей пары равен
а момент результирующей пары равен  Рассмотрим произвольную точку О, не лежащую на линии действия результирующего вектора
Рассмотрим произвольную точку О, не лежащую на линии действия результирующего вектора  и добавим к системе два скользящих вектора
и добавим к системе два скользящих вектора  лежащих на прямой, проходящей через точку О и
лежащих на прямой, проходящей через точку О и
параллельной вектору  направленных в противоположные стороны, а по величине равных величине вектора
направленных в противоположные стороны, а по величине равных величине вектора  Векторы
Векторы  и
и  представляют пару с моментом
представляют пару с моментом

которую можно сложить с первоначальной результирующей парой с моментом  полученной при приведении системы к точке О. Сложение этих пар дает новую результирующую пару с моментом
полученной при приведении системы к точке О. Сложение этих пар дает новую результирующую пару с моментом

Новая система скользящих векторов эквивалентна первоначальной системе и состоит из скользящего вектора  линия действия которого проходит через точку О, и пары с моментом
линия действия которого проходит через точку О, и пары с моментом 
Рассмотрим инвариантные величины по отношению к изменению точки приведения системы скользящих векторов. Первым таким инвариантом является, очевидно, величина и направление результирующего вектора, не изменяющиеся при изменении точки приведения. Результирующий вектор остается скользящим вектором. Вторым инвариантом является скалярное произведение результирующего вектора на момент результирующей пары. В самом деле,

или, переписывая этот инвариант в другом виде, имеем

С другой стороны, скалярное произведение двух векторов равно

Здесь  является инвариантной величиной, следовательно произведение модуля момента результирующей пары на косинус угла между направлениями результирующего вектора и момента результирующей пары, т. е. проекция момента результирующей пары на направление результирующего вектора также есть инвариант.
является инвариантной величиной, следовательно произведение модуля момента результирующей пары на косинус угла между направлениями результирующего вектора и момента результирующей пары, т. е. проекция момента результирующей пары на направление результирующего вектора также есть инвариант.
д) Приведение системы скользящих векторов к винту.
Как мы уже имели возможность заметить, при изменении точки приведения системы скользящих векторов не изменяется величина проекции момента результирующей пары на направление результирующего вектора, так что если момент результирующей пары  представить в виде суммы двух свободных векторов
представить в виде суммы двух свободных векторов  из которых
из которых  направлен вдоль линии действия вектора
направлен вдоль линии действия вектора  а
а  ему ортогонален, то при изменении точки приведения системы будет изменяться только составляющий вектор
ему ортогонален, то при изменении точки приведения системы будет изменяться только составляющий вектор  При изменении точки приведения добавляется пара. Выберем точку О так (рис. 23), чтобы плоскость этой добавочной пары была бы ортогональна к
При изменении точки приведения добавляется пара. Выберем точку О так (рис. 23), чтобы плоскость этой добавочной пары была бы ортогональна к
вектору  , а ее момент был бы равен по величине вектору
, а ее момент был бы равен по величине вектору  но направлен в противоположную сторону, т. е. чтобы
но направлен в противоположную сторону, т. е. чтобы

Тогда при приведении к точке О для момента результирующей пары будем иметь


Рис. 23

Рис. 24
Этот момент коллинеарен с вектором  Из условия коллинеарности векторов
Из условия коллинеарности векторов  получим
получим

Если теперь начало координат выбрать в точке О, а координаты точки О обозначить через х, у, z, то, принимая во внимание, что проекции вектора

определяются из матрицы

можно записать уравнение (а) в виде

Полученное уравнение определяет прямую линию, параллельную линии действия вектора  и проходящую через точку О. Прямую эту назовем винтовой осью. Для всех точек винтовой оси момент результирующей пары имеет наименьшее значение по сравнению со всеми другими точками пространства, равное величине проекции момента результирующей пары относительно
и проходящую через точку О. Прямую эту назовем винтовой осью. Для всех точек винтовой оси момент результирующей пары имеет наименьшее значение по сравнению со всеми другими точками пространства, равное величине проекции момента результирующей пары относительно
произвольной точки на направление линии действия результирующего вектора.
е) Различные случаи приведения системы скользящих векторов.
При изменении точки приведения системы скользящих векторов остаются инвариантными две величины: 1) величина и направление результирующего вектора; 2) скалярное произведение результирующего вектора на момент результирующей пары, т. е.

В зависимости от значений этих инвариантов можно различить четыре различных случая приведения системы скользящих векторов.

В этом случае для точек винтовой оси момент результирующей пары будет принимать нулевое значение, и система приведется к одному результирующему вектору, который называют равнодействующим вектором системы.

Система приводится к одной результирующей паре, которую будем называть равнодействующей парой.

При приведении к винтовой оси момент результирующей пары получает наименьшее значение, отличное от нуля. Система приводится к винту.

В этом случае система скользящих векторов эквивалентна нулю.
Пример 4 Система скользящих векторов приведена к началу координат, причем результирующий вектор  , а момент результирующей пары
, а момент результирующей пары  Написать уравнение винтовой оси.
Написать уравнение винтовой оси.
Проекции момента добавочной пары определяются из матрицы

а ось винта является линией пересечения плоскостей

Пример 5. Система скользящих векторов приведена к началу координат, причем результирующий вектор  и момент результирующей пары
и момент результирующей пары  образуют угол а Определить ось виита.
образуют угол а Определить ось виита.
Приведем геометрическое решение задачи (рис. 24). Из точки О проведем прямую I, ортогональную к плоскости, построенной на векторах  . На этой прямой выберем точки
. На этой прямой выберем точки  так чтобы момент вектора
так чтобы момент вектора  относительно точки
относительно точки 
был бы направлен в сторону, противоположную направлению вектора  а расстояние
а расстояние  до точки
до точки  было бы равно
было бы равно

В точке  добавим систему скользящих векторов, эквивалентную нулю, состоящую из векторов
добавим систему скользящих векторов, эквивалентную нулю, состоящую из векторов  и
и  Вся система будет эквивалентна одному скользящему вектору
Вся система будет эквивалентна одному скользящему вектору  линия действия которого проходит через точку
линия действия которого проходит через точку  и паре, момент которой по величине равен
и паре, момент которой по величине равен

и направлен параллельно вектору 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. ОСНОВЫ ТЕОРИИ ВЕКТОРОВ
- § 1. СВОБОДНЫЕ ВЕКТОРЫ
- 2. Сложение свободных векторов.
- 3. Проекция вектора на ось.
- 4. Инварианты системы свободных векторов.
- § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ
- 2. Координаты скользящего вектора.
- 3. Момент скользящего вектора. Плюккеровы координаты.
- 4. Аналитическое определение момента скользящего вектора.
- 5. Проекция момента на ось.
- 6. Момент скользящего вектора относительно оси
- § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Произвольная система скользящих векторов. Элементарные операции.
- 3. Приведение системы скользящих векторов к простейшей эквивалентной форме.
- 4. Плоская система скользящих векторов.
- 5. Свойства системы параллельных скользящих векторов.
- § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ
- § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ
- Глава II. КИНЕМАТИКА
- § 1. КИНЕМАТИКА ТОЧКИ
- 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат.
- 3. Скорость и ускорение точки в полярных координатах.
- 4. Движение точки по окружности.
- 5. Проекции ускорения на оси естественного трехгранника.
- 6. Теорема о сложении скоростей в сложном движении точки.
- 7. Метод Роберваля построения касательных к плоским кривым.
- 8. Аналитическое доказательство теоремы о сложении скоростей.
- 9. Сложение скоростей в общем случае сложного движения точки.
- § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- 2. Элементарные движения твердого тела.
- 3. Мгновенные движения твердого тела.
- 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела.
- 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела.
- 6. Мгновенное движение твердого тела с одной неподвижной точкой.
- 7. Плоскопараллельное движение твердого тела.
- § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ
- 2. Замечание о дифференцировании единичного вектора.
- 3. Векторный вывод теоремы Кориолиса.
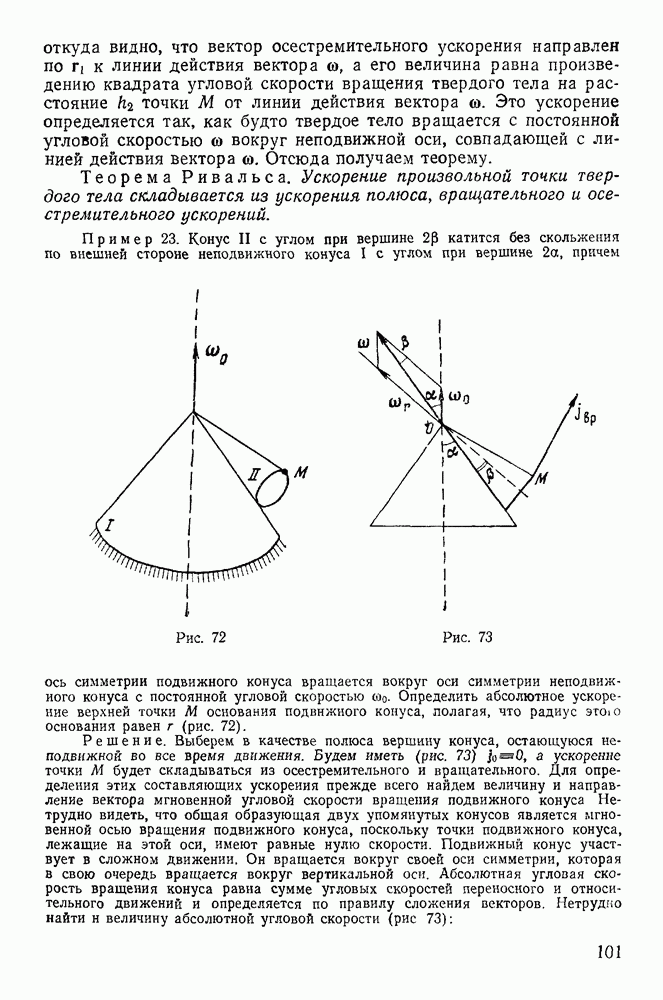
- 4. Теорема Ривальса.
- § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА
- 2. Мгновенный центр ускорений.
- § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА
- Глава III. СТАТИКА
- I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА
- § 1. АКСИОМЫ СТАТИКИ
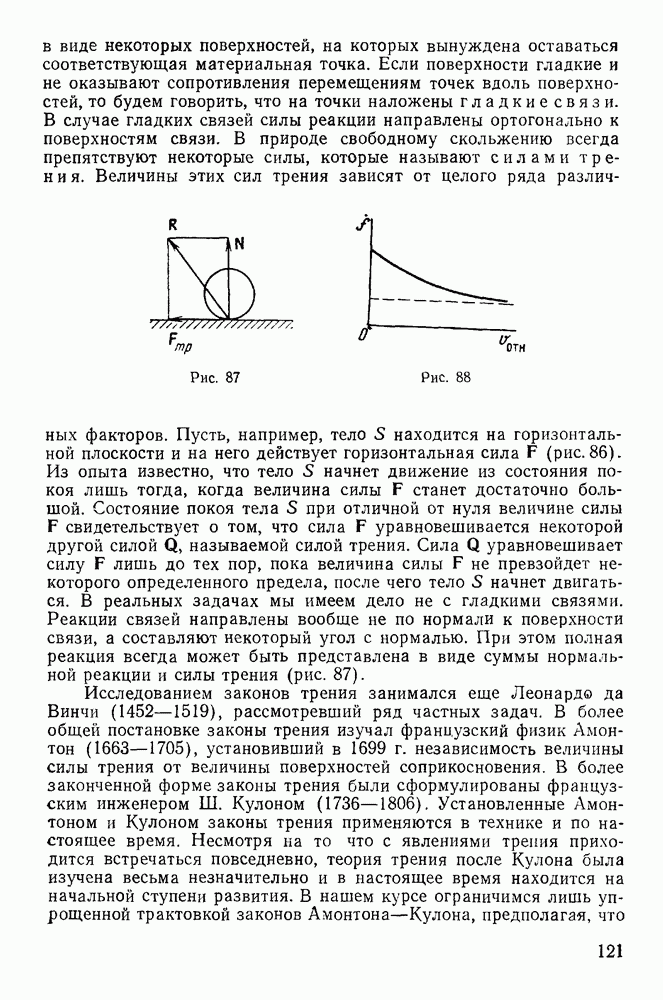
- § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ
- § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ
- 2. Равновесие трех сил.
- § 4. МОМЕНТ СИЛЫ
- 2. Момент силы относительно оси.
- 3. Теорема Вариньона для системы сходящихся сил.
- § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО
- § 7. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО, К ДИНАМЕ. УРАВНЕНИЯ РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
- § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ
- § 9. ПЛОСКАЯ СИСТЕМА СИЛ
- § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА
- 2. Частные случаи равновесия твердого тела.
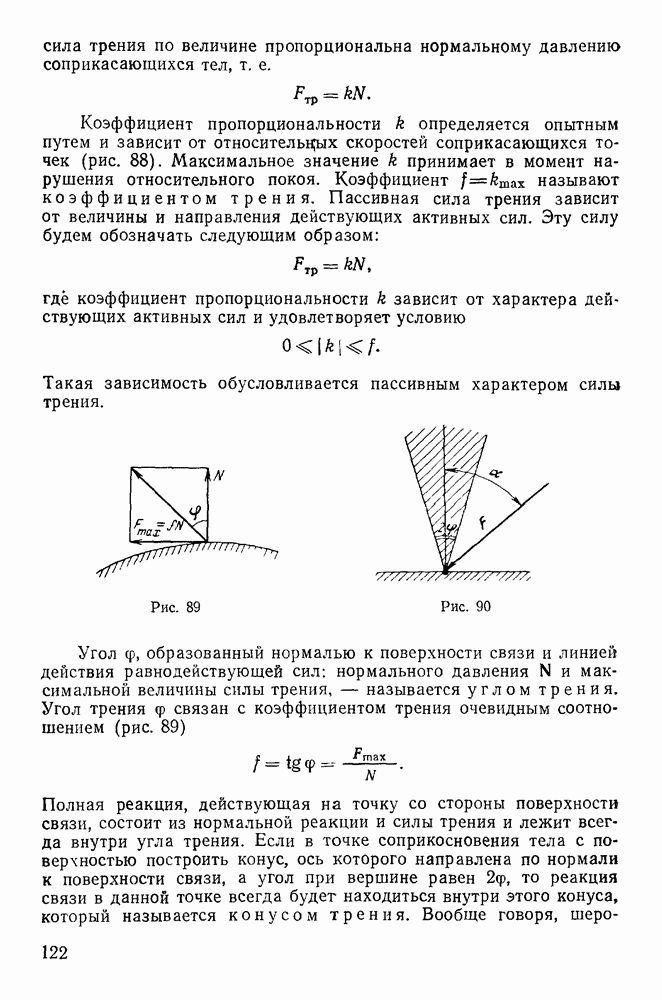
- § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ
- § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ
- II. АНАЛИТИЧЕСКАЯ СТАТИКА
- § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ
- § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- 2. Теорема Лагранжа о равновесии системы.
- 3. Принцип Торричелли.
- § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ
- 3. Общие теоремы о равновесии системы материальных точек.
- 4. Метод неопределенных множителей Лагранжа.
- 5. Определение реакций.
- § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ
- § 5. РАВНОВЕСИЕ НИТИ
- 2. Естественные уравнения равновесия нити.
- Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ
- § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ
- § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
- § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Теорема об изменении момента количества движения.
- 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки.
- 4. Теорема живых сил.
- 5. Интеграл живых сил.
- 6. Устойчивость равновесия. Теорема Лагранжа.
- § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ
- § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ
- 2. Формулы Бине
- 3. Задача о движении планет
- § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ
- § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ
- 2. Движение материальной точки по поверхности.
- § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- 1. Теорема живых сил в относительном движении точки.
- 2. Уравнения относительного равновесия точки.
- 3. Равновесие материальной точки на поверхности Земли. Вес.
- 4. Задача о падении тяжелой точки в пустоте.
- 5. Маятник Фуко.
- § 10. ПРИНЦИП ДАЛАМБЕРА
- Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
- § 1. УЧЕНИЕ О СВЯЗЯХ
- § 2. ПРИНЦИП ДАЛАМБЕРА — ЛАГРАНЖА
- § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ
- 2. Теорема об изменении момента количества движения.
- 3. Теорема живых сил.
- § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА)
- 2. Теорема об изменении момента количества движения системы относительно осей Кёнига.
- 3. Теорема живых сил в движении системы относительно осей Кёнига.
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА
- 2. Случай существования силовой функции.
- 3. Замечание о лагранжевых координатах.
- § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА
- 2. Метод Рауса игнорирования циклических координат.
- 3. Обобщение теоремы и интеграла живых сил.
- § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
- Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ
- 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку.
- 3. Эллипсоид инерции.
- 4. Определение главных осей инерции для произвольной точки.
- § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
- § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ
- 2. Уравнения движения твердого тела с одной неподвижной точкой.
- § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ
- 2. Интегрирование уравнений движения тяжелого твердого тела.
- 3. Случай Эйлера — Пуансо.
- Регулярная прецессия твердого тела в случае Эйлера.
- Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера.
- Устойчивость постоянных вращений твердого тела.
- 4. Случай Лагранжа.
- Особенные случаи движения твердого тела. Спящий волчок.
- Гироскоп. Приближенная теория.
- Некоторые применения гироскопов.
- Регулярная прецессия в случае Лагранжа.
- Вынужденная регулярная прецессия.
- 5. Случай Ковалевской.
- § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА
- § 7. ГИРОСТАТЫ
- Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА
- § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- 1. Преобразования Лежандра.
- 2. Канонические уравнения Гамильтона.
- 3. Функция Гамильтона и ее свойства.
- § 2. ПРИНЦИП ГАМИЛЬТОНА — ОСТРОГРАДСКОГО
- 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского.
- 3. Принцип Гамильтона в форме Пуанкаре.
- § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА
- 2. Канонические преобразования.
- 3. Бесконечно малые канонические преобразования.
- 4. Теорема Лиувилля.
- 5. Теорема Якоби.
- 6. Интегрирование уравнения Гамильтона—Якоби.
- Метод Имшенецкого разделения переменных.
- 7. Скобки Пуассона.
- § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- 2. Принцип Лагранжа.
- 3. Принцип наименьшего действия в форме Якоби.
- Вывод уравнений Лагранжа второго рода из принципа Якоби.
- Сравнение принципа Якоби с принципом Гамильтона.
- 4. Оптико-механическая аналогия.
- 5. Интегральные инварианты.
- Линейные интегральные инварианты.
- Интегральный инвариант Пуанкаре — Картана.
- 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля.
- 7. Уравнения Рауса.
- § 5. МАЛЫЕ КОЛЕБАНИЯ
- Затухающие колебания.
- Вынужденные колебания. Резонанс.
- Параметрический резонанс.
- Нелинейные колебания.
- Диссипативные системы.
- 2. Общий случай малых колебаний системы около положения устойчивого равновесия.
- Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия.
- Замечание об устойчивости стационарных движений.
- Малые колебания системы около положения устойчивого равновесия.
- Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия.
- § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- Прямой метод Ляпунова
- Теорема об асимптотической устойчивости.
- Теорема Четаева о неустойчивости движения.
- 2. Влияние новых связей на малые колебания системы около положения равновесия.
- 3. Влияние диссипативных сил на устойчивость равновесия.
- 4. Влияние гироскопических сил на устойчивость равновесия.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- Устойчивость консервативных систем.
- 2. Метод изменения произвольных постоянных.
- Глава VIII. ТЕОРИЯ УДАРА
- § 2. ТЕОРЕМЫ КАРНО
- § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА
- § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ
- § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА
- § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ
- Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
- § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО
- § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
- Литература