| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
475. Теорема Лиувилля.
Лиувилль указал очень распространенный случай, когда уравнения движения интегрируются в квадратурах. Рассмотрим систему без трения, связи которой не зависят  времени и кинетическая энергия которой выражается в функции параметров
времени и кинетическая энергия которой выражается в функции параметров  в виде
в виде

где  являются функциями одного только параметра
являются функциями одного только параметра  одного только параметра
одного только параметра  Движение этой системы может быть вычислено при помощи квадратур, когда на нее не действуют никакие силы или, в более общем случае, когда действующие на нее активные силы имеют силовую функцию
Движение этой системы может быть вычислено при помощи квадратур, когда на нее не действуют никакие силы или, в более общем случае, когда действующие на нее активные силы имеют силовую функцию  вида
вида

где  зависит только от
зависит только от  только от
только от  — только от
— только от  Частный случай этой теоремы был указан в конце первого тома (п. 305).
Частный случай этой теоремы был указан в конце первого тома (п. 305).
Метод Якоби дает сразу искомое движение. Переменные  в рассматриваемом случае определяются равенствами
в рассматриваемом случае определяются равенствами

Определяя отсюда  и подставляя их значения в Т, найдем для функции
и подставляя их значения в Т, найдем для функции  вследствие однородности Т относительно
вследствие однородности Т относительно 

Следовательно, уравнение с частными производными Якоби, если положить

будет иметь вид

Оно имеет полный интеграл вида

где  зависит только от
зависит только от  — только от
— только от  — только от
— только от  . В самом деле, подставим это значение
. В самом деле, подставим это значение  в предыдущее равенство и отбросим знаменатель. Мы получим уравнение, которое можно написать так:
в предыдущее равенство и отбросим знаменатель. Мы получим уравнение, которое можно написать так:

Первая скобка зависит только от  вторая — только от
вторая — только от  Так как в уравнении с частными производными эти переменные независимы, то последнее уравнение может быть удовлетворено лишь в том случае, если
Так как в уравнении с частными производными эти переменные независимы, то последнее уравнение может быть удовлетворено лишь в том случае, если
каждая скобка в отдельности равна постоянной. Следовательно, мы должны иметь

где  обозначают постоянные, сумма которых равна нулю,
обозначают постоянные, сумма которых равна нулю,  этих постоянных
этих постоянных  будут произвольными, и мы имеем
будут произвольными, и мы имеем

Тогда, интегрируя, получим

Заменяя в выражении (7) функции  этими значениями, мы получим полный интеграл с
этими значениями, мы получим полный интеграл с  произвольными постоянными
произвольными постоянными  Окончательно уравнения движения будут следующие:
Окончательно уравнения движения будут следующие:

Выполняя дифференцирование и применяя соотношение (8), получим

Таким образом, задача разрешена в квадратурах.
Адамар, совершенствуя метод Штауде (Staude), исследовал преобразования этих уравнений для случая, когда интервалы изменения каждого из параметров  ограничены с двух сторон (Hadamard, Bulletin des Sciences mathematiques, т. XXXV, 1911).
ограничены с двух сторон (Hadamard, Bulletin des Sciences mathematiques, т. XXXV, 1911).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ОТ ИЗДАТЕЛЬСТВА
- ДИНАМИКА СИСТЕМЫ
- ГЛАВА XVII. МОМЕНТЫ ИНЕРЦИИ
- I. Определения и примеры
- 314. Определение моментов инерции.
- II. Общие теоремы
- 317. Изменение момента инерции системы относительно оси, перемещающейся параллельно самой себе.
- 318. Изменение момента инерции относительно осей, проходящих через одну и ту же точку.
- 319. Условия, при которых ось Oz является главной для точки О.
- 320. Замечание.
- 321. Задача Бине.
- 322. Геометрическое место точек О, для которых момент инерции относительно одной из главных осей в точке О имеет заданное значение.
- 323. Экспериментальное определение моментов инерции.
- ГЛАВА XVIII. ОБЩИЕ ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ. СЕМЬ УНИВЕРСАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ
- I. Теоремы проекций и моментов количеств движения
- 327. Примеры.
- 328. Доказательство теоремы моментов количеств движения или кинетических моментов.
- 329. Теорема площадей.
- 330. Геометрическая интерпретация обеих теорем.
- 331. Частный случай, когда главный момент внешних сил относительно точки О равен нулю. Плоскость максимума площадей.
- 332. Сумма моментов количеств движения точек твердого тела относительно оси, вокруг которой тело вращается.
- 333. Примеры.
- 334. Движение относительно системы осей, совершающих прямолинейное и равномерное переносное движение.
- 335. Общий случай, когда теоремы проекций и моментов количеств движения дают первый интеграл.
- II. Теорема кинетической энергии
- 337. Примечание о твердом теле.
- 338. Случай, когда взаимодействие двух точек системы зависит только от расстояния между ними.
- 339. Случай, когда теорема кинетической энергии дает первый интеграл.
- 340. Размерности. Пусть в качестве основных единиц приняты единицы длины, времени и массы.
- 341. Пример.
- 342. Деление сил на силы задаваемые и реакции связей.
- 343. Важный частный случай, когда работа реакций связей равна нулю.
- 344. Приложение.
- 345. 1°. Приложение к движению болта в неподвижной гайке без трения.
- 346. Семь общих уравнений движения.
- III. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- 349. Вычисление кинетической энергии.
- IV. Теоремы моментов и кинетической энергии в относительном движении вокруг центра тяжести
- 351. Теорема кинетической энергии в относительном движении вокруг центра тяжести.
- 352. Наибольшее число независимых общих уравнений.
- 353. Произвольная часть системы.
- 354. Пример I.
- V. Энергия
- 356. Потенциальная энергия. Механический смысл.
- 357. Сохранение энергии.
- 368. Механический смысл полной энергии.
- ГЛАВА XIX. ДИНАМИКА ТВЕРДОГО ТЕЛА. ДВИЖЕНИЯ, ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ
- 360. Реакции оси.
- 361. Постоянные и свободные оси вращения.
- 362. Физический маятник.
- 363. Исследование изменения длины синхронного математического маятника при перемещении оси подвеса заданного тела.
- 364. Машина Атвуда.
- II. Движение твердого тела параллельно неподвижной плоскости
- 366. Пример I.
- III. Трение скольжения и сопротивление среды
- 368. Трение скольжения.
- 369. Возможные разрывы в уравнениях движения.
- 370. Пример I.
- 371. Пример II.
- 372. Трение цапф в подшипниках.
- 373. Регулятор с лопатками.
- 374. Самоторможение.
- 375. О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлёве.
- IV. Трение качения
- 377. Качение.
- 378. Пример I.
- 379. О стремлгнии материальных систем избегать трения.
- ГЛАВА XX. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ
- I. Общие уравнения
- 381. Вспомогательные сведения из геометрии. Переменные, определяющие положение подвижного триэдра относительно неподвижного триэдра с той же вершиной.
- 382. Вспомогательные сведения из кинематики. Мгновенное вращение подвижного триэдра.
- 383. Твердое тело, движущееся вокруг неподвижной точки; применение триэдра, неизменно связанного с телом.
- 384. Уравнения Эйлера.
- 385. Реакция неподвижной точки.
- 386. Применение осей, движущихся в теле.
- II. Первое приложение уравнений Эйлера к случаю, когда внешние силы приводятся к одной равнодействующей, проходящей через неподвижную точку
- 388. Исследование движения. Интегрирование при помощи эллиптических функций.
- 389. Частные случаи.
- 390. Случай, когда эллипсоид инерции является эллипсоидом вращения.
- 391. Краткие указания к вычислению девяти косинусов в функции времени.
- 392. Геометрическое представление движения по Пуансо.
- 393. Уравнение герполодии.
- III. Движение тяжелого твердого тела вокруг неподвижной точки
- 396. Случай Лагранжа и Пуассона.
- 396. Частный случай.
- 397. Интегрирование в эллиптических функциях.
- 398. Кинематическая картина движения.
- 339. Случай интегрируемости Ковалевской.
- IV. Другие задачи; применение осей, движущихся относительно тела и относительно пространства; трение и сопротивление среды
- 401. О некоторых свойствах быстро вращающихся тел вращения.
- 402. Трение.
- 403. Сопротивление среды.
- ГЛАВА XXI. СВОБОДНОЕ ТВЕРДОЕ ТЕЛО
- 495. Движение нескольких твердых тел.
- II. Тяжелое тело, соприкасающееся с горизонтальной плоскостью
- 407. Тяжелое тело вращения, скользящее без трения по неподвижной горизонтальной плоскости.
- 408. Замечание Томсона.
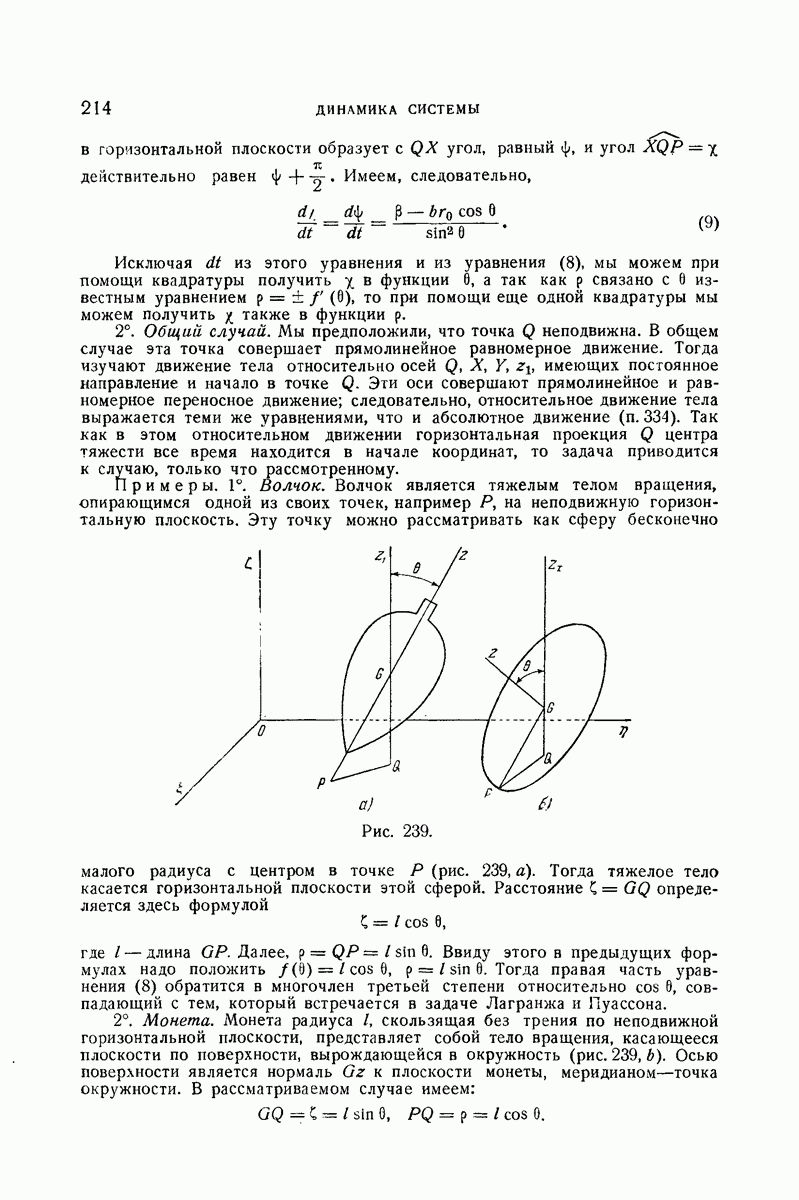
- 409. Тяжелое тело, касающееся гладкой горизонтальной плоскости цилиндрической поверхностью.
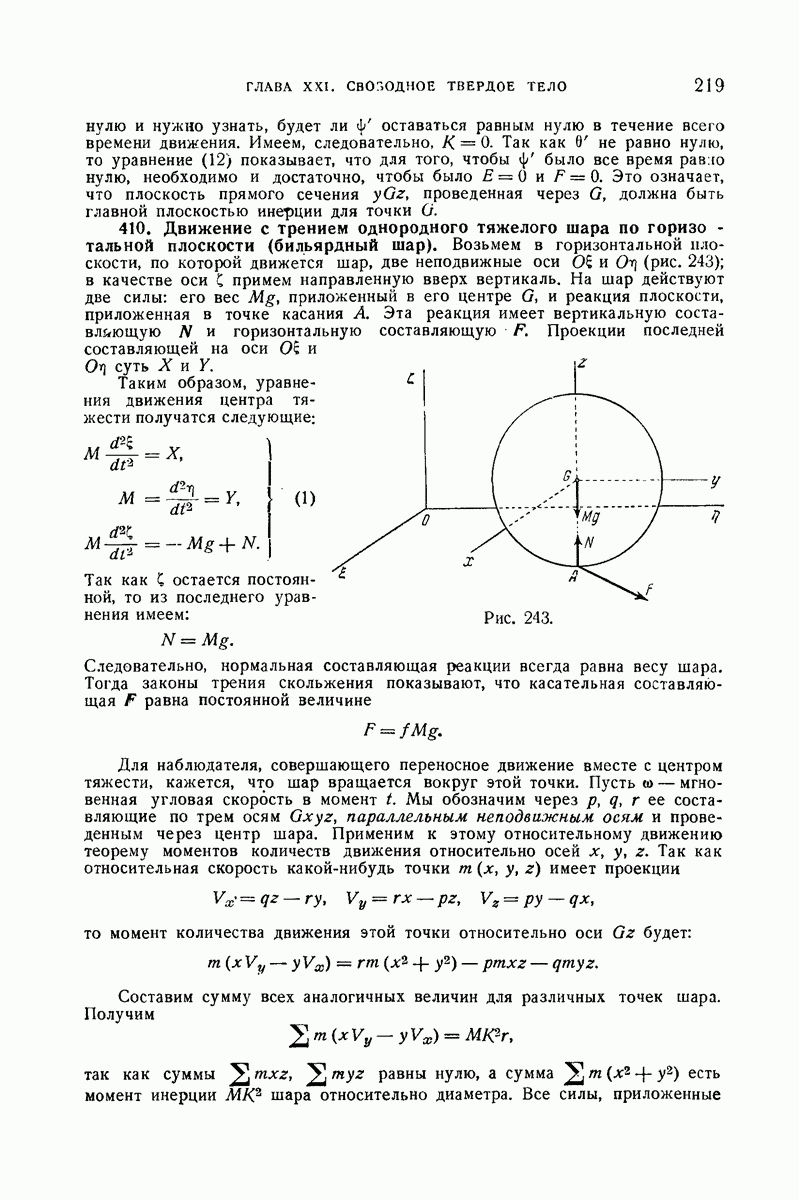
- 410. Движение с трением однородного тяжелого шара по горизонтальной плоскости (бильярдный шар).
- 411. Обруч.
- 412. Координаты твердого тела по Штуди (Study).
- ГЛАВА XXII. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ
- 414. Кинетическая энергия в относительном движении.
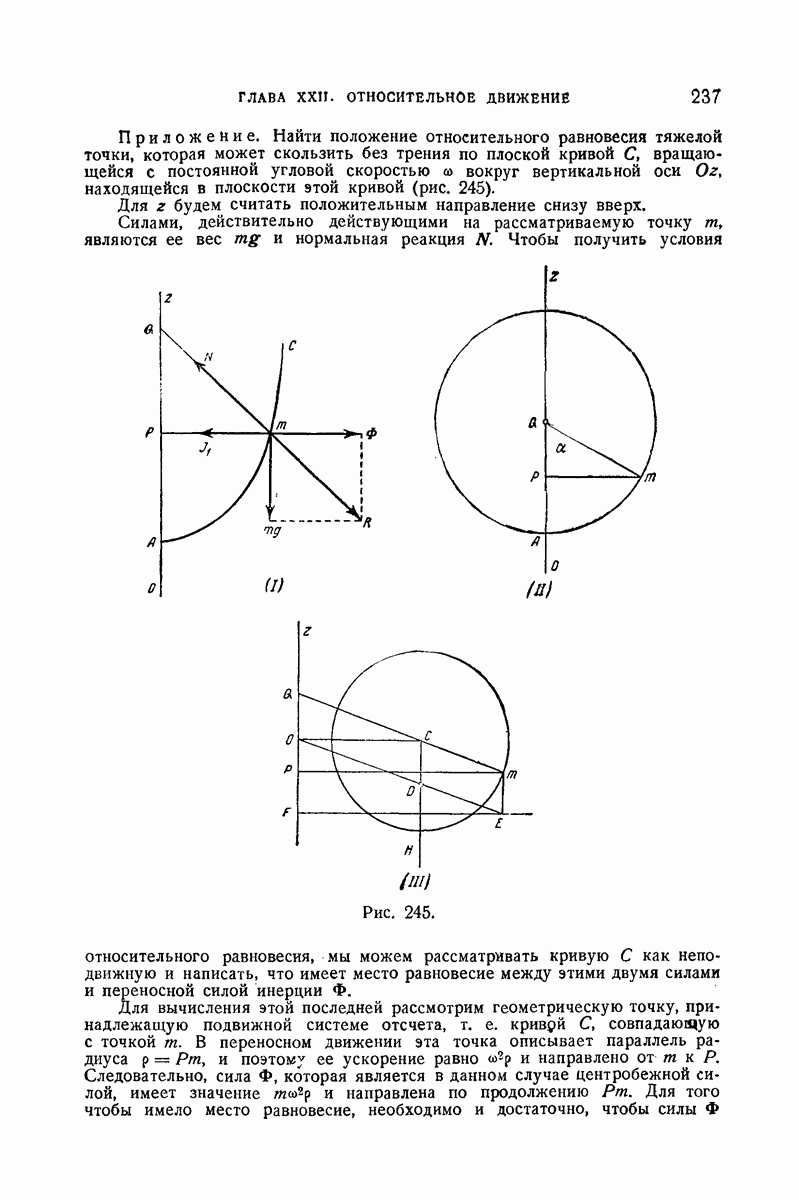
- 415. Относительное равновесие.
- 416. Относительное движение по отношению к осям, совершающим поступательное движение.
- 417. Упражнение.
- II. Относительное движение и равновесие системы
- 420. Пример относительного движения.
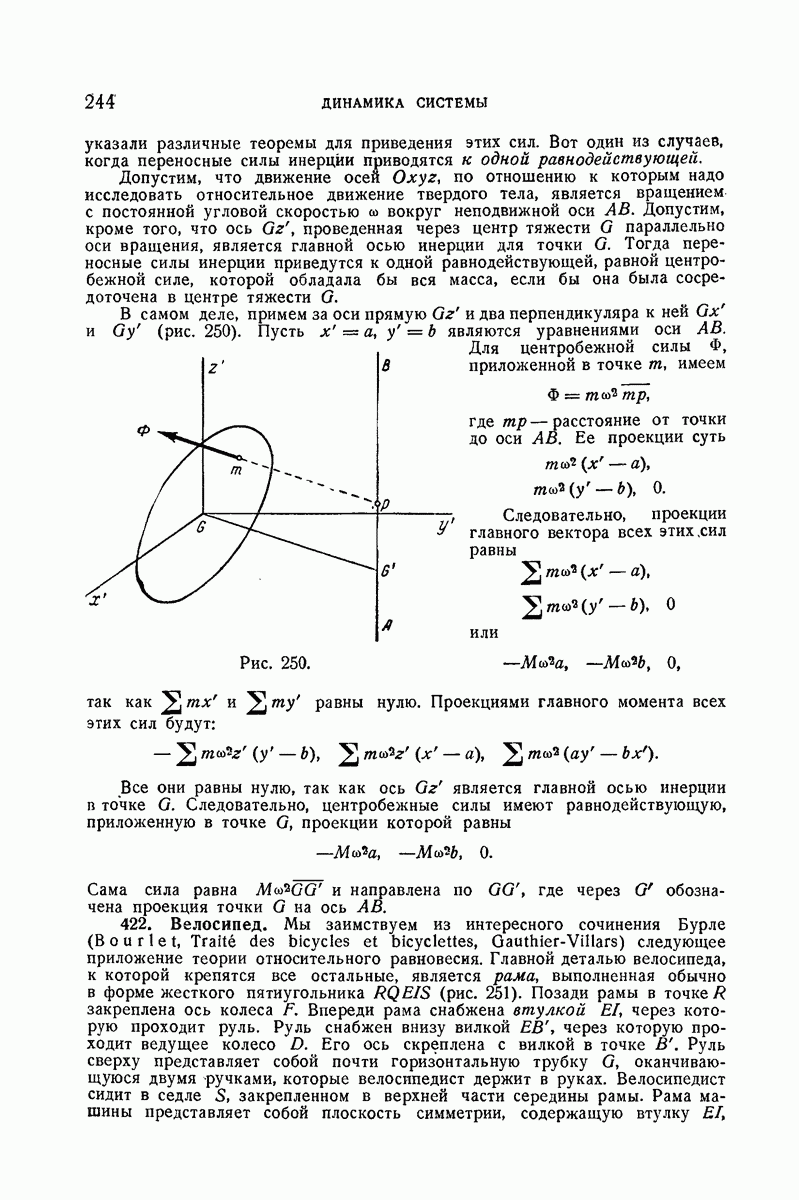
- 421. Твердое тело.
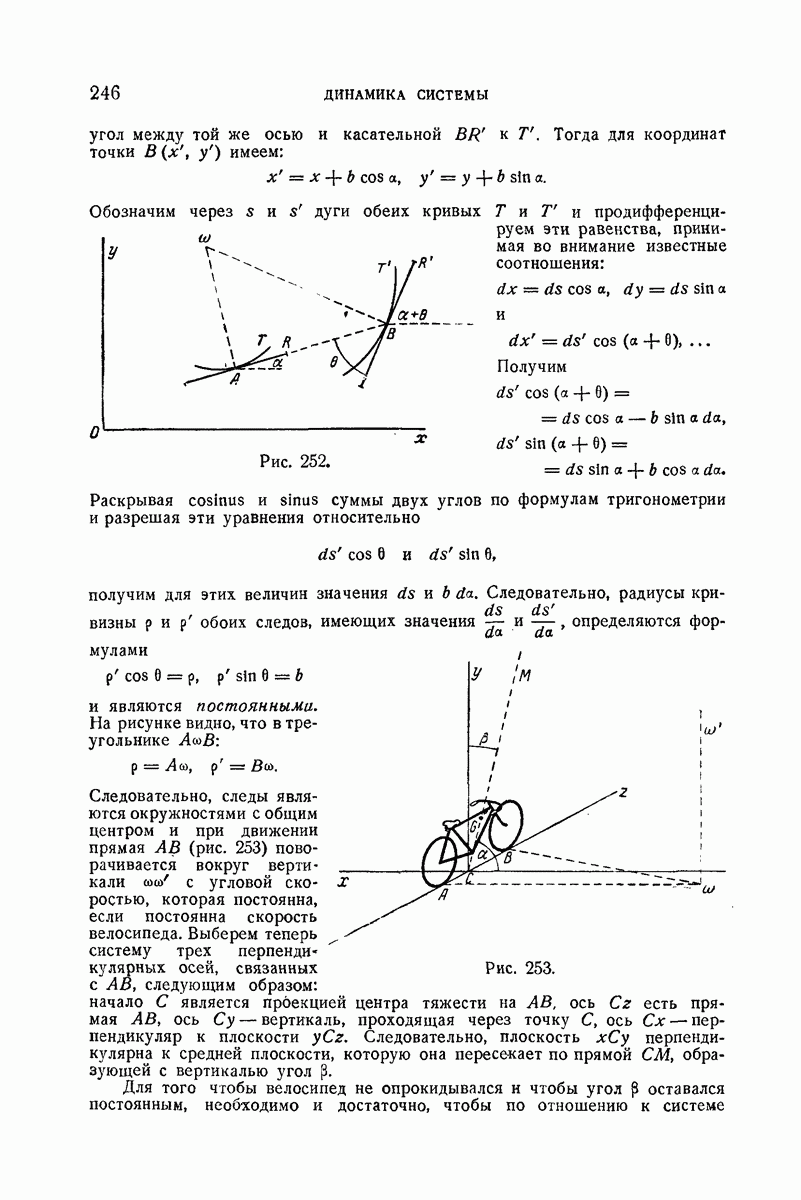
- 422. Велосипед.
- III. Относительное равновесие и относительное движение на поверхности Земли
- 424. Относительное равновесие на поверхности Земли.
- 426. Относительное движение на поверхности Земли.
- 426. Свободное падение тяжелой точки.
- 427. Маятник Фуко.
- 428. Гироскоп.
- ГЛАВА XXIII. ПРИНЦИП ДАЛАМБЕРА
- 430. Случай системы со связями.
- 431. Общее уравнение динамики для системы со связями без трения.
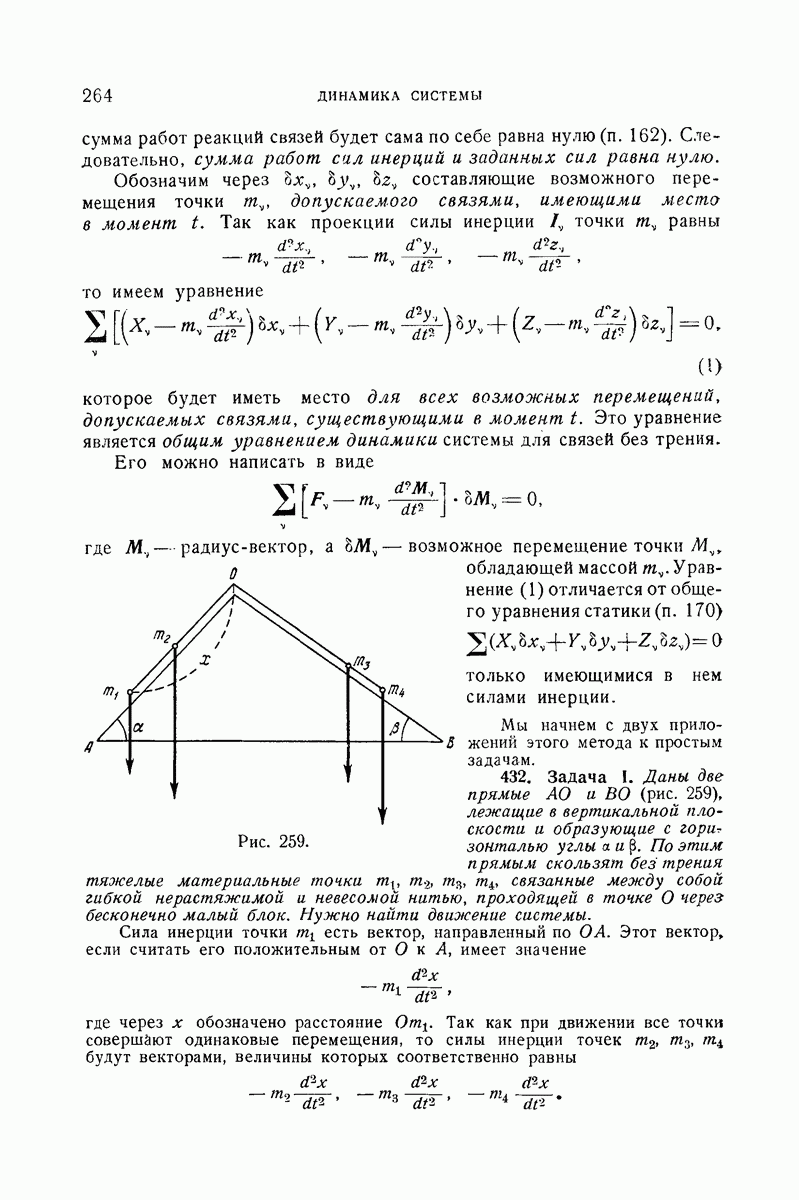
- 432. Задача I.
- 433. Приведение уравнений движения к наименьшему числу.
- 434. Голономные системы; координаты голономной системы.
- 435. Метод множителей Лагранжа для голономной системы.
- II. Теоремы, выводимые из принципа Даламбера
- 437. Частный случай теоремы моментов.
- 438. Частный случай теоремы кинетической энергии.
- III. Приложение принципа Даламбера к случаю трения скольжения
- ГЛАВА XXIV. ОБЩИЕ УРАВНЕНИЯ АНАЛИТИЧЕСКОЙ ДИНАМИКИ
- I. Голономные системы. Уравнения Лагранжа
- 442. Первый пример. Задача.
- 443. Уравнения Эйлера.
- 444. Пример связей, зависящих от времени.
- II. Приложения уравнений Лагранжа
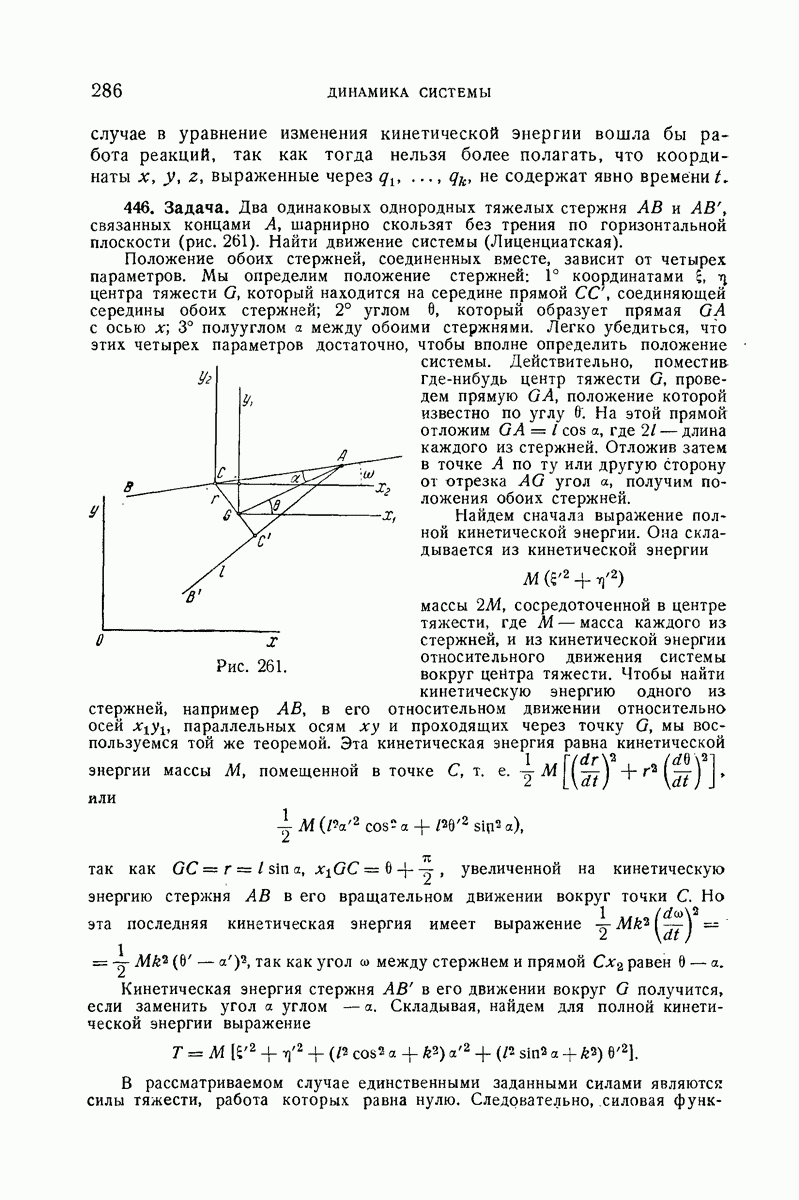
- 446. Задача.
- 447. Тяжелое тело вращения, скользящее без трения по горизонтальной плоскости.
- 448. Интеграл Пенлеве, аналогичный интегралу энергии в некоторых случаях связей, зависящих от времени.
- III. Малые колебания голономных систем около положения устойчивого равновесия
- 450. Малые колебания.
- 451. Малые колебания, вызванные периодической возмущающей силой.
- IV. Колебания около устойчивого движения
- V. Приложение уравнений Лагранжа к относительному движению
- 457. Смешанный метод Жильбера.
- 458. Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли.
- 459. Пример.
- 460. Гироскопический компас Фуко.
- 461. Барогироскоп Жильбера.
- VI. Системы неголономные
- 463. Применение уравнений Лагранжа в сочетании с методом множителей.
- 464. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров.
- 465. Общая форма уравнений движения, пригодная как для голономных, так и для неголономных систем
- 466. Примеры.
- 467. Теорема, аналогичная теореме Кёнига. Приложение к обручу.
- 468. Уравнения движения, получаемые путем нахождения минимума функции второй степени.
- 469. О невозможности охарактеризовать неголономную систему одной только функцией Т.
- VII. Системы, содержащие сервосвязи
- ГЛАВА XXV. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМЫ ЯКОБИ И ПУАССОНА. ПРИНЦИПЫ ГАМИЛЬТОНА, НАИМЕНЬШЕГО ДЕЙСТВИЯ И НАИМЕНЬШЕГО ПРИНУЖДЕНИЯ
- II. Теорема Якоби и ее приложения
- 473. Частный случай, когда t не содержится в коэффициентах уравнения Якоби.
- 474. Примеры.
- 475. Теорема Лиувилля.
- 476. Теорема Штеккеля (Staeckel).
- 477. Приложение преобразования Лежандра к уравнению Якоби
- III. Теорема Пуассона
- 479. Условие, при котором f=С, есть первый интеграл; скобки Пуассона.
- 480. Тождество Пуассона.
- 481. Теорема Пуассона.
- 482. Случай, когда Н не содержит t. Замечание об интеграле энергии.
- 483. Пример.
- IV. Принцип Гамильтона. Принцип наименьшего действия
- 485. Вывод уравнений Лагранжа из принципа Гамильтона.
- 486. Принцип наименьшего действия.
- 487. Геодезические линии.
- 488. Вычисление действия вдоль траектории.
- 439. Геометрические свойства траекторий.
- 490. Расширение понятия силовой функции. Силовая функция, зависящая от времени и от скоростей.
- 491. Задача Майера для случая внутренних сил.
- V. Множитель Якоби
- 493. Уравнение множителя.
- 494. Инвариантность множителя.
- 495. Использование множителя.
- 496. Последний множитель.
- 497. Пример.
- 498. Приложение к каноническим уравнениям.
- 499. Приложение. Задача Бруна (Brun).
- VI. Свойства интегралов. Интегральные инварианты
- 501. Теорема Кёнигса.
- 502. Теорема Пуассона.
- 503. Интегральные инварианты.
- VII. Принцип наименьшего принуждения Гаусса
- ГЛАВА XXVI. УДАР
- I. Удар, приложенный к материальной точке
- II. Удары, приложенные к системе
- III. Приложение общих теорем
- 511. Удары, приложенные к телу, вращающемуся вокруг неподвижной оси Oz.
- 512. Случай, когда действует один удар. Центр удара.
- 513. Баллистический маятник.
- 514. Твердое тело, движущееся вокруг неподвижной точки.
- 515. Свободное твердое тело.
- IV. Общее уравнение теории удара. Теорема Карно
- 517. О связях, существующих в момент удара.
- 518. Следствия из общего уравнения.
- 519. Теорема Карно.
- 520. Распространение теоремы Карно на случай, когда имеются заданные удары.
- 521. Теорема Г. Робена.
- V. Применение уравнений Лагранжа в теории удара
- 523. Замечания о неголономных системах.
- ГЛАВА XXVII. ПОНЯТИЕ О МАШИНАХ. ПОДОБИЕ
- 526. Аналитическое выражение кинетической энергии.
- 527. Движение машины.
- 528. Причины нарушения равномерности хода при установившемся движении.
- 529. Приближенное выражение работы.
- 530. Маховики.
- 531. Регуляторы.
- II. Подобие в механике. Модели