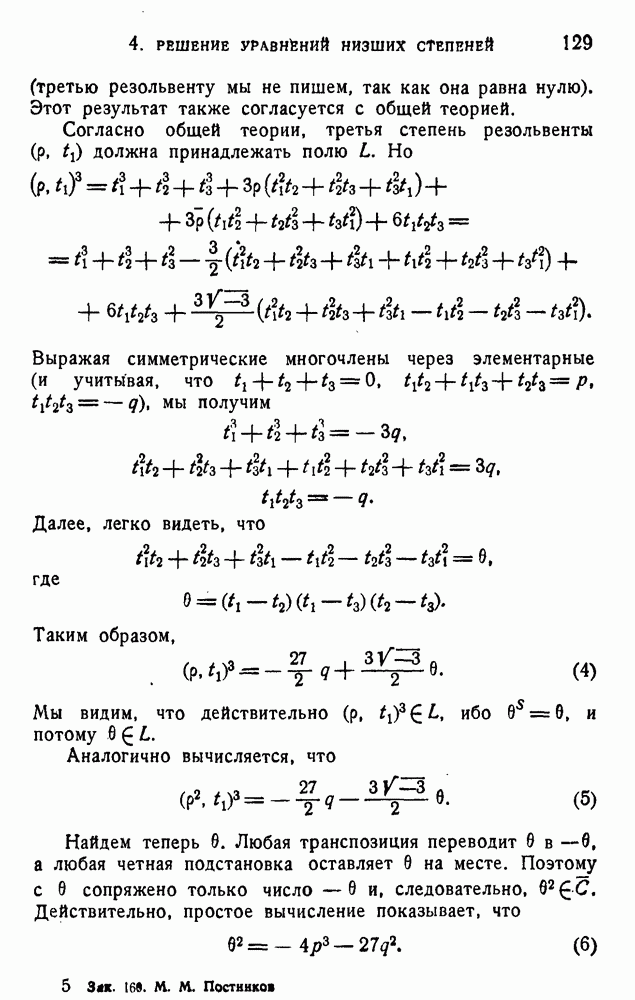| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Примарные группы
Пусть О — произвольная группа. Ее элемент  называется центральным, если он перестановочен с любым элементом группы О, т. е. если для любого элемента
называется центральным, если он перестановочен с любым элементом группы О, т. е. если для любого элемента  имеет место равенство
имеет место равенство

В абелевых группах (и только в них) все элементы центральны. В произвольной группе единица  всегда центральна.
всегда центральна.
Совокупность Z всех центральных элементов группы О называется ее центром. Легко видеть, что центр любой группы является ее (очевидно, абелевым) нормальным делителем (возможно состоящим лишь из единицы  ). Действительно, во-первых, он непуст (содержит единицу
). Действительно, во-первых, он непуст (содержит единицу  ), во-вторых, является подгруппой (если
), во-вторых, является подгруппой (если  то для любого элемента
то для любого элемента  имеет место равенство
имеет место равенство  , в-третьих, для любого элемента
, в-третьих, для любого элемента  из включения
из включения  вытекает включение
вытекает включение 
Элемент  группы О называется сопряженным элементу g, если существует такой элемент
группы О называется сопряженным элементу g, если существует такой элемент  что
что  Совокупность всех элементов группы О, сопряженных некоторому элементу
Совокупность всех элементов группы О, сопряженных некоторому элементу  называется классом сопряженных элементов (определенным элементом g) и обозначается символом
называется классом сопряженных элементов (определенным элементом g) и обозначается символом 
Каждый класс  содержит элемент g (ибо
содержит элемент g (ибо  ), любой элемент
), любой элемент  класса
класса  определяет тот же класс, т. е.
определяет тот же класс, т. е.  (действительно, по условию
(действительно, по условию  и если
и если  то
то  ),
),  , а если
, а если  так что любые два класса либо совпадают, либо не пересекаются. Таким образом, группа О распадается на непересекающиеся классы
так что любые два класса либо совпадают, либо не пересекаются. Таким образом, группа О распадается на непересекающиеся классы  сопряженных элементов.
сопряженных элементов.
Понятие класса сопряженных элементов тесно связано с понятием нормального делителя. Именно, подгруппа Н группы О тогда и только тогда является нормальным делителем этой группы, когда для любого элемента  весь класс
весь класс  содержится в Н. Другими словами, нормальные делители можно определить как подгруппы, состоящие из нескольких полных классов сопряженных элементов.
содержится в Н. Другими словами, нормальные делители можно определить как подгруппы, состоящие из нескольких полных классов сопряженных элементов.
Класс  вполне может состоять лишь из одного элемента. Очевидно, что это имеет место тогда и только тогда, когда элемент g централен.
вполне может состоять лишь из одного элемента. Очевидно, что это имеет место тогда и только тогда, когда элемент g централен.
Рассмотрим теперь совокупность  всех элементов группы О, перестановочных с элементом
всех элементов группы О, перестановочных с элементом  т. е. совокупность всех таких элементов
т. е. совокупность всех таких элементов  что
что

Эта совокупность непуста (ибо содержит все степени элемента g) и является подгруппой группы О (докажите!). Она называется централизатором элемента g в группе О. Очевидно, что элемент g тогда и только тогда централен, когда его централизатор  совпадает со всей группой О.
совпадает со всей группой О.
Каждому элементу  класса
класса  сопоставим смежный класс
сопоставим смежный класс  группы О по централизатору
группы О по централизатору  положив
положив  , где h — такой элемент группы О, что
, где h — такой элемент группы О, что 
Легко видеть, что это определение законно, т. е. смежный класс  не зависит от выбора элемента h. Действительно, если
не зависит от выбора элемента h. Действительно, если  , то
, то  и. потому
и. потому 
Далее, легко видеть, что если  где
где  то
то 
Действительно, пусть  . Тогда равенство
. Тогда равенство  означает, что
означает, что  . Поэтому
. Поэтому  .
.
Наконец, очевидно, что любой смежный класс  группы О по подгруппе
группы О по подгруппе  имеет вид
имеет вид  где
где  (за элемент
(за элемент  можно принять элемент
можно принять элемент  ).
).
Таким образом, отображение осуществляет взаимнооднозначное соответствие между классом  и множеством всех смежных классов группы О по централизатору
и множеством всех смежных классов группы О по централизатору  Следовательно, (предполагается, конечно, что класс
Следовательно, (предполагается, конечно, что класс  состоит из конечного числа элементов) число элементов, содержащихся в классе
состоит из конечного числа элементов) число элементов, содержащихся в классе  равно индексу централизатора
равно индексу централизатора 
Для конечной группы отсюда и из теоремы Лагранжа вытекает, что число элементов, содержащихся в любом классе сопряженных элементов конечной группы О делит порядок этой группы.
Применим эти общие теоремы (относящиеся к произвольным группам) к так называемым примарным (по некоторому простому числу  ) группам, которые определяются как конечные группы, порядок которых имеет вид
) группам, которые определяются как конечные группы, порядок которых имеет вид  где
где 
В первую очередь мы докажем, что любая примарная группа О содержит отличные от единицы центральные элементы.
Действительно, как мы знаем, группа О распадается на непересекающиеся классы сопряженных элементов. Пусть  -числа элементов этих классов. Тогда сумма
-числа элементов этих классов. Тогда сумма  равна порядку
равна порядку  группы О:
группы О:

Все числа  делят порядок
делят порядок  , где
, где  причем хотя бы одно из этих чисел равно единице (так как существует класс — именно класс, определяемый единицей
причем хотя бы одно из этих чисел равно единице (так как существует класс — именно класс, определяемый единицей  группы О, — состоящий только из одного элемента). Отсюда и из равенства (1) вытекает, что по крайней мере
группы О, — состоящий только из одного элемента). Отсюда и из равенства (1) вытекает, что по крайней мере  чисел
чисел  равны единице, т. е. что существует по крайней мере
равны единице, т. е. что существует по крайней мере  центральных элементов. Теорема доказана.
центральных элементов. Теорема доказана.
Докажем теперь, что любая примарная группа О разрешима.
Пусть  — порядок группы О. Проведем доказательство индукцией по числу
— порядок группы О. Проведем доказательство индукцией по числу  . Для
. Для  (а также для
(а также для  теорема очевидна. Предполагая, что теорема уже доказана для всех примарных групп порядка
теорема очевидна. Предполагая, что теорема уже доказана для всех примарных групп порядка  где
где  рассмотрим центр Z группы О. По только что доказанному порядок центра Z отличен от единицы, т. е. имеет вид
рассмотрим центр Z группы О. По только что доказанному порядок центра Z отличен от единицы, т. е. имеет вид  , где
, где  . Поэтому порядок
. Поэтому порядок  факторгруппы
факторгруппы  меньше
меньше  и следовательно, по предположению индукции, эта факторгруппа разрешима. Таким образом, группа О обладает разрешимым (дажа абелевым) нормальным делителем Z, факторгруппа по которому разрешима. Следовательно (см. ч. II, гл. 1, п. 4), сама группа G также разрешима.
и следовательно, по предположению индукции, эта факторгруппа разрешима. Таким образом, группа О обладает разрешимым (дажа абелевым) нормальным делителем Z, факторгруппа по которому разрешима. Следовательно (см. ч. II, гл. 1, п. 4), сама группа G также разрешима.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- I. ОСНОВЫ ТЕОРИИ ГАЛУА
- ГЛАВА 1. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЕЙ
- 2. Некоторые важные типы расширений
- 3. Минимальный многочлен. Строение простых алгебраических расширений
- 4. Алгебраичность конечных расширений
- 5. Строение составных алгебраических расширений
- 6. Составные конечные расширения
- 7. Теорема о том, что составное алгебраическое расширение является простым
- 8. Поле алгебраических чисел
- 9. Композит полей
- ГЛАВА 2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ГРУПП
- 1. Определение группы
- 2. Порядки элементов
- 3. Подгруппы, нормальные делители и факторгруппы
- 4. Гомоморфные отображения
- ГЛABA 3. ТЕОРИЯ ГАЛУА
- 2. Автоморфизмы полей. Группа Галуа
- 3. Порядок группы Галуа
- 4. Соответствие Галуа
- 5. Теорема о сопряженных элементах
- 6. Группа Галуа нормального подполя
- 7. Группа Галуа композита двух полей
- II. РЕШЕНИЕ УРАВНЕНИЙ В РАДИКАЛАХ
- 1. Обобщение теоремы о гомоморфизмах
- 2. Нормальные ряды
- 3. Циклические группы
- 4. Разрешимые и абелевы группы
- 5. Группы Zn и Mn
- ГЛАВА 2. УРАВНЕНИЯ, РАЗРЕШИМЫЕ В РАДИКАЛАХ
- 1. Простые радикальные расширения
- 2. Циклические расширения
- 3. Радикальные расширения
- 4. Нормальные поля с разрешимой группой Галуа
- 5. Уравнения, разрешимые в радикалах
- ГЛАВА 3. ПОСТРОЕНИЕ УРАВНЕНИЙ, НЕРАЗРЕШИМЫХ В РАДИКАЛАХ
- 1. Группа Галуа уравнения как группа подстановок
- § 2. Разложение подстановок в произведение циклов
- 3. Четные подстановки. Знакопеременная группа
- 4. Строение знакопеременной и симметрической групп
- 5. Пример уравнения с симметрической группой Галуа
- 6. Обсуждение полученных результатов
- ГЛАВА 4. НЕРАЗРЕШИМОСТЬ В РАДИКАЛАХ ОБЩЕГО УРАВНЕНИЯ СТЕПЕНИ n >= 5
- 1. Поле формальных степенных рядов
- 2. Поле дробностепенных рядов
- 3. Группа Галуа общего уравнения степени n
- 4. Решение уравнений низших степеней
- III. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ГАЛУА
- ГЛАВА 1. ПРАКТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ГРУПП ГАЛУА УРАВНЕНИЙ
- 2. Сопряженные группы подстановок
- 3. Вычисление группы Галуа произвольного многочлена
- 4. Пример: уравнения, группы Галуа которых содержатся в знакопеременной группе
- 5. Уравнения третьей и четвертой степени
- ГЛАВА 2. УРАВНЕНИЯ ПЯТОЙ СТЕПЕНИ
- 1. Транзитивные группы подстановок
- 2. Транзитивные группы простой степени
- 3. Транзитивные группы пятой степени
- 4. Вычисление группы Галуа неприводимого уравнения пятой степени
- 5. Определяющий многочлен для метациклической группы
- 6. Случай уравнений в нормальном виде
- 7. Уравнения пятой степени, разрешимые в радикалах
- 8. Приведение уравнения пятой степени к нормальному виду
- ГЛАВА 3. РЕШЕНИЕ УРАВНЕНИЙ В НЕПРИВОДИМЫХ РАДИКАЛАХ
- 2. Сведение основной теоремы к двум частным случаям
- 3. Доказательство теоремы А
- 4. Мультипликативная группа классов по примарному модулю
- 6. Группы Галуа примарных круговых расширений
- 6. Доказательство теоремы В
- ГЛАВА 4. УРАВНЕНИЯ ДЕЛЕНИЯ КРУГА
- 1. Строение полей деления круга простого показателя
- 2. Решение уравнений деления круга
- 3. Прием Гаусса
- 4. Уравнение деления круга на 17 частей
- ГЛАВА 5. ПОСТРОЕНИЯ ЦИРКУЛЕМ И ЛИНЕЙКОЙ
- 2. Примарные группы
- 3. Пифагоровы расширения
- 4. Некоторые конкретные задачи на построение