| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Преобразование скоростей
Главное отличие принципа относительности Эйнштейна от принципа относительности Ньютона заключается в том, что законы преобразований, связывающих координаты и времена в системах, движущихся относительно друг друга, различны. Правильный закон преобразований (Лоренца) таков:
 (16.1)
(16.1)
Эти
уравнения отвечают сравнительно простому случаю, когда наблюдатели движутся
относительно друг друга вдоль общей оси ![]() . Конечно, мыслимы и другие
направления движения, но самое общее преобразование Лоренца выглядит довольно
сложно: в нем перемешаны все четыре числа. Мы и впредь будем пользоваться этой
простой формулой, так как она содержит в себе все существенные черты теории
относительности.
. Конечно, мыслимы и другие
направления движения, но самое общее преобразование Лоренца выглядит довольно
сложно: в нем перемешаны все четыре числа. Мы и впредь будем пользоваться этой
простой формулой, так как она содержит в себе все существенные черты теории
относительности.
Рассмотрим
теперь дальнейшие следствия этого преобразования. Прежде всего интересно
разрешить эти уравнения относительно ![]() . Это система четырех линейных
уравнений для четырех неизвестных, и их можно решить - выразить
. Это система четырех линейных
уравнений для четырех неизвестных, и их можно решить - выразить ![]() через
через ![]() . Результат этот
потому интересен, что он говорит нам, как «покоящаяся» система координат
выглядит с точки зрения «движущейся». Ясно, что из-за относительности движения
и постоянства скорости тот, кто «движется», может, если пожелает, счесть себя
неподвижным, другого - движущимся. А поскольку он движется в обратную сторону,
то получит то же преобразование, но с противоположным знаком у скорости. Это в
точности то, что дает и прямое решение системы, так что все сходится. Вот если
бы не сошлось, было бы от чего встревожиться!
. Результат этот
потому интересен, что он говорит нам, как «покоящаяся» система координат
выглядит с точки зрения «движущейся». Ясно, что из-за относительности движения
и постоянства скорости тот, кто «движется», может, если пожелает, счесть себя
неподвижным, другого - движущимся. А поскольку он движется в обратную сторону,
то получит то же преобразование, но с противоположным знаком у скорости. Это в
точности то, что дает и прямое решение системы, так что все сходится. Вот если
бы не сошлось, было бы от чего встревожиться!
 (16.2)
(16.2)
Теперь займемся интересным вопросом о сложении скоростей в теории относительности. Напомним, что первоначально загадка состояла в том, что свет проходит 300000 км/сек во всех системах, даже если они движутся друг относительно друга. Это - частный случай более общей задачи. Приведем пример. Пусть предмет внутри космического корабля движется вперед со скоростью 200000 км/сек; скорость самого корабля тоже 200000 км/сек. С какой скоростью перемещается предмет с точки зрения внешнего наблюдателя? Хочется сказать: 400000 км/сек, но эта цифра уж больно подозрительна: получается скорость большая, чем скорость света! Разве можно себе это представить?
Общая
постановка задачи такова. Пусть скорость тела внутри корабля равна ![]() (с точки зрения
наблюдателя на корабле), а сам корабль имеет скорость
(с точки зрения
наблюдателя на корабле), а сам корабль имеет скорость ![]() по отношению к Земле. Мы
желаем знать, с какой скоростью
по отношению к Земле. Мы
желаем знать, с какой скоростью ![]() это тело движется с точки зрения
земного наблюдателя. Впрочем, это тоже не самый общий случай, потому что
движение происходит в направлении
это тело движется с точки зрения
земного наблюдателя. Впрочем, это тоже не самый общий случай, потому что
движение происходит в направлении ![]() . Могут быть формулы для
преобразования скоростей в направлении
. Могут быть формулы для
преобразования скоростей в направлении ![]() или в любом другом; если они будут
нужны, их всегда можно вывести. Внутри корабля скорость тела равна
или в любом другом; если они будут
нужны, их всегда можно вывести. Внутри корабля скорость тела равна ![]() . Это значит, что
перемещение
. Это значит, что
перемещение ![]() равно
скорости, умноженной на время:
равно
скорости, умноженной на время:
![]() . (16.3)
. (16.3)
Остается
только подсчитать, какие у тела значения ![]() и
и ![]() с точки зрения внешнего наблюдателя,
если
с точки зрения внешнего наблюдателя,
если ![]() и
и ![]() связаны
соотношением (16.3). Подставим (16.3) в (16.2) и получим
связаны
соотношением (16.3). Подставим (16.3) в (16.2) и получим
 . (16.4)
. (16.4)
Но
здесь ![]() выражено
через
выражено
через ![]() . А
скорость с точки зрения внешнего наблюдателя - это «его» расстояние, деленное
на «его» время, а не на время другого наблюдателя! Значит, надо и время подсчитать
с его позиций
. А
скорость с точки зрения внешнего наблюдателя - это «его» расстояние, деленное
на «его» время, а не на время другого наблюдателя! Значит, надо и время подсчитать
с его позиций
 . (16.5)
. (16.5)
А
теперь разделим ![]() на
на
![]() . Квадратные
корни сократятся, останется же
. Квадратные
корни сократятся, останется же
![]() . (16.6)
. (16.6)
Это
и есть искомый закон: суммарная скорость не равна сумме скоростей (это привело
бы ко всяким несообразностям), но «подправлена» знаменателем ![]() .
.
Что
же теперь будет получаться? Пусть ваша скорость внутри корабля равна половине
скорости света, а скорость корабля тоже равна половине скорости света. Значит,
и ![]() равно
равно
![]() , и
, и ![]() равно
равно ![]() , но в знаменателе
, но в знаменателе
![]() равно
равно ![]() , так что
, так что
![]() .
.
Выходит
по теории относительности, что ![]() и
и ![]() дают не 1, а
дают не 1, а ![]() . Небольшие скорости,
конечно, можно складывать, как обычно, потому что, пока скорости по сравнению
со скоростью света малы, о знаменателе
. Небольшие скорости,
конечно, можно складывать, как обычно, потому что, пока скорости по сравнению
со скоростью света малы, о знаменателе ![]() можно забыть, но на больших
скоростях положение меняется.
можно забыть, но на больших
скоростях положение меняется.
Возьмем
предельный случай. Положим, что человек на борту корабля наблюдает, как
распространяется свет. Тогда ![]() . Что обнаружит земной наблюдатель?
Ответ будет такой:
. Что обнаружит земной наблюдатель?
Ответ будет такой:
![]() .
.
Значит, если что-то движется со скоростью света внутри корабля, то, с точки зрения стороннего наблюдателя, скорость не изменится, она по-прежнему будет равна скорости света! Это именно то, ради чего в первую очередь предназначал Эйнштейн свою теорию относительности.
Конечно,
бывает, что движение тела не совпадает по направлению с равномерным движением
корабля. Например, тело движется «вверх» со скоростью ![]() по отношению к кораблю, а
корабль движется «горизонтально». Проделывая такие же манипуляции (только
по отношению к кораблю, а
корабль движется «горизонтально». Проделывая такие же манипуляции (только ![]() надо заменить на
надо заменить на ![]() ), получаем
), получаем
![]() ,
,
так
что при ![]()
 . (16.7)
. (16.7)
Итак,
боковая скорость тела уже не ![]() , a
, a ![]() . Этот результат мы получили,
пользуясь формулами преобразований. Но он вытекает и прямо из принципа
относительности по следующей причине (всегда бывает полезно докопаться до
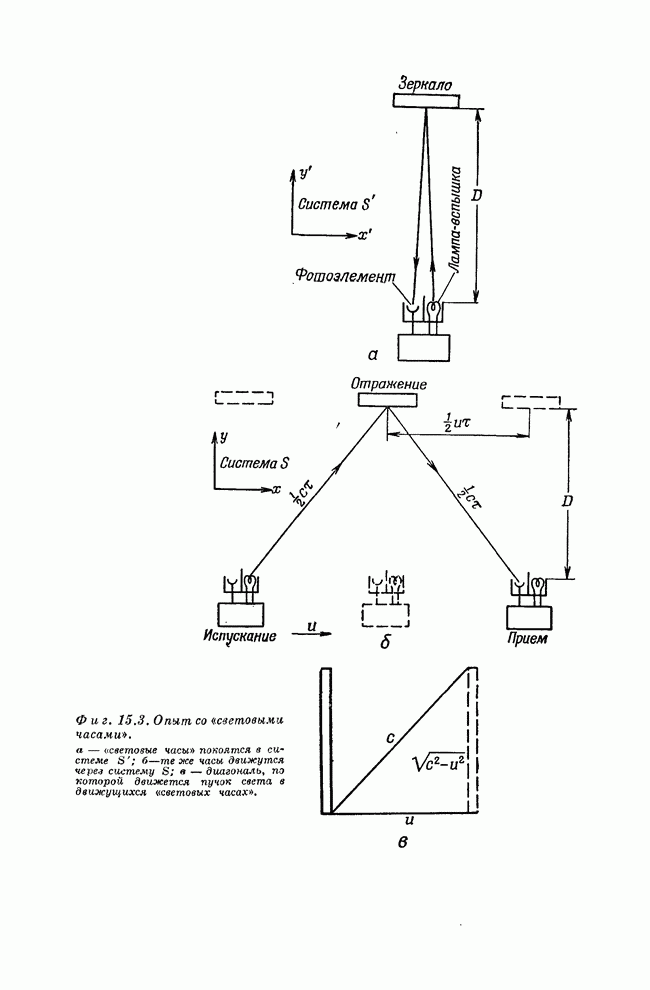
первоначальной причины). Мы уже раньше рассуждали (см. фиг. 15.3) о том, как
могут работать движущиеся часы; свет кажется распространяющимся наискось со
скоростью
. Этот результат мы получили,
пользуясь формулами преобразований. Но он вытекает и прямо из принципа
относительности по следующей причине (всегда бывает полезно докопаться до
первоначальной причины). Мы уже раньше рассуждали (см. фиг. 15.3) о том, как
могут работать движущиеся часы; свет кажется распространяющимся наискось со
скоростью ![]() в
неподвижной системе, в то время как в движущейся системе он просто движется
вертикально с той же скоростью. Мы нашли, что вертикальная компонента скорости
в неподвижной системе меньше скорости света на множитель
в
неподвижной системе, в то время как в движущейся системе он просто движется
вертикально с той же скоростью. Мы нашли, что вертикальная компонента скорости
в неподвижной системе меньше скорости света на множитель ![]() [см. уравнение (15.3)].
Пусть теперь материальная частица движется в тех же «часах» взад-вперед со
скоростью, равной
[см. уравнение (15.3)].
Пусть теперь материальная частица движется в тех же «часах» взад-вперед со
скоростью, равной ![]() скорости света (фиг. 16.1). Пока
частица пройдет туда и обратно, свет пройдет этот путь ровно
скорости света (фиг. 16.1). Пока
частица пройдет туда и обратно, свет пройдет этот путь ровно ![]() раз (
раз (![]() - целое число).
Значит, каждое тиканье «часов с частицей» совпадет с
- целое число).
Значит, каждое тиканье «часов с частицей» совпадет с ![]() -м тиканьем «световых
часов». Этот факт должен остаться верным и тогда, когда тело движется, потому
что физическое явление совпадения остается совпадением в любой системе. Ну а
поскольку скорость
-м тиканьем «световых
часов». Этот факт должен остаться верным и тогда, когда тело движется, потому
что физическое явление совпадения остается совпадением в любой системе. Ну а
поскольку скорость ![]() меньше скорости света, то скорость
меньше скорости света, то скорость ![]() частицы должна
быть меньше соответствующей скорости в том же отношении (с квадратным корнем)!
Вот почему в любой вертикальной скорости появляется корень.
частицы должна
быть меньше соответствующей скорости в том же отношении (с квадратным корнем)!
Вот почему в любой вертикальной скорости появляется корень.

Фиг. 16.1. Траектории светового луча и частицы внутри движущихся часов.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 1. Принцип относительности
- § 2. Преобразование Лоренца
- § 3. Опыт Майкельсона-Морли
- § 4. Преобразование времени
- § 5. Лоренцево сокращение
- § 6. Одновременность
- § 7. Четырехвекторы
- § 8. Релятивистская динамика
- § 9. Связь массы и энергии
- Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС
- § 1. Относительность и «философы»
- § 2. Парадокс близнецов
- § 3. Преобразование скоростей
- § 4. Релятивистская масса
- § 5. Релятивистская энергия
- Глава 17. ПРОСТРАНСТВО-ВРЕМЯ
- § 1. Геометрия пространства-времени
- § 2. Пространственно-временные интервалы
- § 3. Прошедшее, настоящее, будущее
- § 4. Еще о четырехвекторах
- § 5. Алгебра четырехвекторов
- Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ
- § 1. Центр масс
- § 2. Вращение твердого тела
- § 3. Момент количества движения
- § 4. Закон сохранения момента количества движения
- Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ
- § 1. Свойства центра масс
- § 2. Положение центра масс
- § 3. Вычисление момента инерции
- § 4. Кинетическая энергия вращения
- Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ
- § 1. Моменты сил в трехмерном пространстве
- § 2. Уравнения вращения в векторном виде
- § 3. Гироскоп
- § 4. Момент количества движения твердого тела
- Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- § 1. Линейные дифференциальные уравнения
- § 2. Гармонический осциллятор
- § 3. Гармоническое движение и движение по окружности
- § 4. Начальные условия
- § 5. Колебания под действием внешней силы
- Глава 22. АЛГЕБРА
- § 1. Сложение и умножение
- § 2. Обратные операции
- § 3. Шаг в сторону и обобщение
- § 4. Приближенное вычисление иррациональных чисел
- § 5. Комплексные числа
- § 6. Мнимые экспоненты
- Глава 23. РЕЗОНАНС
- § 1. Комплексные числа и гармоническое движение
- § 2. Вынужденные колебания с торможением
- § 3. Электрический резонанс
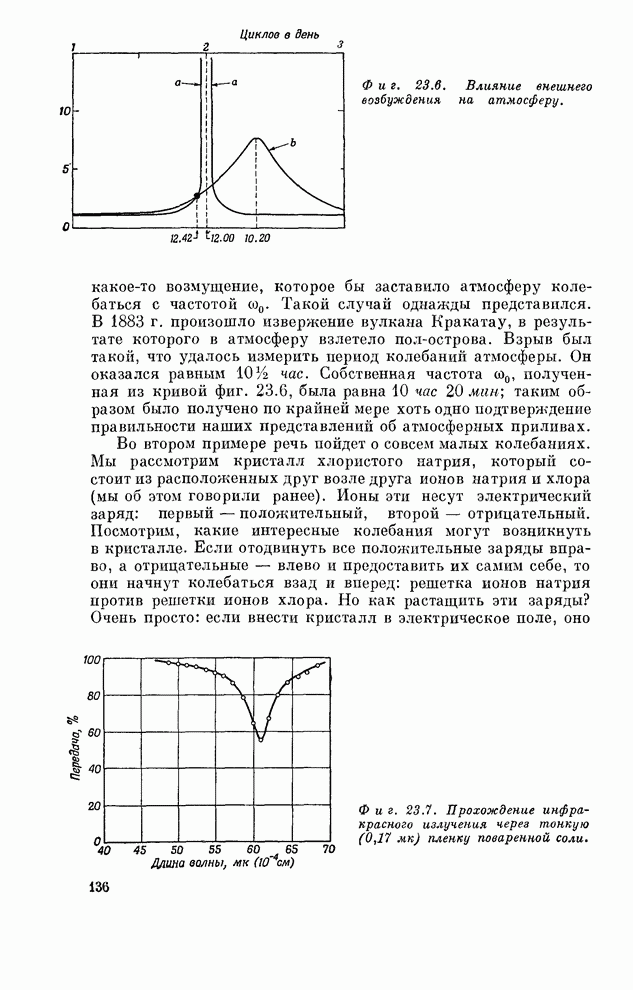
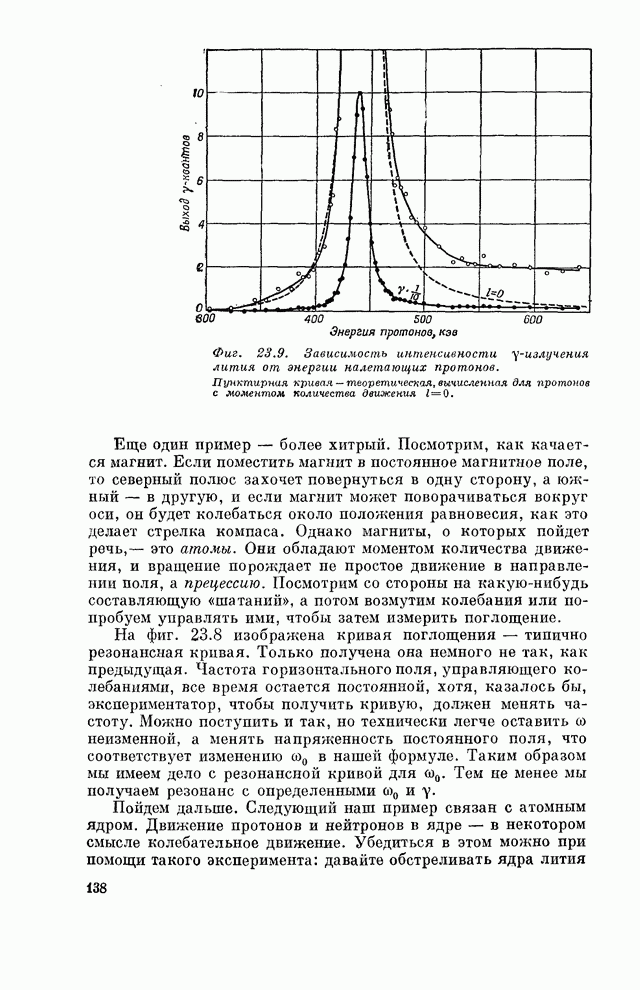
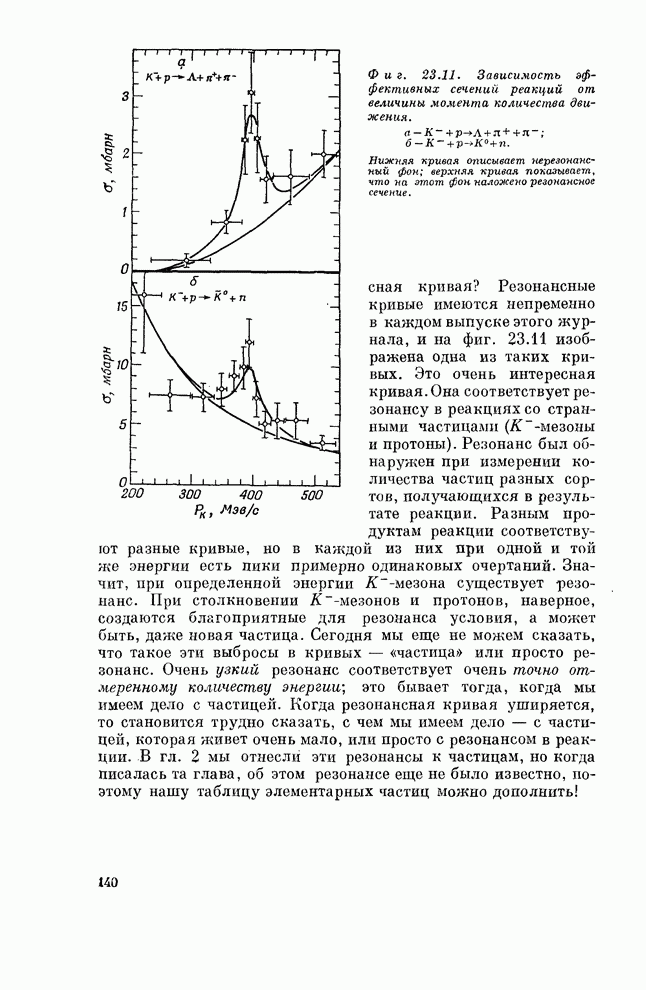
- § 4. Резонанс в природе
- Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ
- § 1. Энергия осциллятора
- § 2. Затухающие колебания
- § 3. Переходные колебания в электрических цепях
- Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР
- § 1. Линейные дифференциальные уравнения
- § 2. Суперпозиция решений
- § 3. Колебания в линейных системах
- § 4. Аналогии в физике
- § 5. Последовательные и параллельные сопротивления