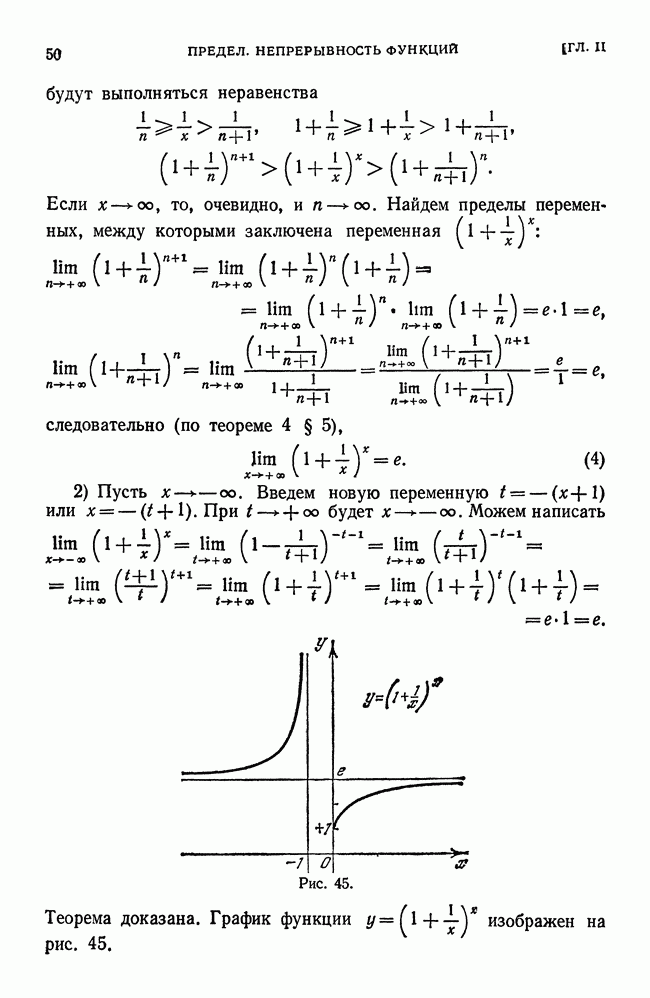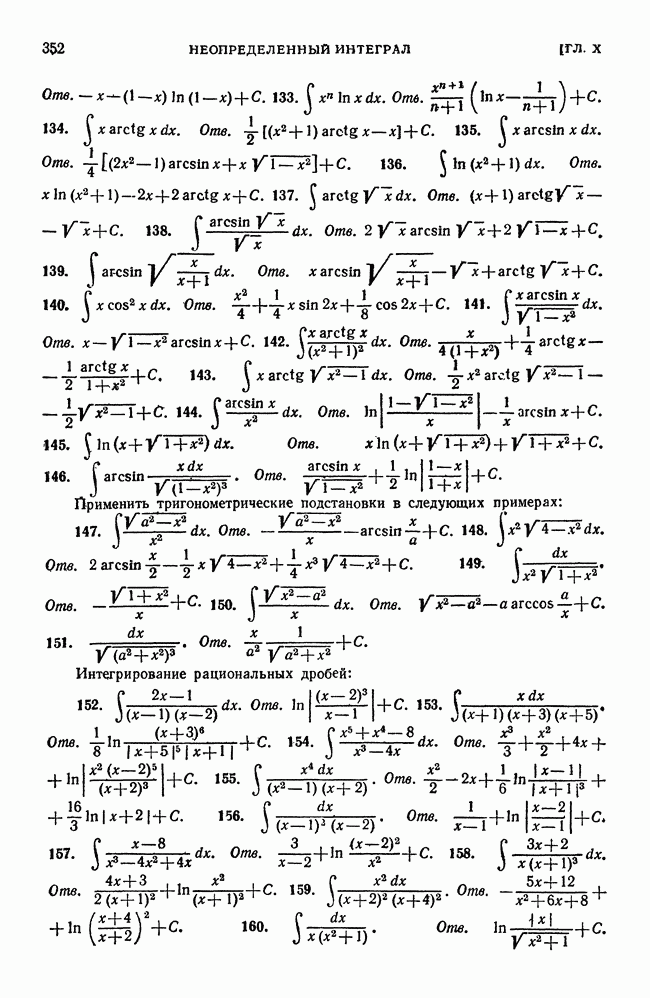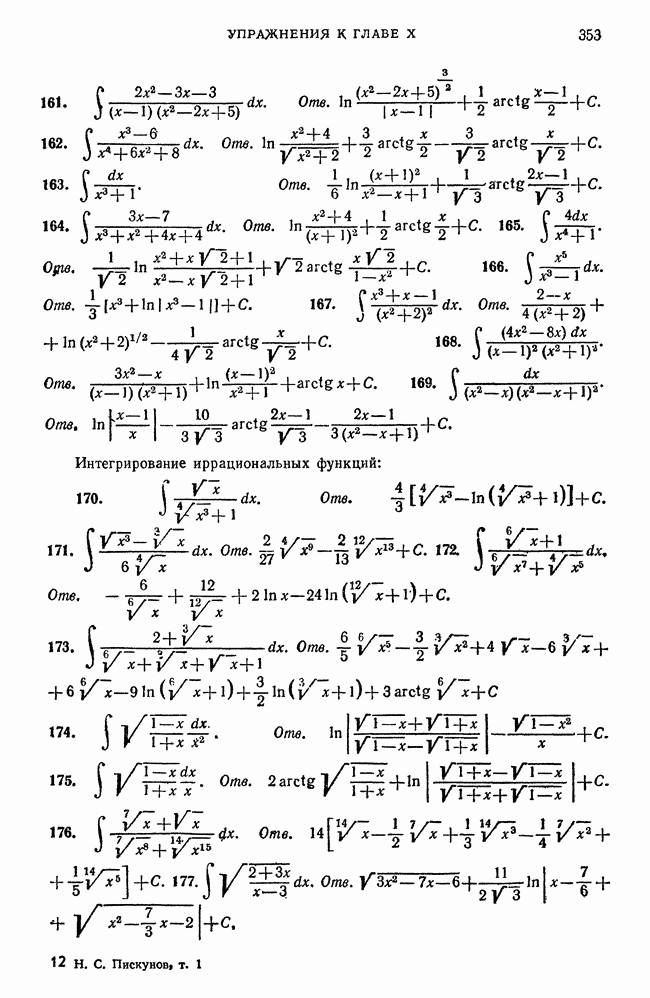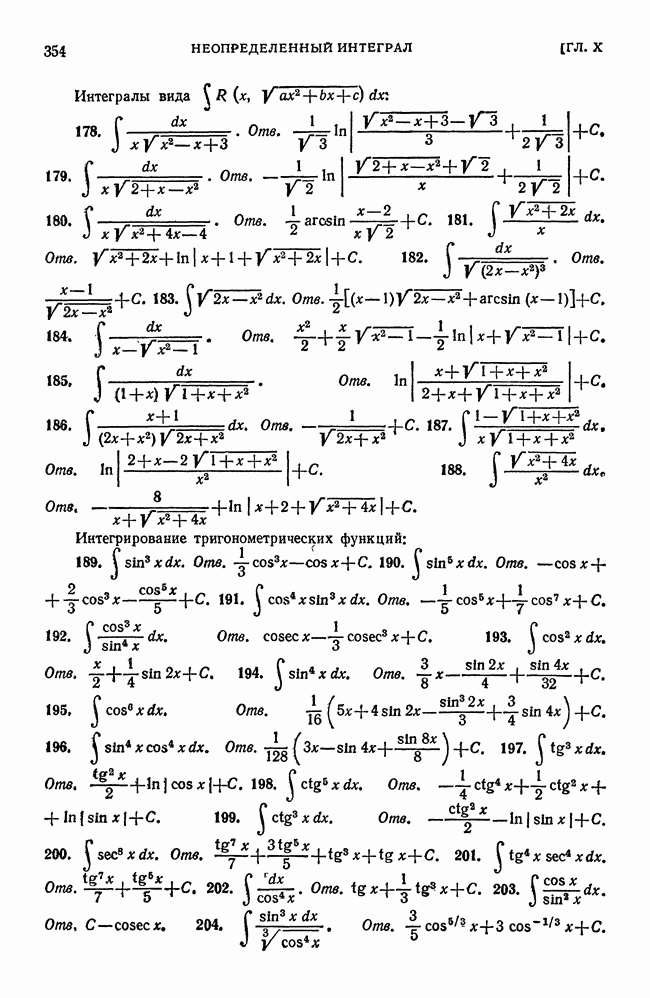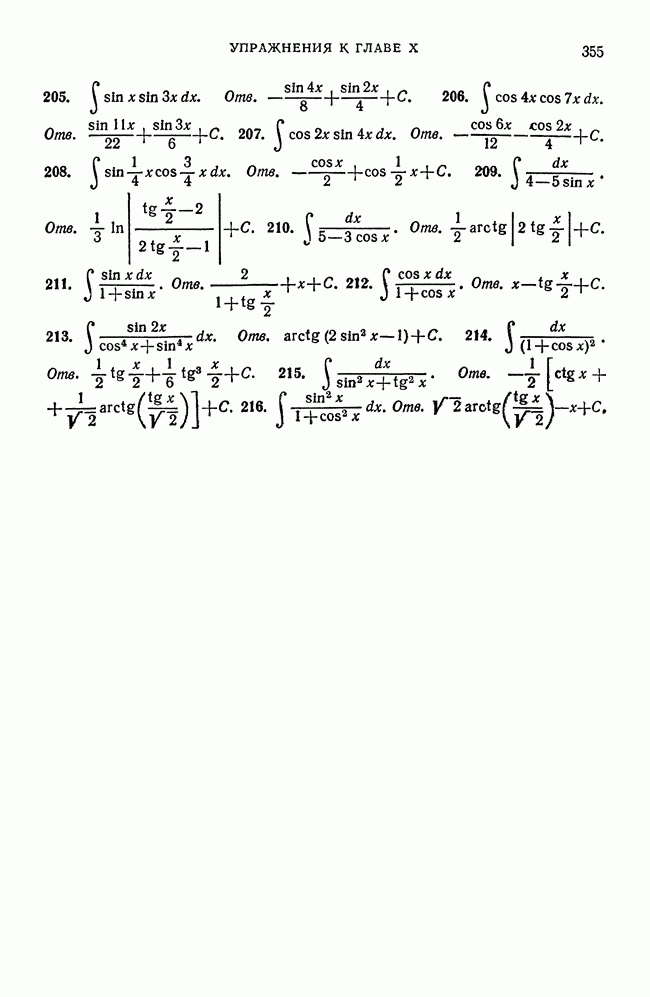| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 4. Бесконечно малые и их основные свойства
В этом параграфе будем рассматривать функции, стремящиеся к нулю при некотором характере изменения, аргумента.
Определение. Функция  называется бесконечно малой при
называется бесконечно малой при  или при
или при  если
если  или
или  .
.
Из определения предела следует, что если, например,  то это значит, что для любого наперед заданного произвольно малого положительного
то это значит, что для любого наперед заданного произвольно малого положительного  найдется
найдется  такое, что для всех
такое, что для всех  удовлетворяющих условию
удовлетворяющих условию  будет удовлетворяться условие
будет удовлетворяться условие 
Пример 1. Функция  есть бесконечно малая при
есть бесконечно малая при  , так как
, так как 
Пример 2. Функция  есть бесконечно малая при
есть бесконечно малая при  пример 3 § 2).
пример 3 § 2).
Установим важное для дальнейшего соотношение:
Теорема 1. Если функция y = f(x) представляется в виде суммы постоянного числа b и бесконечно малой а:

то

Обратно, если  то можно написать
то можно написать  , где а — бесконечно малая.
, где а — бесконечно малая.
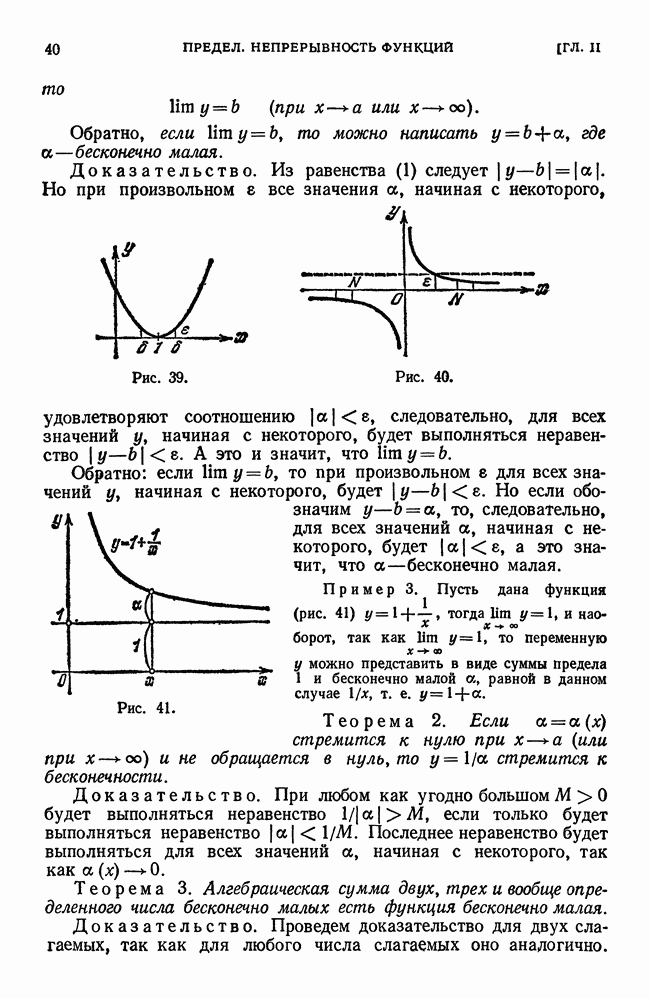
Доказательство. Из равенства (1) следует  Но при произвольном
Но при произвольном  все значения а, начиная с некоторого, удовлетворяют соотношению
все значения а, начиная с некоторого, удовлетворяют соотношению  следовательно, для всех значений у, начиная с некоторого, будет выполняться неравенство
следовательно, для всех значений у, начиная с некоторого, будет выполняться неравенство  это и значит, что
это и значит, что 

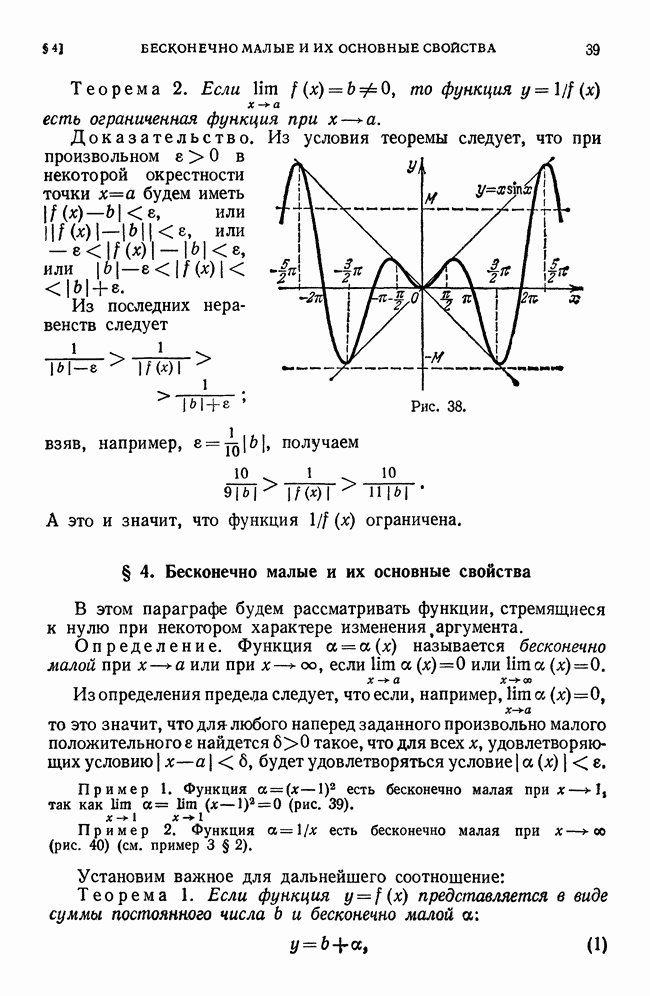
Рис. 39.

Рис. 40.
Обратно: если  , то при произвольном
, то при произвольном  для всех значений у, начиная с некоторого, будет
для всех значений у, начиная с некоторого, будет  Но если обозначим
Но если обозначим  , то, следовательно, для всех значений а, начиная с некоторого, будет
, то, следовательно, для всех значений а, начиная с некоторого, будет  а это значит, что а — бесконечно малая.
а это значит, что а — бесконечно малая.
Пример 3. Пусть дана функция (рис. 41)  , тогда
, тогда  и наоборот, так как
и наоборот, так как  то переменную у можно представить в виде суммы предела 1 и бесконечно малой а, равной в данном случае
то переменную у можно представить в виде суммы предела 1 и бесконечно малой а, равной в данном случае  а.
а.

Рис. 41.
Теорема 2. Если  стремится к нулю при
стремится к нулю при  (или при
(или при  ) и не обращается в нуль, то
) и не обращается в нуль, то  стремится к бесконечности.
стремится к бесконечности.
Доказательство. При любом как угодно большом М > 0 будет выполняться неравенство  если только будет выполняться неравенство
если только будет выполняться неравенство  . Последнее неравенство будет выполняться для всех значений а, начиная с некоторого, так как а
. Последнее неравенство будет выполняться для всех значений а, начиная с некоторого, так как а 
Теорема 3. Алгебраическая сумма двух, трех и вообще определенного числа бесконечно малых есть функция бесконечно малая.
Доказательство. Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно аналогично.
Пусть и  где
где  Докажем, что при произвольном как угодно малом
Докажем, что при произвольном как угодно малом  найдется
найдется  такое, что при удовлетворении неравенства
такое, что при удовлетворении неравенства  будет выполняться неравенство
будет выполняться неравенство  Так как а
Так как а  есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое  что в окрестности с центром в точке а и радиусом будет
что в окрестности с центром в точке а и радиусом будет

Так как  есть бесконечно малая, то найдется такое
есть бесконечно малая, то найдется такое  , что в окрестности с центром в точке а и радиусом
, что в окрестности с центром в точке а и радиусом  будет
будет

Возьмем  равным меньшей из величин
равным меньшей из величин  тогда в окрестности точки а с радиусом
тогда в окрестности точки а с радиусом  будут выполняться неравенства
будут выполняться неравенства  Следовательно, в этой окрестности будет
Следовательно, в этой окрестности будет

т. е. | и | < е, что и требовалось доказать.
Аналогично приводится доказательство и для случая, когда 

Замечание. В дальнейшем нам придется рассматривать такие суммы бесконечно малых величин, что с уменьшением каждого слагаемого число слагаемых увеличивается. В этом случае утверждение теоремы может оказаться и неверным. Рассмотрим, например,  , где
, где  принимает только целые положительные значения
принимает только целые положительные значения  . Очевидно, что каждое слагаемое при
. Очевидно, что каждое слагаемое при  есть бесконечно малая, но сумма
есть бесконечно малая, но сумма  не есть бесконечно малая.
не есть бесконечно малая.
Теорема 4. Произведение бесконечно малой функции  на ограниченную функцию
на ограниченную функцию  при
при  а
а  есть бесконечно малая величина (функция).
есть бесконечно малая величина (функция).
Доказательство Проведем доказательство для случая  Для некоторого
Для некоторого  найдется такая окрестность точки
найдется такая окрестность точки  , в которой будет удовлетворяться неравенство
, в которой будет удовлетворяться неравенство  . Для всякого
. Для всякого  найдется окрестность, в которой будет выполняться неравенство
найдется окрестность, в которой будет выполняться неравенство  . В меньшей из этих двух окрестностей будет выполняться неравенство
. В меньшей из этих двух окрестностей будет выполняться неравенство

А это и значит, что  бесконечно малая. Для случая
бесконечно малая. Для случая  доказательство проводится аналогично. Из данной теоремы вытекают:
доказательство проводится аналогично. Из данной теоремы вытекают:
Следствие 1. Если  , то
, то  , так как
, так как  есть величина ограниченная. Это справедливо для любого конечного числа множителей.
есть величина ограниченная. Это справедливо для любого конечного числа множителей.
Следствие 2. Если  , то
, то  .
.
Теорема 5. Частное  от деления бесконечно малой величины
от деления бесконечно малой величины  на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Доказательство. Пусть  На основании теоремы 2 § 3 следует, что
На основании теоремы 2 § 3 следует, что  есть величина ограниченная. Поэтому дробь
есть величина ограниченная. Поэтому дробь  есть произведение величины бесконечно малой на величину ограниченную, т. е. величина бесконечно малая.
есть произведение величины бесконечно малой на величину ограниченную, т. е. величина бесконечно малая.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
- ГЛАВА I. ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ
- § 1. Действительные числа.
- § 2. Абсолютная величина действительного числа
- § 3. Переменные и постоянные величины
- § 4. Область изменения переменной величины
- § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина
- § 6. Функция
- § 7. Способы задания функции
- § 8. Основные элементарные функции. Элементарные функции
- § 9. Алгебраические функции
- § 10. Полярная система координат
- Упражнения к главе I
- ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
- § 1. Предел переменной величины. Бесконечно большая переменная величина
- § 2. Предел функции
- § 3. Функция, стремящаяся к бесконечности. Ограниченные функции
- § 4. Бесконечно малые и их основные свойства
- § 5. Основные теоремы о пределах
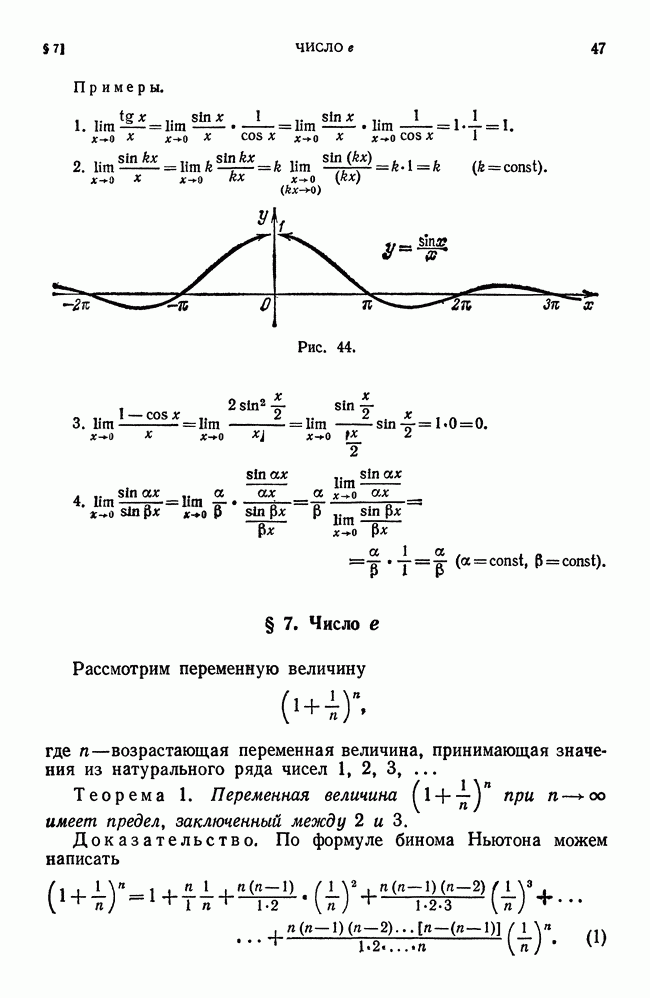
- § 6. Предел функции (sin x)/x при x->0
- § 7. Число e
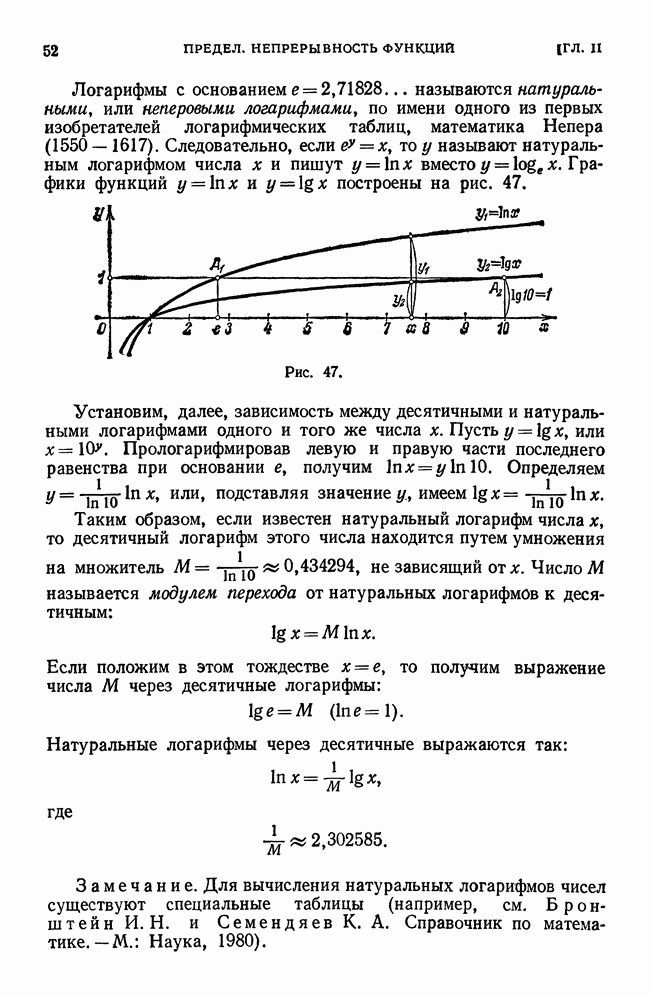
- § 8. Натуральные логарифмы
- § 9. Непрерывность функций
- § 10. Некоторые свойства непрерывных функций
- § 11. Сравнение бесконечно малых
- Упражнения к главе II
- ГЛАВА III. ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
- § 2. Определение производной
- § 3. Геометрическое значение производной
- § 4. Дифференцируемость функций
- § 5. Производная от функции y = x^n при n целом и положительном
- § 6. Производные от функций y = sinx; y = cosx
- § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного
- § 8. Производная логарифмической функции
- § 9. Производная от сложной функции
- § 10. Производные функций y = tgx, y = ctgx, y = ln|x|
- § 11. Неявная функция и ее дифференцирование
- § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции
- § 13. Обратная функция и ее дифференцирование
- § 14. Обратные тригонометрические функции и их дифференцирование
- § 15. Таблица основных формул дифференцирования
- § 16. Параметрическое задание функции
- § 17. Уравнения некоторых кривых в параметрической форме
- § 18. Производная функции, заданной параметрически
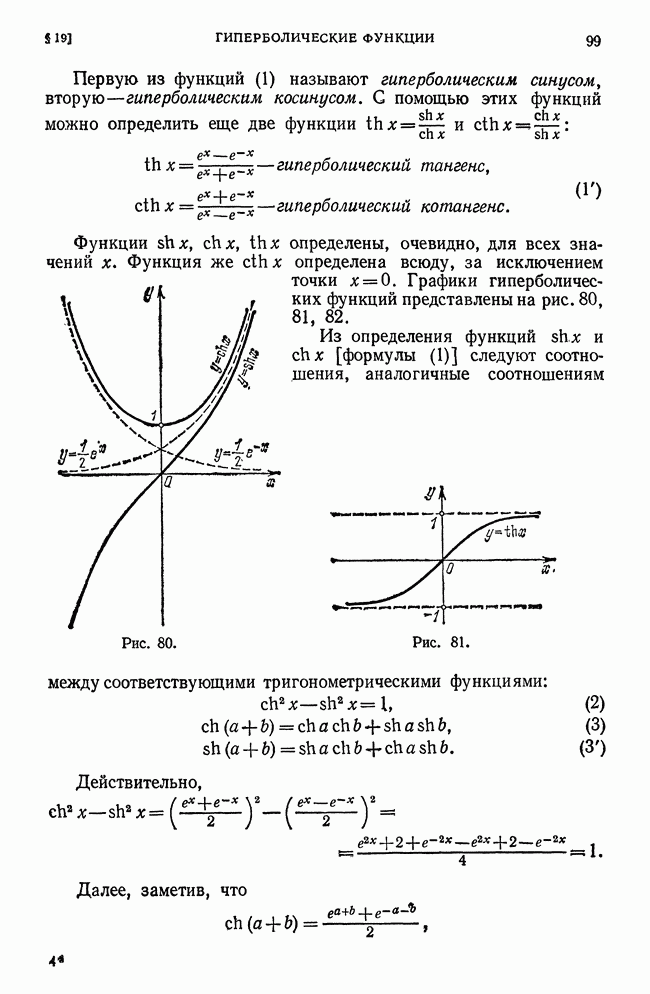
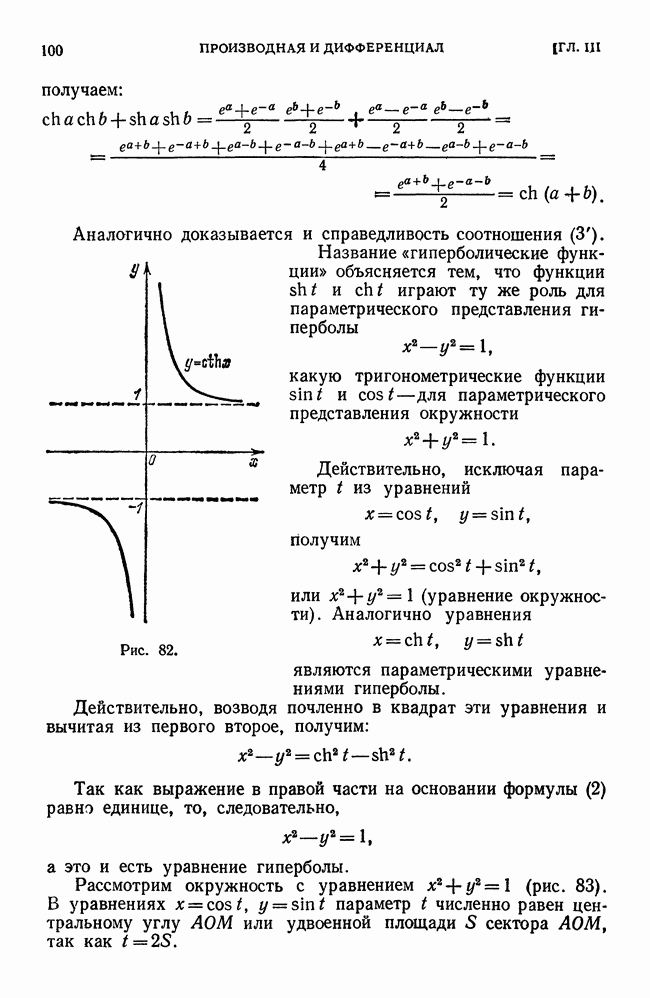
- § 19. Гиперболические функции
- § 20. Дифференциал
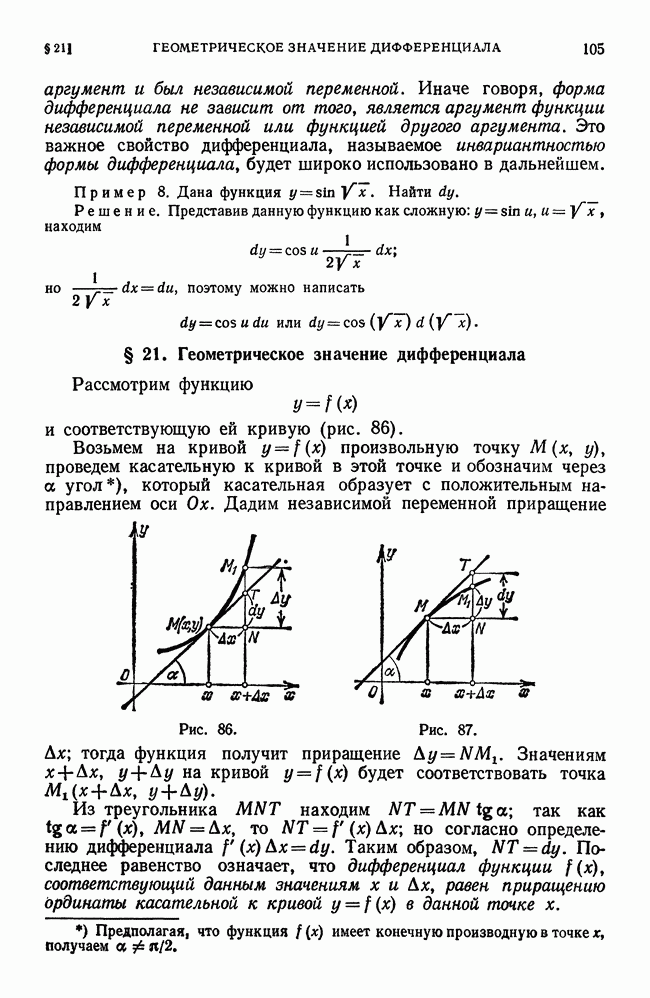
- § 21. Геометрическое значение дифференциала Рассмотрим функцию
- § 22. Производные различных порядков
- § 23. Дифференциалы различных порядков
- § 24. Производные различных порядков от неявных функций и функций, заданных параметрически
- § 25. Механическое значение второй производной
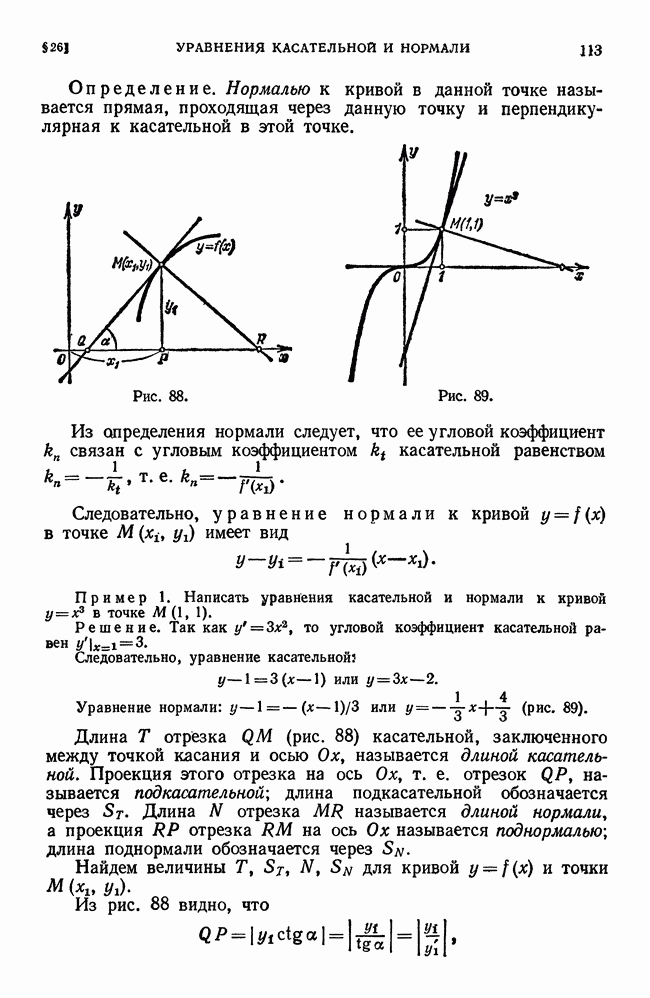
- § 26. Уравнения касательной и нормали. Длины подкасательной и поднормали
- § 27. Геометрическое значение производной радиус-вектора по полярному углу
- Упражнения к главе III
- ГЛАВА IV. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- § 1. Теорема о корнях производной (теорема Ролля)
- § 2. Теорема о конечных приращениях (теорема Лагранжа)
- § 3. Теорема об отношении приращений двух функций (теорема Коши)
- § 4. Предел отношения двух бесконечно малых величин «раскрытие неопределенностей вида 0/0»)
- § 5. Предел отношения двух бесконечно больших величин «раскрытие неопределенностей вида oo/oo»)
- § 6. Формула Тейлора
- § 7. Разложение по формуле Тейлора функций e^x, sin x, cos x
- Упражнения к главе IV
- ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ
- § 2. Возрастание и убывание функции
- § 3. Максимум и минимум функций
- § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной
- § 5. Исследование функции на максимум и минимум с помощью второй производной
- § 6. Наибольшее и наименьшее значения функции на отрезке
- § 7. Применение теории максимума и минимума функций к решению задач
- § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора
- § 9. Выпуклость и вогнутость кривой. Точки перегиба
- § 10. Асимптоты
- § 11. Общий план исследования функций и построения графиков
- § 12. Исследование кривых, заданных параметрически
- Упражнения к главе V
- ГЛАВА VI. КРИВИЗНА КРИВОЙ
- § 1. Длина дуги и ее производная
- § 2. Кривизна
- § 3. Вычисление кривизны
- § 4. Вычисление кривизны линии, заданной параметрически
- § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах
- § 6. Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
- § 7. Свойства эволюты
- § 8. Приближенное вычисление действительных корней уравнения
- Упражнения к главе VI
- ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ
- § 1. Комплексные числа. Исходные определения
- § 2. Основные действия над комплексными числами
- § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа
- § 4. Показательная функция с комплексным показателем и ее свойства
- § 5. Формула Эйлера. Показательная форма комплексного числа
- § 6. Разложение многочлена на множители
- § 7. О кратных корнях многочлена
- § 8. Разложение многочлена на множители в случае комплексных корней
- § 9. Интерполирование. Интерполяционная формула Лагранжа
- § 10. Интерполяционная формула Ньютона
- § 11. Численное дифференцирование
- § 12. О наилучшем приближении функций многочленами. Теория Чебышева
- Упражнения к главе VII
- ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. Определение функции нескольких переменных
- § 2. Геометрическое изображение функции двух переменных
- § 3. Частное и полное приращение функции
- § 4. Непрерывность функции нескольких переменных
- § 5. Частные производные функции нескольких переменных
- § 6. Геометрическая интерпретация частных производных функции двух переменных
- § 7. Полное приращение и полный дифференциал
- § 8. Применение полного дифференциала в приближенных вычислениях
- § 9. Приложение дифференциала к оценке погрешности при вычислениях
- § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции
- § 11. Производная от функции, заданной неявно
- § 12. Частные производные различных порядков
- § 13. Поверхности уровня
- § 14. Производная по направлению
- § 15. Градиент
- § 16. Формула Тейлора для функции двух переменных
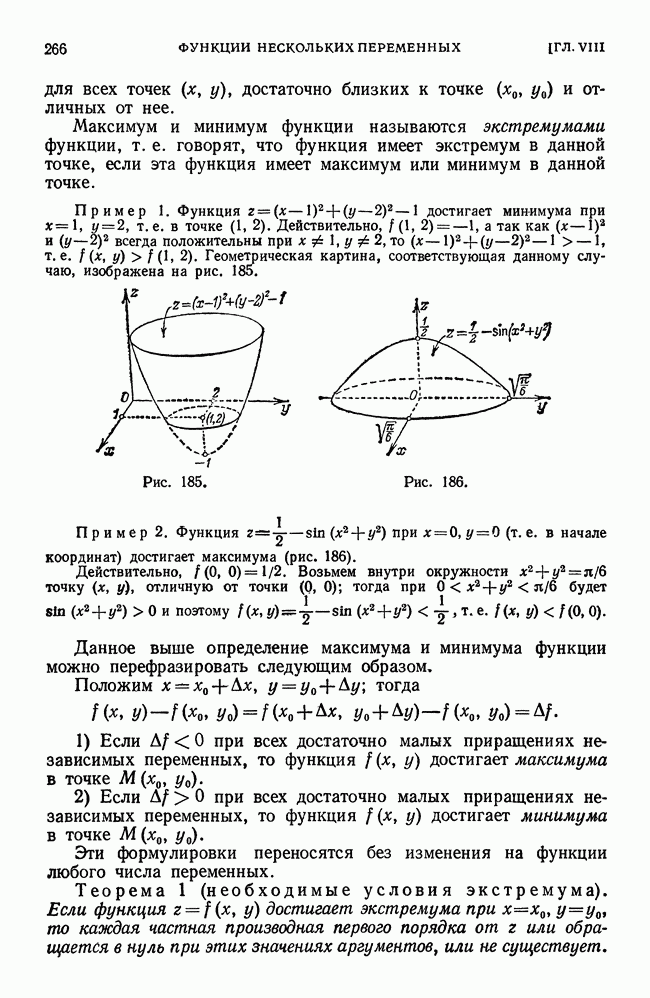
- § 17. Максимум и минимум функции нескольких переменных
- § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы)
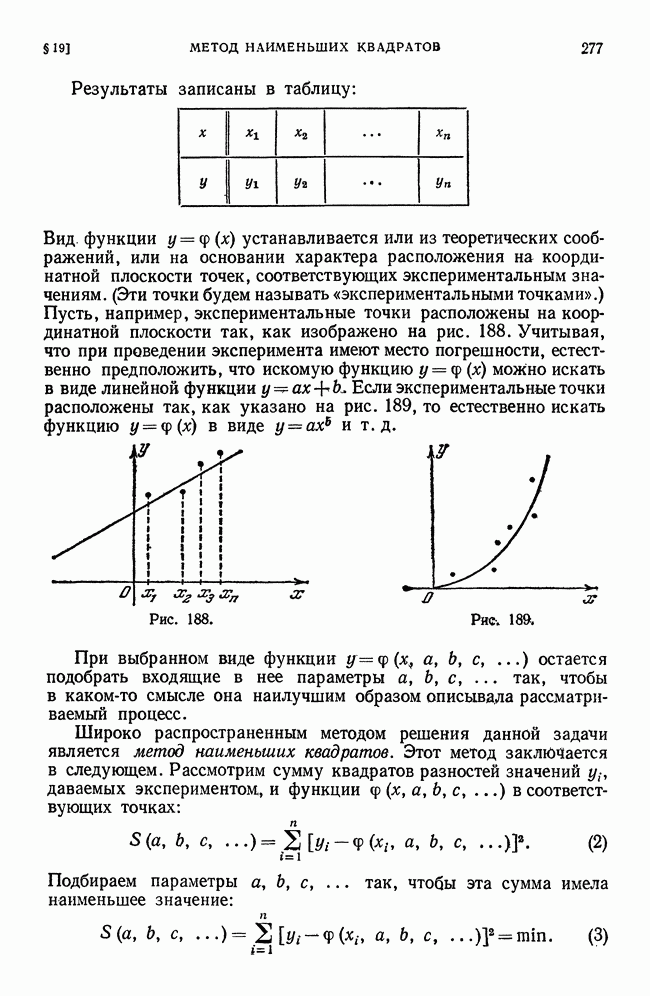
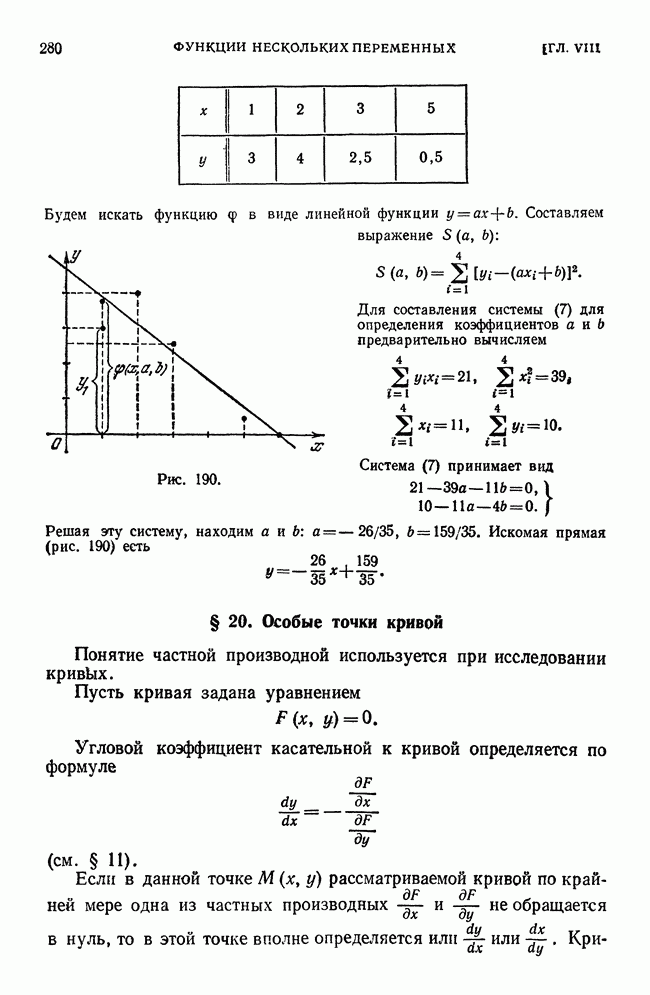
- § 19. Получение функции на основании экспериментальных данных по методу наименьших квадратов
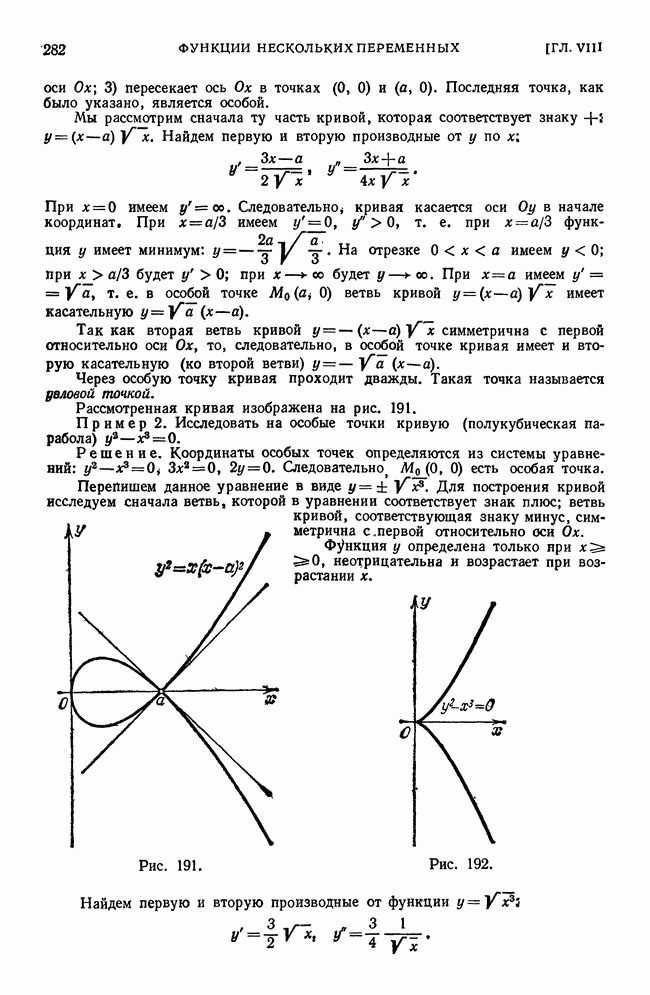
- § 20. Особые точки кривой
- Упражнения к главе VIII
- ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ
- § 1. Уравнения кривой в пространстве
- § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости
- § 3. Правила дифференцирования векторов (векторных функций)
- § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении
- § 5. Соприкасающаяся плоскость. Бинормаль. Кручение.
- § 6. Касательная плоскость и нормаль к поверхности
- Упражнения к главе IX
- ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Первообразная и неопределенный интеграл
- § 2. Таблица интегралов
- § 3. Некоторые свойства неопределенного интеграла
- § 4. Интегрирование методом замены переменной или способом подстановки
- § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен
- § 6. Интегрирование по частям
- § 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- § 8. Разложение рациональной дроби на простейшие
- § 9. Интегрирование рациональных дробей
- § 10. Интегралы от иррациональных функций
- § 11. Интегралы вида …
- § 12. Интегрирование некоторых классов тригонометрических функций
- § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок
- § 14. О функциях, интегралы от которых не выражаются через элементарные функции
- Упражнения к главе X
- ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. Постановка задачи. Нижняя и верхняя интегральные суммы
- § 2. Определенный интеграл. Теорема о существовании определенного интеграла
- § 3. Основные свойства определенного интеграла
- § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница
- § 5. Замена переменной в определенном интеграле
- § 6. Интегрирование по частям
- § 7. Несобственные интегралы
- § 8. Приближенное вычисление определенных интегралов
- § 9. Формула Чебышева
- § 10. Интегралы, зависящие от параметра. Гамма-функция
- § 11. Интегрирование комплексной функции действительной переменной
- Упражнения кглаве XI
- ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. Вычисление площадей в прямоугольных координатах
- § 2. Площадь криволинейного сектора в полярных координатах
- § 3. Длина дуги кривой
- § 4. Вычисление объема тела по площадям параллельных сечений
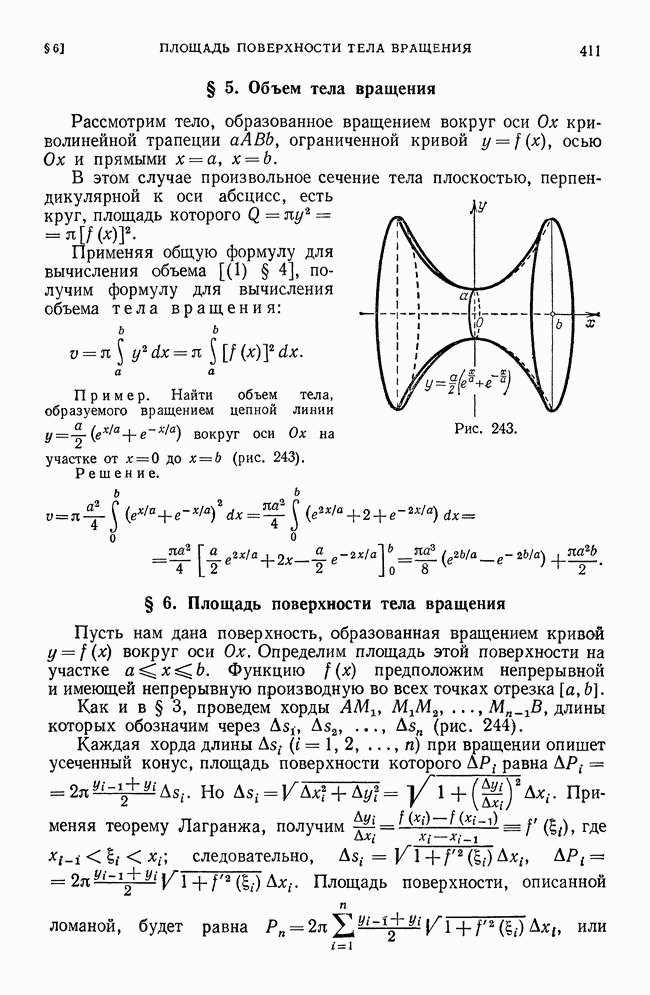
- § 5. Объем тела вращения
- § 6. Площадь поверхности тела вращения
- § 7. Вычисление работы с помощью определенного интеграла
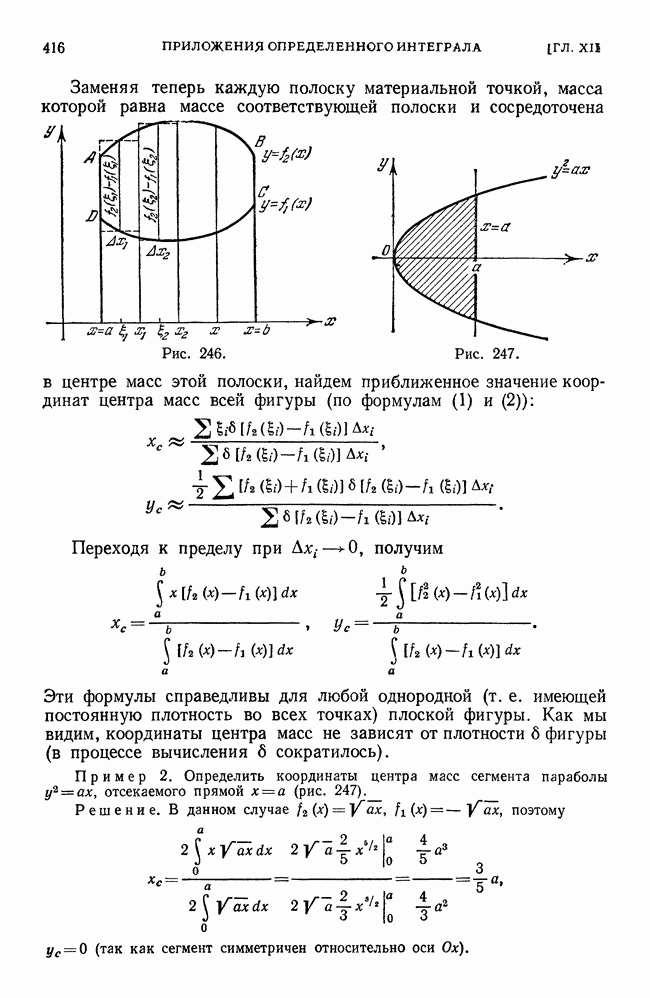
- § 8. Координаты центра масс
- § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла
- Упражнения к главе XII