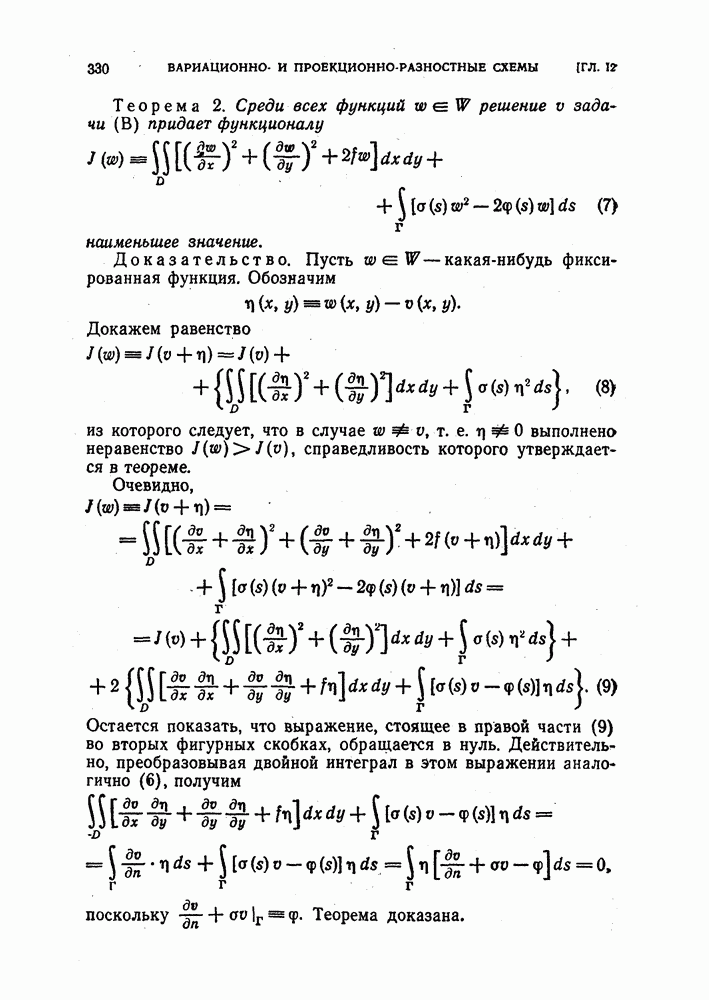| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
В теории краевых задач для аналитических функций, т. е. для решений системы уравнений Коши — Римана, а также для решений более общих систем уравнений с частными производными, применяется метод сингулярных интегральных уравнений. Он состоит в сведении краевых задач к некоторым интегральным уравнениям на границе рассматриваемой области. При этом в дополнение к заданным граничным условиям используются следствия самой системы дифференциальных уравнений — соотношения, которым Должны удовлетворять функции (и их нормальные производные) на границе области, чтобы их можно было доопределить внутри области до некоторого решения соответствующей системы. В случае аналитических функций — это классическое условие Сохоцкого — Племеля, которое возникает при переходе в интегральной формуле Коши

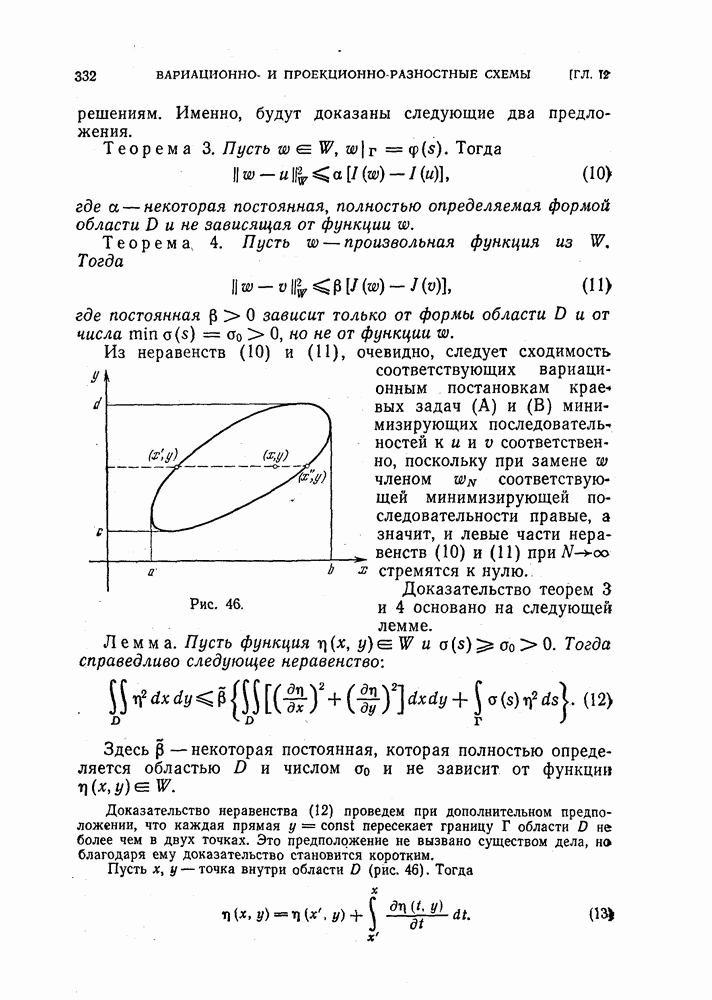
к пределу при стремлении  к границе у. В случае дифференциальных уравнений второго порядка соответствующее условие возникает из формулы Грина, выражающей решение в каждой точке области через значения этого решения и его нормальной производной на границе. Чтобы получить это условие, также надо перейти к пределу при стремлении точки изнутри области к ее границе, воспользовавшись свойствами потенциалов простого и двойного слоев.
к границе у. В случае дифференциальных уравнений второго порядка соответствующее условие возникает из формулы Грина, выражающей решение в каждой точке области через значения этого решения и его нормальной производной на границе. Чтобы получить это условие, также надо перейти к пределу при стремлении точки изнутри области к ее границе, воспользовавшись свойствами потенциалов простого и двойного слоев.
Метод внутренних граничных условий по идее аналогичен описанному методу редукции краевых задач для уравнений с частными производными к интегральным уравнениям на границе. Роль дополнительных граничных условий, аналогичных условию Сохоцкого — Племеля, играют внутренние граничные условия, возникающие из разностного аналога интегральной формулы Коши (или разностного аналога формулы Грина).
1. Класс систем разностных уравнений. Рассматриваются краевые задачи для общих систем разностных уравнений с постоянными коэффициентами, которые в векторной записи имеют вид

где  квадратные матрицы,
квадратные матрицы,  - заданная и
- заданная и  - искомая вектор-функции, К — конечное множество (шаблон). Будем Предполагать, что система (1) удовлетворяет следующему алгебраическому условию: характеристическая матрица
- искомая вектор-функции, К — конечное множество (шаблон). Будем Предполагать, что система (1) удовлетворяет следующему алгебраическому условию: характеристическая матрица

где  - комплексные параметры, не является тождественно по
- комплексные параметры, не является тождественно по  вырожденной:
вырожденной:

Это ограничение естественно: можно показать, что в случае  уравнение (1) имеет решение не при всякой финитной (по
уравнение (1) имеет решение не при всякой финитной (по  ) правой части
) правой части 
2. Фундаментальное решение.
Матричную функцию  назовем фундаментальным решением системы (1), если она однорременно удовлетворяет следующим двум уравнениям:
назовем фундаментальным решением системы (1), если она однорременно удовлетворяет следующим двум уравнениям:

Лемма. Пусть  есть произвольный многочлен от произвольного числа t комплексных аргументов, не обращающийся тождественно в нуль. Тогда можно выбрать радиусы
есть произвольный многочлен от произвольного числа t комплексных аргументов, не обращающийся тождественно в нуль. Тогда можно выбрать радиусы  окружностей
окружностей  так, чтобы выполнялось неравенство
так, чтобы выполнялось неравенство  если
если 
Доказательство проведем индукцией по числу аргументов t. При  число корней
число корней  конечно и утверждение очевидно. Считая, что утверждение доказано для
конечно и утверждение очевидно. Считая, что утверждение доказано для  , установим его в случае
, установим его в случае  . Многочлен
. Многочлен  расположим по степеням
расположим по степеням 

где M — некоторое натуральное число и  не обращается тождественно в нуль. Выберем
не обращается тождественно в нуль. Выберем  так, чтобы
так, чтобы  при
при  Это возможно по предположению индукции. Выбирая теперь
Это возможно по предположению индукции. Выбирая теперь  достаточно большим, можно добиться, чтобы при
достаточно большим, можно добиться, чтобы при  выполнялось неравенство
выполнялось неравенство  ,
,
Теорема 1. Матрица  определяемая равенством
определяемая равенством

является фундаментальным решением.
Здесь  в соответствии с леммой выбраны так, чтобы
в соответствии с леммой выбраны так, чтобы  , если
, если 
Доказательство получается непосредственной проверкой. Учитывая свойства вычетов, получаем

3. Граница сеточной области.
Рассмотрим уравнение (1) на некотором ограниченном множестве

где  — произвольная сеточная область определения правой части
— произвольная сеточная область определения правой части  Тогда область определения решения
Тогда область определения решения  есть множество D, которое пробегает точка
есть множество D, которое пробегает точка
 если n и к пробегают независимо
если n и к пробегают независимо  и К соответственно. Сопоставим каждому
и К соответственно. Сопоставим каждому  подмножество
подмножество  множества К, состоящее из всех тех
множества К, состоящее из всех тех  , для которых
, для которых  Границей Г назовем совокупность всех тех точек
Границей Г назовем совокупность всех тех точек  для которых
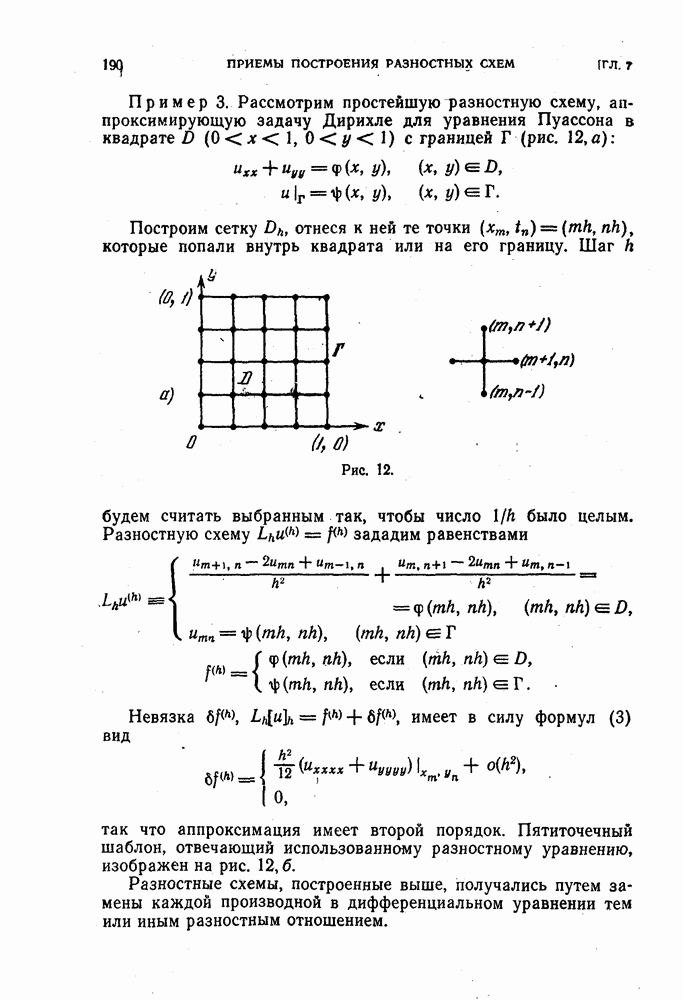
для которых  непусто. Например, для простейшего разностного аналога уравнения Пуассона
непусто. Например, для простейшего разностного аналога уравнения Пуассона

множество  состоит из тех точек
состоит из тех точек  которые попали внутрь квадрата
которые попали внутрь квадрата 

Рис. 57.
Множество К — из пяти векторов  Множество D — совокупность всех целочисленных точек квадрата
Множество D — совокупность всех целочисленных точек квадрата  кроме четырех угловых
кроме четырех угловых  Граница Г состоит из двух слоев точек, отмеченных на рис. 57 крестиками.
Граница Г состоит из двух слоев точек, отмеченных на рис. 57 крестиками.
4. Разностные аналоги интегральных формул Коши и типа Коши.
Лемма. Пусть  — произвольная матрица-функция, для которой имеет смысл умножение справа на квадратную матрицу порядка
— произвольная матрица-функция, для которой имеет смысл умножение справа на квадратную матрицу порядка  , определенная на всей целочисленной сетке. Справедливо следующее тождество:
, определенная на всей целочисленной сетке. Справедливо следующее тождество:

Доказательство. Вектор-функцию  можно записать в виде
можно записать в виде

Левая и правая части тождества (7) линейно зависят от и. Поэтому для доказательства достаточно проверить справедливость тождества (7) для вектор-функции

при каждом фиксированном 

Теорема 2. Пусть  , — произвольное решение уравнения
, — произвольное решение уравнения  произвольное фундаментальное решение. Тогда справедлива формула
произвольное фундаментальное решение. Тогда справедлива формула

Доказательство. Помножим обе части равенства (6) слева на матрицу  и просуммируем по всем
и просуммируем по всем  . Воспользовавшись тождеством (7), а затем равенством (4), получим формулу (8).
. Воспользовавшись тождеством (7), а затем равенством (4), получим формулу (8).
Следствие. Каждое решение  уравнения (6) полностью определяется своими значениями на Г и восстанавливается по этим, значениям по формуле (8).
уравнения (6) полностью определяется своими значениями на Г и восстанавливается по этим, значениям по формуле (8).
Теорема 3. Пусть  произвольная вектор-функция размерности
произвольная вектор-функция размерности  , определенная на Г, и пусть
, определенная на Г, и пусть  произвольное фундаментальное решение. Тогда формула
произвольное фундаментальное решение. Тогда формула

задает некоторое решение уравнения (6).
Доказательство. Применим оператор L к вектор-функции  определенной формулой (9):
определенной формулой (9):

Вычислим правую часть. В силу (4) имеем

Но в силу определения множества  точка
точка  не принадлежит
не принадлежит  так что первое слагаемое в правой части формулы (10) есть нулевой вектор. Второе слагаемое есть, очевидно,
так что первое слагаемое в правой части формулы (10) есть нулевой вектор. Второе слагаемое есть, очевидно,  так что
так что  и теорема доказана.
и теорема доказана.
Равенство (8) аналогично интегральной формуле Коши для аналитических функций  в ограниченной области d с границей у:
в ограниченной области d с границей у:

При этом роль аналитических функций, границы области и ядра Коши - играют соответственно решения  задачи (6), граница
задачи (6), граница  точной области D и выражение
точной области D и выражение  учитывающее через множество
учитывающее через множество  по которому ведется суммирование, структуру границы вблизи точки
по которому ведется суммирование, структуру границы вблизи точки 
Формулу (9) в таком случае естественно сравнить с интегральной формулой типа Коши. Формула (8) аналогична также формуле Грина для уравнения Лапласа.
Подчеркнем, однако, следующее существенное различие между формулами (11) и (8): интегральная формула Коши справедлива только строго внутри области d, а разностная формула (8)- всюду на D, включая точки границы Г.
Аналогичное различие имеется также между формулой (9) и формулой Грина.
5. Внутренние граничные условия.
Теорема 4. Пусть  - какое-нибудь фундаментальное решение уравнения (1). Для того чтобы заданную на Г вектор-функцию
- какое-нибудь фундаментальное решение уравнения (1). Для того чтобы заданную на Г вектор-функцию  можно было доопределить всюду в ограниченной сеточной области D до некоторого решения уравнения (6), необходимо и достаточно, Чтобы при всех
можно было доопределить всюду в ограниченной сеточной области D до некоторого решения уравнения (6), необходимо и достаточно, Чтобы при всех  выполнялись равенства
выполнялись равенства

Доказательство. Если  можно доопределить всюду на D до некоторого решения
можно доопределить всюду на D до некоторого решения  , то, применив к этому решению формулу (8), а затем рассматривая полученное равенство только при
, то, применив к этому решению формулу (8), а затем рассматривая полученное равенство только при  , убедимся в выполнении (12). Обратно, если
, убедимся в выполнении (12). Обратно, если  удовлетворяет (12), то примем
удовлетворяет (12), то примем  и построим некоторое решение
и построим некоторое решение  по формуле (9). В силу (12) граничные значения этого решения
по формуле (9). В силу (12) граничные значения этого решения  совпадут с заданными.
совпадут с заданными.
Доказанная теорема 4 дает основание назвать равенства (12) внутренними граничными условиями: эти условия не задаются извне, а являются следствиями самого разностного уравнения.
Если формулы (8) и (9) трактовать как аналоги интегральных формул Коши и типа Коши, то внутренние граничные условия аналогичны классическим условиям Сохоцкого — Племеля, при которых заданную на границе у области d на комплексной плоскости функцию  можно доопределить всюду в области d до некоторой аналитической функции.
можно доопределить всюду в области d до некоторой аналитической функции.
Формулу (8) можно понимать как адекватную системе (6) разностную формулу Грина, которая неявно учитывает «скачки потенциалов» на границе Г и приводит к внутренним граничным условиям (12).
6. Оператор граничного проектирования.
Возможна отличная от (12) запись внутренних граничных условий. Будем обозначать через  линейное пространство всех сеточных вектор-функций
линейное пространство всех сеточных вектор-функций  , а через
, а через  подпространство тех из них, которые можно доопределить всюду в D до решений
подпространство тех из них, которые можно доопределить всюду в D до решений  однородного уравнения, соответствующего уравнению (6).
однородного уравнения, соответствующего уравнению (6).
Определим линейное отображение  пространства UF в себя следующей формулой:
пространства UF в себя следующей формулой:

Теорема 5. Оператор Р есть оператор проектирования  на
на 
Доказательство. Действительно, при любом  в силу теоремы 3 элемент
в силу теоремы 3 элемент  принадлежит
принадлежит  Если
Если  то в силу теоремы 2 получим
то в силу теоремы 2 получим  Теорема доказана.
Теорема доказана.
Оператор Р, определенный формулой (13), будем называть оператором граничного проектирования. С его помощью внутренние граничные условия (12) в случае  записываются в форме
записываются в форме

Подчеркнем, что оператор граничного проектирования зависит от выбора фундаментального решения 
7. Общая краевая задача.
В силу следствия из теоремы 2 каждое решение уравнения (6) восстанавливается по его значениям на границе Г. Это
дает основание определить общую линейную краевую задачу для уравнения (6) как краевую задачу вида

где  какой-нибудь линейный оператор, отображающий пространство
какой-нибудь линейный оператор, отображающий пространство  на некоторое линейное пространство Ф.
на некоторое линейное пространство Ф.
Естественные разностные схемы, аппроксимирующие первую, вторую или третью краевые задачи для уравнения Пуассона, например, легко записать в виде (15).
Название «общая краевая задача» несколько условно: могут встретиться разностные краевые задачи, имеющие иной, чем (15), вид. Например, таковы естественные разностные схемы для дифференциальных краевых задач, в которых порядок дифференциального уравнения ниже порядка дифференциальных краевых условий.
8. Основная идея метода внутренних граничных условий.
Пусть для простоты  Между разностной краевой задачей
Между разностной краевой задачей

и между задачей

существует тесная связь. Именно, граничные значения  каждого решения
каждого решения  , задачи (16) удовлетворяют в силу теоремы 2 уравнениям (17). Обратно, каждое решение
, задачи (16) удовлетворяют в силу теоремы 2 уравнениям (17). Обратно, каждое решение  задачи (17) в силу теоремы 4 и следствия из теоремы 2 можно единственным образом доопределить всюду в D до решения задачи (16). Основная идея метода внутренних граничных условий состоит в переходе от исходной разностной краевой задачи (16) к системе уравнений (17) на границе Г. Продвижения, которые при этом удается получить, основаны на двух обстоятельствах. Первое из них — малое по сравнению с задачей (16) число неизвестных, участвующих в задаче (17). Второе — специальный вид системы (17), в структуру которой органически включен оператор граничного проектирования.
задачи (17) в силу теоремы 4 и следствия из теоремы 2 можно единственным образом доопределить всюду в D до решения задачи (16). Основная идея метода внутренних граничных условий состоит в переходе от исходной разностной краевой задачи (16) к системе уравнений (17) на границе Г. Продвижения, которые при этом удается получить, основаны на двух обстоятельствах. Первое из них — малое по сравнению с задачей (16) число неизвестных, участвующих в задаче (17). Второе — специальный вид системы (17), в структуру которой органически включен оператор граничного проектирования.
9. Устойчивость внутренних граничных условий.
Можно опасаться, что внутренние граничные условия  «почти вырождены», и поэтому задача (17) плохо обусловлена независимо от вида оператора
«почти вырождены», и поэтому задача (17) плохо обусловлена независимо от вида оператора  так что переход от задачи (16) к задаче (17) связан с потерей вычислительной устойчивости.
так что переход от задачи (16) к задаче (17) связан с потерей вычислительной устойчивости.
Будем считать, что пространство Ф вложено в пространство UF, введем в пространстве  значит, и в пространстве Ф с:
значит, и в пространстве Ф с:  ) норму IMI и докажем теорему, означающую, что при переходе от задачи (16) к задаче (17) не происходит потери вычислительной устойчивости.
) норму IMI и докажем теорему, означающую, что при переходе от задачи (16) к задаче (17) не происходит потери вычислительной устойчивости.
Теорема 6. Пусть задача (17) имеет решение  при любом
при любом  причем выполнена оценка
причем выполнена оценка

где с от  не зависит. Пусть, далее,
не зависит. Пусть, далее,  произвольный элемент из
произвольный элемент из  Обозначим
Обозначим

Тогда справедлива оценка

Если рассматривать (19) как уравнения для определения  , то оценка (20) означает, что чувствительность решения задачи (19) к возмущениям
, то оценка (20) означает, что чувствительность решения задачи (19) к возмущениям  правой части внутренних граничных условий характеризуется постоянной с из оценки (18), т. е. чувствительностью решения к возмущениям правой части заданного граничного условия
правой части внутренних граничных условий характеризуется постоянной с из оценки (18), т. е. чувствительностью решения к возмущениям правой части заданного граничного условия  .
.
Доказательство. Обозначим

В силу теоремы 5 имеем  . Поэтому
. Поэтому

т. e. удовлетворяет системе вида  силу (18) оценке
силу (18) оценке

Отсюда с учетом тождества  следует (20).
следует (20).
10. Дополнительная идея.
Изложим полезную при численном решении краевых задач для уравнений с частными производными идею применительно к следующей задаче.
Пусть функция  определена в некоторой области d с достаточно гладкой границей у как решение задачи Дирихле
определена в некоторой области d с достаточно гладкой границей у как решение задачи Дирихле

и требуется найти производную

в направлении внутренней нормали. Такая задача возникает, если по температуре  на границе у требуется найти установившийся тепловой поток через границу.
на границе у требуется найти установившийся тепловой поток через границу.
Под s понимается длина дуги вдоль границы у. причем будем считать для определенности, что полная длина границы у есть  . Функцию
. Функцию

будем искать приближено в виде частичной суммы

ее ряда Фурье. Для определения коэффициентов  воспользуемся методом внутренних граничных условий.
воспользуемся методом внутренних граничных условий.
Зададим  построим сетку
построим сетку

и разностное уравнение

Отнесем к  все те точки сетки, которые вместе со всеми четырьмя
все те точки сетки, которые вместе со всеми четырьмя
соседними точками принадлежат  Тогда определится сеточная область
Тогда определится сеточная область  ее граница
ее граница  и внутренние граничные условия
и внутренние граничные условия  Идея состоит в том, чтобы по функции
Идея состоит в том, чтобы по функции  и фукнции
и фукнции

записанной в виде ряда с неопределенными коэффициентами, продолжить решение по формуле Тейлора с границы у в приграничную полоску, где лежит граница сеточной области  затем подобрать неопределенные коэффициенты
затем подобрать неопределенные коэффициенты

из условия минимизации невязки, возникающей при подстановке продолженной с границы Y в приграничную полоску функции  во внутренние граничные условия.
во внутренние граничные условия.
11. Сопоставление метода внутренних граничных условий с методом сингулярных интегральных уравнений.
В начале Дополнения мы указывали на аналогию между методом внутренних граничных условий и методом сингулярных интегральных уравнений, которая не является полной. Здесь мы сопоставим эти методы, уточняя аналогию и выявляя существенные различия.
Для сопоставления сначала опишем идею метода сингулярных интегральных уравнений для дифференциальных краевых задач на примере задачи

где  — ограниченная область,
— ограниченная область,  ее граница. Краевое условие (22) связывает решение
ее граница. Краевое условие (22) связывает решение  на границе области и его производную по направлению внутренней нормали
на границе области и его производную по направлению внутренней нормали  Коэффициенты
Коэффициенты  заданные операторы.
заданные операторы.
Выпишем классическую формулу Грина для уравнения (21):

где  - фундаментальное решение уравнения (21), стремящееся к нулю на бесконечности. Устремим
- фундаментальное решение уравнения (21), стремящееся к нулю на бесконечности. Устремим  к границе у. Воспользовавшись свойствами потенциалов простого и двойного слоев, получим на границе Y соотношение вида
к границе у. Воспользовавшись свойствами потенциалов простого и двойного слоев, получим на границе Y соотношение вида

связывающее решение  и его нормальную производную
и его нормальную производную  на границе области;
на границе области;  и
и  некоторые известные интегральные операторы. Переход от задачи (21), (22) к равносильной системе уравнений (22), (24) относительно функций
некоторые известные интегральные операторы. Переход от задачи (21), (22) к равносильной системе уравнений (22), (24) относительно функций  определенных на границе
определенных на границе  и составляет сущность метода сингулярных интегральных уравнений.
и составляет сущность метода сингулярных интегральных уравнений.
Для сравнения рассмотрим теперь метод внутренних граничных условий применительно к следующей общей краевой задаче для разностного аналога уравнения (21) в квадратной сеточной области

Запишем внутренние граничные условия  в удобной для дальнейшего форме.
в удобной для дальнейшего форме.
Легко проверить, что формула (9) в этом случае может быть переписана в форме

где  - совокупность точек Г, лежащих на сторонах квадрата
- совокупность точек Г, лежащих на сторонах квадрата  т. е. на внешнем слое двухслойной границы Г сеточной квадратной области (рис. 57), а
т. е. на внешнем слое двухслойной границы Г сеточной квадратной области (рис. 57), а  разностный аналог производной по направлению внутренней нормали.
разностный аналог производной по направлению внутренней нормали.
Заметим, что формула (27) была бы полным аналогом классической формулы Грина (23), если бы в ее правой части отсутствовало «сингулярное слагаемое» Ьгпиг Однако в таком хлучае равенство (27) имело бы место не при всех  , а лишь при
, а лишь при  Из него нельзя было бы получить тогда внутренние граничные условия
Из него нельзя было бы получить тогда внутренние граничные условия  Эти условия получаются из (27), если
Эти условия получаются из (27), если  пробегает не всю область D, а только точки границы Г, и записываются двумя системами равенств
пробегает не всю область D, а только точки границы Г, и записываются двумя системами равенств

отвечающих, соответственно, точкам  внешнего и точкам
внешнего и точкам  внутреннего слоев двойной границы Г. В качестве
внутреннего слоев двойной границы Г. В качестве  в равенствах (28) и (29) будем использовать ограниченное фундаментальное решение.
в равенствах (28) и (29) будем использовать ограниченное фундаментальное решение.
Можно показать, что внутренние граничные условия  т. е. система уравнений (28), (29), алгебраически равносильна каждой из отдельно взятых подсистем (28) или (29).
т. е. система уравнений (28), (29), алгебраически равносильна каждой из отдельно взятых подсистем (28) или (29).
Подсистема (28) аналогична интегральному соотношению (24), так что разностным аналогом задачи (22), (24) является задача (27), (28), но не задача

записываемая равенствами  которая рассматривается в методе внутренних граничных условий.
которая рассматривается в методе внутренних граничных условий.
Имеется очевидная разница между внутренними граничными условиями  т. е. системой (28), (29), и одной только подсистемой (28). Внутренние граничные условия
т. е. системой (28), (29), и одной только подсистемой (28). Внутренние граничные условия

содержат избыточные равенства (29). В этом смысле разностные внутренние граничные условия

больше похожи не на интегральное соотношение (24), а на условия Сохоцкого — Племеля для аналитических функций. Эти последние представляют собой два вещественных соотношения, связывающих две вещественных функции, но они не независимы, и многообразие удовлетворяющих условиям Сохоцкого — Племеля пар функций зависит от одной произвольной вещественной функции.
Отметим, что внутренние граничные условия

выгодно отличаются от равносильной им подсистемы (28) тем, что в их структуру входит оператор граничного проектирования. Благодаря этому обстоятельству задача

устойчива в смысле теоремы 6 относительно возмущения правой части  . В общем случае при вычеркивании части уравнений из числа составляющих систему
. В общем случае при вычеркивании части уравнений из числа составляющих систему  может получиться подсистема, алгебраически равносильная исходной, но уже не обладающая свойством устойчивости.
может получиться подсистема, алгебраически равносильная исходной, но уже не обладающая свойством устойчивости.
Можно показать, что в нашем примере (25), (26) вместо

удобнее использовать не подсистему (28), а подсистему (29), которая устойчива и в отличие от подсистемы (28) состоит из независимых уравнений — ее ранг равен числу составляющих ее уравнений.
Итак, в рассматриваемом примере аналогия между методом внутренних граничных условий и методом сингулярных интегральных уравнений, аналогичных условию Сохоцкого — Племеля, не является полной.
Тем более, нет полной аналогии с классическим методом интегральных уравнений, в котором искомой функцией является не само решение исходной задачи (21), (22) на границе, а некоторая вспомогательная плотность потенциала простого или двойного слоя.
В заключение заметим, что мы употребляем выражение «метод сингулярных интегральных уравнений», поскольку условие Сохоцкого — Племеля содержит сингулярный интеграл. В примере этого пункта условие (26) содержит сходящиеся несобственные интегралы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ЧАСТЬ ПЕРВАЯ. ОБЫКНОВЕННЫЕ РАЗНОСТНЫЕ УРАВНЕНИЯ
- ГЛАВА 1. РАЗНОСТНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА. ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- ЗАДАЧИ
- § 2. Разностное уравнение первого порядка
- ЗАДАЧИ
- § 3. Разностное уравнение второго порядка
- 2. Общее решение неоднородного уравнения. Фундаментальное решение.
- 3. Оценка фундаментального решения через коэффициенты разностного уравнения.
- ЗАДАЧИ
- ГЛАВА 2. КРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- § 4. Постановка задачи. Признаки хорошей обусловленности
- 2. Определение хорошей обусловленности.
- 3. Достаточный признак хорошей обусловленности.
- 4. Критерий хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 5. Критерий хорошей обусловленности задачи с переменными коэффициентами.
- 6. Обоснование критерия хорошей обусловленности краевой задачи с постоянными коэффициентами.
- 7. Общие краевые задачи для систем разностных уравнений.
- ЗАДАЧИ
- § 5. Алгоритм решения краевой задачи — прогонка
- 2. Пример вычислительно неустойчивого алгоритма.
- ЗАДАЧИ
- ГЛАВА 3. ОБОСНОВАНИЕ МЕТОДА ПРОГОНКИ
- § 6. Свойства хорошо обусловленных краевых задач
- 2. Доказательство критерия хорошей обусловленности.
- 3. Свойства хорошо обусловленных задач.
- § 7. Обоснование метода прогонки для хорошо обусловленных краевых задач
- 2. Оценка влияния на результат ошибок округления в процессе вычислений.
- ЧАСТЬ ВТОРАЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- ГЛАВА 4. ЭЛЕМЕНТАРНЫЕ ПРИМЕРЫ РАЗНОСТНЫХ СХЕМ
- 2. Скорость сходимости решения разностного уравнения.
- 3. Порядок аппроксимации.
- § 9. Неустойчивая разностная схема
- ГЛАВА 5. СХОДИМОСТЬ РЕШЕНИЯ РАЗНОСТНЫХ УРАВНЕНИЙ КАК СЛЕДСТВИЕ АППРОКСИМАЦИИ И УСТОЙЧИВОСТИ
- § 10. Сходимость разностной схемы
- 2. Сходящиеся разностные схемы.
- 3. Проверка сходимости разностной схемы.
- § 11. Аппроксимация дифференциальной краевой задачи разностной схемой
- 3. Аппроксимация порядка h^k.
- 4. Примеры.
- 5. Разбиение разностной схемы на подсистемы.
- 6. Замена производных разностными отношениями.
- 7. Другие спосрбы построения разностных схем.
- § 12. Определение устойчивости разностной схемы. Сходимость как следствие аппроксимации и устойчивости
- 2. Зависимость между аппроксимацией, устойчивостью к сходимостью.
- 3. Сходящаяся разностная схема для интегрального уравнения.
- § 13. О выборе норм
- § 14. Достаточный признак устойчивости разностных схем решения задачи Коши
- 2. Каноническая запись разностной схемы.
- 3. Устойчивость как ограниченность норм степеней оператора перехода.
- 4. Примеры исследования устойчивости.
- 5. Неединственность канонической записи.
- ЗАДАЧИ
- § 15. Необходимый спектральный признак устойчивости
- 2. Спектральный признак устойчивости.
- 3. Обсуждение спектрального признака устойчивости.
- ЗАДАЧИ
- § 16. Ошибки округления
- 2. Ошибки в вычислениях.
- § 17. Количественная характеристика устойчивости
- § 18. Прием исследования устойчивости нелинейных задач
- ГЛАВА 6. УПОТРЕБИТЕЛЬНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 19. Схемы Рунге — Кутта и Адамса
- 2. Схемы Адамса.
- 3. Замечания об устойчивости.
- 4. Обобщение на системы уравнений.
- § 20. Методы решения краевых задач
- 2. Метод прогонки.
- 3. Метод Ньютона.
- ЧАСТЬ ТРЕТЬЯ. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ. ОСНОВНЫЕ ПОНЯТИЯ
- ГЛАВА 7. ПРОСТЕЙШИЕ ПРИЕМЫ ПОСТРОЕНИЯ И ИССЛЕДОВАНИЯ РАЗНОСТНЫХ СХЕМ
- 2. Определение аппроксимации.
- 3. Определение устойчивости.
- ЗАДАЧИ
- § 22. Простейшие приемы построения аппроксимирующих разностных схем
- 2. Метод неопределенных коэффициентов.
- 3. Схемы с пересчетом, или схемы предиктор-корректор.
- 4. О других приемах.
- ЗАДАЧИ
- § 23. Примеры конструирования граничных условий при построении разностных схем
- ЗАДАЧИ
- § 24. Условие Куранта, Фридрихса и Леви, необходимое для сходимости
- 2. Примеры разностных схем для задачи Коши.
- 3. Примеры разностных схем для задачи Дирихле.
- ЗАДАЧИ
- ГЛАВА 8. НЕКОТОРЫЕ ОСНОВНЫЕ ПРИЕМЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
- § 25. Спектральный анализ разностной задачи Коши
- 2. Необходимое спектральное условие устойчивости.
- 3. Примеры.
- 4. Интегральное представление решения.
- 5. Выглаживание разностного решения как действие аппроксимационной вязкости.
- ЗАДАЧИ
- § 26. Принцип замороженных коэффициентов
- 2. Признак Бабенко и Гельфанда.
- ЗАДАЧИ
- § 27. Представление решений некоторых модельных задач в виде конечных рядов Фурье
- 2. Представление решений разностных схем для уравнения теплопроводности на отрезке.
- 3. Представление решений разностных схем для двумерной задачи теплопроводности.
- 4. Представление решения разностной схемы для задачи о колебаниях струны.
- ЗАДАЧИ
- § 28. Принцип максимума
- 2. Неявная разностная схема.
- 3. Сопоставление явной и неявной разностных схем.
- ГЛАВА 9. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ ДЛЯ РАСЧЕТА ОБОБЩЕННЫХ РЕШЕНИИ
- 2. Определение обобщенного решения.
- 3. Условие на линии разрыва решения.
- 5. Другое определение обобщенного решения.
- § 30. Построение разностных схем
- 2. Метод характеристик.
- 3. Дивергентные разностные схемы.
- ЧАСТЬ ЧЕТВЕРТАЯ. ЗАДАЧИ С ДВУМЯ ПРОСТРАНСТВЕННЫМИ ПЕРЕМЕННЫМИ
- ГЛАВА 10. ПОНЯТИЕ О РАЗНОСТНЫХ СХЕМАХ РАСЩЕПЛЕНИЯ
- § 32. Экономичные разностные схемы
- § 33. Расщепление по физическим факторам
- ГЛАВА 11. ЭЛЛИПТИЧЕСКИЕ ЗАДАЧИ
- § 34. Простейшая разностная схема для задачи Дирихле
- § 35. Метод установления
- 2. Анализ явной схемы установления.
- 3. Схема переменных направлений.
- 4. Выбор точности.
- 5. Границы применимости методов.
- ЗАДАЧИ
- § 36. Итерации с переменным шагом
- § 37. Метод Федоренко
- ГЛАВА 12. ПОНЯТИЕ О ВАРИАЦИОННО-РАЗНОСТНЫХ И ПРОЕКЦИОННО-РАЗНОСТНЫХ СХЕМАХ
- § 38. Вариационные и проекционные методы
- 2. Сходимость минимизирующих последовательностей.
- 3. Вариационный метод Ритца.
- 4. Проекционный метод Галеркина.
- 5. Способы решения алгебраической системы.
- 6. Вычислительная устойчивость.
- ЗАДАЧИ
- § 39. Построение и свойства вариационно-разностных и проекционно-разностных схем
- 2. Пример вариационно-разностной схемы для первой краевой задачи.
- 3. Пример вариационно-разностной схемы для третьей краевой задачи.
- 4. О методике доказательства сходимости.
- 5. Сопоставление вариационно-разностных, схем с общими вариационными и обычными разностными.
- ЗАДАЧА
- ЧАСТЬ ПЯТАЯ. УСТОЙЧИВОСТЬ эволюционных РАЗНОСТНЫХ КРАЕВЫХ ЗАДАЧ КАК ОГРАНИЧЕННОСТЬ НОРМ СТЕПЕНЕЙ НЕКОТОРОГО ОПЕРАТОРА
- ГЛАВА 13. КОНСТРУКЦИЯ ОПЕРАТОРА ПЕРЕХОДА
- § 41. Запись разностных краевых задач в виде …
- 2. Устойчивость как равномерная ограниченность норм степеней Rh.
- 3. Пример.
- ЗАДАЧИ
- § 42. Использование частных решений при конструировании оператора перехода
- § 43. Некоторые способы оценки норм степеней операторов
- 2. Спектральный критерий ограниченности степеней самосопряженного оператора.
- 3. Признаки самосопряженности.
- 4. Оценки собственных значений оператора Rh.
- 5. Выбор скалярного умножения.
- 6. Критерии устойчивости Самарского.
- ГЛАВА 14. СПЕКТРАЛЬНЫЙ ПРИЗНАК УСТОЙЧИВОСТИ НЕСАМОСОПРЯЖЕННЫХ ЭВОЛЮЦИОННЫХ КРАЕВЫХ ЗАДАЧ
- § 44. Спектр семейства операторов {Rh}
- 3. Необходимое условие устойчивости.
- 4. Обсуждение понятия спектра семейства операторов {Rh}.
- 5. Близость необходимого признака устойчивости к достаточному.
- § 45. Алгоритм вычисления спектра семейства разностных операторов над сеточными функциями на отрезке
- 2. Алгоритм вычисления спектра в общем случае.
- ЗАДАЧИ
- § 46. Ядра спектров семейств операторов
- § 47. Об устойчивости итерационных алгоритмов решения несамосопряженных разностных уравнений
- ДОПОЛНЕНИЕ. МЕТОД ВНУТРЕННИХ ГРАНИЧНЫХ УСЛОВИЙ
- БИБЛИОГРАФИЧЕСКИЕ КОММЕНТАРИИ
- ЛИТЕРАТУРА