| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Момент вектора относительно оси.
Пусть в пространстве дан вектор  и ось
и ось  направление которой задано ортом е. Возьмем на оси
направление которой задано ортом е. Возьмем на оси  точку О и найдем момент вектора
точку О и найдем момент вектора  относительно этой точки; очевидно, что
относительно этой точки; очевидно, что  будет зависеть по величине и направлению от выбранной точки О. Однако проекция этого момента на ось
будет зависеть по величине и направлению от выбранной точки О. Однако проекция этого момента на ось  не зависит от выбора точки на оси. Докажем это. Пусть на оси
не зависит от выбора точки на оси. Докажем это. Пусть на оси  выбраны две точки О и
выбраны две точки О и  Тогда
Тогда

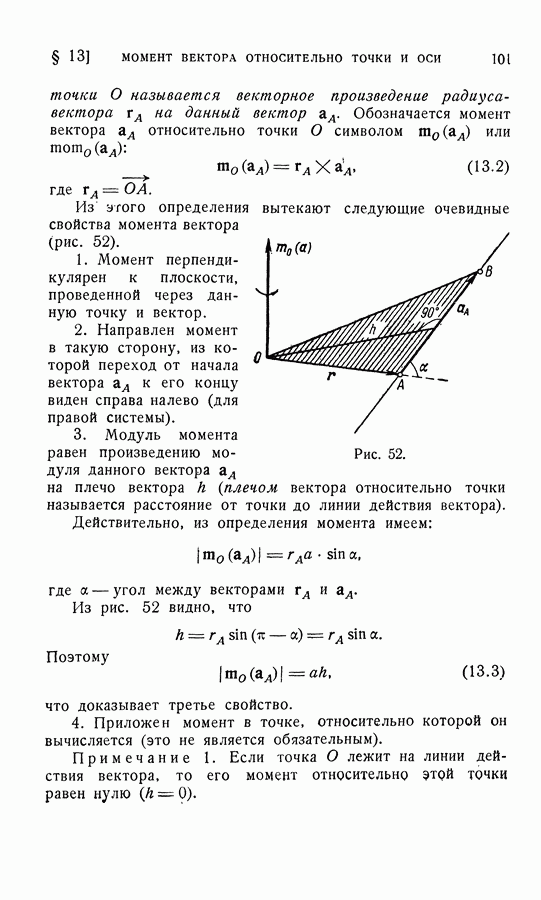
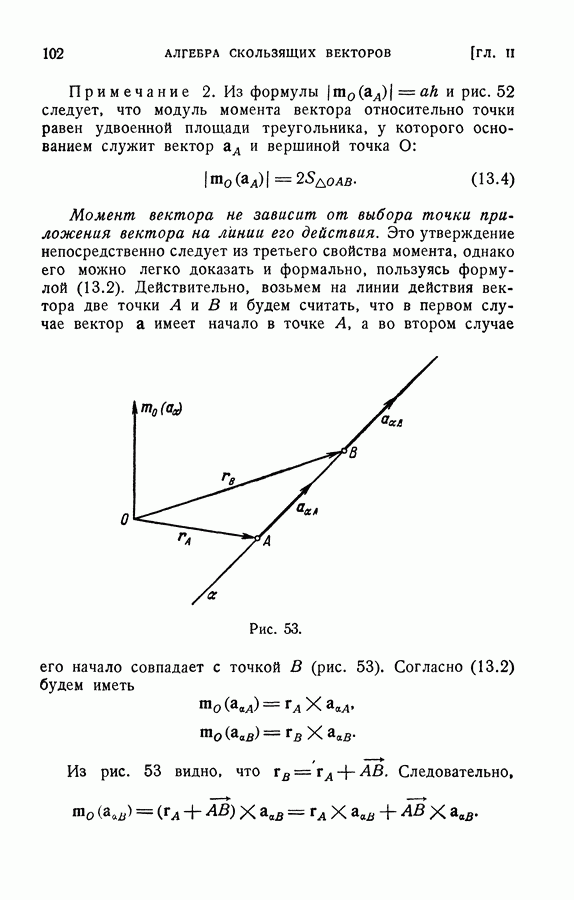
где А — точка приложения вектора а.
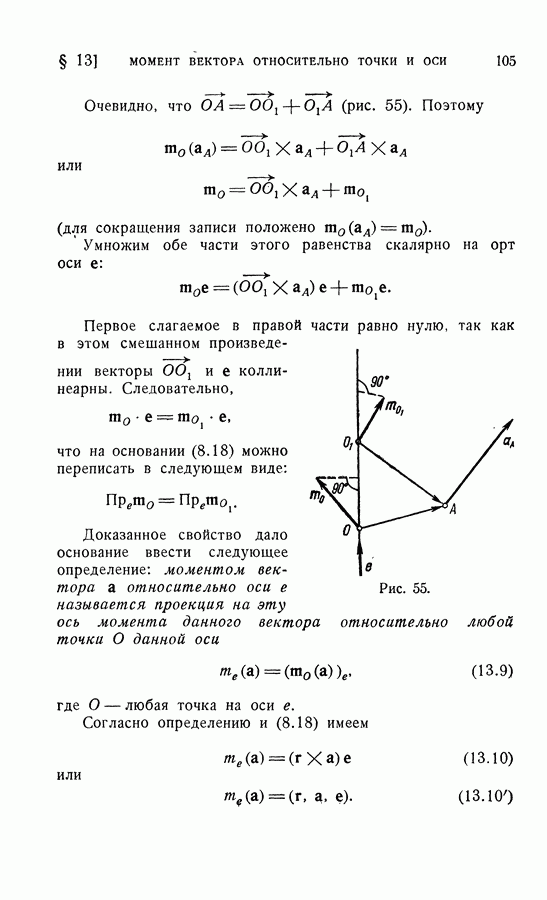
Очевидно, что  (рис. 55). Поэтому
(рис. 55). Поэтому

или

(для сокращения записи положено 
Умножим обе части этого равенства скалярно на орт оси 

Первое слагаемое в правой части равно нулю, так как в этом смешанном произведении векторы  коллинеарны. Следовательно,
коллинеарны. Следовательно,

что на основании (8.18) можно переписать в следующем виде:


Рис. 55.
Доказанное свойство дало основание ввести следующее определение: моментом вектора а относительно оси  называется проекция на эту ось момента данного вектора относительно любой точки О данной оси
называется проекция на эту ось момента данного вектора относительно любой точки О данной оси

где О — любая точка на оси  .
.
Согласно определению и (8.18) имеем

или

Пользуясь выражением для смешанного произведения (10.3), получим

где  — координаты любой точки на оси
— координаты любой точки на оси  ; х, у, z — координаты любой точки на линии действия вектора;
; х, у, z — координаты любой точки на линии действия вектора;  — проекции вектора
— проекции вектора  — направляющие косинусы оси е.
— направляющие косинусы оси е.
Если ось, относительно которой вычисляется момент вектора, проходит через начало координат, то  и последняя формула принимает более простой вид
и последняя формула принимает более простой вид

Пусть ось  совпадает с осью х. Тогда
совпадает с осью х. Тогда  , следовательно,
, следовательно,

Сравнивая с (13.8), видим, что  аналогично
аналогично  т. е. моменты относительно осей координат равны проекциям момента относительно начала координат на соответствующие оси (этот вывод следует также непосредственно из определений). На этом основании в формулах (13.8) можно опустить индекс О и писать просто
т. е. моменты относительно осей координат равны проекциям момента относительно начала координат на соответствующие оси (этот вывод следует также непосредственно из определений). На этом основании в формулах (13.8) можно опустить индекс О и писать просто  и
и 

Момент вектора относительно оси удобно часто вычислять не с помощью формул (13.9) - (13.13), а из простых геометрических соображений. Построим плоскость  перпендикулярную к оси, обозначим точку пересечения
перпендикулярную к оси, обозначим точку пересечения
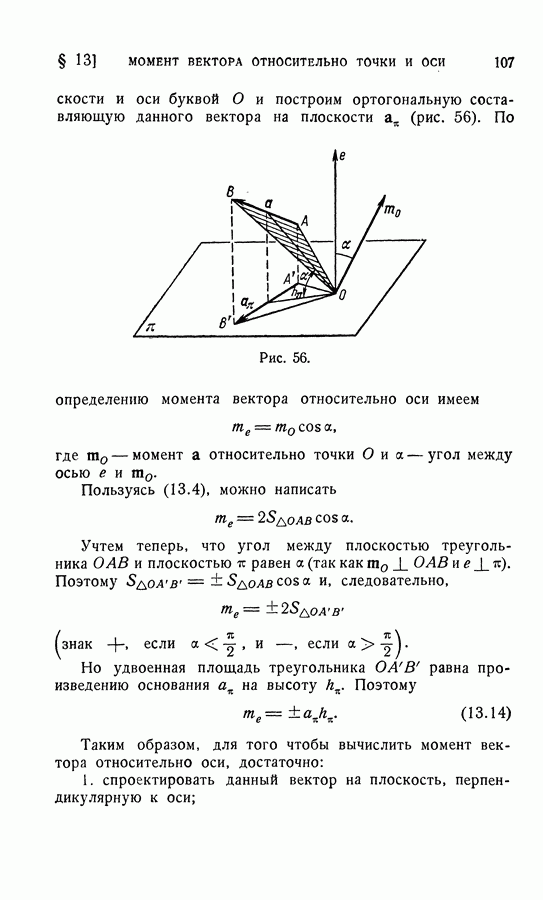
плоскости и оси буквой О и построим ортогональную составляющую данного вектора на плоскости 

Рис. 56.
По определению момента вектора относительно оси имеем

где  — момент а относительно точки О и а — угол между осью
— момент а относительно точки О и а — угол между осью 
Пользуясь (13.4), можно написать

Учтем теперь, что угол между плоскостью треугольника  и плоскостью
и плоскостью  равен а (так как
равен а (так как  и
и  Поэтому
Поэтому  , и, следовательно,
, и, следовательно,

Но удвоенная площадь треугольника  равна произведению основания
равна произведению основания  на высоту
на высоту  Поэтому
Поэтому

Таким образом, для того чтобы вычислить момент вектора относительно оси, достаточно:
1. спроектировать данный вектор на плоскость, перпендикулярную к оси;
2. умножить величину этой проекции атс на расстояние  от точки пересечения плоскости с осью до линии действия составляющей.
от точки пересечения плоскости с осью до линии действия составляющей.
Тогда момент вектора относительно оси будет равен этому произведению, взятому со знаком если со стороны положительного направления оси переход от начала вектора аж к его концу виден справа налево (в этом случае  знаком — в противном случае.
знаком — в противном случае.
Это правило особенно удобно в тех случаях, когда вектор лежит в плоскости, перпендикулярной к оси; в сложных случаях удобнее пользоваться общей формулой.
Очень важное значение имеет вопрос о равенстве нулю момента вектора относительно оси. Из (13.14) видно, что  в двух случаях: либо
в двух случаях: либо  либо
либо  первом случае вектор а параллелен оси, а во втором случае линия действия вектора пересекает ось. Таким образом, если вектор параллелен оси или линия его действия пересекает ось, то момент вектора относительно оси равен нулю.
первом случае вектор а параллелен оси, а во втором случае линия действия вектора пересекает ось. Таким образом, если вектор параллелен оси или линия его действия пересекает ось, то момент вектора относительно оси равен нулю.

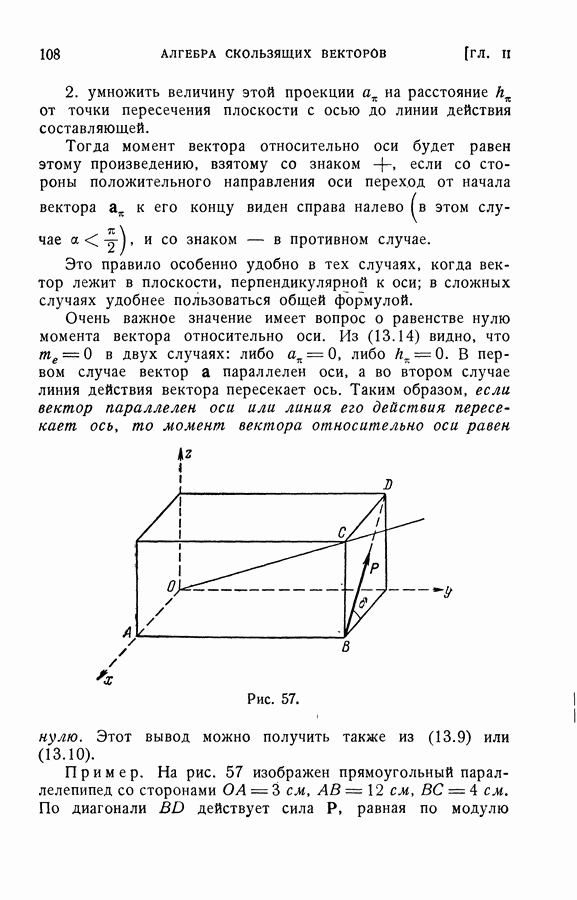
Рис. 57.
Этот вывод можно получить также из (13.9) или (13.10).
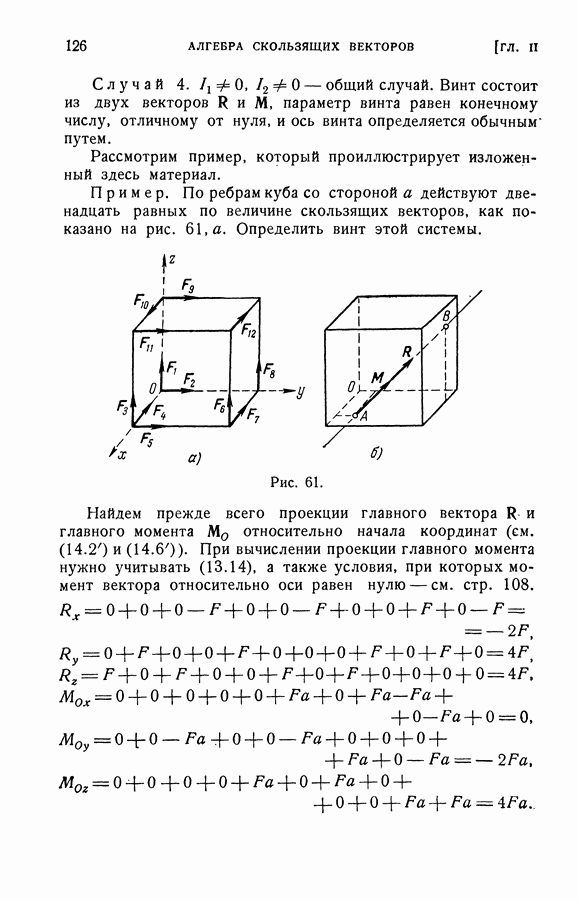
Пример. На рис. 57 изображен прямоугольный параллелепипед со сторонами  см. По диагонали
см. По диагонали  действует сила Р, равная по модулю
действует сила Р, равная по модулю
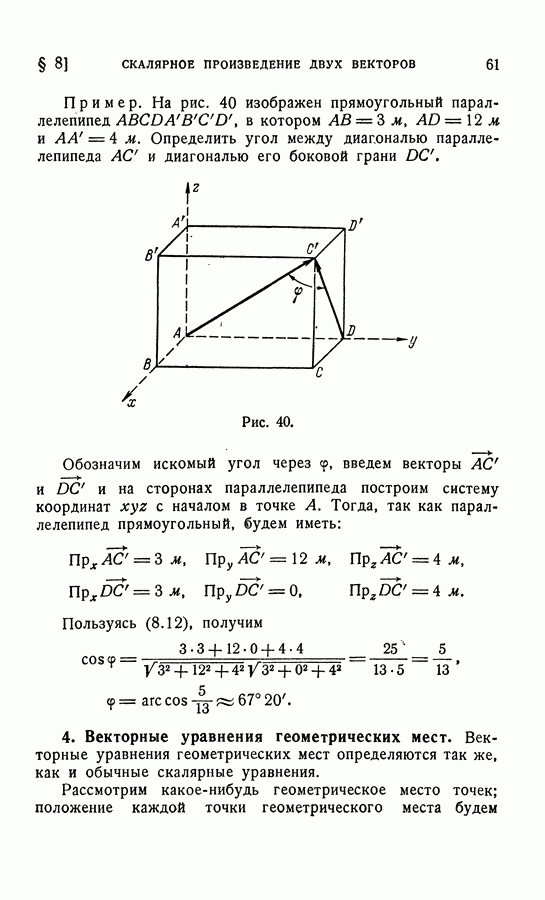
 Определить момент этой силы относительно точки О и ее момент относительно оси ОС.
Определить момент этой силы относительно точки О и ее момент относительно оси ОС.
Построим на сторонах параллелепипеда систему координатных осей  (рис. 57) и найдем проекции силы Р на эти оси.
(рис. 57) и найдем проекции силы Р на эти оси.
Имеем

Согласно (13.13) или (13.14) получим

Отсюда

Для определения момента относительно оси  найдем длину диагонали параллелепипеда
найдем длину диагонали параллелепипеда  а затем направляющие косинусы:
а затем направляющие косинусы:

Пользуясь теперь формулой (13.12), будем иметь:

При вычислениях мы взяли на линии действия вектора Р точку  . Читателю полезно проверить, что результаты не изменятся, если на линии действия вектора Р выбрать любую другую точку, например точку
. Читателю полезно проверить, что результаты не изменятся, если на линии действия вектора Р выбрать любую другую точку, например точку  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
- 2. Определение вектора.
- 3. Классификация векторов.
- 4. Равенство векторов.
- 5. Перенос вектора.
- 6. Нуль-вектор.
- 7. Компланарность и коллинеарность векторов.
- 8. Прямопротивоположные векторы.
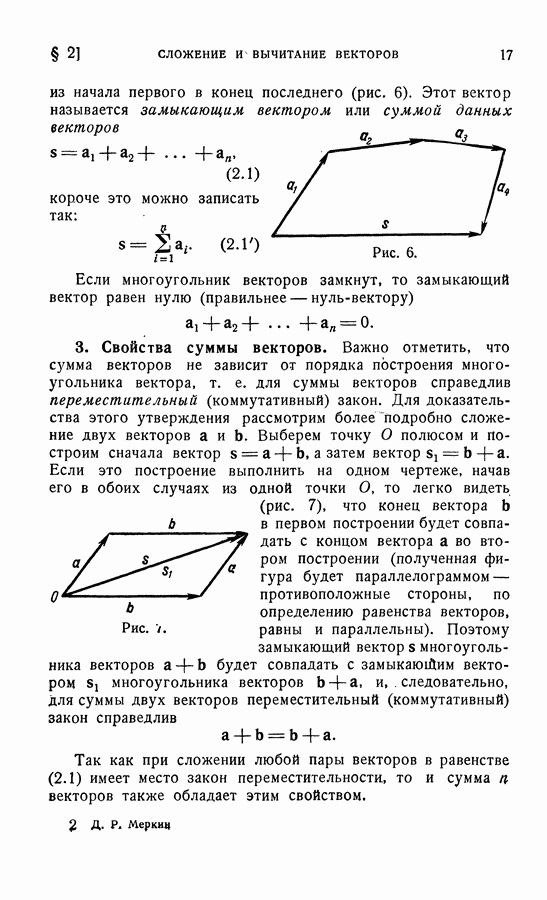
- § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
- 2. Сумма векторов.
- 3. Свойства суммы векторов.
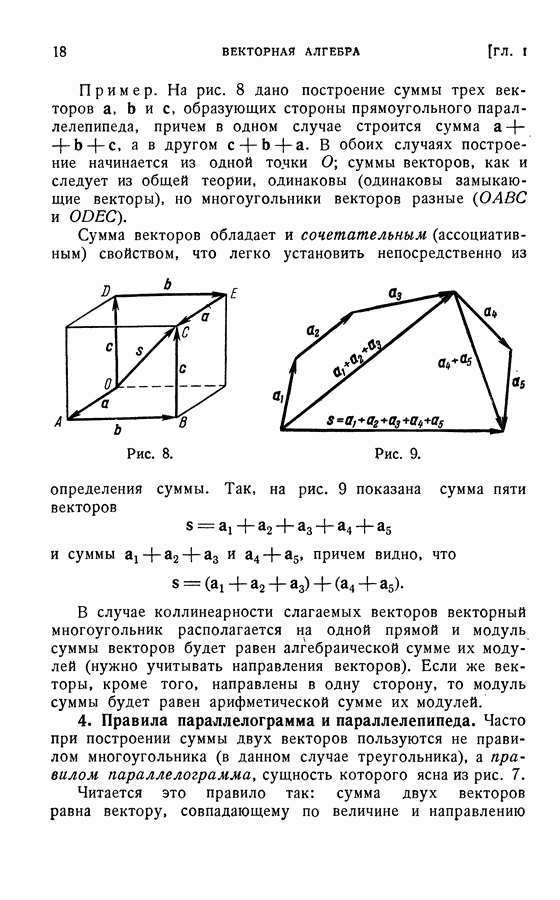
- 4. Правила параллелограмма и параллелепипеда.
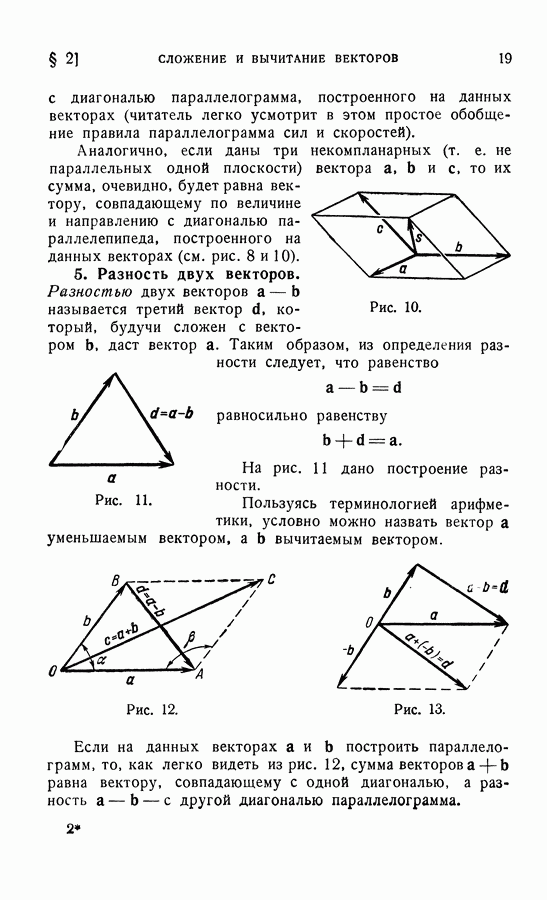
- 5. Разность двух векторов.
- 6. Свойства модуля суммы векторов.
- § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
- 2. Свойства произведения.
- 3. Деление вектора на число.
- 4. Единичные векторы.
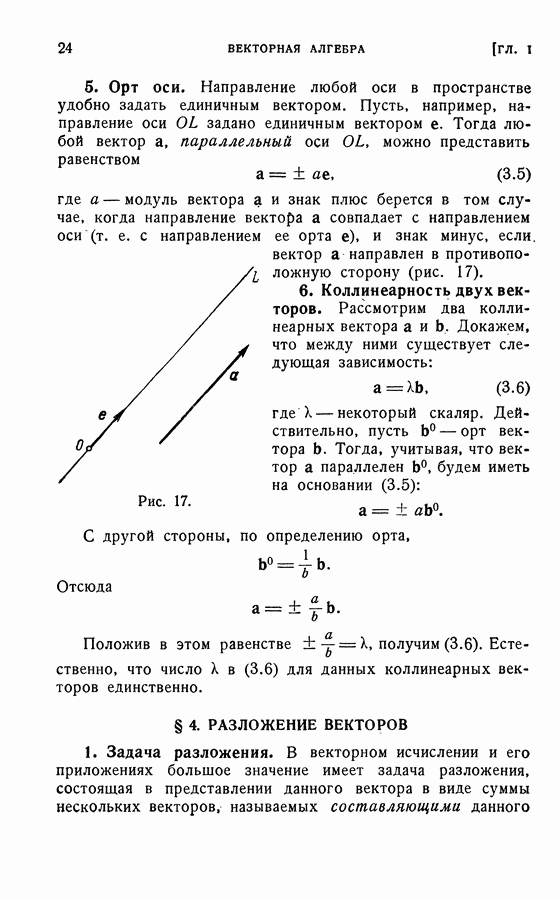
- 5. Орт оси.
- 6. Коллинеарность двух векторов.
- § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
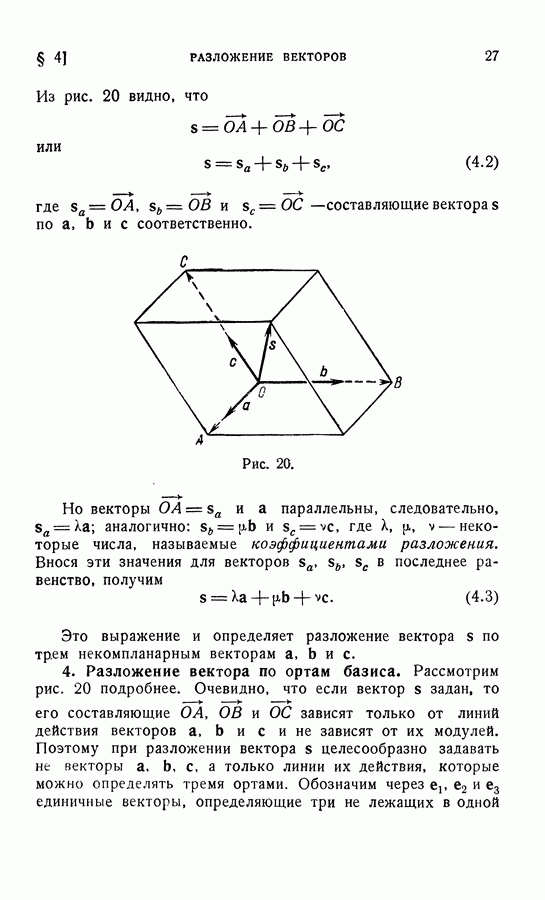
- 3. Разложение вектора по трем другим векторам.
- 4. Разложение вектора по ортам базиса.
- § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
- 2. Условие коллинеарности двух векторов.
- 3. Условие компланарности трех векторов.
- 4. Линейная зависимость четырех векторов.
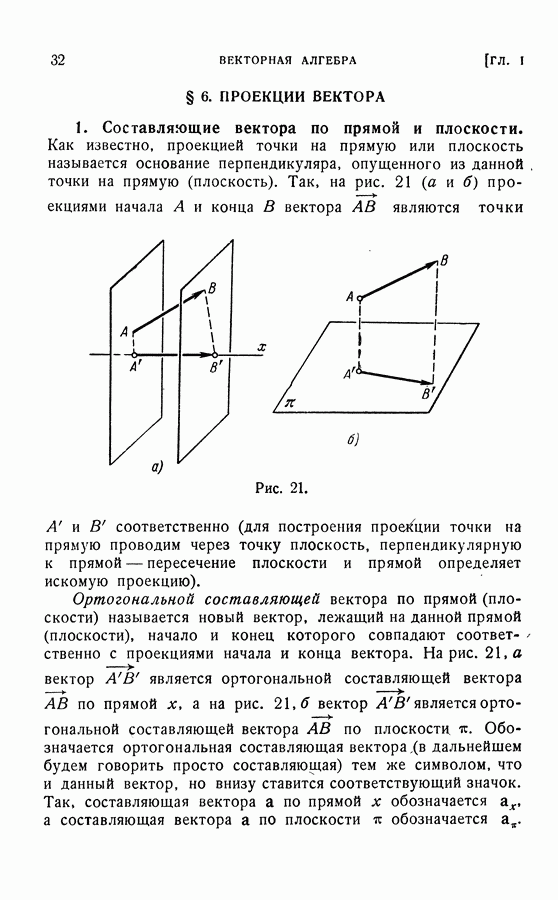
- § 6. ПРОЕКЦИИ ВЕКТОРА
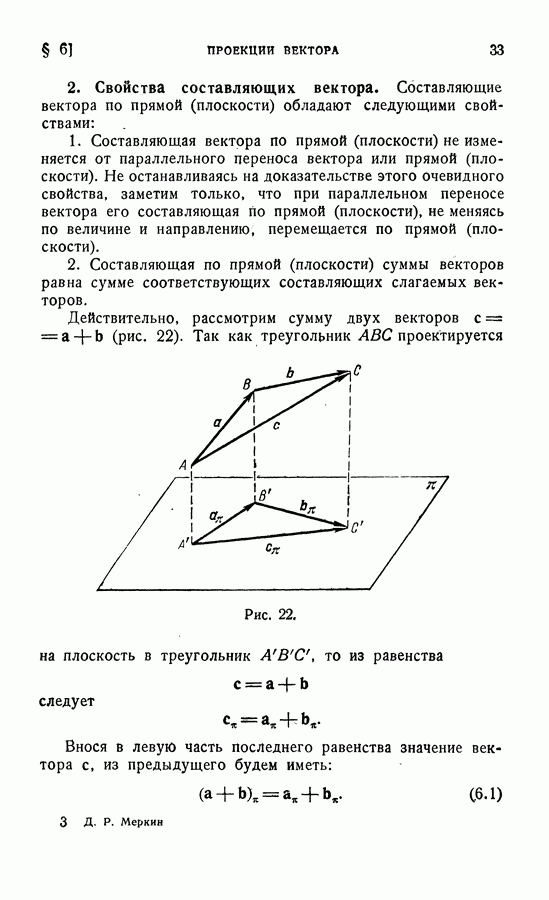
- 2. Свойства составляющих вектора.
- 3. Проекция вектора на ось.
- 4. Свойства проекций.
- 5. Угол между векторами.
- 6. Вычисление проекций вектора.
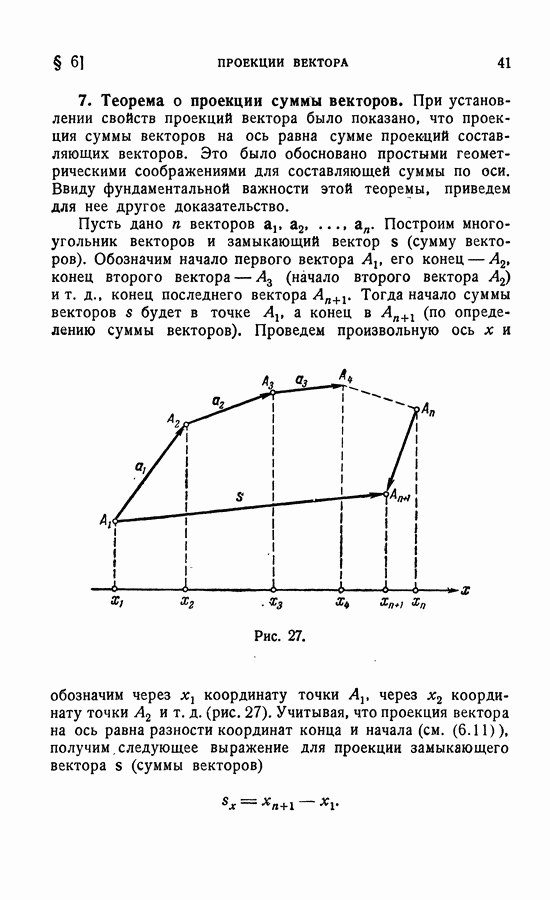
- 7. Теорема о проекции сумммы векторов.
- 8. Псевдоскаляры.
- § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
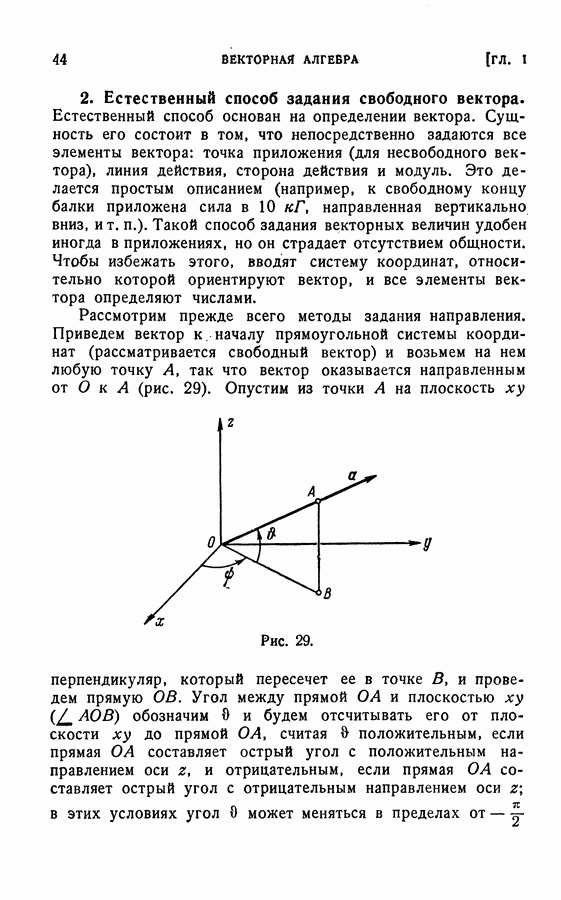
- 2. Естественный способ задания свободного вектора.
- 3. Задание свободного вектора с помощью его проекций (координатный метод).
- 4. Связь между естественным и координатным способами задания вектора.
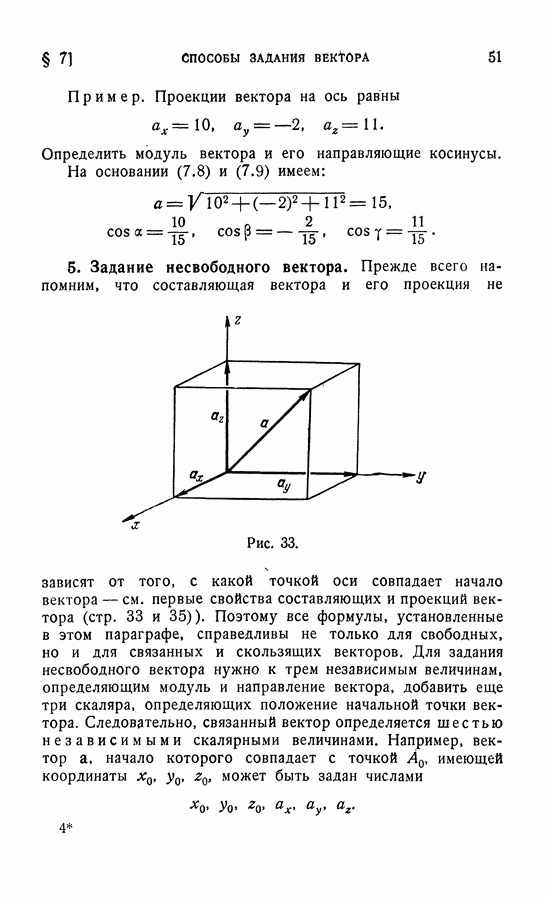
- 5. Задание несвободного вектора.
- 6. Задание скользящего вектора.
- 7. Некоторые приложения.
- § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
- 2. Свойства скалярного произведения.
- 3. Выражение скалярного произведения через проекции векторов.
- 4. Векторные уравнения геометрических мест.
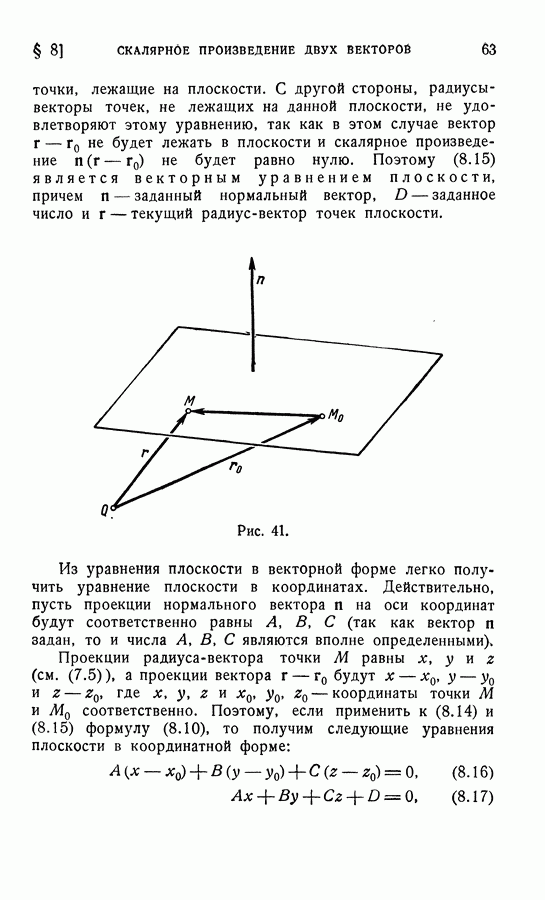
- 5. Уравнение плоскости.
- 7. Изменение проекций вектора при преобразовании координат.
- 8. Другое определение вектора.
- § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
- 2. Примеры из физики.
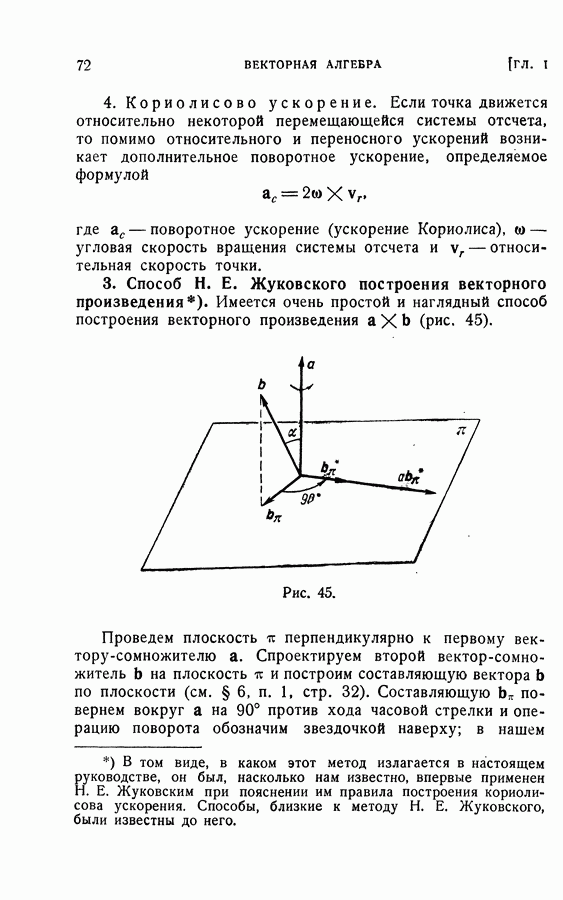
- 3. Способ Н. Е. Жуковского построения векторного произведения.
- 4. Свойства векторного произведения.
- 5. Разложение вектора-произведения по координатным ортам.
- 6. Условие коллинеарности двух векторов.
- 7. Тождество Лагранжа.
- 8. Полярные и аксиальные векторы.
- § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
- 2. Двойное векторное произведение.
- 3. Разложение вектора по трем другим векторам.
- 4. Скалярное произведение двух векторных произведений.
- 5. Векторное произведение двух векторных произведений.
- 6. Произведение двух смешанных произведений.
- 7. Взаимные реперы.
- § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
- 2. Уравнение прямой, проходящей через две заданные точки.
- 3. Плюкерово уравнение прямой в пространстве.
- 4. Прямая как пересечение двух плоскостей.
- § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
- ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
- § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
- 2. Момент вектора относительно точки.
- 3. Проекции момента.
- 4. Момент вектора относительно оси.
- 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
- § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
- 2. Главный вектор системы векторов.
- 3. Главный момент системы векторов.
- 4. Система двух равнопротивоположных векторов.
- 5. Первая теорема Вариньона.
- 6. Изменение главного момента с изменением полюса.
- 7. Инварианты системы векторов.
- 8. Минимальный момент и центральная ось системы.
- 9. Распределение главных моментов в пространстве.
- 10. Понятие о винте.
- 11. Винт системы векторов.
- § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
- 2. Основные определения и аксиомы.
- § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).
- § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
- 2. Условия эквивалентности двух систем скользящих векторов.
- 3. Преобразование эквивалентных систем.
- § 19. ТЕОРИЯ ПАР
- 1. Пара векторов и ее момент.
- 2. Свойства пар.
- 3. Винт
- § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
- 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).
- 3. Приведение системы скользящих векторов к вектору и паре.
- 4. Пример из кинематики.
- 5. Приведение системы скользящих векторов к винту.
- 6. Примеры.
- 7. Уравнения равновесия векторов.
- 8. Вторая теорема Вариньона.
- § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
- 2. Плоская система скользящих векторов.
- 3. Система параллельных скользящих векторов.
- 4. Центр системы параллельных векторов.