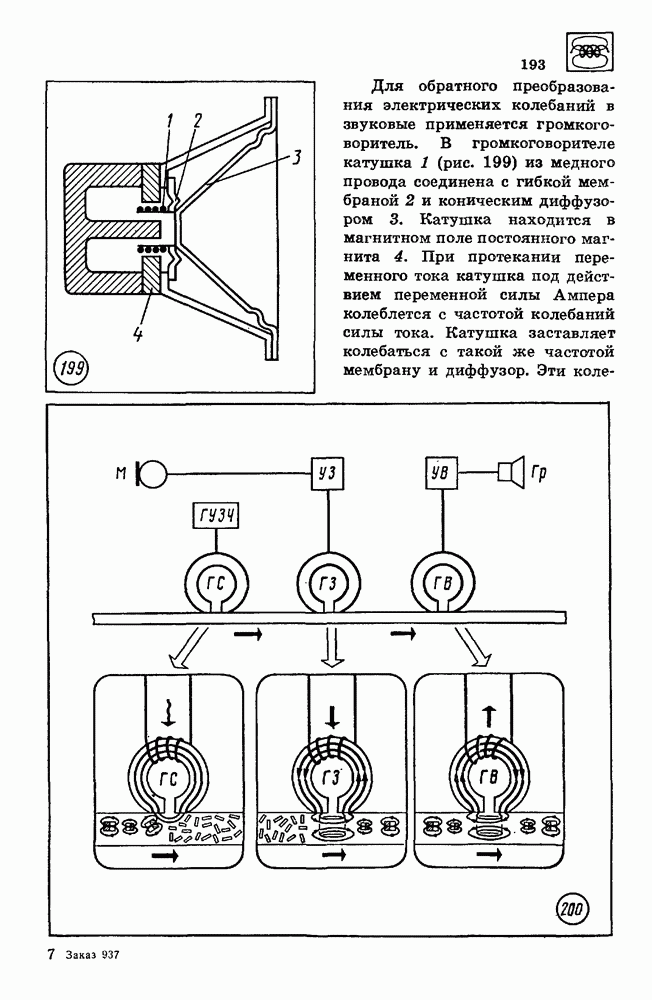
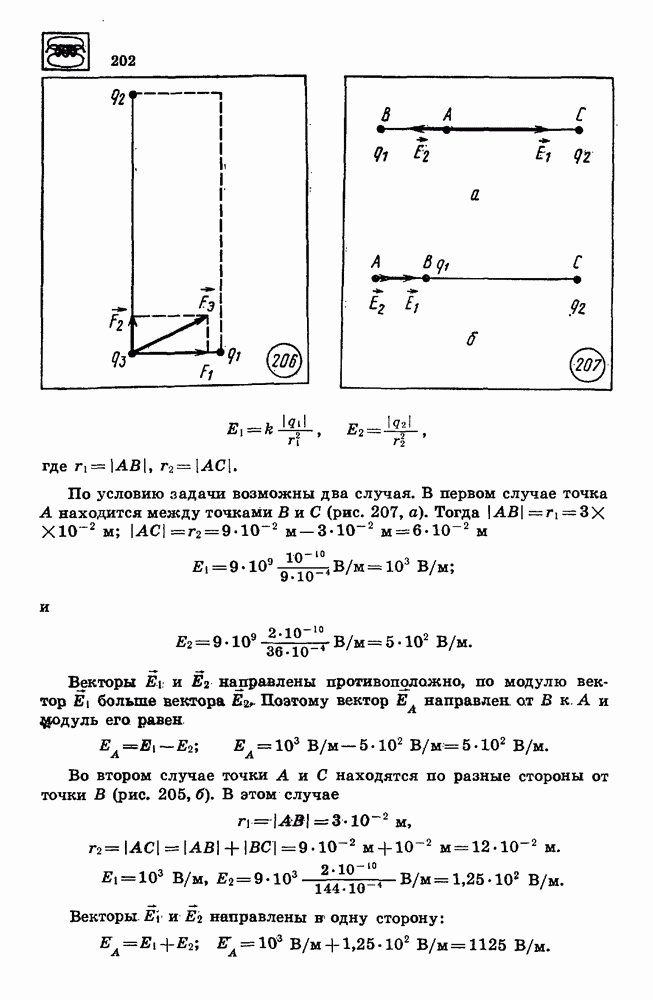
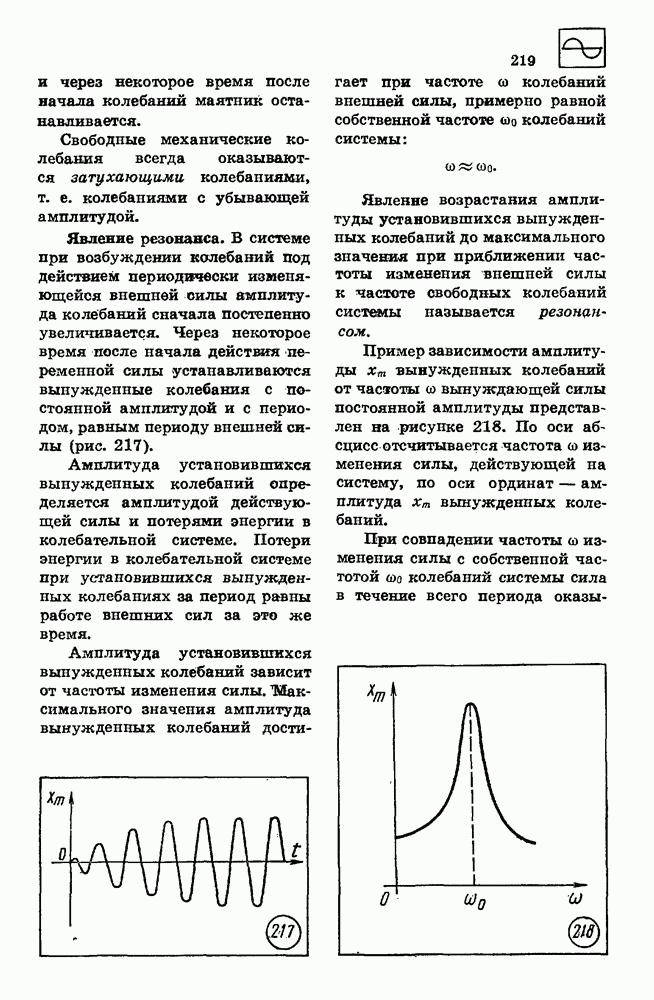
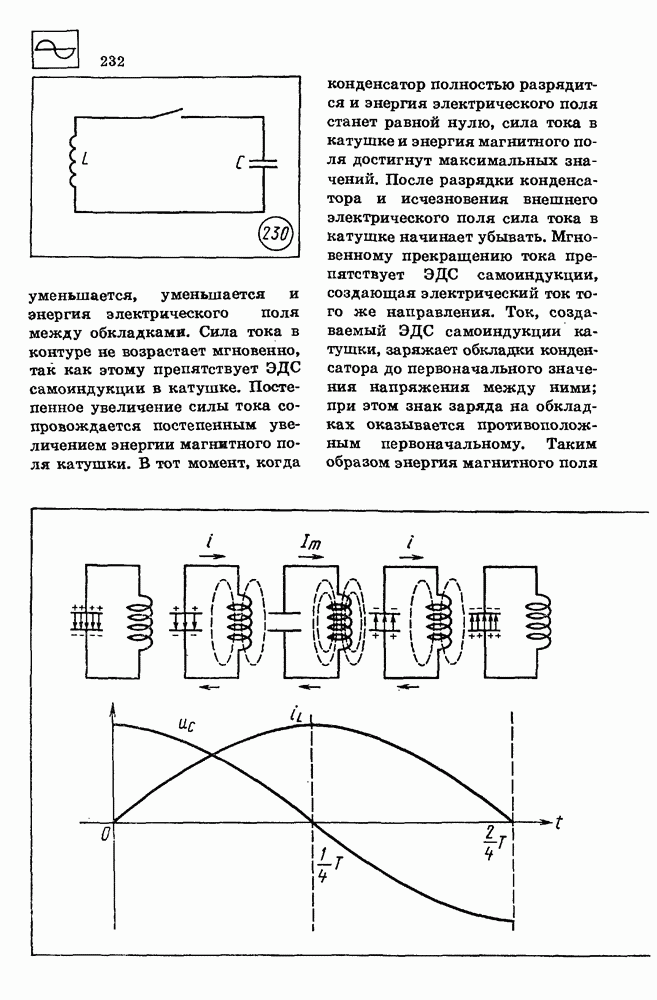
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Свободное падение тел.
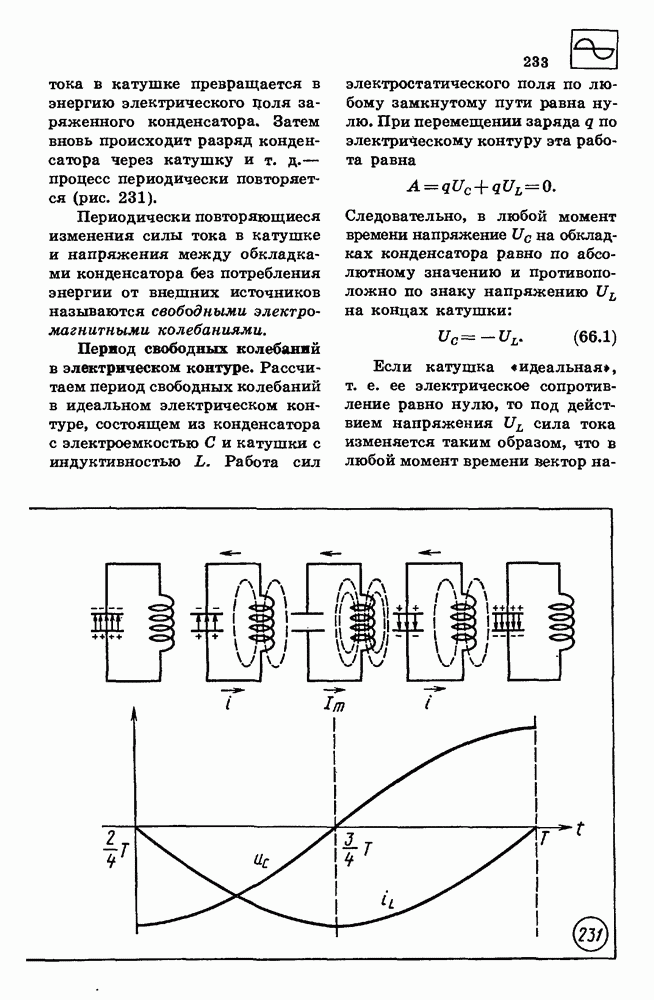
Падение тел на Землю в пустоте называется свободным падением тел. При падении в стеклянной трубке, из которой с помощью насоса откачан воздух, кусок свинца, пробка и легкое перо достигают дна одновременно (рис. 26). Следовательно, при свободном падении все тела независимо от их массы движутся одинаково.
Свободное падение является равноускоренным движением.
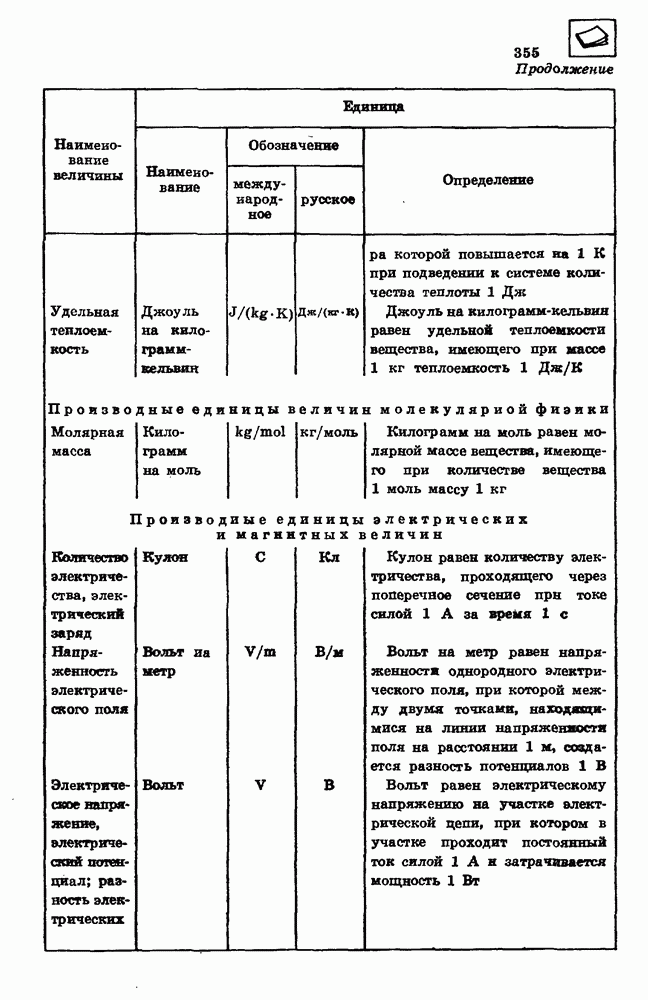
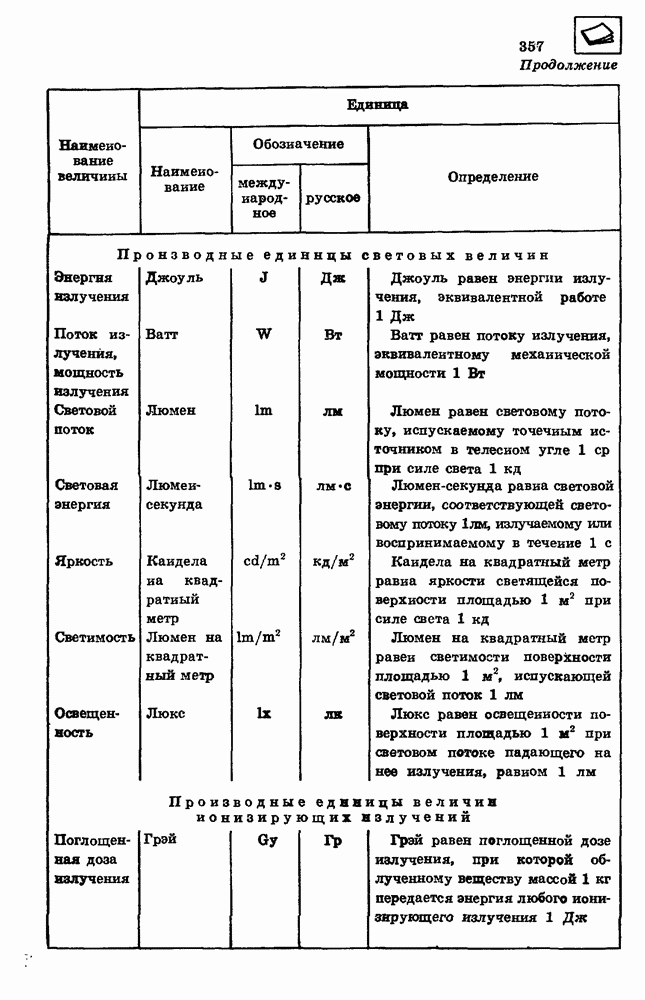
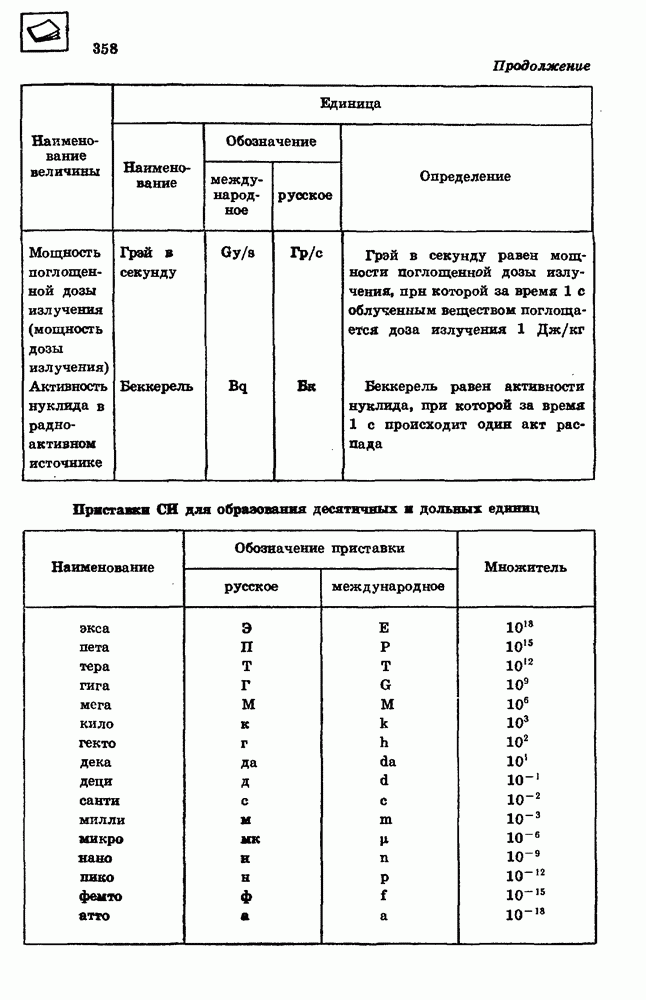
Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения. Ускорение свободного падения обозначается буквой g. У поверхности земного шара модуль ускорения свободного падения примерно равен

Если в расчетах не требуется высокая точность, то принимают, что модуль ускорения свободного падения у поверхности Земли равен 
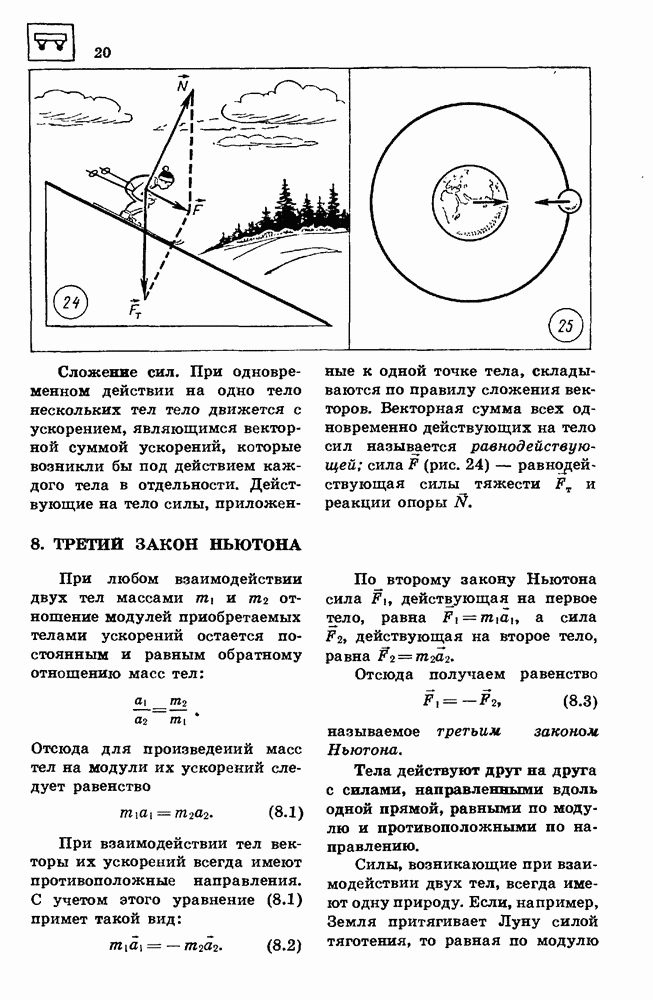
Одинаковое значение ускорения свободно падающих тел, имеющих разную массу, свидетельствует о том, что сила, под действием которой тело приобретает ускорение свободного падения, пропорциональна массе тела. Эта сила притяжения, действующая со стороны Земли на все тела, называется силой тяжести:



Сила тяжести действует на любое тело у поверхности Земли и на расстоянии  от поверхности, и на расстоянии 10 км, где летают самолеты. А действует ли сила тяжести на еще больших расстояниях от Земли? Зависят ли сила тяжести и ускорение свободного падения от расстояния до Земли? Над этими вопросами думали многие ученые, но впервые ответы на них дал в XVII в. великий английский физик Исаак Ньютон (1643— 1727).
от поверхности, и на расстоянии 10 км, где летают самолеты. А действует ли сила тяжести на еще больших расстояниях от Земли? Зависят ли сила тяжести и ускорение свободного падения от расстояния до Земли? Над этими вопросами думали многие ученые, но впервые ответы на них дал в XVII в. великий английский физик Исаак Ньютон (1643— 1727).
Зависимость силы тяжести от расстояния.
Ньютон предположил, что сила тяжести действует на любом расстоянии от Земли, но ее значение убывает обратно пропорционально квадрату расстояния от центра Земли. Проверкой этого предположения могло быть измерение силы притяжения какого-то тела, находящегося на большом расстоянии от Земли, и сравнение ее с силой притяжения того же тела у поверхности Земли.
Для определения ускорения движения тела под действием силы тяжести на большом расстоянии от Земли Ньютон воспользовался результатами астрономических наблюдений за движением Луны.
Он предположил, что сила притяжения, действующая со стороны Земли на Луну, есть та же самая сила тяжести, которая действует на любые тела у поверхности Земли. Следовательно, центростремительное ускорение при движении Луны по орбите вокруг Земли представляет собой ускорение свободного падения Луны на Землю.
Расстояние от центра Земли до центра Луны равно  км. Это примерно в 60 раз больше расстояния от центра Земли до ее поверхности.
км. Это примерно в 60 раз больше расстояния от центра Земли до ее поверхности.
Если сила тяжести убывает обратно пропорционально квадрату расстояния от центра Земли, то ускорение свободного падения на орбите Луны должно быть в  раза меньше ускорения свободного падения у поверхности Земли
раза меньше ускорения свободного падения у поверхности Земли 

По известным значениям радиуса орбиты Луны и периода ее обращения вокруг Земли Ньютон вычислил центростремительное ускорение Луны. Оно оказалось действительно равным 
Теоретически предсказанное значение ускорения свободного падения совпало со значением, полученным в результате астрономических наблюдений. Это доказывало справедливость предположения Ньютона о том, что сила тяжести убывает обратно пропорционально квадрату расстояния  от центра Земли:
от центра Земли:

Закон всемирного тяготения.
Подобно тому как Луна движется вокруг Земли, Земля в свою очередь обращается вокруг Солнца. Вокруг Солнца обращаются Меркурий, Венера, Марс, Юпитер и другие планеты
Солнечной системы. Ньютон доказал, что движение планет вокруг Солнца происходит под действием силы притяжения, направленной к Солнцу и убывающей обратно пропорционально квадрату расстояния от него. Земля притягивает Луну, а Солнце — Землю, Солнце притягивает Юпитер, а Юпитер — свои спутники и т. д. Отсюда Ньютон сделал вывод, что все тела во Вселенной взаимно притягивают друг друга.
Силу взаимного притяжения, действующую между Солнцем, планетами, кометами, звездами и другими телами во Вселенной, Ньютон назвал силой всемирного тяготения.
Сила всемирного тяготения, действующая на Луну со стороны Земли, пропорциональна массе Луны (см. формулу 9.1). Очевидно, что снла всемирного тяготения, действующая со стороны Луны на Землю, пропорциональна массе Земли. Эти силы по третьему закону Ньютона равны между собой. Следовательно, сила всемирного тяготения, действующая между Луной и Землей, пропорциональна массе Земли и массе Луны, т. е. пропорциональна произведению их масс.
Распространив установленные закономерности — зависимость силы тяжести от расстояния и от масс взаимодействующих тел — на взаимодействие всех тел во Вселенной, Ньютон открыл в 1682 г. закон всемирного тяготения: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними:

Векторы сил всемирного тяготения направлены вдоль прямой, соединяющей тела.
Закон всемирного тяготения в такой форме может быть использован для вычисления сил взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними. Ньютон доказал, что для однородных шарообразных тел закон всемирного тяготения в данной форме применим при любых расстояниях между телами. За расстояние  между телами в этом случае принимается расстояние между центрами шаров.
между телами в этом случае принимается расстояние между центрами шаров.
Силы всемирного тяготения называют гравитационными силами, а коэффициент пропорциональности  в законе всемирного тяготения называют гравитационной постоянной.
в законе всемирного тяготения называют гравитационной постоянной.
Гравитационная постоянная.
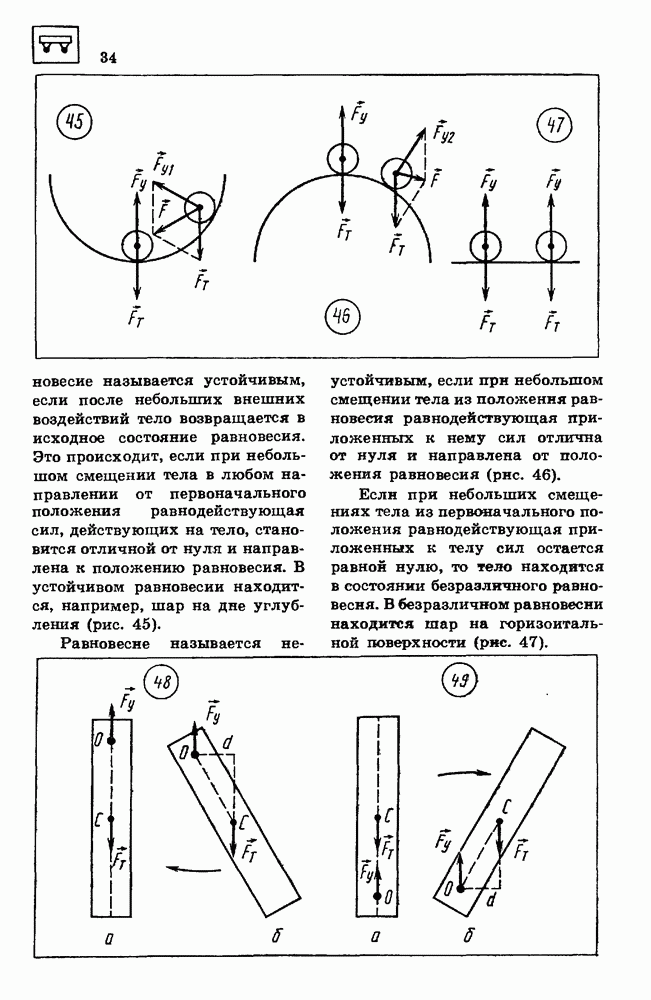
Если существует сила притяжения между земным шаром и куском мела, то, вероятно, существует сила притяжения и между половиной земного шара и куском мела. Продолжая мысленно такой процесс деления земного шара, мы придем к выводу, что гравитационные силы должны действовать между любыми телами, начиная от звезд и планет и кончая молекулами, атомами и элементарными частицами. Это предположение было доказано экспериментально английским физиком Генри Кавендишем (1731—1810) в 1788 г.
Кавендиш выполнил опыты по обнаружению гравитационного взаимодействия тел небольших
размеров с помощью крутильных весов. Два одинаковых небольших свинцовых шара диаметром примерно 5 см были укреплены на стержне длиной около  подвешенном на тонкой медной проволоке. Против малых шаров он устанавливал большие свинцовые шары диаметром 20 см каждый (рис. 27). Опыты показали, что при этом стержень с малыми шарами поворачивался, что говорит о наличии силы притяжения между свинцовыми шарами.
подвешенном на тонкой медной проволоке. Против малых шаров он устанавливал большие свинцовые шары диаметром 20 см каждый (рис. 27). Опыты показали, что при этом стержень с малыми шарами поворачивался, что говорит о наличии силы притяжения между свинцовыми шарами.
Повороту стержня препятствует сила упругости, возникающая при закручивании подвеса.
Эта сила пропорциональна углу поворота. Силу гравитационного взаимодействия шаров можно определить по углу поворота подвеса.
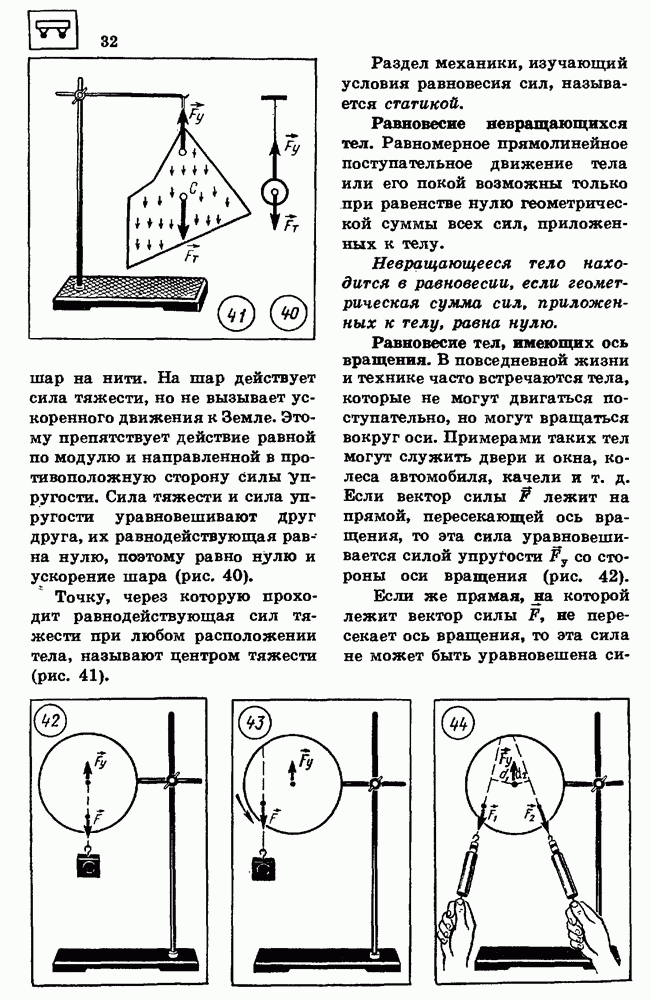
Массы шаров  расстояние
расстояние  между ними в опыте Кавендиша были известны, сила гравитационного взаимодействия
между ними в опыте Кавендиша были известны, сила гравитационного взаимодействия  измерялась непосредственно; поэтому опыт позволил определить гравитационную постоянную
измерялась непосредственно; поэтому опыт позволил определить гравитационную постоянную  в законе всемирного тяготения. По современным данным она равна
в законе всемирного тяготения. По современным данным она равна

| << Предыдущий параграф | Следующий параграф >> |
- 1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ
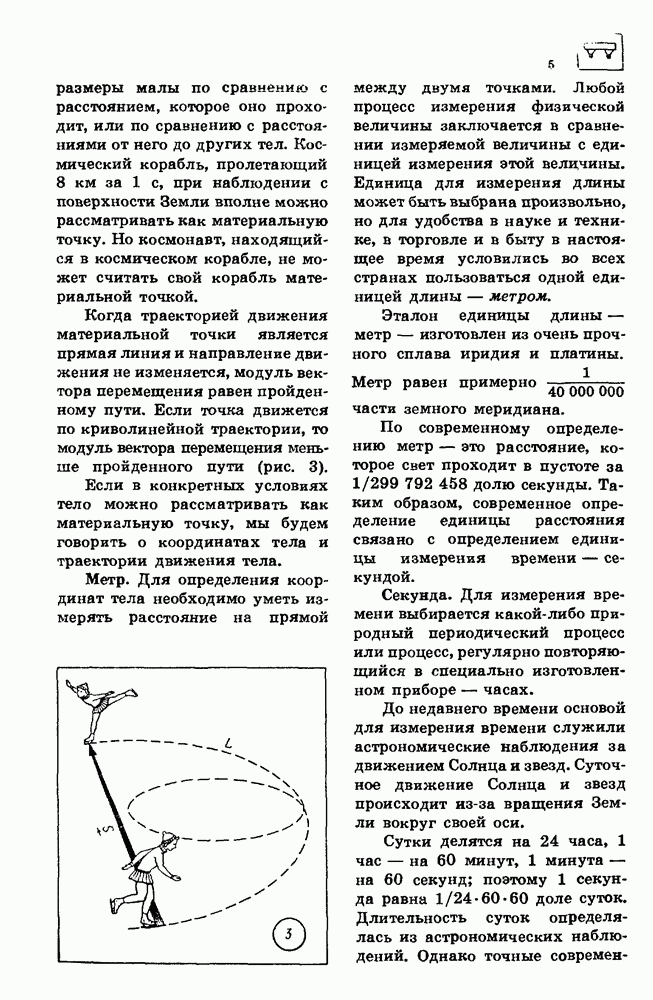
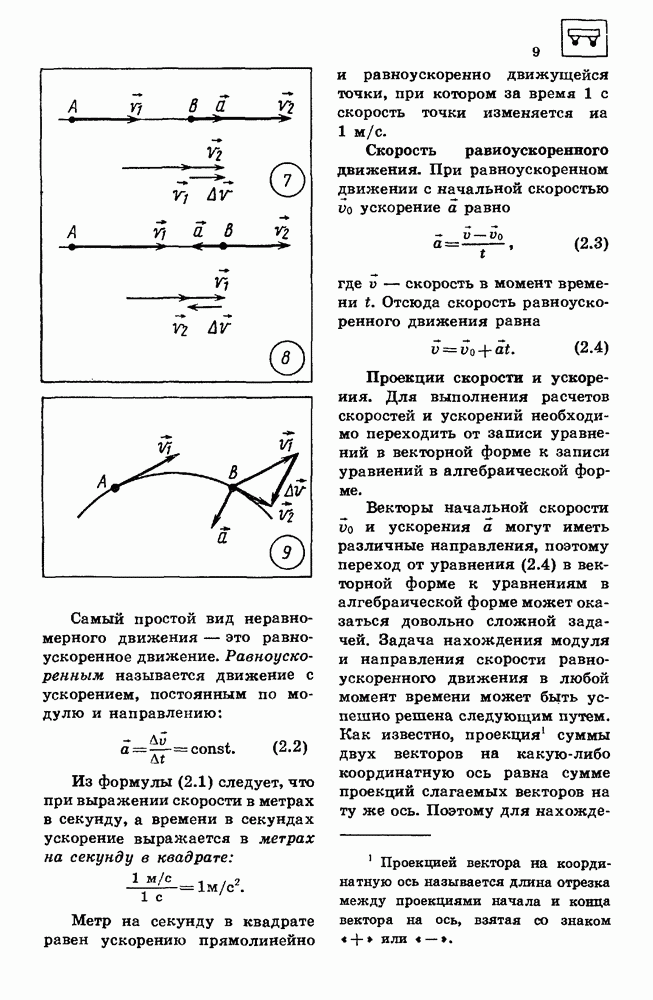
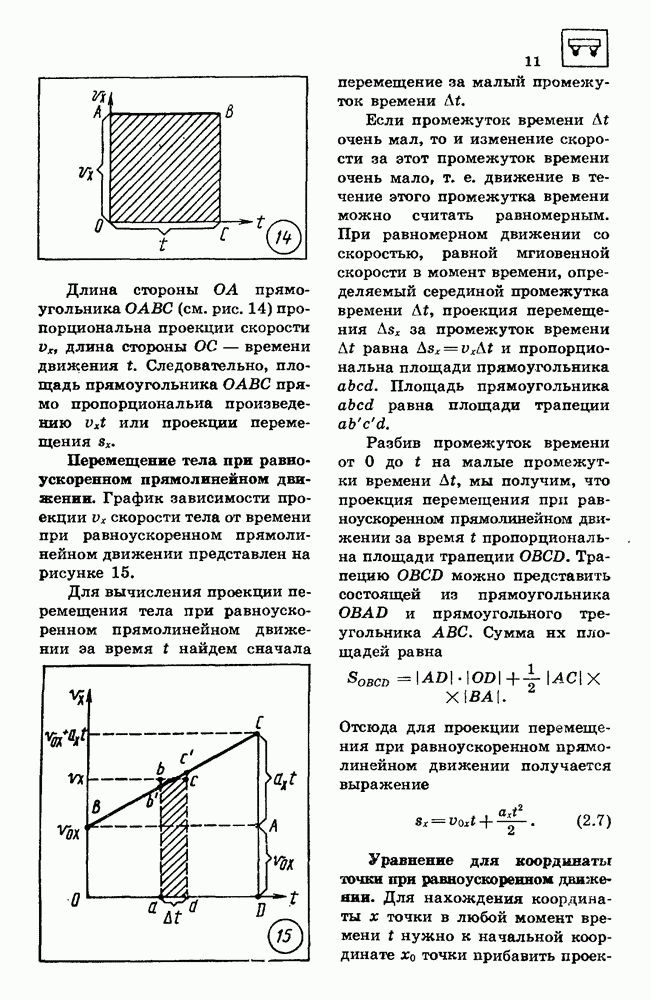
- 2. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ
- 3. РАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
- 4. ПЕРВЫЙ ЗАКОН НЬЮТОНА
- 5. МАССА ТЕЛА
- 6. СИЛА
- 7. ВТОРОЙ ЗАКОН НЬЮТОНА
- 8. ТРЕТИЙ ЗАКОН НЬЮТОНА
- 9. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
- 10. ВЕС И НЕВЕСОМОСТЬ
- 11. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
- 12. СИЛА УПРУГОСТИ
- 13. СИЛЫ ТРЕНИЯ
- 14. УСЛОВИЯ РАВНОВЕСИЯ ТЕЛ
- 15. ЭЛЕМЕНТЫ ГИДРОСТАТИКИ
- 16. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
- 17. РЕАКТИВНОЕ ДВИЖЕНИЕ
- 18. МЕХАНИЧЕСКАЯ РАБОТА
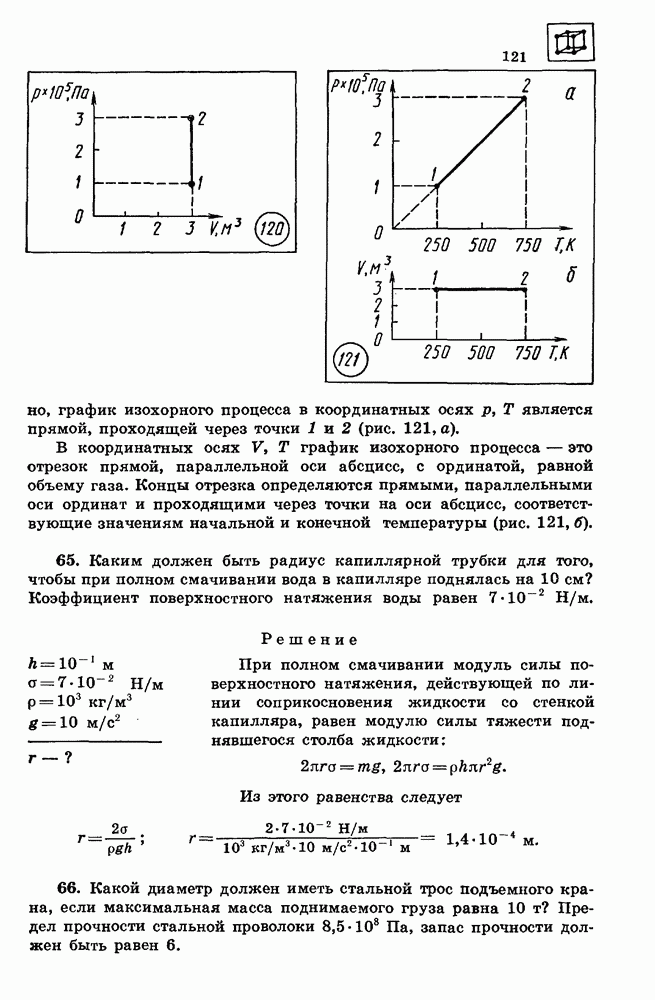
- 19. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
- 20. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
- 21. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ В МЕХАНИЧЕСКИХ ПРОЦЕССАХ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 22. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ И ИХ ОПЫТНОЕ ОБОСНОВАНИЕ
- 23. МАССА МОЛЕКУЛ
- 24. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОИ ТЕОРИИ ИДЕАЛЬНОГО ГАЗА
- 25. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- 28. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- 27. СВОЙСТВА ЖИДКОСТЕЙ
- 28. ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- 29. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
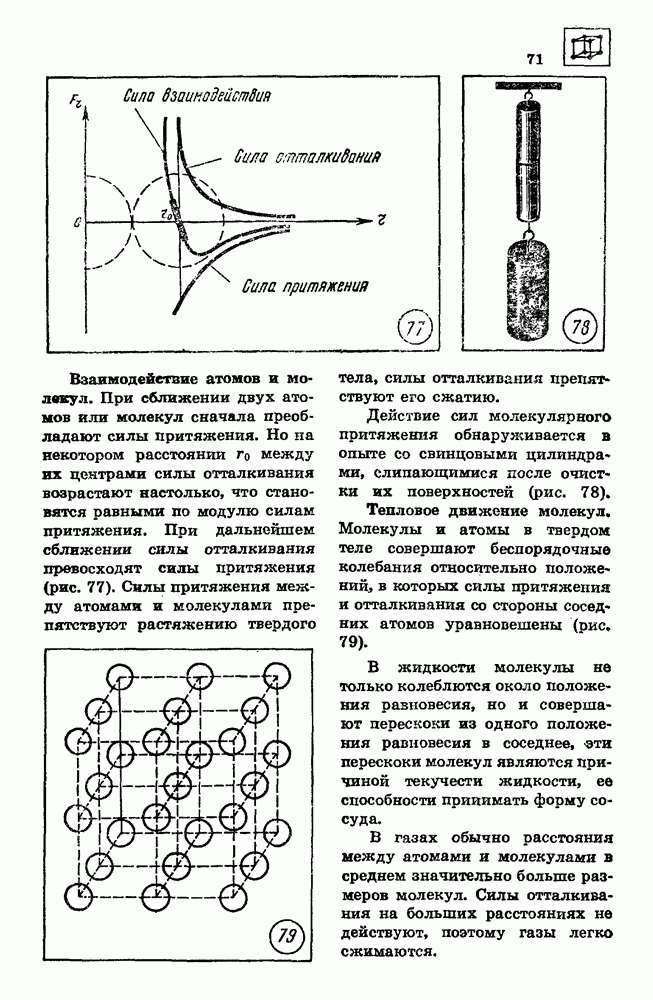
- 30. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ЦЕЛ
- 31. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- 32. КОЛИЧЕСТВО ТЕПЛОТЫ
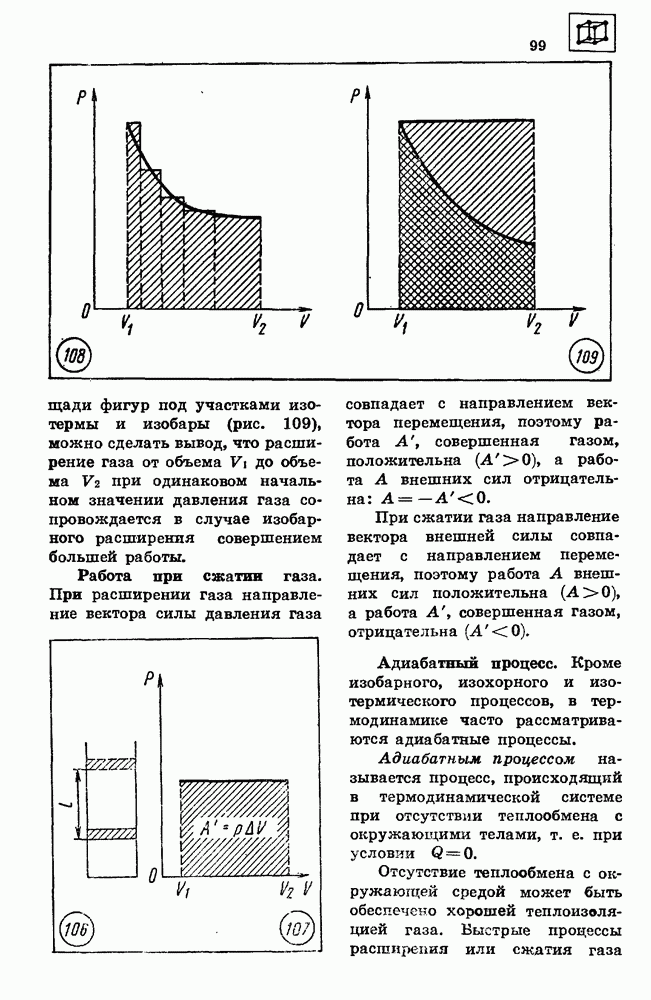
- 33. РАБОТА ПРИ ИЗМЕНЕНИИ ОБЪЕМА ГАЗА
- 34. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДБИГАТЕЛЕЙ
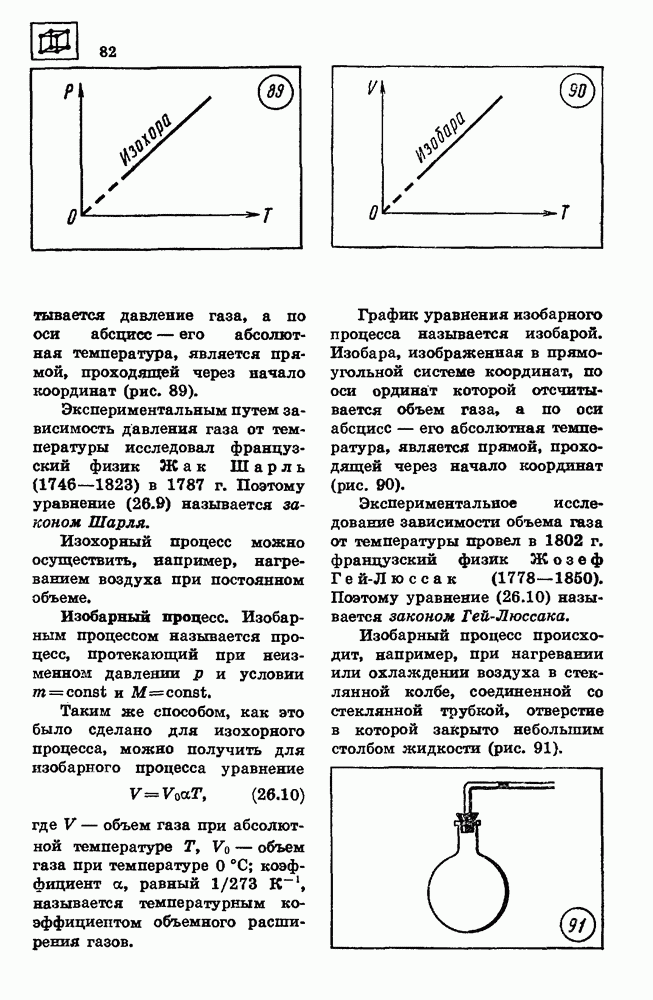
- 35. ТЕПЛОВЫЕ МАШИНЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 36. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- 37. ЗАКОН КУЛОНА
- 38. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
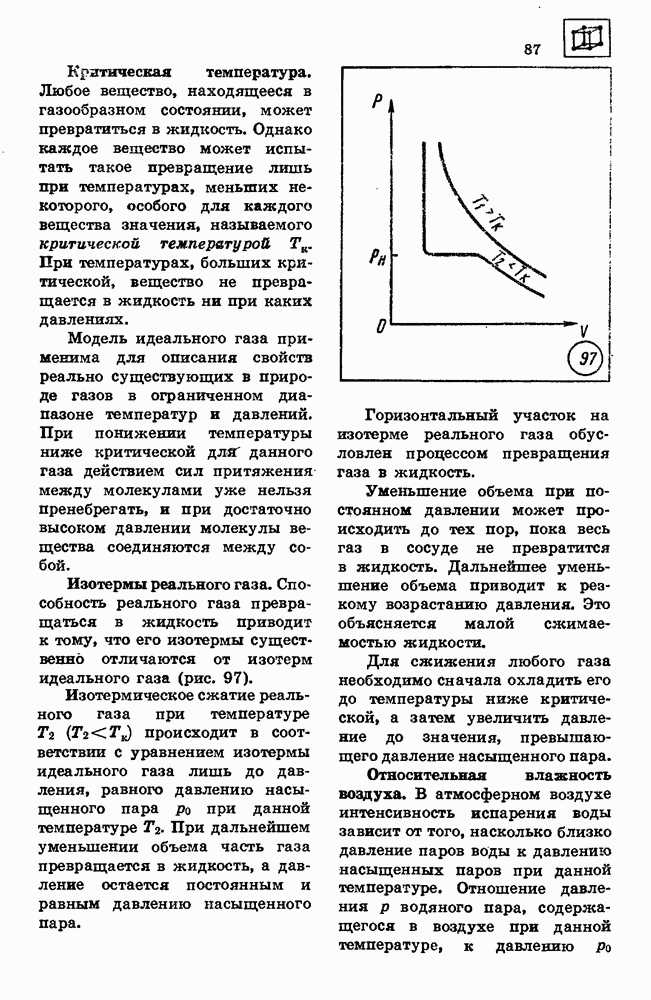
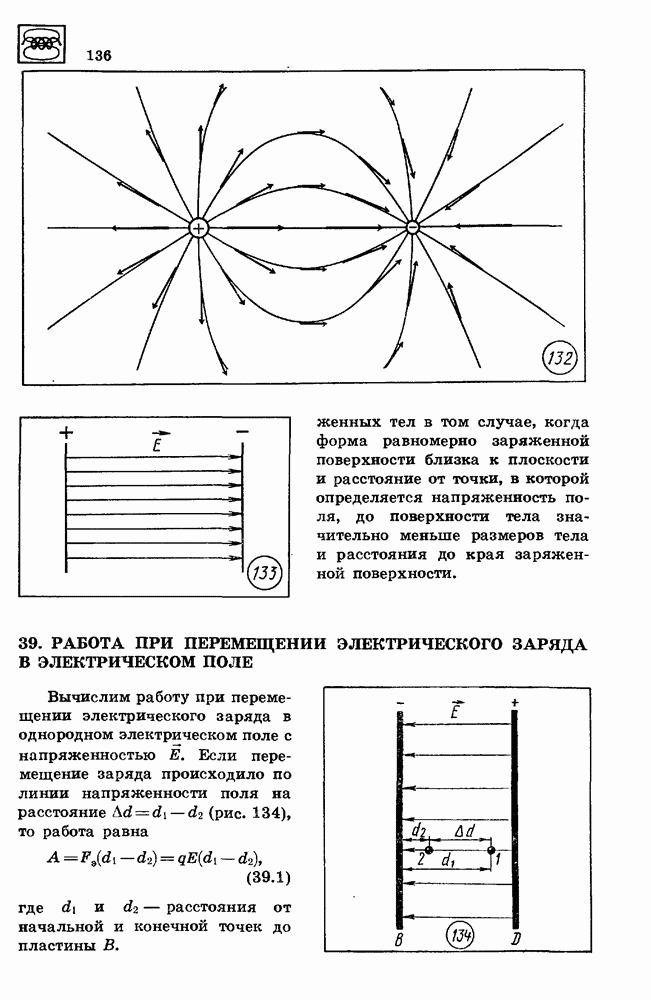
- 39. РАБОТА ПРИ ПЕРЕМЕЩЕНИИ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 40. ПОТЕНЦИАЛ
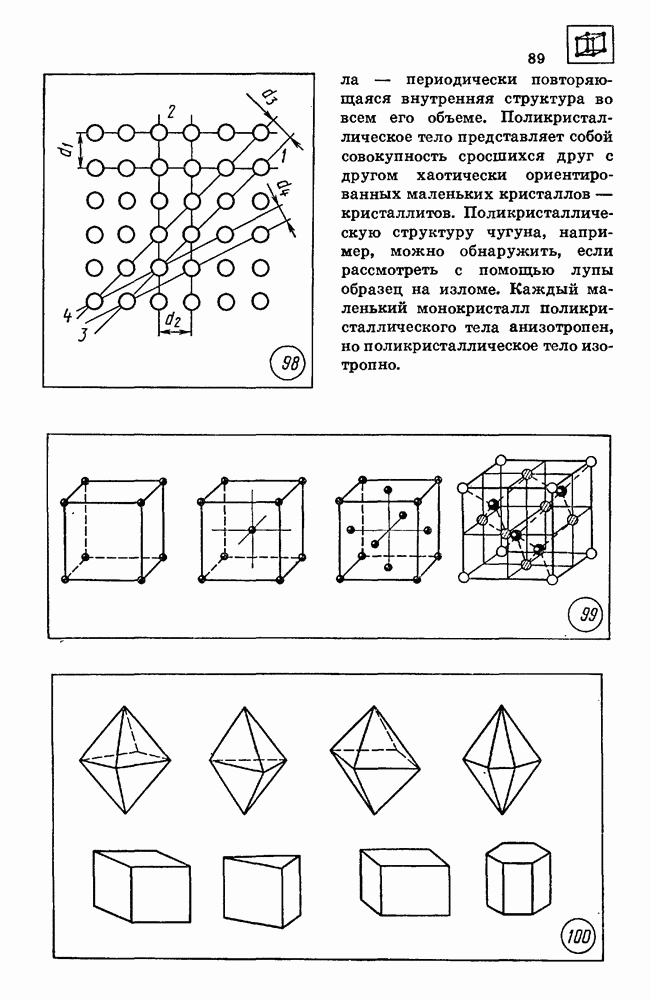
- 41. ВЕЩЕСТВО В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- 42. ЭЛЕКТРОЕМКОСТЬ
- 43. ЗАКОН ОМА
- 44. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
- 45. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
- 46. ПОЛУПРОВОДНИКОВЫЕ ПРИБОРЫ
- 47. ЭЛЕКТРИЧЕСКИЙ ТОК В ЭЛЕКТРОЛИТАХ
- 48. ОТКРЫТИЕ ЭЛЕКТРОНА
- 49. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- 50. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ
- 51. МАГНИТНОЕ ПОЛЕ
- 52. СИЛА ЛОРЕНЦА
- 53. ВЕЩЕСТВО В МАГНИТНОМ ПОЛЕ
- 54. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- 55. САМОИНДУКЦИЯ
- 56. МАГНИТНАЯ ЗАПИСЬ ИНФОРМАЦИИ
- 57. МАШИНА ПОСТОЯННОГО ТОКА
- 58. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 59. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
- 60. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- 61. ПРЕВРАЩЕНИЯ ЭНЕРГИИ ПРИ МЕХАНИЧЕСКИХ КОЛЕБАНИЯХ
- 62. РАСПРОСТРАНЕНИЕ КОЛЕБАНИИ В УПРУГОЙ СРЕДЕ
- 63. ЗВУКОВЫЕ ВОЛНЫ
- 64. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛН
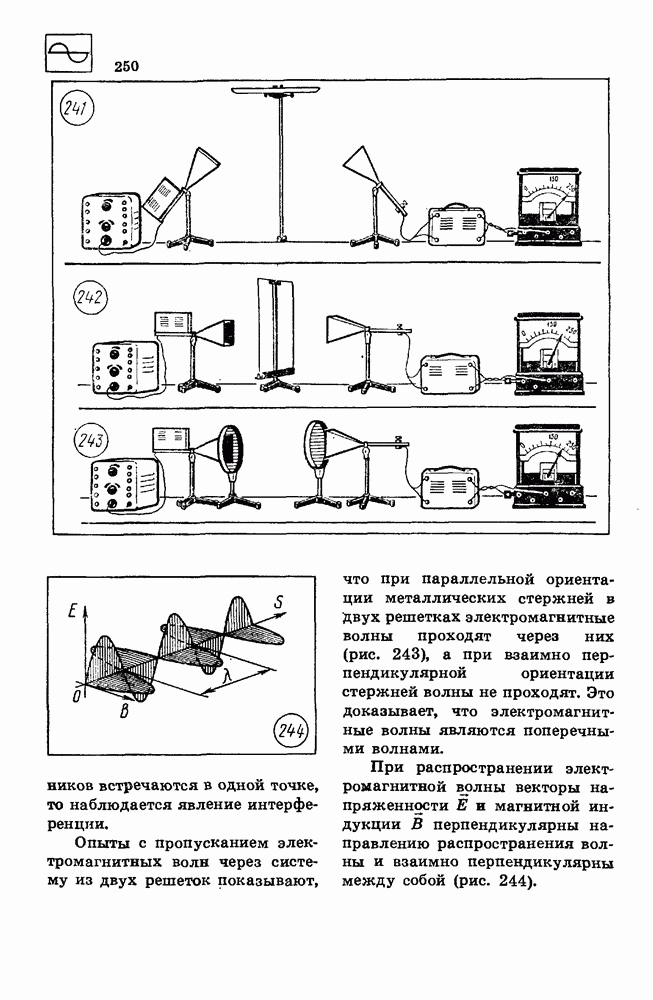
- 65. ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ И ПОЛЯРИЗАЦИЯ ВОЛН
- 66. СВОБОДНЫЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- 67. АВТОКОЛЕБАТЕЛЬНЫЙ ГЕНЕРАТОР НЕЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИИ
- 68. ПЕРЕМЕННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- 69. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 70. ИНДУКТИВНОСТЬ И ЕМКОСТЬ В ЦКТТИ ПЕРЕМЕННОГО ТОКА
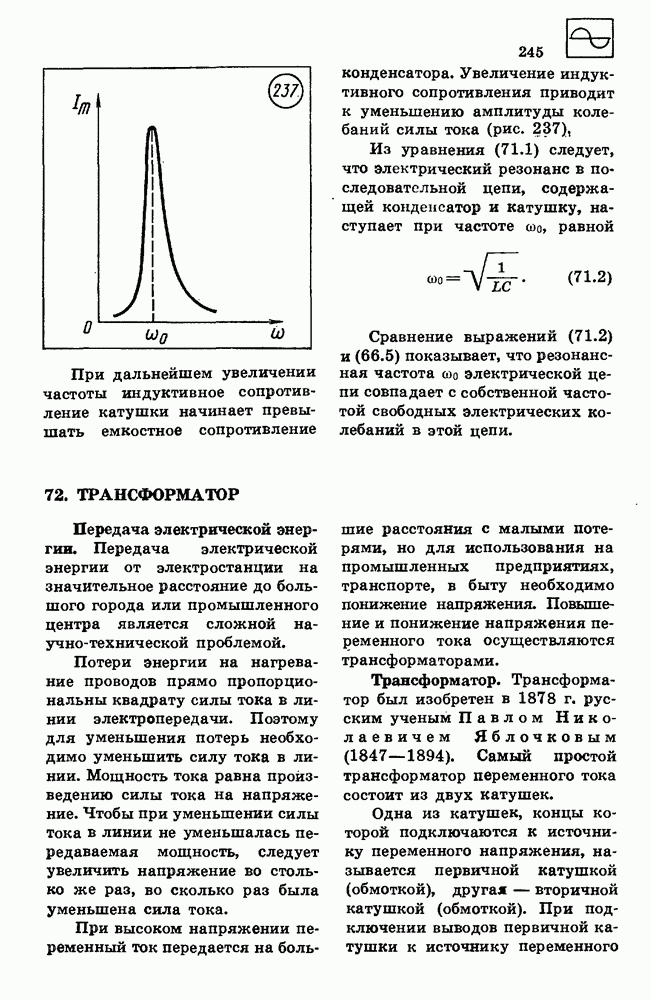
- 71. РЕЗОНАНС В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
- 72. ТРАНСФОРМАТОР
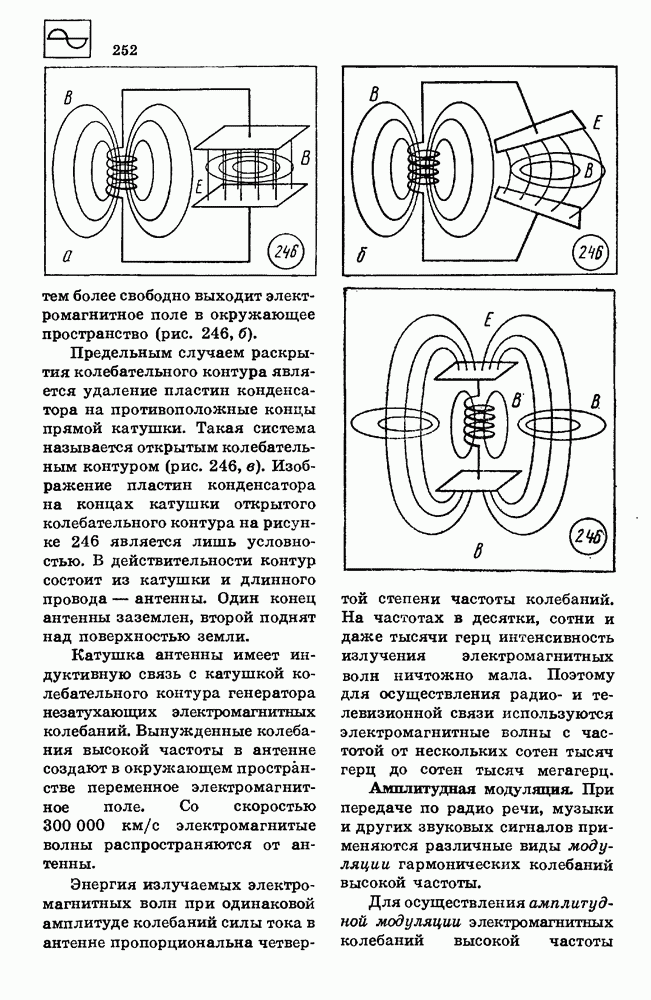
- 73. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- 74. ПРИНЦИПЫ РАДИОСВЯЗИ
- 75. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 76. РАЗВИТОЕ ПРЕДСТАВЛЕНИИ О ПРИРОДЕ СВЕТА
- 77. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
- 78. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 79. ОПТИЧЕСКИЕ ПРИБОРЫ
- 80. СПЕКТР ЭЛЕКТРОМАГНИТНЫХ ИЗЛУЧЕНИЙ
- 81. ЭЛЕМЕНТЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- 82. КВАНТОВЫЕ СВОЙСТВА СВЕТА
- 83. ДОКАЗАТЕЛЬСТВА СЛОЖНОЙ СТРУКТУРЫ АТОМОВ
- 84. КВАНТОВЫЕ ПОСТУЛАТЫ БОРА
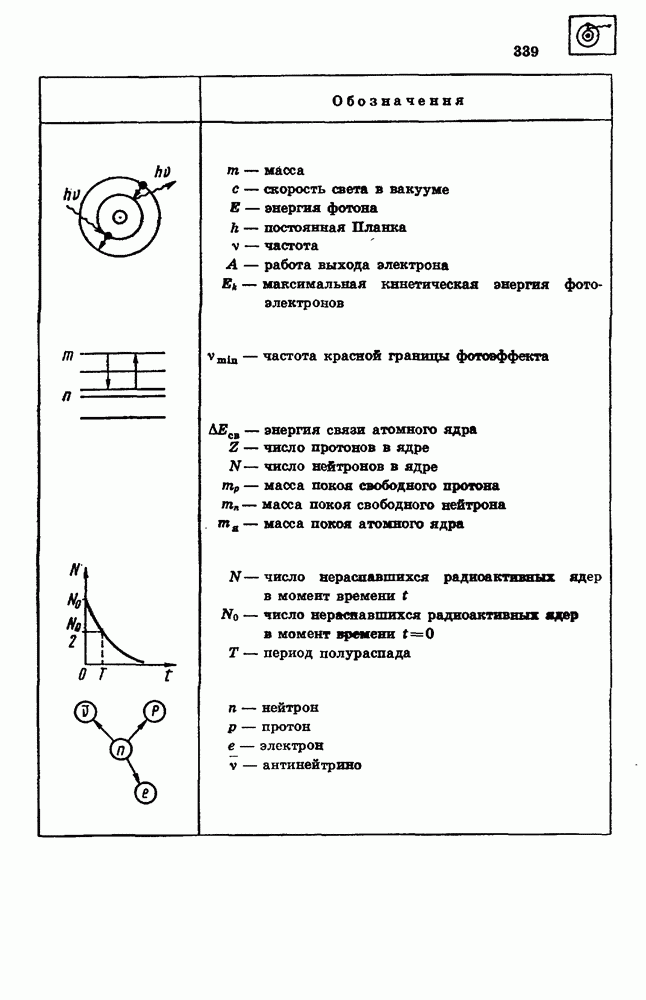
- 86. АТОМНОЕ ЯДРО
- 87. РАДИОАКТИВНОСТЬ
- 88. СВОЙСТВА ЯДЕРНЫХ ИЗЛУЧЕНИЙ
- 89. ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫ РЕГИСТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ
- 90. ЦЕПНАЯ РЕАКЦИЯ ДЕЛЕНИЯ ЯДЕР УРАНА
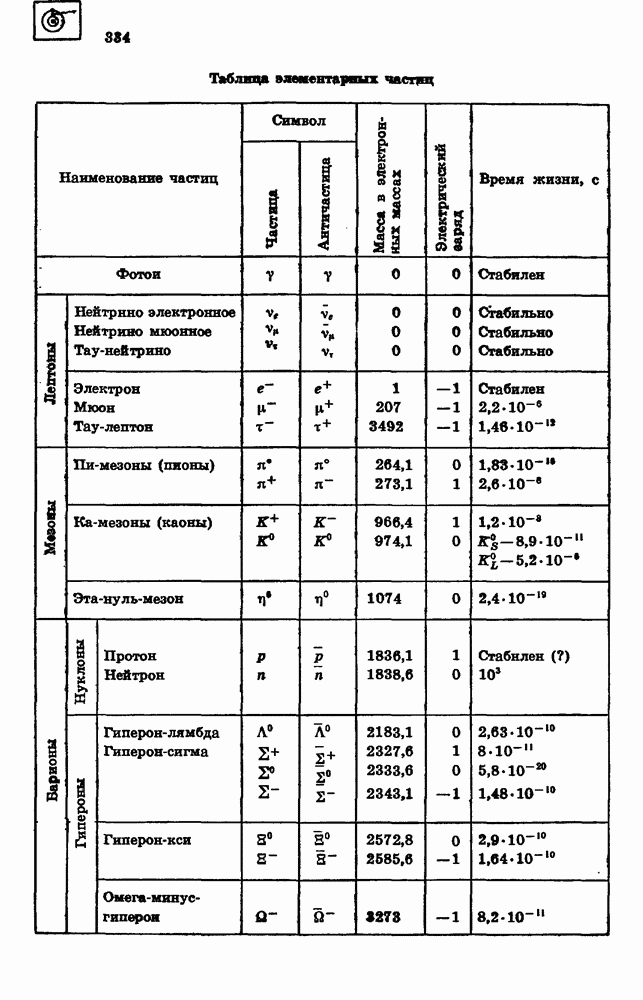
- 91. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- ПРИЛОЖЕНИЯ