| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
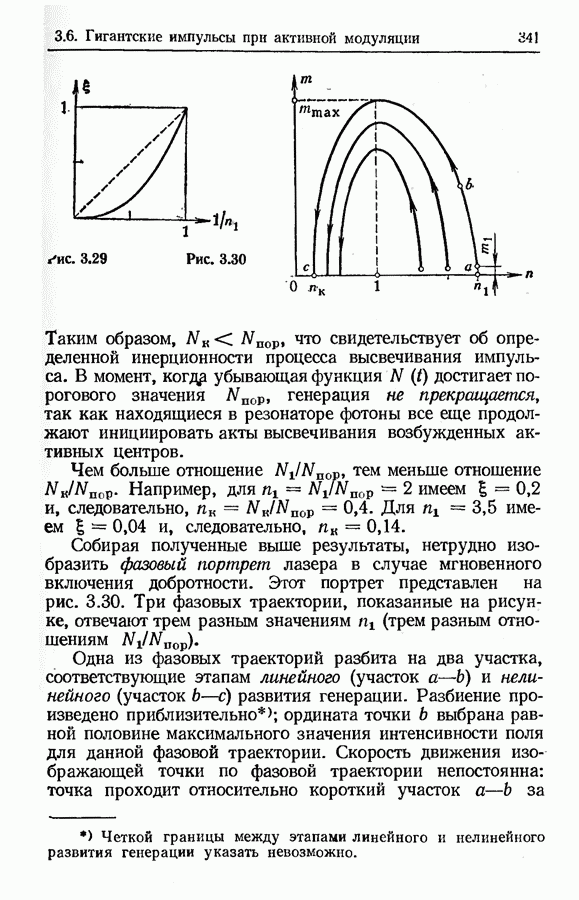
Режим генерации гигантских импульсов при различных временах включения добротности.
Усредненные по длине резонатора балансные уравнения (уравнения Статца—Де Марса) могут достаточно точно описывать процесс генерации лишь в тех случаях, когда длительность импульса больше времени двойного прохода излучения по резонатору. При рассмотрении же генерации достаточно коротких импульсов (длительностью менее 10 нс) требуется учет

Рис. 3.34
пространственных эффектов; в этом случае усредненные балансные  уравнения не годятся.
уравнения не годятся.
Более корректный подход основан на использовании балансных уравнений в частных производных (иначе говоря, балансных уравнений, не усредненных по длине резонатора). Входящие в эти уравнения плотности излучения и инверсной заселенности являются функциями не только времени, но и продольной пространственной координаты. Такой подход предпринят в [24]; была использована следующая система балансных уравнений в частных производных:

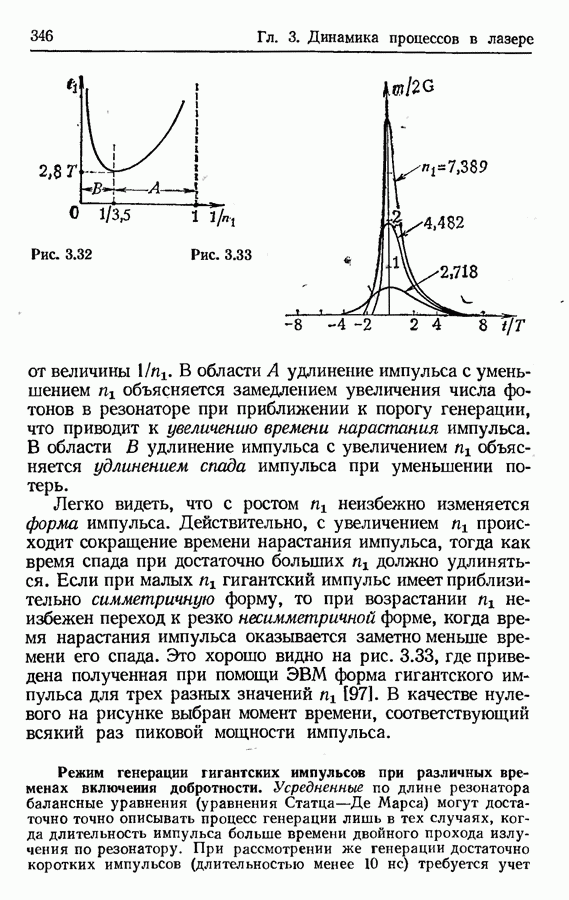
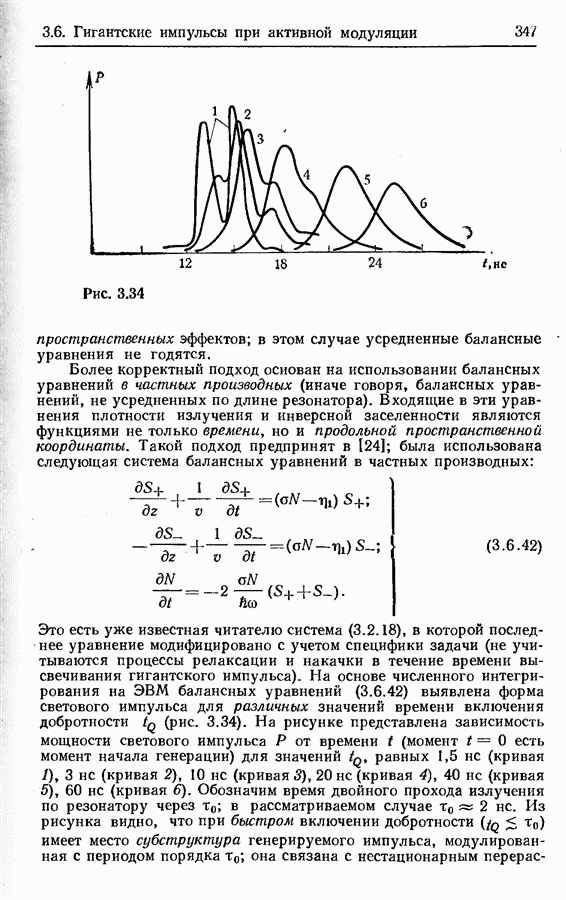
Это есть уже известная читателю система (3.2.18), в которой последнее уравнение модифицировано с учетом специфики задачи (не учитываются процессы релаксации и накачки в течение времени высвечивания гигг тского импульса). На основе численного интегрирования на ЭВМ балансных уравнений (3.6.42) выявлена форма светового импульса для различных значений времени включения добротности  (рис. 3.34). На рисунке представлена зависимость мощности светового импульса Р от времени
(рис. 3.34). На рисунке представлена зависимость мощности светового импульса Р от времени  (момент
(момент  есть момент начала генерации) для значений
есть момент начала генерации) для значений  равных 1,5 не (кривая 1), 3 не (кривая 2), 10 не (кривая 3), 20 не (кривая 4), 40 не (кривая 5), 60 не (кривая 6). Обозначим время двойного прохода излучения по резонатору через
равных 1,5 не (кривая 1), 3 не (кривая 2), 10 не (кривая 3), 20 не (кривая 4), 40 не (кривая 5), 60 не (кривая 6). Обозначим время двойного прохода излучения по резонатору через  в рассматриваемом случае
в рассматриваемом случае  не. Из рисунка видно, что при быстром включении добротности
не. Из рисунка видно, что при быстром включении добротности  имеет место субструктура генерируемого импульса, модулированная с периодом порядка
имеет место субструктура генерируемого импульса, модулированная с периодом порядка  она связана с нестационарным перераспределением
она связана с нестационарным перераспределением

Рис. 3.35
интенсивности поля и плотности инверсной заселенности по длине активного элемента.
Увеличение времени включения добротности приводит к исчезновению указанной выше субструктуры гигантского импульса, при этом наблюдается возрастание времени линейного развития импульса (времени  ) и падение энергии импульса. Последнее связано с тем, что при
) и падение энергии импульса. Последнее связано с тем, что при  развитие генерации начинает протекать в условиях больших потерь.
развитие генерации начинает протекать в условиях больших потерь.
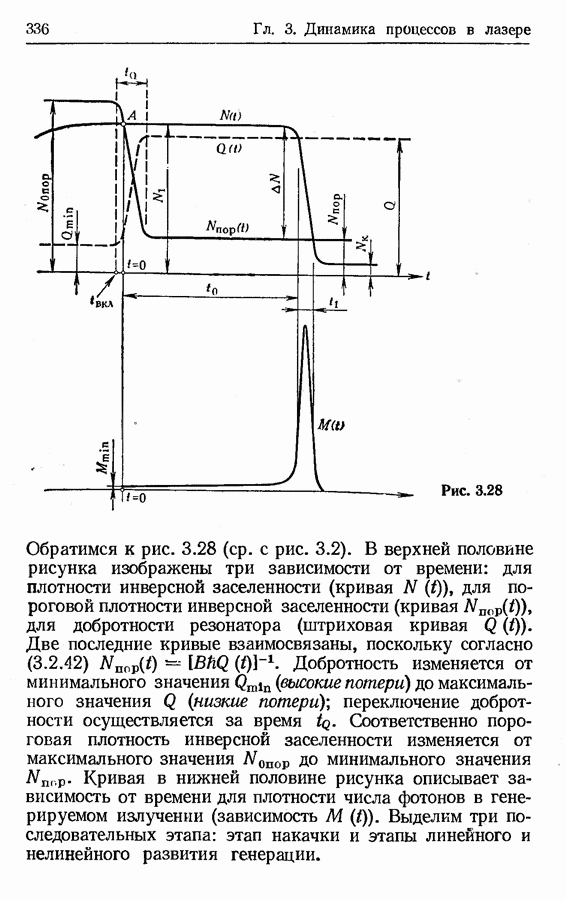
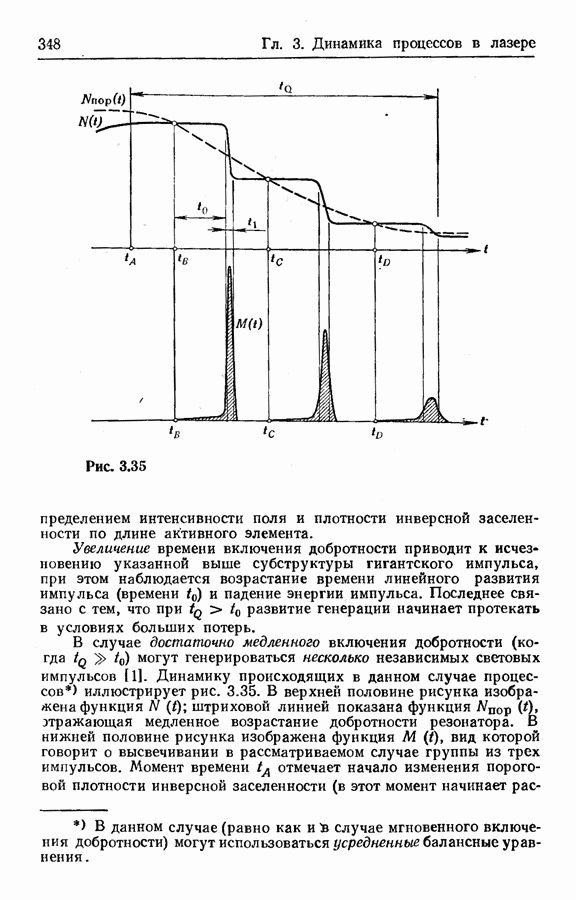
В случае достаточно медленного включения добротности (когда  ) могут генерироваться несколько независимых световых импульсов [1]. Динамику происходящих в данном случае процессов иллюстрирует рис. 3.35. В верхней половине рисунка изображена функция
) могут генерироваться несколько независимых световых импульсов [1]. Динамику происходящих в данном случае процессов иллюстрирует рис. 3.35. В верхней половине рисунка изображена функция  штриховой линией показана функция
штриховой линией показана функция  отражающая медленное возрастание добротности резонатора. В нижней половине рисунка изображена функция
отражающая медленное возрастание добротности резонатора. В нижней половине рисунка изображена функция  вид которой говорит о высвечивании в рассматриваемом случае группы из трех импульсов. Момент времени
вид которой говорит о высвечивании в рассматриваемом случае группы из трех импульсов. Момент времени  отмечает начало изменения пороговой плотности инверсной заселенности (в этот момент начинает
отмечает начало изменения пороговой плотности инверсной заселенности (в этот момент начинает

Рис. 3.36

Рис. 3.37
расти добротность). В момент  кривые
кривые  пересекаются — начинается генерация первого импульса, проходящая последовательно этапы линейного (длительность
пересекаются — начинается генерация первого импульса, проходящая последовательно этапы линейного (длительность  и нелинейного (М развития. В результате высвечивания первого импульса инверсная заселенность падает ниже порога. Продолжающееся понижение порога, обусловливает в момент времени
и нелинейного (М развития. В результате высвечивания первого импульса инверсная заселенность падает ниже порога. Продолжающееся понижение порога, обусловливает в момент времени  новое пересечение кривых
новое пересечение кривых  ; в этот момент начинается генерация второго импульса. Позднее, в момент
; в этот момент начинается генерация второго импульса. Позднее, в момент  начинается генерация третьего импульса. Процесс высвечивания импульсов прекращается, когда устанавливается постоянное значение порога, отвечающее максимальной добротности.
начинается генерация третьего импульса. Процесс высвечивания импульсов прекращается, когда устанавливается постоянное значение порога, отвечающее максимальной добротности.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава I. СПОСОБЫ ПОЛУЧЕНИЯ ИНВЕРТИРОВАННЫХ АКТИВНЫХ СРЕД
- Квантовый выход и коэффициент полезного действия лазера.
- Условие инверсии для четырехуровневой модели (стационарная накачка).
- Механизмы заселения уровней (механизмы возбуждения).
- Механизмы очищения уровней (механизмы релаксации).
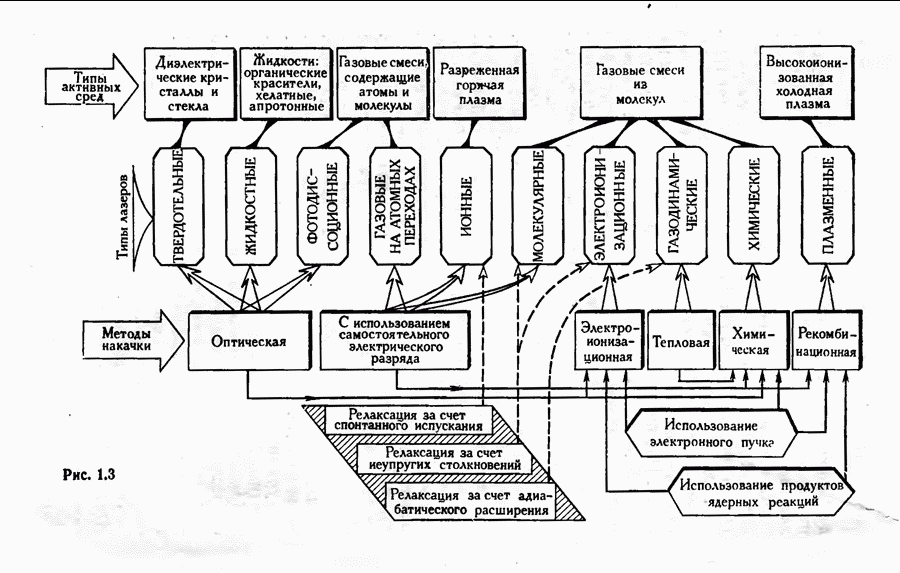
- Классификация лазеров с учетом различных методов накачки.
- Некоторые проблемы, возникающие при непрерывной генерации; столкновительные лазеры.
- Преимущества импульсной накачки; генерация на самоограниченных переходах.
- Лазеры на разлетных молекулах.
- 1.2. Оптическая накачка. Твердотельные лазеры
- Условия реализации стационарной инверсии при оптической накачке.
- Твердотельные лазеры: вопросы практической реализации оптической накачки, рабочие схемы лазеров.
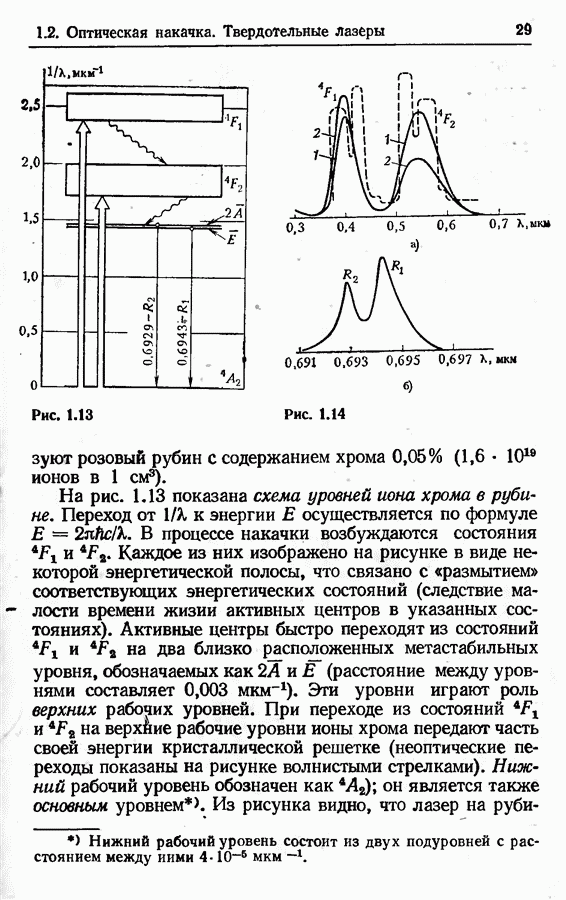
- Лазер на рубине.
- Лазер на иттрий-алюминиевом гранате с неодимом.
- Оптическая накачка полупроводниковым лазером или светодиодом.
- 1.3. Лазеры на органических красителях
- Оптическая накачка лазеров на красителях.
- Схема уровней и основные переходы.
- Перестройка длины волны генерации; селективные резонаторы.
- Проблема расширения диапазона перестройки длины волны генерации.
- 1.4. Газовые лазеры с широкополосной оптической накачкой
- Возможность широкополосной оптической накачки в газах; фотодиссоционные лазеры.
- Фотодиссоционный йодный лазер.
- Проблема прямого преобразования солнечной энергии в лазерное излучение.
- 1.5. Накачка с использованием самостоятельного электрического разряда в разреженных газах
- Электрические разряды, применяемые в газоразрядных лазерах.
- Аргоновый лазер [39].
- Механизм возникновения инверсии в аргоновом лазере.
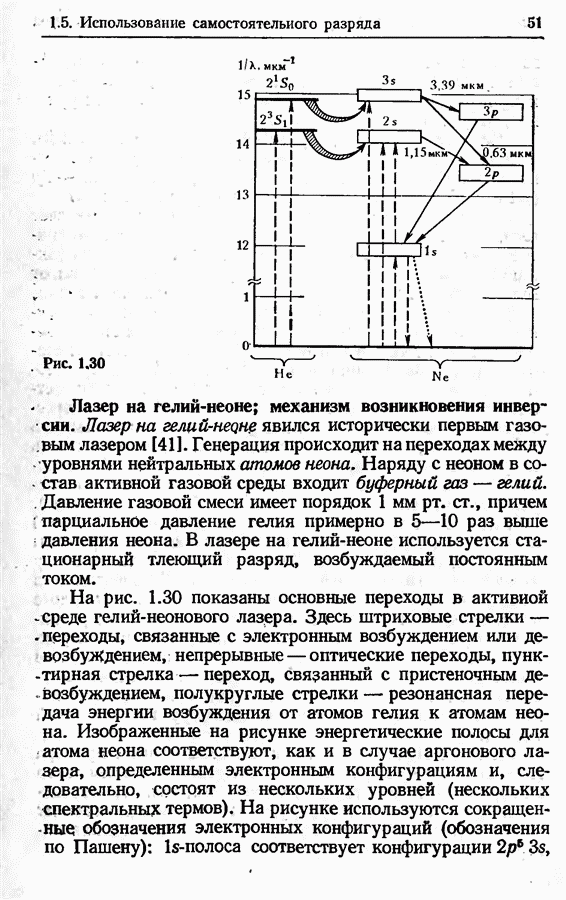
- Лазер на гелий-неоне; механизм возникновения инверсии.
- Лазер на парах меди [5].
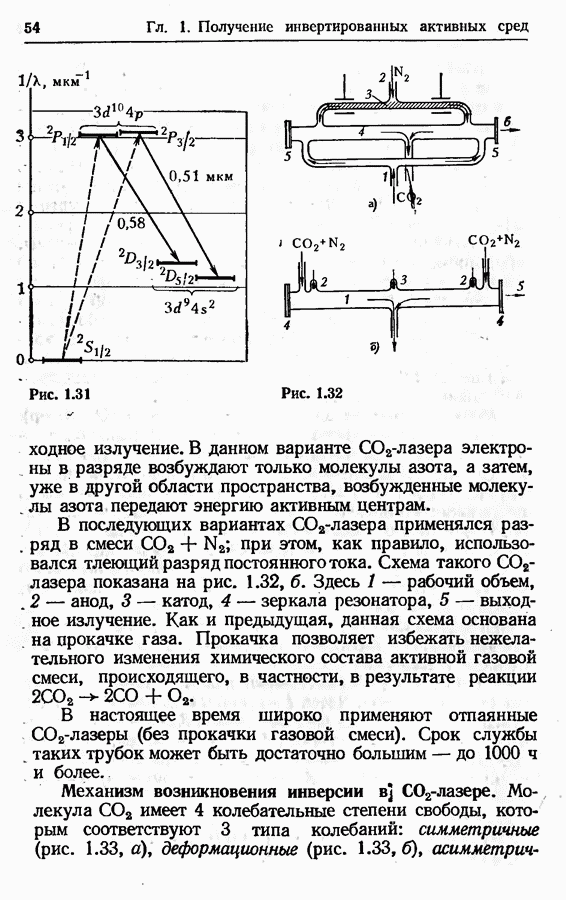
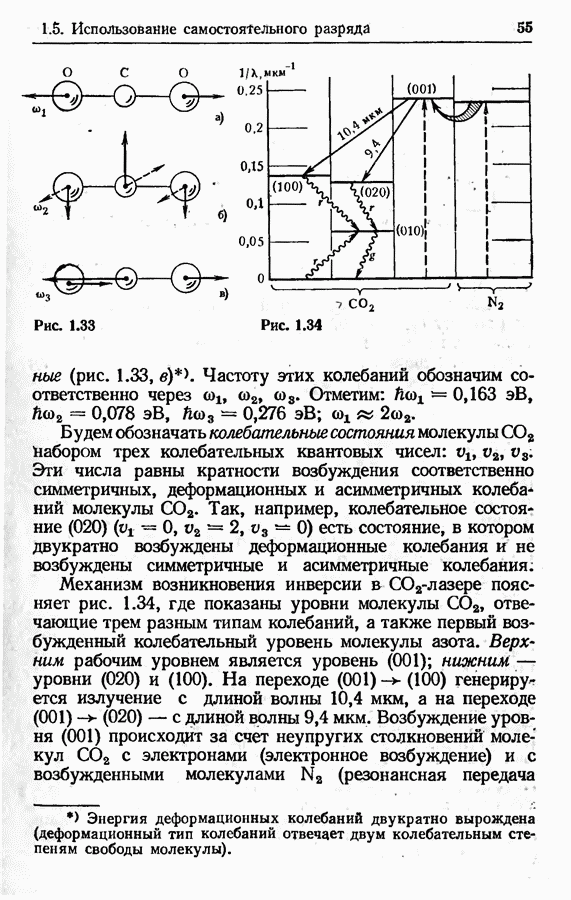
- Молекулярный лазер на двуокиси углерода (CO2-лазер).
- Механизм возникновения инверсии в CO2-лазере.
- 1.6. Электроионизационные лазеры
- Электроионизационный метод накачки газовых лазеров высокого давления.
- Электроионизационный CO2-лазер.
- Использование различных активных сред.
- Способы ионизации.
- 1.7. Газодинамические лазеры (тепловая накачка)
- Газодинамический CO2-лазер.
- Механизм возникновения инверсии в газодинамическом CO2-лазере.
- Пути повышения КПД газодинамических лазеров.
- 1.8. Химические лазеры
- Цепной характер химических реакций; химическая и лазерная длина цепи.
- Лазеры с прямым и непрямым образованием инверсии.
- Химический лазер на фторводородной смеси с непрямым образованием инверсии [63].
- Химические лазеры на сероуглероде (химические СО-лазеры).
- Химические лазеры на электронных переходах молекул.
- 1.9. Плазменные лазеры (рекомбинационная накачка)
- Принципиальные вопросы создания лазера на рекомбинирующей плазме.
- «Открытая» двухуровневая модель плазменного лазера.
- Проблема очищения нижнего рабочего уровня.
- Импульсные плазменные лазеры.
- Плазменные лазеры с использованием жестких ионизаторов; реактор-лазер.
- Плазмодинамические лазеры.
- Плазмохимические лазеры.
- Список литературы
- Глава 2. ФОРМИРОВАНИЕ ПОЛЯ ИЗЛУЧЕНИЯ В РЕЗОНАТОРЕ ЛАЗЕРА
- Начальный коэффициент усиления для оптически разрешенных и запрещенных рабочих переходов.
- Зависимость начального коэффициента усиления от скорости накачки.
- Зависимость начального коэффициента усиления от частоты.
- 2.2. Онтический резонатор и лазерное излучение (начальные сведения)
- Резонансные частоты.
- Моды (типы колебаний) оптического резонатора.
- Роль оптического резонатора в лазере.
- Пассивные и активные резонаторы.
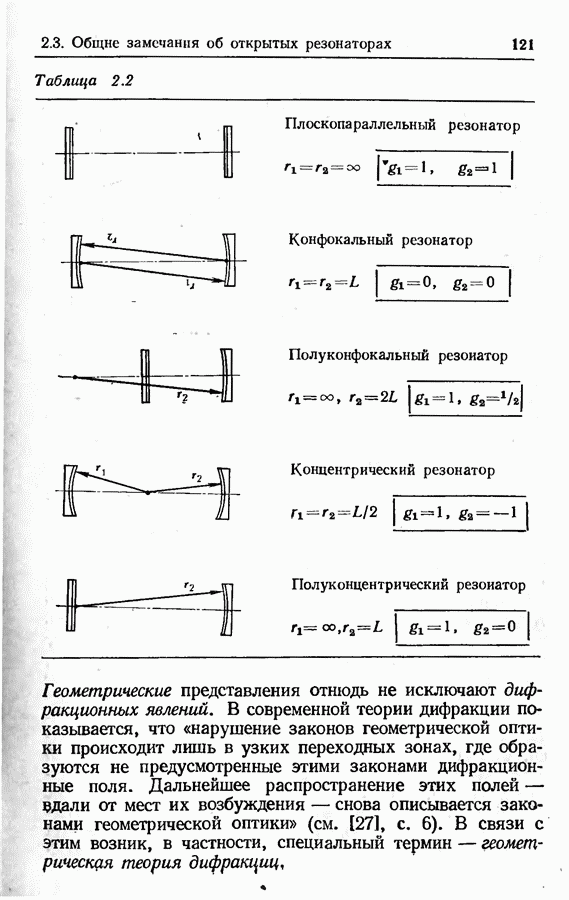
- 2.3. Общие замечания об открытых резонаторах
- Добротность резонатора.
- Добротность и моды открытого резонатора.
- Дифракционные потери. Число Френеля.
- Основные параметры пассивного резонатора, образованного двумя зеркалами (сферическими либо плоскими).
- Геометрическое приближение.
- 2.4. Линзовые волноводы и открытые резонаторы (приближение геометрической оптики)
- Условие устойчивости для линзового волновода с чередующимися линзами.
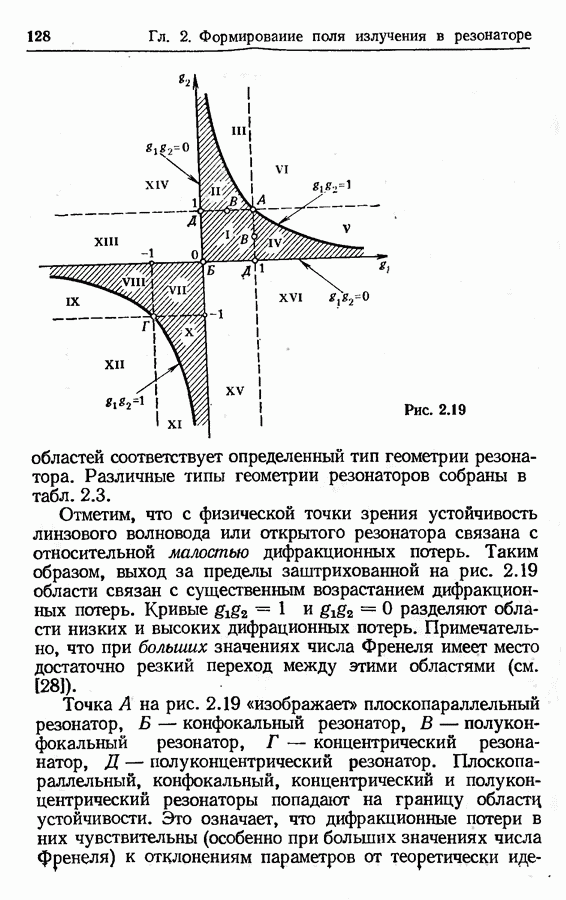
- Устойчивые и неустойчивые открытые резонаторы; диаграмма устойчивости.
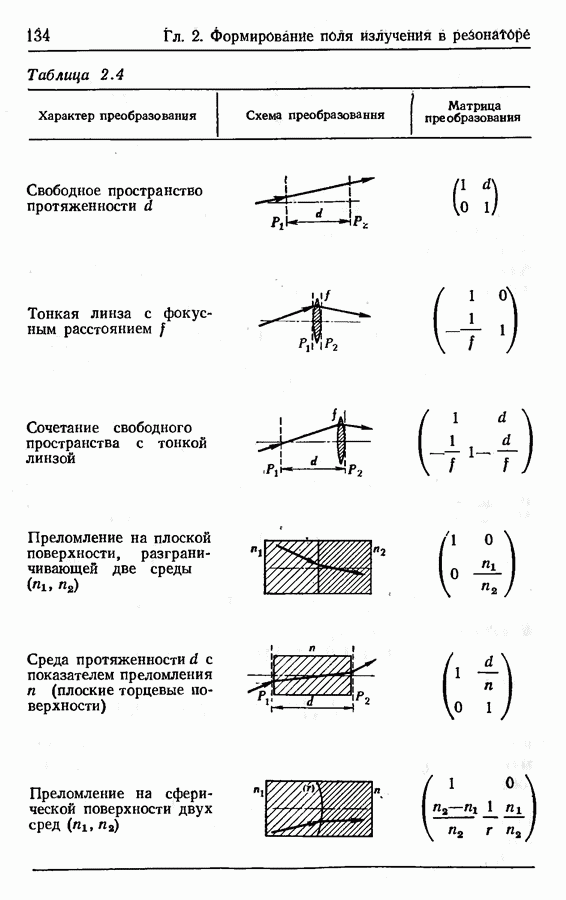
- Матрица передачи светового луча.
- Матрица передачи луча для двойного прохода резонатора.
- 2.5. Расстройка открытого резонатора
- Резонатор с разъюстированным оптическим элементом.
- 2.6. Рассмотрение открытых резонаторов на основе итерационного метода Фокса — Ли. Эквивалентные резонаторы
- Интегральное уравнение Фокса — Ли.
- Поперечные моды открытого резонатора.
- Резонатор, образованный двумя сферическими зеркалами.
- Конфокальный резонатор
- Учет величины апертуры зеркал резонатора.
- Эквивалентные резонаторы.
- Резонатор, эквивалентный резонатору с внутренней линзой.
- Резонатор с диафрагмой.
- 2.7. Гауссовы пучки
- Распространение гауссова пучка в свободном пространстве.
- Радиус кривизны поверхности постоянной фазы.
- Основные соотношения, связывающие параметры гауссова пучка.
- Комплексные параметры гауссова пучка.
- Гауссов пучок как решение параболического уравнения.
- Обобщение на моды высоких порядков.
- 2.8. Преобразование и согласование гауссовых пучков
- Линза как фазовый корректор.
- Преобразование гауссова пучка в линзе.
- Преобразование гауссова пучка в линзовой системе.
- Преобразование гауссова пучка в квадратичной среде.
- Согласование гауссовых пучков.
- 2.9. Гауссовы пучки в устойчивых резонаторах
- Гауссов пучок в резонаторе (большие апертуры зеркал).
- Замечания, связанные с учетом апертуры зеркал.
- Фазовый сдвиг для гауссова пучка и спектр резонансных частот.
- Применение закона ABCD к рассмотрению поля в резонаторе.
- Неопределенность каустики конфокального резонатора с неограниченными апертурами зеркал.
- Конфокальный резонатор с конечными апертурами зеркал.
- Конфокальный резонатор с диафрагмой.
- 2.10. Неустойчивые резонаторы
- Потери в неустойчивом резонаторе по геометрооптической теории.
- Применение закона ABCD к неустойчивым резонаторам.
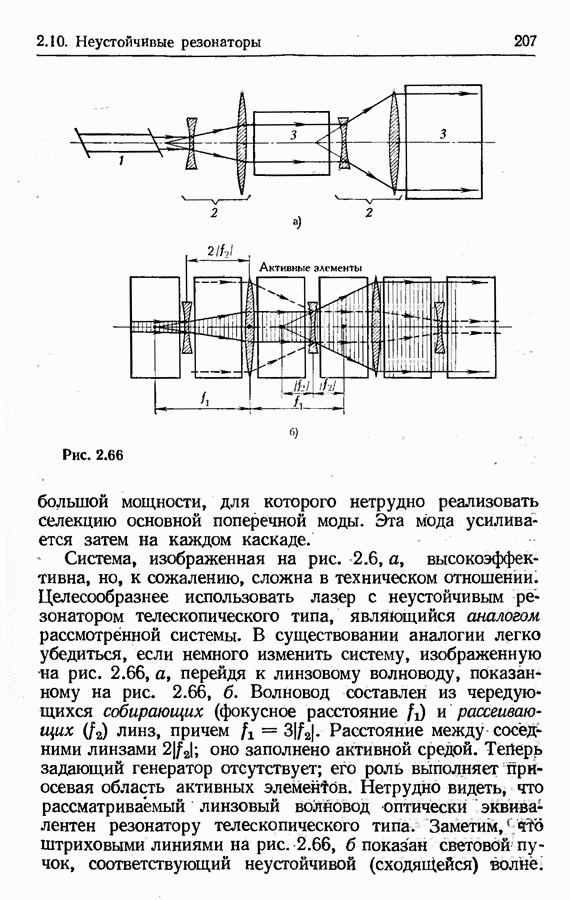
- Лазер с неустойчивым резонатором телескопического типа.
- Учет дифракции на крае зеркала; эквивалентное число Френеля.
- Преимущества неустойчивых резонаторов.
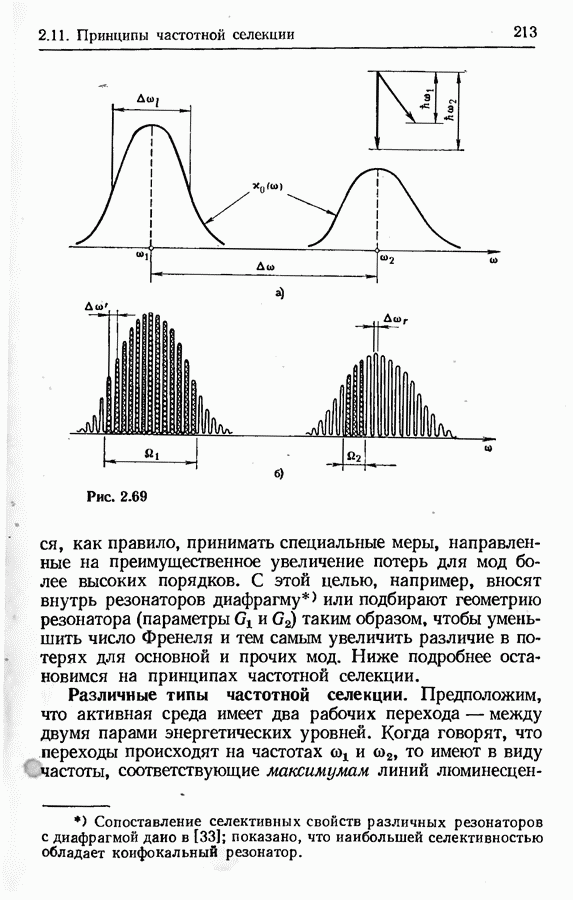
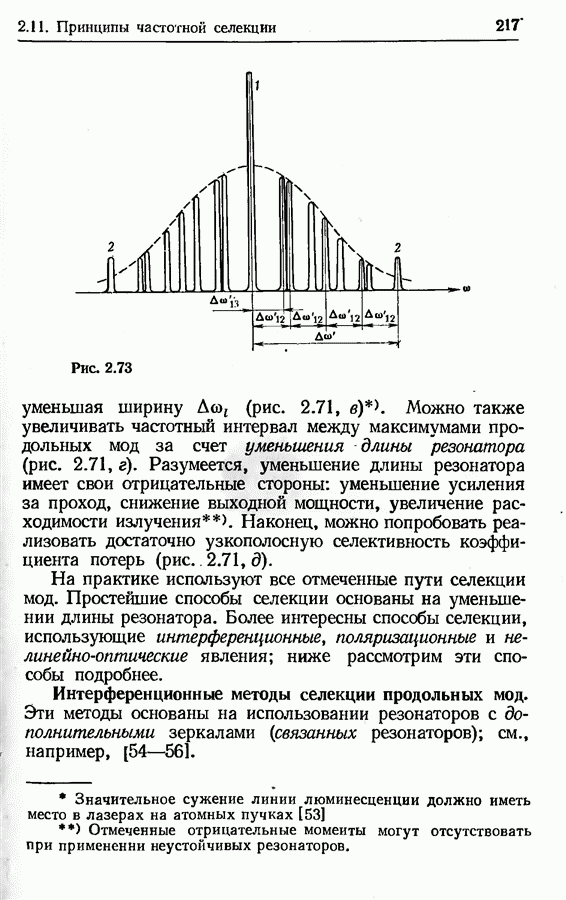
- 2.11. Принципы частотной селекции
- Применение широкополосных поглощающих фильтров и дисперсионных элементов.
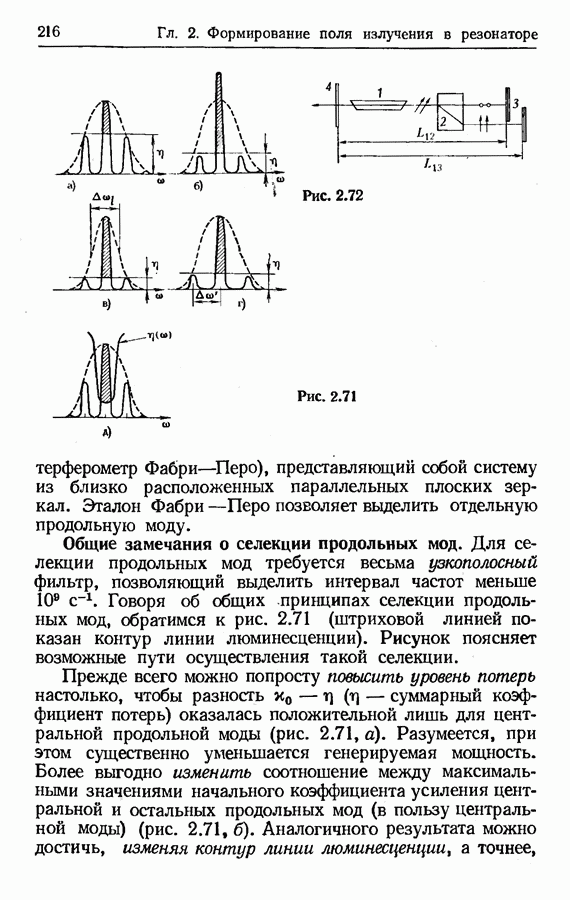
- Общие замечания о селекции продольных мод.
- Интерференционные методы селекции продольных мод.
- Резонаторы с анизотропными элементами.
- Нелинейно-оптический метод частотной селекции.
- 2.12. Эффекты «выгорания дыр» и затягивания частот
- Насыщение усиления при однородном и неоднородном уширении линий; эффект «выгорания дыр».
- Специфика рассмотрения насыщения усиления при неоднородном уширении линнн перехода.
- Эффект затягивания частот.
- Эффект затягивания частот для случаев однородного и неоднородного уширения.
- 2.13. Тепловая линза
- Термоупругие напряжения; термические искажения резонатора.
- Фокусное расстояние и главные плоскости тепловой линзы.
- Учет тепловой линзы в лазерных системах.
- 2.14. Волноводные резонаторы
- Число волноводных мод в резонаторе.
- Волноводный резонатор половинного типа.
- Преимущества волноводных резонаторов.
- 2.15. Оптическое излучение в тонкопленочном волноводе. Распределенная обратная связь
- Волноводные моды в тонкой пленке.
- Число волноводных мод в пленке.
- Распределение поля в волноводных модах.
- Методы ввода и вывода излучения для тонкопленочного волновода.
- Принцип действия элемента связи призма — пленка.
- Распределенная обратная связь.
- Пленочные РОС-лазеры.
- Пленочные лазеры с периодической структурой в качестве зеркала резонатора.
- Список литературы
- Глава 3. ДИНАМИКА ПРОЦЕССОВ В ЛАЗЕРЕ
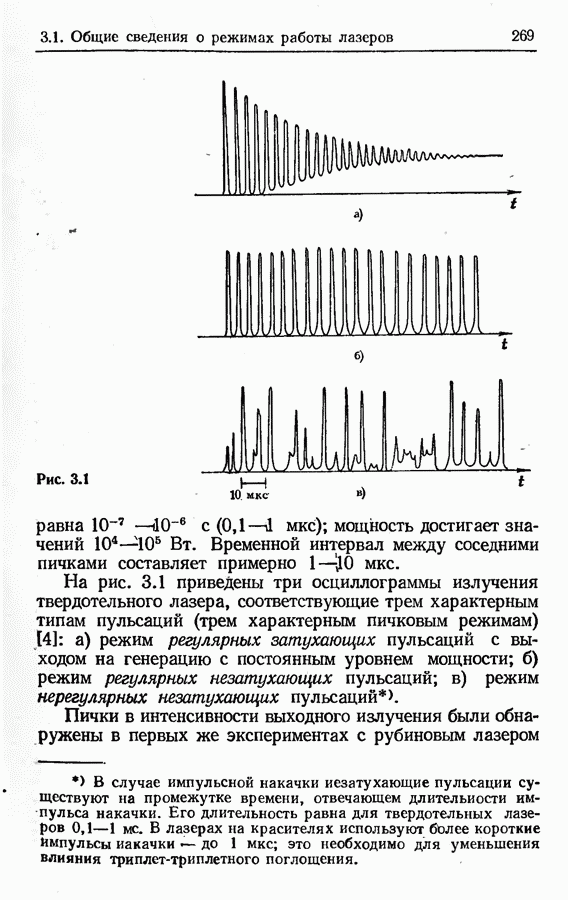
- 3.1. Общие сведения о режимах работы лазеров
- Режим свободной генерации.
- Режим генерации гигантских импульсов при активной модуляции добротности резонатора.
- Режим генерации гигантских импульсов при пассивной модуляции добротности резонатора.
- Режим синхронизации продольных мод (режим генерации сверхкоротких световых импульсов).
- Режим синхронизации поперечных мод.
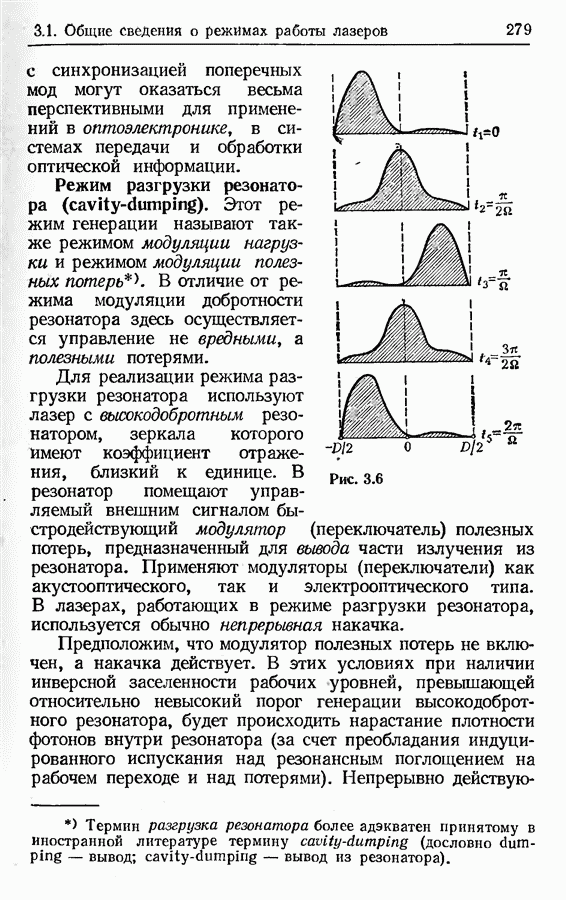
- Режим разгрузки резонатора (cavity-dumping).
- Генерация последовательности импульсов в лазерах с непрерывной накачкой.
- Использование отрицательной обратной связи для получения импульсов микросекундной длительности.
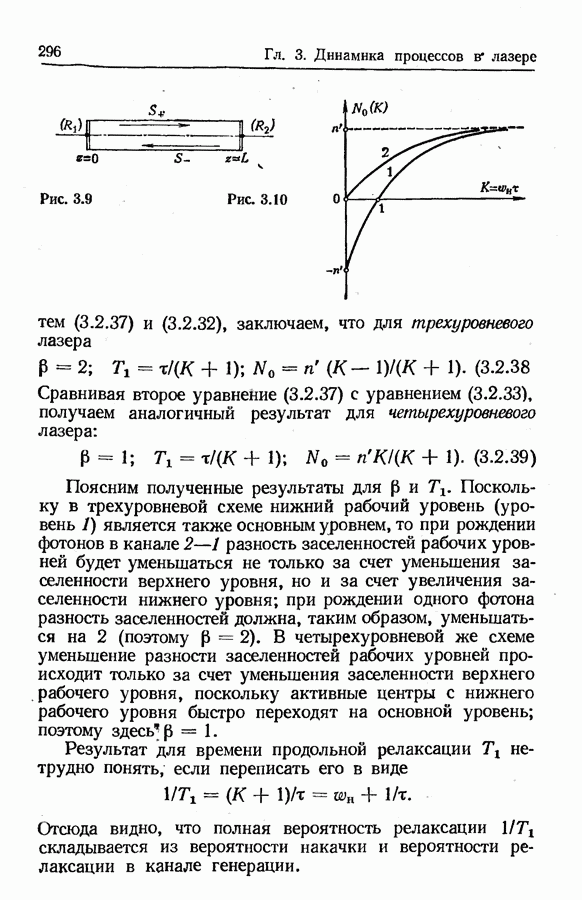
- 3.2. Приближенные уравнения для описания динамики процессов в лазерах (балансные уравнения)
- Дифференциальные уравнения для плотности инверсной заселенности (трехуровневый и четырехуровневый лазеры).
- Полная система балансных уравнений в частных производных.
- Усредненные балансные уравнения (скоростные уравнения).
- Уравнения Статца — Де Марса.
- Сопоставление уравнений Статца — Де Марса и системы усредненных балансных уравнений.
- Пороговая плотность инверсной заселенности и условие генерации.
- Безразмерная форма записи уравнений Статца—Де Марса.
- Учет вклада спонтанного излучения в интенсивность поля.
- Общие замечания о методе балансных уравнений.
- Лазер как распределенная автоколебательная система.
- 3.3. Режим свободной генерации. Регулярные затухающие пульсации мощности излучения
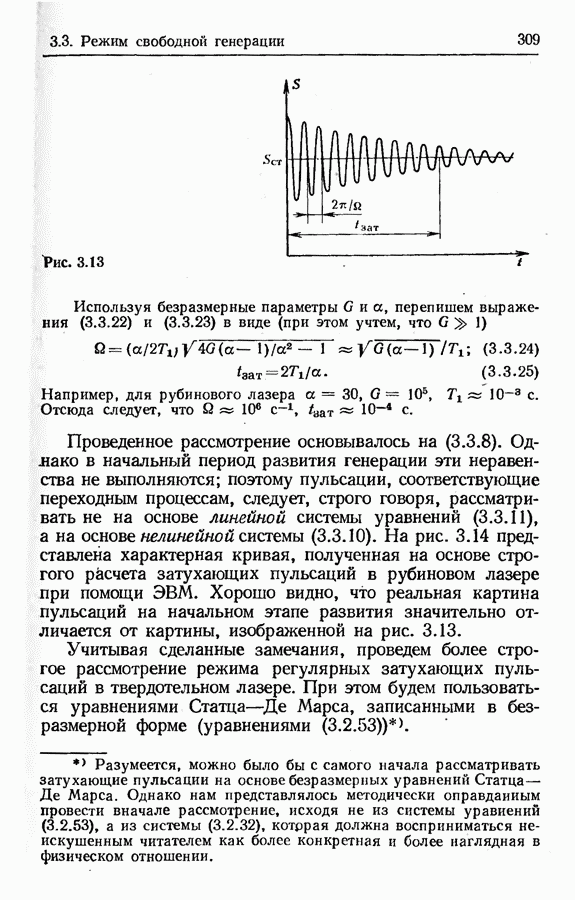
- Переходные процессы, сопровождающие возникновение генерации (регулярные затухающие пульсации мощности излучения).
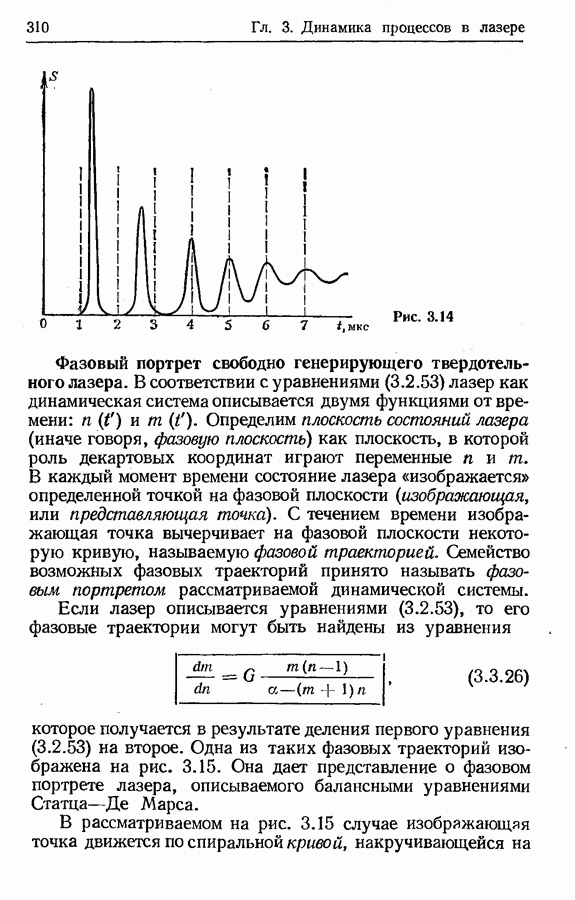
- Фазовый портрет свободно генерирующего твердотельного лазера.
- Выявление структуры фазового портрета лазера.
- Замечания о свободной генерации в многомодовом лазере.
- 3.4. Лазер с нестационарным резонатором. Незатухающие пульсации мощности излучения
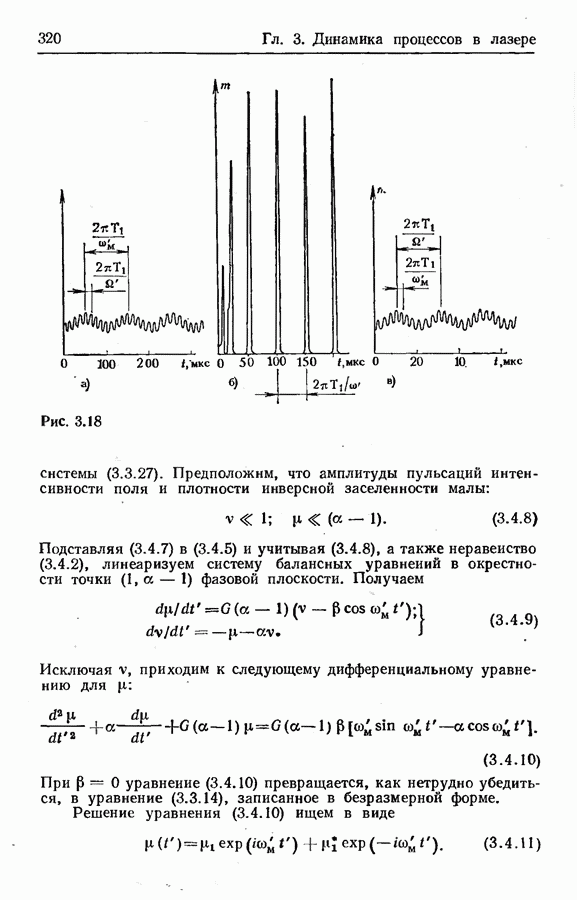
- Пульсации малой амплитуды.
- Замечания о возможности реализации незатухающих пульсаций большой амплитуды.
- Периодическая модуляция добротности при равномерном движении отражающей плоскости.
- Природа незатухающих пульсаций в режиме свободной генерации.
- 3.5. Активная модуляция добротности резонатора
- Электрооптическая модуляция добротности.
- Акустооптическая модуляция добротности.
- Акустооптическая и электрооптическая модуляция добротности (сопоставление).
- Модуляция полезных потерь.
- 3.6. Режим генерации гигантских импульсов при активной модуляции добротности резонатора
- Балансные уравнения. Мгновенное включение добротности.
- Фазовый портрет лазера при мгновенном включении добротности.
- Анализ этапа линейного развития генерации.
- Энергетические характеристики гигантского импульса.
- Длительность и форма гигантского импульса.
- Режим генерации гигантских импульсов при различных временах включения добротности.
- Замечания о развитии импульса в поперечном к оси резонатора направлении.
- 3.7. Лазеры с просветляющимся фильтром
- Дифференциальное уравнение для усредненной плотности светового потока.
- Полная система балансных уравнений для лазера с просветляющимся фильтром.
- Стационарные решения системы балансных уравнений.
- Неустойчивость исходного стационарного состояния и условие самовозбуждения генерации в лазере с просветляющимся фильтром.
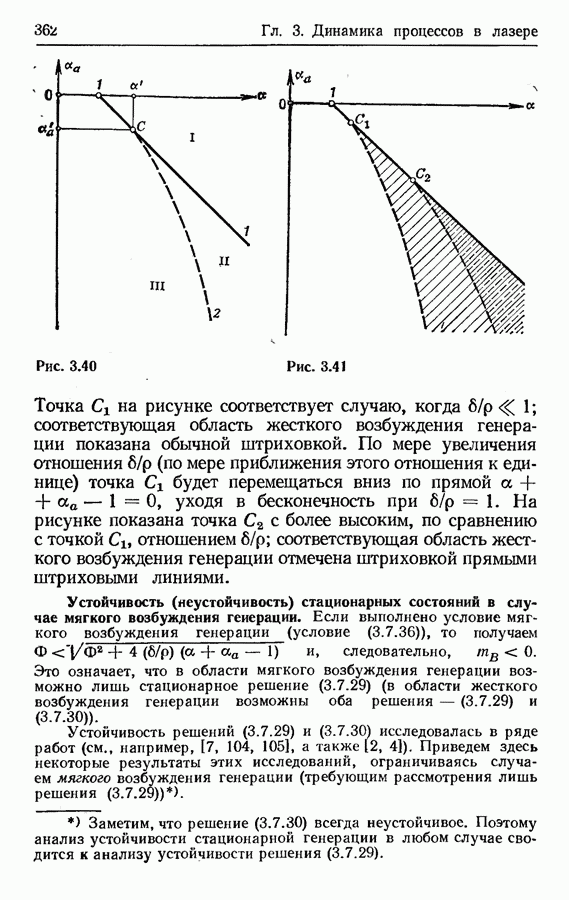
- Мягкое и жесткое возбуждение генерации.
- Устойчивость (неустойчивость) стационарных состояний в случае мягкого возбуждения генерации.
- Режимы генерации лазера с просветляющимся фильтром.
- 3.8. Режим генерации гигантских импульсов при пассивной модуляции добротности резонатора
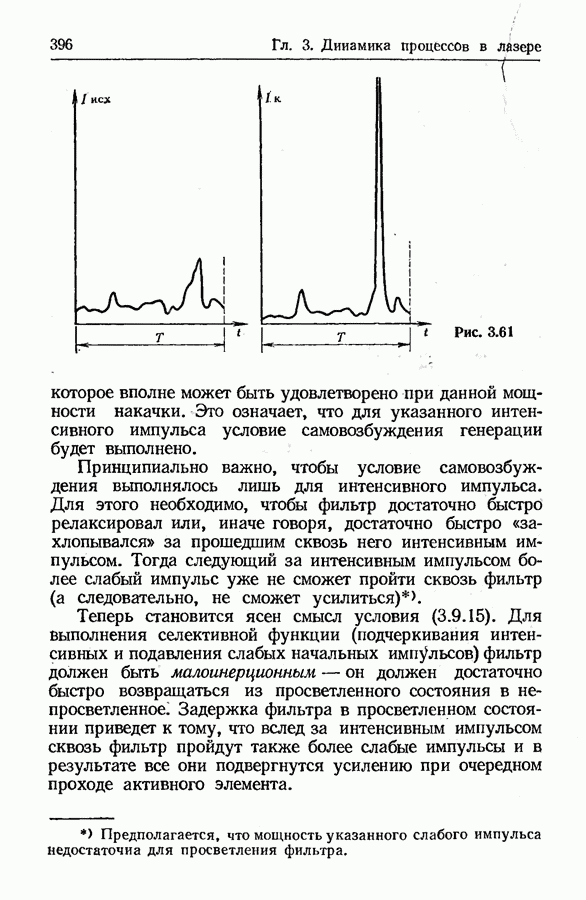
- Развитие гигантского импульса в лазере с просветляющимся фильтром.
- Балансные уравнения; аналогия со случаем мгновенного включения добротности.
- Сопоставление режимов генерации гигантских импульсов при активной и пассивной модуляции добротности; комбинированная модуляция добротности.
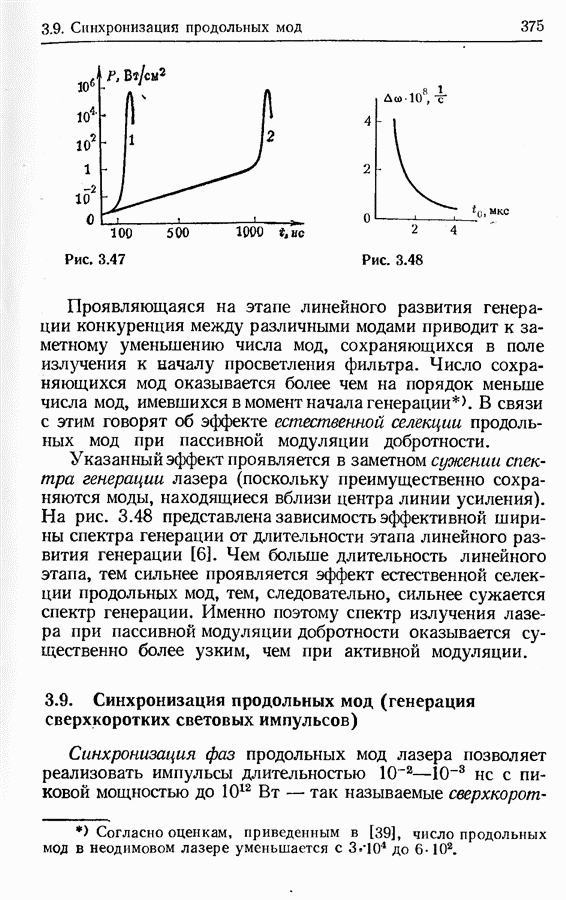
- Естественная селекция продольных мод при пассивной модуляции добротности.
- 3.9. Синхронизация продольных мод (генерация сверхкоротких световых импульсов)
- Неселективный резонатор.
- Активная синхронизация мод.
- Пассивная синхронизация мод (самосинхронизация мод).
- Комбинированный метод синхронизации мод.
- Способы уменьшения времени релаксации просветляющихся фильтров.
- Влияние эффекта самофокусировки света.
- 3.10. Измерение длительности сверхкоротких световых импульсов
- Метод, использующий генерацию второй гармоники.
- Двухфотонная методика.
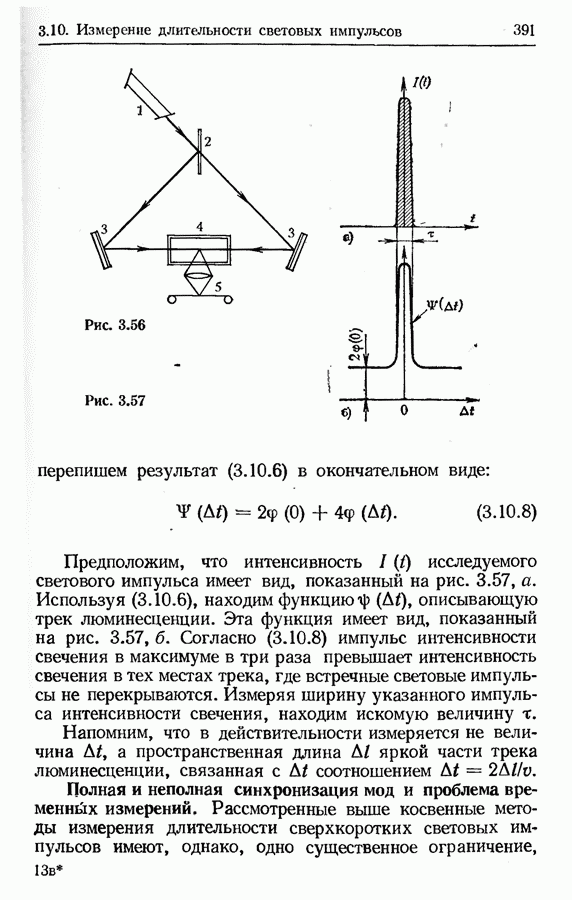
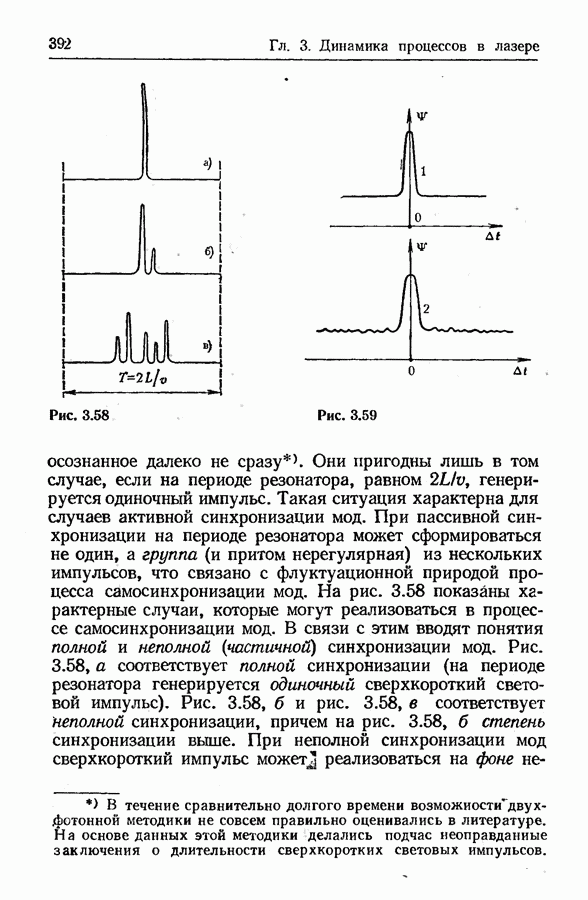
- Полная и неполная синхронизация мод и проблема временных измерений.
- Методика, основанная на измерении структуры спектра сигнала.
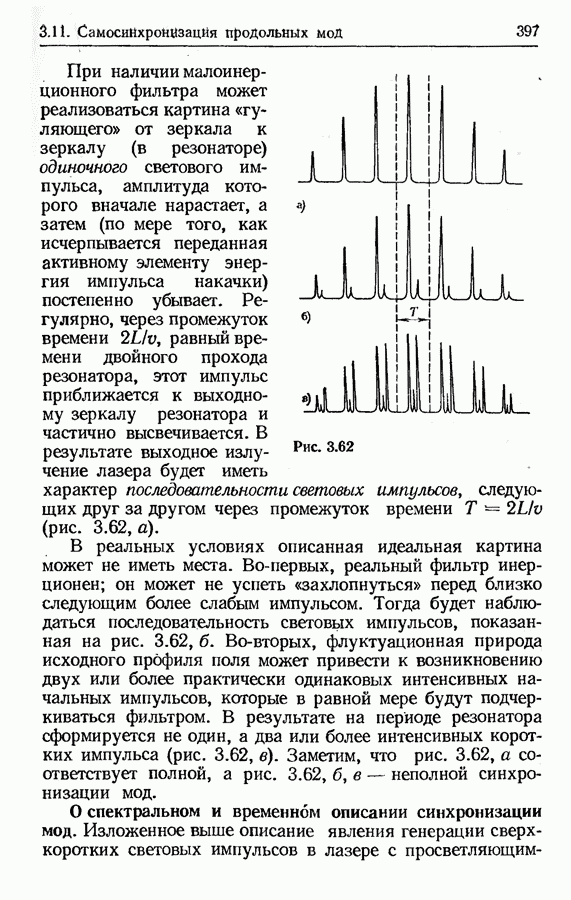
- 3.11. Рассмотрение самосинхронизации продольных мод в лазере с просветляющимся фильтром на основе флуктуационных представлений
- О спектральном и временном описании синхронизации мод.
- Исходный профиль поля излучения.
- Показатель нелинейности.
- Преобразование профиля поля при взаимодействии излучения с фильтром на этапе просветления.
- О возможности синхронизации мод в случае генерации второй гармоники.
- Условия полной самосинхронизации мод.
- 3.12. Временное описание активной синхронизации продольных мод в лазере с однородно уширенной линией усиления
- Изменение светового импульса при его прохождении через активный элемент и модулятор.
- Система дифференциальных уравнений, описывающая процесс установления режима синхронизации мод.
- Замечания о фазовых (электрооптических) и амплитудных (акустооптических) синхронизаторах мод.
- Список литературы
- ПРИЛОЖЕНИЕ 1. ПОЛИНОМЫ ЭРМИТА
- ПРИЛОЖЕНИЕ 2. ГАУССОВ ПУЧОК В СВОБОДНОМ ПРОСТРАНСТВЕ
- ПРИЛОЖЕНИЕ 3. УСТОЙЧИВАЯ И НЕУСТОЙЧИВАЯ СФЕРИЧЕСКИЕ ВОЛНЫ В НЕУСТОЙЧИВОМ РЕЗОНАТОРЕ
- ПРИЛОЖЕНИЕ 4. МАТРИЦЫ ДЖОНСА
- ПРИЛОЖЕНИЕ 5. ОСОБЫЕ ТОЧКИ ДВУМЕРНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ