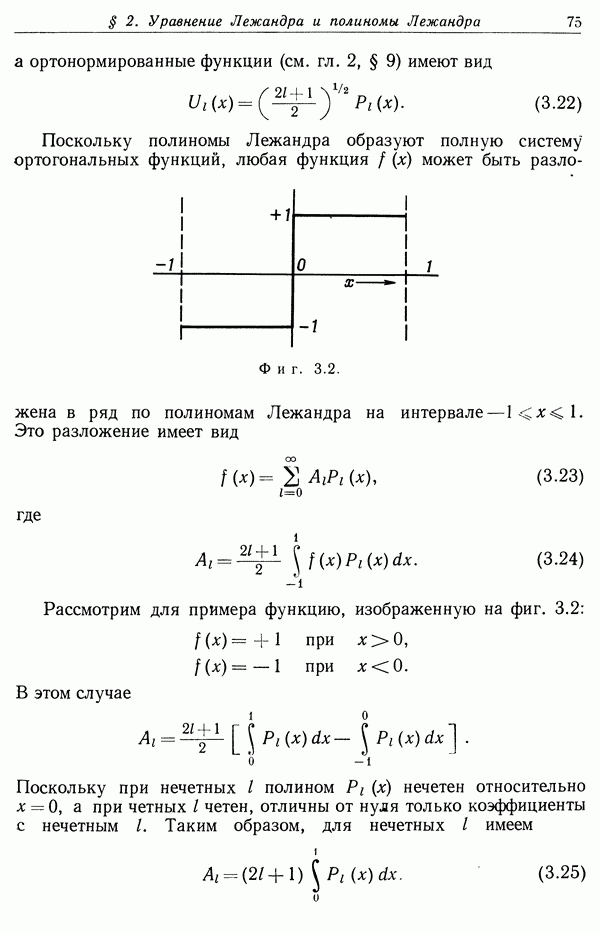| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Влияние плотности на потери энергии при соударении
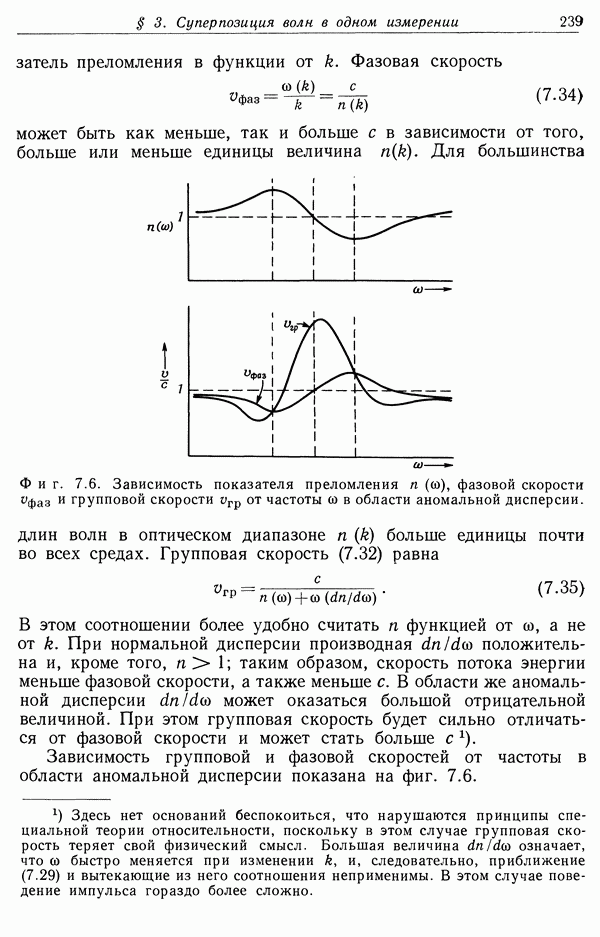
Экспериментально наблюдаемые потери энергии при прохождении частиц всех видов в различных материальных средах для не слишком релятивистских частиц весьма точно описываются соотношением (13.44) [или (13.36), если  Однако для ультрарелятивистских частиц наблюдаемые потери несколько меньше рассчитываемых с помощью соотношения (13.44), особенно для веществ с большой плотностью. На графике зависимости
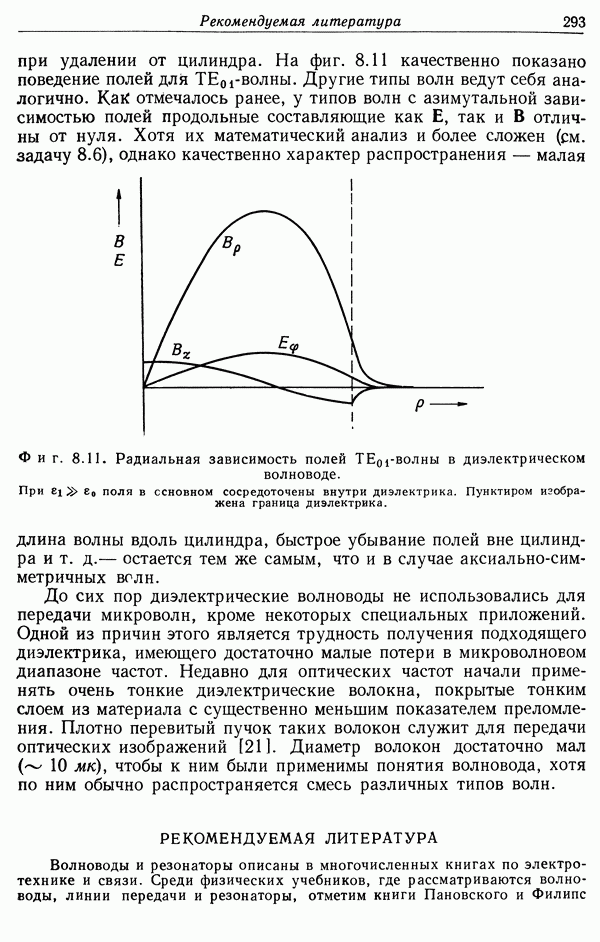
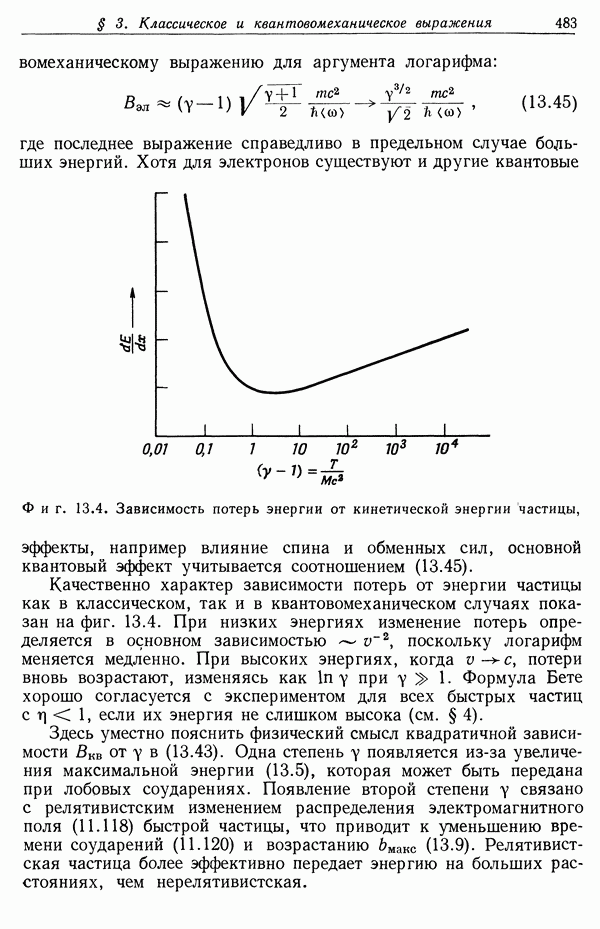
Однако для ультрарелятивистских частиц наблюдаемые потери несколько меньше рассчитываемых с помощью соотношения (13.44), особенно для веществ с большой плотностью. На графике зависимости  от энергии частиц типа фиг. 13.4 это сказывается в том, что реальная кривая потерь энергии возрастает после прохождения минимума приблизительно вдвое медленнее, чем расчетная; это соответствует зависимости аргумента логарифма в (13.44) не от второй, а от первой степени у. Потери энергии в фотоэмульсиях, измеряемые по плотности зерен серебра, после прохождения минимума очень слабовозрастают, а затем образуют на графике плато, простирающееся до наивысших исследованных значений энергии частиц. Это также соответствует понижению степени у на единицу, в данном случае в выражении (13.50) для
от энергии частиц типа фиг. 13.4 это сказывается в том, что реальная кривая потерь энергии возрастает после прохождения минимума приблизительно вдвое медленнее, чем расчетная; это соответствует зависимости аргумента логарифма в (13.44) не от второй, а от первой степени у. Потери энергии в фотоэмульсиях, измеряемые по плотности зерен серебра, после прохождения минимума очень слабовозрастают, а затем образуют на графике плато, простирающееся до наивысших исследованных значений энергии частиц. Это также соответствует понижению степени у на единицу, в данном случае в выражении (13.50) для 
Указанное уменьшение потерь энергии частицы, известное как эффект плотности (или поляризационный эффект), впервые было исследовано теоретически Ферми (1940 г.). До сих пор мы неявно принимали одно допущение, которое перестает выполняться для плотных сред. Мы считали возможным вычислять вначале действие поля налетающей частицы на отдельный атомный электрон, а затем простым суммированием определять передачу энергии всем электронам для всех атомов с  Но величина Ьшакс очень велика по сравнению с размерами атома, особенно при больших у. Следовательно, при значении 6, сравнимом с Ьмакс, в плотных средах между траекторией налетающей частицы и рассматриваемым
Но величина Ьшакс очень велика по сравнению с размерами атома, особенно при больших у. Следовательно, при значении 6, сравнимом с Ьмакс, в плотных средах между траекторией налетающей частицы и рассматриваемым
атомом находится большое число атомов. Поле быстрой частицы влияет на эти атомы, что в свою очередь приводит к появлению возмущающих полей в месте расположения рассматриваемого атома. Иными словами, в плотных средах вследствие поляризации диэлектрика поле частицы в свободном пространстве заменяется характерным макроскопическим полем в диэлектрике. Это изменение поля, обусловленное поляризацией среды, следует учитывать при расчете энергии, передаваемой в дальних соударениях. В близких соударениях налетающая частица взаимодействует одновременно лишь с одним атомом. Поэтому в данном случае применимы расчеты, основанные на значении поля свободной частицы без учета поляризационных эффектов. Значение прицельного параметра, разграничивающее близкие и дальние соударения, по порядку величины совпадает с атомными размерами. Так как окончательный результат получается сопряжением двух логарифмических величин, нет необходимости определять разграничивающее значение b с большой точностью.
Определим теперь потери энергии при дальних соударениях  в предположении, что электромагнитные поля в веществе можно рассчитывать, считая среду непрерывной и имеющей макроскопическую диэлектрическую проницаемость
в предположении, что электромагнитные поля в веществе можно рассчитывать, считая среду непрерывной и имеющей макроскопическую диэлектрическую проницаемость  Если а есть величина порядка размеров атома, то это приближение перестает выполняться для дальних соударений со значениями 6, близкими к нижнему пределу, но справедливо для подавляющего большинства соударений.
Если а есть величина порядка размеров атома, то это приближение перестает выполняться для дальних соударений со значениями 6, близкими к нижнему пределу, но справедливо для подавляющего большинства соударений.
Задача об определении электрического поля быстрой частицы, движущейся с постоянной скоростью в среде, легче всего решается с помощью преобразования Фурье. Осуществляя в соответствии с общим правилом фурье-преобразование потенциалов  и плотности источников
и плотности источников  по координатам и времени
по координатам и времени
 (13-53)
(13-53)
приходим к следующим волновым уравнениям для спектральных амплитуд:

Появление в (13.54) диэлектрической проницаемости  определяется тем, что в макроскопические уравнения Максвелла входит вектор электрической индукции D. Фурье-преобразование плотностей заряда и тока
определяется тем, что в макроскопические уравнения Максвелла входит вектор электрической индукции D. Фурье-преобразование плотностей заряда и тока
 (13.55)
(13.55)
легко выполняется; при этом получаем

Как следует из (13.54), фурье-преобразование потенциалов дает
 (13.57)
(13.57)
Используя соотношения, выражающие электромагнитные поля через потенциалы, для фурье-амплитуд полей получаем
 (13.58)
(13.58)
Как видно из формулы (13.23), для вычисления потерь энергии нужно знать временное фурье-представление электрического поля на расстоянии b по нормали от траектории частицы, движущейся вдоль оси  . Очевидно,
. Очевидно,
 (13.59)
(13.59)
где точка наблюдения имеет координаты  . Чтобы проиллюстрировать метод вычисления
. Чтобы проиллюстрировать метод вычисления  найдем
найдем  — составляющую вектора
— составляющую вектора  параллельную вектору v. Согласно (13.57) и (13.58),
параллельную вектору v. Согласно (13.57) и (13.58),

Интегрирование по  может быть проведено сразу. В результате имеем
может быть проведено сразу. В результате имеем

где

Интеграл по  равен
равен  таким образом,
таким образом,  можно переписать в виде
можно переписать в виде

Оставшийся интеграл имеет тот же вид, что и интеграл в (13.28). Окончательно получим

где знак квадратного корня при определении X с помощью (13.62) выбирается так, чтобы значение X находилось в четвертом квадранте. Аналогичные вычисления приводят к следующим выражениям для других составляющих полей:

Как легко видеть, в предельном случае  выражения для полей (13.64) и (13.65) переходят в ранее полученные выражения (13.30) и (13.29).
выражения для полей (13.64) и (13.65) переходят в ранее полученные выражения (13.30) и (13.29).
Для определения энергии, передаваемой атому при соударении с прицельным параметром b, достаточно представить (13.23) в более общем виде
 (13.66)
(13.66)
где  — амплитуда колебаний атомного электрона
— амплитуда колебаний атомного электрона  типа. Вместо того чтобы воспользоваться формулой (13.19) для
типа. Вместо того чтобы воспользоваться формулой (13.19) для  выразим сумму дипольных моментов через поляризуемость молекул и тем самым через диэлектрическую проницаемость
выразим сумму дипольных моментов через поляризуемость молекул и тем самым через диэлектрическую проницаемость
 (13.67)
(13.67)
где N — число атомов в единице объема. При этом выражение для передаваемой энергии принимает вид
 (13.68)
(13.68)
Потери энергии на единице длины за счет соударений с прицельными параметрами  можно, очевидно, записать как
можно, очевидно, записать как

Подставляя в (13.68) и (13.69) выражения для полей (13.64) и (13.65), после ряда вычислений приходим к результату, полученному Ферми:

где к определяется соотношением (13.62). Этот же результат можно получить более изящно, вычисляя электромагнитную энергию, излученную через поверхность цилиндра радиусом а, окружающего траекторию налетающей частицы. В силу закона сохранения энергии эта величина совпадает с энергией, теряемой частицей в единицу времени. Таким образом,
 (13.71)
(13.71)
Интеграл по  для данного момента времени эквивалентен интегралу по всем моментам времени для фиксированной точки на цилиндре. Введя
для данного момента времени эквивалентен интегралу по всем моментам времени для фиксированной точки на цилиндре. Введя  получим
получим

Обычным способом можно преобразовать его в интеграл по частотам:
 (13.73)
(13.73)
Используя выражения для полей (13.64) и (13.65), вновь приходим к результату Ферми (13.70).
Выражение Ферми (13.70) для потерь энергии внешне мало похоже на приведенные нами ранее результаты, например формулу (13.35). Однако если влияние поляризационных эффектов незначительно, то оно дает прежний результат. Например, для нерелятивистских частиц  как ясно из (13.62), величина
как ясно из (13.62), величина  не зависит от
не зависит от  . В этом случае модифицированные функции Бесселя в (13.70) действительны. Значение интеграла определяется лишь мнимой частью функции
. В этом случае модифицированные функции Бесселя в (13.70) действительны. Значение интеграла определяется лишь мнимой частью функции  . Пренебрегая поляризационной
. Пренебрегая поляризационной
поправкой Лоренца (4.67) для внутреннего поля в атоме, можно представить диэлектрическую проницаемость в виде

где при вычислении дипольного момента использовано выражение (13.19). Если второй член предполагается малым, то мнимую часть функции  легко вычислить и подставить ее в (13.70). При этом в том же приближении, которое использовалось при выводе соотношений (13.24) — (13.26), интеграл по
легко вычислить и подставить ее в (13.70). При этом в том же приближении, которое использовалось при выводе соотношений (13.24) — (13.26), интеграл по  может быть преобразован к нерелятивистскому выражению (13.35). Если принебречь отличием К от
может быть преобразован к нерелятивистскому выражению (13.35). Если принебречь отличием К от  но не делать других допущений, то (13.70) приводит точно к формуле Бора (13.35).
но не делать других допущений, то (13.70) приводит точно к формуле Бора (13.35).
Поляризационный эффект проявляется, очевидно, в комплексности аргумента модифицированных функций Бесселя, что соответствует учету члена с  в (13.62). Так как величина
в (13.62). Так как величина  входит в (13.62) в виде произведения на
входит в (13.62) в виде произведения на  ясно, что этот эффект фактически заметен лишь при больших энергиях. Подробные вычисления для всех энергий с использованием явного выражения для
ясно, что этот эффект фактически заметен лишь при больших энергиях. Подробные вычисления для всех энергий с использованием явного выражения для  типа (13.74) весьма сложны и не приводят к сколько-нибудь наглядным результатам. Поэтому мы ограничимся лишь рассмотрением ультрарелятивистского предельного случая
типа (13.74) весьма сложны и не приводят к сколько-нибудь наглядным результатам. Поэтому мы ограничимся лишь рассмотрением ультрарелятивистского предельного случая  Кроме того, так как в интеграле по
Кроме того, так как в интеграле по  наиболее важны оптические частоты, а радиус а имеет порядок атомных размеров, величина
наиболее важны оптические частоты, а радиус а имеет порядок атомных размеров, величина  Следовательно, можно использовать приближенные выражения для функций Бесселя (3.103), справедливые в предельном случае малых аргументов. Выражение Ферми (13.70) в ультрарелятивистском предельном случае принимает вид
Следовательно, можно использовать приближенные выражения для функций Бесселя (3.103), справедливые в предельном случае малых аргументов. Выражение Ферми (13.70) в ультрарелятивистском предельном случае принимает вид
 (13.75)
(13.75)
Здесь уместно подчеркнуть, что аргумент второго логарифмического члена в действительности равен  ]. В частном случае
]. В частном случае  этот логарифмический член дает множитель у под логарифмом, что соответствует ранее приведенному результату (13.36). Если же
этот логарифмический член дает множитель у под логарифмом, что соответствует ранее приведенному результату (13.36). Если же  , то этот множитель можно переписать в виде
, то этот множитель можно переписать в виде  вследствие чего из аргумента логарифма исчезает одна степень у в согласии с экспериментом.
вследствие чего из аргумента логарифма исчезает одна степень у в согласии с экспериментом.
Интеграл по положительным действительным  в (13.75), где
в (13.75), где  определяется согласно (13.74), легко преобразуется с помощью теоремы Коши в интеграл по положительным чисто мнимым со.
определяется согласно (13.74), легко преобразуется с помощью теоремы Коши в интеграл по положительным чисто мнимым со.
В этом случае величина  становится чисто действительной на пути интегрирования. Следовательно, значение действительной части интеграла будет определяться лишь фазами логарифмов. В приближении
становится чисто действительной на пути интегрирования. Следовательно, значение действительной части интеграла будет определяться лишь фазами логарифмов. В приближении  результат интегрирования можно представить в простом виде
результат интегрирования можно представить в простом виде

где  — электронная плазменная частота
— электронная плазменная частота

Соответствующее релятивистское выражение без учета поляризационного эффекта, как следует из (13.36), имеет вид

Сравнение показывает, что учет поляризационного эффекта приводит к более простому асимптотическому выражению для потерь энергии, которые перестают зависеть от деталей структуры атома [величина  описываемая соотношением (13.38), не входит в (13.76)] и определяются лишь числом электронов в единице объема, входящим в
описываемая соотношением (13.38), не входит в (13.76)] и определяются лишь числом электронов в единице объема, входящим в  Потери энергии для ультрарелятивистских частиц в двух веществах с совершенно различной структурой атомов будут одинаковы, если плотность электронов в этих веществах одинакова.
Потери энергии для ультрарелятивистских частиц в двух веществах с совершенно различной структурой атомов будут одинаковы, если плотность электронов в этих веществах одинакова.
Так как в литературе приведено большое Число рассчитанных по формуле Бете (13.44) кривых потерь энергии, очень часто оказывается удобным знать величину уменьшения потерь, обусловленную влиянием поляризации. Это уменьшение определяется разностью выражений (13.78) и (13.76)

Для фотоэмульсий энергетические потери определяются соотношениями (13.49) и (13.50) с  При учете поляризационной поправки потери при больших энергиях стремятся к постоянной величине
При учете поляризационной поправки потери при больших энергиях стремятся к постоянной величине

Для бромистого серебра  Для однозарядных частиц отношение величины потерь (13.80) к плотности оказывается равным приблизительно
Для однозарядных частиц отношение величины потерь (13.80) к плотности оказывается равным приблизительно  Это значение потерь энергии хорошо согласуется с экспериментальными данными; оно соответствует
Это значение потерь энергии хорошо согласуется с экспериментальными данными; оно соответствует
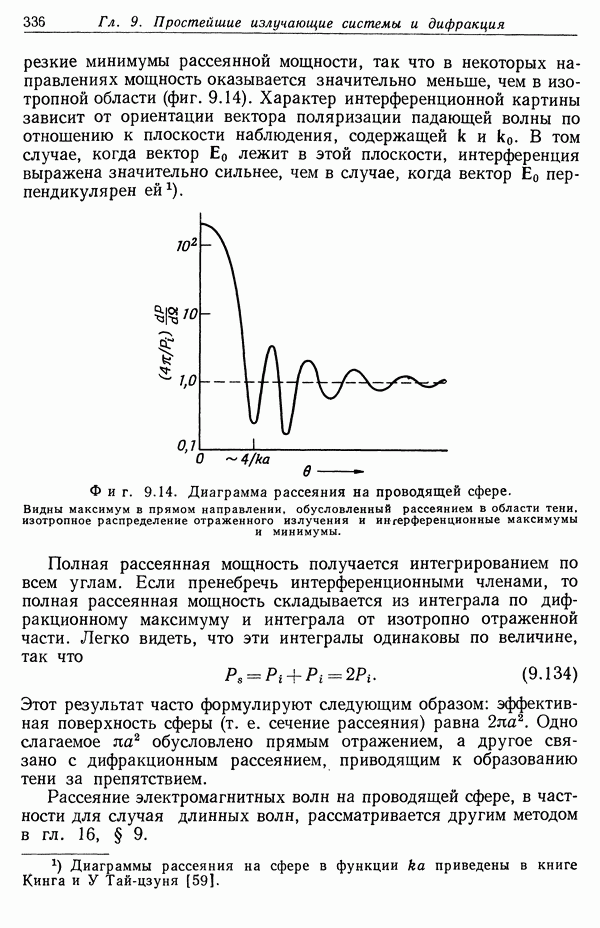
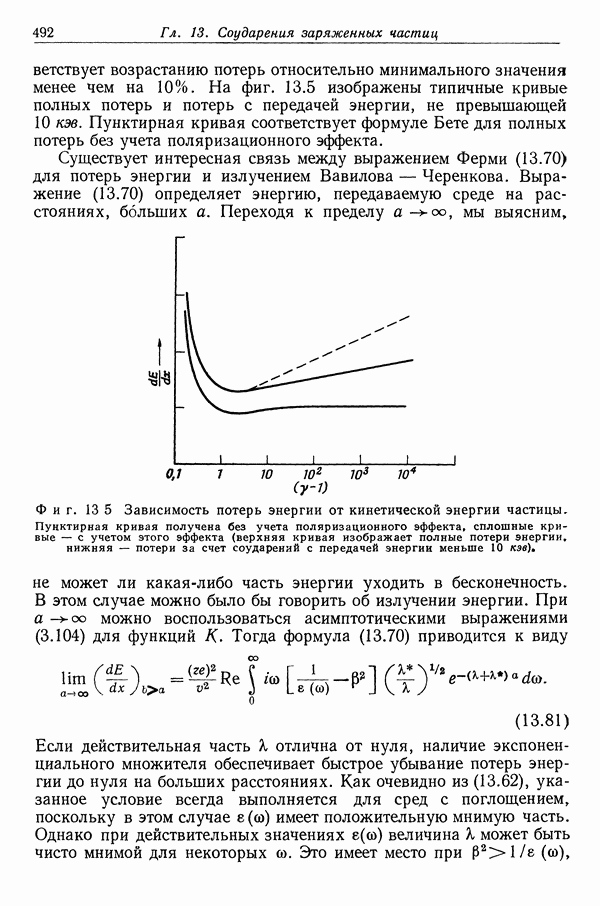
возрастанию потерь относительно минимального значения менее чем на 10%. На фиг. 13.5 изображены типичные кривые полных потерь и потерь с передачей энергии, не превышающей 10 кэв. Пунктирная кривая соответствует формуле Бете для полных потерь без учета поляризационного эффекта.
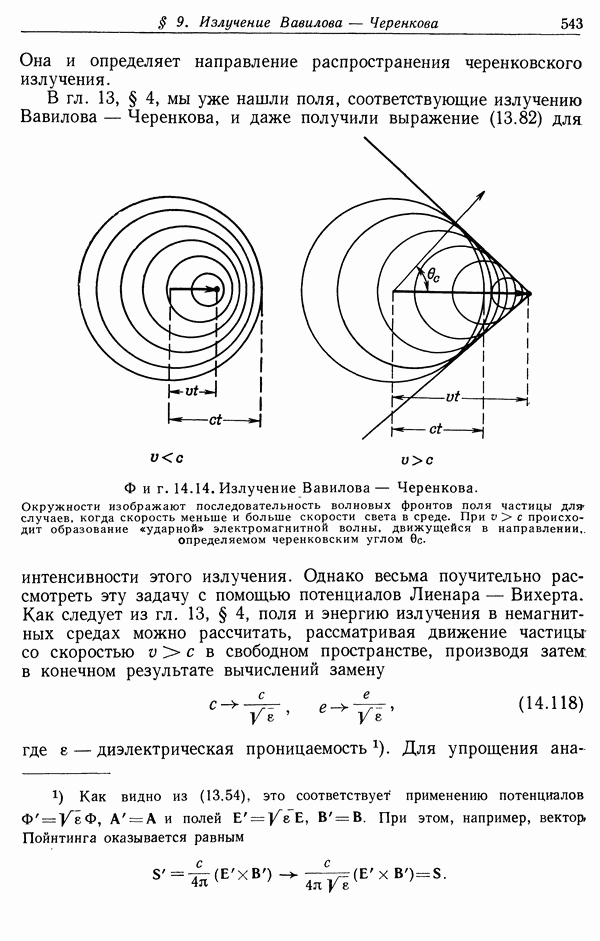
Существует интересная связь между выражением Ферми (13.70) для потерь энергии и излучением Вавилова — Черенкова. Выражение (13.70) определяет энергию, передаваемую среде на расстояниях, больших а. Переходя к пределу  мы выясним, не может ли какая-либо часть энергии уходить в бесконечность.
мы выясним, не может ли какая-либо часть энергии уходить в бесконечность.

Фиг. 13 5 Зависимость потерь энергии от кинетической энергии частицы. Пунктирная кривая получена без учета поляризационного эффекта, сплошные кривые — с учетом этого эффекта (верхняя кривая изображает полные потери энергии» нижняя — потери за счет соударений с передачей энергии меньше  .
.
В этом случае можно было бы говорить об излучении энергии. При а  можно воспользоваться асимптотическими выражениями (3.104) для функций К. Тогда формула (13.70) приводится к виду
можно воспользоваться асимптотическими выражениями (3.104) для функций К. Тогда формула (13.70) приводится к виду
 (13.81)
(13.81)
Если действительная часть X отлична от нуля, наличие экспоненциального множителя обеспечивает быстрое убывание потерь энергии до нуля на больших расстояниях. Как очевидно из (13.62), указанное условие всегда выполняется для сред с поглощением, поскольку в этом случае  имеет положительную мнимую часть. Однако при действительных значениях
имеет положительную мнимую часть. Однако при действительных значениях  величина X может быть чисто мнимой для некоторых
величина X может быть чисто мнимой для некоторых  . Это имеет место при
. Это имеет место при  ,
,
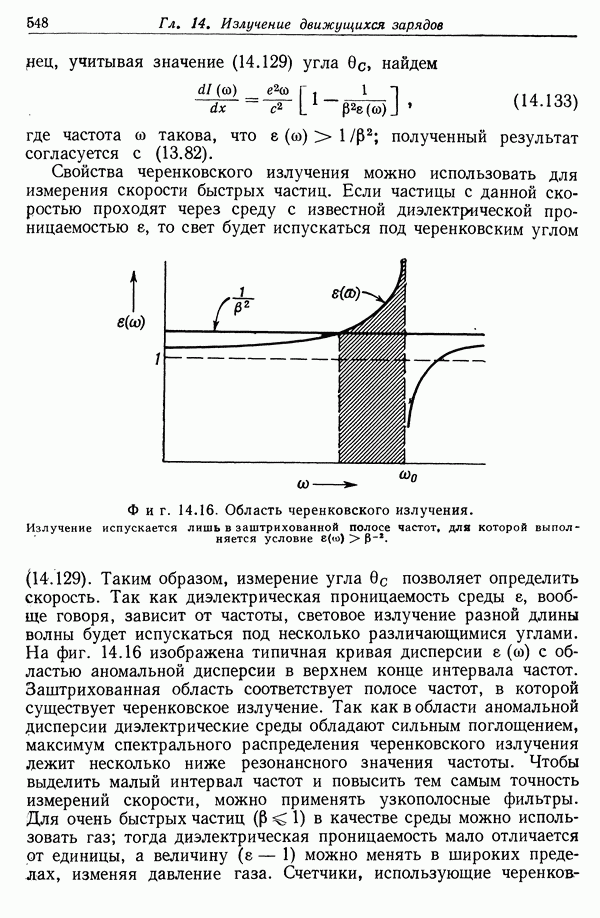
т. е. в том случае, когда скорость частицы превышает фазовую скорость света в среде. В этом и состоит условие существования излучения Вавилова — Черенкова. Для таких частот  . При этом экспоненциальный множитель обращается в единицу и, следовательно,
. При этом экспоненциальный множитель обращается в единицу и, следовательно,

Так как полученное выражение не зависит от радиуса цилиндра а, оно представляет собой истинное излучение. Это выражение полностью совпадает с формулой Франка и Тамма (1937 г.) для полной энергии излучения Вавилова — Черенкова на единице пути. Более детально излучение Вавилова — Черенкова как радиационный процесс будет рассмотрено в гл. 14, § 9.
Для сред, в которых поляризационные эффекты играют существенную роль в процессе потерь энергии, поглощение почти всегда столь велико, что возбуждаемое излучение Вавилова — Черенкова поглощается в непосредственной близости от траектории частицы.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
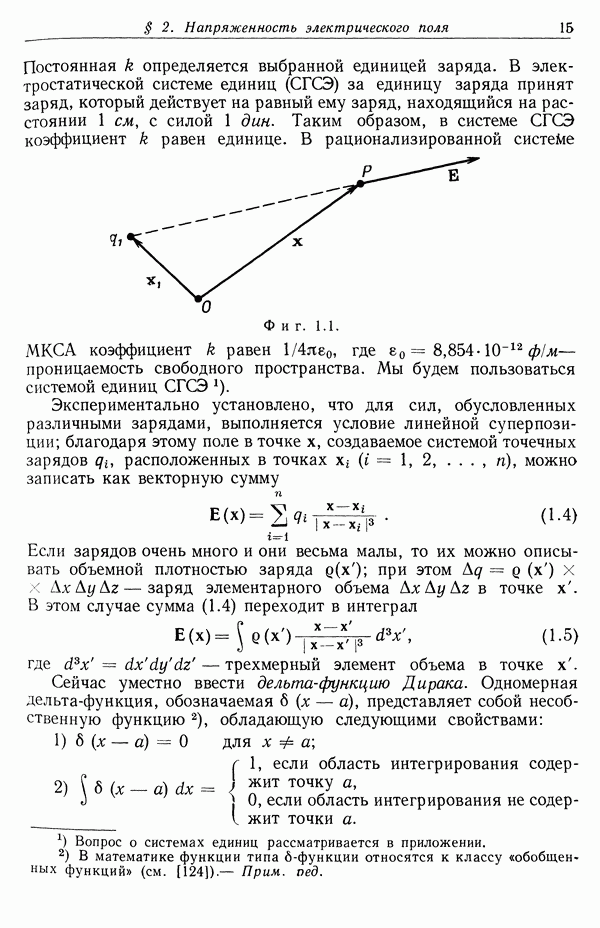
- § 2. Напряженность электрического поля
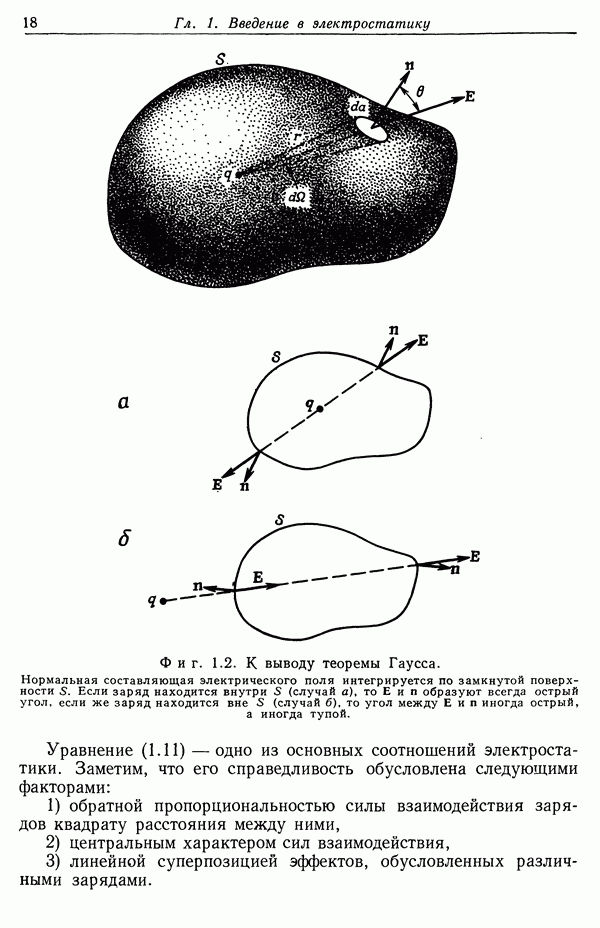
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
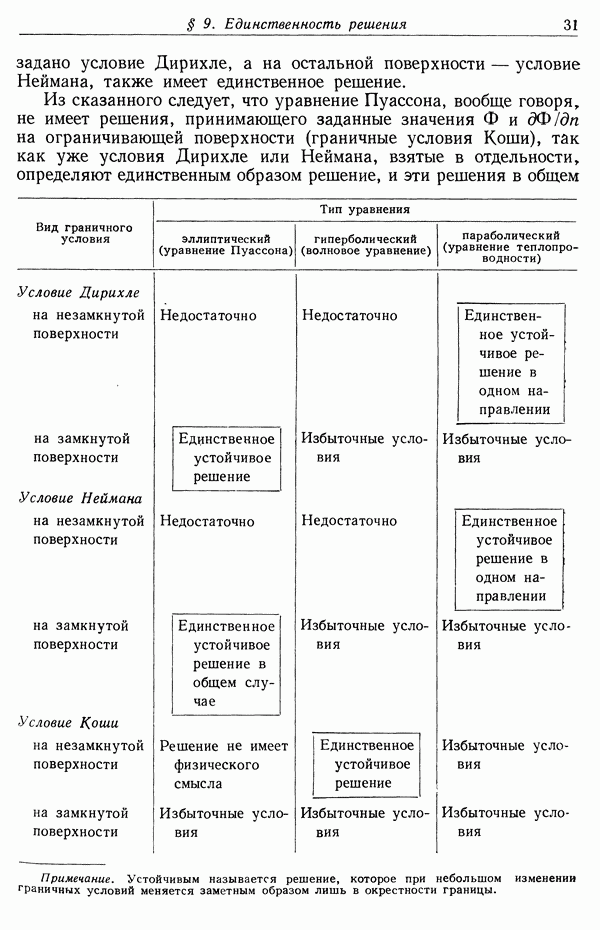
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
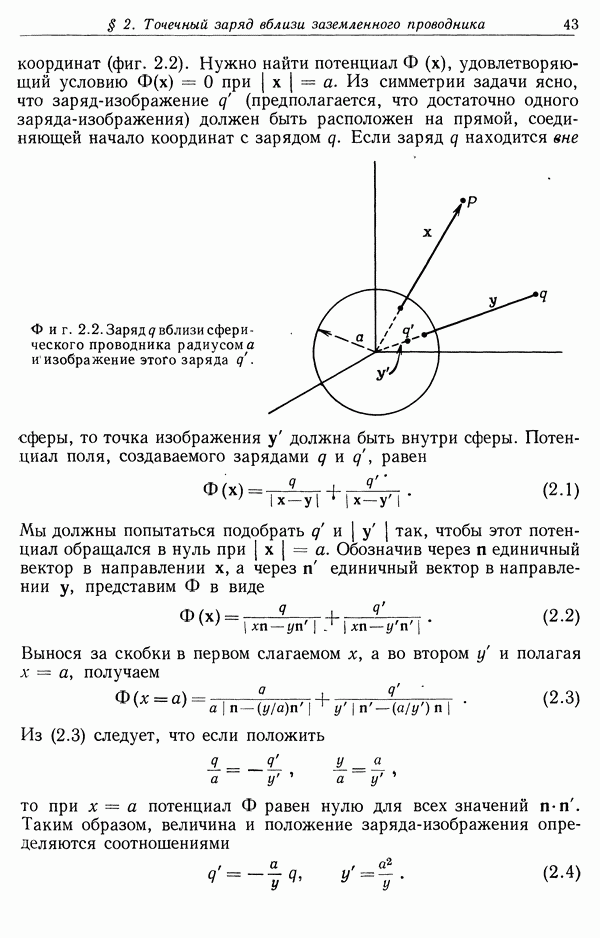
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
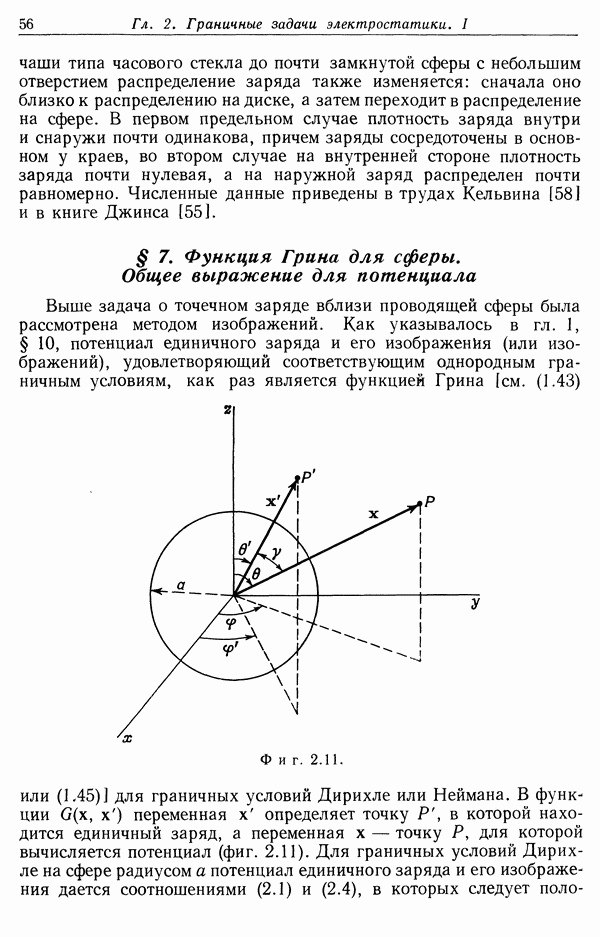
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
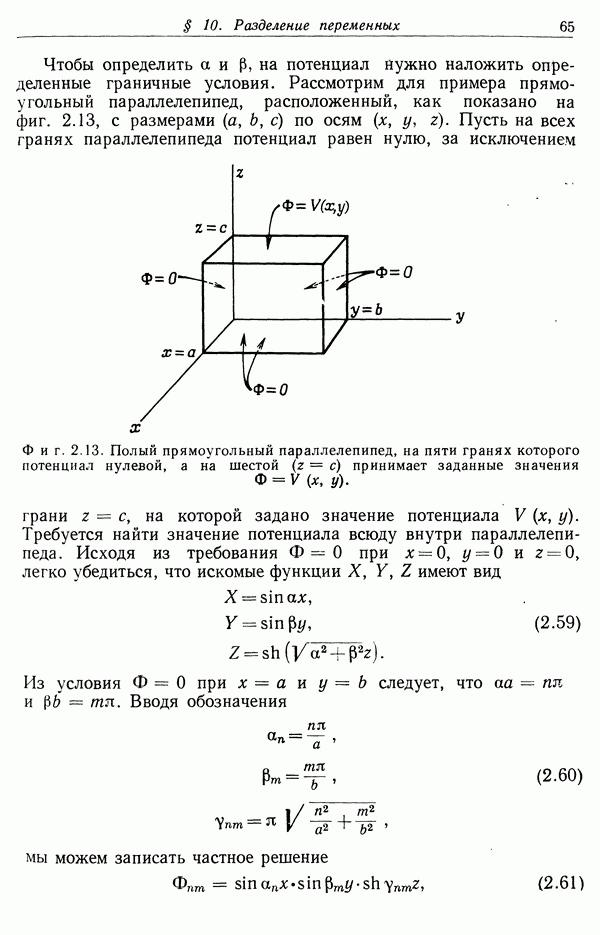
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
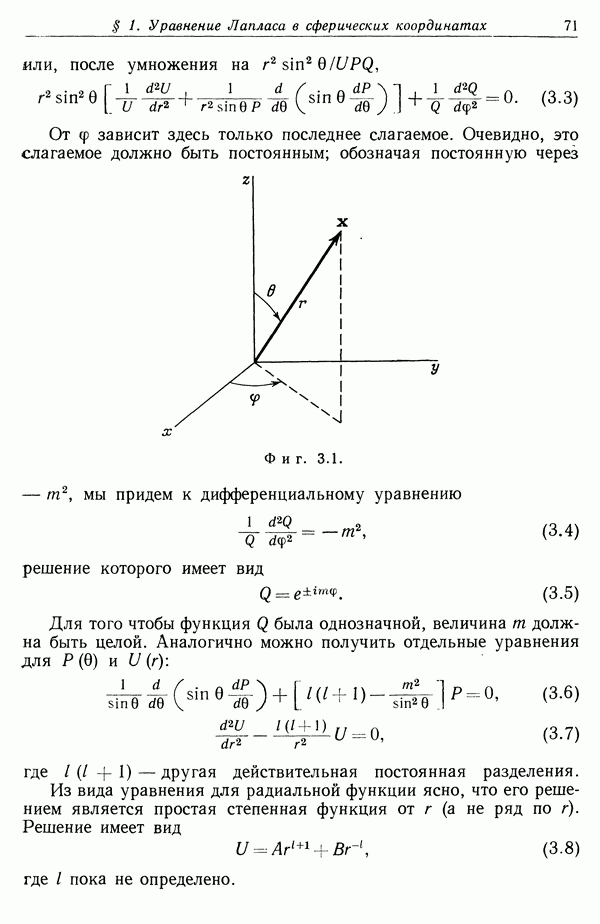
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
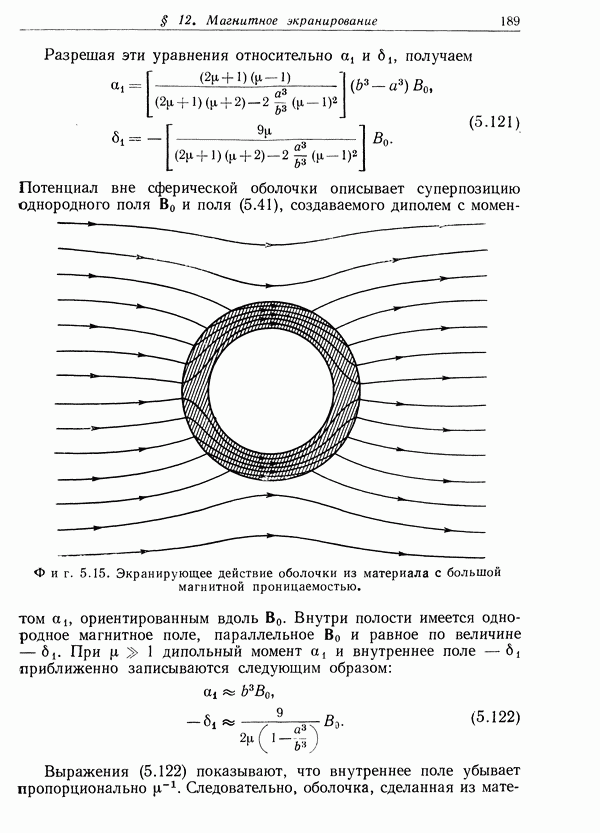
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
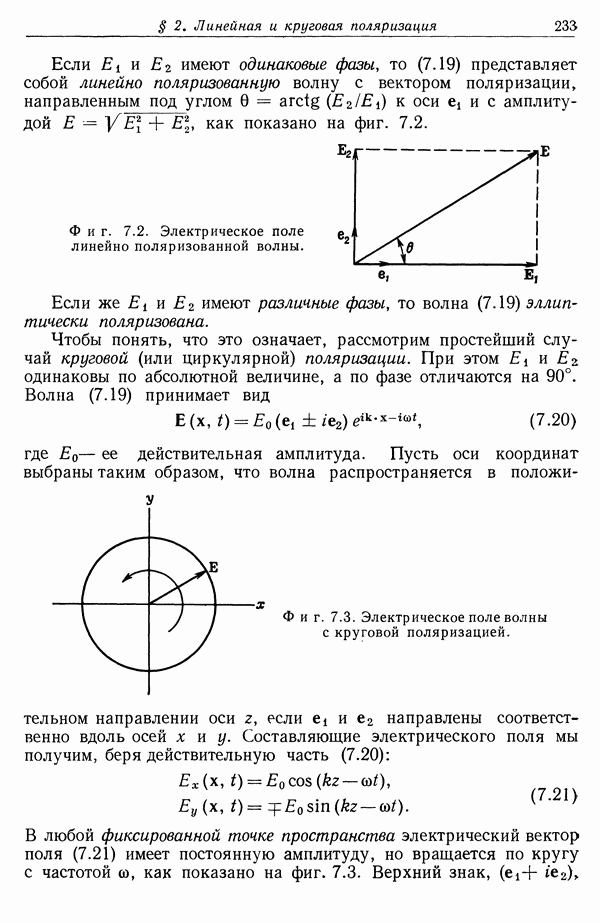
- § 2. Линейная и круговая поляризация
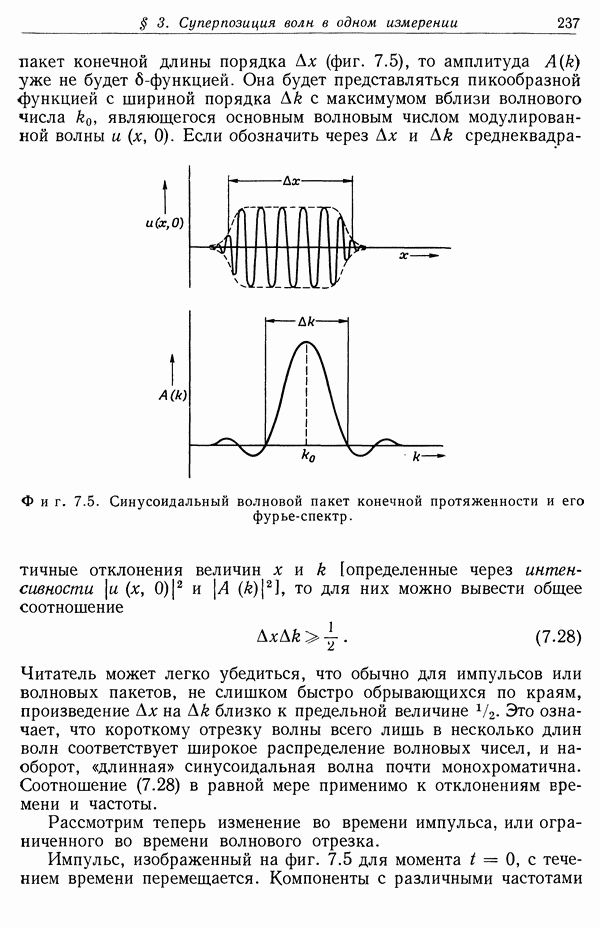
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
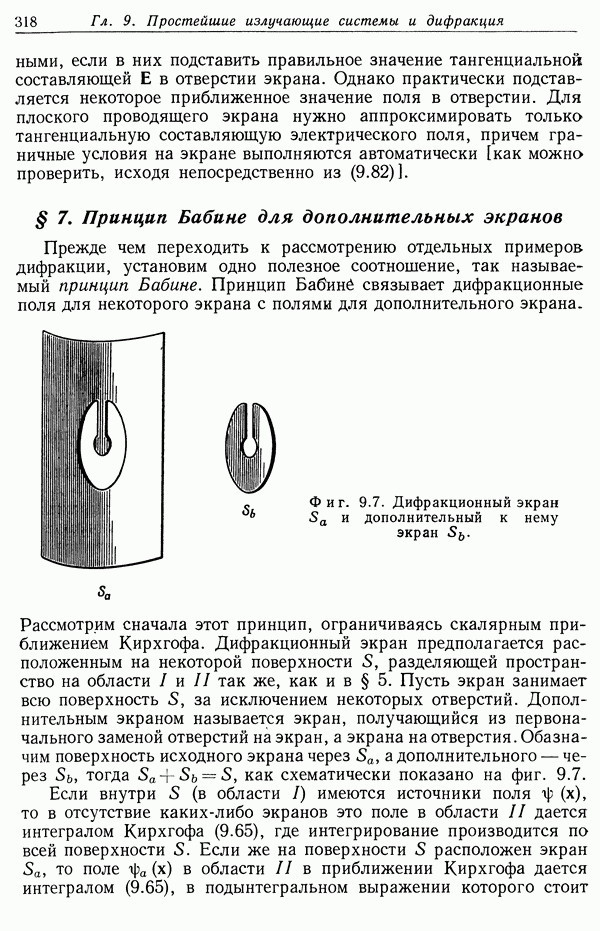
- § 7. Принцип Бабине для дополнительных экранов
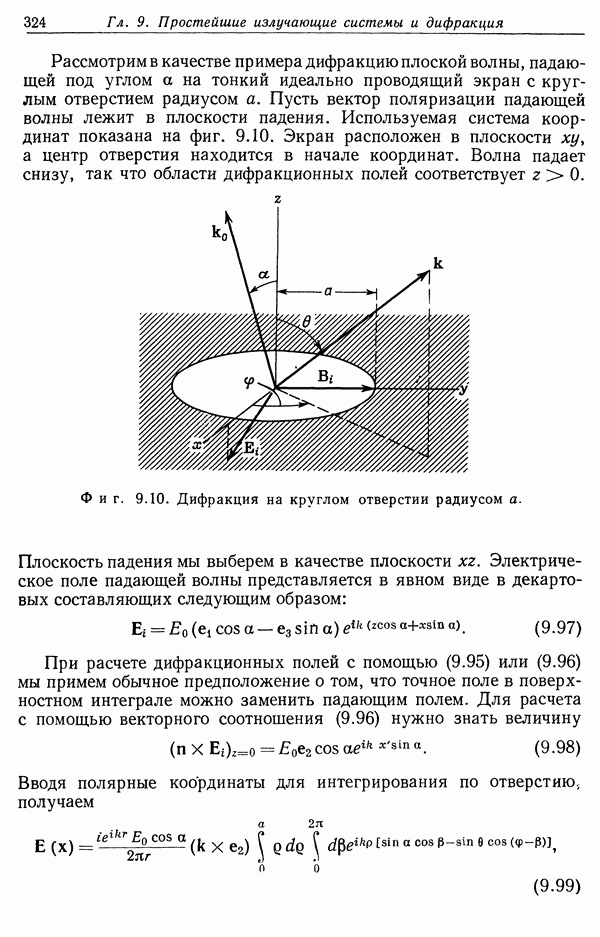
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
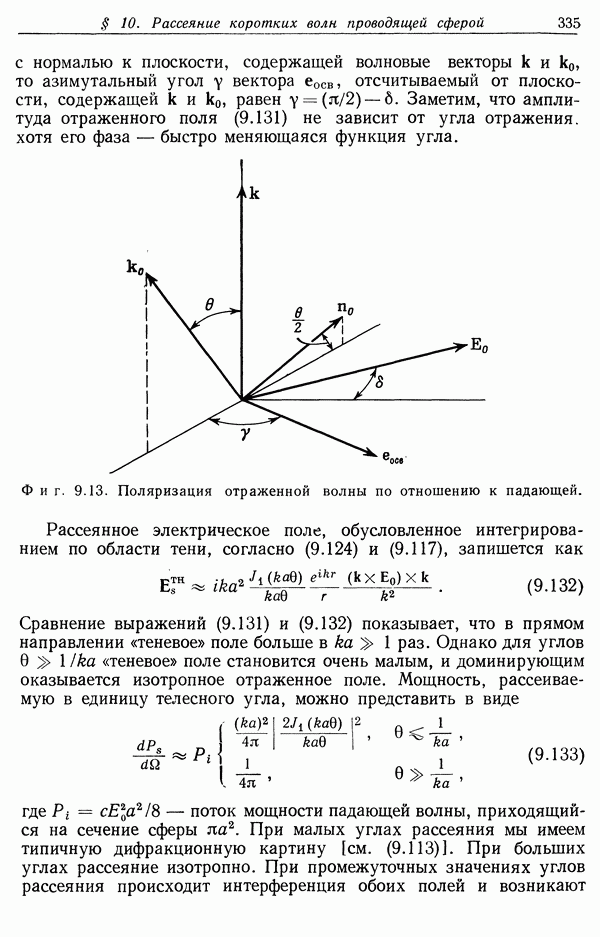
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
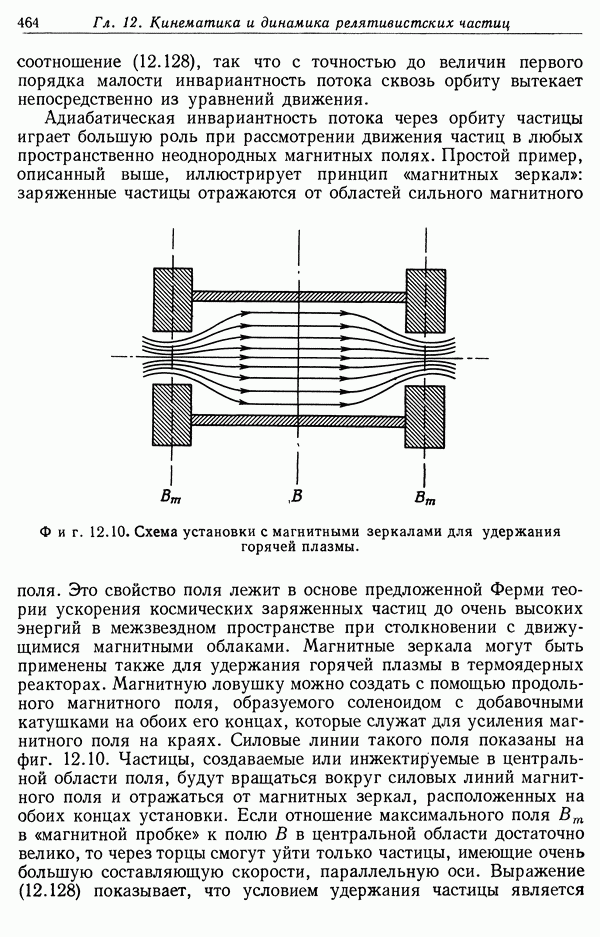
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ