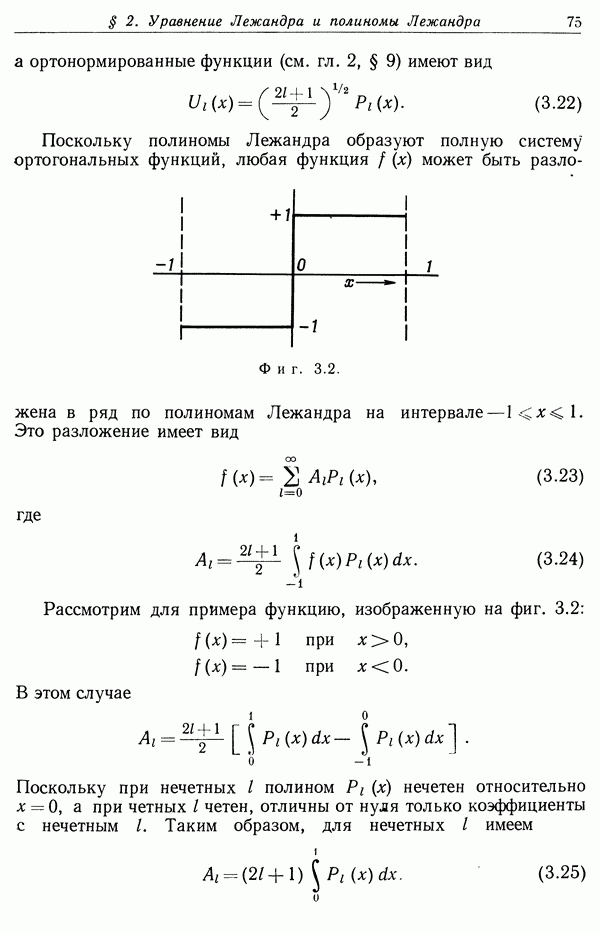| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6. Метод инверсии
Изложенные в предыдущих параграфах примеры применения метода изображений к сфере наводят на мысль о том, что решения электростатических задач, связанных обратным преобразованием радиуса

в каком-то смысле эквивалентны. Эта эквивалентность является основой так называемого метода инверсии, а преобразование (2.16) называется преобразованием инверсии на сфере. Радиус сферы называют радиусом инверсии, а ее центр — центром инверсии. Математический смысл эквивалентности ясен из следующей теоремы:
Пусть  потенциал, обусловленный системой точечных зарядов
потенциал, обусловленный системой точечных зарядов  в точках
в точках  Тогда функция
Тогда функция

является потенциалом системы зарядов

расположенных в точках 
Докажем эту теорему. Потенциал  можно представить в виде
можно представить в виде

где  — угол между радиусами-векторами
— угол между радиусами-векторами  При преобразовании (2.16) углы не меняются. Следовательно, новый потенциал Ф имеет вид
При преобразовании (2.16) углы не меняются. Следовательно, новый потенциал Ф имеет вид

Вынося  за знак радикала, мы можем переписать Ф в виде
за знак радикала, мы можем переписать Ф в виде

откуда и следует справедливость теоремы.
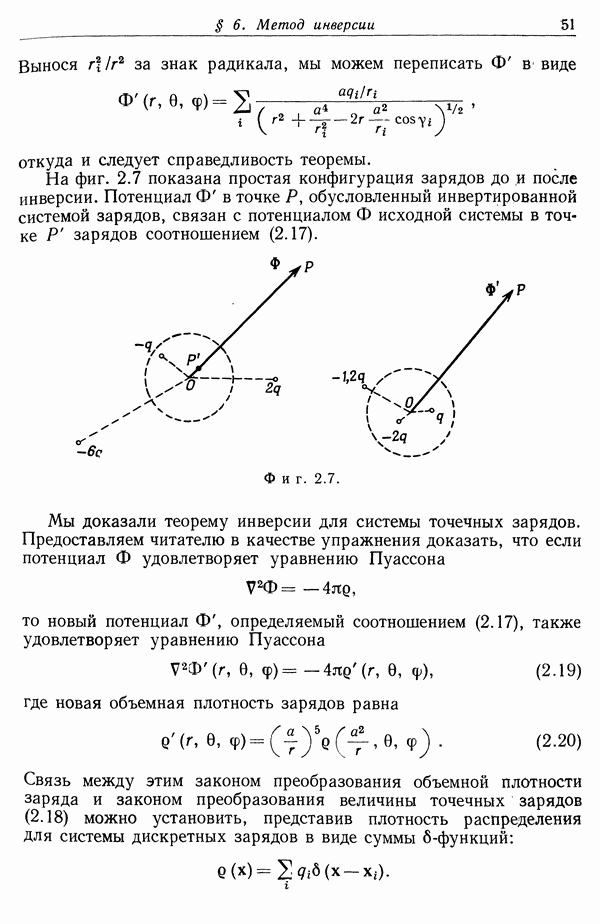
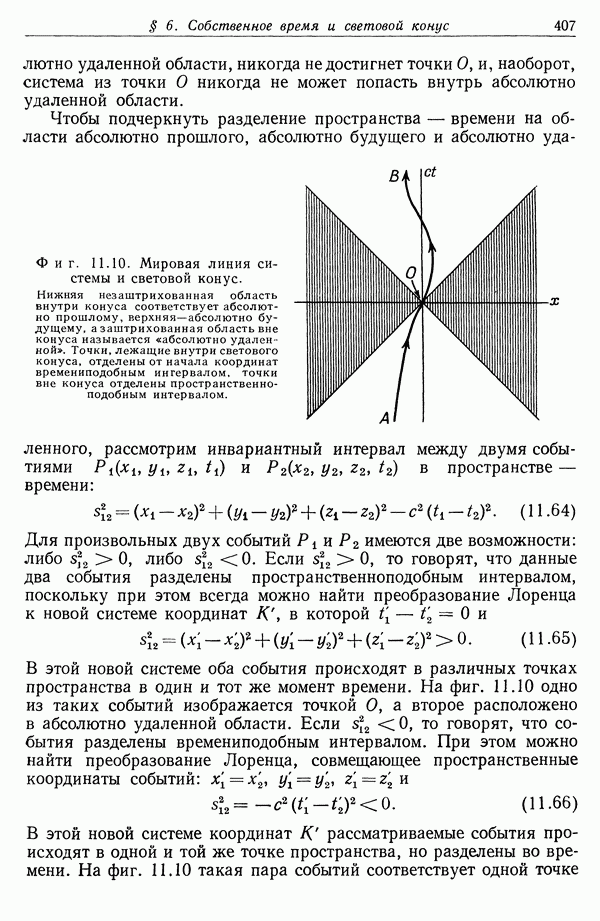
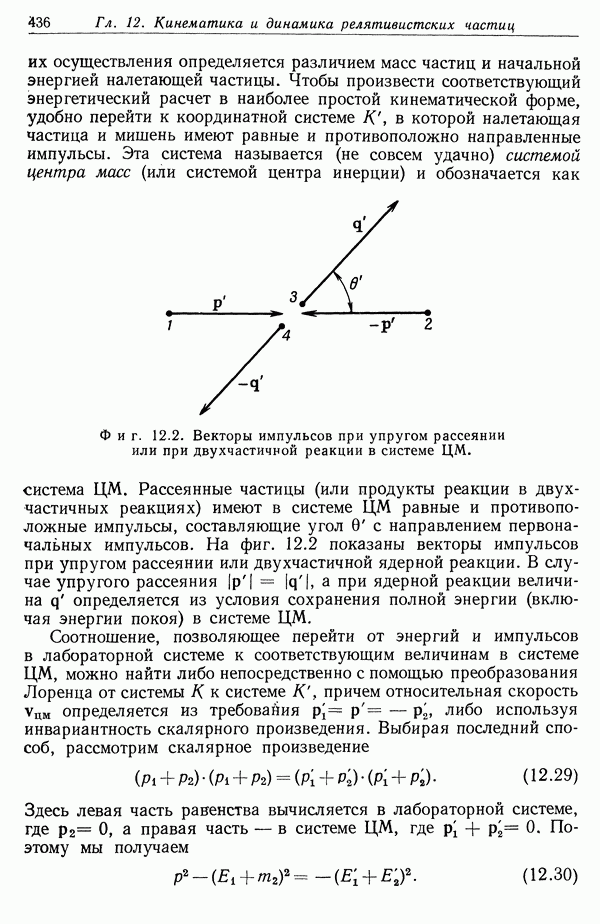
На фиг. 2.7 показана простая конфигурация зарядов до ,и после инверсии. Потенциал Ф в точке Р, обусловленный инвертированной системой зарядов, связан с потенциалом Ф исходной системы в точке Р зарядов соотношением (2.17).

Фиг. 2.7.
Мы доказали теорему инверсии для системы точечных зарядов. Предоставляем читателю в качестве упражнения доказать, что если потенциал Ф удовлетворяет уравнению Пуассона

то новый потенциал Ф, определяемый соотношением (2.17), также удовлетворяет уравнению Пуассона

где новая объемная плотность зарядов равна

Связь между этим законом преобразования объемной плотности заряда и законом преобразования величины точечных зарядов (2.18) можно установить, представив плотность распределения для системы дискретных зарядов в виде суммы  -функций:
-функций:

В сферических координатах с началом координат в центре инверсии объемная плотность заряда запишется в виде

где  — угловая
— угловая  -функция, интеграл от которой по телесному углу дает единицу, а
-функция, интеграл от которой по телесному углу дает единицу, а  — радиальная
— радиальная  -функция. При инверсии угловая зависимость не меняется. Следовательно,
-функция. При инверсии угловая зависимость не меняется. Следовательно,

Как указано в гл. 1, § 2, радиальную  -функцию можно преобразовать следующим образом:
-функцию можно преобразовать следующим образом:

так что

а новая объемная плотность заряда принимает, согласно (2.20), вид

где  что совпадает с (2.18).
что совпадает с (2.18).
Для поверхностной плотности зарядов закон преобразования при инверсии имеет вид

такую зависимость и следовало ожидать из сопоставления соотношений (2.18) и (2.20).
Прежде чем перейти к примерам применения метода инверсии, следует остановиться на нескольких вопросах физического и геометрического характера.
В отношении физических свойств преобразования инверсии заметим сначала, что, если в первоначальной задаче на некоторых поверхностях был задан постоянный потенциал, после инверсии на инвертированных поверхностях потенциал не будет, вообще
говоря, постоянным. Это видно из соотношения (2.17): из-за множителя  потенциал Ф инвертированной поверхности не будет постоянным, даже если потенциал Ф первоначальной поверхности был постоянным. Единственным исключением является случай, когда потенциал Ф равен нулю на некоторой поверхности; тогда и потенциал Ф равен нулю на инвертированной поверхности.
потенциал Ф инвертированной поверхности не будет постоянным, даже если потенциал Ф первоначальной поверхности был постоянным. Единственным исключением является случай, когда потенциал Ф равен нулю на некоторой поверхности; тогда и потенциал Ф равен нулю на инвертированной поверхности.
Может показаться, что, поскольку потенциал Ф содержит произвольную аддитивную постоянную, мы можем приравнять нулю потенциал произвольной поверхности первоначальной конфигурации, обеспечив тем самым нулевой потенциал инвертированной поверхности.

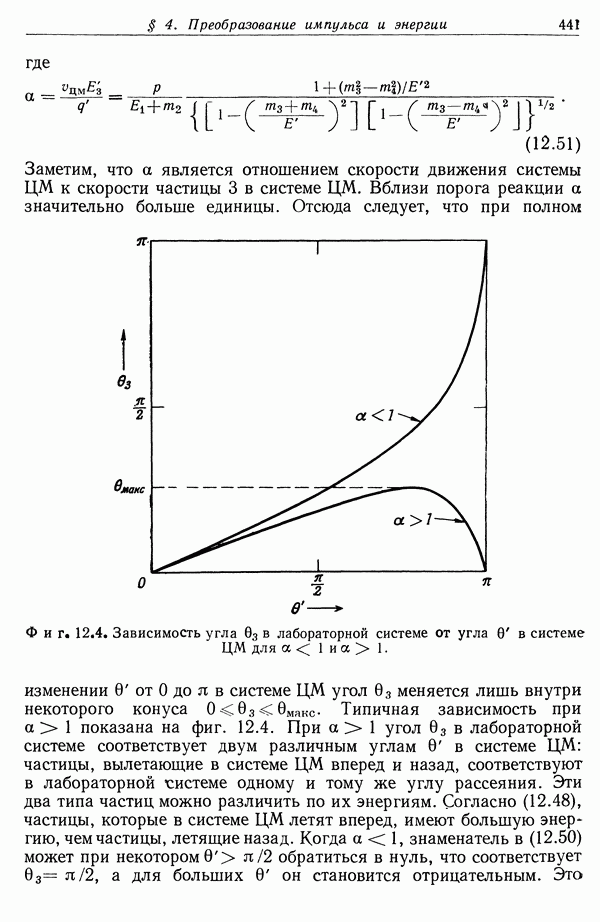
Фиг. 2.8. Преобразование инверсии. Поверхность S преобразуется в S, и наоборот; О — центр инверсии, а — радиус инверсии.
Однако тут мы сталкиваемся со вторым характерным физическим свойством преобразования инверсии. Оказывается, потенциалы, получающиеся по методу инверсии для двух задач, в которых потенциалы первоначальных систем различаются лишь на постоянную  соответствуют физически различным системам зарядов, а именно распределение зарядов отличается на точечный заряд
соответствуют физически различным системам зарядов, а именно распределение зарядов отличается на точечный заряд  расположенный в центре инверсии. Это легко видеть из (2.17): добавление постоянного слагаемого
расположенный в центре инверсии. Это легко видеть из (2.17): добавление постоянного слагаемого  к Ф приводит к увеличению Ф на
к Ф приводит к увеличению Ф на  Соответственно при применении метода инверсии следует иметь в виду, что при отображении бесконечно удаленной точки в начало координат там может появиться точечный заряд. Если он не требуется по условиям задачи, то его следует убрать надлежащей линейной суперпозицией.
Соответственно при применении метода инверсии следует иметь в виду, что при отображении бесконечно удаленной точки в начало координат там может появиться точечный заряд. Если он не требуется по условиям задачи, то его следует убрать надлежащей линейной суперпозицией.
Приведем теперь несколько простых геометрических свойств преобразования инверсии, в справедливости которых легко убедиться. Пусть О — центр инверсии, а — радиус инверсии (фиг. 2.8). Пересечение сферы инверсии с плоскостью чертежа показано на фиг. 2.8 пунктиром. Пусть кривая АВ — след пересечения
поверхности S с плоскостью чертежа. Инвертированная поверхность S, определяемая преобразованием (2.16), пересекается с плоскостью чертежа по кривой АВПри инверсии справедливы следующие положения, доказательства которых мы приводить не будем:
а) углы пересечения не меняются;
б) величина элементарной площадки  на поверхности S связана с величиной соответствующей площадки
на поверхности S связана с величиной соответствующей площадки  на инвертированной поверхности S соотношением
на инвертированной поверхности S соотношением 
в) сфера переходит в сферу (в частности, бесконечного радиуса, см.  );
);
г) плоскость переходит в сферу, проходящую через центр инверсии, и наоборот.

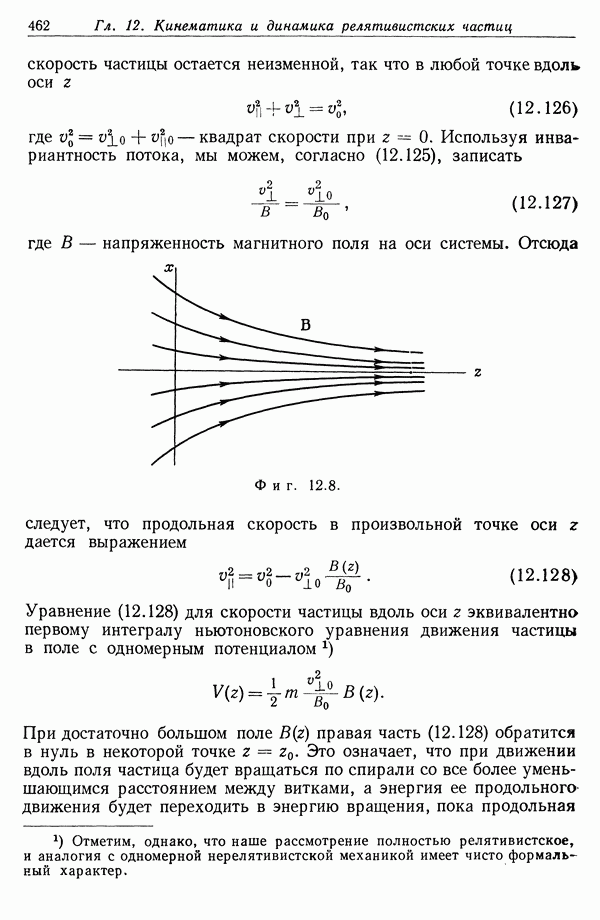
Фиг. 2.9. Различные варианты инверсии сферы. Если центр О инверсии расположен на поверхности S сферы, то инвертированная поверхность S представляет собой плоскость, в остальных случаях — сферу. Сфера инверсии показана пунктиром.
На фиг. 2.9 показаны различные варианты инверсии сферы, соответствующие п. «в» и «г» для случаев, когда центр инверсии расположен вне сферы, на ее поверхности и внутри сферы.
В качестве простейшего примера решения электростатической задачи методом инверсии рассмотрим проводящую сферу радиусом  , несущую заряд Q. Внутри этой сферы потенциал постоянен и равен
, несущую заряд Q. Внутри этой сферы потенциал постоянен и равен  а вне сферы убывает обратно пропорционально расстоянию от ее центра. Надлежащим выбором центра инверсии и соответствующих параметров мы можем с помощью метода инверсии найти потенциал точечного заряда q, расположенного на расстоянии d от бесконечной проводящей заземленной плоскости. Очевидно, если поместить центр инверсии О на поверхности сферы
а вне сферы убывает обратно пропорционально расстоянию от ее центра. Надлежащим выбором центра инверсии и соответствующих параметров мы можем с помощью метода инверсии найти потенциал точечного заряда q, расположенного на расстоянии d от бесконечной проводящей заземленной плоскости. Очевидно, если поместить центр инверсии О на поверхности сферы
радиусом R, то в результате преобразования она перейдет в плоскость (фиг. 2.10). Далее, если принять произвольную постоянную  в потенциале равной
в потенциале равной  то сфера и получающаяся при ее преобразовании плоскость будут иметь нулевой потенциал, а в центре инверсии появится точечный заряд
то сфера и получающаяся при ее преобразовании плоскость будут иметь нулевой потенциал, а в центре инверсии появится точечный заряд  Чтобы получить точечный заряд q на расстоянии d от плоскости, следует положить радиус инверсии а равным
Чтобы получить точечный заряд q на расстоянии d от плоскости, следует положить радиус инверсии а равным  а начальный заряд Q равным -
а начальный заряд Q равным -  .
.

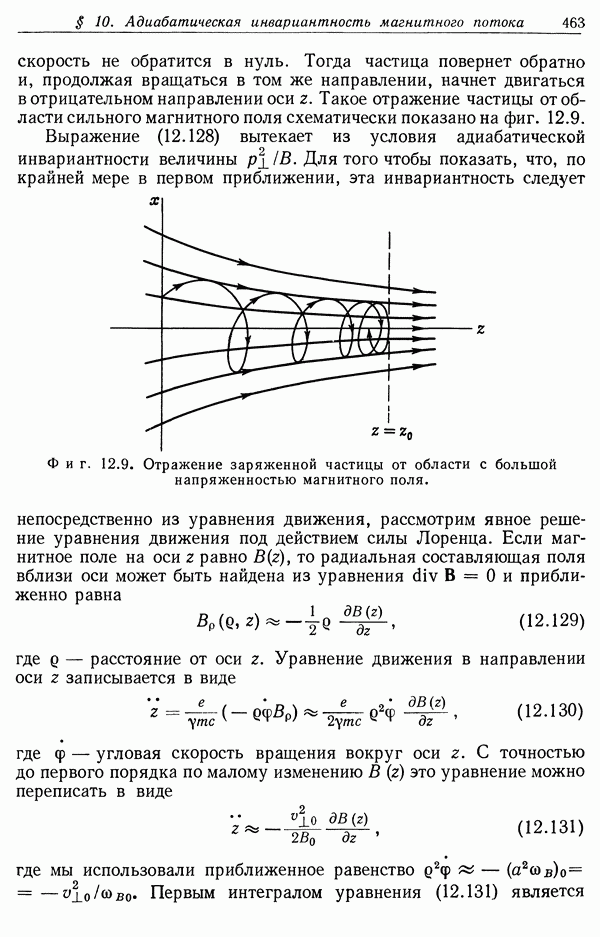
Фиг. 2.10. Нахождение потенциала точечного заряда методом инверсии. Потенциал изолированной заряженной проводящей сферы переходит при преобразовании инверсии в потенциал точечного заряда, находящегося на расстоянии d от бесконечной проводящей плоскости.
Поверхностная плотность заряда, индуцируемая на плоскости, легко находится с помощью соотношения (2.21). Поскольку на поверхности сферы поверхностная плотность постоянна, на плоскости она меняется обратно пропорционально кубу расстояния от начала координат (это легко проверить методом изображений; см. задачу 2.1).
Если центр инверсии находится вне изолированной проводящей сферы, то, как видно из фиг. 2.9, преобразованием инверсии можно решить задачу о поле точечного заряда вблизи заземленной проводящей сферы (в § 2 она была решена методом изображений). Предоставляем читателю убедиться в этом (см. задачу 2.9).
Весьма интересно применил метод инверсии лорд Кельвин в 1847 г. Он рассчитал распределение плотности заряда на внутренней и внешней сторонах тонкой заряженной проводящей «чаши», получающейся срезанием верхушки у сферической поверхности. В качестве исходного потенциала, подвергавшегося инверсии, был принят потенциал тонкого плоского заряженного круглого диска (см. гл. 3, § 12). По мере изменения формы поверхности от мелкой
чаши типа часового стекла до почти замкнутой сферы с небольшим отверстием распределение заряда также изменяется: сначала оно близко к распределению на диске, а затем переходит в распределение на сфере. В первом предельном случае плотность заряда внутри и снаружи почти одинакова, причем заряды сосредоточены в основном у краев, во втором случае на внутренней стороне плотность заряда почти нулевая, а на наружной заряд распределен почти равномерно. Численные данные приведены в трудах Кельвина [58] и в книге Джинса [55].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
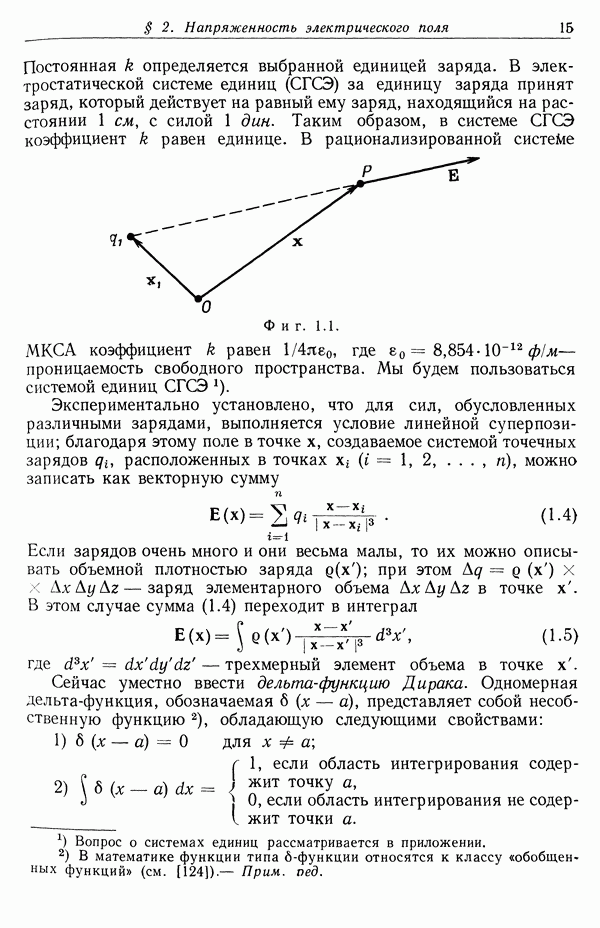
- § 2. Напряженность электрического поля
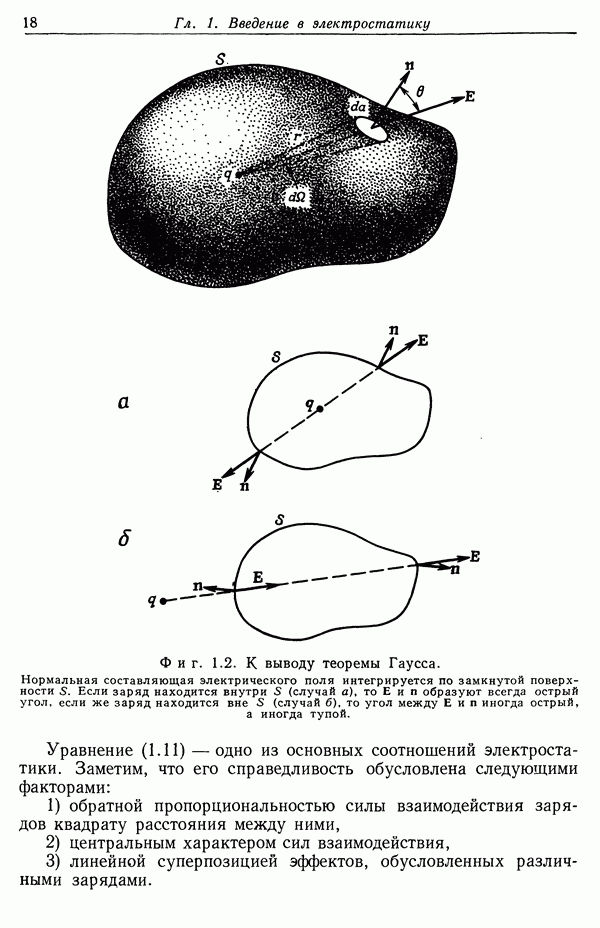
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
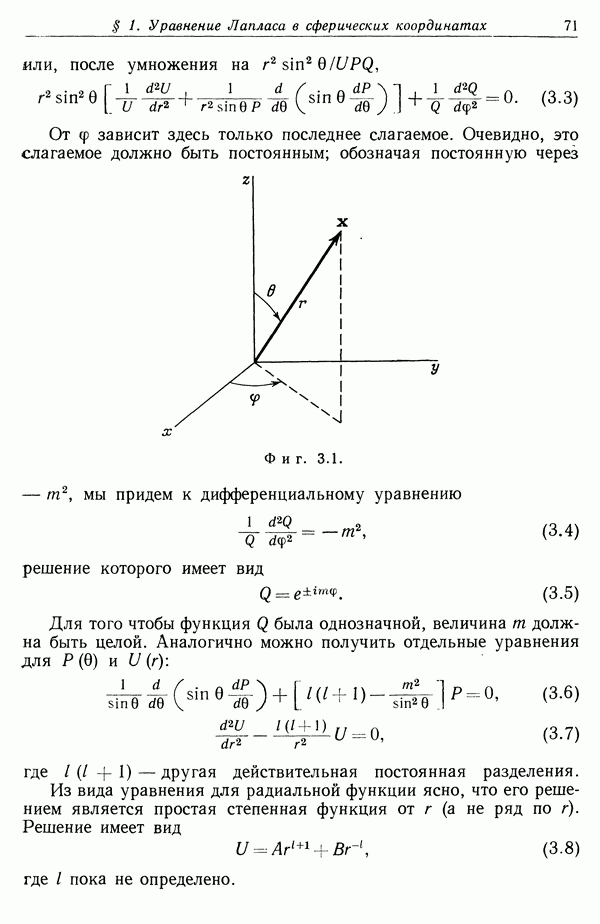
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
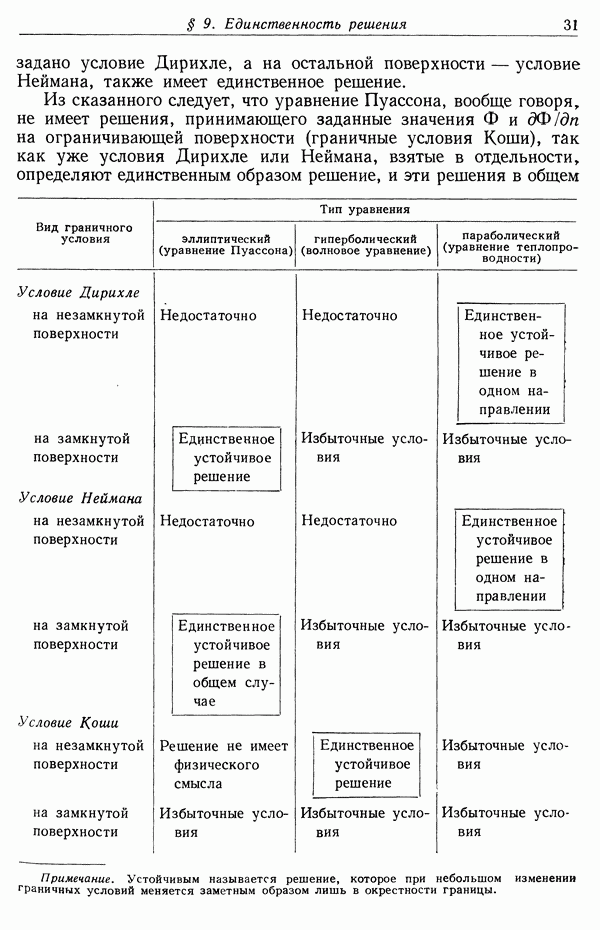
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
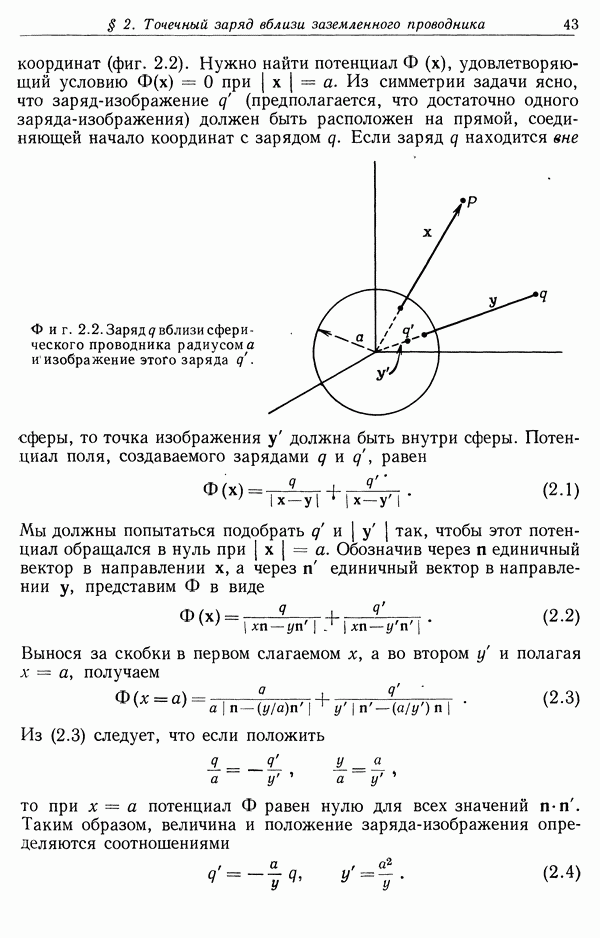
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
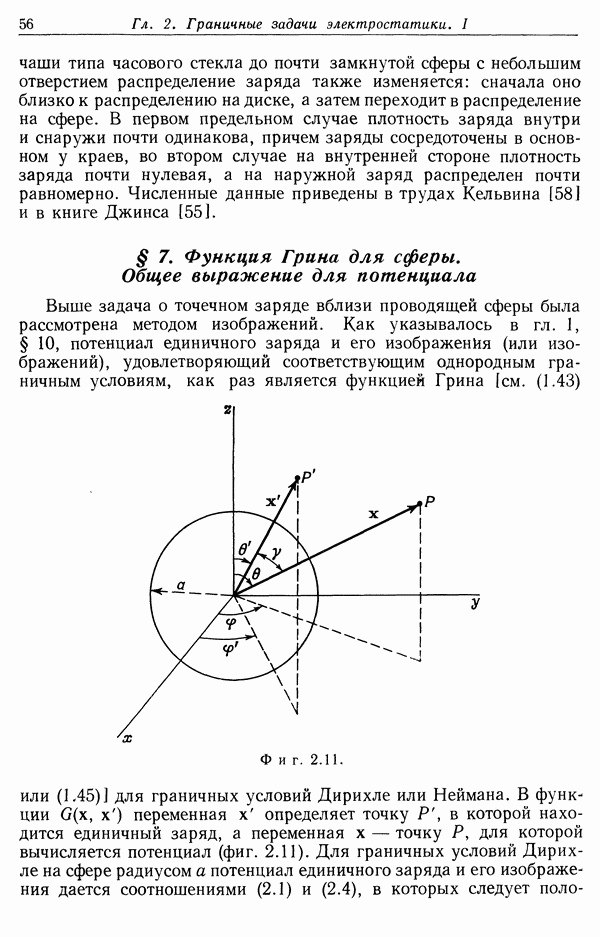
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
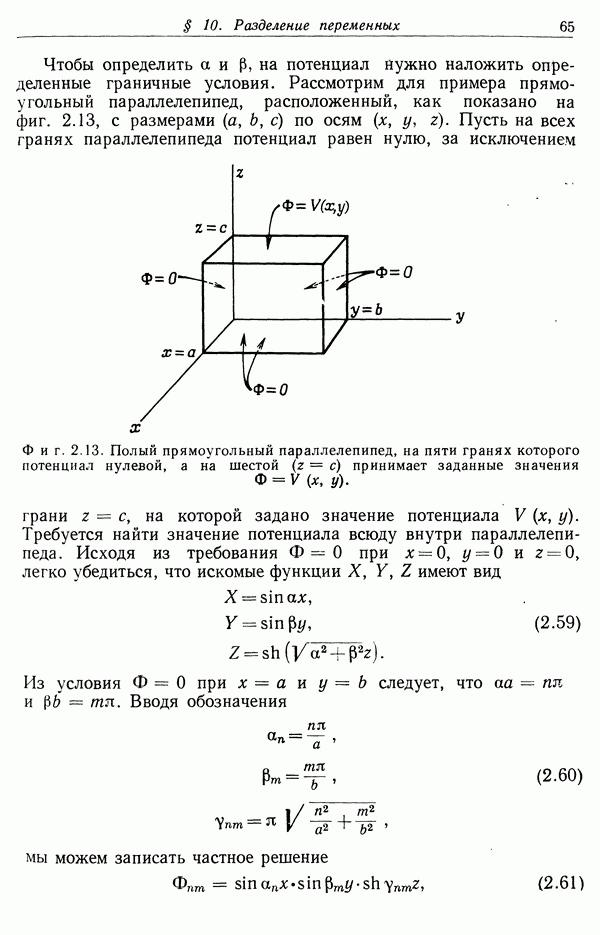
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
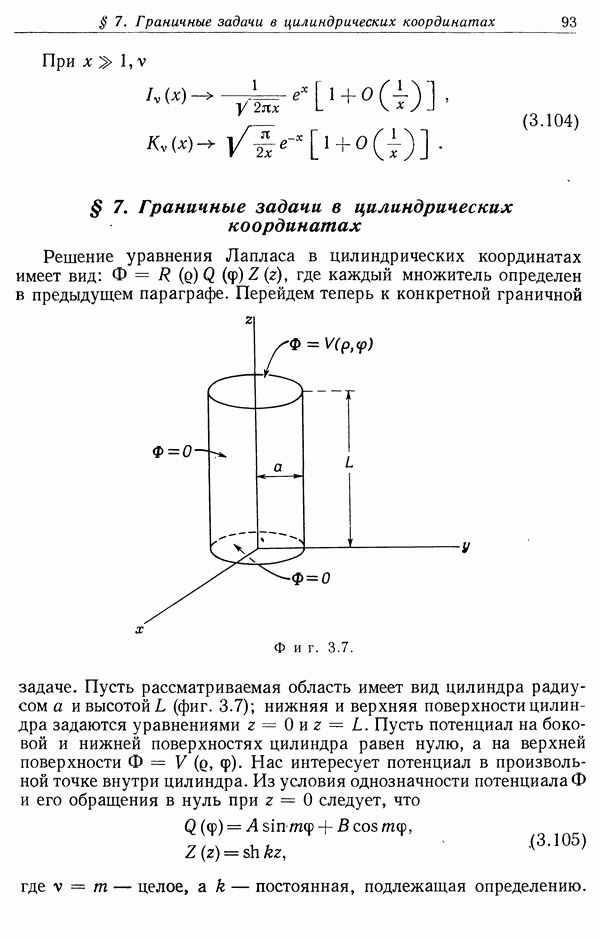
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
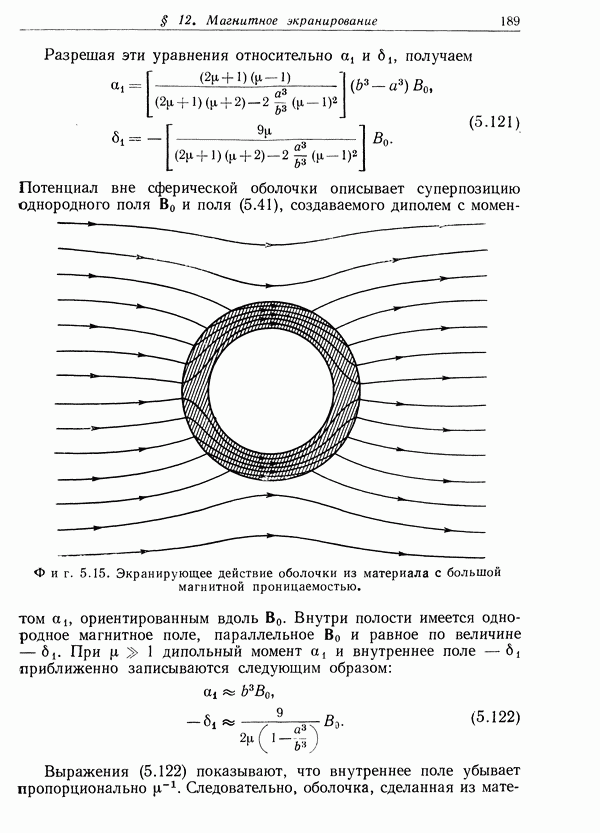
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
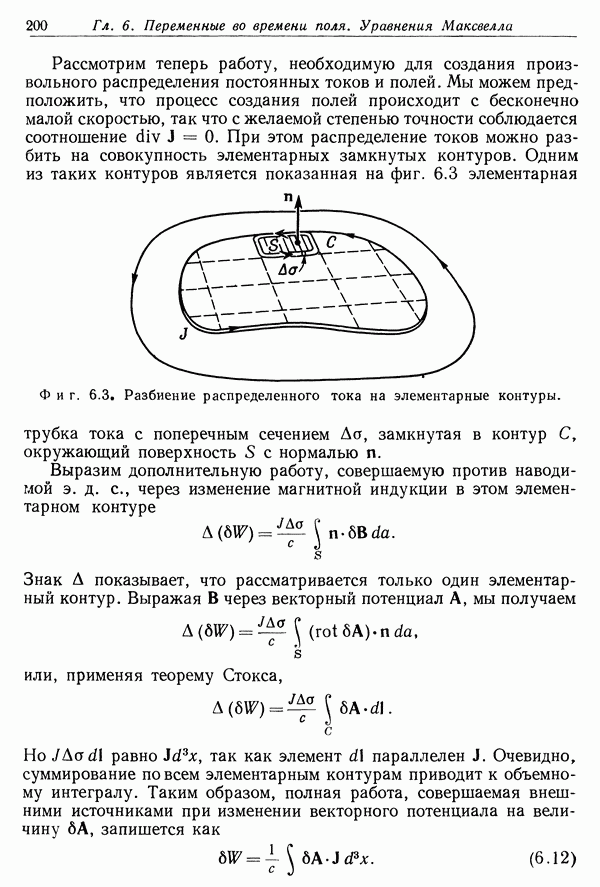
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
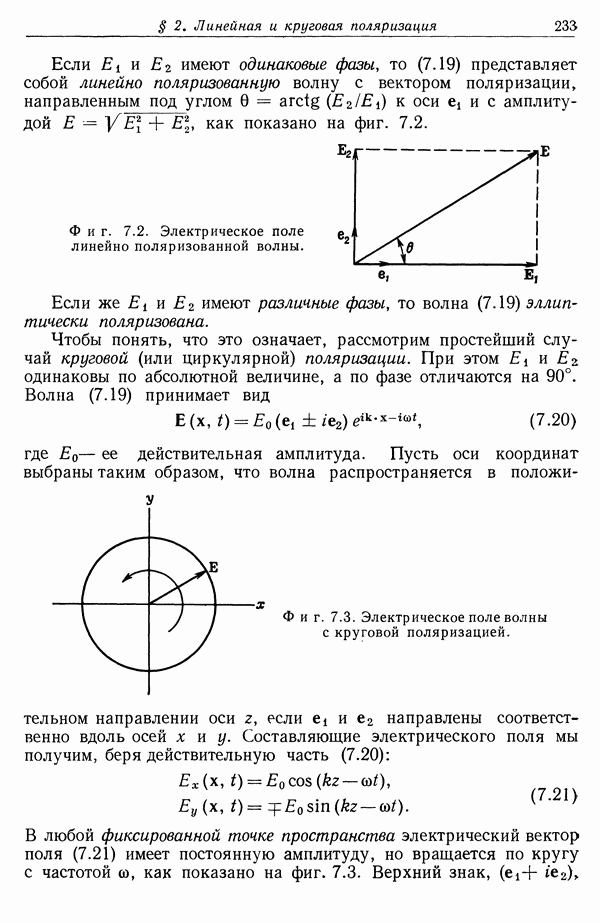
- § 2. Линейная и круговая поляризация
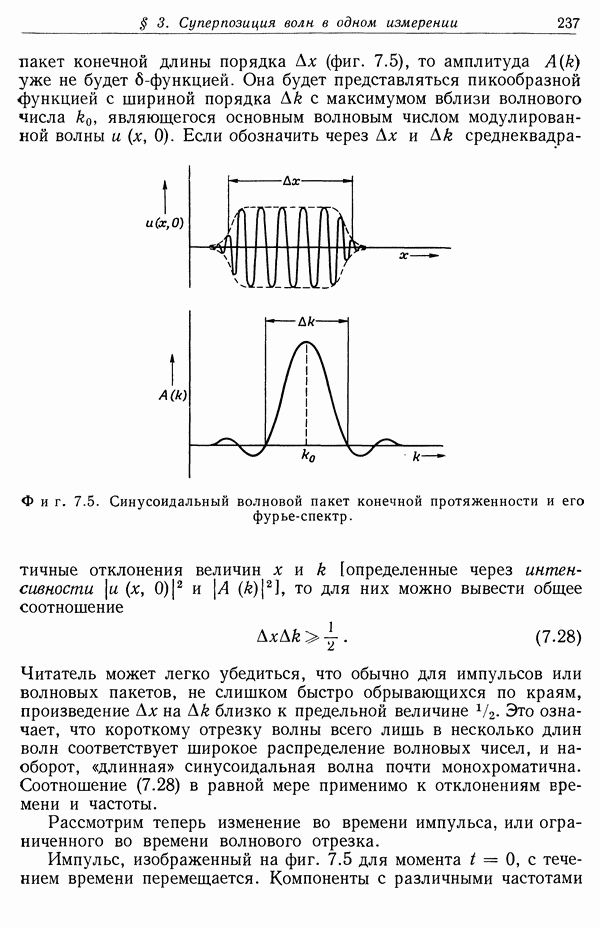
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
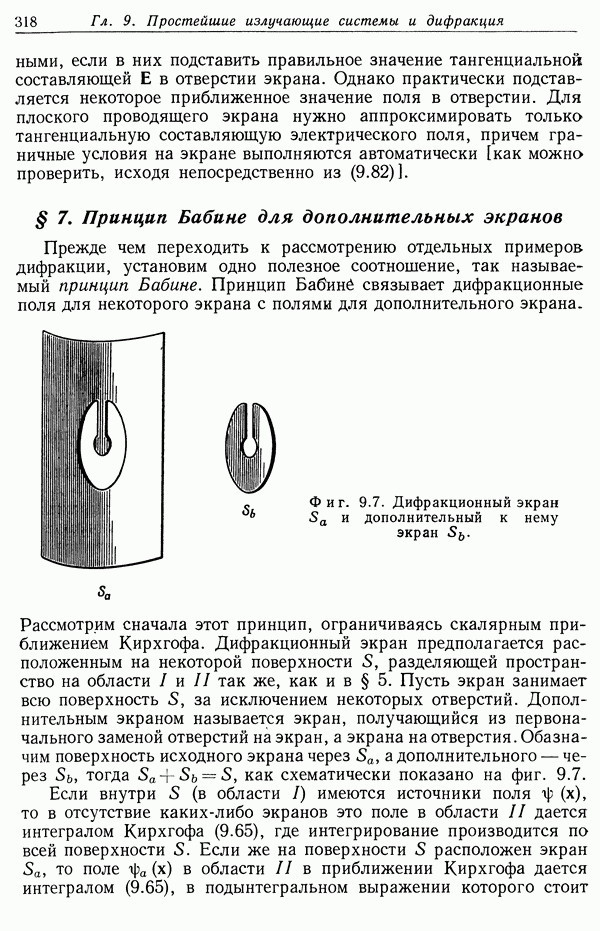
- § 7. Принцип Бабине для дополнительных экранов
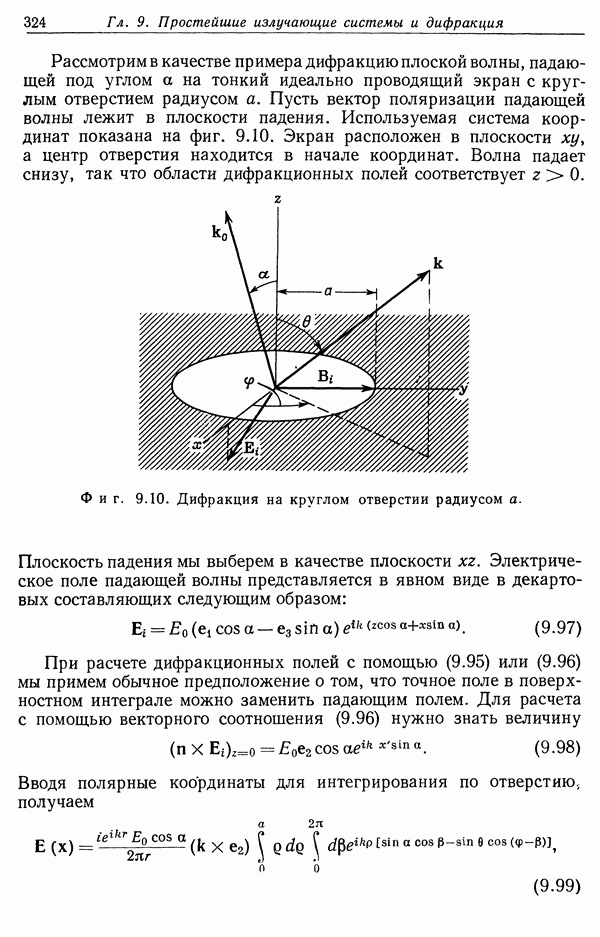
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
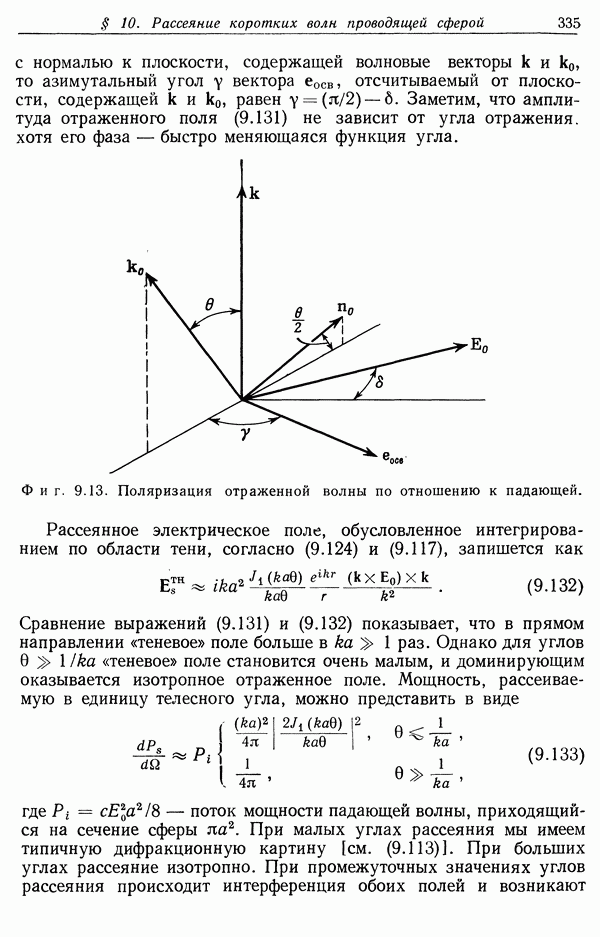
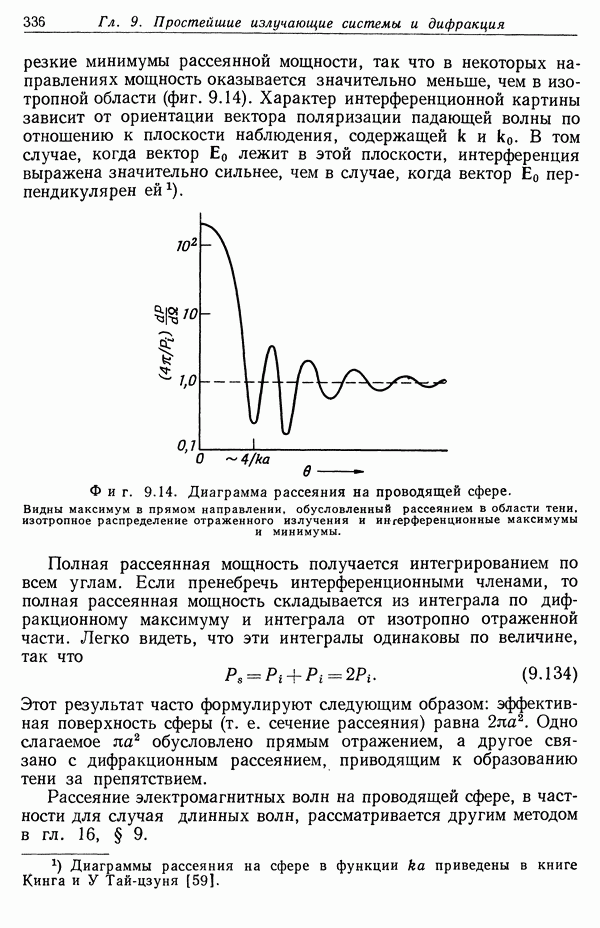
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
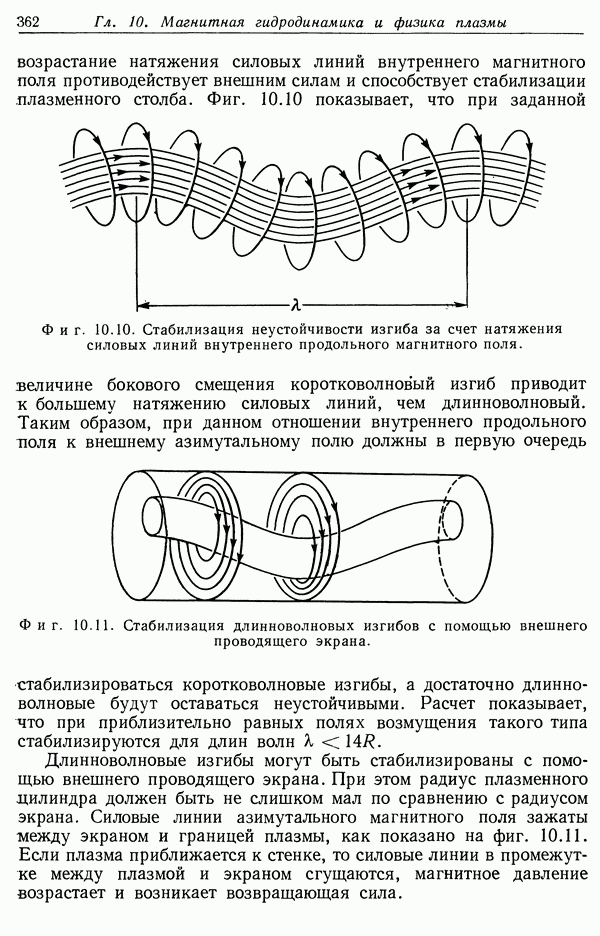
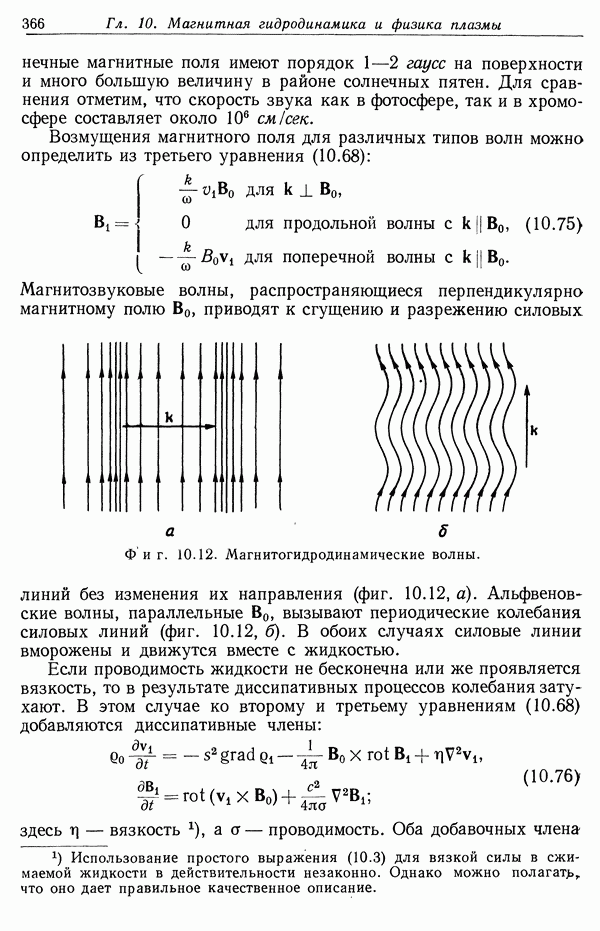
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
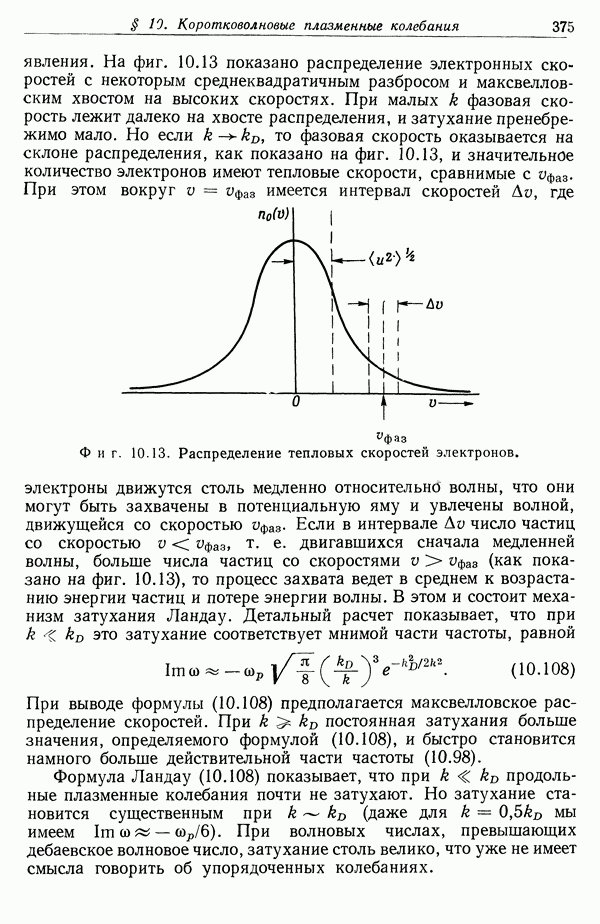
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
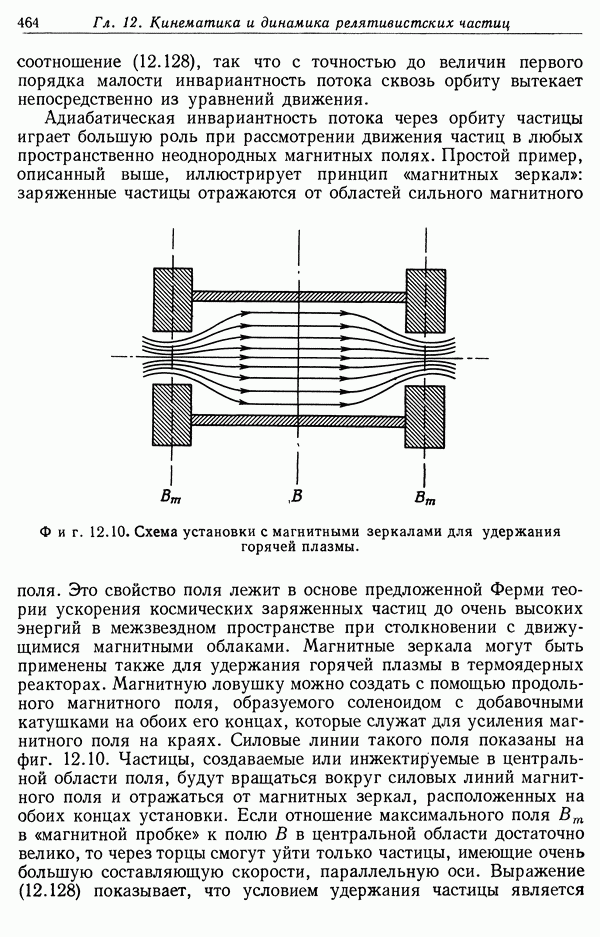
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
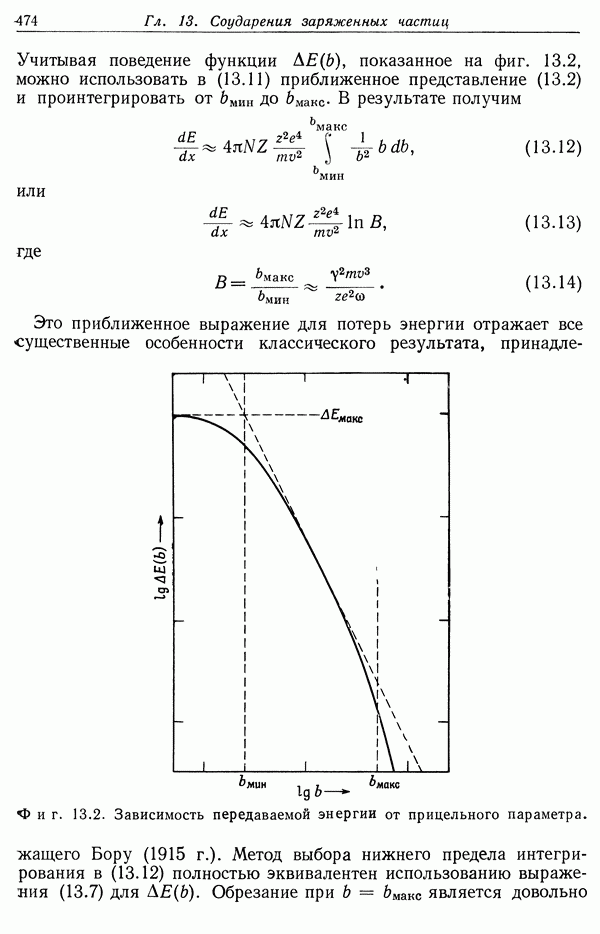
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
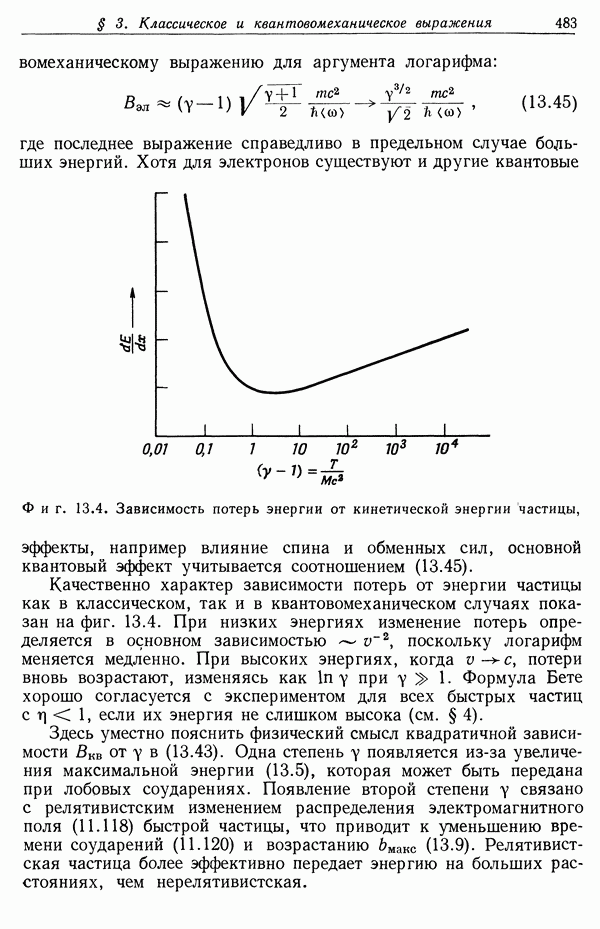
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
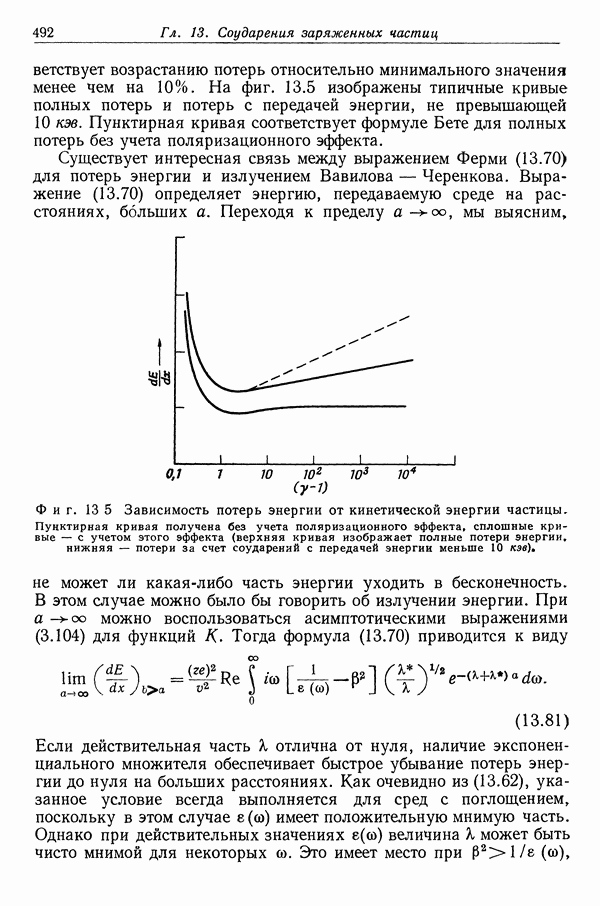
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
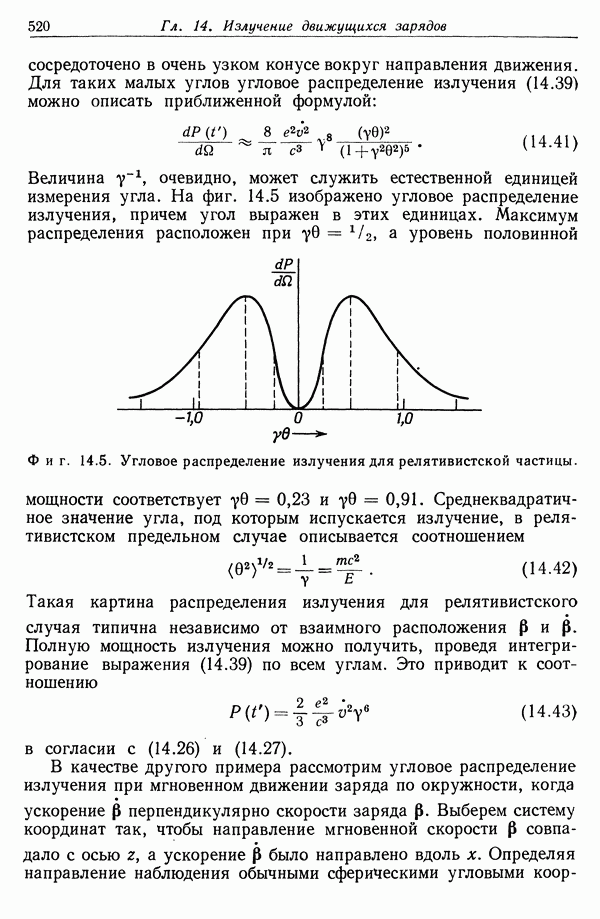
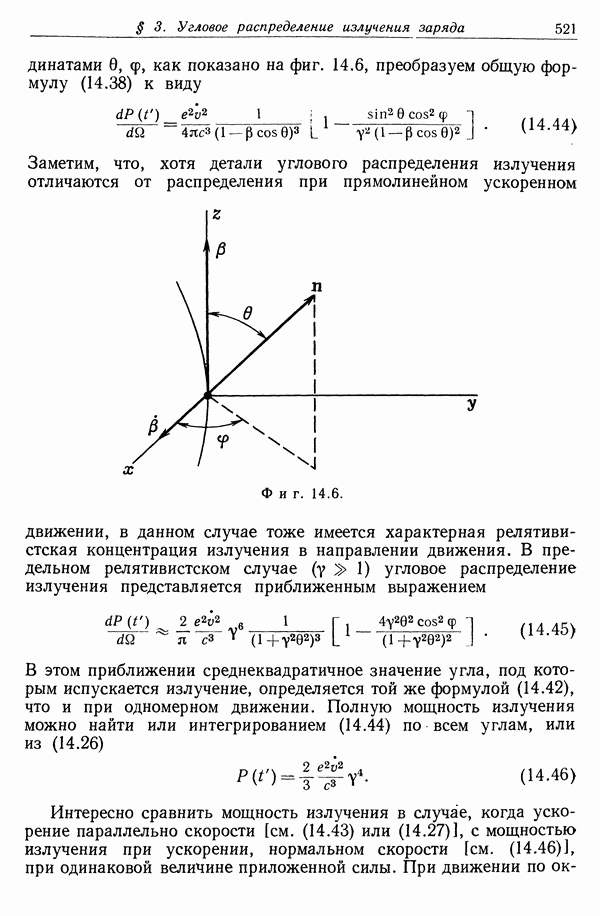
- § 3. Угловое распределение излучения ускоряемого заряда
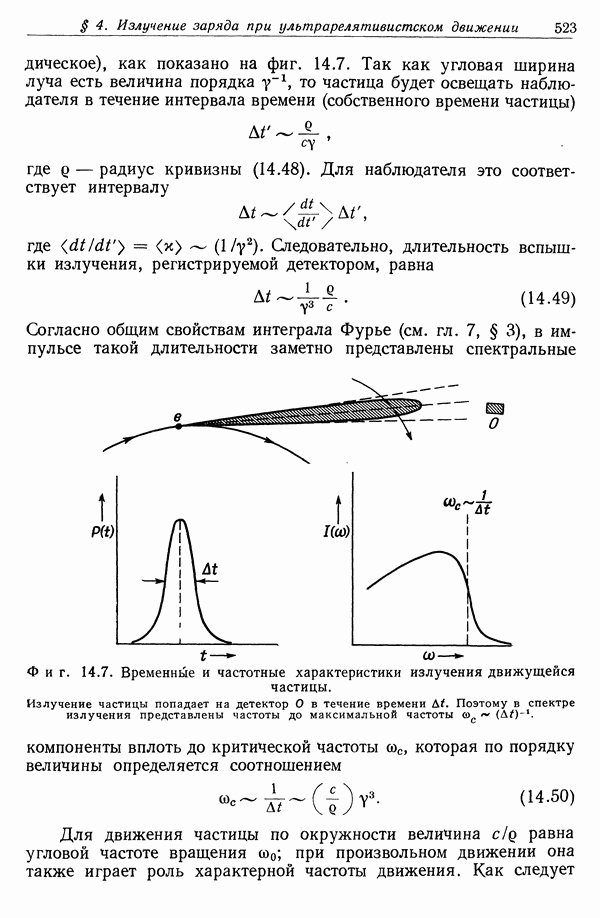
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
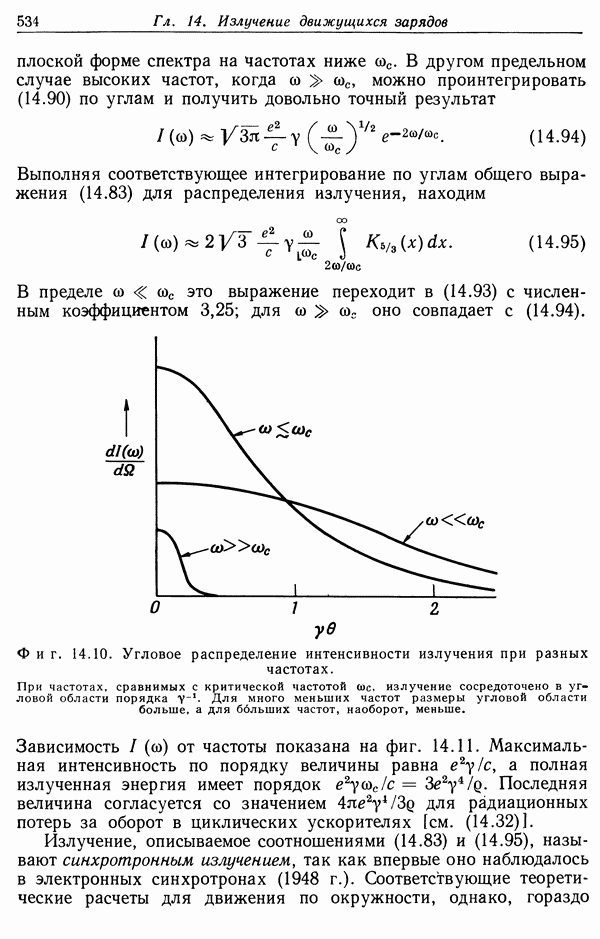
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
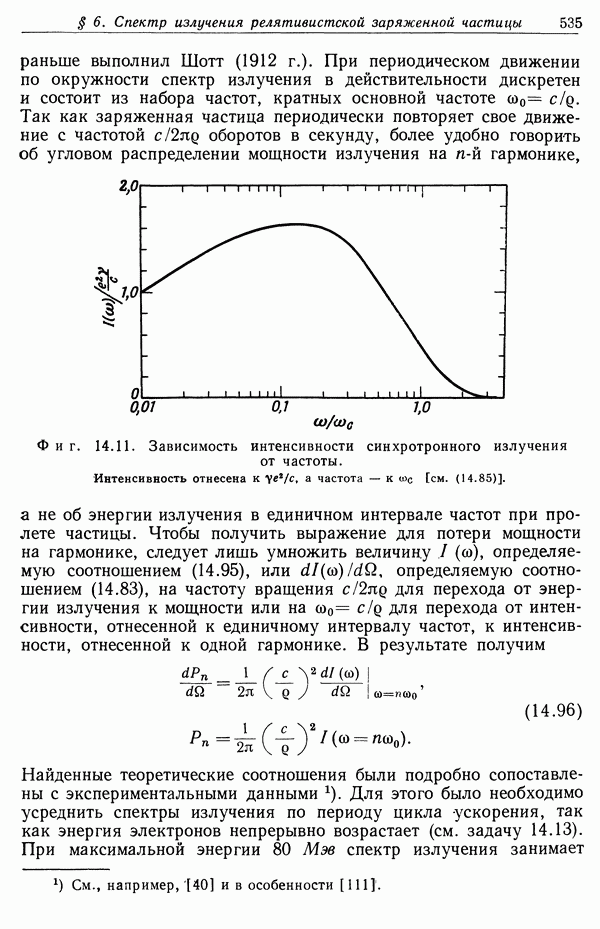
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
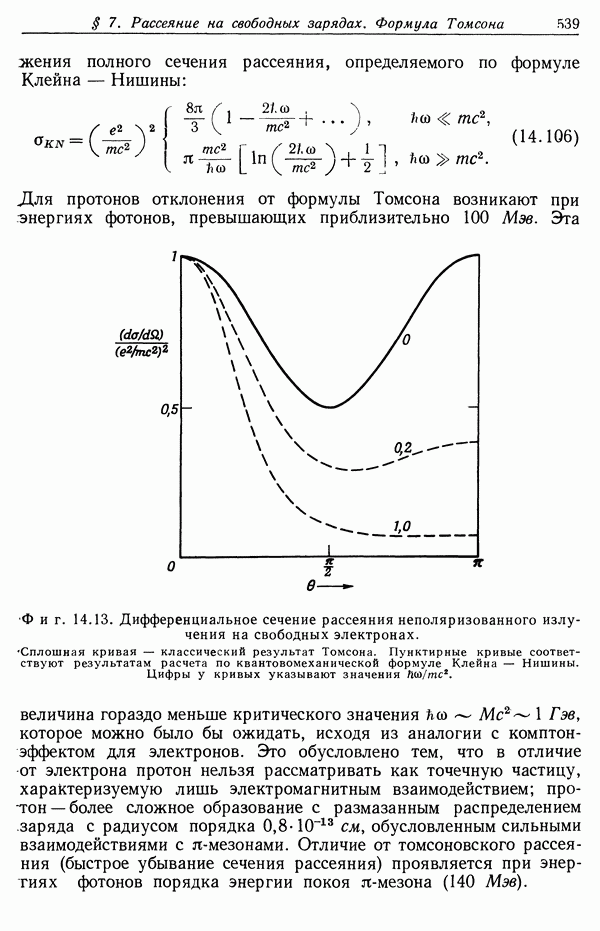
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
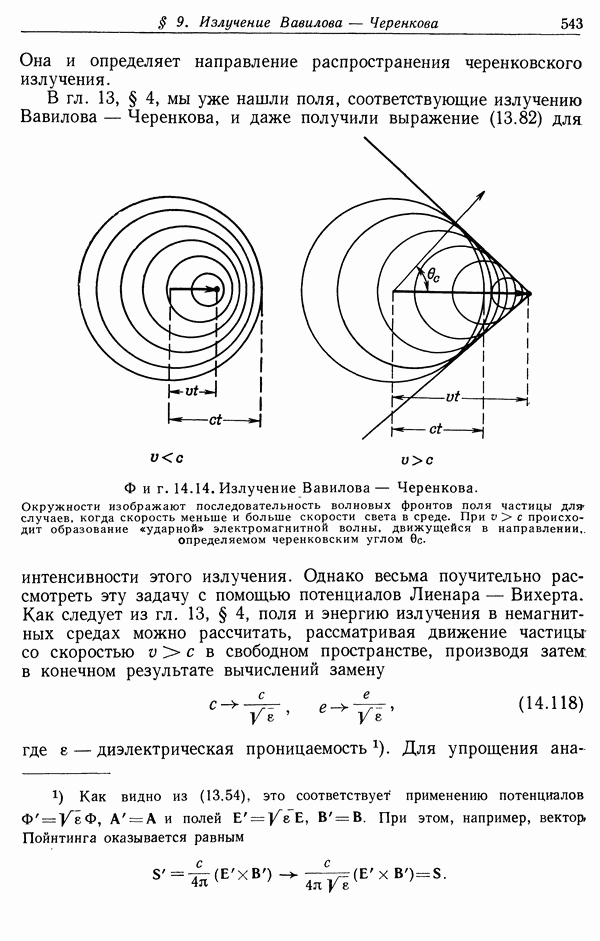
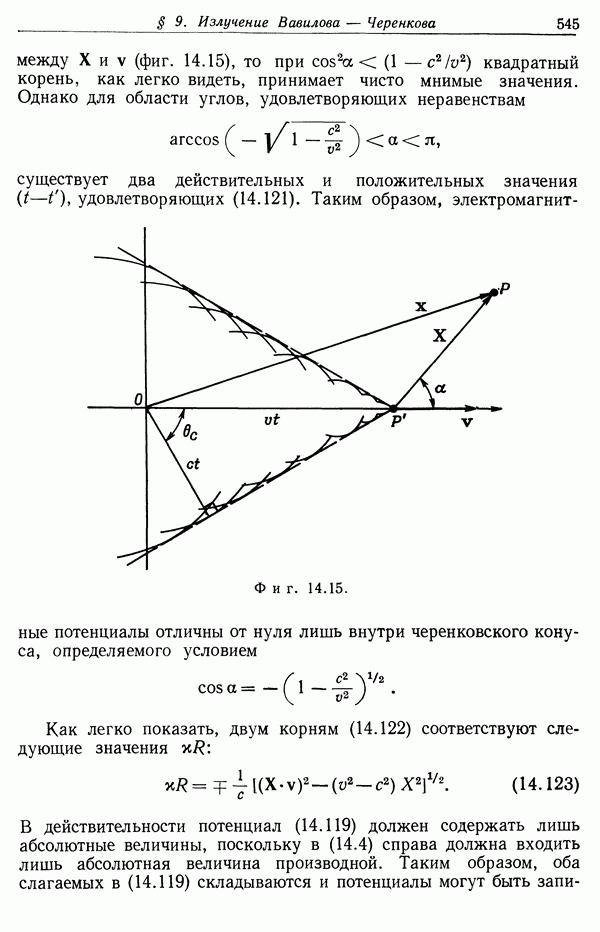
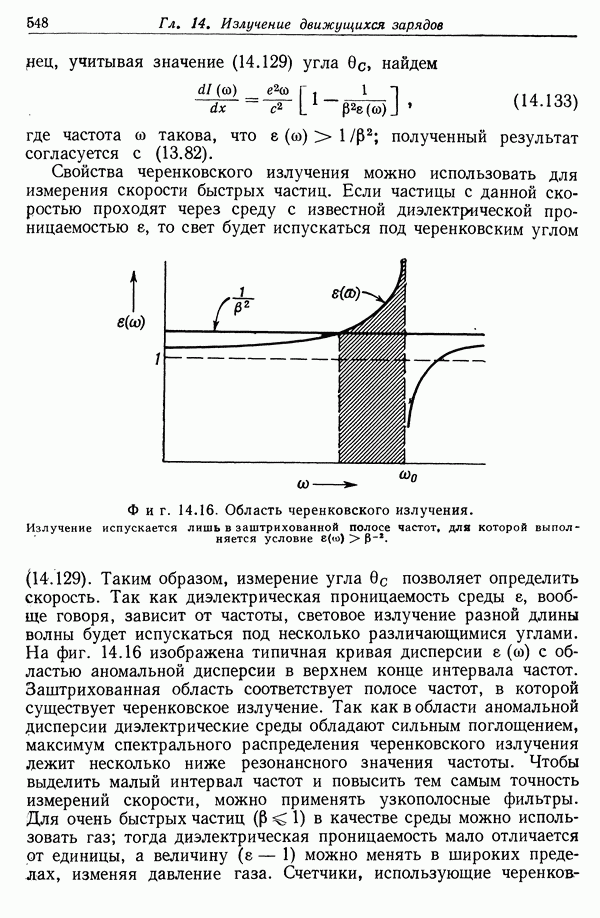
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
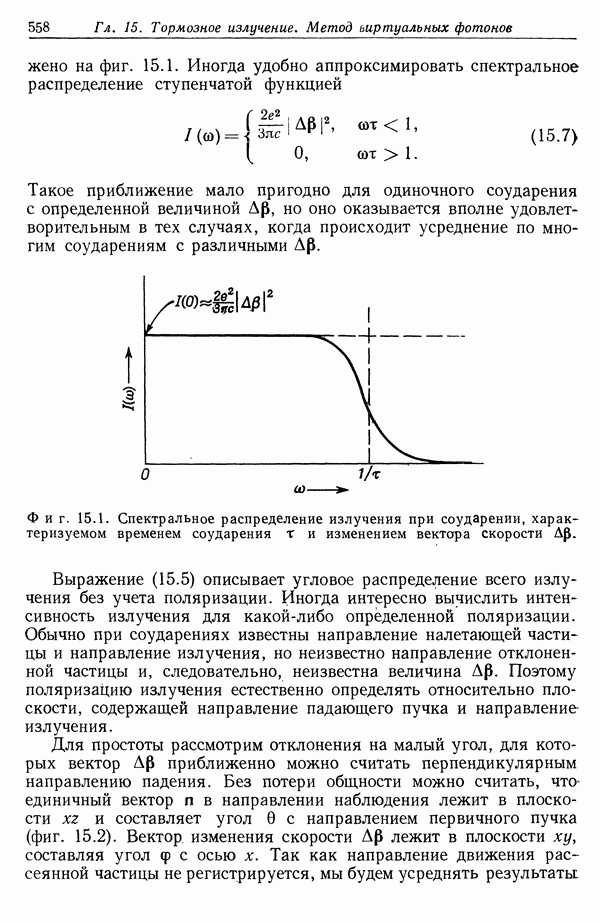
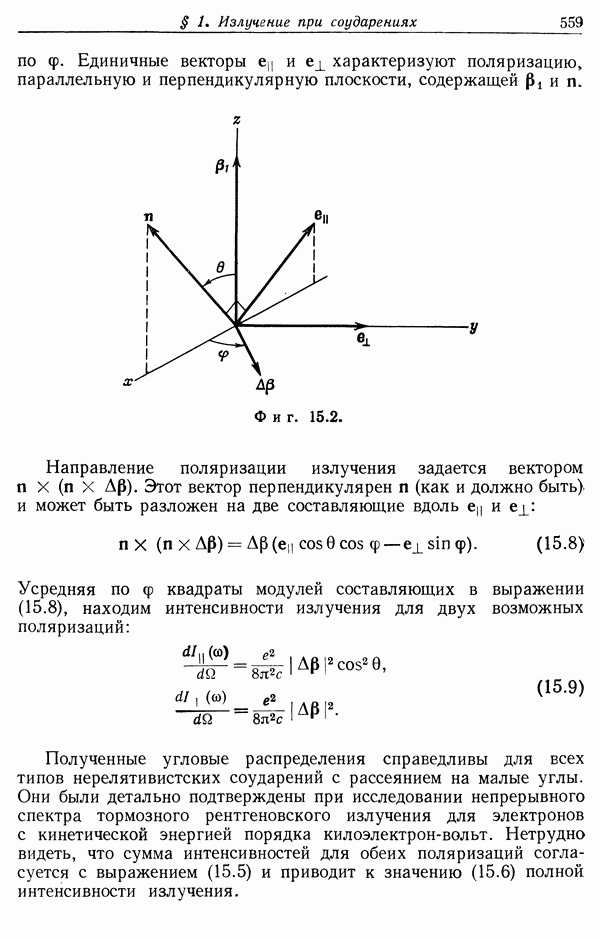
- § 1. Излучение при соударениях
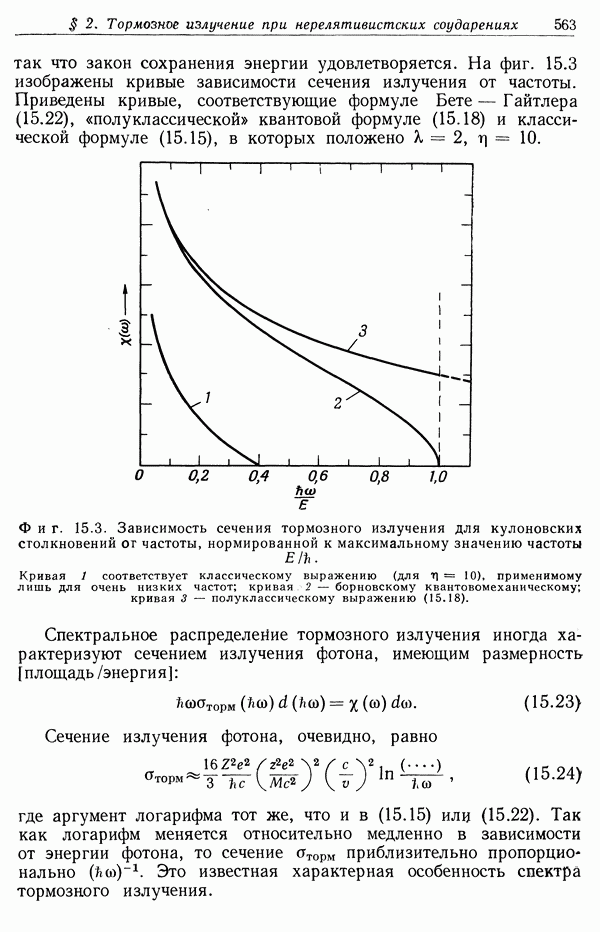
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
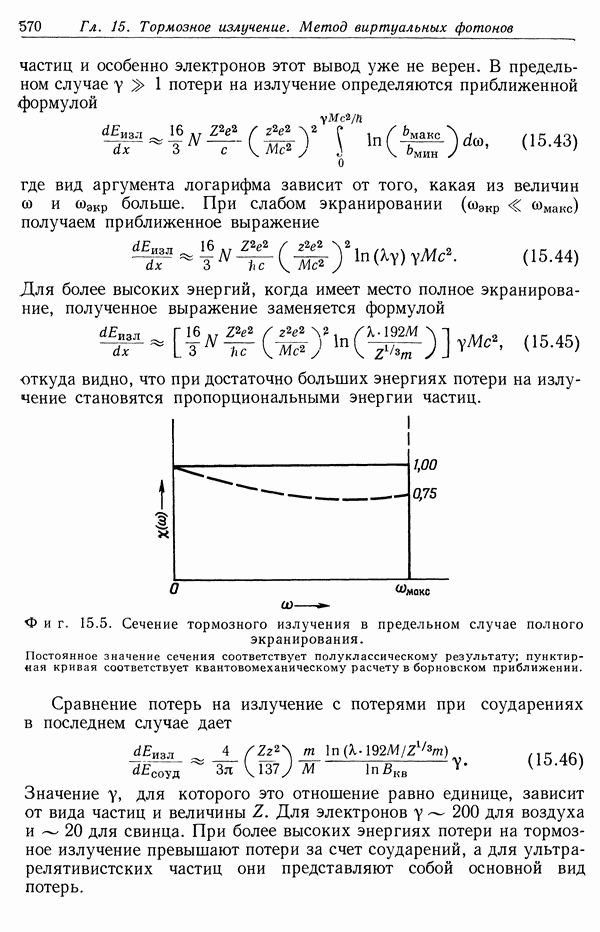
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ