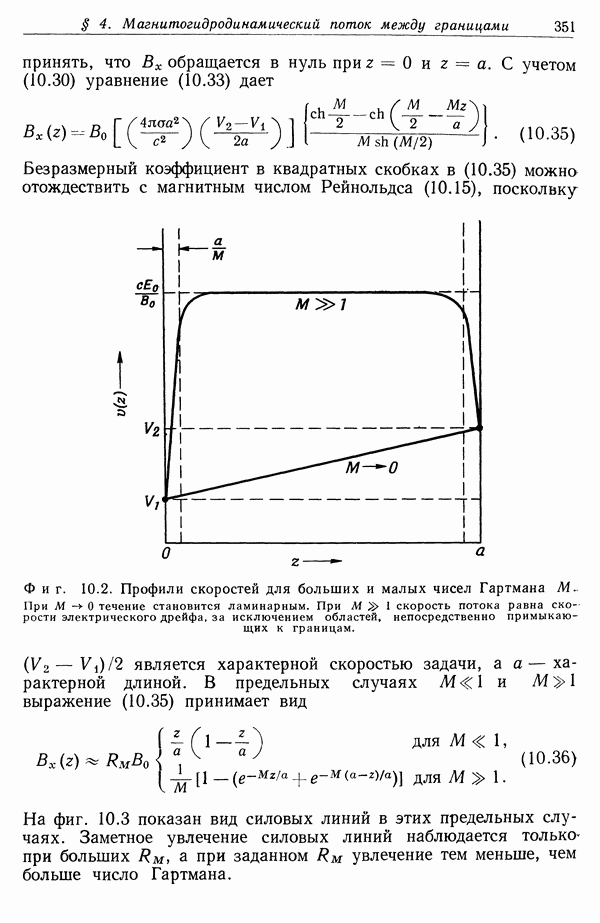
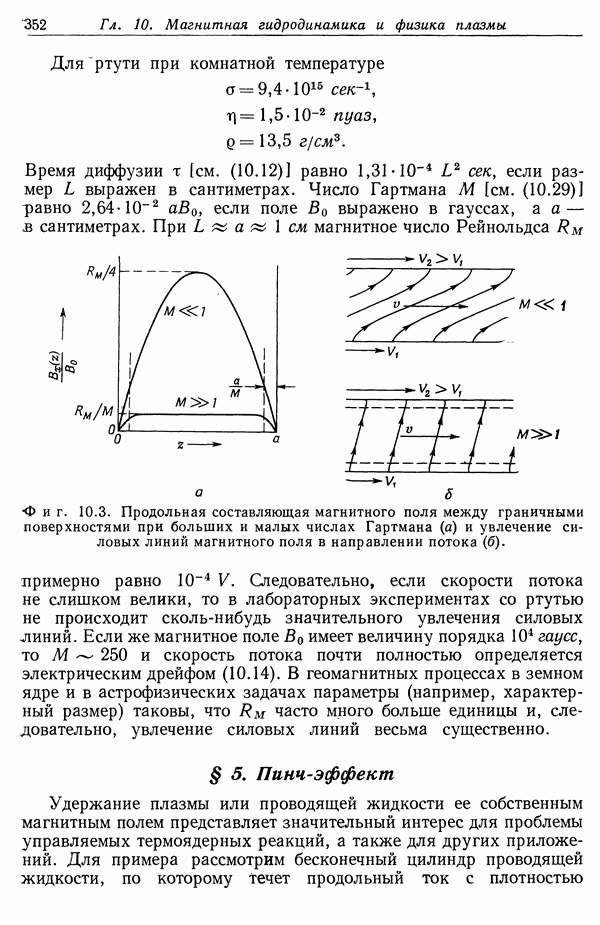
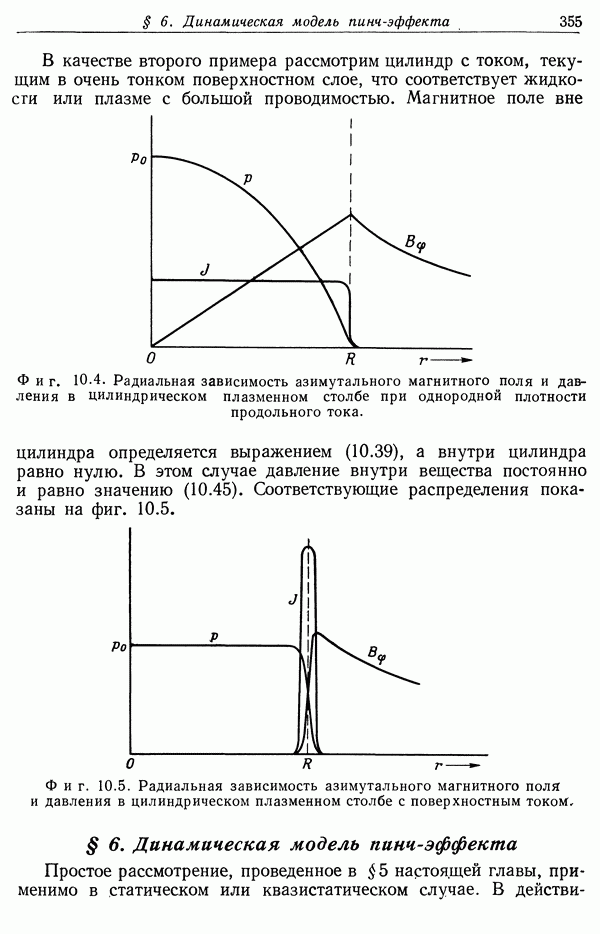
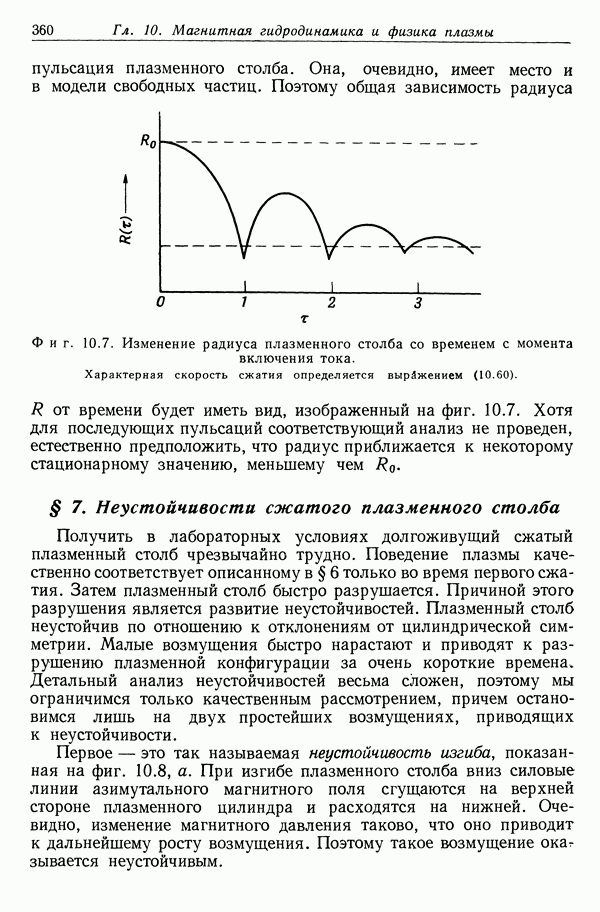
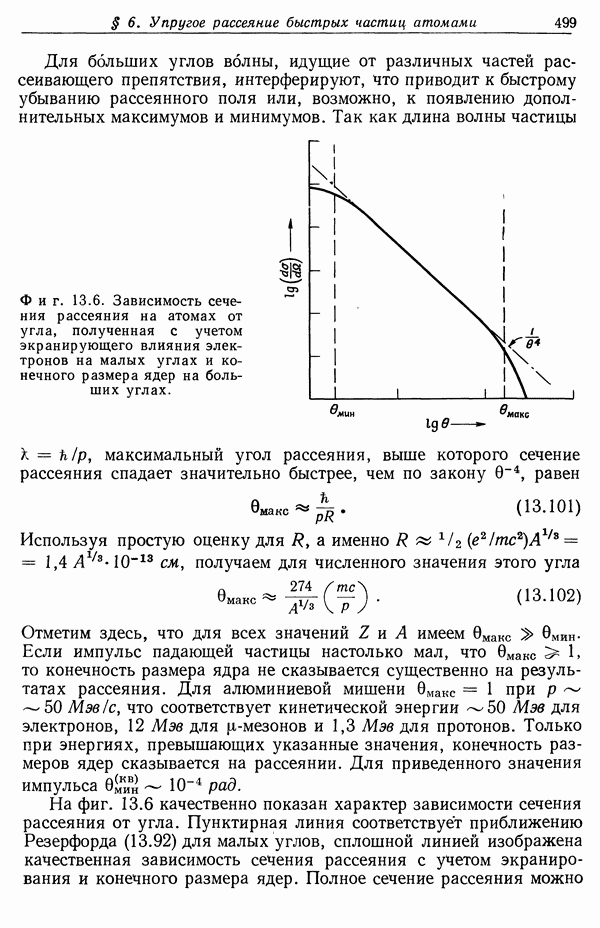
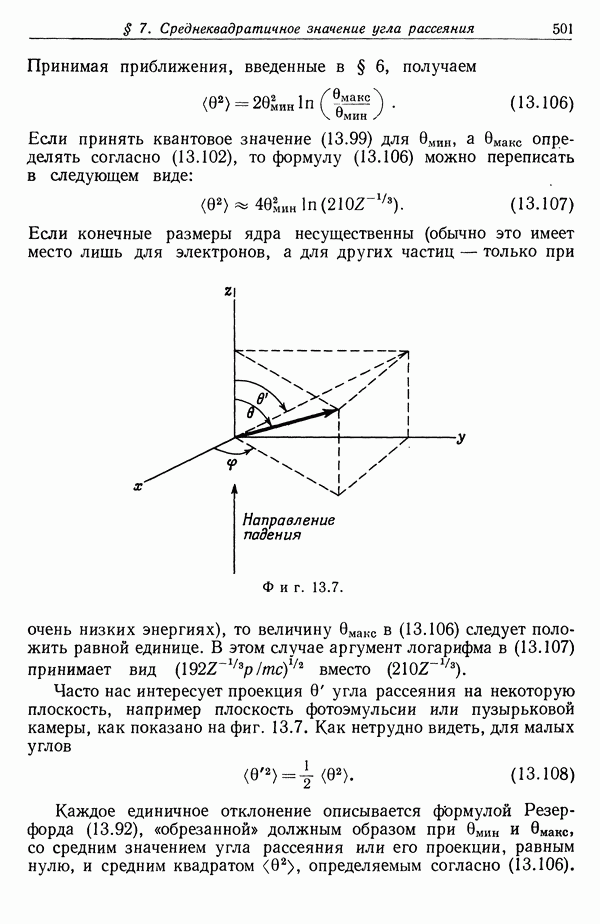
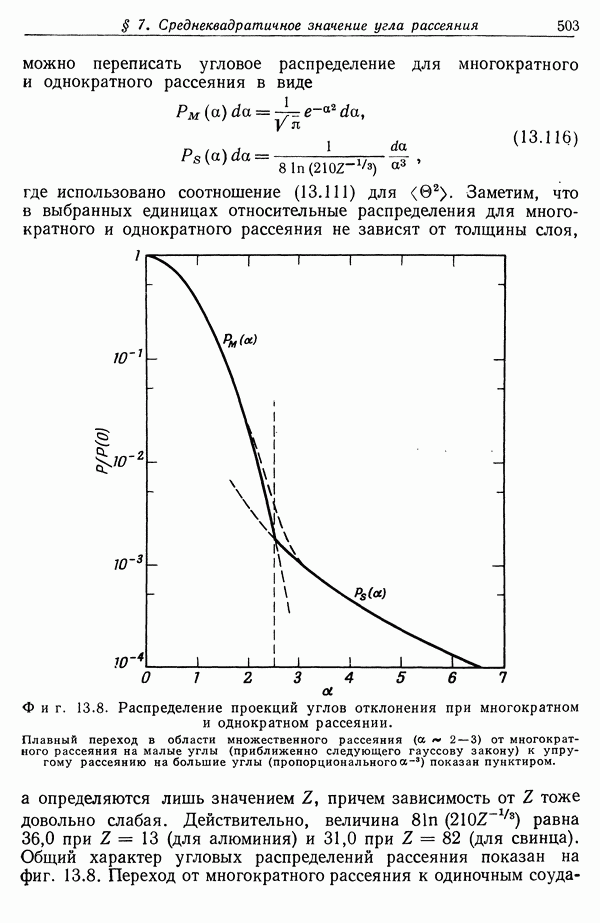
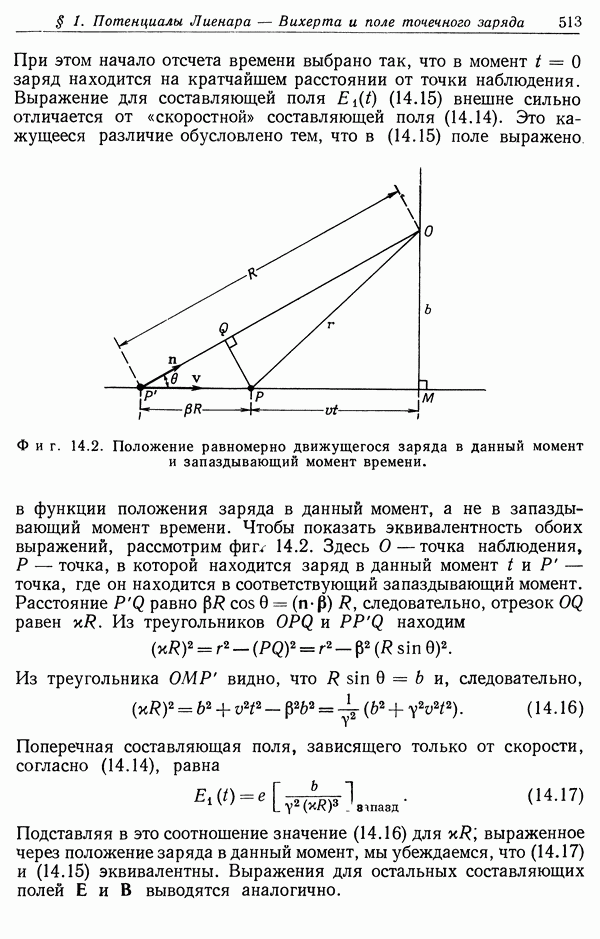
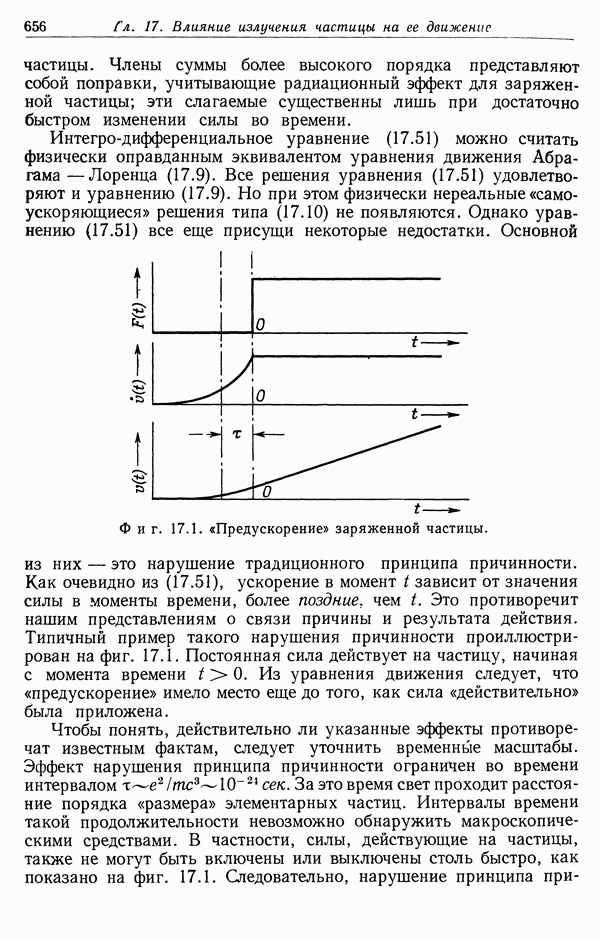
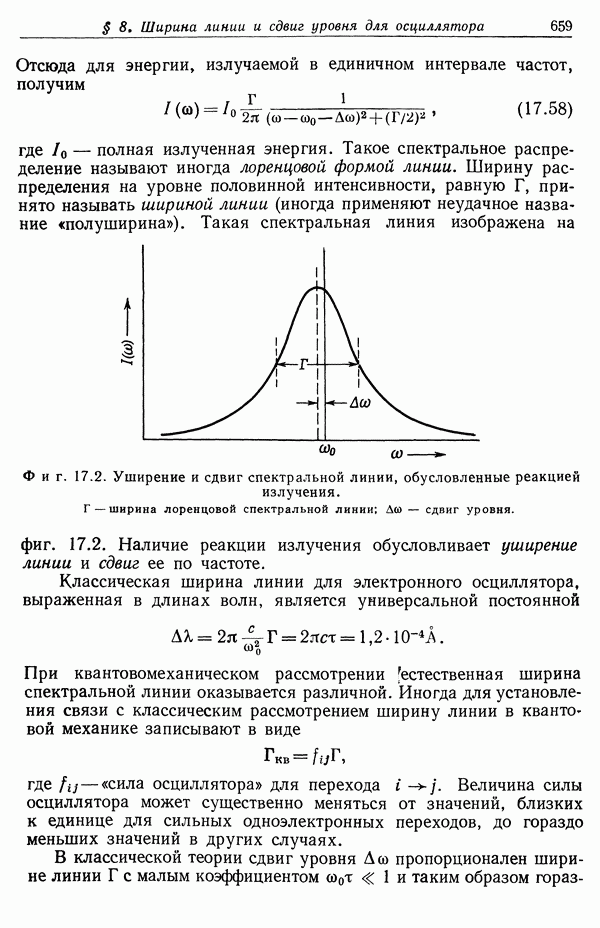
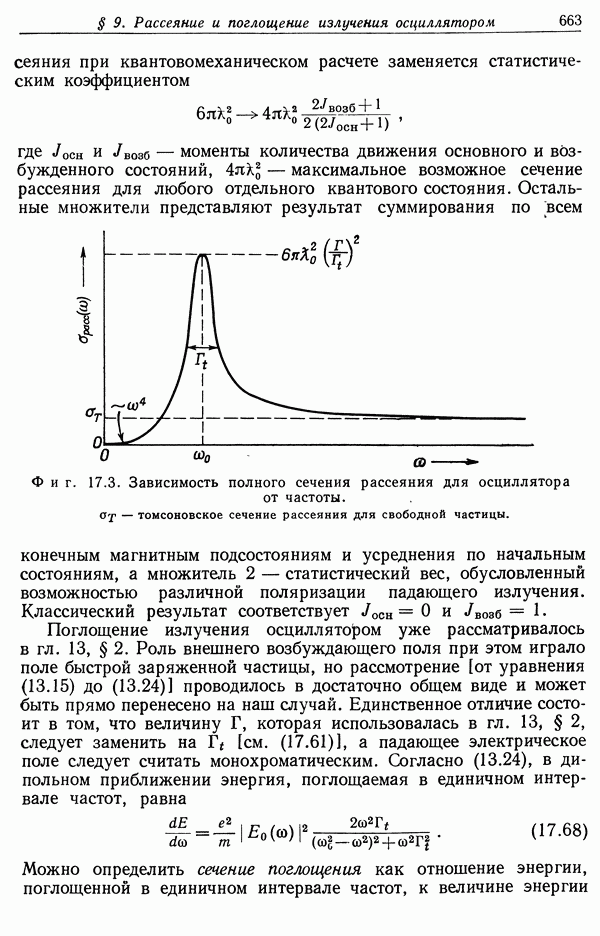
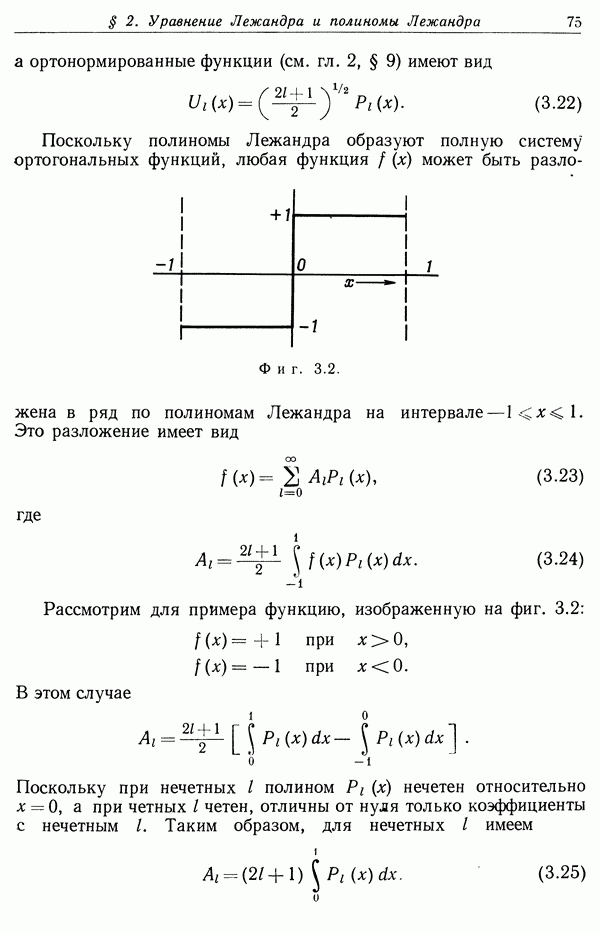| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
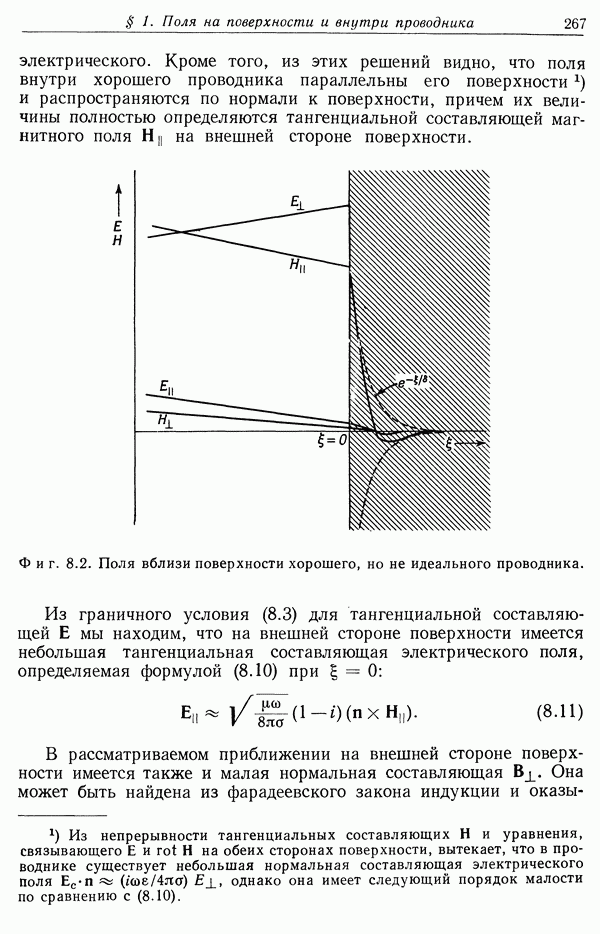
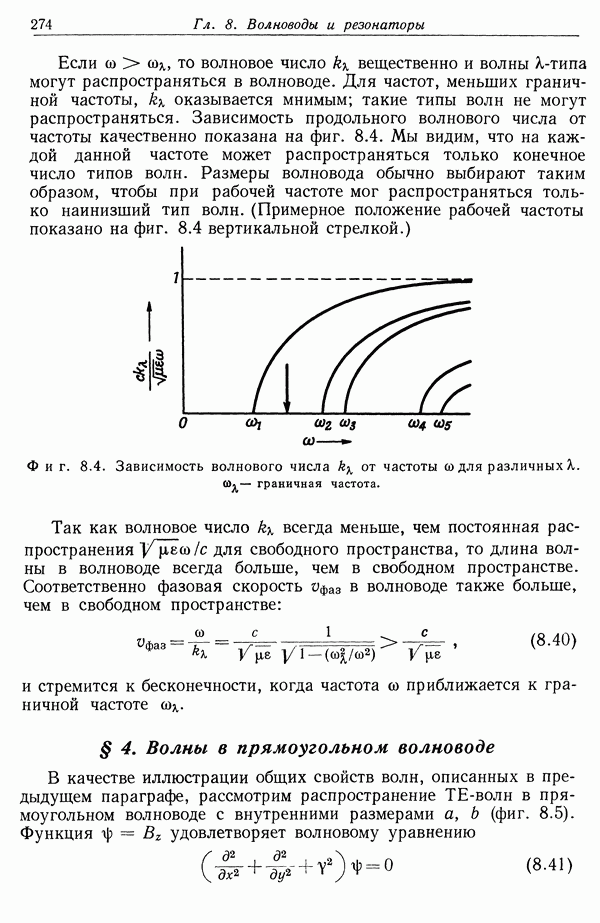
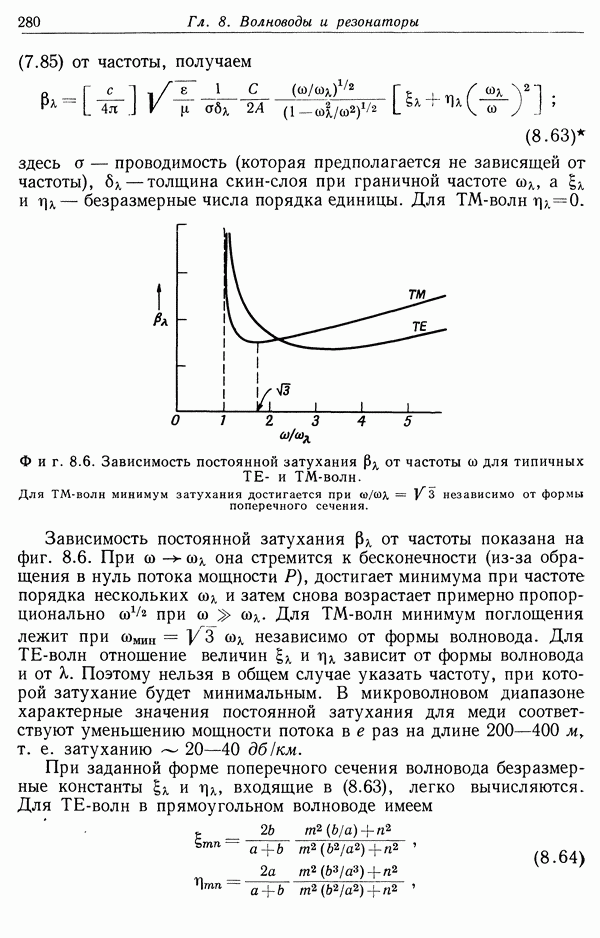
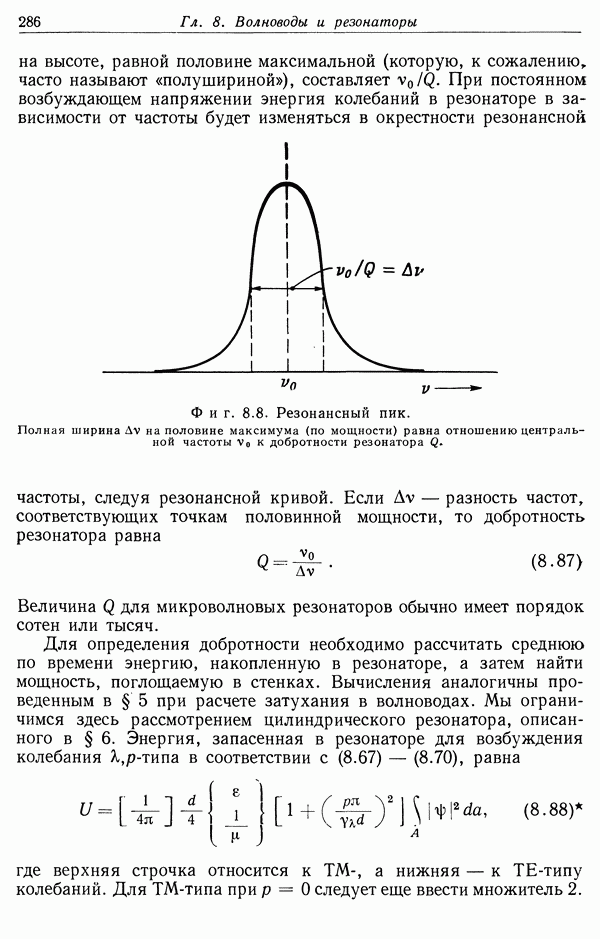
§ 3. Теорема Гаусса
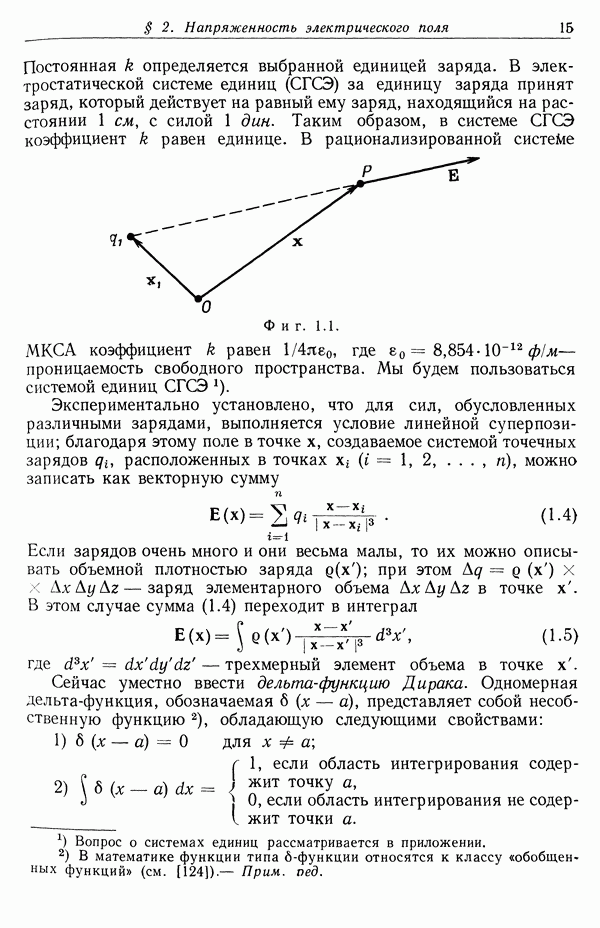
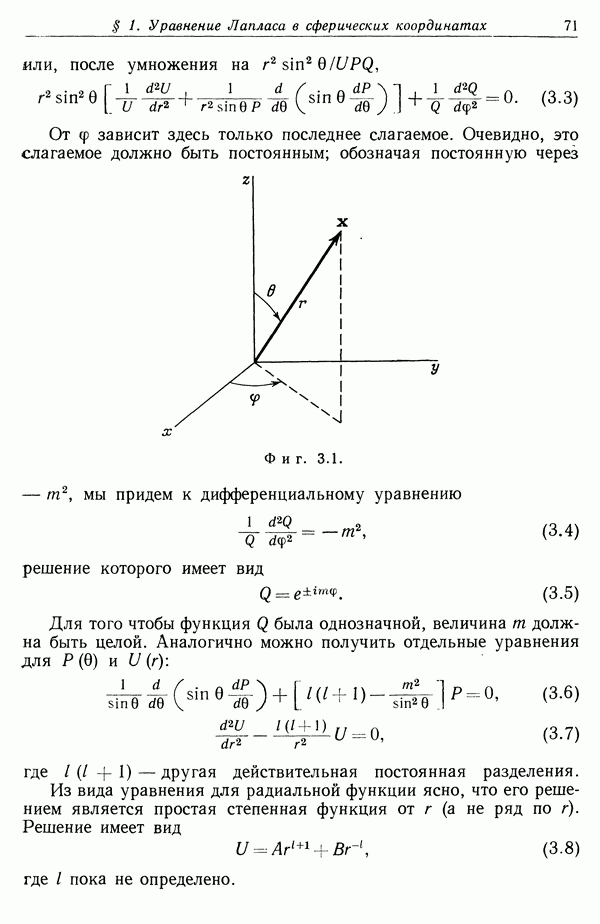
Интегральное выражение (1.5) не очень удобно для расчета электрического поля. Существует другое интегральное соотношение, носящее название теоремы Гаусса, которое иногда значительно удобнее и которое, кроме того, позволяет найти дифференциальное уравнение для  Чтобы получить теорему Гаусса, рассмотрим сначала отдельный точечный заряд q и замкнутую поверхность S (фиг. 1.2). Пусть
Чтобы получить теорему Гаусса, рассмотрим сначала отдельный точечный заряд q и замкнутую поверхность S (фиг. 1.2). Пусть  — расстояние от заряда до точки на поверхности
— расстояние от заряда до точки на поверхности  — единичный вектор, направленный по внешней нормали к поверхности S в этой точке,
— единичный вектор, направленный по внешней нормали к поверхности S в этой точке,  — элемент площади поверхности. Если создаваемое зарядом q электрическое поле Е в рассматриваемой точке поверхности образует угол
— элемент площади поверхности. Если создаваемое зарядом q электрическое поле Е в рассматриваемой точке поверхности образует угол  с единичным вектором нормали
с единичным вектором нормали  , то произведение нормальной составляющей вектора Е на элемент площади равно
, то произведение нормальной составляющей вектора Е на элемент площади равно
 (1.7)
(1.7)
Поскольку вектор Е направлен по прямой, соединяющей заряд q с элементом поверхности  , то
, то  , где
, где  — элемент телесного угла, под которым видна площадка
— элемент телесного угла, под которым видна площадка  из точки нахождения заряда. Таким образом,
из точки нахождения заряда. Таким образом,

Если теперь проинтегрировать нормальную составляющую Е по всей поверхности, то легко видеть, что

Это и есть теорема Гаусса для единичного точечного заряда. Очевидно, для системы дискретных точечных зарядов она запишется в виде

где сумма берется лишь по тем зарядам, которые находятся внутри S. Для непрерывного распределения зарядов с плотностью  теорема Гаусса имеет вид
теорема Гаусса имеет вид

где V — объем, ограниченный поверхностью S.

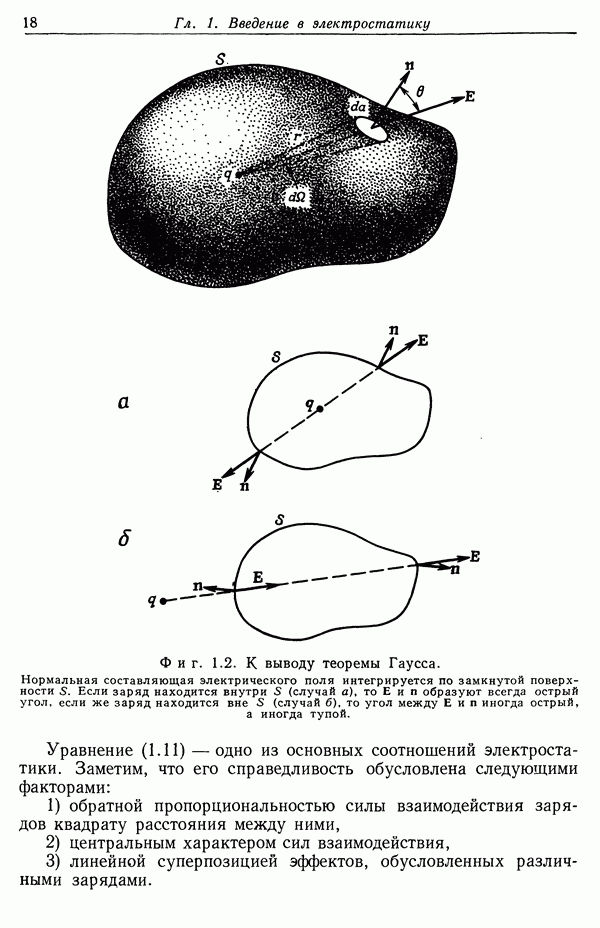
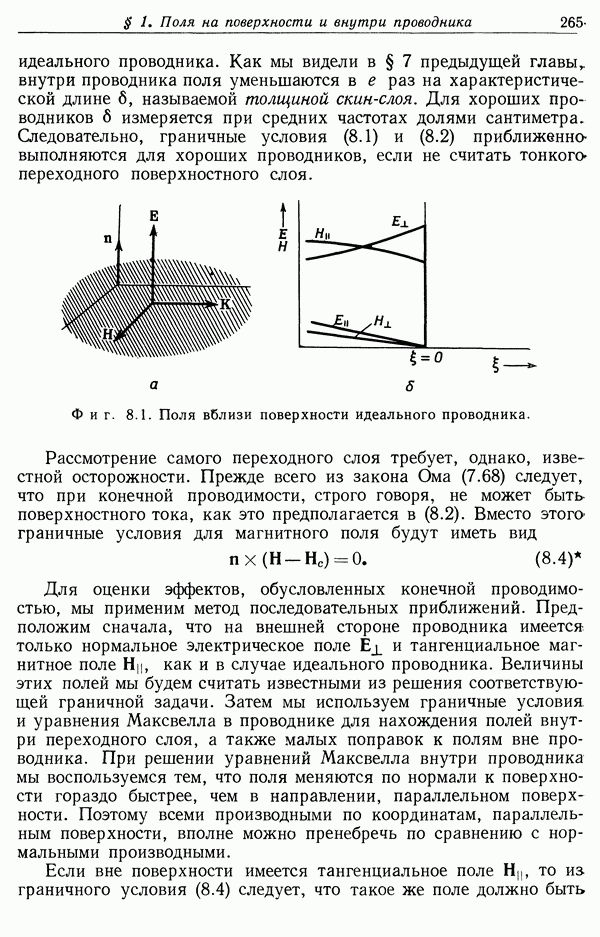
Фиг. 1.2. К выводу теоремы Гаусса. Нормальная составляющая электрического поля интегрируется по замкнутой поверхности S. Если заряд находится внутри 5 (случай а), то  образуют всегда острый угол, если же заряд находится вне S (случай б), то угол между Е и
образуют всегда острый угол, если же заряд находится вне S (случай б), то угол между Е и  иногда острый, а иногда тупой.
иногда острый, а иногда тупой.
Уравнение (1.11) — одно из основных соотношений электростатики. Заметим, что его справедливость обусловлена следующими факторами:
1) обратной пропорциональностью силы взаимодействия зарядов квадрату расстояния между ними,
2) центральным характером сил взаимодействия,
3) линейной суперпозицией эффектов, обусловленных различными зарядами.
Очевидно, теорема Гаусса справедлива и для ньютоновских гравитационных сил, конечно, если плотность заряда заменить плотностью распределения материи.
Интересно заметить, что Кэвендиш еще до опытов Кулона, применив фактически непосредственно теорему Гаусса, поставил опыт с двумя концентрическими проводящими сферами и показал, что сила взаимодействия зарядов убывает обратно пропорционально  где
где  . Усовершенствовав технику эксперимента, Максвелл показал, что
. Усовершенствовав технику эксперимента, Максвелл показал, что  (см. книги Джинса [55] или Максвелла [73]).
(см. книги Джинса [55] или Максвелла [73]).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
- § 2. Напряженность электрического поля
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
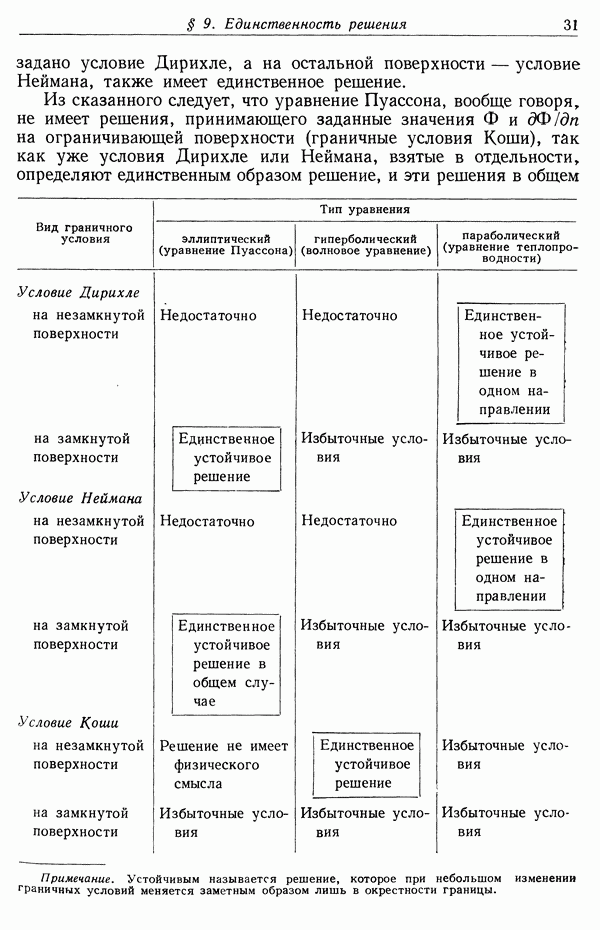
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
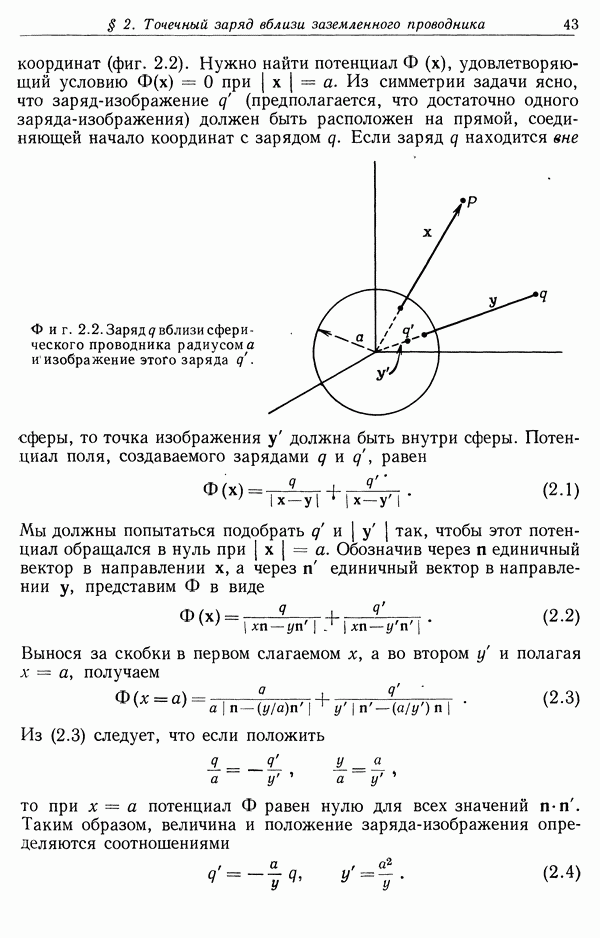
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
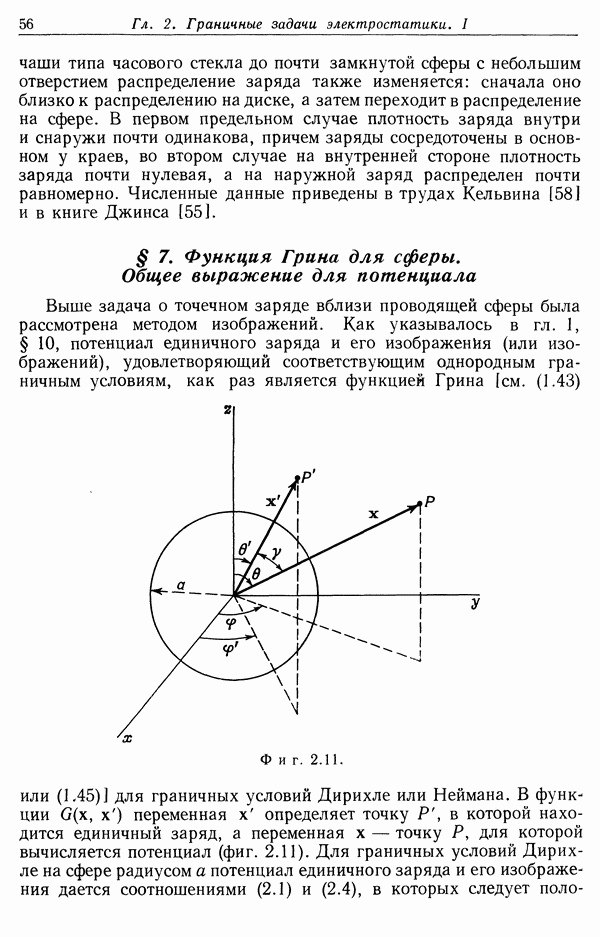
- § 7. Функция Грина для сферы. Общее выражение для потенциала
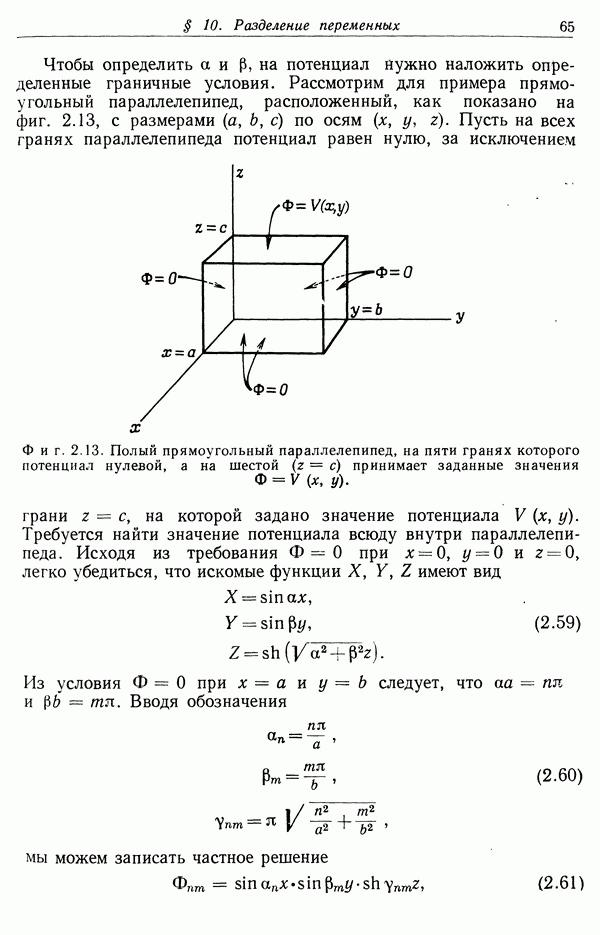
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
- § 2. Уравнение Лежандра и полиномы Лежандра
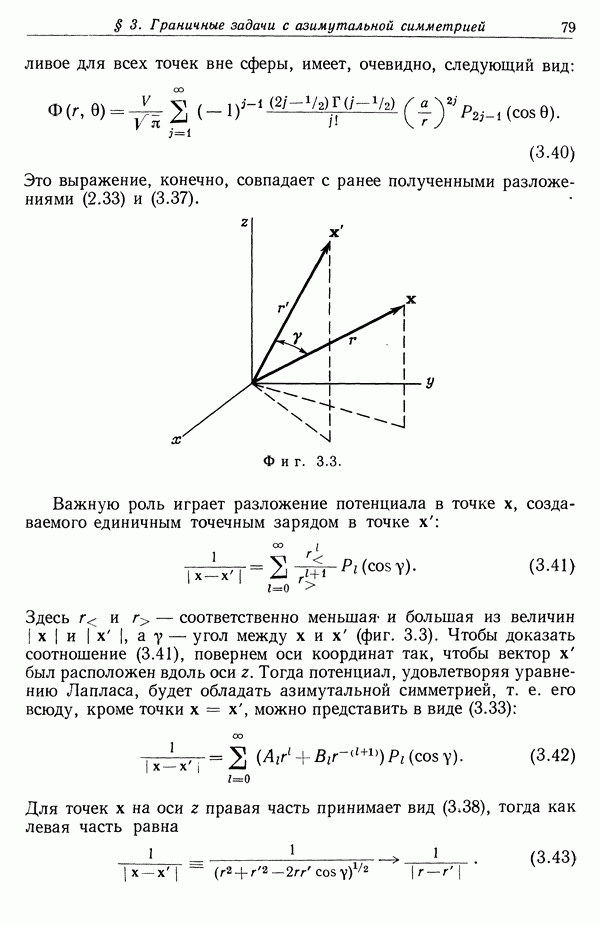
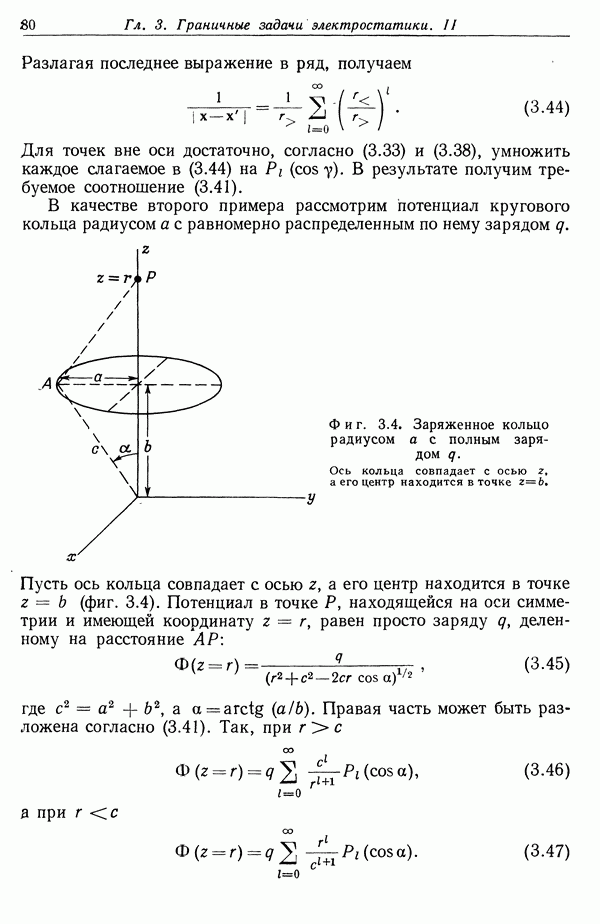
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
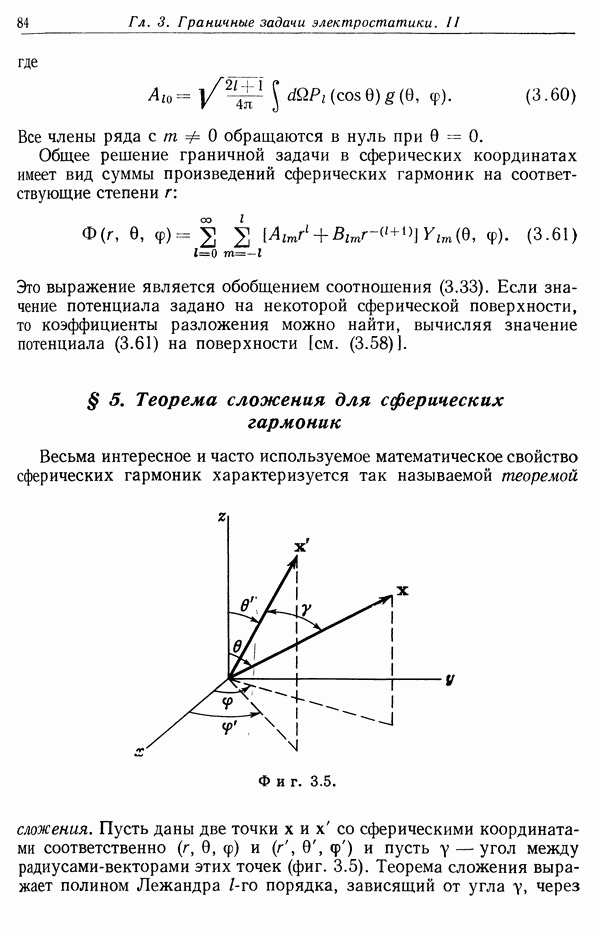
- § 5. Теорема сложения для сферических гармоник
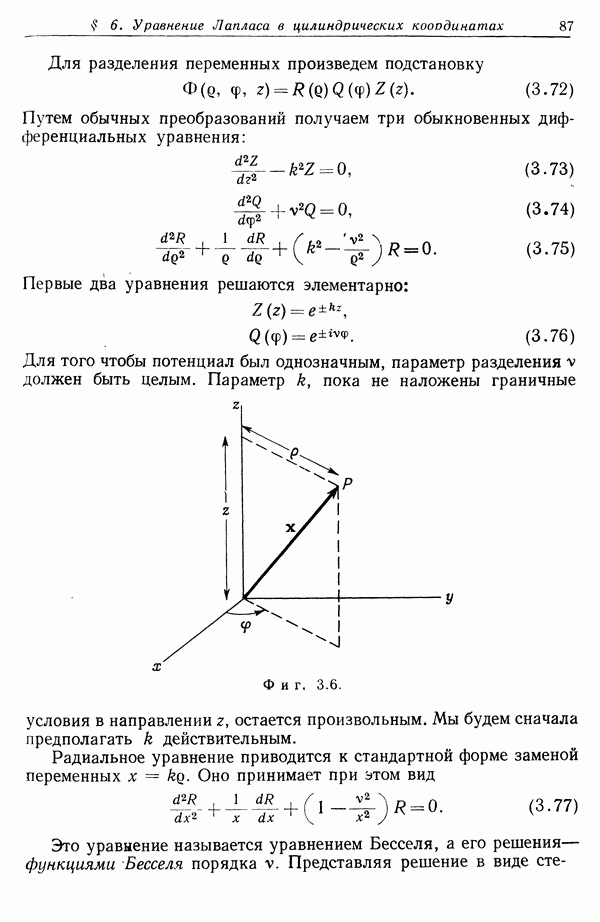
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
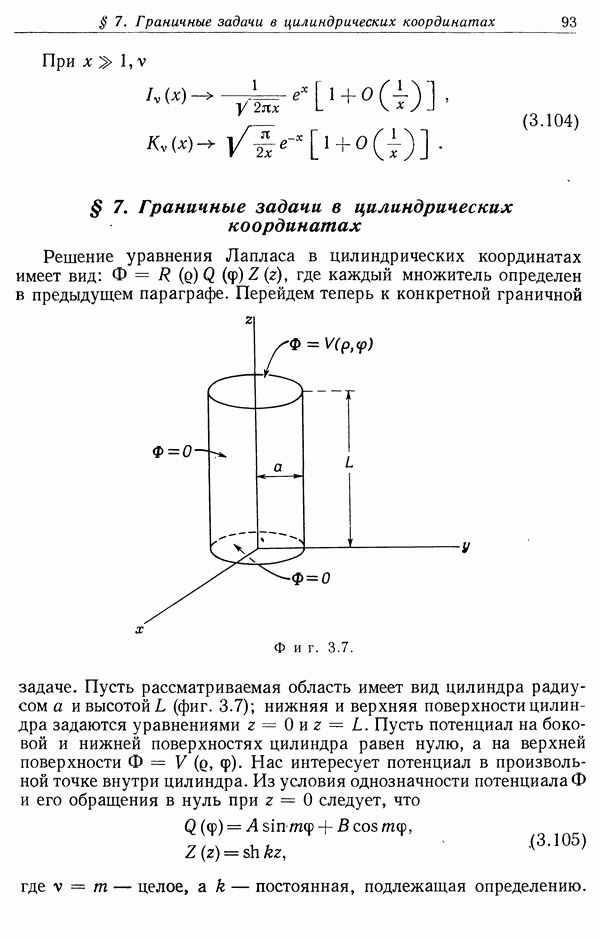
- § 7. Граничные задачи в цилиндрических координатах
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
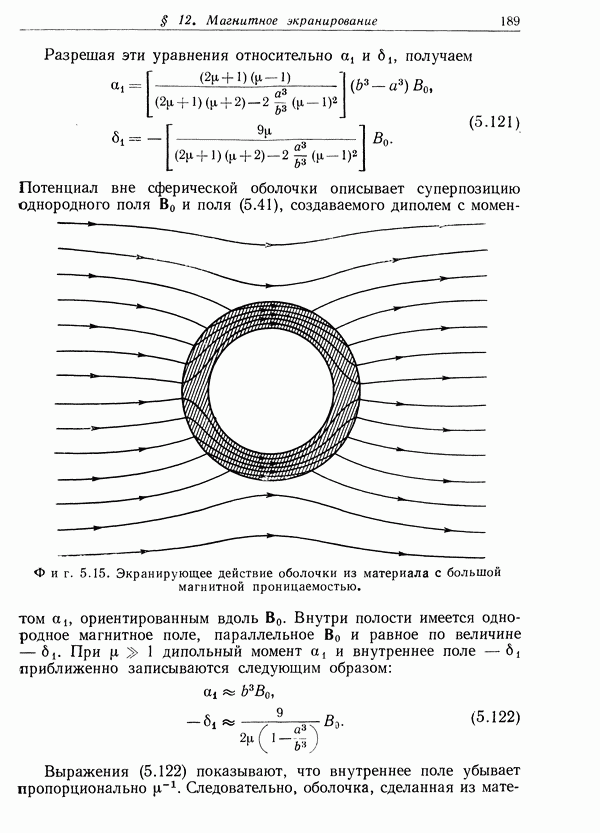
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
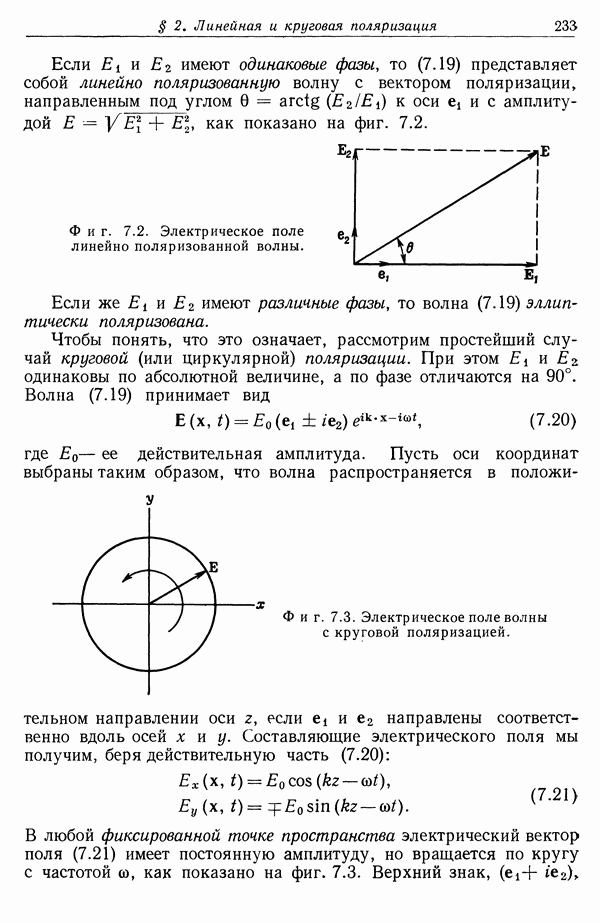
- § 2. Линейная и круговая поляризация
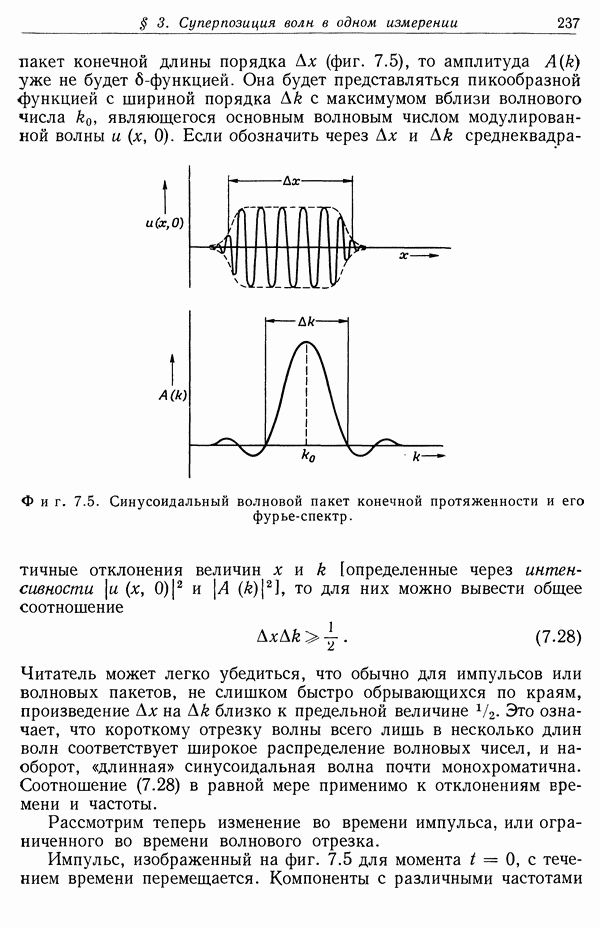
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
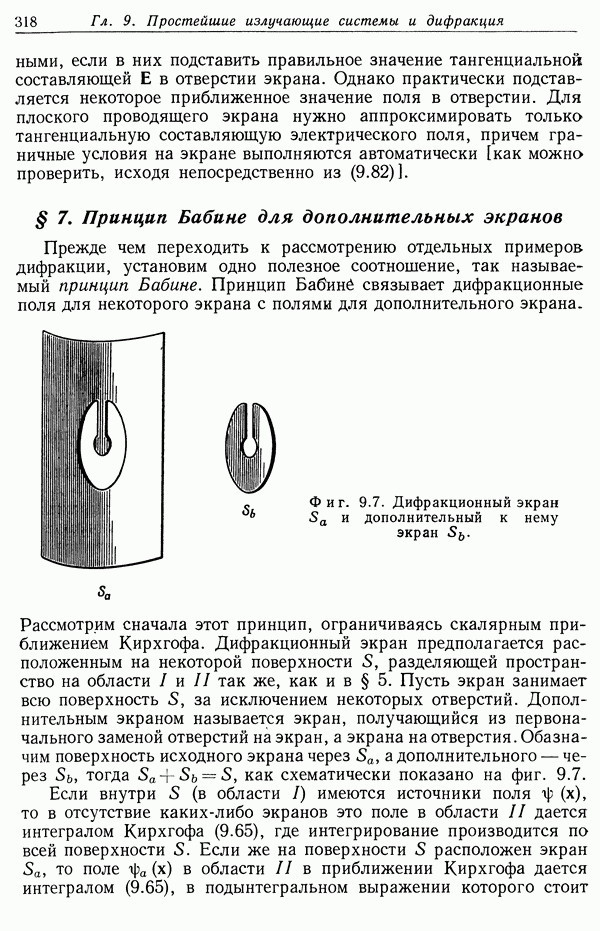
- § 7. Принцип Бабине для дополнительных экранов
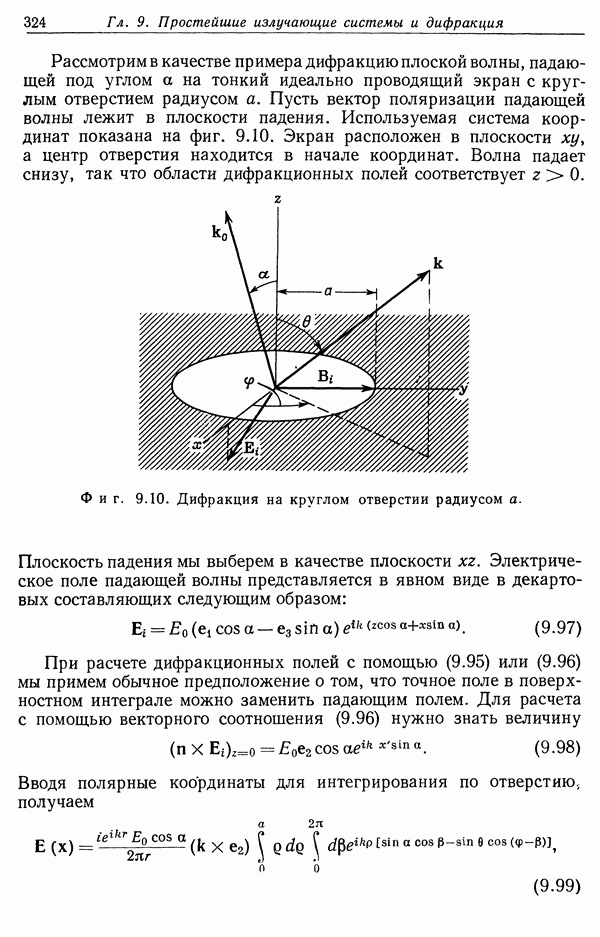
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
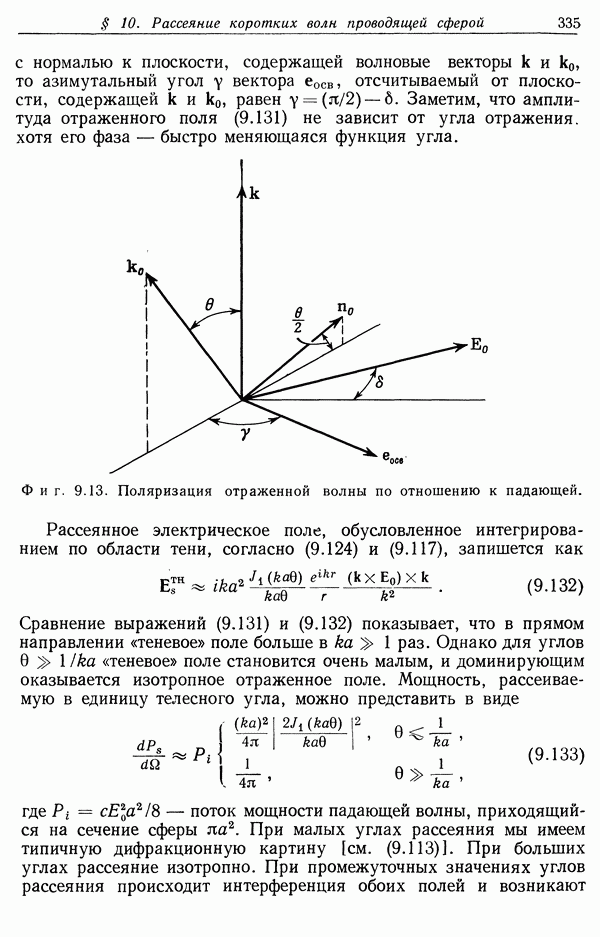
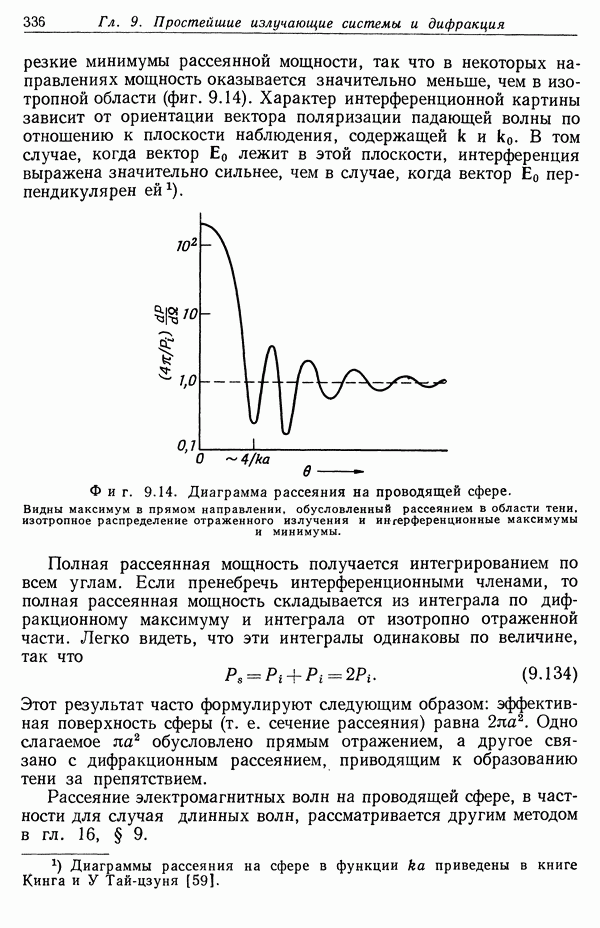
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
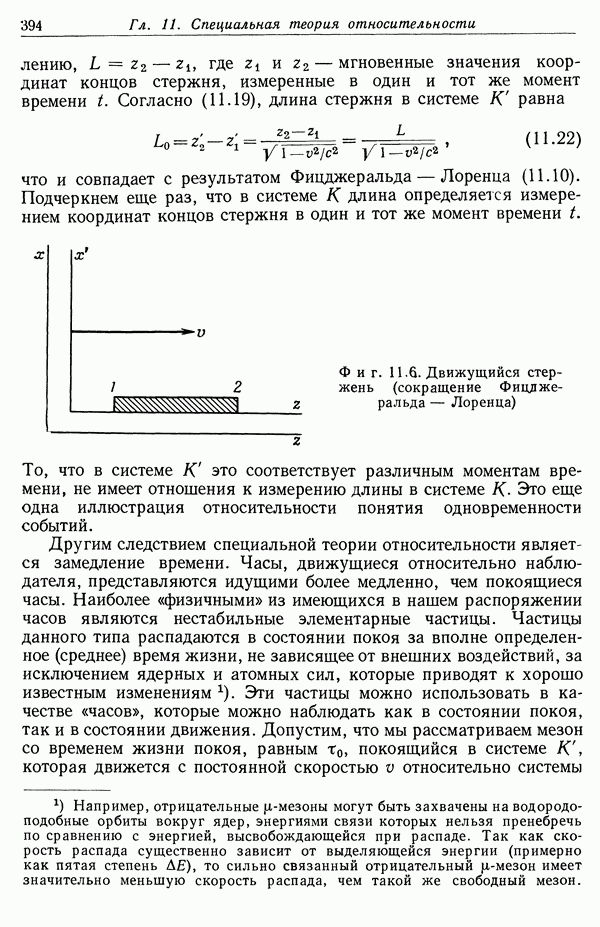
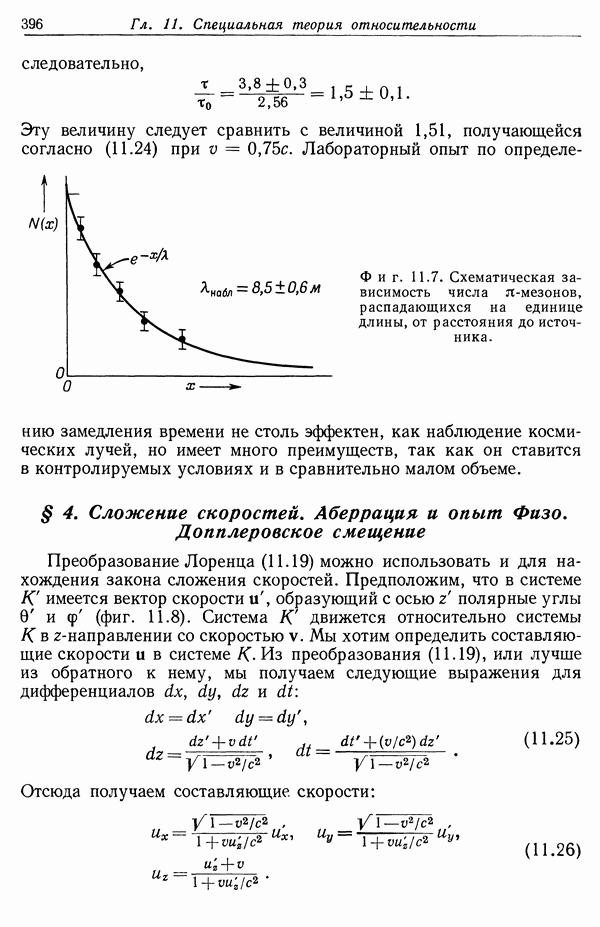
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
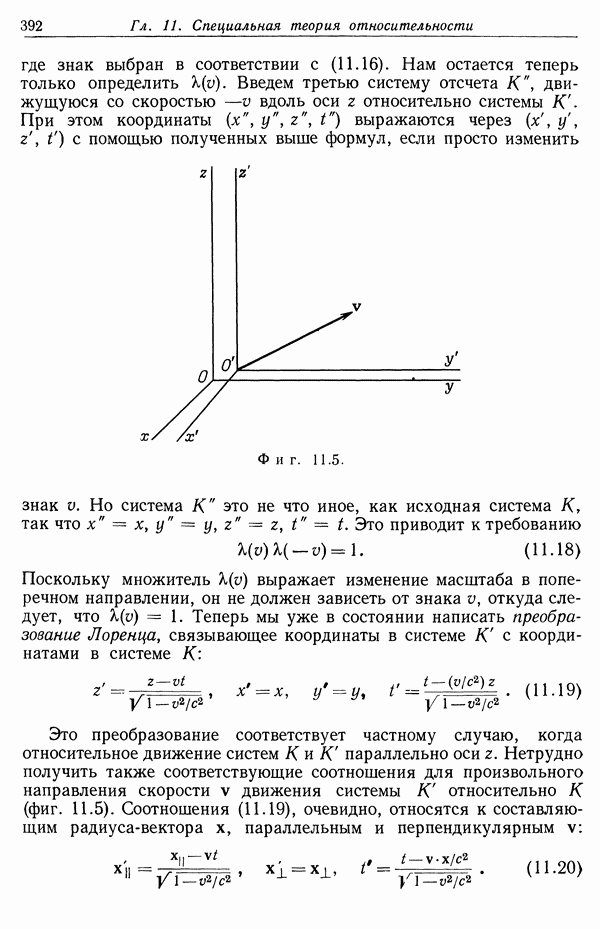
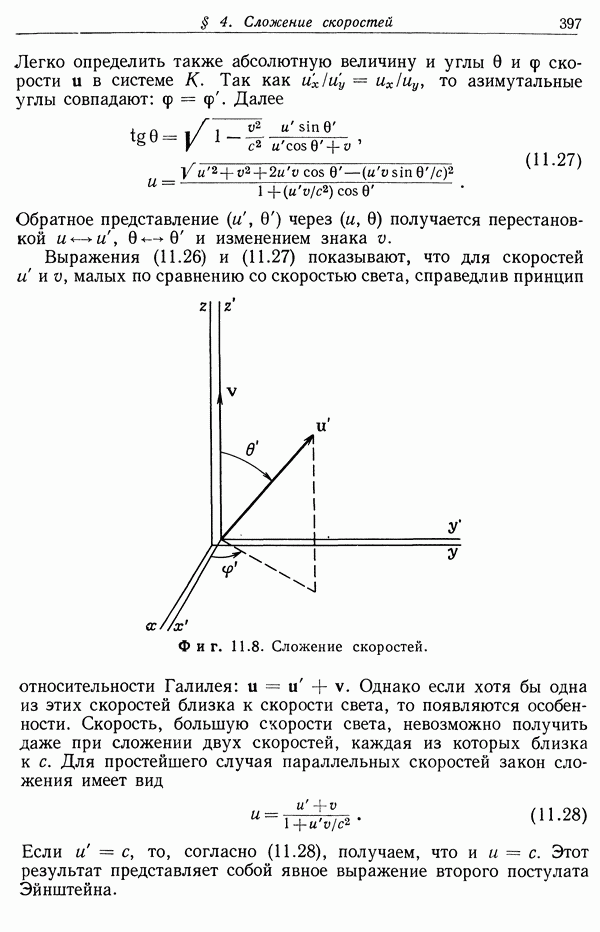
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
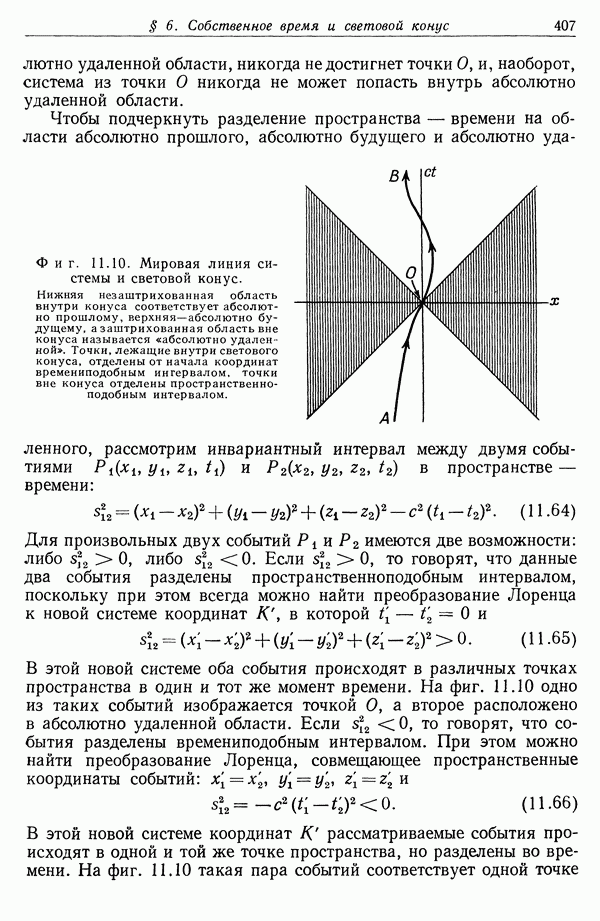
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
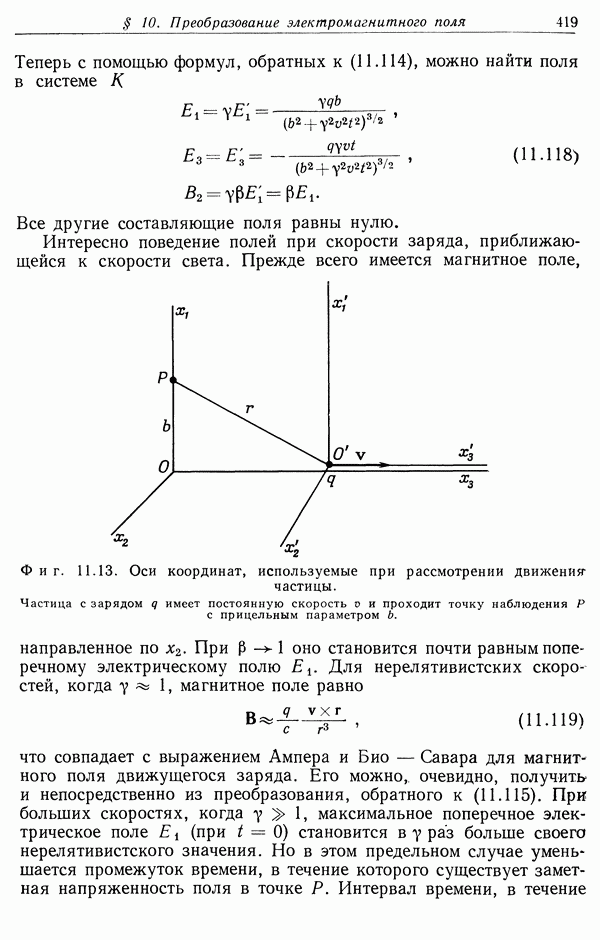
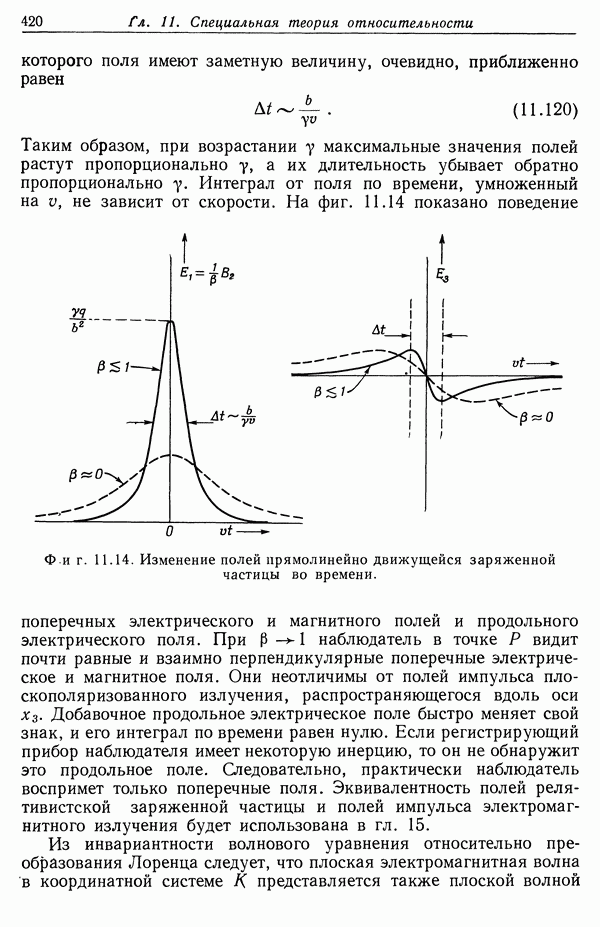
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
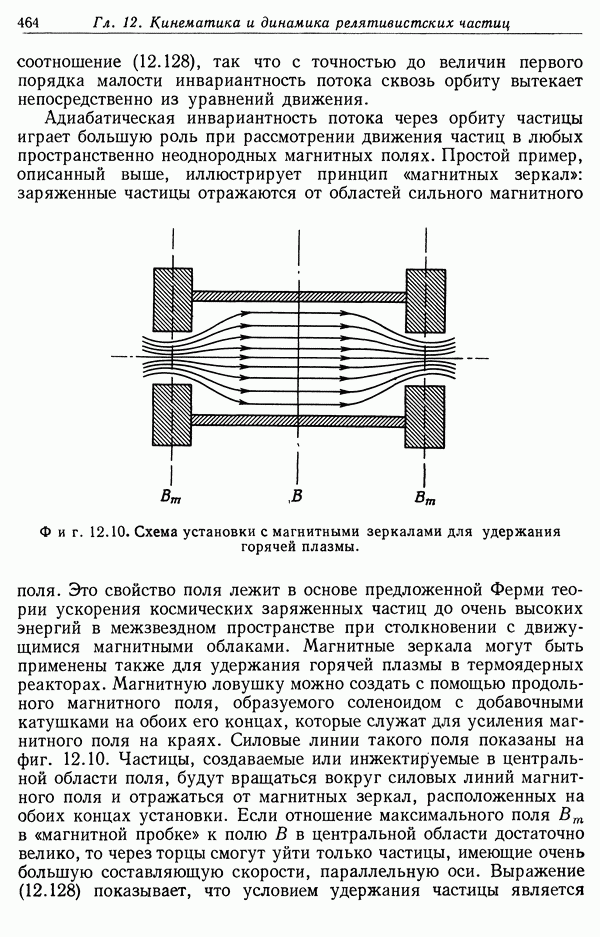
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
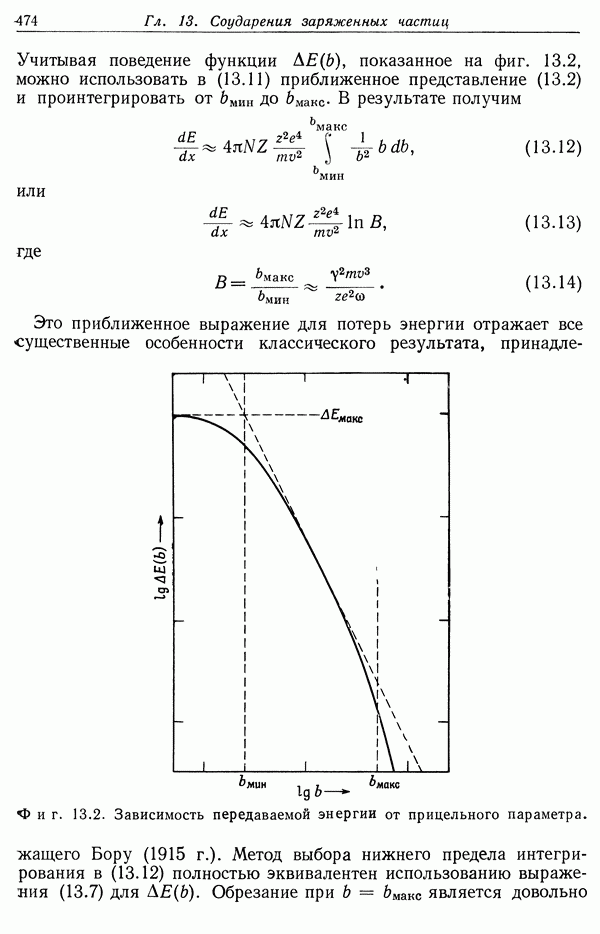
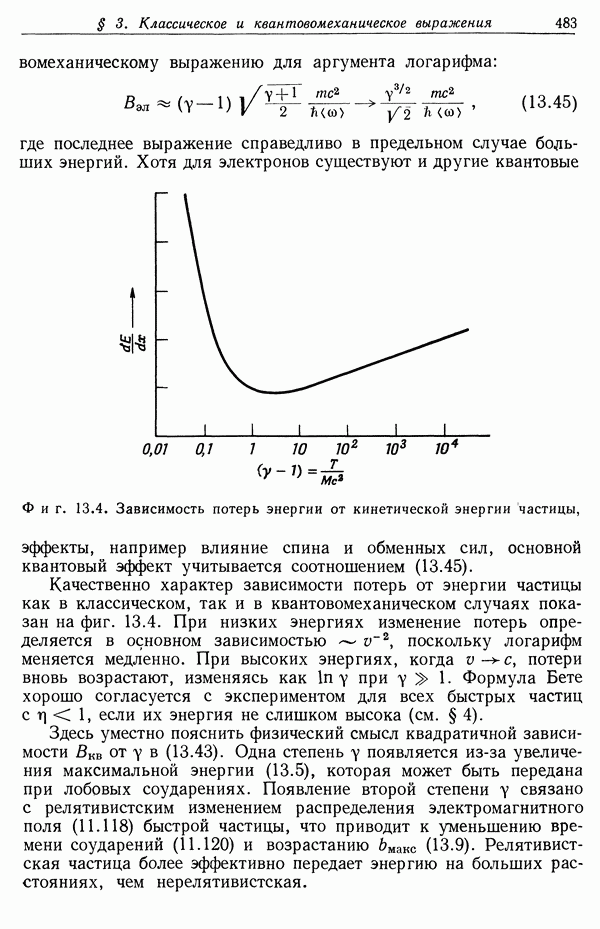
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
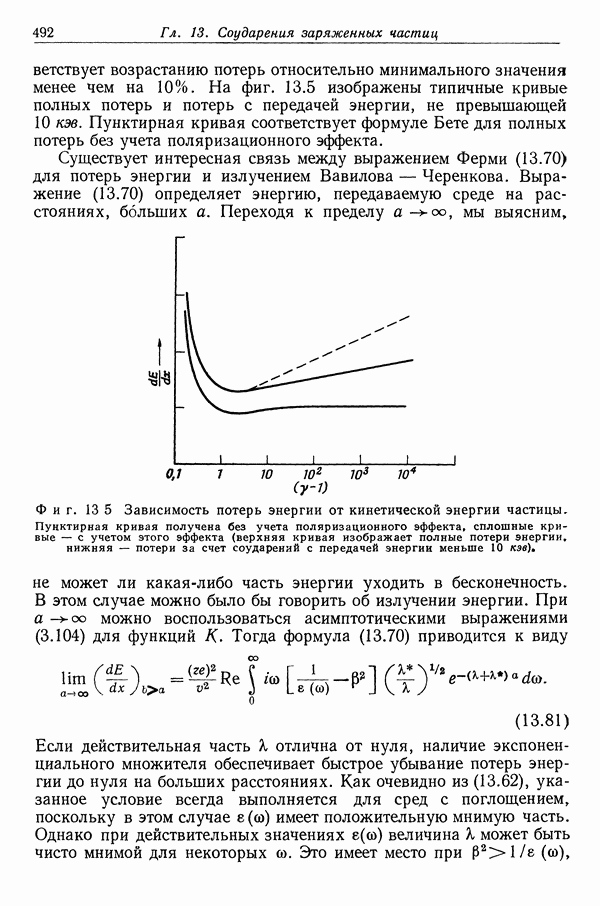
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
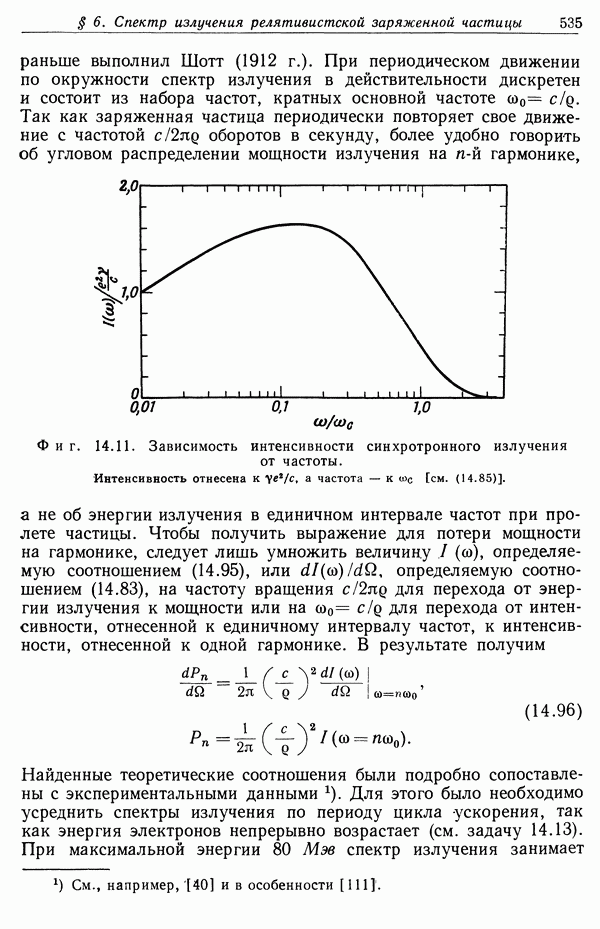
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
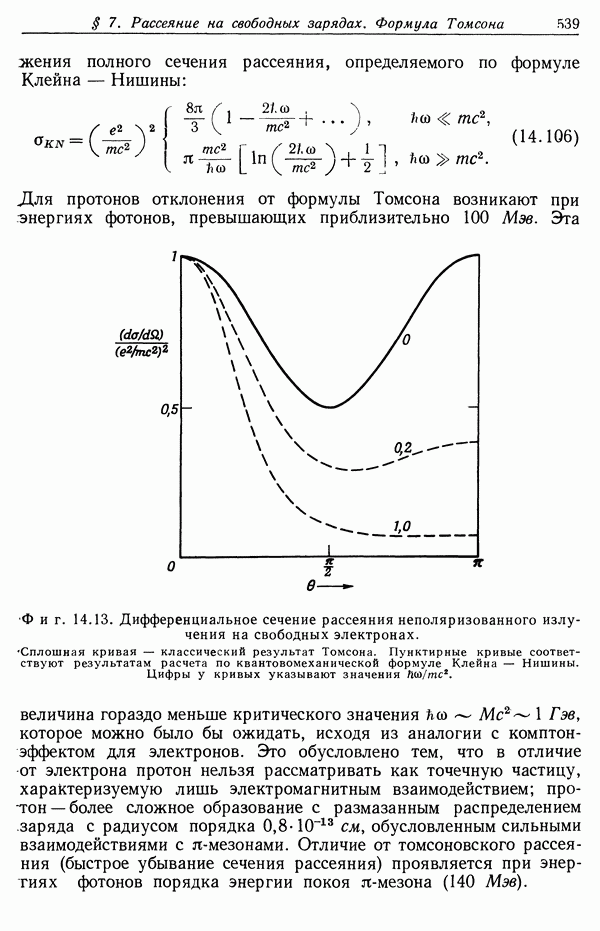
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
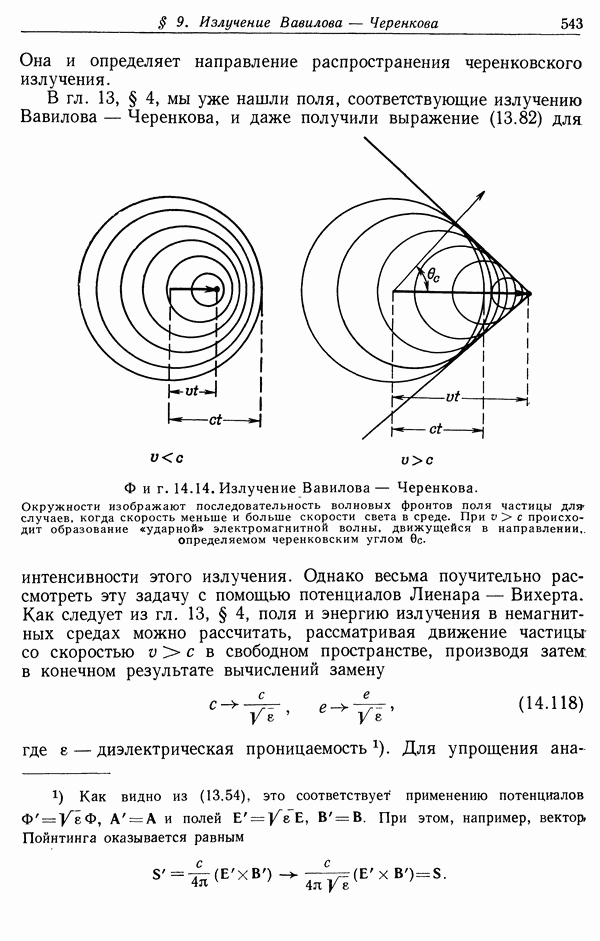
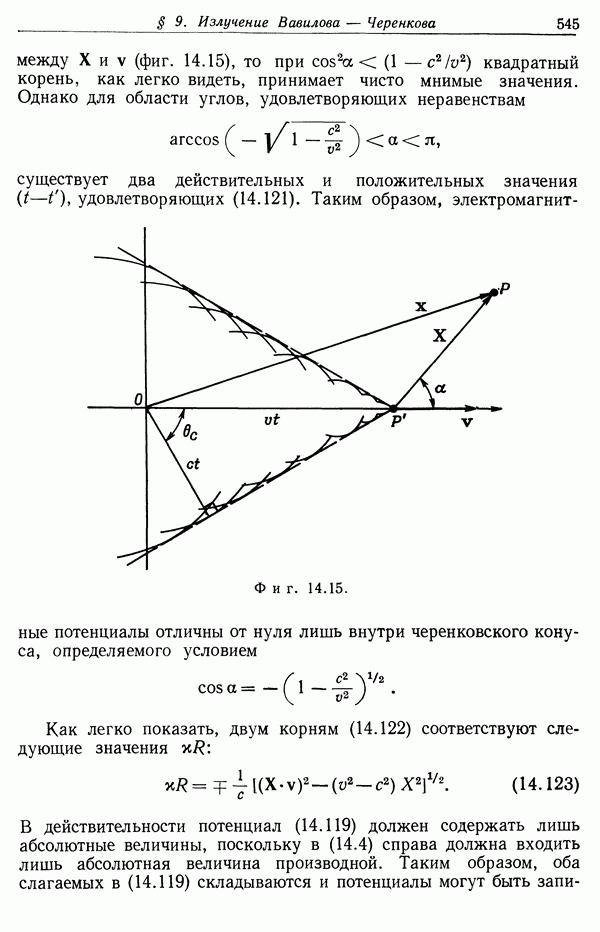
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
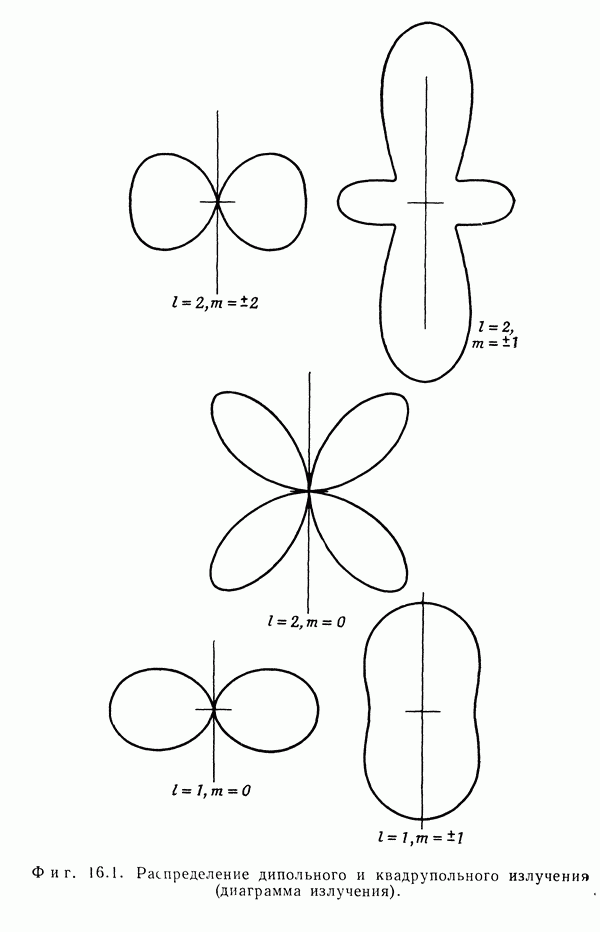
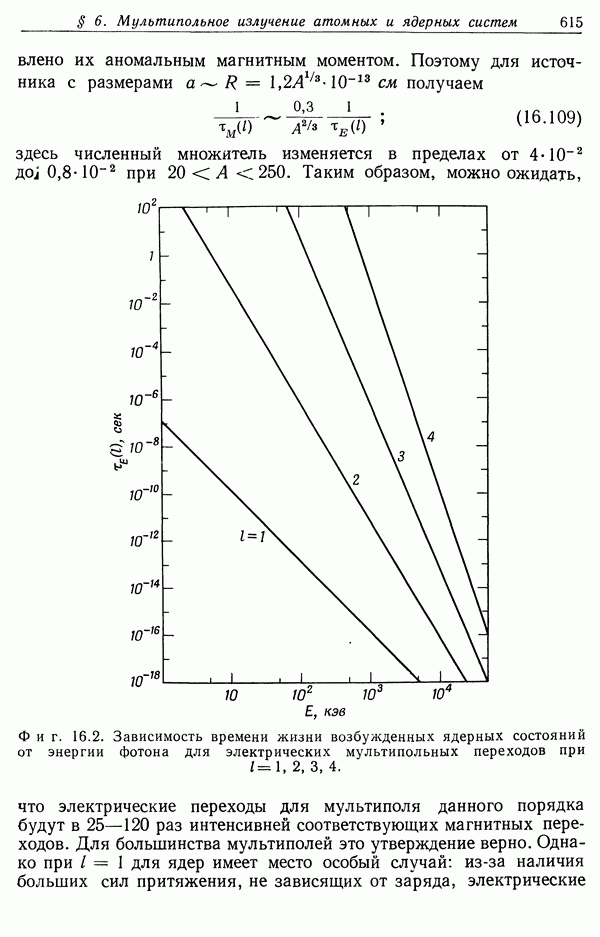
- § 6. Мультипольное излучение атомных и ядерных систем
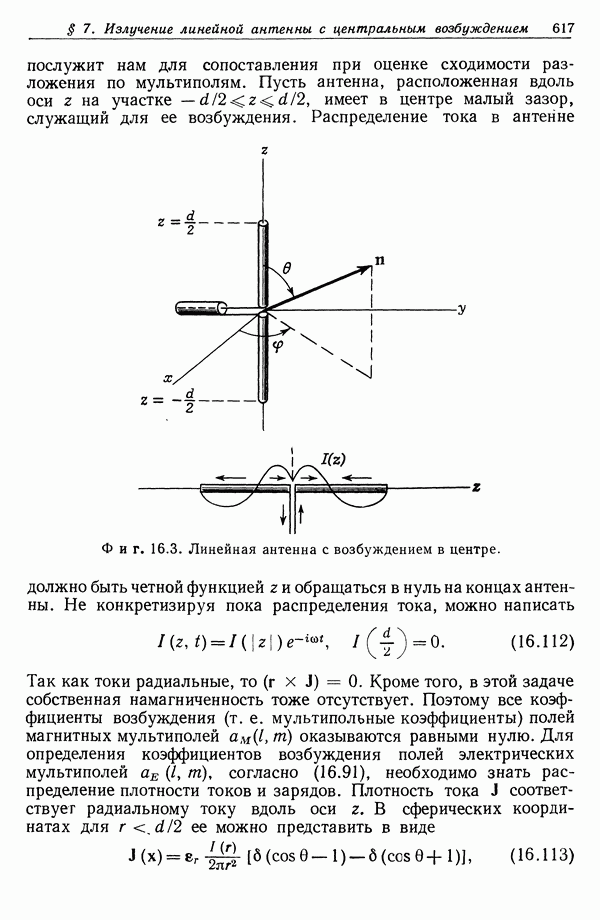
- § 7. Излучение линейной антенны с центральным возбуждением
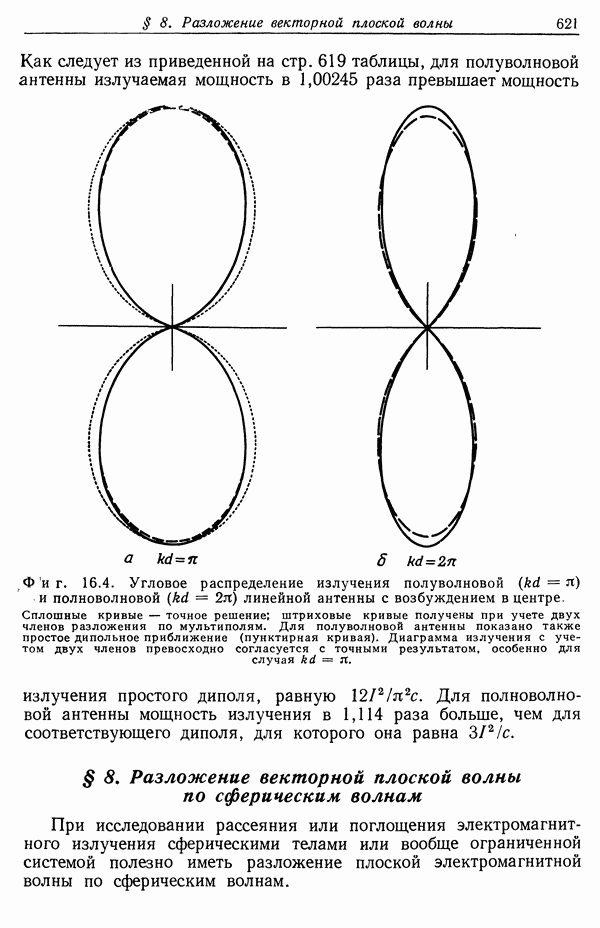
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ