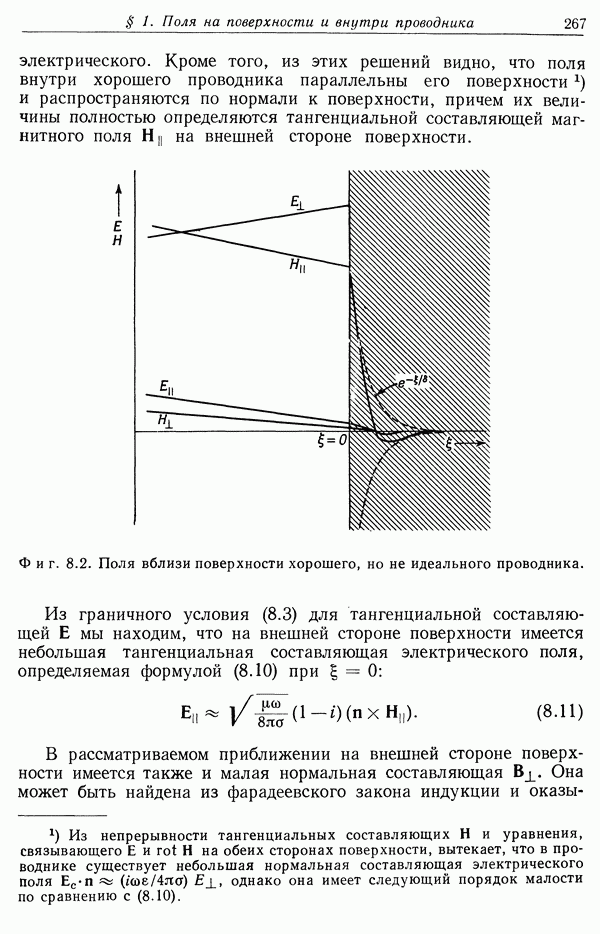
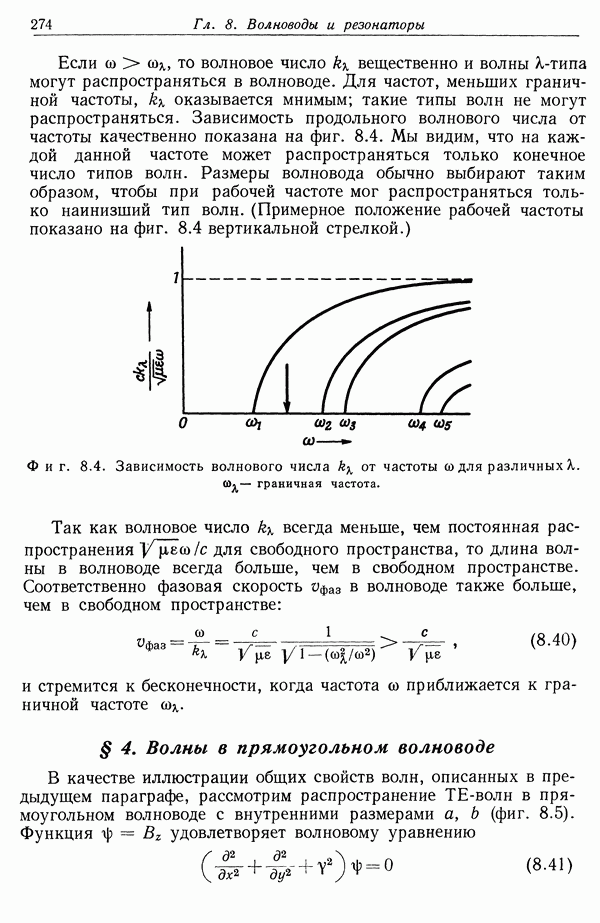
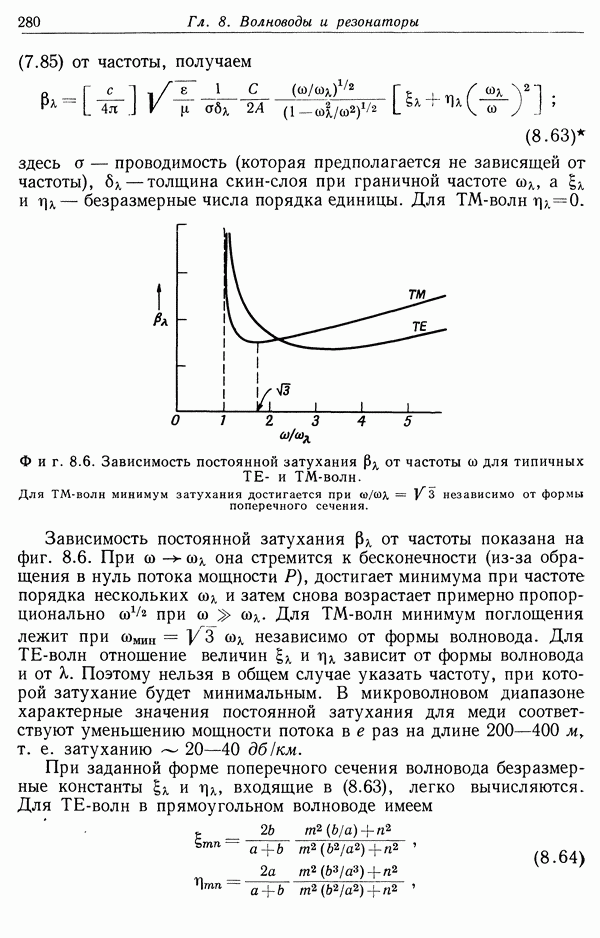
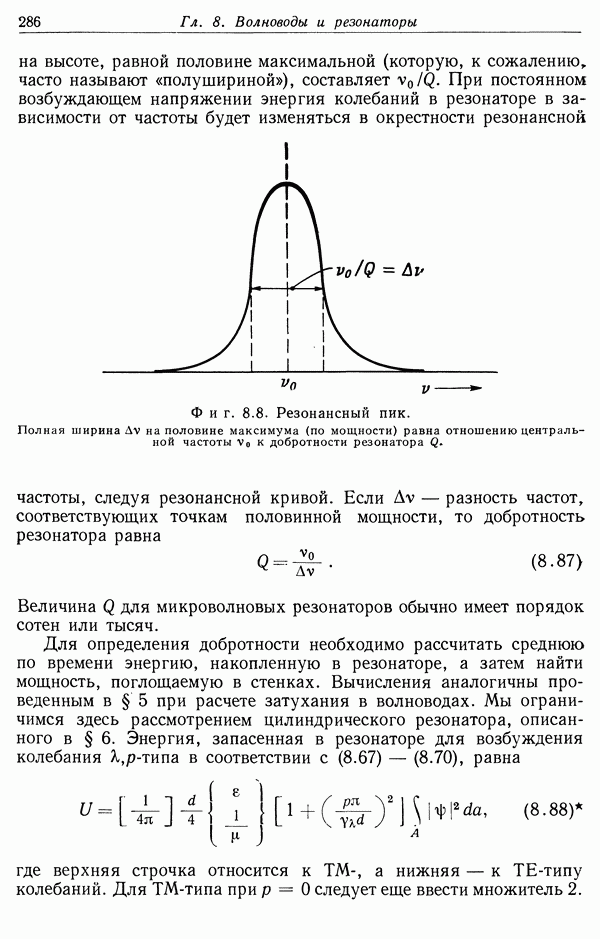
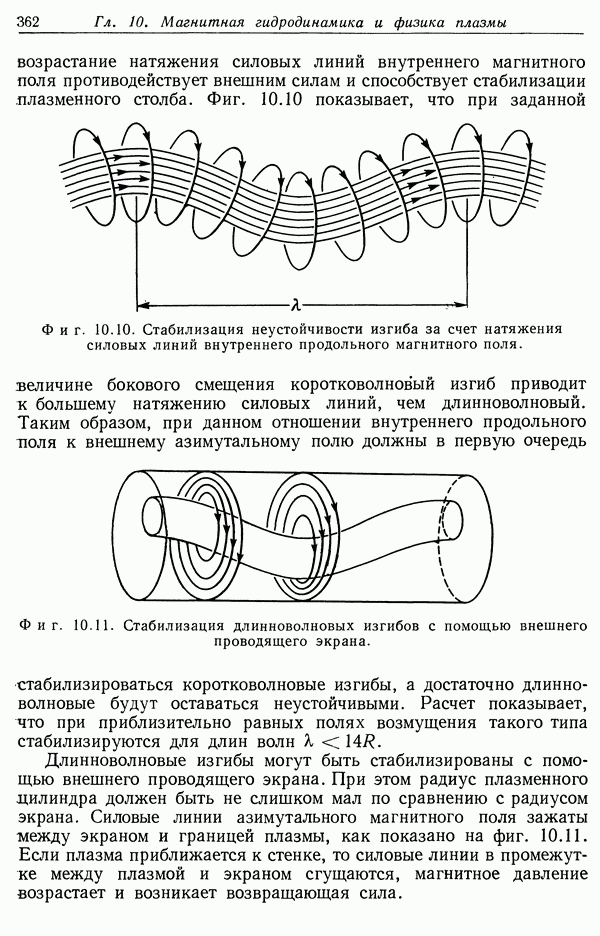
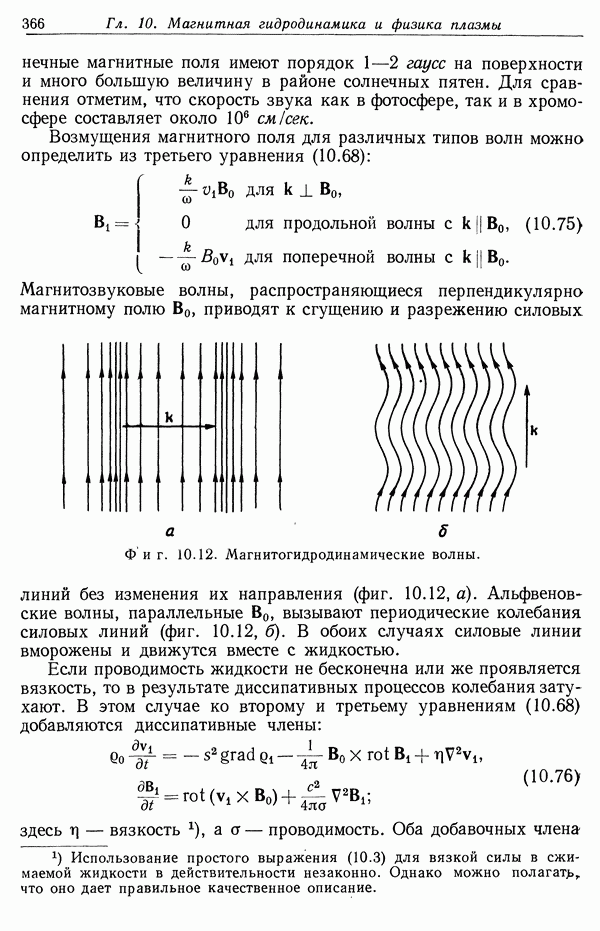
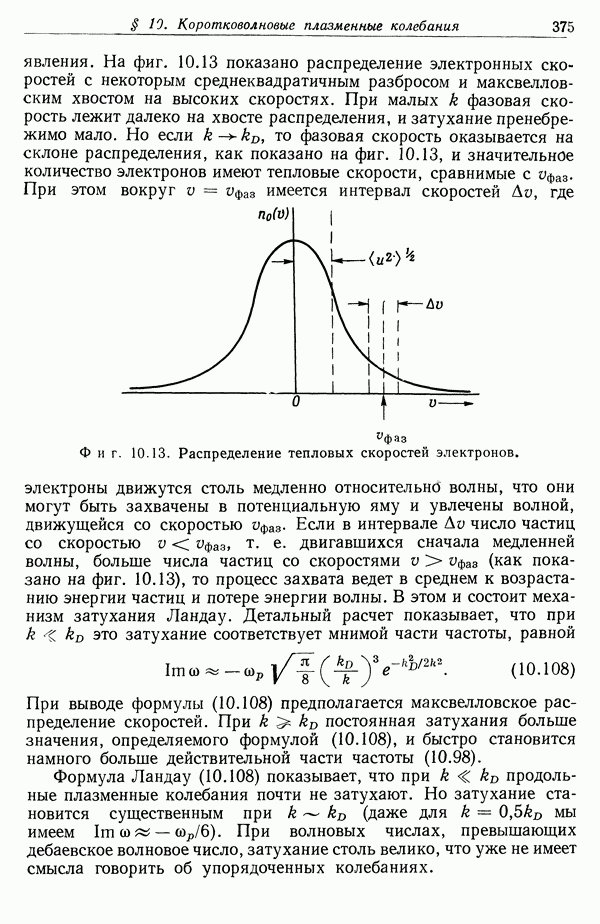
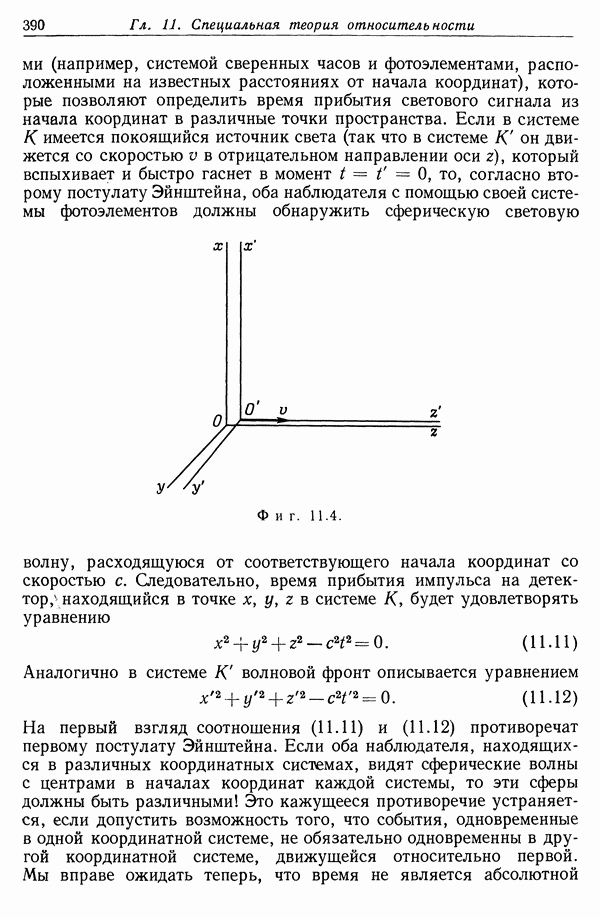
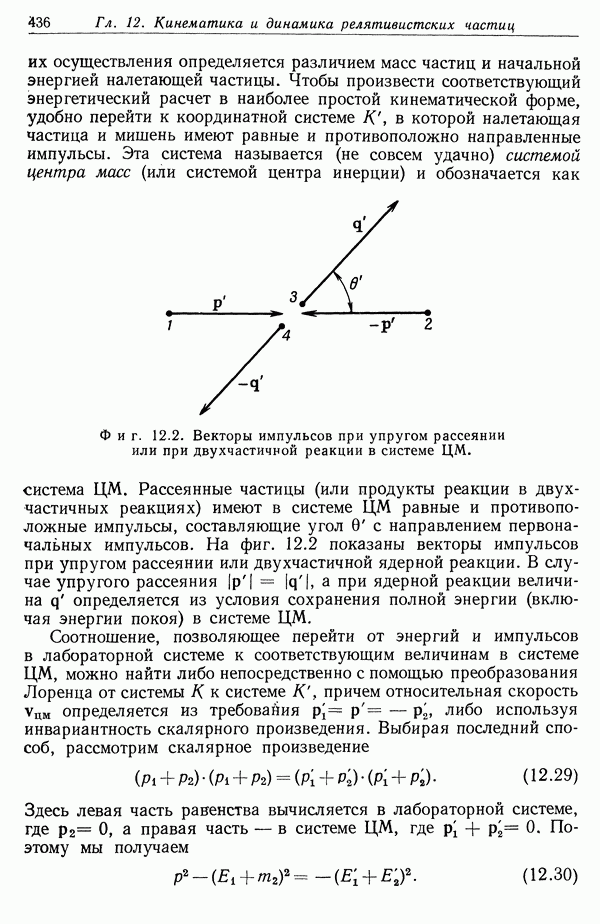
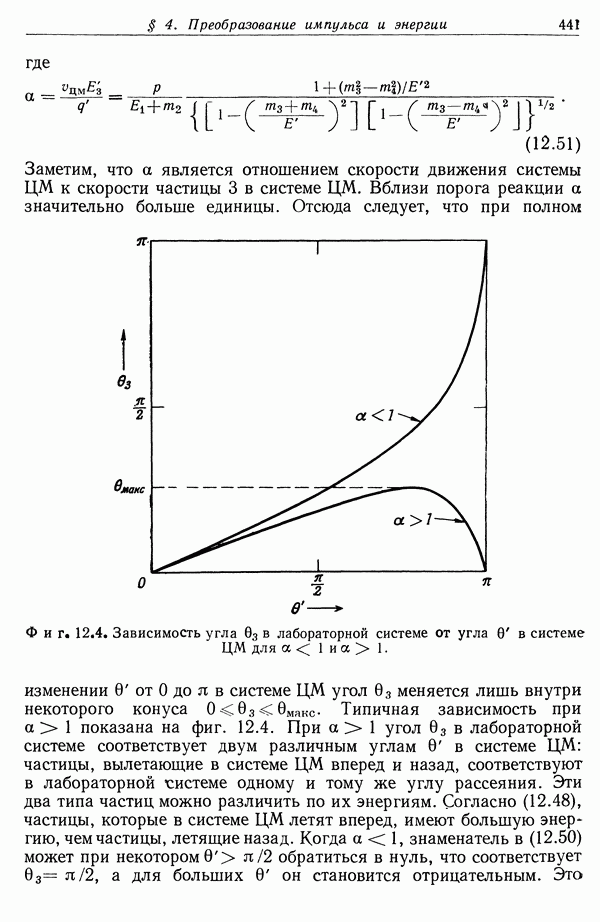
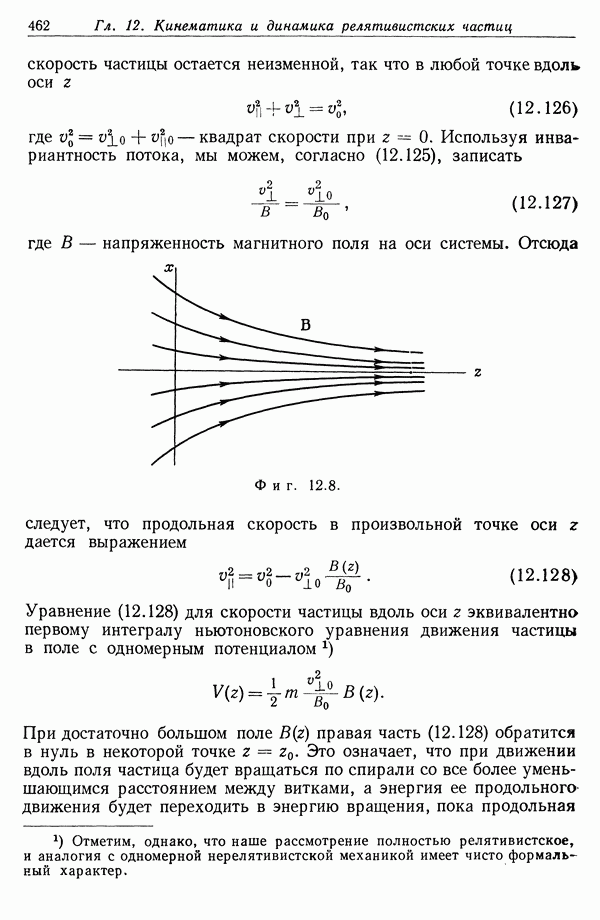
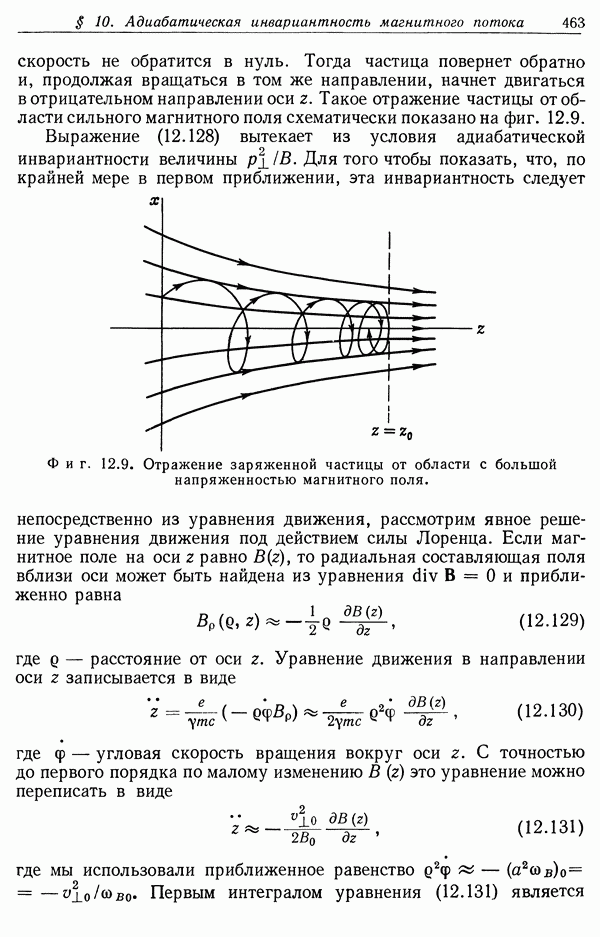
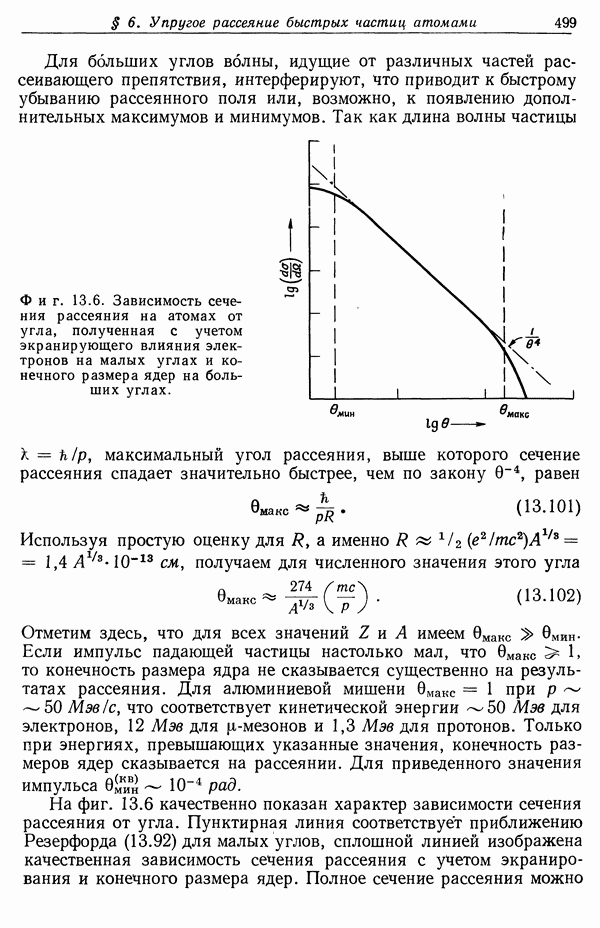
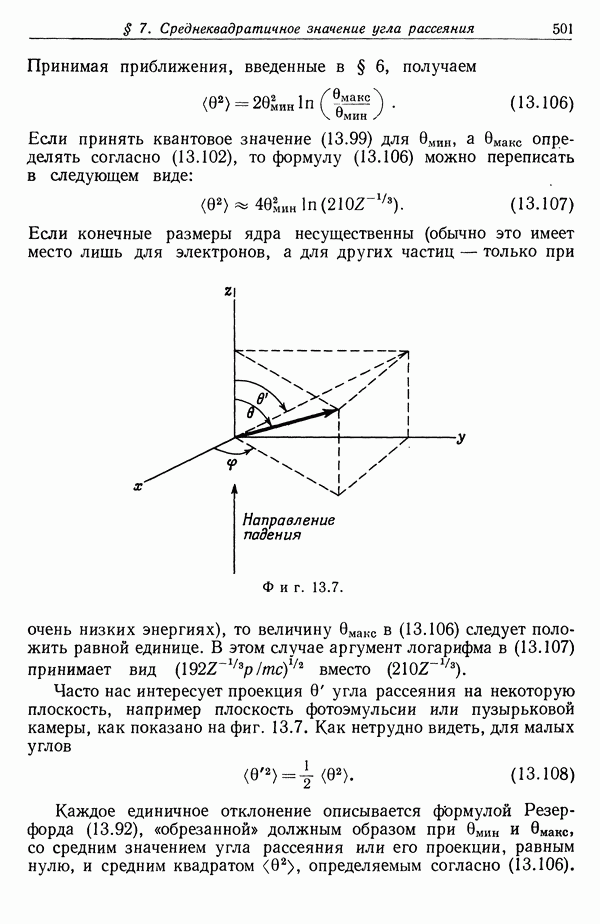
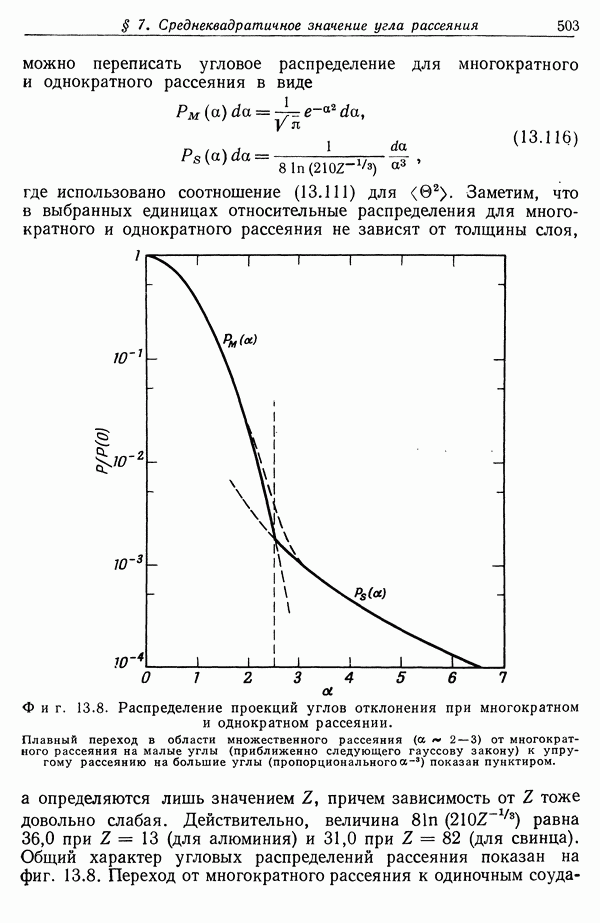
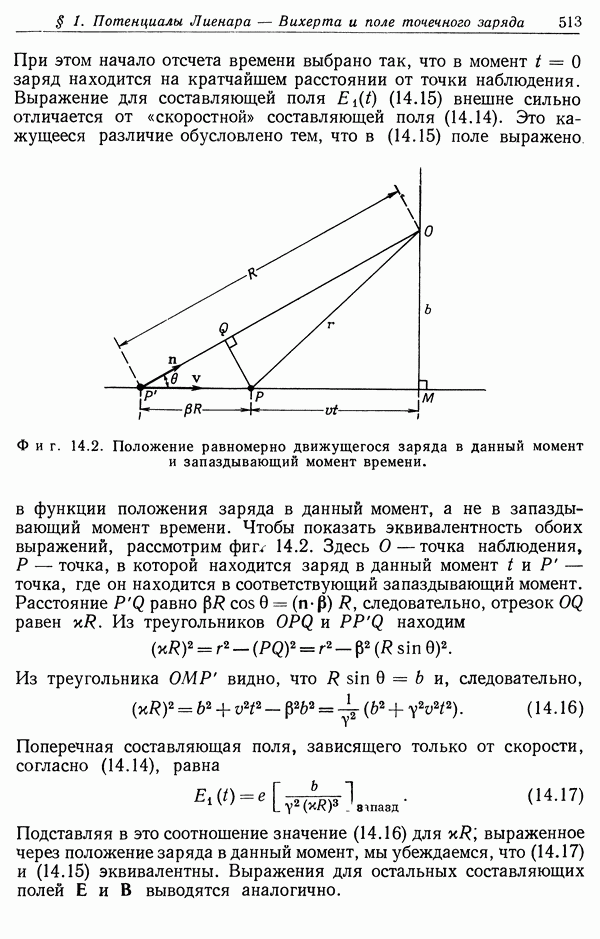
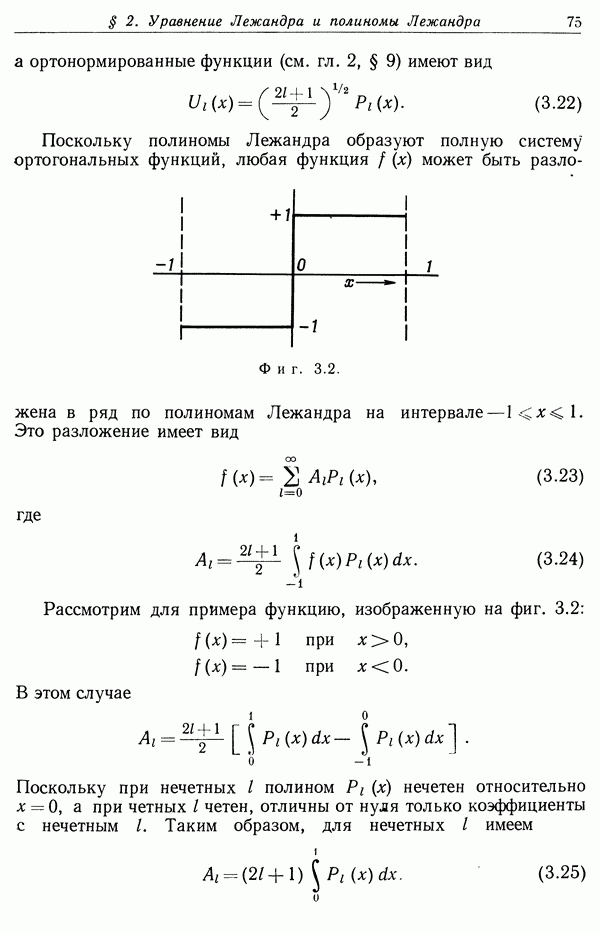| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Энергия электрического поля в диэлектрике
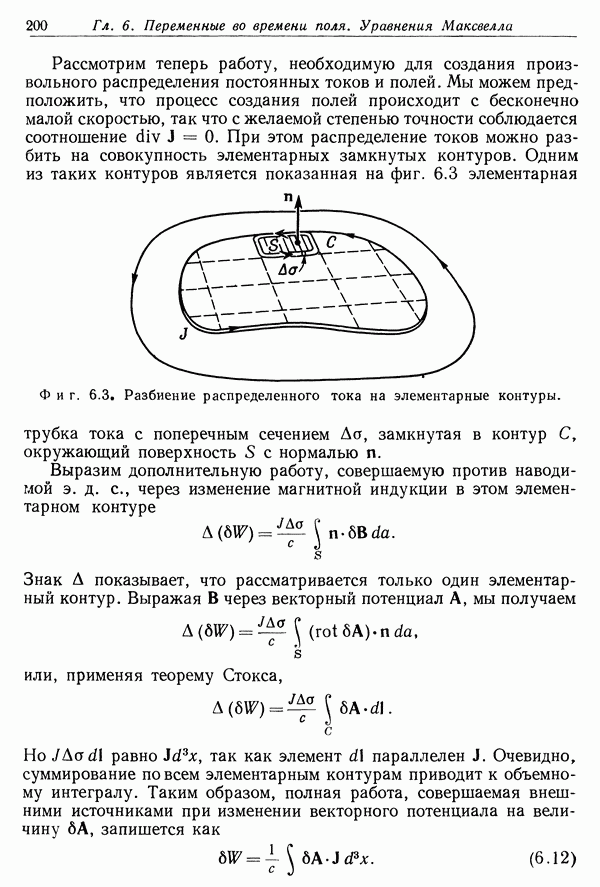
В гл. 1, § 11, была исследована энергия системы зарядов в свободном пространстве. Полученное выражение для энергии системы
с распределением плотности заряда  и потенциалом
и потенциалом 

не может быть, вообще говоря, принято без изменения при макроскопическом описании диэлектрических сред. Причина этого станет более ясной, если напомнить, как было получено выражение (4.86).
Данное распределение заряда мы представляли себе как результат постепенного накопления элементарных зарядов, которые вносятся из бесконечно удаленной точки, причем преодолевается противодействие электрического поля уже существующего заряда. При этом полная работа, совершенная при накоплении заряда, описывается соотношением (4.86). При наличии диэлектрической среды совершаемая работа тратится не только на перенос свободного (макроскопического) заряда в его окончательное положение, но и на увеличение поляризации диэлектрика. Поэтому если понимать под q и Ф в (4.86) макроскопические величины, то заранее не очевидно, что выражение (4.86) определяет полную затраченную работу, включающую и работу на поляризацию диэлектрика.
Для общности рассмотрения мы вначале не будем делать каких-либо допущений о линейности, однородности и тому подобных свойствах реакции диэлектрика на приложенное поле. Рассмотрим малое изменение энергии  обусловленное некоторым изменением
обусловленное некоторым изменением  распределения плотности заряда Q, существующего во всем пространстве.
распределения плотности заряда Q, существующего во всем пространстве.
Работа, требуемая для совершения этого изменения, равна

где  — потенциал, создаваемый уже существующим распределением заряда
— потенциал, создаваемый уже существующим распределением заряда  . Так как
. Так как  , то
, то  можно связать с изменением электрической индукции
можно связать с изменением электрической индукции 

В результате изменение энергии  может быть представлено в виде
может быть представлено в виде

где мы воспользовались соотношением  и приняли, что
и приняли, что  описывает ограниченное распределение заряда. Полную электростатическую энергию можно найти, по крайней мере формально, рассмотрев изменение D от начального значения
описывает ограниченное распределение заряда. Полную электростатическую энергию можно найти, по крайней мере формально, рассмотрев изменение D от начального значения 
до некоторой конечной величины 

Для линейной среды

и полная электростатическая энергия оказывается равной

Последний результат можно преобразовать к виду (4.86), воспользовавшись соотношениями  или же возвращаясь к (4.87) и принимая линейную связь между q и Ф. Таким образом, мы видим, что выражение (4.86) выполняется для макроскопических характеристик лишь в случае линейных сред. В противном случае энергия окончательной конфигурации зарядов должна вычисляться согласно (4.90) и может зависеть от предыстории системы (гистерезис).
или же возвращаясь к (4.87) и принимая линейную связь между q и Ф. Таким образом, мы видим, что выражение (4.86) выполняется для макроскопических характеристик лишь в случае линейных сред. В противном случае энергия окончательной конфигурации зарядов должна вычисляться согласно (4.90) и может зависеть от предыстории системы (гистерезис).
Представляет интерес задача об изменении энергии при внесении диэлектрических тел в электрическое поле фиксированных источников. Пусть первоначально электрическое поле  создается некоторым распределением зарядов
создается некоторым распределением зарядов  в среде с диэлектрической проницаемостью
в среде с диэлектрической проницаемостью  которая может зависеть от координат. При этом начальная электростатическая энергия равна
которая может зависеть от координат. При этом начальная электростатическая энергия равна

где  Пусть теперь при фиксированном положении источников в поле вносится диэлектрическое тело объемом
Пусть теперь при фиксированном положении источников в поле вносится диэлектрическое тело объемом  что приводит к изменению поля от
что приводит к изменению поля от  до Е. При наличии тела диэлектрическая проницаемость
до Е. При наличии тела диэлектрическая проницаемость  равна
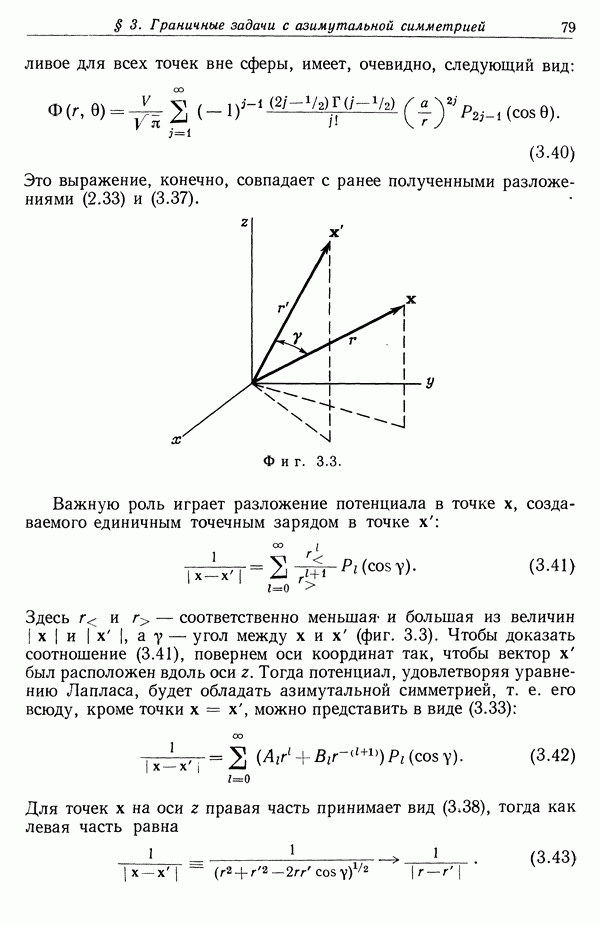
равна  в объеме и
в объеме и  вне
вне  Чтобы обойти математические трудности, будем считать функцию
Чтобы обойти математические трудности, будем считать функцию  достаточно плавной функцией координат, спадающей от
достаточно плавной функцией координат, спадающей от  до
до  вблизи границы объема V быстро, но непрерывно. При наличии тела величина энергии будет равна
вблизи границы объема V быстро, но непрерывно. При наличии тела величина энергии будет равна

где  Разность энергий можно записать в виде
Разность энергий можно записать в виде 

Можно показать, что второй интеграл равен нулю. Действительно, так как  то
то

так что второй интеграл может быть представлен в виде

Интегрирование по частям дает

так как  в силу предположения о том, что распределение плотности заряда
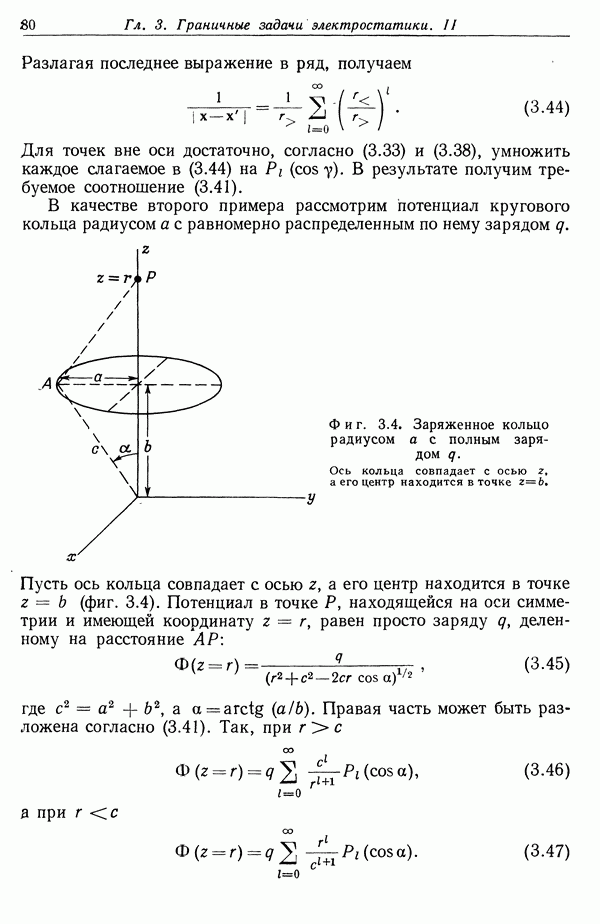
в силу предположения о том, что распределение плотности заряда  не изменилось при внесении диэлектрического тела. Таким образом, изменение энергии определяется выражением
не изменилось при внесении диэлектрического тела. Таким образом, изменение энергии определяется выражением

Интегрирование, которое, казалось бы, надо распространять на все пространство, в действительности следует проводить лишь по объему  занятому телом, так как вне этого объема
занятому телом, так как вне этого объема  Таким образом,
Таким образом,

Если диэлектрическое тело расположено в свободном пространстве, то  Учитывая определение вектора поляризации Р, можно записать (4.95) в виде
Учитывая определение вектора поляризации Р, можно записать (4.95) в виде

где Р — поляризация диэлектрика. Отсюда следует, что плотность энергии в диэлектрике, расположенном в поле  источники которого фиксированы, описывается формулой
источники которого фиксированы, описывается формулой

Это выражение аналогично дипольному члену в разложении (4.17) для энергии распределения зарядов во внешнем поле. Наличие коэффициента 1/2 связано с тем, что (4.97) представляет плотность энергии для поляризуемого диэлектрика во внешнем поле, а не для постоянного диполя. Этот коэффициент имеет то же происхождение, что и в формуле (4.91).
Из выражений (4.95) и (4.96) следует, что при  диэлектрическое тело стремится переместиться в область с большим значением поля
диэлектрическое тело стремится переместиться в область с большим значением поля  Для вычисления действующей на тело силы рассмотрим малое обобщенное смещение тела
Для вычисления действующей на тело силы рассмотрим малое обобщенное смещение тела  Оно приведет к изменению энергии
Оно приведет к изменению энергии  . Так как распределение зарядов фиксировано, то внешние источники энергии отсутствуют и изменение энергии поля должно компенсироваться изменением механической энергии тела. Это значит, что действующая на тело сила определяется выражением
. Так как распределение зарядов фиксировано, то внешние источники энергии отсутствуют и изменение энергии поля должно компенсироваться изменением механической энергии тела. Это значит, что действующая на тело сила определяется выражением

где индекс Q у частной производной показывает, что источники поля остаются неизменными.
В практических задачах с перемещением диэлектриков электрическое поле часто создается заданной конфигурацией электродов, на которых с помощью внешнего источника, например батареи, поддерживается постоянный потенциал. При перемещении диэлектрика заряд будет течь к батарее или от нее так, чтобы потенциал оставался постоянным. Это означает, что внешний источник в данном случае затрачивает некоторую энергию. Интересно сравнить эту энергию с найденным выше изменением энергии для фиксированных источников поля. Будем рассматривать лишь линейные среды, для которых справедливо выражение (4.86). При этом достаточно рассмотреть лишь малые изменения первоначально существовавшей конфигурации. Как видно из (4.86), изменение энергии, соответствующее изменению плотности заряда  и изменению потенциала
и изменению потенциала  равно
равно

Сопоставление с выражением (4.87) показывает, что при неизменных свойствах диэлектрика оба слагаемых в (4.99) равны. Если, однако, свойства диэлектрика меняются:
 (4.100)
(4.100)
то слагаемые (4.99) могут быть не равными.
Действительно, мы сейчас нашли изменение энергии, обусловленное введением диэлектрического тела в электрическое поле, создаваемое фиксированными источниками  Это изменение энергии объясняется появлением наведенных зарядов. Изменение свойств диэлектрика в соответствии с (4.100) вызывает изменение плотности связанного заряда. Поэтому если интерпретировать соотношение (4.99) как интеграл от плотности и свободного, и свят занного зарядов (т. е. как микроскопическое уравнение), то оба
Это изменение энергии объясняется появлением наведенных зарядов. Изменение свойств диэлектрика в соответствии с (4.100) вызывает изменение плотности связанного заряда. Поэтому если интерпретировать соотношение (4.99) как интеграл от плотности и свободного, и свят занного зарядов (т. е. как микроскопическое уравнение), то оба
слагаемых оказываются всегда равными. Однако часто удобно иметь дело с макроскопическими величинами. При этом указанное равенство обоих слагаемых имеет место лишь при неизменных свойствах диэлектрика.
Можно считать, что любой процесс изменения свойств диэлектрика (перемещением диэлектрических тел, изменением их восприимчивостей и т. д.) при заданных потенциалах на электродах совершается в два этапа. На первом этапе электроды отсоединены от батарей и заряд на них поддерживается постоянным  Изменение энергии при изменении свойств диэлектрика (4.100) выражается формулой
Изменение энергии при изменении свойств диэлектрика (4.100) выражается формулой

где  — изменение потенциала. Можно показать, что это соотношение приводится к (4.95). На втором этапе батареи подключаются к электродам и на электродах вновь восстанавливается первоначальный потенциал. Изменение потенциала —
— изменение потенциала. Можно показать, что это соотношение приводится к (4.95). На втором этапе батареи подключаются к электродам и на электродах вновь восстанавливается первоначальный потенциал. Изменение потенциала —  сопровождается потоком заряда
сопровождается потоком заряда  от батареи. Изменение энергии на втором этапе равно
от батареи. Изменение энергии на втором этапе равно
 (4.102)
(4.102)
так как оба слагаемых равны друг другу. Мы видим, что изменение энергии, обусловленное внешними источниками на втором этапе, вдвое больше, чем на первом, и имеет противоположный знак. В результате полное изменение энергии
 (4.103)
(4.103)
Символически можно записать
 (4.104)
(4.104)
где индекс соответствует фиксированному параметру.
Если диэлектрик с  вносится в область с большей напряженностью поля, то в случае фиксированных потенциалов энергия возрастает, а не убывает. При этом действующая на тело механическая сила, соответствующая обобщенному смещению равна
вносится в область с большей напряженностью поля, то в случае фиксированных потенциалов энергия возрастает, а не убывает. При этом действующая на тело механическая сила, соответствующая обобщенному смещению равна

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие редактора перевода
- Предисловие
- Глава 1. ВВЕДЕНИЕ В ЭЛЕКТРОСТАТИКУ
- § 1. Закон Кулона
- § 2. Напряженность электрического поля
- § 3. Теорема Гаусса
- § 4. Дифференциальная форма теоремы Гаусса
- § 5. Второе уравнение электростатики и скалярный потенциал
- § 6. Поверхностные распределения зарядов и диполей. Скачки электрического поля и потенциала
- § 7. Уравнения Лапласа и Пуассона
- § 8. Теорема Грина
- § 9. Единственность решения при граничных условиях Дирихле или Неймана
- § 10. Формальное решение граничных задач электростатики с помощью функции Грина
- § 11. Потенциальная энергия и плотность энергии электростатического поля
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 2. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ.
- § 2. Точенный заряд вблизи заземленного сферического проводника
- § 3. Точечный заряд вблизи заряженного изолированного сферического проводника
- § 4. Точечный заряд вблизи сферического проводника с заданным потенциалом
- § 5. Сферический проводник в однородном электрическом поле
- § 6. Метод инверсии
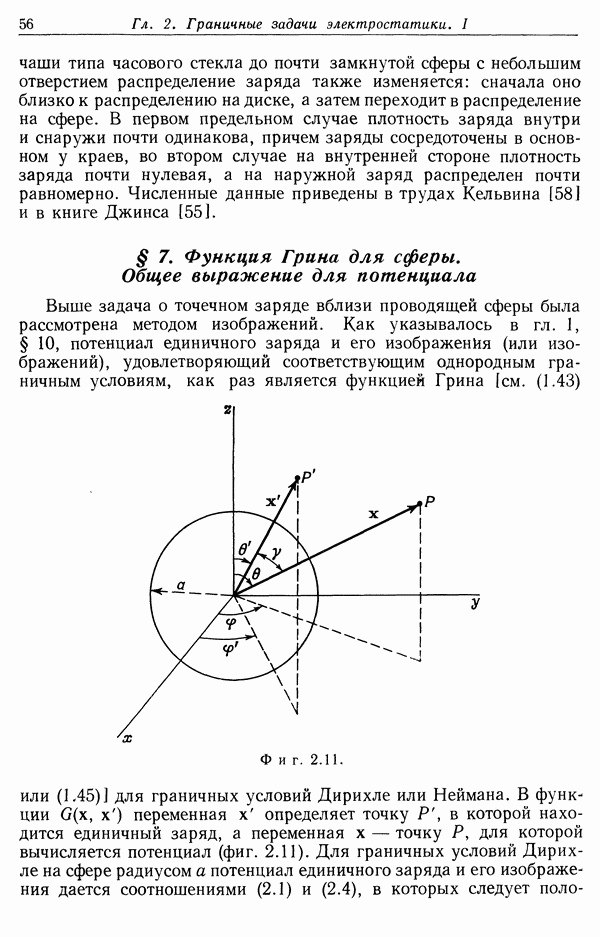
- § 7. Функция Грина для сферы. Общее выражение для потенциала
- § 8. Две примыкающие проводящие полусферы, имеющие различный потенциал
- § 9. Разложение по ортогональным функциям
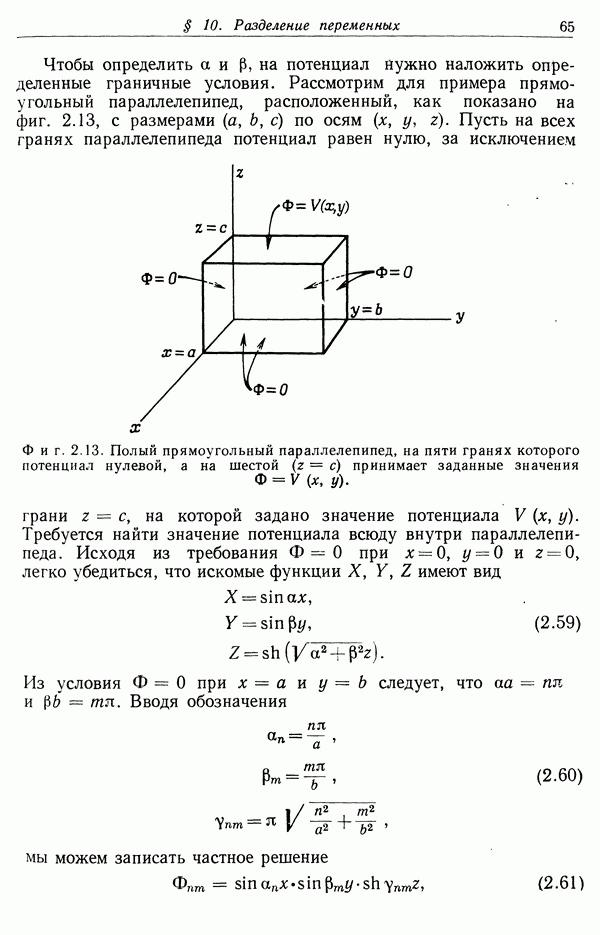
- § 10. Разделение переменных. У равнение Лапласа в декартовых координатах
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 3. ГРАНИЧНЫЕ ЗАДАЧИ ЭЛЕКТРОСТАТИКИ II
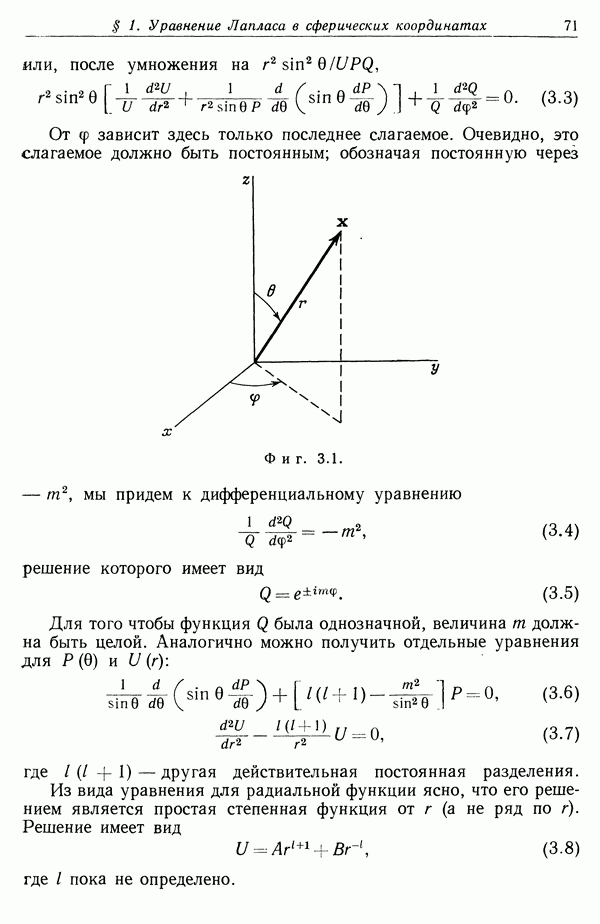
- § 2. Уравнение Лежандра и полиномы Лежандра
- 3. Граничные задачи с азимутальной симметрией
- § 4. Присоединенные функции Лежандра и сферические гармоники …
- § 5. Теорема сложения для сферических гармоник
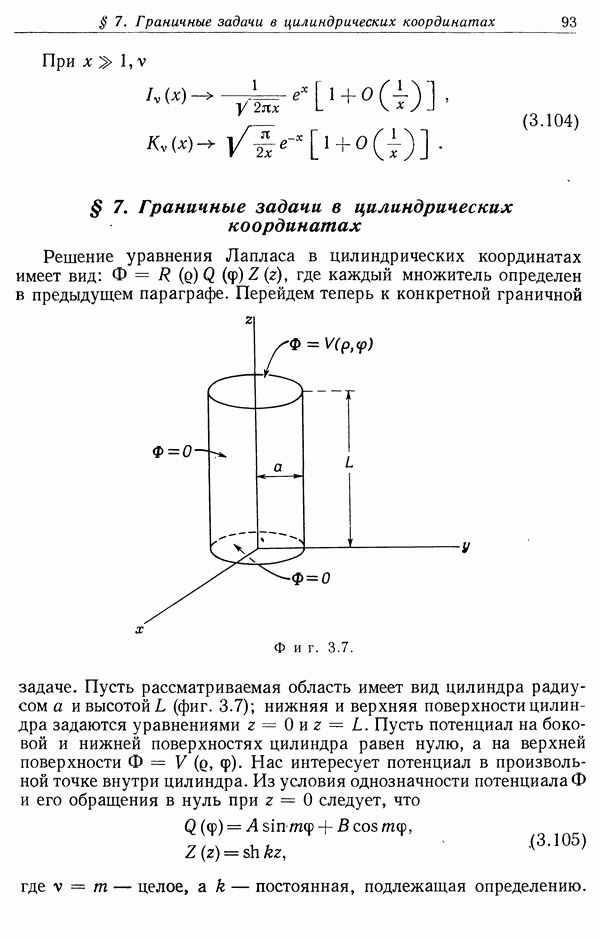
- § 6. Уравнение Лапласа в цилиндрических координатах. Функции Бесселя
- § 7. Граничные задачи в цилиндрических координатах
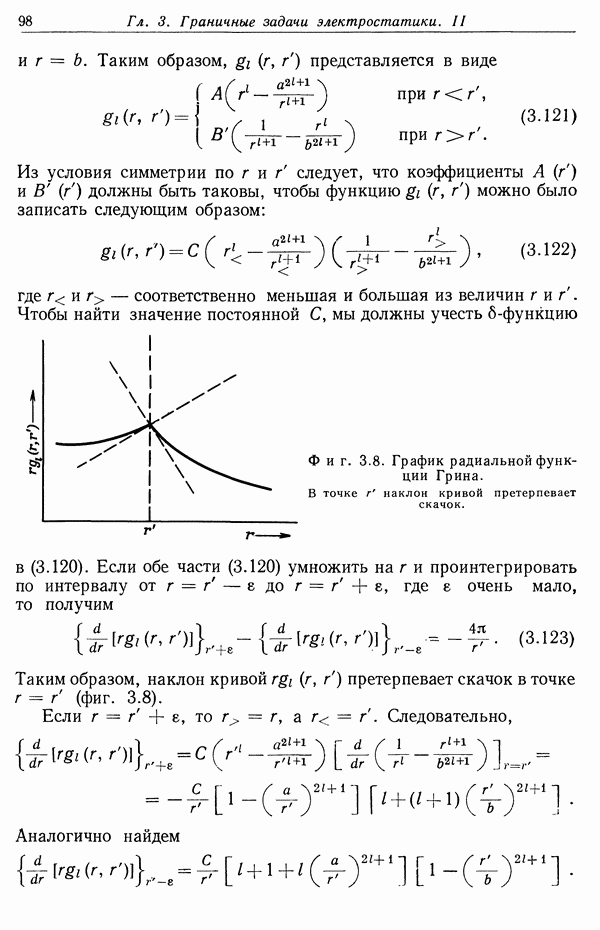
- § 8. Разложение функций Грина в сферических координатах
- § 9. Нахождение потенциала с помощью разложений для сферических функций Грина
- § 10. Разложение функций Грина в цилиндрических координатах
- § 11. Разложение функций Грина по собственным функциям
- § 12. Смешанные граничные условия. Заряженный проводящий диск
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 4. МУЛЬТИПОЛИ. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОСТАТИКА МАТЕРИАЛЬНЫХ СРЕД. ДИЭЛЕКТРИКИ
- § 2. Разложение по мультиполям энергии распределения зарядов во внешнем поле
- § 3. Макроскопическая электростатика. Эффекты совокупного действия атомов
- § 4. Изотропные диэлектрики и граничные условия
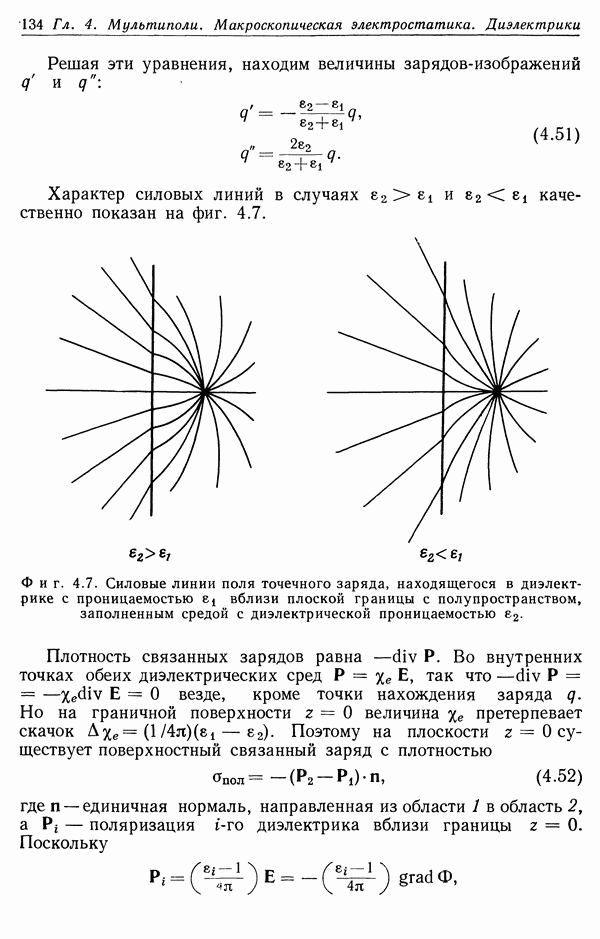
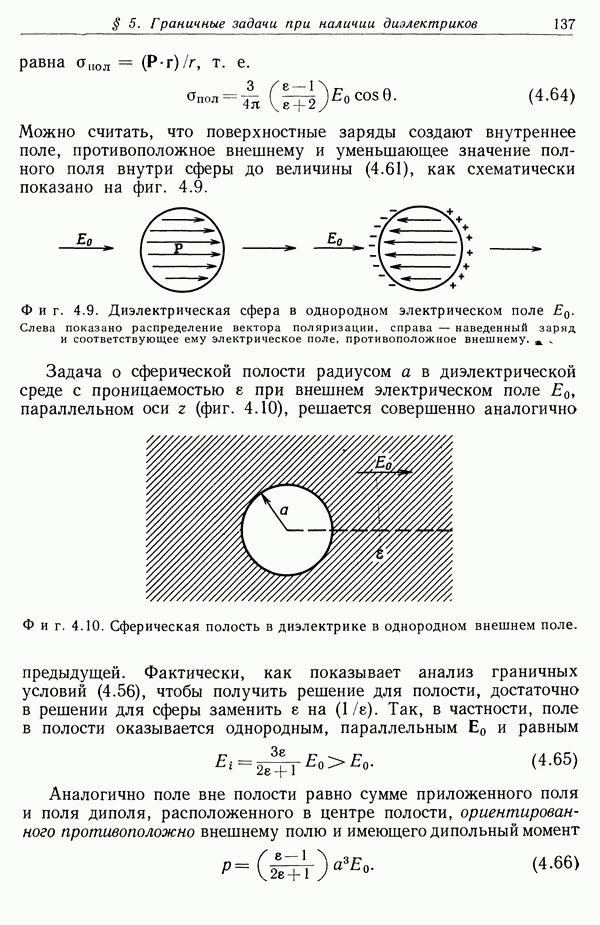
- § 5. Граничные задачи при наличии диэлектриков
- § 6. Поляризуемость молекул и диэлектрическая восприимчивость
- § 7. Модели поляризуемости молекул
- § 8. Энергия электрического поля в диэлектрике
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 5. МАГНИТОСТАТИКА
- § 2. Закон Био и Савара
- § 3. Дифференциальные уравнения магнитостатики и закон Ампера
- § 4. Векторный потенциал
- § 5. Векторный потенциал и магнитная индукция кругового витка тока
- § 6. Магнитное поле ограниченного распределения токов. Магнитный момент
- § 7. Сила и момент, действующие на ограниченное распределение тока во внешнем магнитном поле
- § 8. Макроскопические уравнения
- § 9. Граничные условия для магнитной индукции и поля
- § 10. Однородно намагниченный шар
- § 11. Намагниченный шар во внешнем поле. Постоянные магниты
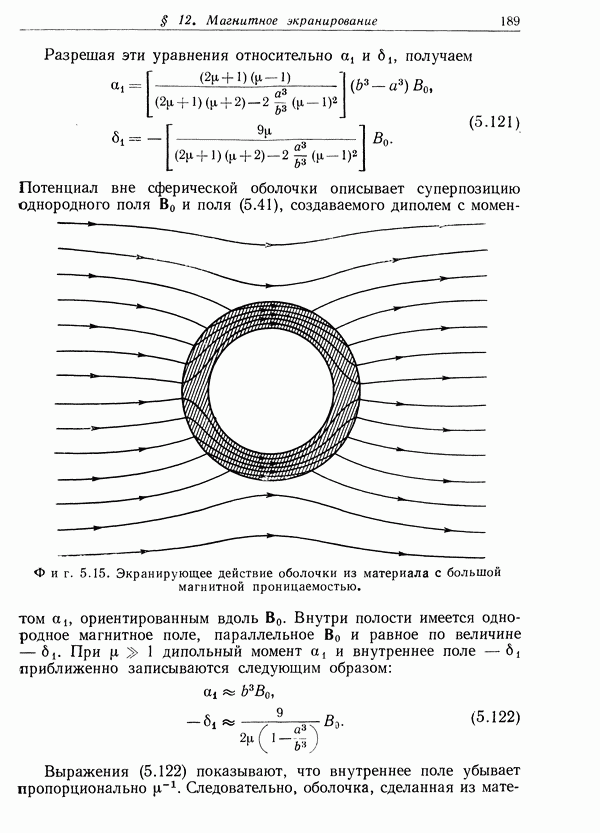
- § 12. Магнитное экранирование. Сферическая оболочка из магнитного материала в однородном поле
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 6. ПЕРЕМЕННЫЕ ВО ВРЕМЕНИ ПОЛЯ. УРАВНЕНИЯ МАКСВЕЛЛА. ЗАКОНЫ СОХРАНЕНИЯ
- § 1. Закон индукции. Фарадея
- § 2. Энергия магнитного поля
- § 3. Максвелловский ток смещения. Уравнения Максвелла
- § 4. Векторный и скалярный потенциалы
- § 5. Калибровочные преобразования. Лоренцовская калибровка. Кулоновская калибровка
- § 6. Функция Грина для волнового уравнения
- § 7. Задача с начальными условиями. Интегральное представление Кирхгофа
- § 8. Теорема Пойнтинга
- § 9. Законы сохранения для системы заряженных частиц и электромагнитных полей
- § 10. Макроскопические уравнения
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 7. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
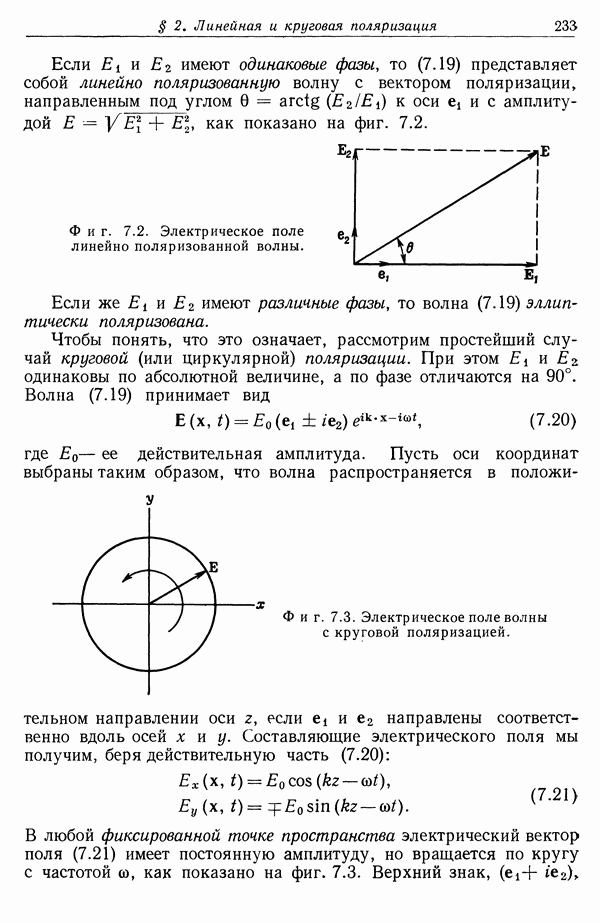
- § 2. Линейная и круговая поляризация
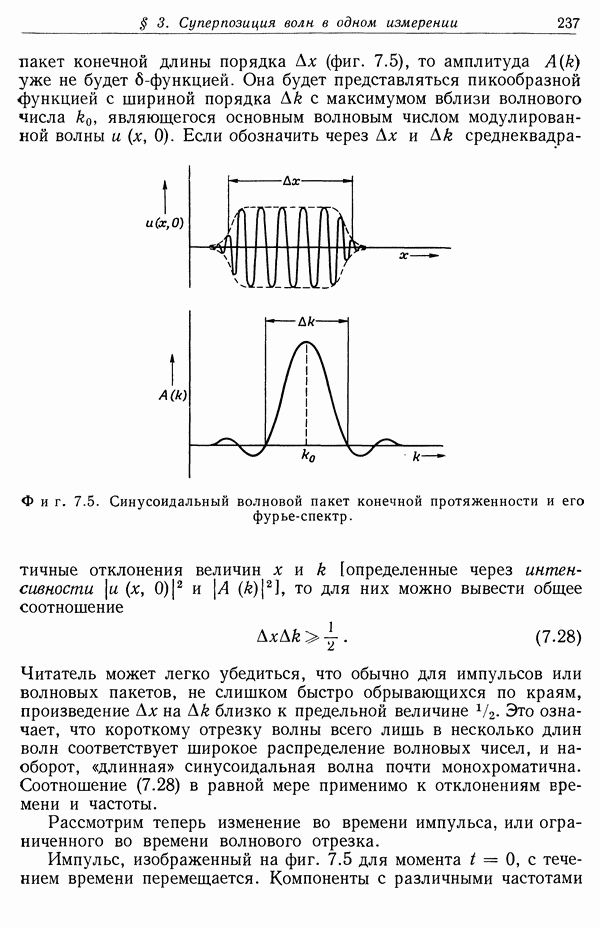
- § 3. Суперпозиция волн в одном измерении. Групповая скорость
- § 4. Примеры распространения импульсов в диспергирующей среде
- § 5. Отражение и преломление электромагнитных волн на плоской границе раздела между диэлектриками
- § 6. Поляризация при отражении и полное внутреннее отражение
- § 7. Волны в проводящей среде
- § 8. Простая модель проводимости
- § 9. Поперечные волны в разреженной плазме
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 8. ВОЛНОВОДЫ И РЕЗОНАТОРЫ
- § 2. Цилиндрические резонаторы и волноводы
- § 3. Волноводы
- § 4. Волны в прямоугольном волноводе
- § 5. Поток энергии и затухание в волноводах
- § 6. Резонаторы
- § 7. Потери мощности в резонаторе. Добротность резонатора
- § 8. Диэлектрические волноводы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 9. ПРОСТЕЙШИЕ ИЗЛУЧАЮЩИЕ СИСТЕМЫ И ДИФРАКЦИЯ
- § 2. Электрическое диполъное поле и излучение
- § 3. Магнитные диполъные и электрические квадрупольные поля
- § 4. Линейная антенна с центральным возбуждением
- § 5. Интеграл Кирхгофа
- § 6. Векторные эквиваленты интеграла Кирхгофа
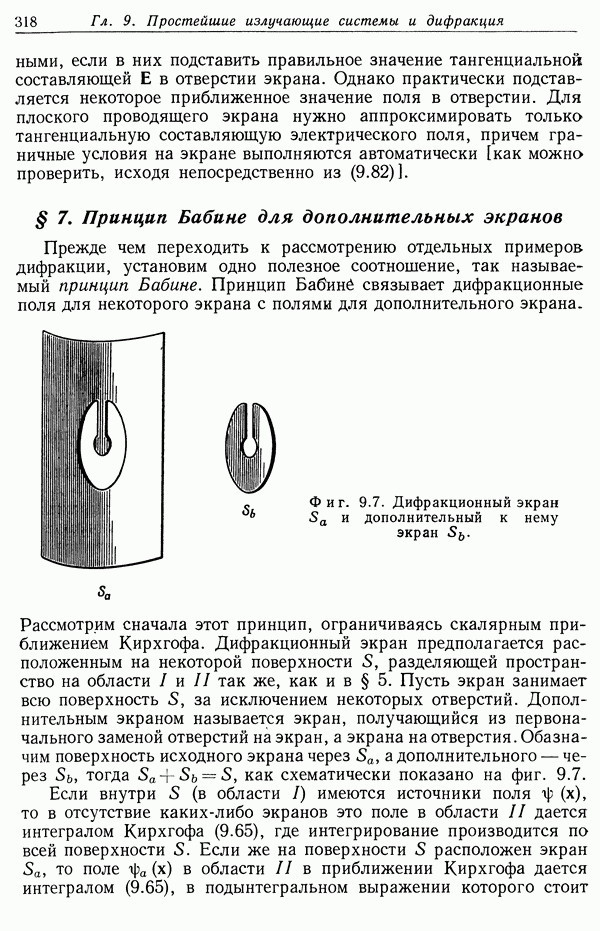
- § 7. Принцип Бабине для дополнительных экранов
- § 8. Дифракция на круглом отверстии
- § 9. Дифракция на малых отверстиях
- § 10. Рассеяние коротких волн проводящей сферой
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 10. МАГНИТНАЯ ГИДРОДИНАМИКА И ФИЗИКА ПЛАЗМЫ
- § 2. Уравнения магнитной гидродинамики
- § 4. Магнитогидродинамический поток между границами в скрещенных электрическом и магнитном полях
- § 5. Пинч-эффект
- § 6. Динамическая модель пинч-эффекта
- § 7. Неустойчивости сжатого плазменного столба
- § 8. Магнитогидродинамические волны
- § 9. Высокочастотные плазменные колебания
- § 10. Коротковолновые плазменные колебания. Дебаевский радиус экранирования
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 11. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 2. Постулаты специальной теории относительности и преобразование Лоренца
- § 3. Сокращение Фицджеральда — Лоренца и замедление времени
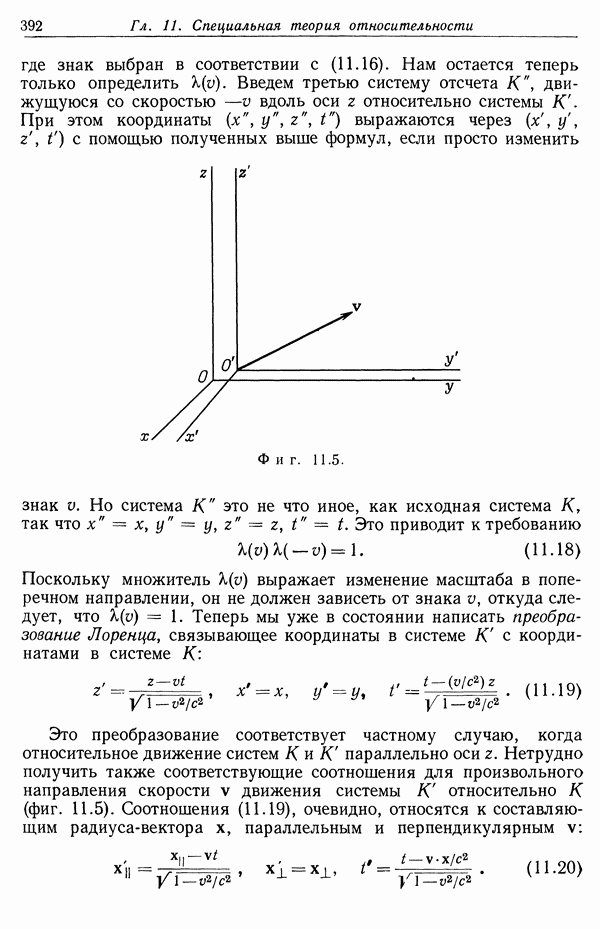
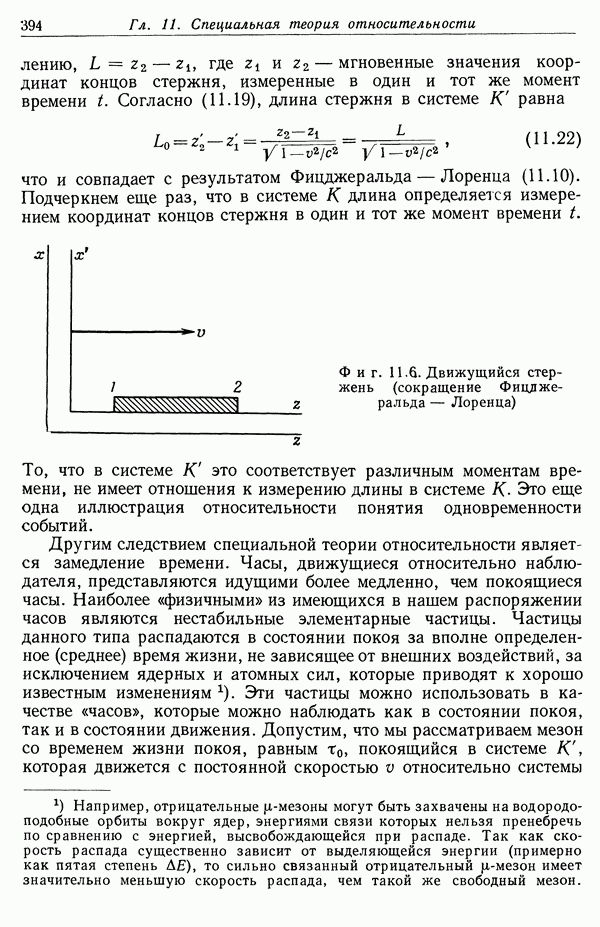
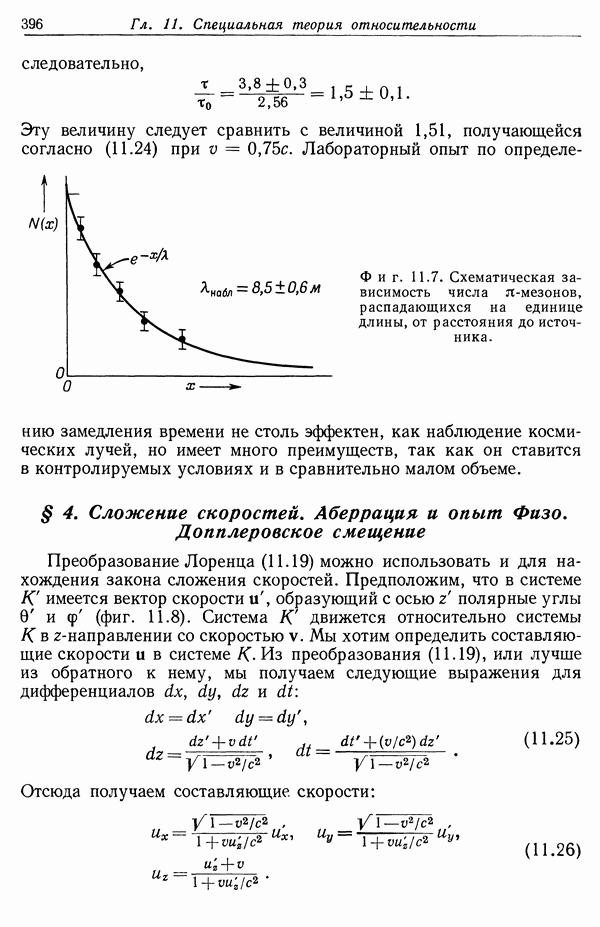
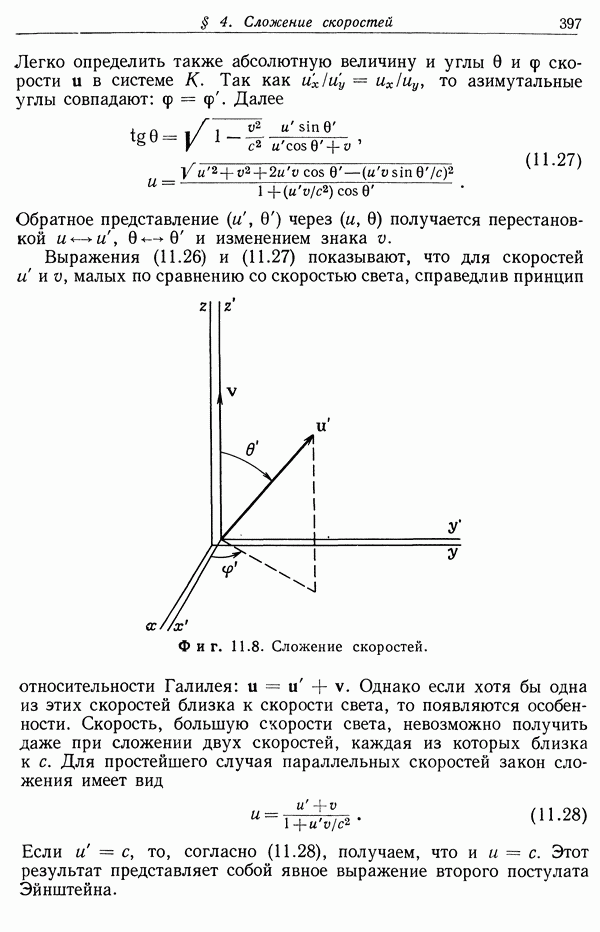
- § 4. Сложение скоростей. Аберрация и опыт Физо. Допплеровское смещение
- § 5. Прецессия Томаса
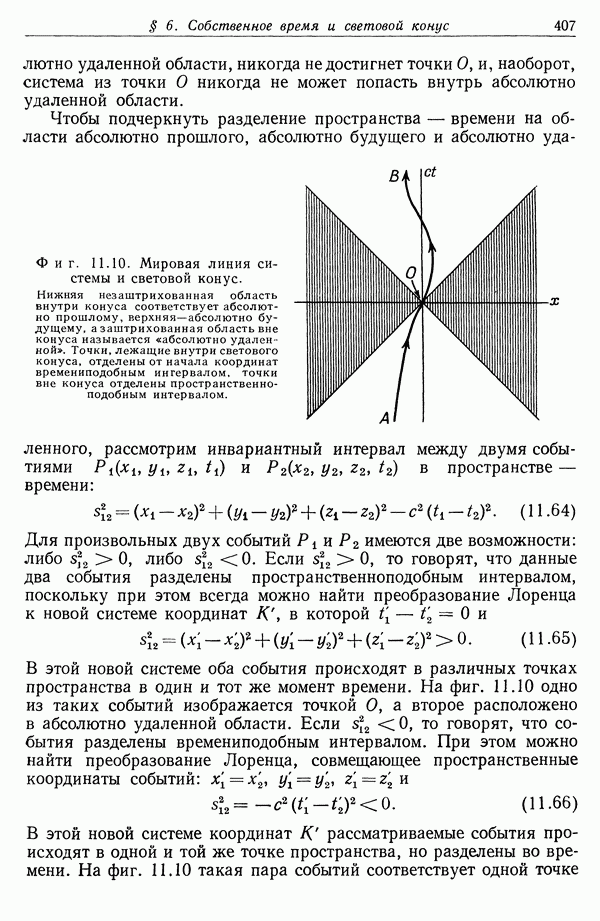
- § 6. Собственное время и световой конус
- § 7. Преобразования Лоренца как ортогональные преобразования в четырехмерном пространстве
- § 8. Четырехвекторы и четырехтензоры. Ковариантность уравнений физики
- § 9. Ковариантность уравнений электродинамики
- § 10. Преобразование электромагнитного поля
- § 11. Ковариантность выражения для силы Лоренца и законов сохранения
- РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 12. КИНЕМАТИКА И ДИНАМИКА РЕЛЯТИВИСТСКИХ ЧАСТИЦ
- § 2. Кинематика осколков при распаде нестабильной частицы
- § 3. Преобразование к системе центра масс и пороги реакций
- § 4. Преобразование импульса и энергии из системы центра масс в лабораторную систему
- § 5. Ковариантные уравнения движения. Лагранжиан и гамильтониан для релятивистской заряженной частицы
- § 6. Релятивистские поправки первого порядка для лагранжиана взаимодействующих заряженных частиц
- § 7. Движение в однородном статическом магнитном поле
- § 8. Движение в однородных статических электрическом и магнитном полях
- § 9. Дрейф частиц в неоднородном статическом магнитном поле
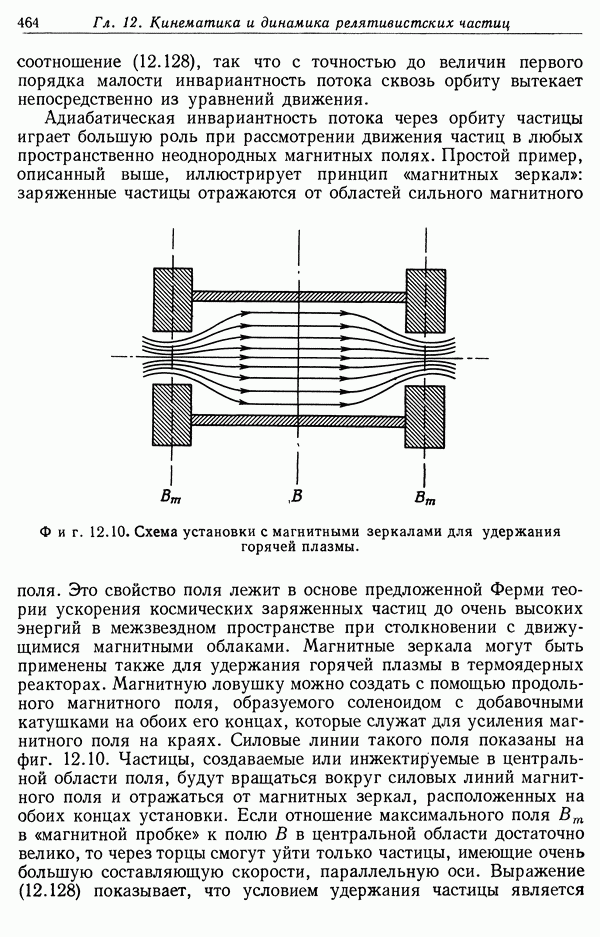
- § 10. Адиабатическая инвариантность магнитного потока сквозь орбиту частицы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 13. СОУДАРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ. ПОТЕРИ ЭНЕРГИИ. РАССЕЯНИЕ
- § 1. Передача энергии при кулоновских соударениях
- § 2. Передача энергии гармоническому осциллятору
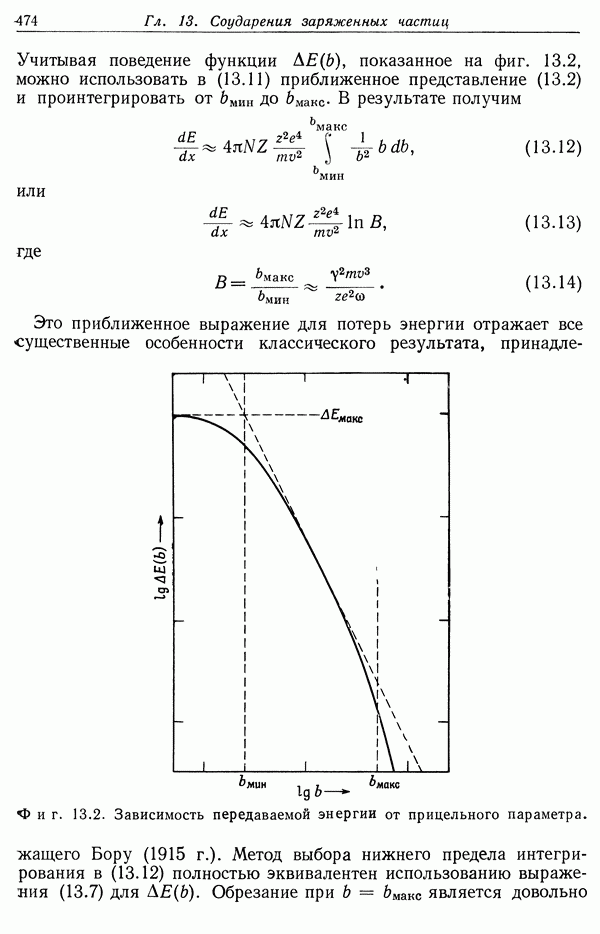
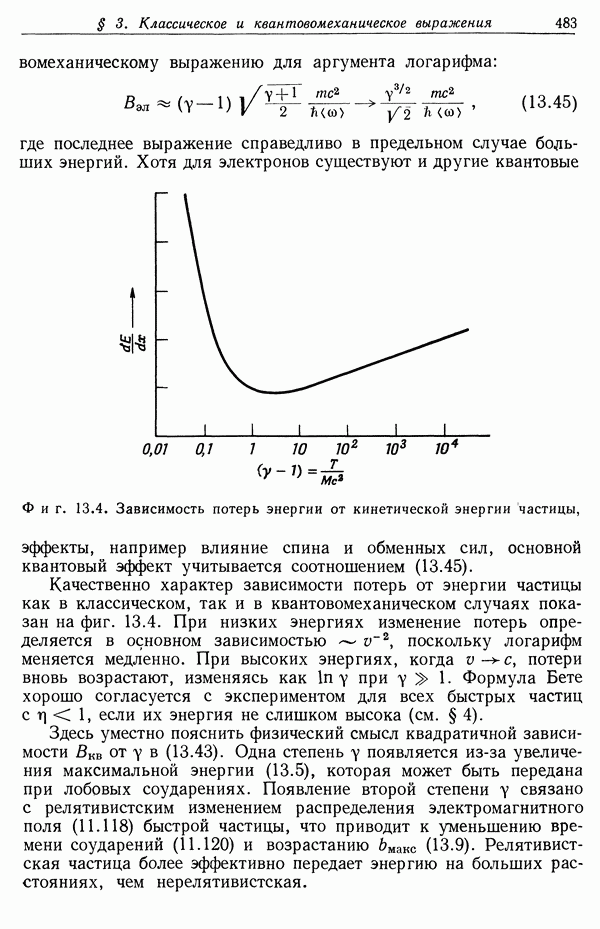
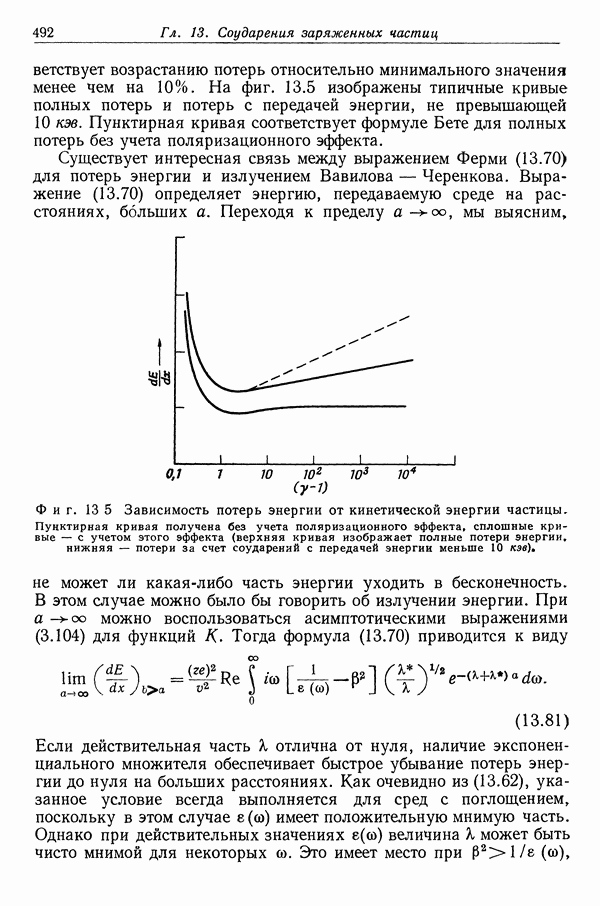
- § 3. Классическое и квантовомеханическое выражения для потерь энергии
- § 4. Влияние плотности на потери энергии при соударении
- § 5. Потери энергии в электронной плазме
- § 6. Упругое рассеяние быстрых частиц атомами
- § 7. Среднеквадратичное значение угла рассеяния и угловое распределение при многократном рассеянии
- § 8. Электропроводность плазмы
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 14. ИЗЛУЧЕНИЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
- § 2. Полная мощность, излучаемая ускоренно движущимся зарядом. Формула Лармора и ее релятивистское обобщение
- § 3. Угловое распределение излучения ускоряемого заряда
- § 4. Излучение заряда при произвольном ультрарелятивистском движении
- § 5. Спектральное и угловое распределения энергии, излучаемой ускоренными зарядами
- § 6. Спектр излучения релятивистской заряженной частицы при мгновенном движении по окружности
- § 7. Рассеяние на свободных зарядах. Формула Томсона
- § 8. Когерентное и некогерентное рассеяние
- § 9. Излучение Вавилова—Черенкова
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 15. ТОРМОЗНОЕ ИЗЛУЧЕНИЕ. МЕТОД ВИРТУАЛЬНЫХ ФОТОНОВ. ИЗЛУЧЕНИЕ ПРИ БЕТА-РАСПАДЕ
- § 1. Излучение при соударениях
- § 2. Тормозное излучение при нерелятивистских кулоновских соударениях
- § 3. Тормозное излучение при релятивистском движении
- § 4. Влияние экранирования. Потери на излучение в релятивистском случае
- § 5. Метод виртуальных фотонов Вейцзеккера — Вильямса
- § 6. Тормозное излучение как рассеяние виртуальных фотонов
- § 7. Излучение при бета-распаде
- § 8. Излучение при захвате орбитальных электронов. Исчезновение заряда и магнитного момента
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глаза 16. ПОЛЯ МУЛЬТИПОЛЕЙ
- § 2. Разложение электромагнитных полей по мультиполям
- § 3. Свойства полей мультиполей. Энергия и момент количества движения мультипольного излучения
- § 4. Угловое распределение мультипольного излучения
- § 5. Источники мультипольного излучения. Мулътипольные моменты
- § 6. Мультипольное излучение атомных и ядерных систем
- § 7. Излучение линейной антенны с центральным возбуждением
- § 8. Разложение векторной плоской волны по сферическим волнам
- § 9. Рассеяние электромагнитных волн на проводящей сфере
- § 10. Решение граничных задач с помощью разложений по мультиполям
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Глава 17. ВЛИЯНИЕ ИЗЛУЧЕНИЯ ЧАСТИЦЫ НА ЕЕ ДВИЖЕНИЕ. СОБСТВЕННОЕ ПОЛЕ ЧАСТИЦЫ
- § 2. Определение силы реакции излучения из закона сохранения энергии
- § 3. Вычисление силы реакции излучения по Абрагаму и Лоренцу
- § 4. Трудности модели Абрагама—Лоренца
- § 5. Трансформационные свойства модели Абрагама — Лоренца. Натяжения Пуанкаре
- § 6. Ковариантное определение собственной электромагнитной энергии и импульса заряженной частицы
- § 7. Интегро-дифференциальное уравнение движения с учетом радиационного затухания
- § 8. Ширина линии и сдвиг уровня для осциллятора
- § 9. Рассеяние и поглощение излучения осциллятором
- РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
- ЗАДАЧИ
- Приложение. ЕДИНИЦЫ ИЗМЕРЕНИЯ И РАЗМЕРНОСТИ
- § 2. Единицы измерения и уравнения электродинамики
- § 3. Различные системы электромагнитных единиц
- § 4. Перевод формул и численных значений величин из гауссовой системы единиц в систему МКС
- БИБЛИОГРАФИЯ