| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Закон сохранения момента количества движения
Посмотрим
теперь, что получается в случае большого количества частиц, т. е. когда тело
состоит из множества частичек со множеством сил, действующих между ними и
извне. Разумеется, мы уже знаем, что момент силы, действующий на любую ![]() -ю частицу (т. е.
произведение силы, действующей на
-ю частицу (т. е.
произведение силы, действующей на ![]() -ю частицу, на ее плечо), равен
скорости изменения момента количества движения этой частицы, а момент
количества движения
-ю частицу, на ее плечо), равен
скорости изменения момента количества движения этой частицы, а момент
количества движения ![]() -й частицы в свою очередь равен
произведению импульса частицы на его плечо. Допустим теперь, что мы сложили
моменты сил
-й частицы в свою очередь равен
произведению импульса частицы на его плечо. Допустим теперь, что мы сложили
моменты сил ![]() всех
частиц и назвали это полным моментом сил
всех
частиц и назвали это полным моментом сил ![]() . Эта величина должна быть равна скорости
изменения суммы моментов количества движения всех частиц
. Эта величина должна быть равна скорости
изменения суммы моментов количества движения всех частиц ![]() . Эту сумму можно принять
за определение новой величины, которую мы назовем полным моментом количества
движения
. Эту сумму можно принять
за определение новой величины, которую мы назовем полным моментом количества
движения ![]() .
Точно так же, как импульс тела равен сумме импульсов составляющих его частиц,
момент количества движения тела тоже равен сумме моментов составляющих его
частиц. Таким образом, скорость изменения полного момента количества движения
.
Точно так же, как импульс тела равен сумме импульсов составляющих его частиц,
момент количества движения тела тоже равен сумме моментов составляющих его
частиц. Таким образом, скорость изменения полного момента количества движения ![]() равна полному
моменту сил
равна полному
моменту сил
![]() . (18.18)
. (18.18)
С непривычки может показаться, что полный момент сил - ужасно сложная штука. Ведь нужно учитывать все внутренние и внешние силы. Однако если мы вспомним, что по закону Ньютона силы действия и противодействия не только равны, но и (что особенно важно!) действуют по одной и той же прямой в противоположных направлениях (неважно, говорил ли об этом сам Ньютон или нет, неявно он подразумевал это), то два момента внутренних сил между двумя взаимодействующими частицами должны быть равны друг другу и направлены противоположно, поскольку для любой оси плечи их будут одинаковы. Поэтому все внутренние моменты сил взаимно сокращаются и получается замечательная теорема: скорость изменения момента количества движения относительно любой оси равна моменту внешних сил относительно этой же оси!
![]() . (18.19)
. (18.19)
Итак, мы получили в руки мощную теорему о движении большого коллектива частиц, которая позволяет нам изучать общие свойства движения, не зная деталей его внутреннего механизма. Эта теорема верна для любого набора частиц, независимо от того, образуют ли они твердое тело или нет.
Особенно важным частным случаем этой теоремы является закон сохранения момента количества движения, который гласит: если на систему частиц не действуют никакие внешние моменты сил, то ее момент количества движения остается постоянным.
Рассмотрим
один очень важный частный случай набора частиц, когда они образуют твердое
тело, т. е. объект, который всегда имеет определенную форму и геометрический
размер и может только крутиться вокруг какой-то оси. Любая часть такого объекта
в любой момент времени расположена одинаковым образом относительно других его
частей. Попытаемся теперь найти полный момент количества движения твердого
тела. Если масса ![]() -й
частицы его равна
-й
частицы его равна ![]() , а положение ее
, а положение ее ![]() , то задача сводится к
определению момента количества движения этой частицы, поскольку полный момент
количества движения равен сумме моментов количества движения всех таких частиц,
образующих тело. Для движущейся по окружности точки момент количества движения
равен, конечно, произведению ее массы на скорость и на расстояние до оси
вращения, а скорость в свою очередь равна угловой скорости, умноженной на
расстояние до оси:
, то задача сводится к
определению момента количества движения этой частицы, поскольку полный момент
количества движения равен сумме моментов количества движения всех таких частиц,
образующих тело. Для движущейся по окружности точки момент количества движения
равен, конечно, произведению ее массы на скорость и на расстояние до оси
вращения, а скорость в свою очередь равна угловой скорости, умноженной на
расстояние до оси:
![]() . (18.20)
. (18.20)
Суммируя
![]() ; для
всех частиц, получаем
; для
всех частиц, получаем
![]() , (18.21)
, (18.21)
где
![]() . (18.22)
. (18.22)
Это
выражение очень похоже на формулу для импульса, который равен произведению
массы на скорость. Скорость при этом заменяется на угловую скорость, а масса,
как видите, заменяется на некоторую новую величину, называемую моментом инерции
![]() . Вот
что играет роль массы при вращении! Уравнения (18.21) и (18.22) говорят нам,
что инерция вращения тела зависит не только от масс составляющих его частичек,
но и от того, насколько далеко расположены они от оси. Так что если мы имеем
два тела равной массы, но в одном из них массы расположены дальше от оси, то
его инерция вращения будет больше. Это легко продемонстрировать на устройстве,
изображенном на фиг. 18.4. Масса
. Вот
что играет роль массы при вращении! Уравнения (18.21) и (18.22) говорят нам,
что инерция вращения тела зависит не только от масс составляющих его частичек,
но и от того, насколько далеко расположены они от оси. Так что если мы имеем
два тела равной массы, но в одном из них массы расположены дальше от оси, то
его инерция вращения будет больше. Это легко продемонстрировать на устройстве,
изображенном на фиг. 18.4. Масса ![]() в этом устройстве не может падать
слишком быстро, потому что она должна крутить тяжелый стержень. Расположим
сначала массы
в этом устройстве не может падать
слишком быстро, потому что она должна крутить тяжелый стержень. Расположим
сначала массы ![]() около
оси вращения, причем грузик
около
оси вращения, причем грузик ![]() будет как-то ускоряться. Однако
после того, как мы изменим момент инерции, расположив массы
будет как-то ускоряться. Однако
после того, как мы изменим момент инерции, расположив массы ![]() гораздо дальше от оси, мы
увидим, что грузик
гораздо дальше от оси, мы
увидим, что грузик ![]() ускоряется гораздо медленнее, чем
прежде. Происходит это вследствие возрастания инертности вращения, которая
составляет физический смысл момента инерции - суммы произведений всех масс на
квадраты их расстояний от оси вращения.
ускоряется гораздо медленнее, чем
прежде. Происходит это вследствие возрастания инертности вращения, которая
составляет физический смысл момента инерции - суммы произведений всех масс на
квадраты их расстояний от оси вращения.

Фиг. 18.4. Зависимость инерции вращения от плеча масс.
Между
массой и моментом инерции имеется существенная разница, которая проявляется
удивительным образом. Дело в том, что масса объекта обычно не изменяется, тогда
как момент инерции легко изменить. Представьте себе, что вы встали на стол,
который может вращаться без трения, и держите в вытянутых руках гантели, а сами
медленно вращаетесь. Можно легко изменить момент инерции, согнув руки; при этом
наша масса останется той же самой. Когда мы проделаем все это, то закон
сохранения момента количества движения будет творить чудеса, произойдет нечто
удивительное. Если моменты внешних сил равны нулю, то момент количества
движения равен моменту инерции ![]() , умноженному на угловую скорость
, умноженному на угловую скорость ![]() , т. е. ваш момент
количества движения равен
, т. е. ваш момент
количества движения равен ![]() . Согнув затем руки, вы тем самым
уменьшили момент инерции до величины
. Согнув затем руки, вы тем самым
уменьшили момент инерции до величины ![]() . Но поскольку из-за закона сохранения
момента количества движения произведение
. Но поскольку из-за закона сохранения
момента количества движения произведение ![]() должно остаться тем же самым, то
должно остаться тем же самым, то ![]() должно быть равно
должно быть равно
![]() . Так
что если вы уменьшили момент инерции, то ваша угловая скорость в результате
этого должна возрасти.
. Так
что если вы уменьшили момент инерции, то ваша угловая скорость в результате
этого должна возрасти.
| << Предыдущий параграф | Следующий параграф >> |
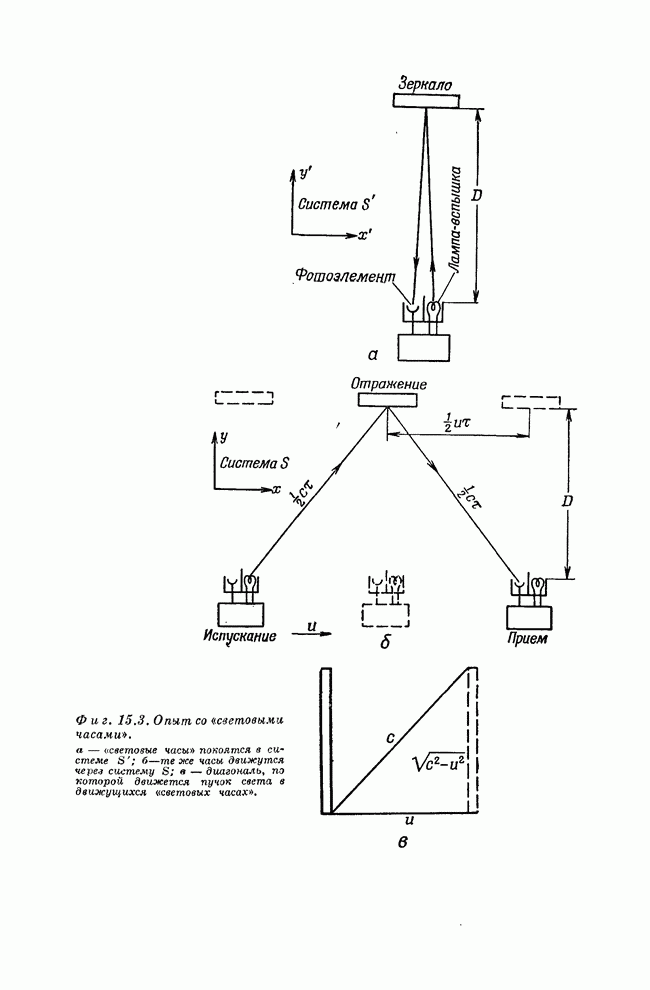
- Глава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 1. Принцип относительности
- § 2. Преобразование Лоренца
- § 3. Опыт Майкельсона-Морли
- § 4. Преобразование времени
- § 5. Лоренцево сокращение
- § 6. Одновременность
- § 7. Четырехвекторы
- § 8. Релятивистская динамика
- § 9. Связь массы и энергии
- Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС
- § 1. Относительность и «философы»
- § 2. Парадокс близнецов
- § 3. Преобразование скоростей
- § 4. Релятивистская масса
- § 5. Релятивистская энергия
- Глава 17. ПРОСТРАНСТВО-ВРЕМЯ
- § 1. Геометрия пространства-времени
- § 2. Пространственно-временные интервалы
- § 3. Прошедшее, настоящее, будущее
- § 4. Еще о четырехвекторах
- § 5. Алгебра четырехвекторов
- Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ
- § 1. Центр масс
- § 2. Вращение твердого тела
- § 3. Момент количества движения
- § 4. Закон сохранения момента количества движения
- Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ
- § 1. Свойства центра масс
- § 2. Положение центра масс
- § 3. Вычисление момента инерции
- § 4. Кинетическая энергия вращения
- Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ
- § 1. Моменты сил в трехмерном пространстве
- § 2. Уравнения вращения в векторном виде
- § 3. Гироскоп
- § 4. Момент количества движения твердого тела
- Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- § 1. Линейные дифференциальные уравнения
- § 2. Гармонический осциллятор
- § 3. Гармоническое движение и движение по окружности
- § 4. Начальные условия
- § 5. Колебания под действием внешней силы
- Глава 22. АЛГЕБРА
- § 1. Сложение и умножение
- § 2. Обратные операции
- § 3. Шаг в сторону и обобщение
- § 4. Приближенное вычисление иррациональных чисел
- § 5. Комплексные числа
- § 6. Мнимые экспоненты
- Глава 23. РЕЗОНАНС
- § 1. Комплексные числа и гармоническое движение
- § 2. Вынужденные колебания с торможением
- § 3. Электрический резонанс
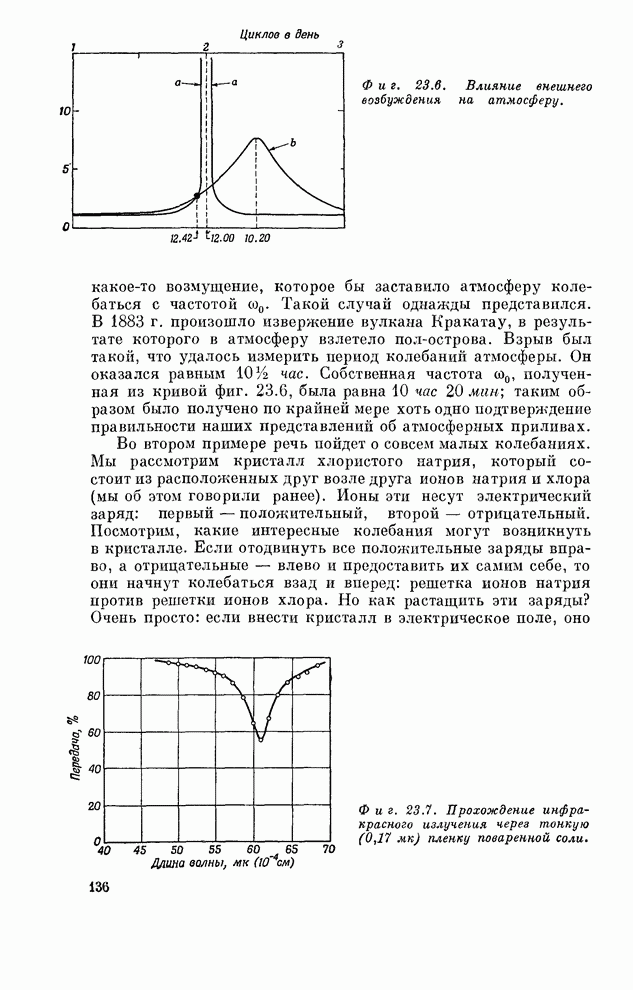
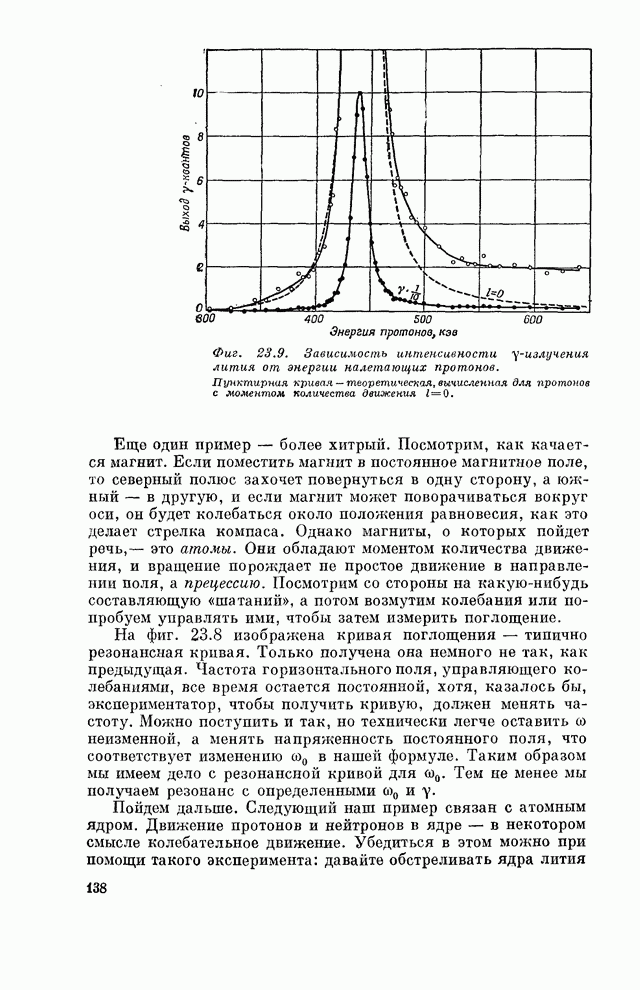
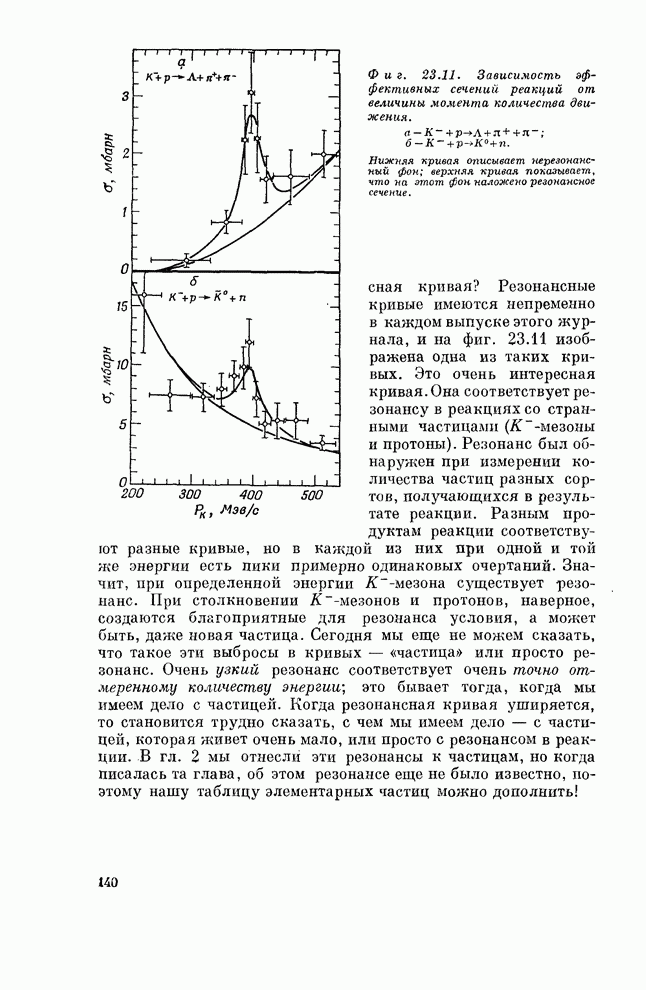
- § 4. Резонанс в природе
- Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ
- § 1. Энергия осциллятора
- § 2. Затухающие колебания
- § 3. Переходные колебания в электрических цепях
- Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР
- § 1. Линейные дифференциальные уравнения
- § 2. Суперпозиция решений
- § 3. Колебания в линейных системах
- § 4. Аналогии в физике
- § 5. Последовательные и параллельные сопротивления