| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Резонанс в природе
Хотя мы детально разобрали вопрос о резонансе в электрических цепях, можно приводить пример за примером из любых наук и отыскивать в них резонансные кривые. В природе очень часто что-нибудь «колеблется» и так же часто наступает резонанс. Об этом уже говорилось в одной из предыдущих глав; приведем теперь некоторые примеры. Зайдите в библиотеку, возьмите с полки несколько книг, полистайте их; вы обнаружите кривые, похожие на кривые фиг. 23.2, и уравнения, похожие на уравнения, приведенные в этой главе. Много ли найдется таких книг? Для убедительности возьмем всего пять-шесть книг, и они обеспечат вас полным набором примеров резонансов.
Первые
два относятся к механике. Самый первый грандиозен - речь идет о колебаниях
атмосферы. Если бы атмосфера, которая, по нашим представлениям, шарообразна и
обволакивает нашу Землю равномерно со всех сторон, под влиянием Луны вытянулась
бы в одну сторону, то атмосфера приняла бы форму вытянутой дыни. Если
предоставить атмосферу, имеющую форму дыни, самой себе, то возникнут колебания.
Так получается осциллятор. Этими колебаниями управляет Луна, которая вращается
вокруг Земли. Чтобы понять, как это происходит, представим себе, что Луна стоит
неподвижно на каком-то расстоянии от Земли, а Земля вращается вокруг своей оси.
Поэтому проекция силы, скажем, на ось ![]() имеет периодическую составляющую.
Отклик атмосферы на приливно-отливные толчки Луны будет обычным откликом
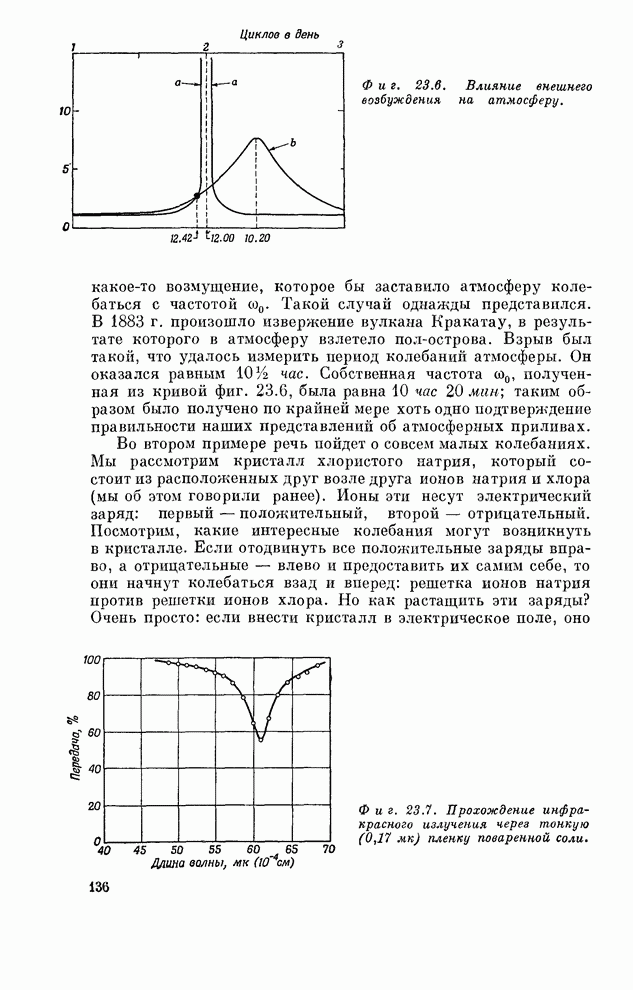
осциллятора на периодическую силу. Кривая b на фиг. 23.6 изображает ожидаемый отклик атмосферы
(кривая a приведена на заимствованном нами
рисунке из книги Мунка и Мак-Дональда по другому поводу и нас не касается).
Может показаться странным, что удалось начертить эту кривую: ведь Земля
вращается с постоянной скоростью, и поэтому можно получить только одну точку на
кривой - точку, приблизительно соответствующую периоду 12 - 12,7 час (приливы
бывают дважды в сутки) плюс еще немного, потому что надо учесть движение Луны.
Но, измеряя величину атмосферных приливов и время их задержки - фазу, можно
найти обе характеристики отклика
имеет периодическую составляющую.
Отклик атмосферы на приливно-отливные толчки Луны будет обычным откликом
осциллятора на периодическую силу. Кривая b на фиг. 23.6 изображает ожидаемый отклик атмосферы
(кривая a приведена на заимствованном нами
рисунке из книги Мунка и Мак-Дональда по другому поводу и нас не касается).
Может показаться странным, что удалось начертить эту кривую: ведь Земля
вращается с постоянной скоростью, и поэтому можно получить только одну точку на
кривой - точку, приблизительно соответствующую периоду 12 - 12,7 час (приливы
бывают дважды в сутки) плюс еще немного, потому что надо учесть движение Луны.
Но, измеряя величину атмосферных приливов и время их задержки - фазу, можно
найти обе характеристики отклика ![]() и
и ![]() . По ним можно вычислить
. По ним можно вычислить ![]() и
и ![]() , а затем
начертить уже всю кривую! Вот пример чистой науки. Из двух чисел получают два
числа, по этим двум числам чертят очень красивую кривую, которая, конечно,
проходит через ту же точку, по которой построена кривая! Кривая эта, конечно,
бесполезна, пока нельзя измерить еще чего-нибудь, а в геофизике сделать это
зачастую очень трудно. В нашем случае тем, что нужно было бы еще измерить,
могут служить колебания атмосферы с собственной частотой
, а затем
начертить уже всю кривую! Вот пример чистой науки. Из двух чисел получают два
числа, по этим двум числам чертят очень красивую кривую, которая, конечно,
проходит через ту же точку, по которой построена кривая! Кривая эта, конечно,
бесполезна, пока нельзя измерить еще чего-нибудь, а в геофизике сделать это
зачастую очень трудно. В нашем случае тем, что нужно было бы еще измерить,
могут служить колебания атмосферы с собственной частотой ![]() ; необходимо какое-то
возмущение, которое бы заставило атмосферу колебаться с частотой
; необходимо какое-то
возмущение, которое бы заставило атмосферу колебаться с частотой ![]() . Такой случай
однажды представился. В 1883 г. произошло извержение вулкана Кракатау, в
результате которого в атмосферу взлетело пол-острова. Взрыв был такой, что
удалось измерить период колебаний атмосферы. Он оказался равным 10½ час.
Собственная частота
. Такой случай
однажды представился. В 1883 г. произошло извержение вулкана Кракатау, в
результате которого в атмосферу взлетело пол-острова. Взрыв был такой, что
удалось измерить период колебаний атмосферы. Он оказался равным 10½ час.
Собственная частота ![]() , полученная из кривой фиг. 23.6,
была равна 10 час 20 мин; таким образом было получено по крайней мере хоть одно
подтверждение правильности наших представлений об атмосферных приливах.
, полученная из кривой фиг. 23.6,
была равна 10 час 20 мин; таким образом было получено по крайней мере хоть одно
подтверждение правильности наших представлений об атмосферных приливах.

Фиг. 23.6. Влияние внешнего возбуждения на атмосферу.
Во втором примере речь пойдет о совсем малых колебаниях. Мы рассмотрим кристалл хлористого натрия, который состоит из расположенных друг возле друга ионов натрия и хлора (мы об этом говорили ранее). Ионы эти несут электрический заряд: первый - положительный, второй - отрицательный. Посмотрим, какие интересные колебания могут возникнуть в кристалле. Если отодвинуть все положительные заряды вправо, а отрицательные - влево и предоставить их самим себе, то они начнут колебаться взад и вперед: решетка ионов натрия против решетки ионов хлора. Но как растащить эти заряды? Очень просто: если внести кристалл в электрическое поле, оно отодвинет положительные заряды в одну сторону, а отрицательные - в другую! Значит, имея внешнее электрическое поле, можно, пожалуй, вызвать колебания кристалла. Но для этого частота электрического поля должна быть столь большой, что она соответствует инфракрасному излучению! Таким образом попытаемся построить резонансную кривую, измеряя поглощение инфракрасного света хлористым натрием. Такая кривая изображена на фиг. 23.7. По абсциссе отложена не частота, а длина волны, но это техническая деталь; между частотой и длиной волны существует строго определенное соотношение, так что мы все-таки имеем дело со шкалой частот, и одна из этих частот - резонансная частота.
Ну,
а что можно сказать о ширине резонансной кривой? Чем эта ширина определяется?
Очень часто кривая выглядит гораздо шире, чем ей предписывается теоретическим
значением ![]() (эта
ширина называется естественной шириной). Есть две причины уширения резонансной
кривой. Мы наблюдаем колебания многих осцилляторов сразу, а их частоты могут
немного отличаться. К этому приводят, например, натяжения в отдельных частях
кристалла. Поэтому мы видим сразу много резонансных кривых, проходящих рядом.
Они сливаются в одну кривую с большей шириной. Вторая причина очень проста - не
всегда можно точно измерить частоту. Сколько со спектрометром ни возись, он
всегда зарегистрирует не одну частоту, а целый спектр частот
(эта
ширина называется естественной шириной). Есть две причины уширения резонансной
кривой. Мы наблюдаем колебания многих осцилляторов сразу, а их частоты могут
немного отличаться. К этому приводят, например, натяжения в отдельных частях
кристалла. Поэтому мы видим сразу много резонансных кривых, проходящих рядом.
Они сливаются в одну кривую с большей шириной. Вторая причина очень проста - не
всегда можно точно измерить частоту. Сколько со спектрометром ни возись, он
всегда зарегистрирует не одну частоту, а целый спектр частот ![]() . Поэтому может
оказаться, что разрешающая сила спектрометра недостаточна для определения
точной формы кривой. Так или иначе, но, глядя на фиг. 23.7, трудно сказать, что
там за ширина - естественная или та, что соответствует неоднородностям
кристалла или разрешающей силе спектрометра .
. Поэтому может
оказаться, что разрешающая сила спектрометра недостаточна для определения
точной формы кривой. Так или иначе, но, глядя на фиг. 23.7, трудно сказать, что
там за ширина - естественная или та, что соответствует неоднородностям
кристалла или разрешающей силе спектрометра .

Фиг. 23.7. Прохождение инфракрасного излучения через тонкую (0,17 мк) пленку поваренной соли.
Еще один пример - более хитрый. Посмотрим, как качается магнит. Если поместить магнит в постоянное магнитное поле, то северный полюс захочет повернуться в одну сторону, а южный - в другую, и если магнит может поворачиваться вокруг оси, он будет колебаться около положения равновесия, как это делает стрелка компаса. Однако магниты, о которых пойдет речь,- это атомы. Они обладают моментом количества движения, и вращение порождает не простое движение в направлении поля, а прецессию. Посмотрим со стороны на какую-нибудь составляющую «шатаний», а потом возмутим колебания или попробуем управлять ими, чтобы затем измерить поглощение.
На
фиг. 23.8 изображена кривая поглощения - типично резонансная кривая. Только
получена она немного не так, как предыдущая. Частота горизонтального поля,
управляющего колебаниями, все время остается постоянной, хотя, казалось бы,
экспериментатор, чтобы получить кривую, должен менять частоту. Можно поступить
и так, но технически легче оставить ![]() неизменной, а менять напряженность
постоянного поля, что соответствует изменению
неизменной, а менять напряженность
постоянного поля, что соответствует изменению ![]() в нашей формуле. Таким образом мы
имеем дело с резонансной кривой для
в нашей формуле. Таким образом мы
имеем дело с резонансной кривой для ![]() . Тем не менее мы получаем резонанс с
определенными
. Тем не менее мы получаем резонанс с
определенными ![]() и
и
![]() .
.

Фиг. 23.8. Зависимость потери магнитной энергии в парамагнитном органическом соединении от напряженности приложенного поля.
Пойдем
дальше. Следующий наш пример связан с атомным ядром. Движение протонов и
нейтронов в ядре - в некотором смысле колебательное движение. Убедиться в этом
можно при помощи такого эксперимента: давайте обстреливать ядра лития
протонами. Мы обнаружим, что в ядрах при этом будут происходить какие-то
реакции, в результате которых возникает ![]() -излучение. Кривая, изображающая
количество испущенного излучения, имеет очень острый, типично резонансный
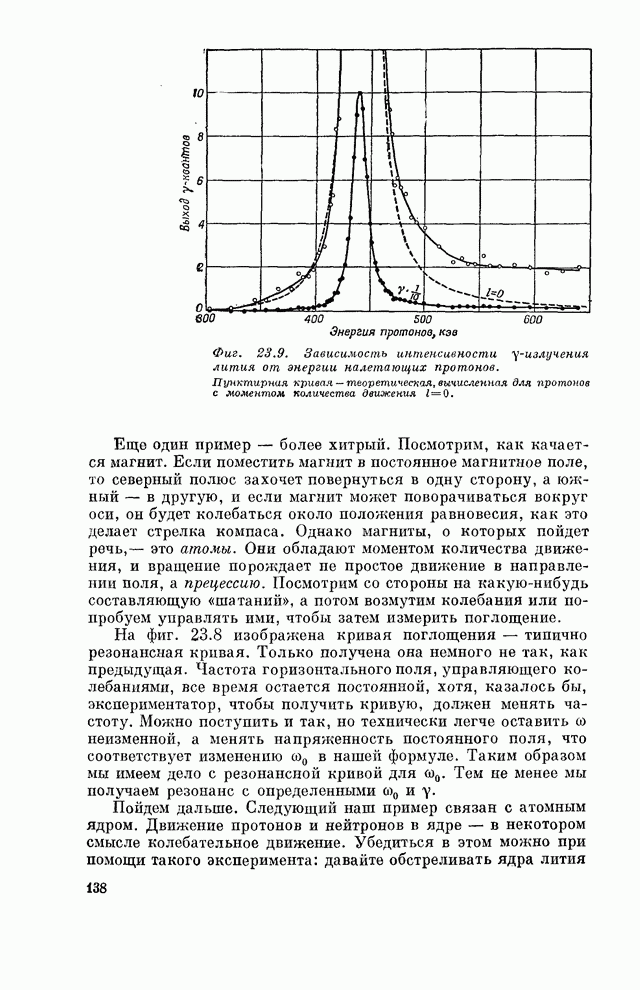
максимум. Это изображено на фиг. 23.9. Однако приглядитесь к рисунку
повнимательнее: на горизонтальной шкале отложена не частота, как обычно, а
энергия! Дело в том, что та величина, которую в классической физике мы привыкли
считать энергией, в квантовой механике оказывается определенным образом
связанной с частотой некоторой волны. Если в привычной нам крупномасштабной
физике при анализе какого-нибудь явления приходится иметь дело с частотой, то в
квантовомеханических явлениях, связанных с атомным веществом, аналогичные
кривые будут зависеть от энергии. Кривая на фиг. 23.9 иллюстрирует эту связь.
Размышляя над этой кривой, можно прийти к мысли, что частота и энергия имеют
глубокую взаимосвязь; так оно и есть на самом деле.
-излучение. Кривая, изображающая
количество испущенного излучения, имеет очень острый, типично резонансный
максимум. Это изображено на фиг. 23.9. Однако приглядитесь к рисунку
повнимательнее: на горизонтальной шкале отложена не частота, как обычно, а
энергия! Дело в том, что та величина, которую в классической физике мы привыкли
считать энергией, в квантовой механике оказывается определенным образом
связанной с частотой некоторой волны. Если в привычной нам крупномасштабной
физике при анализе какого-нибудь явления приходится иметь дело с частотой, то в
квантовомеханических явлениях, связанных с атомным веществом, аналогичные
кривые будут зависеть от энергии. Кривая на фиг. 23.9 иллюстрирует эту связь.
Размышляя над этой кривой, можно прийти к мысли, что частота и энергия имеют
глубокую взаимосвязь; так оно и есть на самом деле.

Фиг. 23.9. Зависимость
интенсивности ![]() -излучения
лития от энергии налетающих протонов. Пунктирная кривая - теоретическая,
вычисленная для протонов с моментом количества движения
-излучения
лития от энергии налетающих протонов. Пунктирная кривая - теоретическая,
вычисленная для протонов с моментом количества движения ![]() .
.
Вот
еще одна резонансная кривая, полученная в результате опытов с атомными ядрами;
она очень узкая, уже всех предыдущих. На фиг. 23.10 величина ![]() соответствует
энергии 10000 эв, а ширина
соответствует
энергии 10000 эв, а ширина ![]() равна приблизительно
равна приблизительно ![]() эв; иначе говоря,
эв; иначе говоря,
![]() !
Построив такую кривую, экспериментатор измерил
!
Построив такую кривую, экспериментатор измерил ![]() самого добротного из ныне известных
осцилляторов. Это проделал Р. Мёссбауэр, получивший за свои работы Нобелевскую
премию. На горизонтальной шкале отложена скорость, потому что для сдвига
частоты использовался эффект Допплера, получающийся в результате относительного
движения источника и поглотителя. Цифры дают некоторое представление о тонкости
эксперимента - пришлось измерять скорости в несколько сантиметров в секунду!
Если продолжить горизонтальную шкалу влево, то нулевую частоту мы найдем на
расстоянии
самого добротного из ныне известных
осцилляторов. Это проделал Р. Мёссбауэр, получивший за свои работы Нобелевскую
премию. На горизонтальной шкале отложена скорость, потому что для сдвига
частоты использовался эффект Допплера, получающийся в результате относительного
движения источника и поглотителя. Цифры дают некоторое представление о тонкости
эксперимента - пришлось измерять скорости в несколько сантиметров в секунду!
Если продолжить горизонтальную шкалу влево, то нулевую частоту мы найдем на
расстоянии ![]() см!
Страницы для этого, пожалуй, не хватит!
см!
Страницы для этого, пожалуй, не хватит!

Фиг. 23.10. Кривая поглощения ![]() -излучения,
полученная Р. Мессбауэром.
-излучения,
полученная Р. Мессбауэром.
Наконец,
возьмем какой-нибудь выпуск журнала Physical Review, скажем, за 1 января 1962
г. Найдется ли в нем резонансная кривая? Резонансные кривые имеются непременно
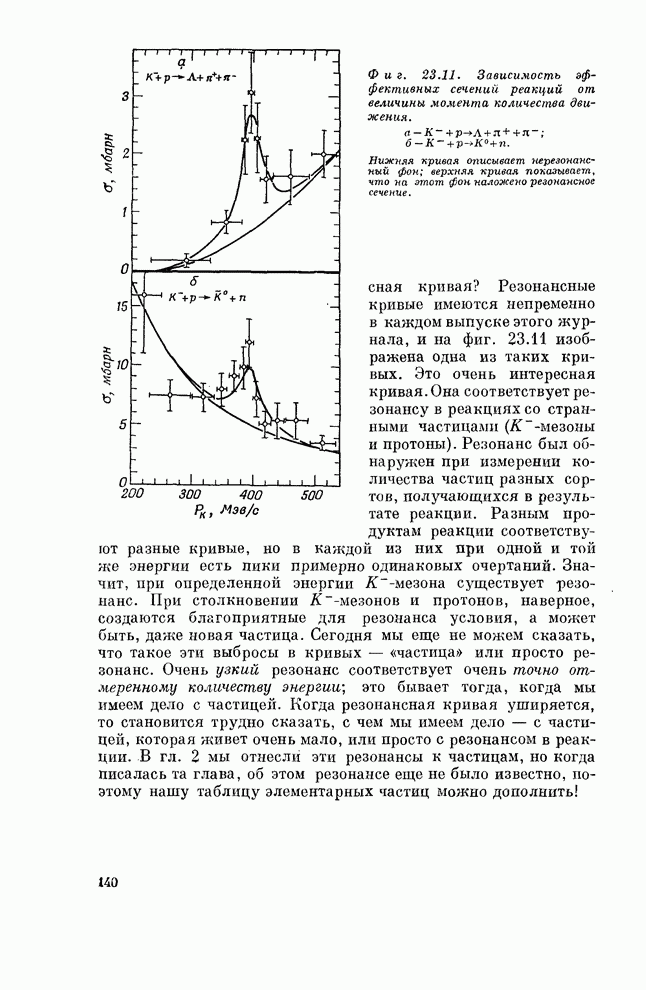
в каждом выпуске этого журнала, и на фиг. 23.11 изображена одна из таких
кривых. Это очень интересная кривая.Она соответствует резонансу в реакциях со
странными частицами (![]() -мезоны и протоны). Резонанс был
обнаружен при измерении количества частиц разных сортов, получающихся в
результате реакции. Разным продуктам реакции соответствуют разные кривые, но в
каждой из них при одной и той же энергии есть пики примерно одинаковых очертаний.
Значит, при определенной энергии
-мезоны и протоны). Резонанс был
обнаружен при измерении количества частиц разных сортов, получающихся в
результате реакции. Разным продуктам реакции соответствуют разные кривые, но в
каждой из них при одной и той же энергии есть пики примерно одинаковых очертаний.
Значит, при определенной энергии ![]() -мезона существует резонанс. При
столкновении
-мезона существует резонанс. При
столкновении ![]() -мезонов
и протонов, наверное, создаются благоприятные для резонанса условия, а может
быть, даже новая частица. Сегодня мы еще не можем сказать, что такое эти
выбросы в кривых - «частица» или просто резонанс. Очень узкий резонанс
соответствует очень точно отмеренному количеству энергии; это бывает тогда,
когда мы имеем дело с частицей. Когда резонансная кривая уширяется, то
становится трудно сказать, с чем мы имеем дело - с частицей, которая живет
очень мало, или просто с резонансом в реакции. В гл. 2 мы отнесли эти резонансы
к частицам, но когда писалась та глава, об этом резонансе еще не было известно,
поэтому нашу таблицу элементарных частиц можно дополнить!
-мезонов
и протонов, наверное, создаются благоприятные для резонанса условия, а может
быть, даже новая частица. Сегодня мы еще не можем сказать, что такое эти
выбросы в кривых - «частица» или просто резонанс. Очень узкий резонанс
соответствует очень точно отмеренному количеству энергии; это бывает тогда,
когда мы имеем дело с частицей. Когда резонансная кривая уширяется, то
становится трудно сказать, с чем мы имеем дело - с частицей, которая живет
очень мало, или просто с резонансом в реакции. В гл. 2 мы отнесли эти резонансы
к частицам, но когда писалась та глава, об этом резонансе еще не было известно,
поэтому нашу таблицу элементарных частиц можно дополнить!

Фиг. 23.11. Зависимость эффективных сечении реакций от величины момента количества движения.

Нижняя кривая описывает нерезонансный фон; верхняя кривая показывает, что на этот фон наложено резонансное сечение.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
- § 1. Принцип относительности
- § 2. Преобразование Лоренца
- § 3. Опыт Майкельсона-Морли
- § 4. Преобразование времени
- § 5. Лоренцево сокращение
- § 6. Одновременность
- § 7. Четырехвекторы
- § 8. Релятивистская динамика
- § 9. Связь массы и энергии
- Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС
- § 1. Относительность и «философы»
- § 2. Парадокс близнецов
- § 3. Преобразование скоростей
- § 4. Релятивистская масса
- § 5. Релятивистская энергия
- Глава 17. ПРОСТРАНСТВО-ВРЕМЯ
- § 1. Геометрия пространства-времени
- § 2. Пространственно-временные интервалы
- § 3. Прошедшее, настоящее, будущее
- § 4. Еще о четырехвекторах
- § 5. Алгебра четырехвекторов
- Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ
- § 1. Центр масс
- § 2. Вращение твердого тела
- § 3. Момент количества движения
- § 4. Закон сохранения момента количества движения
- Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ
- § 1. Свойства центра масс
- § 2. Положение центра масс
- § 3. Вычисление момента инерции
- § 4. Кинетическая энергия вращения
- Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ
- § 1. Моменты сил в трехмерном пространстве
- § 2. Уравнения вращения в векторном виде
- § 3. Гироскоп
- § 4. Момент количества движения твердого тела
- Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- § 1. Линейные дифференциальные уравнения
- § 2. Гармонический осциллятор
- § 3. Гармоническое движение и движение по окружности
- § 4. Начальные условия
- § 5. Колебания под действием внешней силы
- Глава 22. АЛГЕБРА
- § 1. Сложение и умножение
- § 2. Обратные операции
- § 3. Шаг в сторону и обобщение
- § 4. Приближенное вычисление иррациональных чисел
- § 5. Комплексные числа
- § 6. Мнимые экспоненты
- Глава 23. РЕЗОНАНС
- § 1. Комплексные числа и гармоническое движение
- § 2. Вынужденные колебания с торможением
- § 3. Электрический резонанс
- § 4. Резонанс в природе
- Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ
- § 1. Энергия осциллятора
- § 2. Затухающие колебания
- § 3. Переходные колебания в электрических цепях
- Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР
- § 1. Линейные дифференциальные уравнения
- § 2. Суперпозиция решений
- § 3. Колебания в линейных системах
- § 4. Аналогии в физике
- § 5. Последовательные и параллельные сопротивления