| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.2. КОНДЕНСАЦИОННЫЙ И КОАГУЛЯЦИОННЫЙ РОСТ КАПЕЛЬ В ОБЛАКАХ
Уже в мощных кучевых облаках встречаются крупные капли радиусом до 50-100 мкм, а в кучево-дождевых облаках наблюдаются значительно большие капли и ледяные частицы. Рост частиц в облаках определяется двумя механизмами — конденсацией или сублимацией водяного пара и коагуляцией.
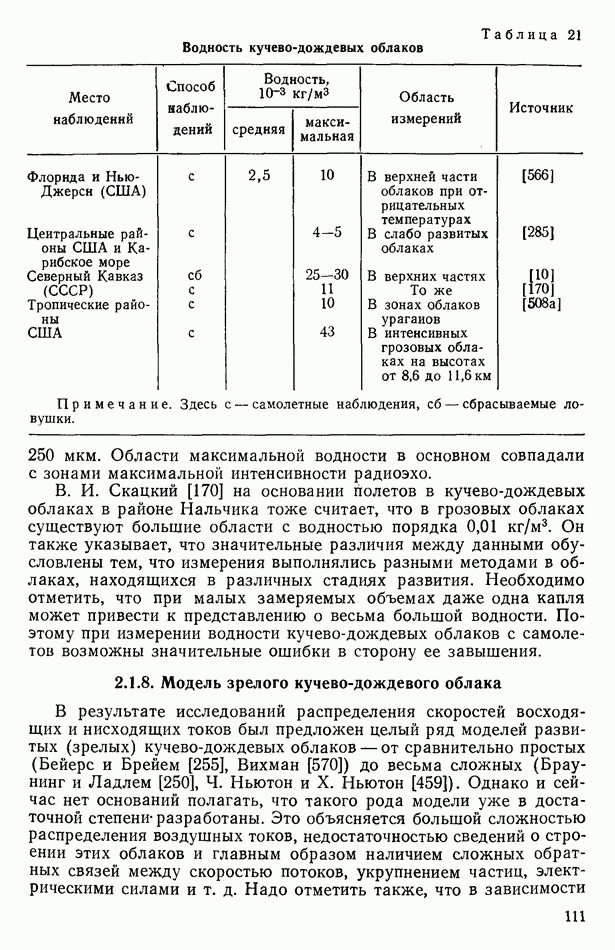
Бест [230] произвел расчеты скорости роста капельки для температуры воздуха 273 К и давления  Он получил, что при конденсации водяного пара на сравнительно больших ядрах рост капелек радиусом от 0,75 до 1-2 мкм происходит весьма быстро, за доли секунды. В этих пределах капельки являются достаточно концентрированными растворами, что и является причиной понижения равновесной упругости пара и интенсивной конденсации водяного пара. Но при дальнейшем росте концентрация раствора играет малую роль. Для ядер конденсации с массой
Он получил, что при конденсации водяного пара на сравнительно больших ядрах рост капелек радиусом от 0,75 до 1-2 мкм происходит весьма быстро, за доли секунды. В этих пределах капельки являются достаточно концентрированными растворами, что и является причиной понижения равновесной упругости пара и интенсивной конденсации водяного пара. Но при дальнейшем росте концентрация раствора играет малую роль. Для ядер конденсации с массой  время роста капелек до радиуса 15 мкм составляет почти 50 мин. Следовательно, в быстро развивающихся конвективных облаках образование облачных капелек радиусом более 10 мкм нельзя объяснить конденсацией водяного пара. Расчеты показали, что электрические силы могут влиять на скорость конденсационного роста капелек радиусом не более 1 мкм.
время роста капелек до радиуса 15 мкм составляет почти 50 мин. Следовательно, в быстро развивающихся конвективных облаках образование облачных капелек радиусом более 10 мкм нельзя объяснить конденсацией водяного пара. Расчеты показали, что электрические силы могут влиять на скорость конденсационного роста капелек радиусом не более 1 мкм.
Предпринимались попытки более точно вычислить скорость конденсационного роста капель в условиях пересыщения водяного пара, в частности И. П. Мазиным [110], В. И. Смирновым [171] и др.; результаты этих расчетов не изменили вывода, сделанного на основании вычислений Беста. В дальнейшем привлекались представления о влиянии на конденсационный рост размеров ядер конденсации, в особенности «гигантских», и пульсаций пересыщения в облаках, а также представление о коагуляционном росте капель.
Процесс коагуляции капелек состоит из их сближения под действием каких-либо сил и слияния. К коагуляции капелек могут привести гравитационные, гидродинамические и электрические силы, а также турбулентность воздуха и броуновское движение.
Рассмотрим коагуляцию двух капель, падающих в неподвижном воздухе под действием гравитационных сил. Капля с большим радиусом  имеющая большую скорость падения,
имеющая большую скорость падения,
догонит меньшую каплю радиусом  и при соударении может с ней слиться. Такая задача была решена Лэнгмюром [109], у которого большая неподвижная капля обтекается воздушным потоком с капельками. Вдали от капли капельки движутся со скоростью потока V, соответствующей скорости падения капли радиусом
и при соударении может с ней слиться. Такая задача была решена Лэнгмюром [109], у которого большая неподвижная капля обтекается воздушным потоком с капельками. Вдали от капли капельки движутся со скоростью потока V, соответствующей скорости падения капли радиусом  Вблизи капли происходит ее обтекание потоком воздуха, который только частично увлекает за собой капельки. Часть капелек вследствие инерции попадает на поверхность капли. Размеры капелек не учитывались.
Вблизи капли происходит ее обтекание потоком воздуха, который только частично увлекает за собой капельки. Часть капелек вследствие инерции попадает на поверхность капли. Размеры капелек не учитывались.

Рис. 4. Соударение капельки радиусом  с каплей радиусом
с каплей радиусом 
Для определения вероятности соударения капелек с крупной каплей Лэнгмюр использовал понятие о коэффициенте соударения как отношении числа капелек, которые соударялись с каплей, к числу капелек, которые соударялись бы с каплей, если бы не было отклоняющего действия потока. Как видно из рис. 4, число капелек, которые могут соудариться с каплей, пропорционально  а число капелек, действительно соударяющихся с каплей, пропорционально
а число капелек, действительно соударяющихся с каплей, пропорционально  расстояние критической траектории капелек на бесконечности от оси, проходящей через центр капли). Капельки, лежащие вне этой траектории, не соударяются с каплей. Следовательно,
расстояние критической траектории капелек на бесконечности от оси, проходящей через центр капли). Капельки, лежащие вне этой траектории, не соударяются с каплей. Следовательно,

Если число Рейнольдса, соответствующее капле радиусом  меньше единицы, то силы вязкости будут определяющими вблизи капли и движение капелек будет подчиняться закону Стокса. Для этого случая Лэнгмюр, учитывая скорость
меньше единицы, то силы вязкости будут определяющими вблизи капли и движение капелек будет подчиняться закону Стокса. Для этого случая Лэнгмюр, учитывая скорость  падения капелек радиусом
падения капелек радиусом  получил выражение для коэффициента соударения
получил выражение для коэффициента соударения

где

Здесь  соответственно плотность воды и воздуха;
соответственно плотность воды и воздуха;  кинематическая вязкость воздуха;
кинематическая вязкость воздуха;  число Стокса.
число Стокса.
Из (10) вытекает, что существует некоторое критическое значение  При
При  Это означает, что капельки радиусом
Это означает, что капельки радиусом  и меньше не соударяются с каплей радиусом
и меньше не соударяются с каплей радиусом  а увлекаются потоком. Общая теория, позволяющая определить
а увлекаются потоком. Общая теория, позволяющая определить  в зависимости от условий обтекания, была разработана
в зависимости от условий обтекания, была разработана  Левиным [100, 102, 103].
Левиным [100, 102, 103].
Для значительно больших капель, например дождевых  инерция превалирует над силами вязкости, и поэтому течение вокруг капли можно считать потенциальным, т. е. соответствующим потоку идеальной жидкости без трения. Но при этом учитывается влияние сил вязкости на капельки. Для такого случая Лэнгмюр получил выражение
инерция превалирует над силами вязкости, и поэтому течение вокруг капли можно считать потенциальным, т. е. соответствующим потоку идеальной жидкости без трения. Но при этом учитывается влияние сил вязкости на капельки. Для такого случая Лэнгмюр получил выражение

Выражение (12) оправдывается при значениях  причем
причем  Для значений
Для значений  равных и меньших
равных и меньших 
Из (11) следует, что при  выражение (10) оказывается непригодным при рассмотрении соударения капелек сопоставимых размеров. Для этого случая необходимо учесть размеры капелек и гидродинамические силы взаимодействия потоков, обтекающих капли. Учет размеров капелек при вычислениях коэффициента соударения был выполнен Н. А. Фуксом [189], Н. С. Шишкиным [200], Мейсоном [115] и др.
выражение (10) оказывается непригодным при рассмотрении соударения капелек сопоставимых размеров. Для этого случая необходимо учесть размеры капелек и гидродинамические силы взаимодействия потоков, обтекающих капли. Учет размеров капелек при вычислениях коэффициента соударения был выполнен Н. А. Фуксом [189], Н. С. Шишкиным [200], Мейсоном [115] и др.
С. В. Пшенай-Северин [160, 161] исследовал для двух случаев влияние взаимодействия малых капель близких размеров, находящихся на одной вертикальной оси, на скорость их падения. В первом случае учитываются только силы вязкости, силами инерции можно пренебречь (стоксовское обтекание); во втором случае силы вязкости и инерции сопоставимы по величине (осееновское обтекание). Пшенай-Северин обнаружил, что при осееновском обтекании возникают силы, зависящие от отношения радиуса капель к расстоянию между ними, которые увеличивают скорость сближения капель.
Пирс и Хилл [467] рассмотрели взаимодействие потоков капель в осееновском приближении. Они пришли к выводу, что в кильватере падающей капли возникает область пониженного давления. Это приводит к появлению турбулизированного течения сзади падающей капли. Для капель радиусом свыше 70 мкм наиболее вероятным является процесс засасывания меньших капель в след более крупных, что приводит к увеличению коэффициента соударения в 10—100 раз по сравнению с коэффициентом соударения, полученным из геометрических соображений.
Для капелек сопоставимых размеров с радиусами от 35 до 100 мкм Телфорд и др. [549], Вудс и Мейсон [580] и др. экспериментально подтвердили существование засасывания капелек меньших размеров в кильватерный след капель больших размеров. Телфорд и др. [549] для капелек радиусом 80 мкм (с учетом замечания Вудса и Мейсона [580] о коррекции значения коэффициента эффективности соударения) получили  Вудс и Мейсон обнаружили, что капельки радиусом до 35 мкм создают кильватерный след, который вызывает некоторое ускорение меньших капель, но этого ускорения недостаточно для их слияния с большей каплей.
Вудс и Мейсон обнаружили, что капельки радиусом до 35 мкм создают кильватерный след, который вызывает некоторое ускорение меньших капель, но этого ускорения недостаточно для их слияния с большей каплей.
Хокинг [339] считает, что выводы Пирса и Хилла неприменимы к каплям, находящимся на близких расстояниях. Он предпринял
вычисления на ЭВМ траекторий движения капель радиусом до 30 мкм, в том числе и капель близких размеров, находящихся на малых расстояниях друг от друга, в стоксовском приближении с учетом взаимодействия потоков капель (рис. 5). Из них вытекает, что нижняя граница радиусов капель, для которых возможна коагуляция, 18 мкм. Лэнгмюр [109] получил соответствующее граничное значение, равное 14,5 мкм; согласно же Пирсу и Хиллу, такое граничное значение вообще отсутствует.

Рис. 5. Зависимость коэффициента эффективности соударения К от отношения радиусов капель  По Хокингу [339]. Значения R (мкм): 1) 19, 2) 20, 3) 25, 4) 30.
По Хокингу [339]. Значения R (мкм): 1) 19, 2) 20, 3) 25, 4) 30.
Мейсон [579] выполнил интерполяцию между значениями коэффициентов соударения Хокинга для капель с  и Лэнгмюра для капель с 200 мкм для величин
и Лэнгмюра для капель с 200 мкм для величин  Данные для капель радиусом 60 и 100 мкм представлены на рис. 6. Здесь же приведены результаты вычислений Шафрира и Нейбургера [513] и данные экспериментальных исследований Вудса и Мейсона [579]. Экспериментальные данные хорошо совпадают с результатами вычислений Хокинга для капелек радиусом
Данные для капель радиусом 60 и 100 мкм представлены на рис. 6. Здесь же приведены результаты вычислений Шафрира и Нейбургера [513] и данные экспериментальных исследований Вудса и Мейсона [579]. Экспериментальные данные хорошо совпадают с результатами вычислений Хокинга для капелек радиусом  и несколько хуже — с данными вычислений Шафрира и Нейбургера, а также Мейсона для радиусов 40 мкм для отношений
и несколько хуже — с данными вычислений Шафрира и Нейбургера, а также Мейсона для радиусов 40 мкм для отношений  Для
Для  между данными вычислений и экспериментов нет достаточно хорошего совпадения.
между данными вычислений и экспериментов нет достаточно хорошего совпадения.

Рис. 6. Сопоставление вычисленных и экспериментальных значений коэффициентов эффективности соударения капелек. По Вудсу и Мейсону [579]. Вычисленные значения  (Хокинг): 3)
(Хокинг): 3)  (Шафрир и Нейбургер); 5)
(Шафрир и Нейбургер); 5)  (Мейсон). Экспериментальные значения
(Мейсон). Экспериментальные значения  (Пнкиет); 9)
(Пнкиет); 9)  (Вудс и Мейсон).
(Вудс и Мейсон).
Был подтвержден вывод Хокинга о том, что критическое значение радиуса капелек, при котором отсутствует коагуляция, равно 18 мкм.
Сартор и Миллер [499] перевычислили данные Хокинга [339] с некоторыми уточнениями. Для капли с  их вычисления хорошо совпадают. Но уже для капель радиусом 20 мкм, для которых при
их вычисления хорошо совпадают. Но уже для капель радиусом 20 мкм, для которых при  Хокинг получил
Хокинг получил  они нашли
они нашли  соответственно при
соответственно при  и 0,25. Сартор и Миллер отмечают, что обнаруженные различия должны сильно сказываться на определении вероятности коагуляции на ранних стадиях роста капелек, т. е. для
и 0,25. Сартор и Миллер отмечают, что обнаруженные различия должны сильно сказываться на определении вероятности коагуляции на ранних стадиях роста капелек, т. е. для  Девис [275] для капелек с
Девис [275] для капелек с  получил, что вообще отсутствует запрет соударения между капельками с
получил, что вообще отсутствует запрет соударения между капельками с  предсказанный Хокингом. Но значение К для таких капелек мало, меньше 0,06.
предсказанный Хокингом. Но значение К для таких капелек мало, меньше 0,06.
Таким образом, коэффициенты соударения капель радиусом 15-20 мкм с более мелкими капельками весьма малы и у капель меньших размеров мало шансов расти за счет гравитационной коагуляции; поэтому вопрос о росте облачных капель радиусом примерно от 5 до 20 мкм остается нерешенным.
В. Г. Левич [107, 108] исследовал вопрос о влиянии броуновского движения на коагуляцию облачных капелек. Он показал, что вследствие значительного превышения массы капелек над массой молекул воздуха броуновская диффузия весьма мала для частиц размером порядка 1 мкм и ею можно пренебречь.
Турбулентные движения воздуха, которые особенно велики в конвективных облаках, должны оказывать определенное влияние на вероятность соударения капелек. Исследования этого вопроса выполнены В. Г. Левичем [107, 108], Истом и Маршаллом [288] и др. А. И. Ивановский и И. П. Мазин [55], например, вычислили, что для восьмикратного увеличения объема капелек, которые вследствие начального слияния имели двойную массу, требуется 8 ч при скорости диссипации турбулентной энергии в облаке  мин при
мин при  и около 9 мин. при
и около 9 мин. при  . Интенсивная турбулентность, при которой скорость диссипации турбулентной энергии становится равной нескольким десятым
. Интенсивная турбулентность, при которой скорость диссипации турбулентной энергии становится равной нескольким десятым  может обеспечить эффективность соударения капель того же порядка, что и гравитационная коагуляция.
может обеспечить эффективность соударения капель того же порядка, что и гравитационная коагуляция.
Н. А. Вагер [19] обнаружил прирост массы капель радиусом 2,1-2,3 мм при падении в камере с туманом, средний радиус капелек которого 10 мкм. Ганн и Хичфельд [320] получили согласие в пределах точности эксперимента между коэффициентом коагуляции капель радиусом 1,6 мм с капельками тумана в камере и коэффициентом эффективности соударения, рассчитанным по Лэнгмюру. Коэффициент слияния принимался равным единице. М. А. Химач и Н. С. Шишкин [193] наблюдали в облачной камере рост радиусов капель от 25—30 до 400-500 мкм. Радиусы капелек тумана находились в основном в пределах 5-15 мкм. Принимая коэффициент слияния равным единице, они получили согласие
между теорией и экспериментом. Такие же эксперименты были выполнены Кинцером и Коббом [361]. Они нашли, что экспериментальные значения больше вычисленных по Лэнгмюру для радиусов между 150 и 500 мкм.
Для преодоления трудностей, которые весьма велики при лабораторных исследованиях коагуляции капель в воздухе, был поставлен ряд экспериментов (Сартор [494], Скотленд [508], В. Г. Хоргуани [194] и др.), в которых моделировались естественные условия. Пытались заменить водяные капли, падающие в воздухе, каплями разных жидкостей и металлическими шариками, падающими в вязкой жидкости.
Сартор [494] первым предпринял попытку исследовать гравитационную коагуляцию капель, моделируя условия их соударения. Для моделирования он выбрал падение капель воды в минеральном масле. Сартор наблюдал случаи соударения капель, но без их слияния. Возможно, что здесь сказалось влияние масляной пленки между каплями, препятствующей их слиянию при соударении. Он обнаружил засасывание капель в кильватерный след при их падении.
Скотленд [508] моделировал капли стальными шариками, а воздух — раствором сахара в воде. Он получил значения коэффициентов соударения для капель радиусом  от 10 до 22 мкм. Появление значений с
от 10 до 22 мкм. Появление значений с  указывало на существование засасывания верхней, меньшей капли в кильватерный след нижней, большей капли, что противоречит опытам Вудса и Мейсона [580], выполненным с капельками, падающими в воздухе.
указывало на существование засасывания верхней, меньшей капли в кильватерный след нижней, большей капли, что противоречит опытам Вудса и Мейсона [580], выполненным с капельками, падающими в воздухе.
Подобные эксперименты были выполнены В. Г. Хоргуани [194], причем капли моделировались стальными шариками, а воздух — глицерином. Он получил значения коэффициентов соударения для капель сопоставимых размеров. При  обнаруживалось засасывание в кильватерный след нижнего шарика, если вертикальное расстояние между ними составляет
обнаруживалось засасывание в кильватерный след нижнего шарика, если вертикальное расстояние между ними составляет  Сближение шариков приводило к их вращению.
Сближение шариков приводило к их вращению.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ В ОБЛАКАХ
- 1.1. ЭЛЕКТРИЧЕСКОЕ СОСТОЯНИЕ АТМОСФЕРЫ «ХОРОШЕЙ» ПОГОДЫ
- 1.2. КОНДЕНСАЦИОННЫЙ И КОАГУЛЯЦИОННЫЙ РОСТ КАПЕЛЬ В ОБЛАКАХ
- 1.3. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА КОАГУЛЯЦИЮ КАПЕЛЬ
- 1.4. СЛИЯНИЕ КАПЕЛЬ
- 1.5. ВЛИЯНИЕ СИЛЬНЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ И ЗАРЯДОВ НА НЕУСТОЙЧИВОСТЬ И СЛИЯНИЕ КАПЕЛЬ
- 1.6. КРИСТАЛЛИЗАЦИЯ ПЕРЕОХЛАЖДЕННЫХ КАПЕЛЬ ВОДЫ
- 1.6.2. Физические основы и некоторые экспериментальные исследования кристаллизации переохлажденных капель воды
- 1.6.3. Влияние электрических сил на кристаллизацию переохлажденных капель
- 1.6.4. Особенности замерзания капель воды, вторичные ядра замерзания и влияние электрических сил на их эффективность
- 1.7. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА СУБЛИМАЦИОННЫЙ РОСТ ЛЕДЯНЫХ ЧАСТИЦ
- 1.8. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА КОАГУЛЯЦИОННЫЙ РОСТ И АГРЕГАЦИЮ ЛЕДЯНЫХ ЧАСТИЦ
- 1.9. МИКРОФИЗИЧЕСКИЕ ПРОЦЕССЫ ПРИ РОСТЕ КРУПЫ И ГРАДА
- 1.10. РАЗРУШЕНИЕ КАПЕЛЬ И СРЫВАНИЕ ВОДЫ С ГРАДИН
- 1.10.2. Разрушение капель при соударении с градинами. Срывание капель с градин при таянии
- 1.10.3. Относительная потеря массы каплями в сильных электрических полях
- Глава 2. СТРОЕНИЕ И ЭЛЕКТРИЧЕСКАЯ СТРУКТУРА КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 2.1. КУЧЕВО-ДОЖДЕВЫЕ ОБЛАКА
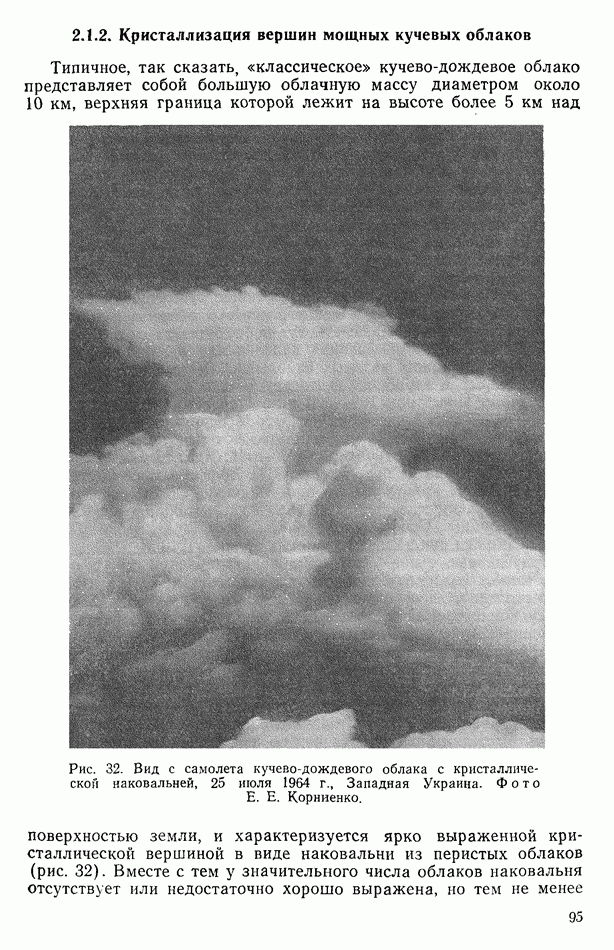
- 2.1.2. Кристаллизация вершин мощных кучевых облаков
- 2.1.3. Макрохарактеристики кучево-дождевых облаков
- 2.1.4. Зарождение и развитие радиоэхо
- 2.1.5. Максимальная интенсивность ливней
- 2.1.6. Токи и турбулентность в кучево-дождевых облаках
- 2.1.7. Микроструктура кучево-дождевых облаков
- 2.1.8. Модель зрелого кучево-дождевого облака
- 2.1.9. Образование ливней и града в кучево-дождевых облаках
- 2.2. ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 2.2.2. Электрическое поле
- 2.2.3. Изменения электрического поля при грозовых разрядах
- 2.2.4. Быстрые изменения электрического поля, обусловленные процессами развития молнии
- 2.2.5. Восстановление электрического поля после грозовых разрядов. Проводимость в грозовых облаках
- 2.2.6. Токи в грозовых облаках
- 2.2.7. Токи с острий под грозовыми облаками
- 2.2.8. Объемные заряды
- 2.2.9. Электричество теплых кучево-дождевых облаков
- 2.2.10. Грозы в теплых облаках
- Глава 3. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ЭЛЕКТРИЗАЦИИ В ГРОЗОВЫХ ОБЛАКАХ
- 3.1.1. Электропроводность и диэлектрическая проницаемость воды в жидкой и твердой фазах
- 3.1.2. Заряжение капель в среде ионов
- 3.1.3. Электризация при контакте и трении ледяных частиц
- 3.1.4. Электризация при замерзании воды и ее растворов
- 3.1.5. Электризация при разрушении замерзающих капель воды
- 3.1.6. Электризация при соударении крупных ледяных частиц с переохлажденными капельками и ледяными кристаллами
- 3.1.7. Баллоэлектрический эффект
- 3.1.8. Электризация при спонтанном разрушении капель при падении
- 3.1.9. Электризация при разрушении капель, соударяющихся с твердыми телами
- 3.1.10. Электризация при разрушении воздушных пузырьков на поверхности воды и при таянии льда
- 3.2. ИНДУКЦИОННЫЕ МЕХАНИЗМЫ ЭЛЕКТРИЗАЦИИ ГИДРОМЕТЕОРОВ
- 3.2.2. Электризация при контакте в электрическом поле
- 3.2.3. Электризация при разрушении капель, соударяющихся с градинами в электрическом поле
- 3.2.4. Электризация при таянии градин в электрическом поле
- 3.2.5. Электризация при разрушении капель в электрическом поле
- 3.2.6. Коронный разряд на каплях и ледяных частицах как причина электризации гидрометеоров
- Глава 4. ТЕОРИИ ГРОЗОВОГО ЭЛЕКТРИЧЕСТВА
- 4.1. СХЕМА ЭЛЬСТЕРА И ГЕЙТЕЛЯ
- 4.2. СХЕМА СИМПСОНА
- 4.3. СХЕМА ВИЛЬСОНА
- 4.4. СХЕМА ФРЕНКЕЛЯ—ШИШКИНА
- 4.5. СХЕМА ВАЛЛЯ
- 4.6. СХЕМА ФИНДЕЙЗЕНА
- 4.7. СХЕМА МЕЙСОНА
- 4.8. СХЕМА ВОРКМЕНА—РЕЙНОЛЬДСА
- 4.9. СХЕМА РЕЙТЕРА
- 4.10. СХЕМА РЕЙНОЛЬДСА
- 4.11. СХЕМА ГРЕНЕ—ВОННЕГУТА
- 4.12. СХЕМА МАК-КРИДИ
- 4.13. СХЕМА ИМЯНИТОВА
- 4.14. ПРЕДСТАВЛЕНИЯ АВТОРА
- 4.14.2. Схема образования гроз умеренных широт
- Глава 5. ПРОБЛЕМА РЕГУЛИРОВАНИЯ ГРОЗОВОГО ЭЛЕКТРИЧЕСТВА
- 5.1. ВОЗДЕЙСТВИЕ НА ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГРОЗОВЫХ ОБЛАКОВ
- 5.2. РЕГУЛИРОВАНИЕ ГРОЗОВОЙ ДЕЯТЕЛЬНОСТИ ПУТЕМ ВОЗДЕЙСТВИЯ НА МИКРО- И МАКРОФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 5.3. ИНИЦИИРУЮЩЕЕ ДЕЙСТВИЕ ТЕЛ, ВНОСИМЫХ В ОБЛАКА
- ЗАКЛЮЧЕНИЕ