| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
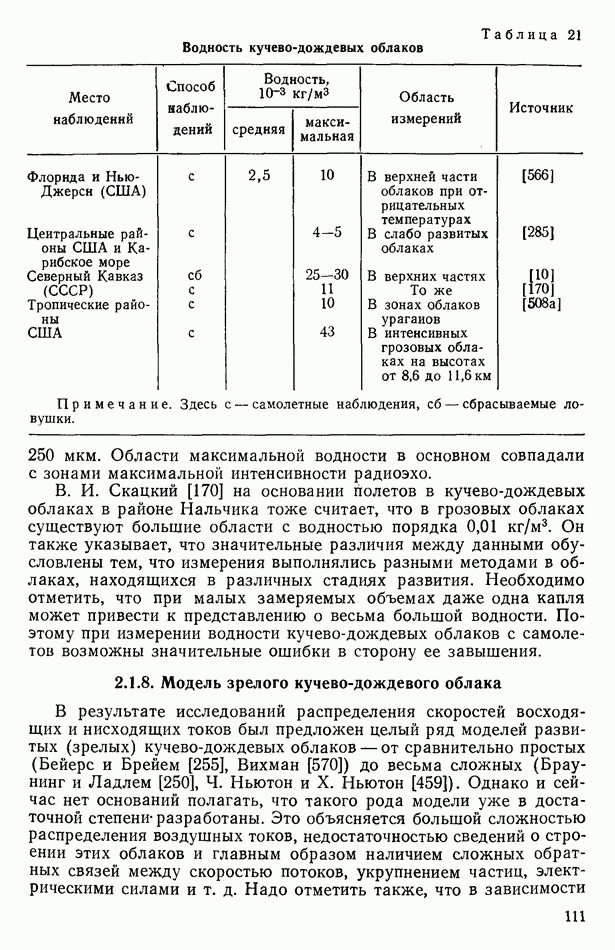
3.2.2. Электризация при контакте в электрическом поле
Возможность электризации капель при контакте в электрическом поле была впервые рассмотрена Эльстером и Гейтелем [290]. Они предположили, что при соударении большей падающей капли с меньшей последняя скользит по поверхности первой и отрывается где-то в верхней ее части (рис. 60 а). Заряд, образующийся на меньшей капле, имеет в поле нормального направления отрицательный знак. В дальнейшем Эльстер и Гейтель [291] допустили, что, кроме скольжения меньших капель по поверхности большей капли,
может происходить также их отражение от нижней части последней. Отражение от нижней части должно особенно хорошо проявляться для больших капель, которые при падении сплющиваются в вертикальном направлении (рис. 60 б). В этом случае меньшая капля в поле нормального направления приобретает положительный заряд.
Сартор [494] выполнил экспериментальное исследование соударения двух капель при их движении в вязкой жидкости в вертикальном электрическом поле. Он обнаружил, что при отсутствии механического контакта между каплями может иметь место электрический контакт вследствие возникновения между каплями поля, напряженность которого может многократно превышать напряженность внешнего электрического поля и достигать пробойного значения.

Рис. 60. Электризация капель при контакте в электрическом поле.
Задача об увеличении напряженности электрического поля между двумя проводящими сферами равных размеров, центры которых лежат на прямой, параллельной направлению однородного поля, в котором они находятся, была решена Сартором. Затем эта задача была решена Девисом [274] в общем виде.
Н. П. Тверская [177] высказала соображение, что возникновение между каплями полей с большой напряженностью приводит к локальному изменению поверхности капель в промежутке между ними. Подобные же соображения были высказаны Сартором [496]. Вследствие искажения поверхности напряженность поля в промежутке между каплями увеличивается, что в свою очередь приводит к дальнейшему искажению поверхности капель в этом промежутке и т. д. Этот процесс при достаточной напряженности внешнего поля для данных размеров капель и длины промежутка между ними может привести к неустойчивому состоянию, возникновению разряда и соединительной перемычки между каплями. Эти соображения были подтверждены экспериментально Сартором и Абботом [498], Азадом и Леземом [218], В. А. Дячуком, В. М. Мучником, Б. Е. Фишманом [47] и др. При сближении капель с противоположными зарядами происходит перенос зарядов искровым разрядом
(Миллер и др. (444]). При этом обнаружилось, что в промежутке между каплями их поверхность искривляется, увеличивая возможность разряда между ними. Процесс разряда сопровождается электромагнитным излучением, которое было экспериментально обнаружено и исследовано в световом и радиоволновом участках спектра Сартором [497], Миллером и др. [444], Аткинсоном и Палуч [214]. Эти процессы существенны не только вследствие их близости к процессам, происходящим с каплями в электрическом поле, но и вследствие их влияния на образование зарядов в грозовых облаках. Их роль может сказаться в уменьшении скорости образования заряженных областей, так как при этих процессах происходит нейтрализация зарядов противоположных знаков.
Сартор и Аббот [498] изучали возникновение разряда между каплями дистиллированной воды равных размеров (радиус капель от 370 до 816 мкм) в сильном горизонтальном электрическом поле. Они установили, что минимальная напряженность электрического поля, при которой происходит искровой разряд между каплями, хорошо выражается формулой

где у — коэффициент усиления поля между сферами, табулированный Девисом (см. табл. 48);  атмосферное давление в
атмосферное давление в 
Сартор и Аббот произвели экспериментальную проверку величины разделяющихся зарядов для капель, вступающих в электрический контакт или соприкасающихся друг с другом, при условии, что линия, проходящая через их центры, параллельна направлению электрического поля. Этот заряд, согласно Сартору [497а], дается выражением

что находится в согласии с данными табл. 46.
Как следует из табл. 47, для полей с напряженностью, значительно меньшей минимальной напряженности, которая требуется для возникновения разряда, экспериментально наблюдаемые заряды меньше или близки к вычисленным на основании (87). Для больших напряженностей поля, приближающихся к разрядным, характерен быстрый рост экспериментальных значений по сравнению с вычисленными, что может обусловливаться влиянием сильного поля на конфигурацию капель в момент их отрыва друг от друга. При вытягивании пары капель в направлении поля их конфигурации приближаются к вытянутым эллипсоидам, что должно привести к увеличению зарядов на разделяющихся каплях.
Монтгомери и Доусон [446] исследовали электризацию при контакте капель радиусом 1 мм в электрическом поле напряженностью от  Относительная скорость соударения капель составляла около 0,5 м/с. Эти авторы обнаружили, что существует зависимость величины разделяемых зарядов и числа сателлитных капелек радиусом 50—200 мкм от электрического поля.
Относительная скорость соударения капель составляла около 0,5 м/с. Эти авторы обнаружили, что существует зависимость величины разделяемых зарядов и числа сателлитных капелек радиусом 50—200 мкм от электрического поля.
Таблица 47 (см. скан) Сравнение вычисленных зарядов, разделяющихся в электрическом поле при контакте капель одинаковых размеров, с экспериментальными. По Сартору и Абботу [498]
В пределах напряженности  наблюдалось резкое возрастание величины зарядов и числа сателлитных капелек, которое указывает на изменение условий слияния капель. По-видимому, при больших напряженностях поля степень слияния больше и отрывание капель друг от друга происходит на большем расстоянии от экватора, чем при малых значениях напряженности поля. Капля, падающая быстрее, скользит вдоль поверхности капли, падающей с меньшей скоростью, и отрывается от ее нижней части. Действительно, знак заряда более быстро падающей капли всегда совпадал со знаком поля.
наблюдалось резкое возрастание величины зарядов и числа сателлитных капелек, которое указывает на изменение условий слияния капель. По-видимому, при больших напряженностях поля степень слияния больше и отрывание капель друг от друга происходит на большем расстоянии от экватора, чем при малых значениях напряженности поля. Капля, падающая быстрее, скользит вдоль поверхности капли, падающей с меньшей скоростью, и отрывается от ее нижней части. Действительно, знак заряда более быстро падающей капли всегда совпадал со знаком поля.
Вопрос об электризации при соударении ледяных частиц рассматривал Мюллер-Гиллебрандт [452]. Он указал на то, что возможность электризации при контакте в электрическом поле обусловливается электропроводностью льда, которая зависит от температуры и частоты колебаний электрического поля. Полное разделение зарядов при контакте будет осуществляться в том случае, если время релаксации меньше времени контакта. Мюллер-Гиллебрандт предположил, что продолжительность контакта достаточно длительна для передачи заряда вследствие того, что при соударении ледяной крупы с ледяными кристаллами последние скользят по ее поверхности, и, кроме того, что этот процесс характеризуется высокочастотным изменением электрического поля. Эти требования
не всегда выполняются. При соударении сферических ледяных частиц существует возможность их отскакивания без скольжения, например, при лобовых и близких к ним соударениях. Мюллер-Гиллебрандт не рассматривал природу высокочастотных колебаний электрического поля. Изменение же поля при сближении частиц вряд ли можно отнести к высокочастотным. Поэтому существует необходимость убедиться в том, что время релаксации всегда меньше времени контакта при соударении ледяных частиц, наблюдаемых в грозовых облаках.
Рассмотрим, согласно [46], время контакта между двумя ледяными сферами, которое определяется упругими свойствами льда. Этот вид контакта можно назвать механическим в отличие от электрического контакта, обусловленного зарядом и электрическим полем, который может иметь место без соприкосновения тел. Время механического контакта для двух упругих сфер с радиусом  можно определить из формулы [97]
можно определить из формулы [97]

где  -приведенная масса сфер;
-приведенная масса сфер;  их относительная скорость соударения;
их относительная скорость соударения;

Здесь  коэффициент Пуассона,
коэффициент Пуассона,  модуль Юнга. Так как плотность льда
модуль Юнга. Так как плотность льда  можно считать равной
можно считать равной  то
то  (в килограммах). Для определения установившейся скорости падения ледяных сфер в воздухе можно использовать формулу (36). Пусть градина с
(в килограммах). Для определения установившейся скорости падения ледяных сфер в воздухе можно использовать формулу (36). Пусть градина с  соударяется с ледяной крупой радиусом
соударяется с ледяной крупой радиусом  на высоте, где температура —10°
на высоте, где температура —10°  Для этих данных
Для этих данных  Подставив эти значения в (88), получим, что
Подставив эти значения в (88), получим, что 
Определим теперь время релаксации  при соударении ледяных сфер в электрическом поле (для простоты предположим, что они не имеют собственных зарядов) на основании формулы (51). Поскольку
при соударении ледяных сфер в электрическом поле (для простоты предположим, что они не имеют собственных зарядов) на основании формулы (51). Поскольку  оказалось порядка
оказалось порядка  то следует для
то следует для  принять
принять  . Подставив эти данные в (51), получаем, что
. Подставив эти данные в (51), получаем, что  Следовательно,
Следовательно,
для рассмотренного случая соударения градины с ледяной крупой время релаксации примерно на порядок меньше времени механического контакта. Если  то
то  согласно (88), будет увеличиваться, и можно считать, что почти всегда время релаксации будет меньше времени механического контакта.
согласно (88), будет увеличиваться, и можно считать, что почти всегда время релаксации будет меньше времени механического контакта.
В действительности время контакта, т. е. время обмена зарядами между частицами, должно быть больше, чем время механического контакта, поскольку электрический контакт всегда наступает до момента соприкосновения частиц. Согласно теории Девиса [274], напряженность электрического поля между двумя проводящими сферами, центры которых находятся на одной прямой, параллельной направлению внешнего электрического поля, в точках на той же прямой равна

где у — некоторый коэффициент, который весьма сложно зависит от радиусов сфер  и кратчайшего расстояния между их поверхностями
и кратчайшего расстояния между их поверхностями  (табл. 48). Теория Девиса получила экспериментальное подтверждение (Лезем и др. [379]).
(табл. 48). Теория Девиса получила экспериментальное подтверждение (Лезем и др. [379]).
Таблица 48 (см. скан) Значения у в формуле (90). По Девису [274]
Для рассматриваемого случая электрический контакт благодаря разряду между сферами в поле с  на высотах около 5 км, где
на высотах около 5 км, где  должен произоити при напряженности поля между сферами
должен произоити при напряженности поля между сферами  Тогда на основании данных табл. 48 и формулы (90) получаем, что для этого момента расстояние между сферами
Тогда на основании данных табл. 48 и формулы (90) получаем, что для этого момента расстояние между сферами  Согласно Сартору [497], Аткинсону и Палуч [214] и др., при разряде в воздушном промежутке между заряженными каплями воды происходит излучение радиоволн с частотой 109—1012 Гц. Поданным [180] и [529] можно принять, что
Согласно Сартору [497], Аткинсону и Палуч [214] и др., при разряде в воздушном промежутке между заряженными каплями воды происходит излучение радиоволн с частотой 109—1012 Гц. Поданным [180] и [529] можно принять, что  при
при  Гц и выше. Труднее использовать данные об электропроводности льда, так как ее зависимость от частоты известна только для частот до
Гц и выше. Труднее использовать данные об электропроводности льда, так как ее зависимость от частоты известна только для частот до  Гц [529]. Поэтому можно получить экстраполяцией только ее грубо приближенное значение для
Гц [529]. Поэтому можно получить экстраполяцией только ее грубо приближенное значение для  Гц, а именно
Гц, а именно  Используя эти значения, на основании (51) получаем
Используя эти значения, на основании (51) получаем 
Время, необходимое для сближения шаров после начала разряда между ними, равно  Относительная скорость соударения двух ледяных сфер принятых размеров равна
Относительная скорость соударения двух ледяных сфер принятых размеров равна  отсюда
отсюда  Таким образом, время релаксации меньше времени, требующегося для соприкосновения двух сфер заданных размеров после наступления электрического разряда между ними. Так как при
Таким образом, время релаксации меньше времени, требующегося для соприкосновения двух сфер заданных размеров после наступления электрического разряда между ними. Так как при  время сближения сфер будет соответственно увеличиваться, то можно утверждать, что время релаксации будет всегда меньше времени, необходимого для сближения ледяных сферических гидрометеоров, и времени механического контакта между ними. Это означает, что за время контакта в электрическом поле частицы к моменту разделения приобретут равновесные заряды.
время сближения сфер будет соответственно увеличиваться, то можно утверждать, что время релаксации будет всегда меньше времени, необходимого для сближения ледяных сферических гидрометеоров, и времени механического контакта между ними. Это означает, что за время контакта в электрическом поле частицы к моменту разделения приобретут равновесные заряды.
Лезем и Мейсон [382] выполнили эксперименты по электризации при контакте ледяных сфер в электрическом поле. Две ледяные сферы радиусом от 0,5 до 2 мм подвешивались на нитях в горизонтальном электрическом поле. Время контакта изменялось от 0,5 с до 5 мин, температура — от —4 до —30° С, напряженность поля — от  до
до  Результаты этих экспериментов полностью подтвердили, что электризация происходит в согласии с формулой Гордона. Лезем и Мейсон исследовали также электризацию при контакте ледяной сферы с ледяными кристаллами разной формы в электрическом поле. Ледяные кристаллы подвешивались на изолированной нити и приводились в соприкосновение с ледяной сферой в электрическом поле постоянной напряженности примерно в течение такого же времени, как и в предыдущих опытах. Масса ледяных кристаллов определялась после их таяния.
Результаты этих экспериментов полностью подтвердили, что электризация происходит в согласии с формулой Гордона. Лезем и Мейсон исследовали также электризацию при контакте ледяной сферы с ледяными кристаллами разной формы в электрическом поле. Ледяные кристаллы подвешивались на изолированной нити и приводились в соприкосновение с ледяной сферой в электрическом поле постоянной напряженности примерно в течение такого же времени, как и в предыдущих опытах. Масса ледяных кристаллов определялась после их таяния.
Таблица 49
Влияние формы ледяных кристаллов на электризацию при контакте с ледяной сферой в электрическом поле. По Лезему и Мейсону [382]
Как видно из табл. 49, форма кристаллов играет заметную роль в электризации при контакте с ледяной сферой в электрическом поле. Наибольшее увеличение характерно для игл с наибольшим отношением  вследствие того, что при этом значительно
вследствие того, что при этом значительно
увеличивается напряженность индуцированного поля на поверхности сферы.
Во всех описанных выше экспериментах время контакта было явно завышенным по сравнению со временем, которое соответствует контакту ледяных частиц в естественных условиях. Поэтому Лезем и Мейсон провели исследование, в котором ледяные кристаллы, двигавшиеся в потоке воздуха, налетали на ледяной цилиндр. Опыты проводились при скоростях потока от 1 до 30 м/с, в поле напряженностью  при температурах
при температурах  Было получено, что за 30 с не происходит сколько-нибудь заметная электризация цилиндра, во всяком случае, его заряд был меньше
Было получено, что за 30 с не происходит сколько-нибудь заметная электризация цилиндра, во всяком случае, его заряд был меньше  Лезем и Мейсон считают, что причиной отсутствия электризации является малое время контакта между ледяными частицами и ледяной сферой.
Лезем и Мейсон считают, что причиной отсутствия электризации является малое время контакта между ледяными частицами и ледяной сферой.

Рис. 61. Зависимость образования зарядов  при соударении ледяных (1) или стальных (2) шариков в электрическом поле от их размеров. По В. А. Дячуку и В. М. Мучнику
при соударении ледяных (1) или стальных (2) шариков в электрическом поле от их размеров. По В. А. Дячуку и В. М. Мучнику 
Напряженность поля  -коэффициент (см. табл. 48).
-коэффициент (см. табл. 48).
Такого же мнения придерживаются Скотт и Левин [510а]. Но это представление явно неверное. Контакт между ледяными кристаллами и поверхностью цилиндра более длительный, чем при соударении двух сфер, так как ледяные кристаллы должны скользить по поверхности цилиндра. Отрывание кристаллов будет происходить где-то вблизи экваториальной линии по отношению к полю. Поэтому заряды будут малы и разных знаков (в зависимости от части цилиндра, от которой они оторвутся), и суммарный заряд, уносимый кристаллами с поляризованного ледяного цилиндра, должен быть близким к нулю.
В. А. Дячуком и В. М. Мучником [46] было проведено исследование, в котором естественные условия соударения ледяных сфер имитировались более полно, чем в экспериментах Лезема и Мейсона. Ледяные шарики из питьевой воды радиусом от 1,5 до 5,5 мм соударялись с ледяным неподвижным шариком радиусом 7,5 мм в вертикальном электрическом поле. Температура в камере менялась от  На рис. 61 представлена зависимость
На рис. 61 представлена зависимость  от
от  согласно (86), для
согласно (86), для  причем значения у брались из табл. 48. Каждая точка на графике соответствует среднему из семи проб. Как следует из рисунка, зависимость
причем значения у брались из табл. 48. Каждая точка на графике соответствует среднему из семи проб. Как следует из рисунка, зависимость  от
от  является
является
линейной, согласно требованиям теории. При разных значениях напряженности поля были выполнены опыты с шариками из льда, изготовленного из питьевой, дистиллированной и бидистиллированной воды (рис. 62). Как видно из рисунка, между величиной зарядов и напряженностью поля существует прямо пропорциональная зависимость в согласии с (86). На эту связь не оказывает влияния температура, что возможно только в том случае, если электропроводность льда достаточно велика и время релаксации меньше времени контакта. Это верно и для дистиллированной, и для бидистиллированной воды: точки, соответствующие этим измерениям, совпадают (в пределах точности эксперимента) с прямыми для опытов со льдом из питьевой воды. Экстраполируя прямую на рис. 61, получаем для случая соударения ледяных сфер радиусом 7,5 и 5,5 мм в поле напряженностью  заряд около
заряд около  а при соударении с ледяной крупой радиусом
а при соударении с ледяной крупой радиусом  около
около  Эти результаты были подтверждены Скоттом и Левиным [510а], которые исследовали электризацию, возникающую при соударении ледяных сфер и естественных снежинок в электрическом поле.
Эти результаты были подтверждены Скоттом и Левиным [510а], которые исследовали электризацию, возникающую при соударении ледяных сфер и естественных снежинок в электрическом поле.

Рис. 62. Зависимость образования зарядов  при соударении ледяных шариков различных размеров с ледяным шаром радиусом 13,5 мм от напряженности поля Е. По В. А. Дячуку и В. М. Мучнику [46].
при соударении ледяных шариков различных размеров с ледяным шаром радиусом 13,5 мм от напряженности поля Е. По В. А. Дячуку и В. М. Мучнику [46].
Радиусы ледяных шариков (мм): 1) 5,5, 2) 4, 3) 2,5, 4) 1,5 из питьевой воды); 5) 4 (из дистиллированной воды); 6) 4 (из бидистиллированной воды).
Лезем и др. [384] моделировали гексагональные кристаллы металлическими пластинками со стороной 6,4 мм и толщиной 0,8 мм (отношение  призматические кристаллы шестигранными призмами длиной 12,7 мм и со стороной 6,4 мм (отношение
призматические кристаллы шестигранными призмами длиной 12,7 мм и со стороной 6,4 мм (отношение  игольчатые кристаллы шестигранными призмами длиной
игольчатые кристаллы шестигранными призмами длиной  и со стороной
и со стороной  (отношение
(отношение  Эти формы представлены на рис. 63. Модели ледяных кристаллов помещались в вертикальное электрическое поле напряженностью от нуля до
Эти формы представлены на рис. 63. Модели ледяных кристаллов помещались в вертикальное электрическое поле напряженностью от нуля до  и сближались до тех пор, пока не происходил перенос зарядов между частицами. Опыты показали, что для каждой пары моделей и их ориентации приданной напряженности поля существует граничное расстояние, начиная с которого наблюдается перенос зарядов между частицами.
и сближались до тех пор, пока не происходил перенос зарядов между частицами. Опыты показали, что для каждой пары моделей и их ориентации приданной напряженности поля существует граничное расстояние, начиная с которого наблюдается перенос зарядов между частицами.

Рис. 63. Модели ледяных кристаллов и их расположение по отношению к направлению электрического поля. По Лезему и др. [384].  пластинки,
пластинки,  иглы,
иглы,  призмы.
призмы.
Таблица 50
Критическое расстояние  для разделения зарядов как функция типов моделей кристаллов и их ориентации относительно направления поля при напряженности
для разделения зарядов как функция типов моделей кристаллов и их ориентации относительно направления поля при напряженности  По Лезему и др. [384]
По Лезему и др. [384]

В табл. 50 ориентация моделей кристаллов соответствует рис. 63. Когда два пластинчатых кристалла перпендикулярны направлению электрического поля, их сближение должно быть весьма тесным, чтобы произошел обмен зарядами. Но если плоскости кристаллов параллельны направлению электрического поля, то перенос зарядов при напряженности  происходит на расстояниях, сопоставимых с их размерами (конфигурации
происходит на расстояниях, сопоставимых с их размерами (конфигурации  и
и  То же самое справедливо и для моделей типа
То же самое справедливо и для моделей типа  Вообще, чем больше кривизна частиц, тем больше критическое расстояние, на котором происходит перенос зарядов: случаи, в которых участвуют конфигурации
Вообще, чем больше кривизна частиц, тем больше критическое расстояние, на котором происходит перенос зарядов: случаи, в которых участвуют конфигурации  характеризуются большими значениями
характеризуются большими значениями  чем любые другие конфигурации, кроме
чем любые другие конфигурации, кроме 
В рассмотренных экспериментах не была исследована зависимость  от отношения диаметра кристалла
от отношения диаметра кристалла  к его длине
к его длине  Для выявления этой зависимости воспользуемся данными табл. 50. В сочетания конфигураций моделей
Для выявления этой зависимости воспользуемся данными табл. 50. В сочетания конфигураций моделей  и
и  входят шестигранные призмы, но с разными соотношениями
входят шестигранные призмы, но с разными соотношениями  соответственно
соответственно  Для
Для  значение лгкр оказывается в 20 раз больше, чем для
значение лгкр оказывается в 20 раз больше, чем для  Согласно [117], отношения
Согласно [117], отношения  для естественных ледяных кристаллов лежат в основном в пределах от
для естественных ледяных кристаллов лежат в основном в пределах от  до
до  Это указывает на возможность разделения зарядов между ледяными кристаллами без их прикосновения при напряженностях поля, наблюдаемых в грозовых облаках.
Это указывает на возможность разделения зарядов между ледяными кристаллами без их прикосновения при напряженностях поля, наблюдаемых в грозовых облаках.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ В ОБЛАКАХ
- 1.1. ЭЛЕКТРИЧЕСКОЕ СОСТОЯНИЕ АТМОСФЕРЫ «ХОРОШЕЙ» ПОГОДЫ
- 1.2. КОНДЕНСАЦИОННЫЙ И КОАГУЛЯЦИОННЫЙ РОСТ КАПЕЛЬ В ОБЛАКАХ
- 1.3. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА КОАГУЛЯЦИЮ КАПЕЛЬ
- 1.4. СЛИЯНИЕ КАПЕЛЬ
- 1.5. ВЛИЯНИЕ СИЛЬНЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЕЙ И ЗАРЯДОВ НА НЕУСТОЙЧИВОСТЬ И СЛИЯНИЕ КАПЕЛЬ
- 1.6. КРИСТАЛЛИЗАЦИЯ ПЕРЕОХЛАЖДЕННЫХ КАПЕЛЬ ВОДЫ
- 1.6.2. Физические основы и некоторые экспериментальные исследования кристаллизации переохлажденных капель воды
- 1.6.3. Влияние электрических сил на кристаллизацию переохлажденных капель
- 1.6.4. Особенности замерзания капель воды, вторичные ядра замерзания и влияние электрических сил на их эффективность
- 1.7. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА СУБЛИМАЦИОННЫЙ РОСТ ЛЕДЯНЫХ ЧАСТИЦ
- 1.8. ВЛИЯНИЕ ЭЛЕКТРИЧЕСКИХ СИЛ НА КОАГУЛЯЦИОННЫЙ РОСТ И АГРЕГАЦИЮ ЛЕДЯНЫХ ЧАСТИЦ
- 1.9. МИКРОФИЗИЧЕСКИЕ ПРОЦЕССЫ ПРИ РОСТЕ КРУПЫ И ГРАДА
- 1.10. РАЗРУШЕНИЕ КАПЕЛЬ И СРЫВАНИЕ ВОДЫ С ГРАДИН
- 1.10.2. Разрушение капель при соударении с градинами. Срывание капель с градин при таянии
- 1.10.3. Относительная потеря массы каплями в сильных электрических полях
- Глава 2. СТРОЕНИЕ И ЭЛЕКТРИЧЕСКАЯ СТРУКТУРА КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 2.1. КУЧЕВО-ДОЖДЕВЫЕ ОБЛАКА
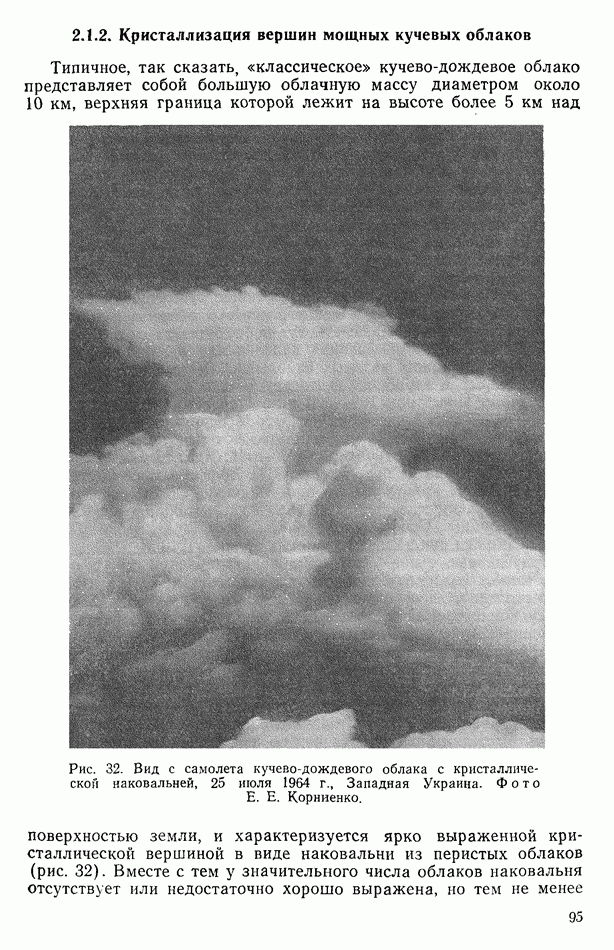
- 2.1.2. Кристаллизация вершин мощных кучевых облаков
- 2.1.3. Макрохарактеристики кучево-дождевых облаков
- 2.1.4. Зарождение и развитие радиоэхо
- 2.1.5. Максимальная интенсивность ливней
- 2.1.6. Токи и турбулентность в кучево-дождевых облаках
- 2.1.7. Микроструктура кучево-дождевых облаков
- 2.1.8. Модель зрелого кучево-дождевого облака
- 2.1.9. Образование ливней и града в кучево-дождевых облаках
- 2.2. ЭЛЕКТРИЧЕСКОЕ СТРОЕНИЕ КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 2.2.2. Электрическое поле
- 2.2.3. Изменения электрического поля при грозовых разрядах
- 2.2.4. Быстрые изменения электрического поля, обусловленные процессами развития молнии
- 2.2.5. Восстановление электрического поля после грозовых разрядов. Проводимость в грозовых облаках
- 2.2.6. Токи в грозовых облаках
- 2.2.7. Токи с острий под грозовыми облаками
- 2.2.8. Объемные заряды
- 2.2.9. Электричество теплых кучево-дождевых облаков
- 2.2.10. Грозы в теплых облаках
- Глава 3. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ЭЛЕКТРИЗАЦИИ В ГРОЗОВЫХ ОБЛАКАХ
- 3.1.1. Электропроводность и диэлектрическая проницаемость воды в жидкой и твердой фазах
- 3.1.2. Заряжение капель в среде ионов
- 3.1.3. Электризация при контакте и трении ледяных частиц
- 3.1.4. Электризация при замерзании воды и ее растворов
- 3.1.5. Электризация при разрушении замерзающих капель воды
- 3.1.6. Электризация при соударении крупных ледяных частиц с переохлажденными капельками и ледяными кристаллами
- 3.1.7. Баллоэлектрический эффект
- 3.1.8. Электризация при спонтанном разрушении капель при падении
- 3.1.9. Электризация при разрушении капель, соударяющихся с твердыми телами
- 3.1.10. Электризация при разрушении воздушных пузырьков на поверхности воды и при таянии льда
- 3.2. ИНДУКЦИОННЫЕ МЕХАНИЗМЫ ЭЛЕКТРИЗАЦИИ ГИДРОМЕТЕОРОВ
- 3.2.2. Электризация при контакте в электрическом поле
- 3.2.3. Электризация при разрушении капель, соударяющихся с градинами в электрическом поле
- 3.2.4. Электризация при таянии градин в электрическом поле
- 3.2.5. Электризация при разрушении капель в электрическом поле
- 3.2.6. Коронный разряд на каплях и ледяных частицах как причина электризации гидрометеоров
- Глава 4. ТЕОРИИ ГРОЗОВОГО ЭЛЕКТРИЧЕСТВА
- 4.1. СХЕМА ЭЛЬСТЕРА И ГЕЙТЕЛЯ
- 4.2. СХЕМА СИМПСОНА
- 4.3. СХЕМА ВИЛЬСОНА
- 4.4. СХЕМА ФРЕНКЕЛЯ—ШИШКИНА
- 4.5. СХЕМА ВАЛЛЯ
- 4.6. СХЕМА ФИНДЕЙЗЕНА
- 4.7. СХЕМА МЕЙСОНА
- 4.8. СХЕМА ВОРКМЕНА—РЕЙНОЛЬДСА
- 4.9. СХЕМА РЕЙТЕРА
- 4.10. СХЕМА РЕЙНОЛЬДСА
- 4.11. СХЕМА ГРЕНЕ—ВОННЕГУТА
- 4.12. СХЕМА МАК-КРИДИ
- 4.13. СХЕМА ИМЯНИТОВА
- 4.14. ПРЕДСТАВЛЕНИЯ АВТОРА
- 4.14.2. Схема образования гроз умеренных широт
- Глава 5. ПРОБЛЕМА РЕГУЛИРОВАНИЯ ГРОЗОВОГО ЭЛЕКТРИЧЕСТВА
- 5.1. ВОЗДЕЙСТВИЕ НА ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГРОЗОВЫХ ОБЛАКОВ
- 5.2. РЕГУЛИРОВАНИЕ ГРОЗОВОЙ ДЕЯТЕЛЬНОСТИ ПУТЕМ ВОЗДЕЙСТВИЯ НА МИКРО- И МАКРОФИЗИЧЕСКИЕ ХАРАКТЕРИСТИКИ КУЧЕВО-ДОЖДЕВЫХ ОБЛАКОВ
- 5.3. ИНИЦИИРУЮЩЕЕ ДЕЙСТВИЕ ТЕЛ, ВНОСИМЫХ В ОБЛАКА
- ЗАКЛЮЧЕНИЕ