| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 1. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ
При решении ряда практических задач (в области экономики, военного дела и т. д.) приходится анализировать ситуации, где налицо две (или более) враждующие стороны, преследующие противоположные цели, причем результат каждого мероприятия одной из сторон зависит от того, какой образ действий выберет противник. Такие ситуации мы будем называть «конфликтными ситуациями».
Можно привести многочисленные примеры конфликтных ситуаций из различных областей практики. Любая ситуация, возникающая в ходе военных действий, принадлежит к конфликтным ситуациям: каждая из борющихся сторон принимает все доступные ей меры для того, чтобы воспрепятствовать противнику достигнуть успеха. К конфликтным принадлежат и ситуации, возникающие при выборе системы вооружения, способов его боевого применения и вообще при планировании военных операций: каждое из решений в этой области должно приниматься в расчете на наименее выгодные для нас действия противника. Ряд ситуаций в области экономики (особенно при наличии свободной конкуренции) принадлежит к конфликтным ситуациям; в роли борющихся сторон выступают торговые фирмы, промышленные предприятия и т. д.
Необходимость анализировать подобные ситуации вызвала к жизни специальный математический аппарат. Теория игр по существу представляет собой не что иное, как математическую теорию конфликтных ситуаций. Цель теории — выработка рекомендаций по рациональному образу действий каждого из противников в ходе конфликтной ситуации.
Каждая непосредственно взятая из практики конфликтная ситуация очень сложна, и анализ ее затруднен наличием многочисленных привходящих факторов. Чтобы сделать возможным математический анализ ситуации, необходимо отвлечься от второстепенных, привходящих факторов и построить упрощенную, формализованную модель ситуации. Такую модель мы будем называть «игрой».
От реальной конфликтной ситуации игра отличается тем, что ведется по вполне определенным правилам. Человечество издавна пользуется такими формализованными моделями конфликтных ситуаций, которые являются играми в буквальном смысле слова. Примерами могут служить шахматы, шашки, карточные игры и т. д. Все эти игры носят характер соревнования, протекающего по известным правилам и заканчивающегося «победой» (выигрышем) того или иного игрока.
Такие формально регламентированные, искусственно организованные игры представляют собой наиболее подходящий материал для иллюстрации и усвоения основных понятий теории игр. Терминология, заимствованная из практики таких игр, применяется и при анализе других конфликтных ситуаций: стороны, участвующие в них, условно именуются «игроками», а результат столкновения — «выигрышем» одной из сторон.
В игре могут сталкиваться интересы двух или более противников; в первом случае игра называется «парной», во втором — «множественной». Участники множественной игры могут в ее ходе образовывать коалиции — постоянные или временные. При наличии двух постоянных коалиций множественная игра обращается в парную. Наибольшее практическое значение имеют парные игры; здесь мы ограничимся рассмотрением только таких игр.
Начнем изложение элементарной теории игр с формулировки некоторых основных понятий. Будем рассматривать парную игру, в которой участвуют два игрока А и В с противоположными интересами. Под «игрой» будем понимать мероприятие, состоящее из ряда действий сторон А и В. Чтобы игра могла быть подвергнута математическому анализу, должны быть точно сформулированы правила игры. Под «правилами игры» разумеется система условий, регламентирующая возможные варианты действий обеих сторон, объем информации каждой стороны о поведении другой, последовательность чередования «ходов» (отдельных peшений,
принятых в процессе игры), а также результат или исход игры, к которому приводит данная совокупность ходов. Этот результат (выигрыш или проигрыш) не всегда имеет количественное выражение, но обычно можно, установив некоторую шкалу измерения, выразить его определенным числом. Например, в шахматной игре выигрышу можно условно приписать значение -+ -1, проигрышу —1, ничьей 0.
Игра называется игрой с нулевой суммой, если один игрок выигрывает то, что проигрывает другой, т. е. сумма выигрышей обеих сторон равна нулю. В игре с нулевой суммой интересы игроков прямо противоположны. Здесь мы будем рассматривать только такие игры.
Так как в игре с нулевой суммой выигрыш одного из игроков равен выигрышу другого с противоположным знаком, то, очевидно, при анализе такой игры можно рассматривать выигрыш только одного из игроков. Пусть это будет, например, игрок А. В дальнейшем мы для удобства сторону А будем условно именовать «мы», а сторону В — «противник».
При этом сторона А («мы») будет всегда рассматриваться как «выигрывающая», а сторона В («противник») как «проигрывающая». Это формальное условие, очевидно, не означает какого-либо реального преимущества для первого игрока; легко видеть, что оно заменяется противоположным, если знак выигрыша изменить на обратный.
Развитие игры во времени мы будем представлять состоящим из ряда последовательных этапов или «ходов». Ходом в теории игр называется выбор одного из предусмотренных правилами игры вариантов. Ходы делятся на личные и случайные.
Личным ходом называется сознательный выбор одним из игроков одного из возможных в данной ситуации ходов и его осуществление.
Пример личного хода — любой из ходов в шахматной игре. Выполняя очередной ход, игрок делает сознательный выбор одного из вариантов, возможных при данном расположении фигур на доске.
Набор возможных вариантов при каждом личном ходе регламентирован правилами игры и зависит от всей совокупности предшествующих ходов обеих сторон.
Случайным ходом называется выбор из ряда возможностей, осуществляемый не решением игрока, а каким-либо механизмом случайного выбора (бросание монеты, игральной
кости, тасовка и сдача карт и т. п.). Например, сдача первой карты одному из игроков в преферанс есть случайный ход с 32 равновозможными вариантами.
Чтобы игра была математически определенной, правила игры должны для каждого случайного хода указывать распределение вероятностей возможных исходов.
Некоторые игры могут состоять только из случайных ходов (так называемые чисто азартные игры) или только из личных ходов (шахматы, шашки). Большинство карточных игр принадлежит к играм смешанного типа, т. е. содержит как случайные, так и личные ходы.
Игры классифицируются не только по характеру ходов (личные, случайные), но и по характеру и по объему информации, доступной каждому игроку относительно действий другого. Особый класс игр составляют так называемые «игры с полной информацией». Игрой с полной информацией называется игра, в которой каждый игрок при каждом личном ходе знает результаты всех предыдущих ходов, как личных, так и случайных. Примерами игр с полной информацией могут служить шахматы, шашки, а также известная игра «крестики и нолики».
Большинство игр, имеющих практическое значение, не принадлежит к классу игр с полной информацией, так как неизвестность по поводу действий противника обычно является существенным элементом конфликтных ситуаций.
Одним из основных понятий теории игр является понятие «стратегии».
Стратегией игрока называется совокупность правил, определяющих однозначно выбор при каждом личном ходе данного игрока в зависимости от ситуации, сложившейся в процессе игры.
Понятие стратегии следует пояснить подробнее.
Обычно решение (выбор) при каждом личном ходе принимается игроком в ходе самой игры в зависимости от сложившейся конкретной ситуации. Однако теоретически дело не изменится, если мы представим себе, что все эти решения принимаются игроком заранее. Для этого игрок должен был бы заблаговременно составить перечень всех возможных в ходе игры ситуаций и предусмотреть свое решение для каждой из них. В принципе (если не практически) это возможно для любой игры. Если такая система решений будет принята, это будет означать, что игрок выбрал определенную стратегию.
Игрок, выбравший стратегию, может теперь не участвовать в игре лично, а заменить свое участие списком правил, которые за него будет применять какое-либо незаинтересованное лицо (судья). Стратегия может быть также задана машине-автомату в виде определенной программы. Именно так в настоящее время играют в шахматы электронные счетные машины.
Чтобы понятие «стратегии» имело смысл, необходимо наличие в игре личных ходов; в играх, состоящих из одних случайных ходов, стратегии отсутствуют.
В зависимости от числа возможных стратегий игры делятся на «конечные» и «бесконечные».
Конечной называется игра, в которой у каждого игрока имеется только конечное число стратегий.
Конечная игра, в которой игрок А имеет  стратегий, а игрок В —
стратегий, а игрок В —  стратегий, называется игрой
стратегий, называется игрой 
Рассмотрим игру  двух игроков А и В («мы» и «противник»).
двух игроков А и В («мы» и «противник»).
Будем обозначать наши стратегии  стратегии противника
стратегии противника 
Пусть каждая сторона выбрала определенную стратегию; для нас это будет  для противника
для противника 
Если игра состоит только из личных ходов, то выбор стратегий  однозначно определяет исход игры — наш выигрыш. Обозначим его
однозначно определяет исход игры — наш выигрыш. Обозначим его 
Если игра содержит, кроме личных, случайные ходы, то выигрыш при паре стратегий  есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае естественной оценкой ожидаемого выигрыша является его среднее значение (математическое ожидание). Мы будем обозначать одним и тем же знаком а как сам выигрыш (в игре без случайных ходов), так и его среднее значение (в игре со случайными ходами).
есть величина случайная, зависящая от исходов всех случайных ходов. В этом случае естественной оценкой ожидаемого выигрыша является его среднее значение (математическое ожидание). Мы будем обозначать одним и тем же знаком а как сам выигрыш (в игре без случайных ходов), так и его среднее значение (в игре со случайными ходами).
Пусть нам известны значения выигрыша (или среднего выигрыша) при каждой паре стратегий. Значения  можно записать в виде прямоугольной таблицы (матрицы), строки которой соответствуют нашим стратегиям
можно записать в виде прямоугольной таблицы (матрицы), строки которой соответствуют нашим стратегиям  а столбцы — стратегиям противника
а столбцы — стратегиям противника  Такая таблица называется платежной матрицей или просто матрицей игры.
Такая таблица называется платежной матрицей или просто матрицей игры.
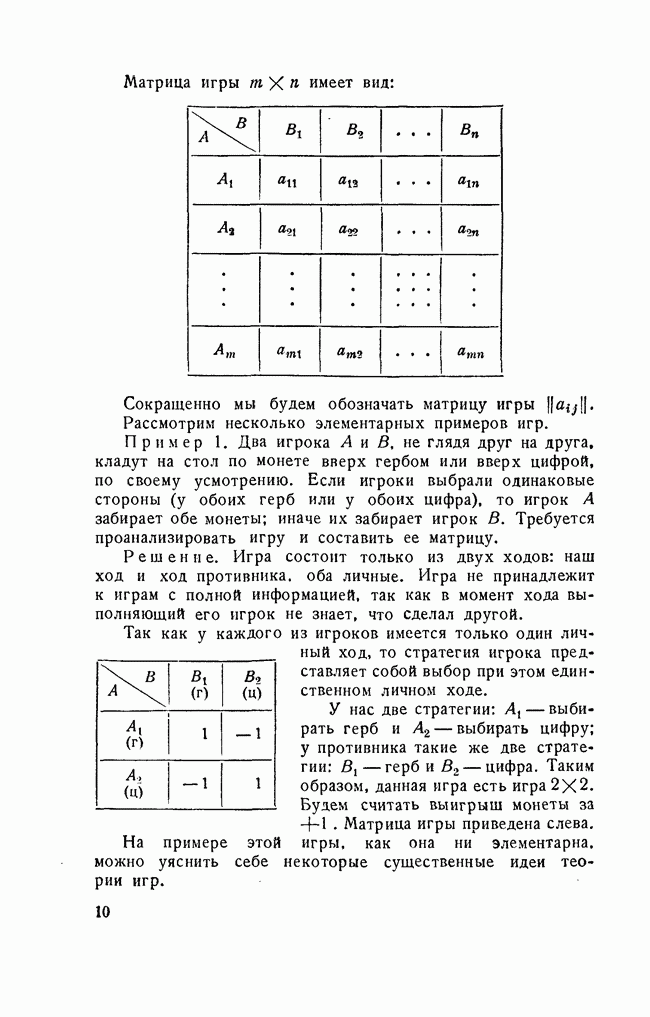
Матрица игры  имеет вид:
имеет вид:

Сокращенно мы будем обозначать матрицу игры 
Рассмотрим несколько элементарных примеров игр.
Пример 1. Два игрока А и В, не глядя друг на друга, кладут на стол по монете вверх гербом или вверх цифрой, по своему усмотрению. Если игроки выбрали одинаковые стороны (у обоих герб или у обоих цифра), то игрок А забирает обе монеты; иначе их забирает игрок В. Требуется проанализировать игру и составить ее матрицу.
Решение. Игра состоит только из двух ходов: наш ход и ход противника, оба личные. Игра не принадлежит к играм с полной информацией, так как в момент хода выполняющий его игрок не знает, что сделал другой.
Так как у каждого из игроков имеется только один личный ход, то стратегия игрока представляет собой выбор при этом единственном личном ходе.

У нас две стратегии:  — выбирать герб и
— выбирать герб и  выбирать цифру; у противника такие же две стратегии:
выбирать цифру; у противника такие же две стратегии:  -герб и
-герб и  цифра. Таким образом, данная игра есть игра 2X2. Будем считать выигрыш монеты за
цифра. Таким образом, данная игра есть игра 2X2. Будем считать выигрыш монеты за  Матрица игры приведена слева.
Матрица игры приведена слева.
На примере этой игры, как она ни элементарна, можно уяснить себе некоторые существенные идеи теории игр.
Предположим сначала, что данная игра выполняется только один раз. Тогда, очевидно, бессмысленно говорить о каких-либо «стратегиях» игроков, более разумных, чем другие. Каждый из игроков с одинаковым основанием может принять любое решение. Однако при повторении игры положение меняется.
Действительно, допустим, что мы (игрок А) выбрали себе какую-то стратегию (скажем,  ) и придерживаемся ее. Тогда уже по результатам первых нескольких ходов противник догадается о нашей стратегии и будет на нее отвечать наименее выгодным для нас образом, т. е. выбирать цифру. Нам явно невыгодно всегда применять какую-то одну стратегию; чтобы не оказаться в проигрыше, мы должны иногда выбирать герб, иногда — цифру. Однако, если мы будем чередовать гербы и цифры в какой-то определенной последовательности (например, через один), противник тоже может догадаться об этом и ответить на эту стратегию наихудшим для нас образом. Очевидно, надежным способом, гарантирующим, что противник не будет знать нашей стратегии, будет такая организация выбора при каждом ходе, когда мы его сами наперед не знаем (это можно обеспечить, например, подбрасыванием монеты). Таким образом, мы путем интуитивных рассуждений подходим к одному из существенных понятий теории игр — к понятию «смешанной стратегии», т. е. такой, когда «чистые» стратегии — в данном случае
) и придерживаемся ее. Тогда уже по результатам первых нескольких ходов противник догадается о нашей стратегии и будет на нее отвечать наименее выгодным для нас образом, т. е. выбирать цифру. Нам явно невыгодно всегда применять какую-то одну стратегию; чтобы не оказаться в проигрыше, мы должны иногда выбирать герб, иногда — цифру. Однако, если мы будем чередовать гербы и цифры в какой-то определенной последовательности (например, через один), противник тоже может догадаться об этом и ответить на эту стратегию наихудшим для нас образом. Очевидно, надежным способом, гарантирующим, что противник не будет знать нашей стратегии, будет такая организация выбора при каждом ходе, когда мы его сами наперед не знаем (это можно обеспечить, например, подбрасыванием монеты). Таким образом, мы путем интуитивных рассуждений подходим к одному из существенных понятий теории игр — к понятию «смешанной стратегии», т. е. такой, когда «чистые» стратегии — в данном случае  и
и  -чередуются случайно с определенными частотами. В данном примере из соображений симметрии заранее ясно, что стратегии
-чередуются случайно с определенными частотами. В данном примере из соображений симметрии заранее ясно, что стратегии  должны чередоваться с одинаковой частотой; в более сложных играх решение может быть далеко не тривиальным.
должны чередоваться с одинаковой частотой; в более сложных играх решение может быть далеко не тривиальным.
Пример 2. Игроки  одновременно и независимо друг от друга записывают каждый одно из трех чисел: 1, 2 или 3.
одновременно и независимо друг от друга записывают каждый одно из трех чисел: 1, 2 или 3.
Если сумма написанных чисел четная, то В платит А эту сумму в рублях; если она нечетная, то, наоборот, А платит В эту сумму. Требуется проанализировать игру и составить ее матрицу.
Решение. Игра состоит из двух ходов; оба — личные. У нас (А) три стратегии:  писать 1;
писать 1;
 - писать
- писать  писать 3. У противника (В) — те же три стратегии.
писать 3. У противника (В) — те же три стратегии.
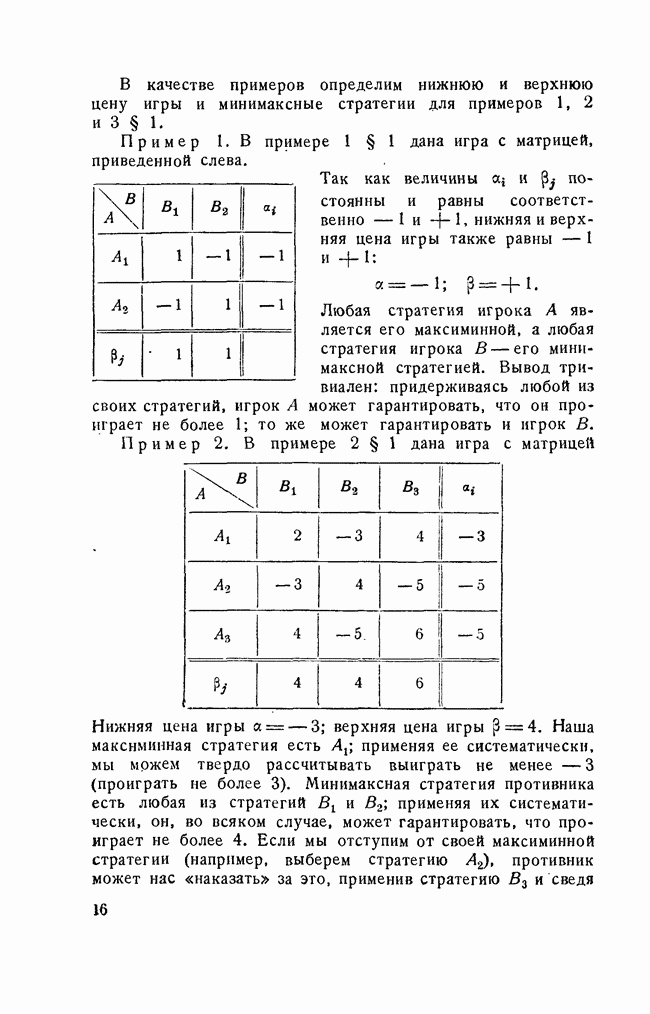
Игра представляет собой игру 3X3 с матрицей, приведенной справа.

Очевидно, как и в предыдущем случае, на любую выбранную нами стратегию противник может ответить наихудшим для нас образом. Действительно, если мы выберем, например, стратегию  противник будет всегда отвечать на нее стратегией
противник будет всегда отвечать на нее стратегией  на стратегию
на стратегию  стратегией
стратегией  на стратегию
на стратегию  стратегией
стратегией  таким образом, любой выбор определенной стратегии неизбежно приведет нас к проигрышу. Решение этой игры (т. е. совокупность наивыгоднейших стратегий обоих игроков) будет дано в § 5.
таким образом, любой выбор определенной стратегии неизбежно приведет нас к проигрышу. Решение этой игры (т. е. совокупность наивыгоднейших стратегий обоих игроков) будет дано в § 5.
Пример 3. В нашем распоряжении имеются три вида вооружения:  ; у противника — три вида самолетов:
; у противника — три вида самолетов:  . Наша задача — поразить самолет; задача противника — сохранить его непораженным. При применении вооружения самолеты
. Наша задача — поразить самолет; задача противника — сохранить его непораженным. При применении вооружения самолеты  поражаются соответственно с вероятностями 0,9, 0,4 и 0,2; при вооружении
поражаются соответственно с вероятностями 0,9, 0,4 и 0,2; при вооружении  вероятностями 0,3, 0,6 и 0,8; при вооружении
вероятностями 0,3, 0,6 и 0,8; при вооружении  вероятностями 0,5, 0,7 и 0,2. Требуется сформулировать ситуацию в терминах теории игр.
вероятностями 0,5, 0,7 и 0,2. Требуется сформулировать ситуацию в терминах теории игр.
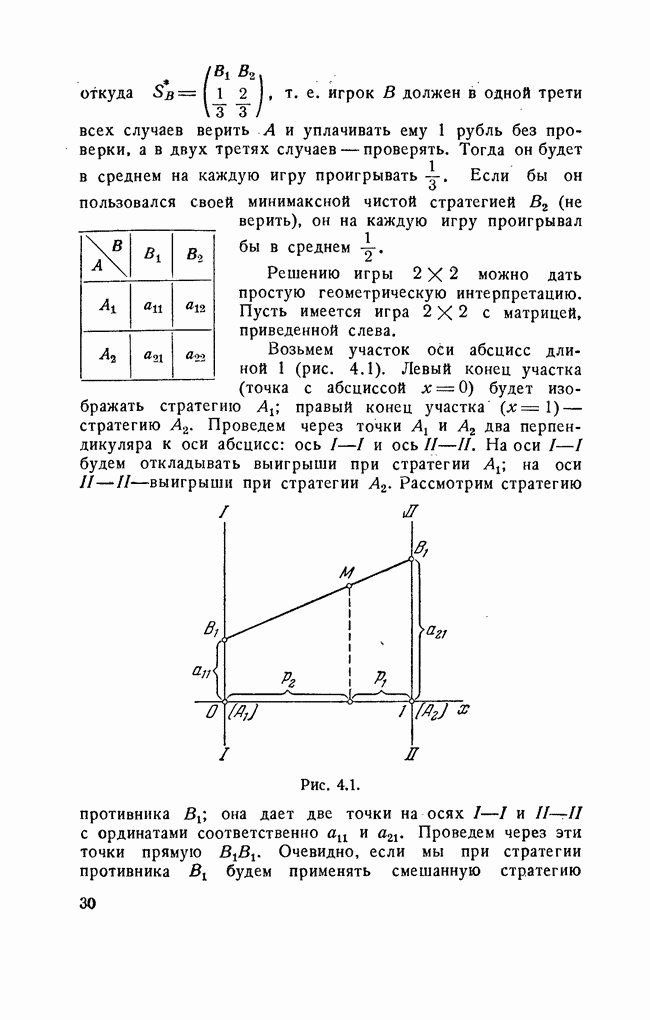
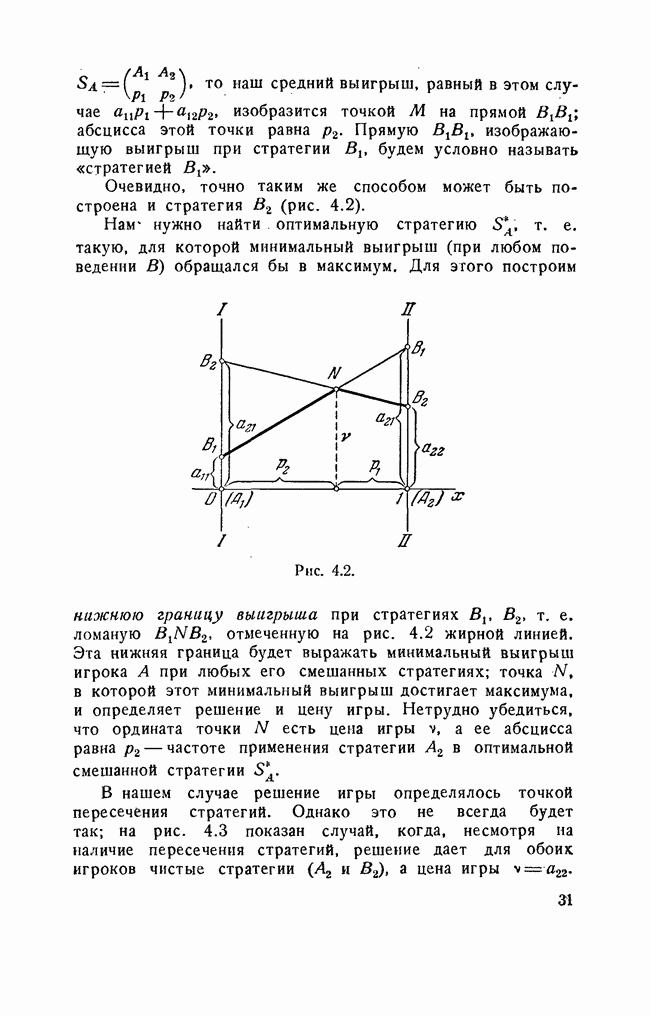
Решение. Ситуация может рассматриваться как игра  с двумя личными ходами и одним случайным. Наш личный ход — выбор типа вооружения; личный ход противника — выбор самолета для участия в бою. Случайный ход — применение вооружения; этот ход может закончиться поражением или непоражением самолета. Наш выигрыш равен единице, если самолет поражен, и равен нулю в противном случае. Нашими стратегиями являются три варианта вооружения; стратегиями противника — три варианта самолетов. Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения данного самолета данным оружием. Матрица игры приведена слева.
с двумя личными ходами и одним случайным. Наш личный ход — выбор типа вооружения; личный ход противника — выбор самолета для участия в бою. Случайный ход — применение вооружения; этот ход может закончиться поражением или непоражением самолета. Наш выигрыш равен единице, если самолет поражен, и равен нулю в противном случае. Нашими стратегиями являются три варианта вооружения; стратегиями противника — три варианта самолетов. Среднее значение выигрыша при каждой заданной паре стратегий есть не что иное, как вероятность поражения данного самолета данным оружием. Матрица игры приведена слева.

Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтных ситуациях, т. е. определение «оптимальной стратегии» каждого из них.
Оптимальной стратегией игрока в теории игр называется такая стратегия, которая при многократном повторении игры обеспечивает данному игроку максимально возможный средний выигрыш (или, что то же, минимально возможный средний проигрыш). При выборе этой стратегии основой рассуждений является предположение, что противник является по меньшей мере таким же разумным, как и мы сами, и делает все для того, чтобы помешать нам добиться своей цели.
В теории игр все рекомендации вырабатывают, исходя именно из этих принципов; следовательно, в ней не учитываются элементы риска, неизбежно присутствующие в каждой реальной стратегии, а также возможные просчеты и ошибки каждого из игроков.
Теория игр, как и всякая математическая модель сложного явления, имеет свои ограничения. Важнейшим из них является то, что выигрыш искусственно сводится к одному - единственному числу. В большинстве практических конфликтных ситуаций при выработке разумной стратегии приходится принимать во внимание не один, а несколько численных параметров — критериев успешности мероприятия. Стратегия, являющаяся оптимальной по одному критерию, необязательно будет оптимальной по другим. Однако, сознавая эти ограничения и поэтому не придерживаясь слепо рекомендаций, получаемых игровыми методами, можно все же разумно использовать математический аппарат теории игр для выработки если не в точности «оптимальной», то, во всяком случае, «приемлемой» стратегии.
| Следующий параграф >> |
- § 1. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ
- § 2. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП «МИНИМАКСА»
- § 3. ЧИСТЫЕ И СМЕШАННЫЕ СТРАТЕГИИ. РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ
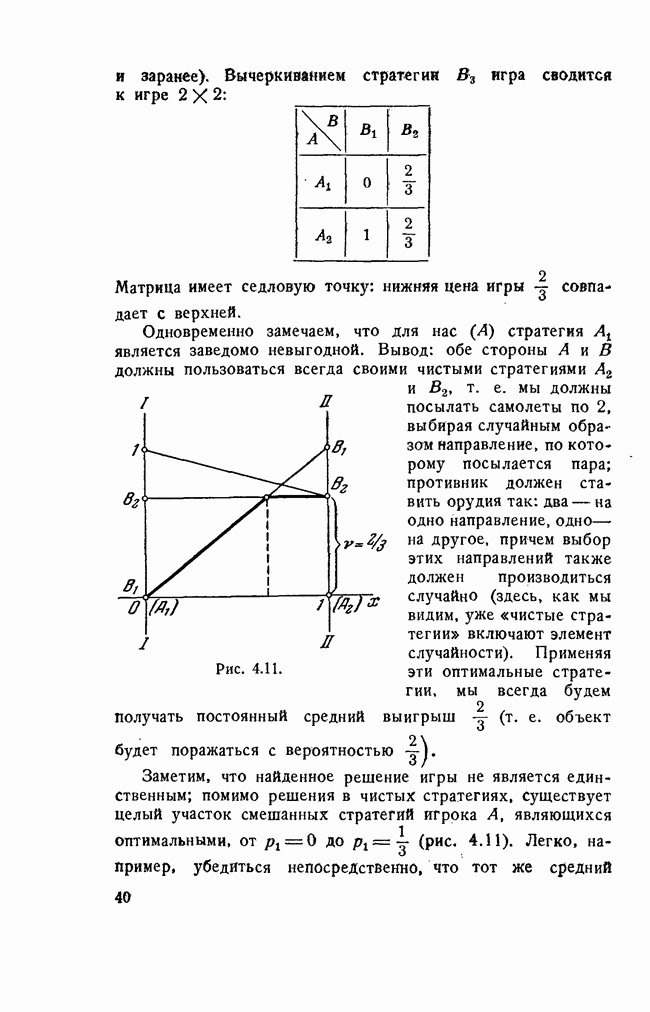
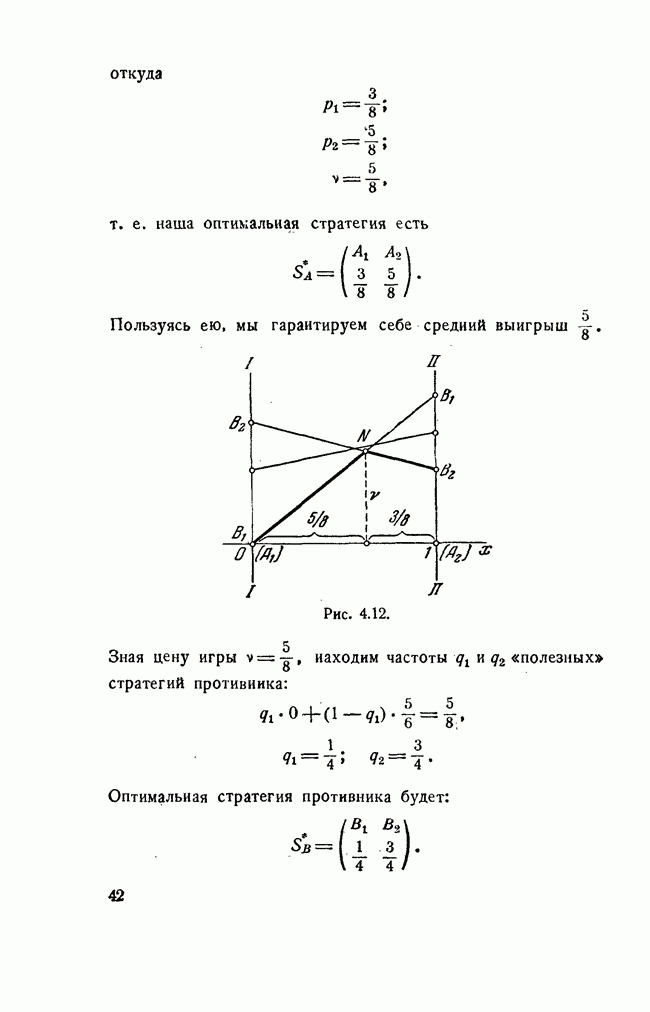
- § 4. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ ИГР. ИГРЫ 2X2 И 2Xn
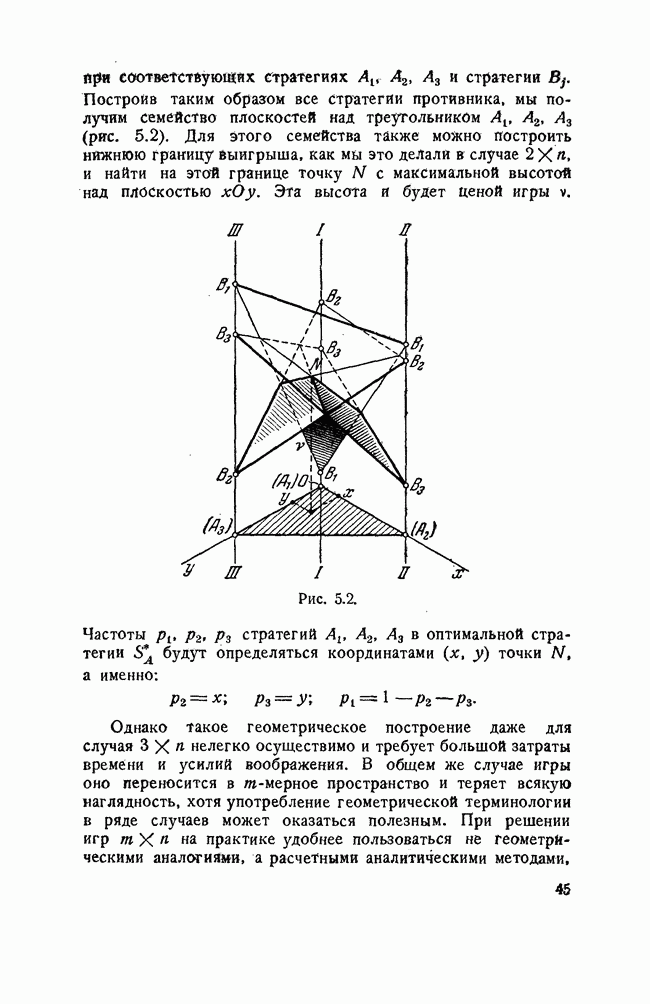
- § 5. ОБЩИЕ МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР
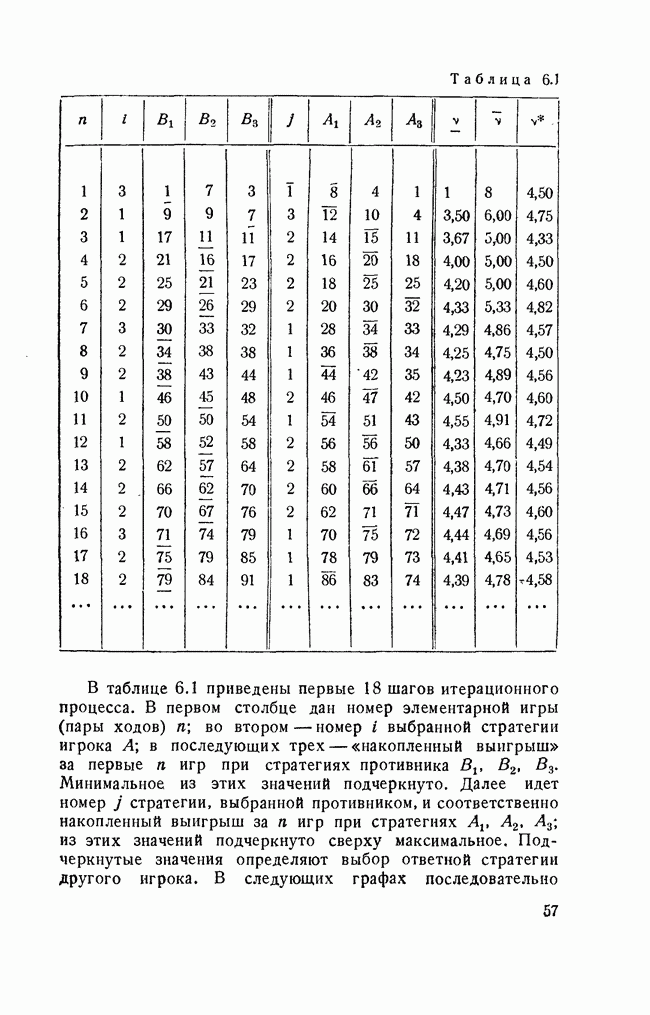
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИГР
- § 7. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР