| << Предыдущий параграф |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР
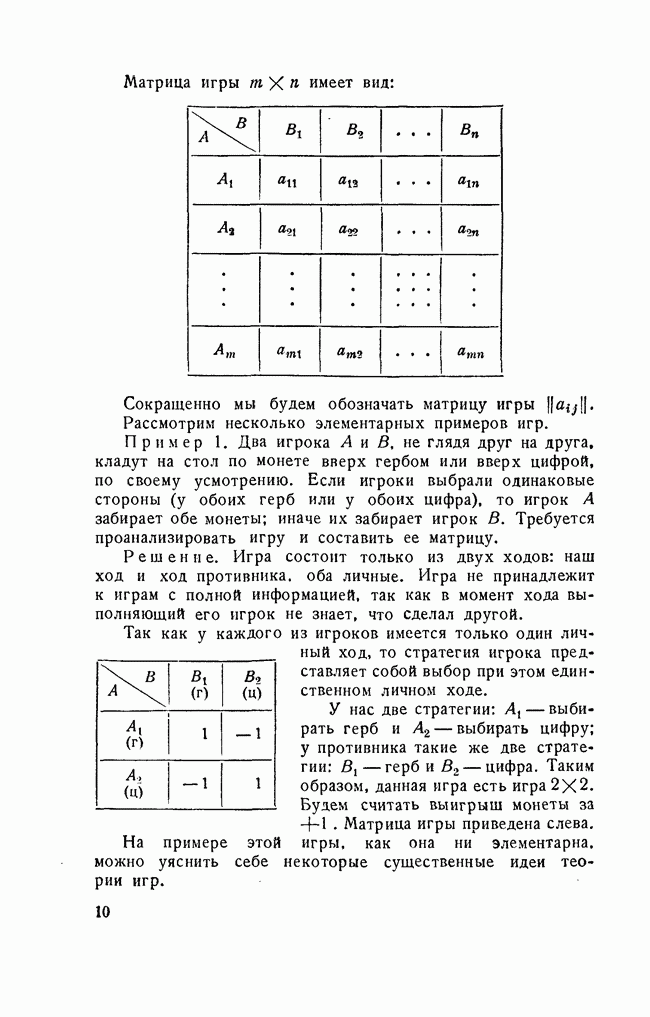
Бесконечной игрой называется игра, в которой по крайней мере одна из сторон имеет бесконечное множество стратегий. Общие методы решения таких игр еще мало разработаны. Однако для практики могут представлять интерес некоторые частные случаи, которые допускают сравнительно простое решение.
Рассмотрим игру двух противников А и В, каждый из которых имеет бесконечное (несчетное) множество стратегий; эти стратегии для игрока А соответствуют различным значениям непрерывно меняющегося параметра  , а для В — параметра у. В данном случае вместо матрицы
, а для В — параметра у. В данном случае вместо матрицы  игру определяет некоторая функция двух непрерывно меняющихся аргументов
игру определяет некоторая функция двух непрерывно меняющихся аргументов  которую мы будем называть функцией выигрыша (заметим, что сама функция
которую мы будем называть функцией выигрыша (заметим, что сама функция  необязательно должна быть непрерывной). Функцию выигрыша
необязательно должна быть непрерывной). Функцию выигрыша  можно представить геометрически некоторой поверхностью
можно представить геометрически некоторой поверхностью  над областью изменения аргументов (х, у) (рис. 7.1)
над областью изменения аргументов (х, у) (рис. 7.1)
Анализ функции выигрыша  производится аналогично анализу платежной матрицы. Сначала находится нижняя цена игры а; для этого определяется для каждого х минимум
производится аналогично анализу платежной матрицы. Сначала находится нижняя цена игры а; для этого определяется для каждого х минимум
функции  по всем у.
по всем у.

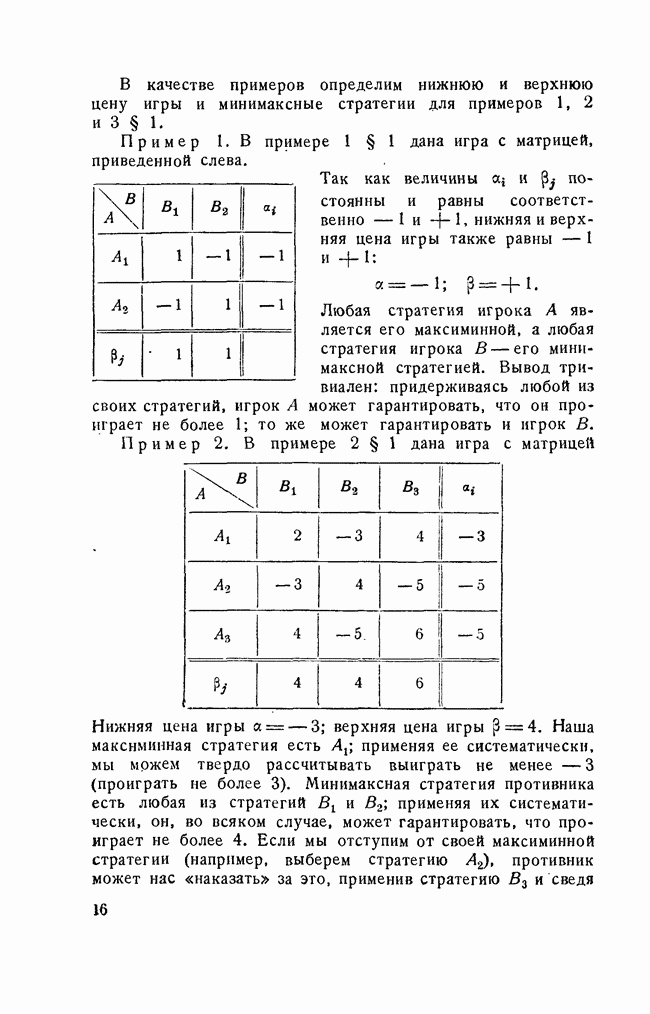
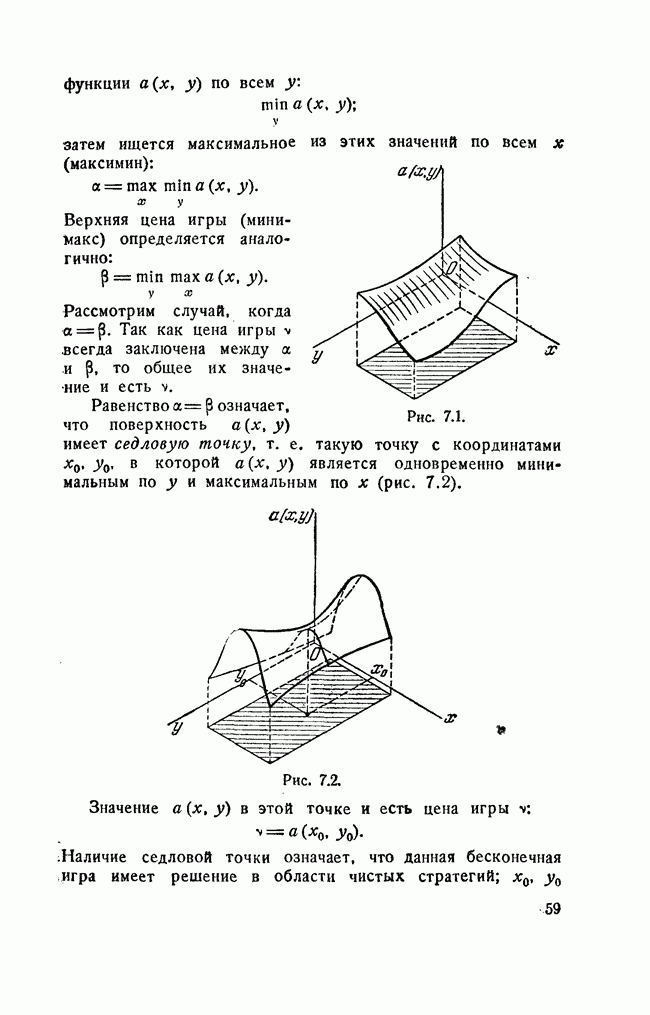
затем ищется максимальное из этих значений по всем х (максимин):

Верхняя цена игры (мини-макс) определяется аналогично:

Рассмотрим случай, когда  Так как цена игры всегда заключена между
Так как цена игры всегда заключена между  , то общее их значение и есть V.
, то общее их значение и есть V.

Рис. 7.1.
Равенство  означает, что поверхность
означает, что поверхность  имеет седловую точку, т. е. такую точку с координатами
имеет седловую точку, т. е. такую точку с координатами  в которой
в которой  является одновременно минимальным по у и максимальным по
является одновременно минимальным по у и максимальным по 

Рис. 7.2.
Значение а  в этой точке и есть цена игры v:
в этой точке и есть цена игры v:

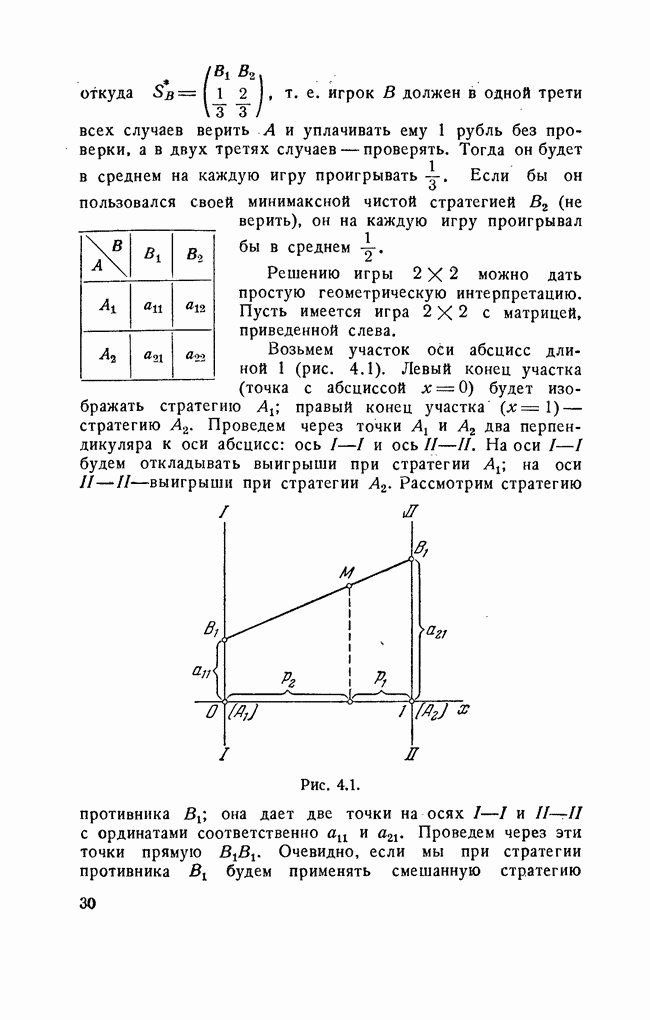
Наличие седловой точки означает, что данная бесконечная игра имеет решение в области чистых стратегий; 
представляют собой оптимальные чистые стратегии А и В. В общем случае, когда  , игра может иметь решение только в области смешанных стратегий (возможно, не единственное). Смешанная стратегия для бесконечных игр есть некоторое распределение вероятностей для стратегий
, игра может иметь решение только в области смешанных стратегий (возможно, не единственное). Смешанная стратегия для бесконечных игр есть некоторое распределение вероятностей для стратегий  и у, рассматриваемых как случайные величины. Это распределение может быть непрерывным и определяться плотностями
и у, рассматриваемых как случайные величины. Это распределение может быть непрерывным и определяться плотностями  может быть дискретным, и тогда оптимальные стратегии состоят из набора отдельных чистых стратегий, выбираемых с какими-то отличными от нуля вероятностями.
может быть дискретным, и тогда оптимальные стратегии состоят из набора отдельных чистых стратегий, выбираемых с какими-то отличными от нуля вероятностями.
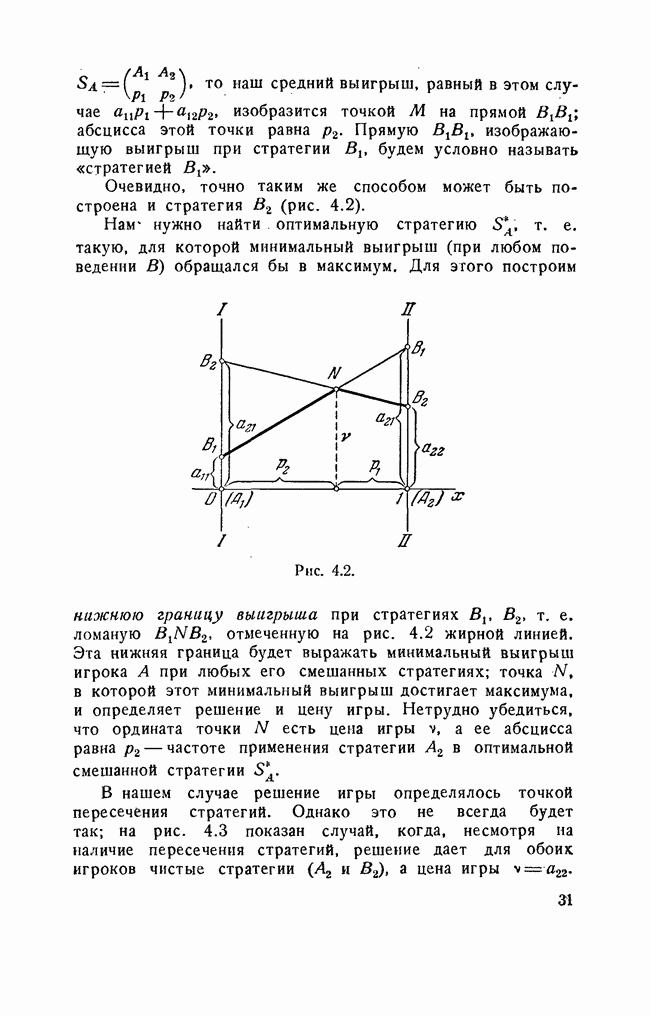
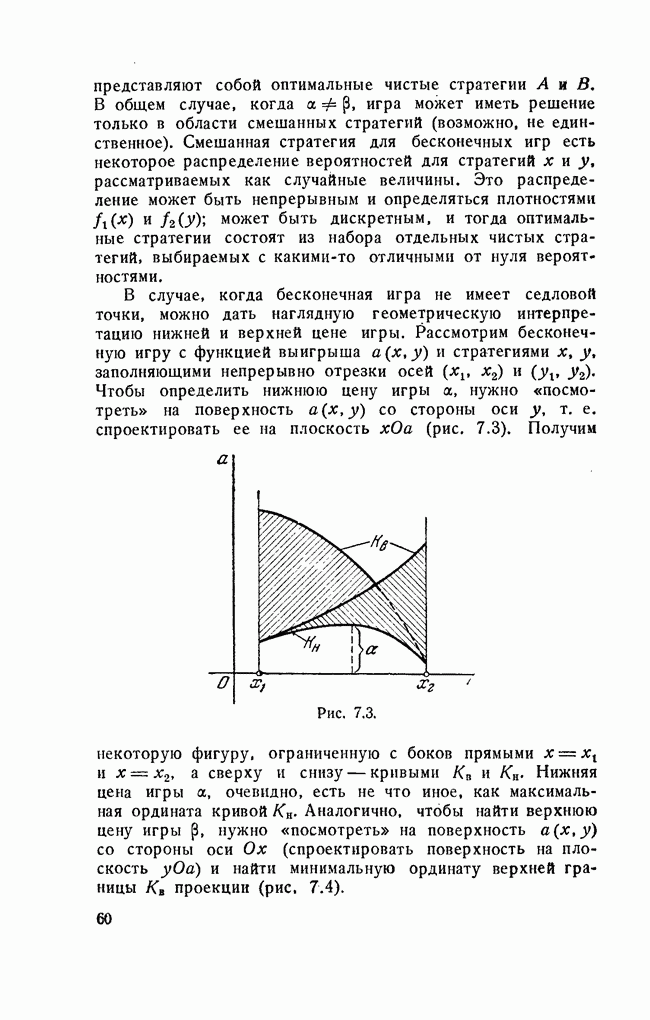
В случае, когда бесконечная игра не имеет седловой точки, можно дать наглядную геометрическую интерпретацию нижней и верхней цене игры. Рассмотрим бесконечную игру с функцией выигрыша  и стратегиями х, у, заполняющими непрерывно отрезки осей
и стратегиями х, у, заполняющими непрерывно отрезки осей  Чтобы определить нижнюю цену игры а, нужно «посмотреть» на поверхность
Чтобы определить нижнюю цену игры а, нужно «посмотреть» на поверхность  со стороны оси у, т. е. спроектировать ее на плоскость
со стороны оси у, т. е. спроектировать ее на плоскость 

Рис. 7.3.
Получим некоторую фигуру, ограниченную с боков прямыми  а сверху и снизу — кривыми
а сверху и снизу — кривыми  и Нижняя цена игры а, очевидно, есть не что иное, как максимальная ордината кривой
и Нижняя цена игры а, очевидно, есть не что иное, как максимальная ордината кривой  . Аналогично, чтобы найти верхнюю цену игры
. Аналогично, чтобы найти верхнюю цену игры  , нужно «посмотреть» на поверхность
, нужно «посмотреть» на поверхность  со стороны оси Ох (спроектировать поверхность на плоскость
со стороны оси Ох (спроектировать поверхность на плоскость  ) и найти минимальную ординату верхней границы
) и найти минимальную ординату верхней границы  проекции (рис, 7.4).
проекции (рис, 7.4).
Рассмотрим два элементарных примера бесконечных игр. Пример 1. Игроки А и В имеют каждый несчетное множество возможных стратегий х и у, причем 

Рис. 7.4.
Функция выигрыша задана выражением

Найти решение игры.
Решение. Поверхность  представляет собой параболический цилиндр (рис. 7.5) и не имеет седловой точки. Определим нижнюю цену игры; очевидно,
представляет собой параболический цилиндр (рис. 7.5) и не имеет седловой точки. Определим нижнюю цену игры; очевидно,  для всех
для всех  отсюда
отсюда 

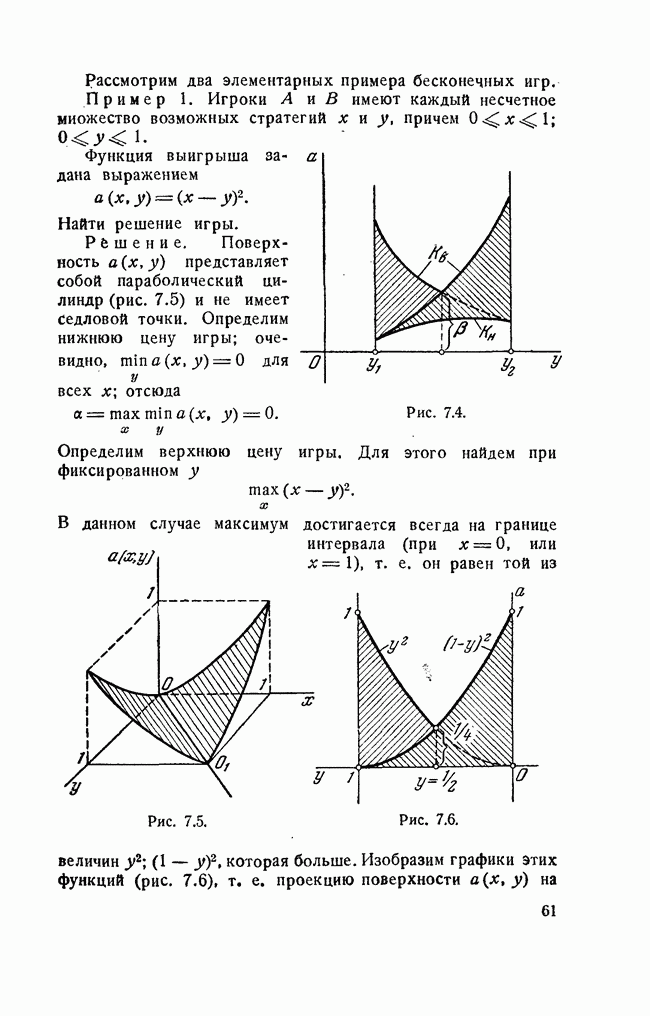
Определим верхнюю цену игры. Для этого найдем при фиксированном у

В данном случае максимум достигается всегда на границе интервала  или
или  т. е. он равен той из величин
т. е. он равен той из величин  которая больше.
которая больше.

Рис. 7.5.

Рис. 7.6.
Изобразим графики этих функций (рис. 7.6), т. е. проекцию поверхности  на
на
плоскость  Жирной линией на рис. 7.6 показана функция
Жирной линией на рис. 7.6 показана функция  Очевидно, ее минимальное значение достигается при
Очевидно, ее минимальное значение достигается при  и равно
и равно  Следовательно, верхняя цена игры
Следовательно, верхняя цена игры 
В данном случае верхняя цена игры совпадает с цеиой игры Действительно, игрок А может применить смешанную стратегию  в которую крайние значения
в которую крайние значения  входят с одинаковыми частотами; тогда при любой стратегии у игрока В средний выигрыш игрока А будет равен;
входят с одинаковыми частотами; тогда при любой стратегии у игрока В средний выигрыш игрока А будет равен;

Нетрудно убедиться, что эта величина при любых значениях у между 0 и 1 имеет значение не меньшее

Таким образом, игрок А применением данной смешанной стратегии может гарантировать себе выигрыш, равный верхней цене игры; так как цена игры не может быть больше верхней цены, то данная стратегия  есть оптимальная:
есть оптимальная:

Остается найти оптимальную стратегию игрока В,
Очевидно, что если цена игры  равна верхней цене игры
равна верхней цене игры  , то оптимальной стратегией игрока В будет всегда его чистая минимаксная стратегия, гарантирующая ему верхнюю цену игры. В данном случае такой стратегией является
, то оптимальной стратегией игрока В будет всегда его чистая минимаксная стратегия, гарантирующая ему верхнюю цену игры. В данном случае такой стратегией является  Действительно, при этой стратегии, что бы ни делал игрок А, выигрыш его не будет больше 1. Это следует из очевидного неравенства
Действительно, при этой стратегии, что бы ни делал игрок А, выигрыш его не будет больше 1. Это следует из очевидного неравенства

Пример 2. Сторона («мы») ведет стрельбу по самолету В противника. Для того чтобы уклониться от
обстрела, противник может маневрировать с некоторой перегрузкой у, которой он по своему усмотрению может придавать значения от  (прямолинейное движение) до
(прямолинейное движение) до  (полет по окружности максимальной кривизны). Будем считать
(полет по окружности максимальной кривизны). Будем считать  единицей измерения, т. е. положим
единицей измерения, т. е. положим 
В борьбе с противником мы можем применять прицельные приспособления, основанные на той или иной гипотезе о движении цели за время полета снаряда. Перегрузка  при этом гипотетическом маневре может полагаться равной любому значению от 0 до 1.
при этом гипотетическом маневре может полагаться равной любому значению от 0 до 1.
Наша задача — поразить противника; задача противника — остаться непораженным. Вероятность поражения для данных х и у приближенно выражается формулой

где у — перегрузка, применяемая противником; х — перегрузка, учтенная в прицеле.

Рис. 7.7.
Требуется определить оптимальные стратегии обеих сторон.
Решение, Очевидно, решение игры не изменится, если мы положим 
Функция выигрыша  изображается поверхностью, представленной на рис. 7.7.
изображается поверхностью, представленной на рис. 7.7.
Это — цилиндрическая поверхность, образующие которой параллельны биссектрисе координатного угла  а сечение плоскостью, перпендикулярной к образующей, есть кривая типа нормальной кривой распределения.
а сечение плоскостью, перпендикулярной к образующей, есть кривая типа нормальной кривой распределения.
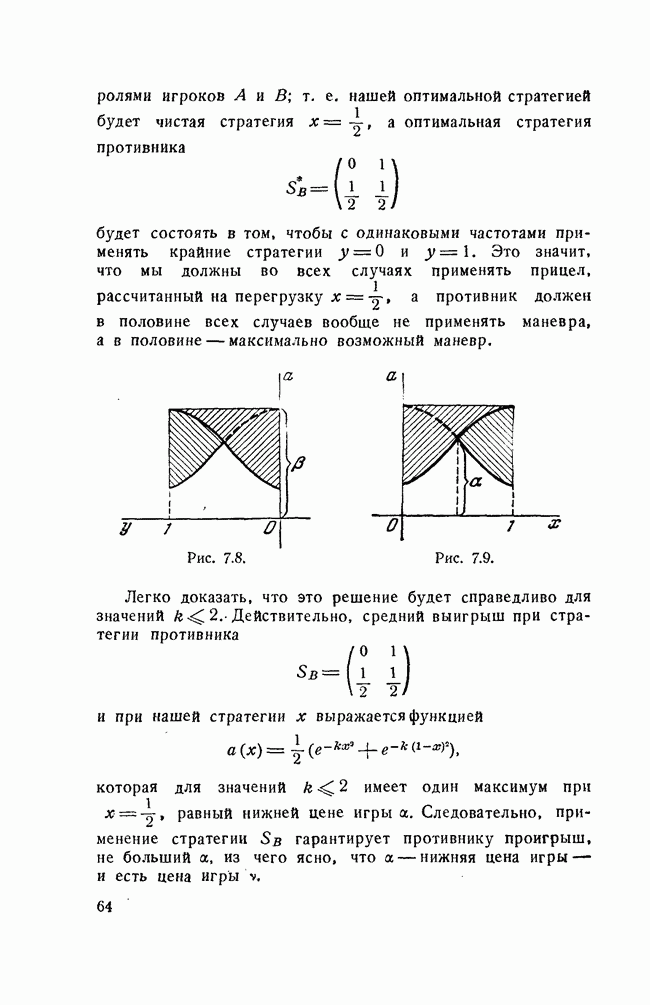
Пользуясь предложенной выше геометрической интерпретацией нижней и верхней цены игры, находим  (рис. 7.8) и
(рис. 7.8) и  (рис. 7.9).
(рис. 7.9).
Игра не имеет седловой точки; решение нужно искать в области смешанных стратегий. Задача до некоторой степени аналогична задаче предыдущего примера. Действительно, при малых значениях к функция  ведет себя примерно как функция
ведет себя примерно как функция  и решение игры получится, если в решении предыдущего примера поменять
и решение игры получится, если в решении предыдущего примера поменять
ролями игроков А и В; т. е. нашей оптимальной стратегией будет чистая стратегия  а оптимальная стратегия противника
а оптимальная стратегия противника

будет состоять в том, чтобы с одинаковыми частотами применять крайние стратегии  и
и  . Это значит, что мы должны во всех случаях применять прицел, рассчитанный на перегрузку
. Это значит, что мы должны во всех случаях применять прицел, рассчитанный на перегрузку  а противник должен в половине всех случаев вообще не применять маневра, а в половине — максимально возможный маневр.
а противник должен в половине всех случаев вообще не применять маневра, а в половине — максимально возможный маневр.

Рис. 7.8.

Рис. 7.9.
Легко доказать, что это решение будет справедливо для значений  . Действительно, средний выигрыш при стратегии противника
. Действительно, средний выигрыш при стратегии противника

и при нашей стратегии  выражается функцией
выражается функцией

которая для значений  имеет один максимум при
имеет один максимум при  равный нижней цене игры а. Следовательно, применение стратегии
равный нижней цене игры а. Следовательно, применение стратегии  гарантирует противнику проигрыш, не больший а, из чего ясно, что а — нижняя цена игры — и есть цена игры
гарантирует противнику проигрыш, не больший а, из чего ясно, что а — нижняя цена игры — и есть цена игры 
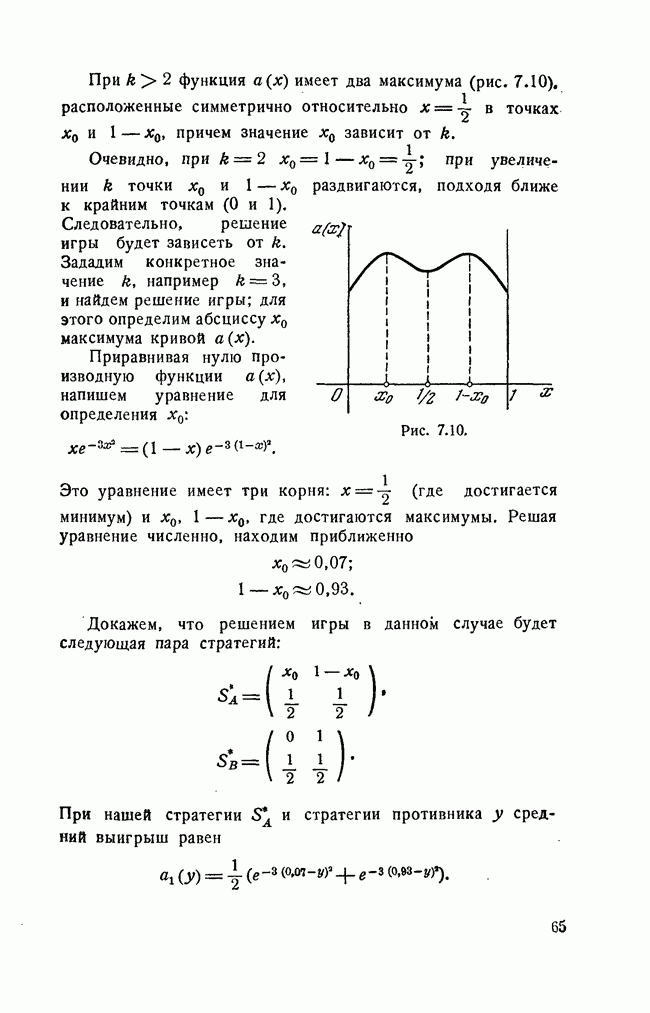
При  функция
функция  имеет два максимума (рис. 7.10). расположенные симметрично относительно
имеет два максимума (рис. 7.10). расположенные симметрично относительно  в точках
в точках  причем значение
причем значение  зависит от k.
зависит от k.
Очевидно, при  при увеличении k точки
при увеличении k точки  раздвигаются, подходя ближе к крайним точкам (0 и 1).
раздвигаются, подходя ближе к крайним точкам (0 и 1).

Рис. 7.10.
Следовательно, решение игры будет зависеть от k.
Зададим конкретное значение k, например  и найдем решение игры; для этого определим абсциссу
и найдем решение игры; для этого определим абсциссу  максимума кривой
максимума кривой 
Приравнивая нулю производную функции  напишем уравнение для определения
напишем уравнение для определения 

Это уравнение имеет три корня:  (где достигается минимум) и
(где достигается минимум) и  , где достигаются максимумы. Решая уравнение численно, находим приближенно
, где достигаются максимумы. Решая уравнение численно, находим приближенно

Докажем, что решением игры в данном случае будет следующая пара стратегий:

При нашей стратегии и стратегии противника у средний выигрыш равен

Найдем минимум  при
при  Функция симметрична относительно
Функция симметрична относительно  и может иметь только один или два максимума; ее минимум, во всяком случае, достигается либо в середине отрезка (0, 1), либо на его концах. Полагая
и может иметь только один или два максимума; ее минимум, во всяком случае, достигается либо в середине отрезка (0, 1), либо на его концах. Полагая  найдем
найдем

Полагая  получаем
получаем

что больше, чем  следовательно, цена игры не меньше, чем
следовательно, цена игры не меньше, чем 

Теперь допустим, что противник применяет стратегию  а мы — стратегию х. Тогда средний выигрыш будет
а мы — стратегию х. Тогда средний выигрыш будет

Но мы выбрали  именно так, чтобы при
именно так, чтобы при  достигался максимум выражения (7.2); следовательно,
достигался максимум выражения (7.2); следовательно,

т. е. противник применением стратегии может не допустить проигрыша, большего 0,530; следовательно,  и есть цена игры, а стратегии и
и есть цена игры, а стратегии и  дают решение. Это значит, что мы должны с одинаковой частотой пользоваться прицелами с
дают решение. Это значит, что мы должны с одинаковой частотой пользоваться прицелами с  , а противник с одинаковой частотой не маневрировать и маневрировать с максимальной перегрузкой.
, а противник с одинаковой частотой не маневрировать и маневрировать с максимальной перегрузкой.
Заметим, что выигрыш  заметно больше, чем нижняя цена игры
заметно больше, чем нижняя цена игры

которую мы могли бы обеспечить себе, применяя свою максиминную стратегию 
Одним из практических способов решения бесконечных игр является их приближенное сведение к конечным. При этом целый диапазон возможных стратегий каждого игрока условно объединяется в одну стратегию. Таким способом, разумеется, можно получить только приближенное решение игры, но в большинстве случаев точного решения и не требуется.
Однако нужно иметь в виду, что при применении этого приема могут появиться решения в области смешанных стратегий даже в случаях, когда решение исходной бесконечной игры возможно в чистых стратегиях, т. е. когда бесконечная игра имеет седловую точку. Если путем сведения бесконечной игры к конечной получено смешанное решение, в которое входят только две соседние «полезные» стратегии, то имеет смысл попытаться применить промежуточную между ними чистую стратегию исходной бесконечной игры.
В заключение заметим, что бесконечные игры в отличие от конечных могут и не иметь решения. Приведем пример бесконечной игры, не имеющей решения. Два игрока называют каждый любое целое число. Назвавший большее число получает от другого 1 рубль. Если оба назвали одно и то же число, игра заканчивается вничью. Игра, очевидно, не может иметь решения. Однако существуют классы бесконечных игр, для которых решение заведомо существует. В частности, можно доказать, что если в бесконечной игре возможные стратегии х, у игроков А, В непрерывно заполняют некоторые промежутки и функция выигрыша  непрерывна, то решение игры (в чистых или смешанных стратегиях) всегда существует.
непрерывна, то решение игры (в чистых или смешанных стратегиях) всегда существует.
| << Предыдущий параграф |
- § 1. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ
- § 2. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП «МИНИМАКСА»
- § 3. ЧИСТЫЕ И СМЕШАННЫЕ СТРАТЕГИИ. РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ
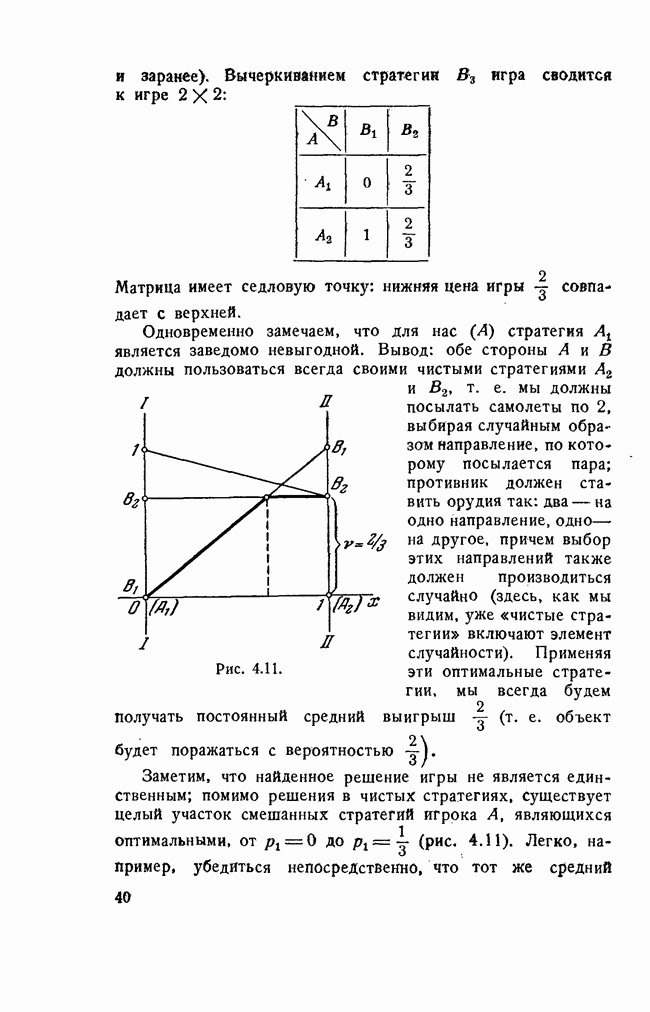
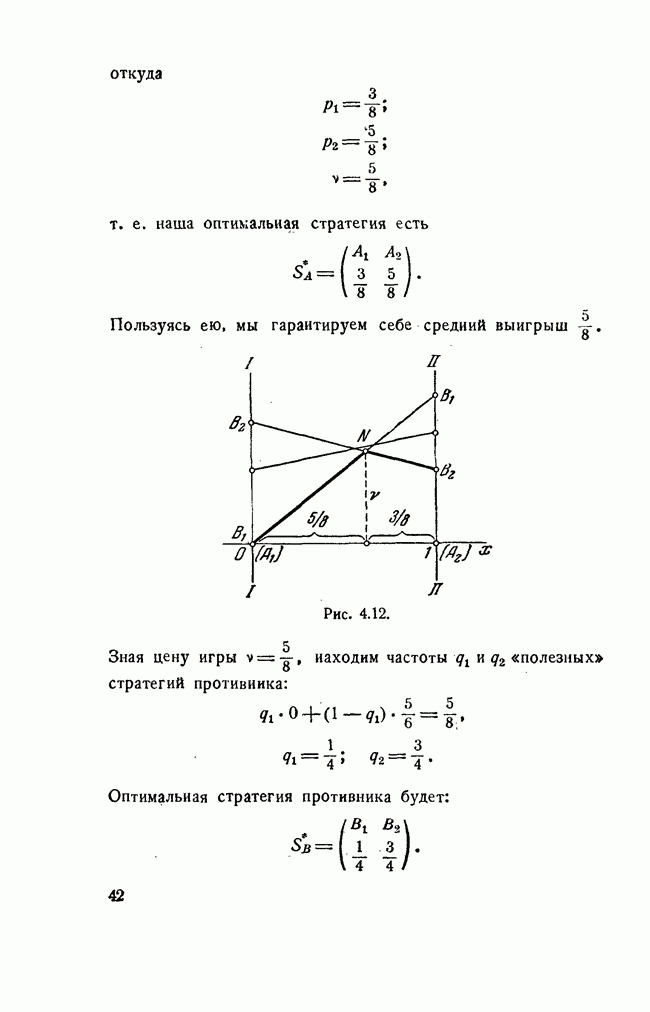
- § 4. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ ИГР. ИГРЫ 2X2 И 2Xn
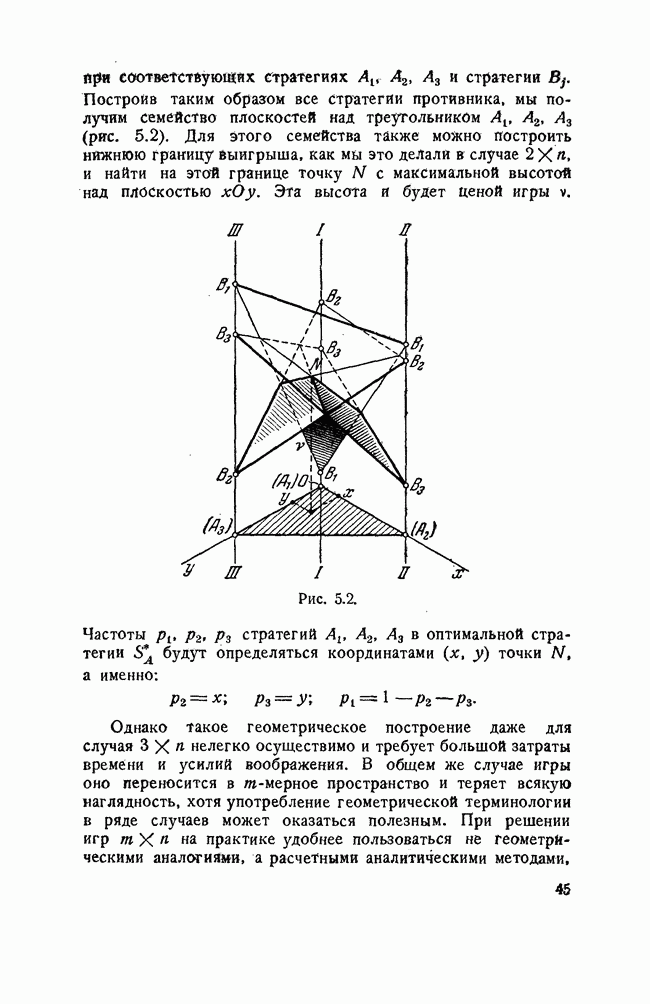
- § 5. ОБЩИЕ МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР
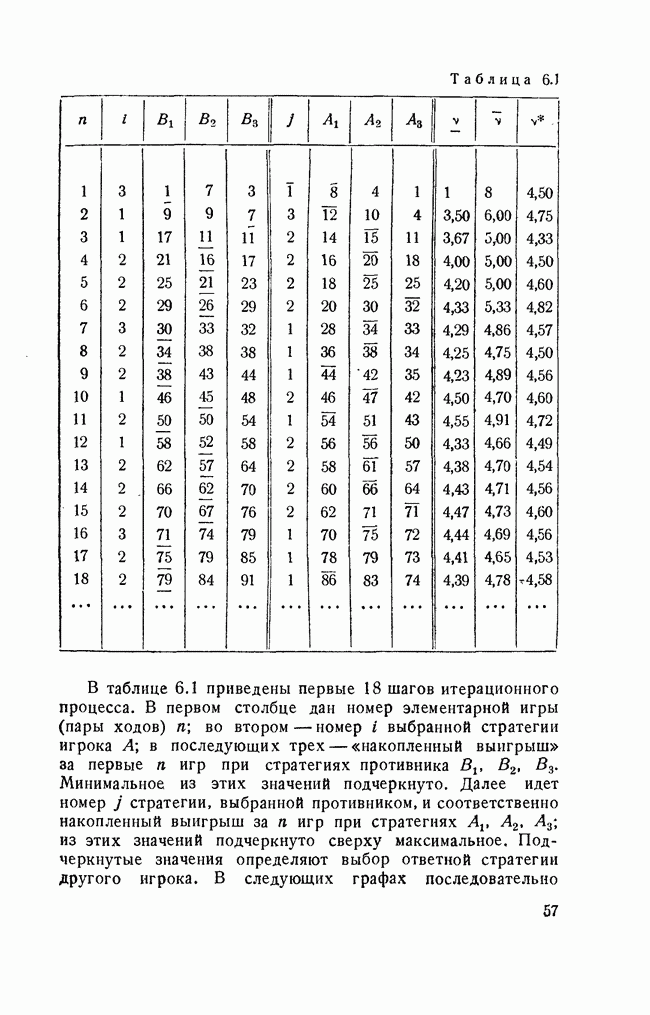
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИГР
- § 7. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР