| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ ИГР. ИГРЫ 2X2 И 2Xn
Если игра  не имеет седловой точки, то нахождение решения есть вообще довольно трудная задача, особенно при больших тип.
не имеет седловой точки, то нахождение решения есть вообще довольно трудная задача, особенно при больших тип.
Иногда эту задачу удается упростить, если предварительно уменьшить число стратегий путем вычеркивания некоторых излишних.
Излишние стратегии бывают а) дублирующие и б) заведомо невыгодные. Рассмотрим, например, игру с матрицей:

Нетрудно убедиться, что стратегия  в точности повторяет («дублирует») стратегию
в точности повторяет («дублирует») стратегию  поэтому любую из этих двух стратегий можно вычеркнуть.
поэтому любую из этих двух стратегий можно вычеркнуть.
Далее, сравнивая почленно строки  видим, что каждый элемент строки А, меньше (или равен) соответствующего элемента строки
видим, что каждый элемент строки А, меньше (или равен) соответствующего элемента строки 

Очевидно, что мы никогда не должны пользоваться стратегией  она является заведомо невыгодной. Вычеркивая
она является заведомо невыгодной. Вычеркивая  приводим матрицу к более простому виду (см. слева). Далее замечаем, что для противника стратегия
приводим матрицу к более простому виду (см. слева). Далее замечаем, что для противника стратегия  заведомо невыгодна; вычеркивая ее, приводим матрицу к окончательному виду (см. ниже). Таким образом, игра 4X4 вычеркиванием дублирующих и заведомо невыгодных стратегий сведена к игре 2X3.
заведомо невыгодна; вычеркивая ее, приводим матрицу к окончательному виду (см. ниже). Таким образом, игра 4X4 вычеркиванием дублирующих и заведомо невыгодных стратегий сведена к игре 2X3.
Процедура вычеркивания дублирующих и заведомо невыгодных стратегий всегда должна предшествовать решению игры.
Наиболее простыми случаями конечных игр, которые всегда

можно решить элементарными способами, являются игры  .
.
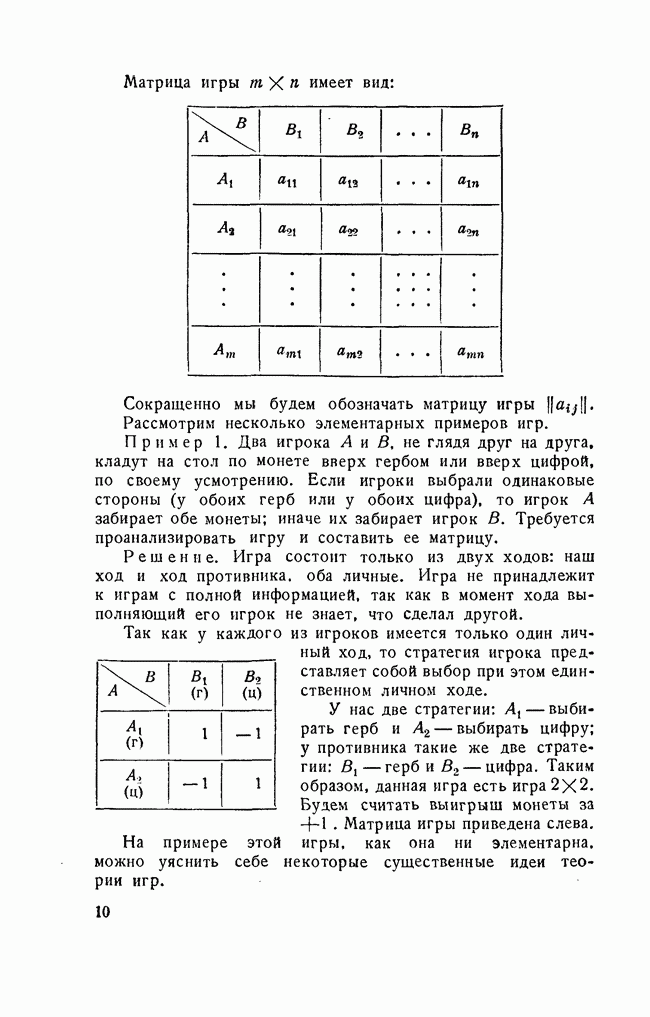
Рассмотрим игру 2X2 с матрицей:

Здесь могут встретиться два случая:
1) игра имеет седловую точку; 2) игра не имеет седловой точки. В первом случае решение очевидно: это пара стратегий, пересекающихся в седловой точке. Заметим кстати, что в игре 2X2 наличие седловой точки всегда соответствует существованию заведомо невыгодных стратегий, которые должны быть вычеркнуты при предварительном анализе.
Пусть седловой точки нет и, следовательно, нижняя цена игры не равна верхней:  Требуется найти оптимальную смешанную стратегию игрока А:
Требуется найти оптимальную смешанную стратегию игрока А:

Она отличается тем свойством, что, каковы бы ни были действия противника (если только он не выходит за пределы своих «полезных» стратегий), выигрыш будет равен цене игры v. В игре 2X2 обе стратегии противника являются «полезными», — иначе игра имела бы решение в области чистых стратегий (седловую точку). Значит, если мы придерживаемся своей оптимальной стратегии  , то противник может пользоваться любой из своих чистых стратегий
, то противник может пользоваться любой из своих чистых стратегий  не изменяя среднего выигрыша V. Отсюда имеем два уравнения:
не изменяя среднего выигрыша V. Отсюда имеем два уравнения:

из которых, принимая во внимание,  получим:
получим:

Цену игры v найдем, подставляя значения  в любое из уравнений (4.1).
в любое из уравнений (4.1).
Если цена игры известна, то для. определения оптимальной стратегии противника  достаточно одного уравнения, например:
достаточно одного уравнения, например:

откуда, учитывая, что  имеем:
имеем:

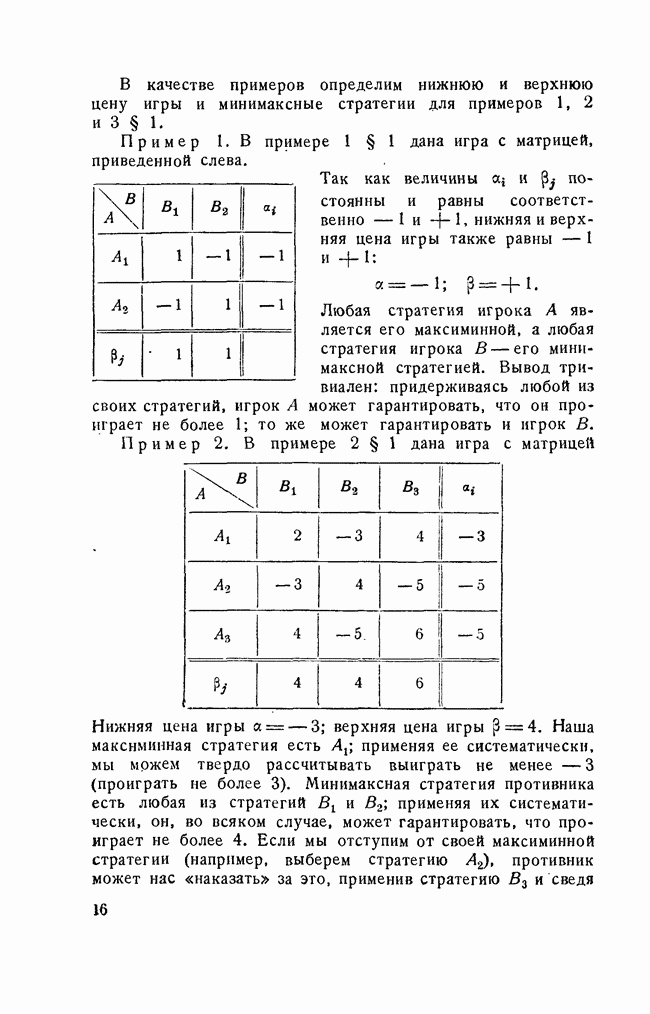
Пример 1. Найдем решение игры  рассмотренной в примере 1 § 1, с матрицей.
рассмотренной в примере 1 § 1, с матрицей.

Игра не имеет седловой точки  и, следовательно, решение должно лежать в области смешанных стратегий:
и, следовательно, решение должно лежать в области смешанных стратегий:

Нужно найти  .
.
Для  имеем уравнение
имеем уравнение

откуда

Аналогично найдем:

Следовательно, оптимальная стратегия для каждого из игроков состоит в том, чтобы случайным образом чередовать обе свои чистые стратегии, пользуясь одинаково часто каждой из них; при этом средний выигрыш будет равен нулю.
Полученный вывод был достаточно ясен заранее. В следующем примере мы рассмотрим более сложную игру, решение которой не является столь очевидным. Пример представляет собой элементарный образец игр, известных под названием игр с «обманом» или «введением в заблуждение». На практике в конфликтных ситуациях часто применяются разные - способы введения противника в заблуждение (дезинформация, расстановка ложных целей и т. д.). Пример, несмотря на свою простоту, довольно поучителен.
Пример 2. Игра состоит в следующем. Имеются две карты: туз и двойка. Игрок А наугад вынимает одну из них; В не видит, какую карту он вынул. Если А вынул туза, он заявляет: «у меня туз», и требует у противника 1 рубль. Если А вынул двойку, то он может либо  сказать «у меня туз» и потребовать у противника 1 рубль, либо
сказать «у меня туз» и потребовать у противника 1 рубль, либо  признаться, что у него двойка, и уплатить противнику 1 рубль.
признаться, что у него двойка, и уплатить противнику 1 рубль.
Противник, если ему добровольно платят 1 рубль, может только принять его. Если же у него потребуют 1 рубль, то он может либо  поверить игроку А, что у него туз, и отдать ему 1 рубль, либо
поверить игроку А, что у него туз, и отдать ему 1 рубль, либо  потребовать проверки с тем, чтобы убедиться, верно ли утверждение А. Если в результате проверки окажется, что у А действительно туз, В должен уплатить А 2 рубля. Если же окажется, что А обманывает и у него двойка, игрок А уплачивает игроку В 2 рубля.
потребовать проверки с тем, чтобы убедиться, верно ли утверждение А. Если в результате проверки окажется, что у А действительно туз, В должен уплатить А 2 рубля. Если же окажется, что А обманывает и у него двойка, игрок А уплачивает игроку В 2 рубля.
Требуется проанализировать игру и найти оптимальную стратегию каждого из игроков.
Решение. Игра имеет сравнительно сложную структуру; она состоит из одного обязательного случайного хода — выбора игроком А одной из двух карт — и двух личных ходов, которые, однако, необязательно осуществляются. Действительно, если А вынул туза, то он не делает никакого личного хода: ему предоставлена только одна возможность — потребовать 1 рубль, что он и делает. В этом случае личный ход — верить или не верить (т. е. платить или не платить 1 рубль,) — передается игроку В. Если А в результате первого случайного хода получил двойку, то ему предоставляется личный ход: уплатить 1 рубль или попытаться обмануть противника и потребовать 1 рубль (короче: «не обманывать» или «обманывать»). Если А выбирает первое, то В остается только принять 1 рубль; если А выбрал второе, то игроку В предоставляется личный
ход: верить или не верить А (т. е. уплатить А 1 рубль или требовать проверки).
Стратегии каждого из игроков представляют собой правила, указывающие, как поступить игроку, когда ему предоставляется личный ход.
Очевидно, у А только две стратегии:
 - обманывать,
- обманывать,  - не обманывать.
- не обманывать.
У В - тоже две стратегии:
 - верить,
- верить,  - не верить.
- не верить.
Построим матрицу игры. Для этого вычислим средний выигрыш при каждой комбинации стратегий.
1.  (А обманывает, В верит).
(А обманывает, В верит).
Если А получил туза вероятность этого то ему не предоставляется личного хода; он требует 1 рубль, и игрок В верит ему; выигрыш А в рублях равен 1.
Если А получил двойку вероятность этого тоже он согласно своей стратегии обманывает и требует 1 рубль; В ему верит и уплачивает; выигрыш А также равен 1.
Средний выигрыш:

2.  (А обманывает, В не верит).
(А обманывает, В не верит).
Если А получил туза, у него нет личного хода; он требует 1 рубль; В согласно своей стратегии не верит и в результате проверки уплачивает 2 рубля (выигрыш А равен  ).
).
Если А получил двойку, он согласно своей стратегии требует 1 рубль; В, согласно своей, не верит; в результате А уплачивает 2 рубля (выигрыш А равен —2). Средний выигрыш равен:

3.  (А не обманывает, В верит).
(А не обманывает, В верит).
Если А вынул туза, он требует 1 рубль; В согласно своей стратегии уплачивает; выигрыш А равен  Если А вынул двойку, он согласно своей стратегии платит 1 рубль; В остается только принять (выигрыш А равен —1). Средний выигрыш равен:
Если А вынул двойку, он согласно своей стратегии платит 1 рубль; В остается только принять (выигрыш А равен —1). Средний выигрыш равен:

4.  (А не обманывает, В не верит).
(А не обманывает, В не верит).
Если А вынул туза, он требует 1 рубль; В проверяет и в результате проверки уплачивает 2 рубля (выигрыш равен +2).
Если А вынул двойку, он уплачивает 1 рубль; В остается только принять (выигрыш равен -1).
Средний выигрыш равен:

Строим матрицу игры (см. справа).

Матрица не имеет седловой точки.
Нижняя цена игры  , верхняя цена игры
, верхняя цена игры  . Найдем решение игры в области смешанных стратегий. Применяя формулу (4.2), получим:
. Найдем решение игры в области смешанных стратегий. Применяя формулу (4.2), получим:

т. е. игрок А должен в одной трети всех случаев пользоваться своей первой стратегией (обманывать), а в двух третях — второй (не обманывать). При этом он будет выигрывать в среднем цену игры

Значение свидетельствует о том, что в данных условиях игра выгодна для А и невыгодна для В. Пользуясь своей оптимальной стратегией, А всегда может себе обеспечить положительный средний выигрыш.
Заметим, что, если бы А пользовался своей наиболее осторожной (максиминной) стратегией (в данном случае обе стратегии  являются максиминными), он имел бы средний выигрыш, равный нулю. Таким образом, применение смешанной стратегии дает А возможность реализовать свое преимущество над В, возникающее при данных правилах игры.
являются максиминными), он имел бы средний выигрыш, равный нулю. Таким образом, применение смешанной стратегии дает А возможность реализовать свое преимущество над В, возникающее при данных правилах игры.
Определим оптимальную стратегию В. Имеем:

откуда  т. e. игрок В должен в одной трети
т. e. игрок В должен в одной трети  всех случаев верить А и уплачивать ему 1 рубль без проверки, а в двух третях случаев — проверять. Тогда он будет в среднем на каждую игру проигрывать Если бы он пользовался своей минимаксной чистой стратегией В2 (не верить), он на каждую игру проигрывал бы в среднем у.
всех случаев верить А и уплачивать ему 1 рубль без проверки, а в двух третях случаев — проверять. Тогда он будет в среднем на каждую игру проигрывать Если бы он пользовался своей минимаксной чистой стратегией В2 (не верить), он на каждую игру проигрывал бы в среднем у.

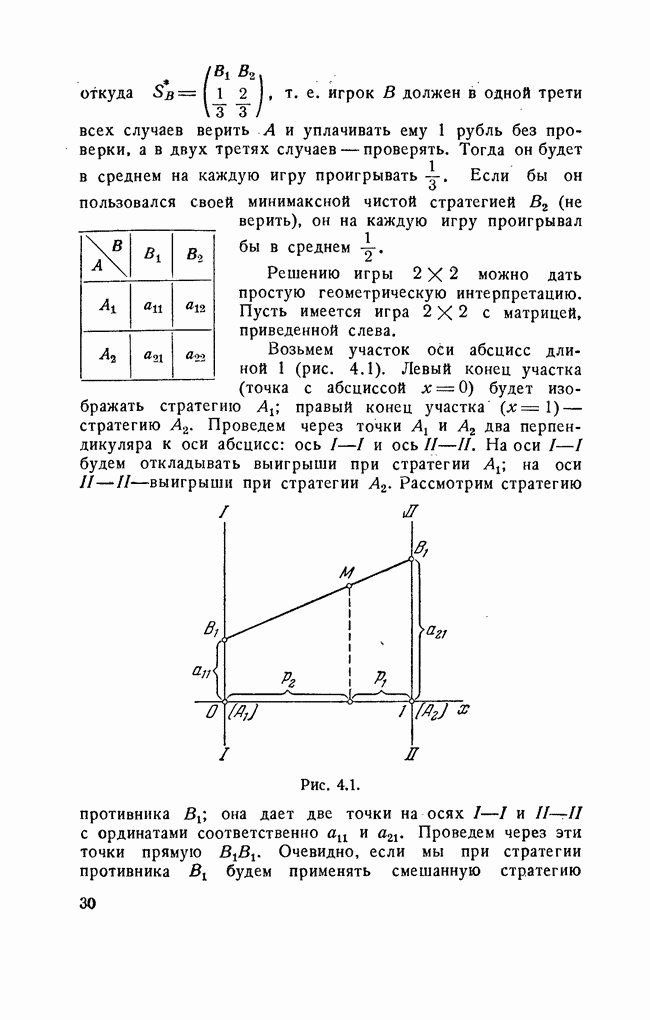
Решению игры 2X2 можно дать простую геометрическую интерпретацию. Пусть имеется игра 2X2 с матрицей, приведенной слева.
Возьмем участок оси абсцисс длиной 1 (рис. 4.1). Левый конец участка (точка с абсциссой  ) будет изображать стратегию правый конец участка
) будет изображать стратегию правый конец участка  стратегию
стратегию  Проведем через точки
Проведем через точки  два перпендикуляра к оси абсцисс: ось
два перпендикуляра к оси абсцисс: ось  и ось II—II. На оси I—I будем откладывать выигрыши при стратегии
и ось II—II. На оси I—I будем откладывать выигрыши при стратегии  ; на оси II—II — выигрыши при стратегии
; на оси II—II — выигрыши при стратегии 

Рис. 4.1.
Рассмотрим стратегию противника  она дает две точки на осях I—I и
она дает две точки на осях I—I и  с ординатами соответственно
с ординатами соответственно  Проведем через эти точки прямую Очевидно, если мы при стратегии противника
Проведем через эти точки прямую Очевидно, если мы при стратегии противника  будем применять смешанную стратегию
будем применять смешанную стратегию
 , то наш средний выигрыш, равный в этом случае
, то наш средний выигрыш, равный в этом случае  изобразится точкой М на прямой В; абсцисса этой точки равна
изобразится точкой М на прямой В; абсцисса этой точки равна  Прямую
Прямую  изображающую выигрыш при стратегии
изображающую выигрыш при стратегии  будем условно называть «стратегией
будем условно называть «стратегией  .
.
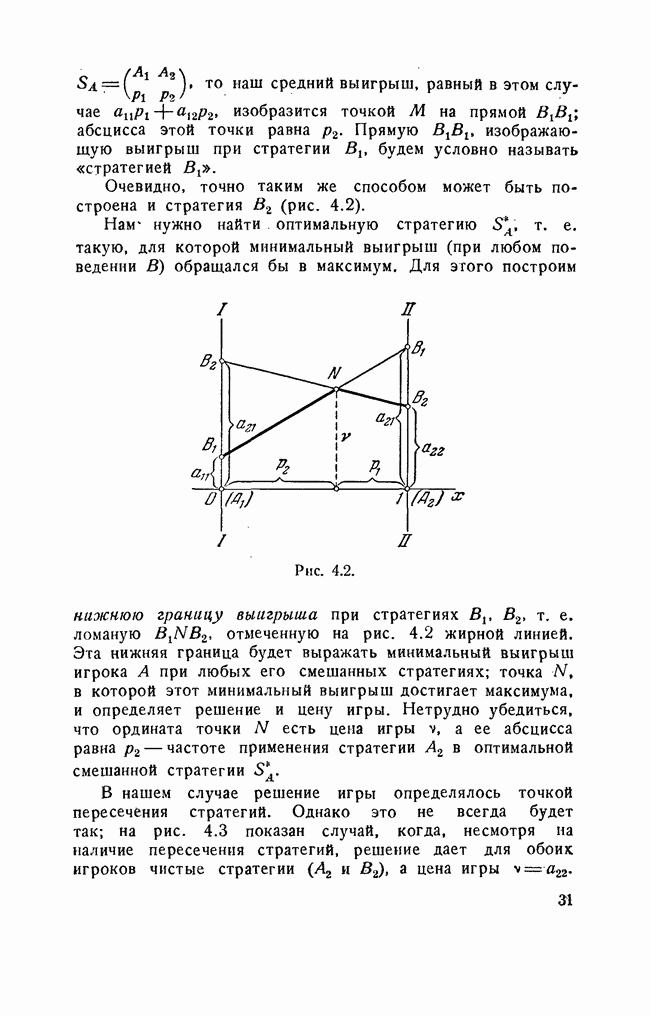
Очевидно, точно таким же способом может быть построена и стратегия 
Нам нужно найти оптимальную стратегию  , т. е. такую, для которой минимальный выигрыш (при любом поведении В) обращался бы в максимум.
, т. е. такую, для которой минимальный выигрыш (при любом поведении В) обращался бы в максимум.

Рис. 4.2.
Для этого построим нижнюю границу выигрыша при стратегиях  т. е. ломаную
т. е. ломаную  отмеченную на рис. 4.2 жирной линией. Эта нижняя граница будет выражать минимальный выигрыш игрока А при любых его смешанных стратегиях; точка N, в которой этот минимальный выигрыш достигает максимума, и определяет решение и цену игры. Нетрудно убедиться, что ордината точки N есть цена игры v, а ее абсцисса равна
отмеченную на рис. 4.2 жирной линией. Эта нижняя граница будет выражать минимальный выигрыш игрока А при любых его смешанных стратегиях; точка N, в которой этот минимальный выигрыш достигает максимума, и определяет решение и цену игры. Нетрудно убедиться, что ордината точки N есть цена игры v, а ее абсцисса равна  частоте применения стратегии
частоте применения стратегии  в оптимальной смешанной стратегии
в оптимальной смешанной стратегии  .
.
В нашем случае решение игры определялось точкой пересечения стратегий. Однако это не всегда будет так; на рис. 4.3 показан случай, когда, несмотря на наличие пересечения стратегий, решение дает для обоих игроков чистые стратегии  а цена игры
а цена игры 
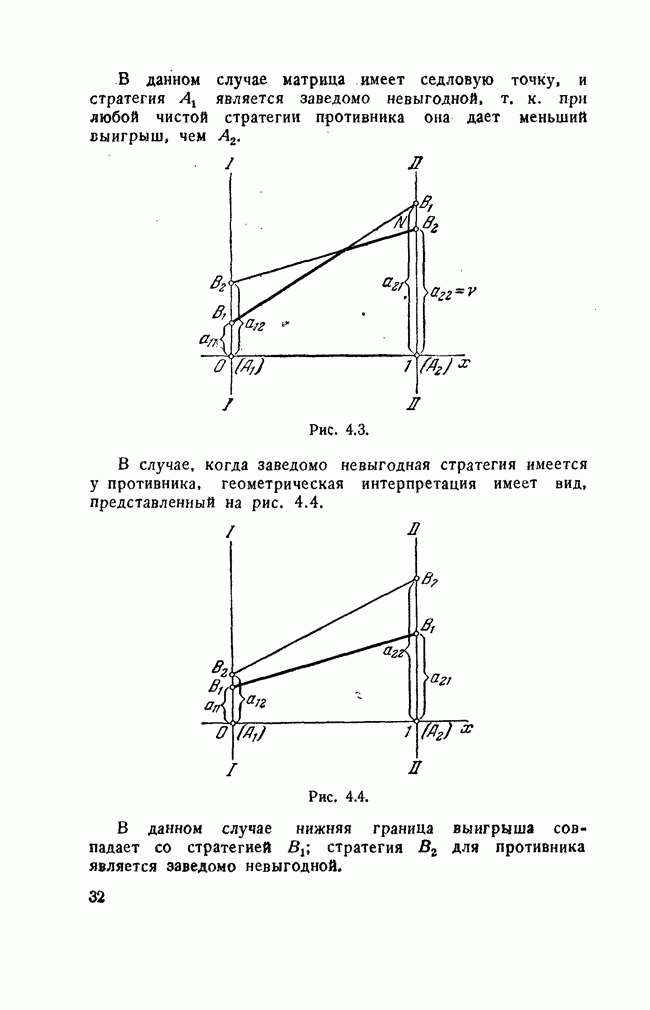
В данном случае матрица имеет седловую точку, и стратегия  является заведомо невыгодной, т. к. при любой чистой стратегии противника она дает меньший выигрыш, чем
является заведомо невыгодной, т. к. при любой чистой стратегии противника она дает меньший выигрыш, чем 

Рис. 4.3.
В случае, когда заведомо невыгодная стратегия имеется у противника, геометрическая интерпретация имеет вид, представленный на рис. 4.4.

Рис. 4.4.
В данном случае нижняя граница выигрыша совпадает со стратегией  стратегия
стратегия  для противника является заведомо невыгодной.
для противника является заведомо невыгодной.
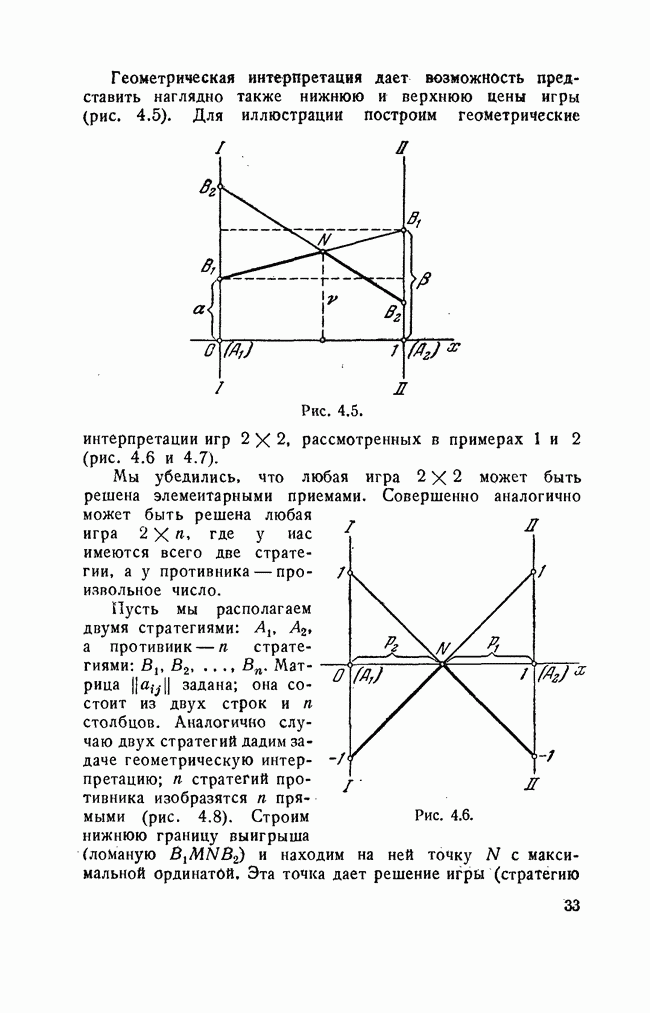
Геометрическая интерпретация дает возможность представить наглядно также нижнюю и верхнюю цены игры (рис. 4.5).

Рис. 4.5.
Для иллюстрации построим геометрические интерпретации игр  , рассмотренных в примерах 1 и 2 (рис. 4.6 и 4.7).
, рассмотренных в примерах 1 и 2 (рис. 4.6 и 4.7).
Мы убедились, что любая игра  может быть решена элементарными приемами. Совершенно аналогично может быть решена любая игра
может быть решена элементарными приемами. Совершенно аналогично может быть решена любая игра  , где у нас имеются всего две стратегии, а у противника — произвольное число.
, где у нас имеются всего две стратегии, а у противника — произвольное число.
Пусть мы располагаем двумя стратегиями:  а противник —
а противник —  стратегиями:
стратегиями:  Матрица
Матрица  задана; она состоит из двух строк и
задана; она состоит из двух строк и  столбцов. Аналогично случаю двух стратегий дадим задаче геометрическую интерпретацию;
столбцов. Аналогично случаю двух стратегий дадим задаче геометрическую интерпретацию;  стратегий противника изобразятся
стратегий противника изобразятся  прямыми (рис. 4.8). Строим нижнюю границу выигрыша (ломаную и находим на ней точку N с максимальной ординатой. Эта точка дает решение игры (стратегию
прямыми (рис. 4.8). Строим нижнюю границу выигрыша (ломаную и находим на ней точку N с максимальной ординатой. Эта точка дает решение игры (стратегию

Рис. 4.6.
 ордината точки N равна цене игры
ордината точки N равна цене игры  , а абсцисса равна частоте
, а абсцисса равна частоте  стратегии
стратегии  .
.
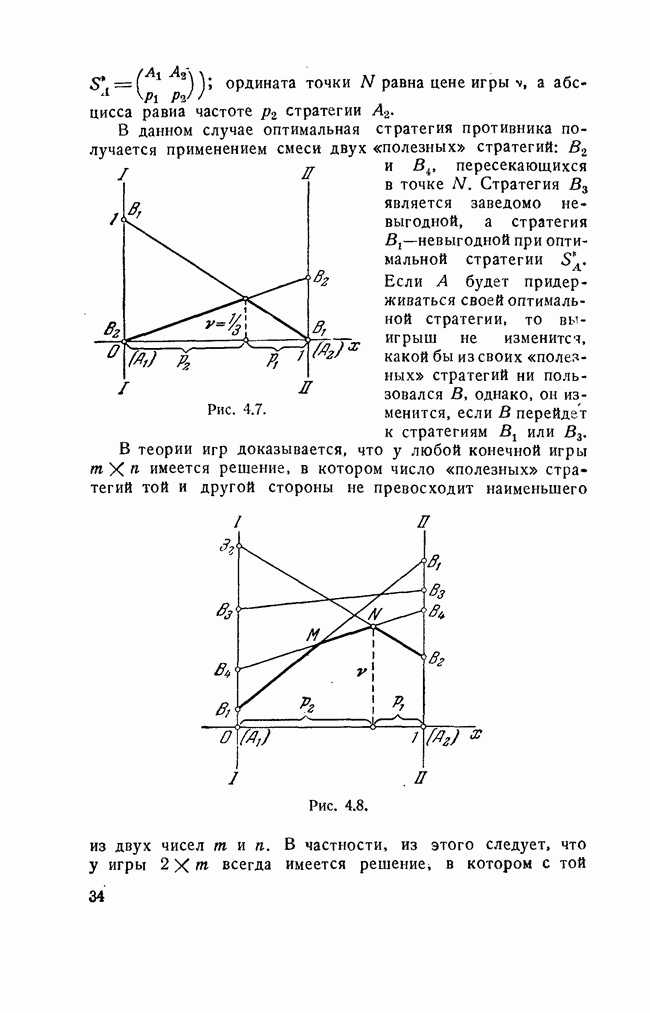
В данном случае оптимальная стратегия противника получается применением смеси двух «полезных» стратегий:  пересекающихся в точке N. Стратегия
пересекающихся в точке N. Стратегия  является заведомо невыгодной, а стратегия
является заведомо невыгодной, а стратегия  невыгодной при оптимальной стратегии
невыгодной при оптимальной стратегии  . Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих «полезных» стратегий ни пользовался В, однако, он изменится, если В перейдет к стратегиям
. Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих «полезных» стратегий ни пользовался В, однако, он изменится, если В перейдет к стратегиям  или
или  . В теории игр доказывается, что у любой конечной игры туп имеется решение, в котором число «полезных» стратегий той и другой стороны не превосходит наименьшего из двух чисел
. В теории игр доказывается, что у любой конечной игры туп имеется решение, в котором число «полезных» стратегий той и другой стороны не превосходит наименьшего из двух чисел  .
.

Рис. 4.7.

Рис. 4.8.
В частности, из этого следует, что у игры  всегда имеется решение в котором с той
всегда имеется решение в котором с той
и другой стороны участвует не более двух «полезных» стратегий.
Пользуясь геометрической интерпретацией, можно дать простой способ решения любой игры 2 X m. Непосредственно по чертежу находим пару «полезных» стратегий противника  пересекающиеся в точке N (если в точке N пересекается более двух стратегий, берем любые две из них). Мы знаем, что если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои «полезные» стратегии, следовательно,
пересекающиеся в точке N (если в точке N пересекается более двух стратегий, берем любые две из них). Мы знаем, что если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои «полезные» стратегии, следовательно,

Из этих уравнений и условия  находим
находим  и цену игры V.
и цену игры V.
Зная цену игры, можно сразу определить оптимальную стратегию  игрока В.
игрока В.
Для этого решается, например, уравнение:

где

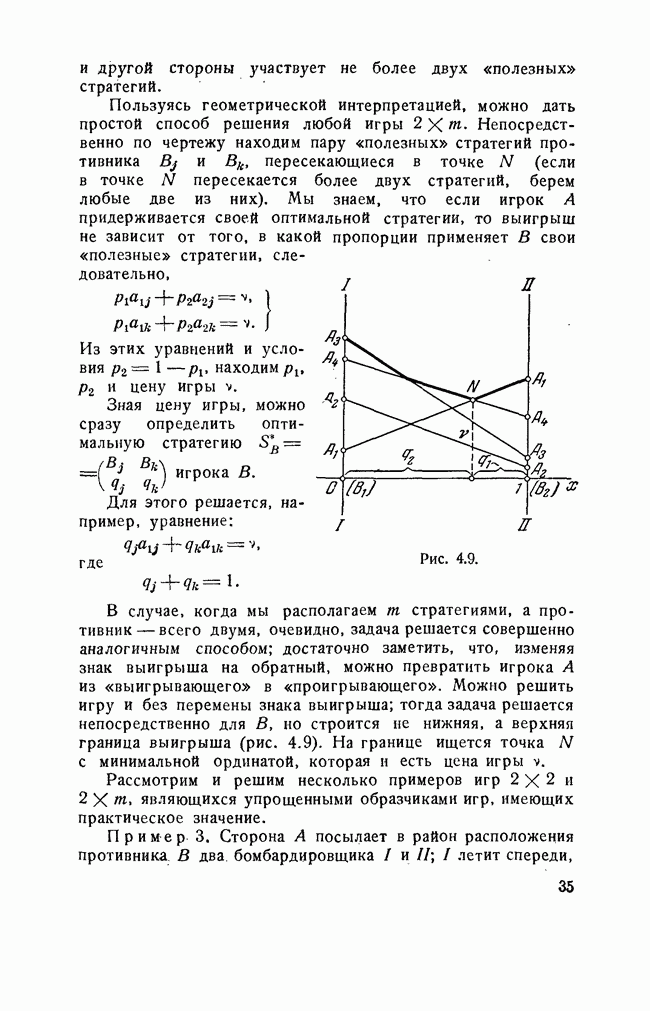
В случае, когда мы располагаем т. стратегиями, а противник — всего двумя, очевидно, задача решается совершенно аналогичным способом; достаточно заметить, что, изменяя знак выигрыша на обратный, можно превратить игрока А из «выигрывающего» в «проигрывающего». Можно решить игру и без перемены знака выигрыша; тогда задача решается непосредственно для В, но строится не нижняя, а верхняя граница выигрыша (рис. 4.9). На границе ищется точка  с минимальной ординатой, которая и есть цена игры
с минимальной ординатой, которая и есть цена игры 
Рассмотрим и решим несколько примеров игр  , являющихся упрощенными образчиками игр, имеющих практическое значение.
, являющихся упрощенными образчиками игр, имеющих практическое значение.
Пример 3. Сторона А посылает в район расположения противника В два бомбардировщика  летит спереди,
летит спереди,

Рис. 4.9.
II — сзади. Один из бомбардировщиков — заранее неизвестно какой — должен нести бомбу, другой выполняет функцию сопровождения. В районе противника бомбардировщики подвергаются нападению истребителя стороны В. Бомбардировщики вооружены пушками различной скорострельности. Если истребитель атакует задний бомбардировщик II, то по нему ведут огонь пушки только этого бомбардировщика; если же он атакует передний бомбардировщик, то по нему ведут огонь пушки обоих бомбардировщиков. Вероятность поражения истребителя в первом случае 0,3, во втором 0,7.
Если истребитель не сбит оборонительным огнем бомбардировщиков, то он поражает выбранную им цель с вероятностью 0,6. Задача бомбардировщиков — донести бомбу до цели; задача истребителя — воспрепятствовать этому, т. е. сбить бомбардировщик-носитель. Требуется выбрать оптимальные стратегии сторон:
а) для стороны А: какой бомбардировщик сделать носителем?
б) для стороны В: какой бомбардировщик атаковать?
Решение. Имеем простой случай игры 2X2; выигрыш — вероятность непоражения носителя.
Наши стратегии:
 - носитель — бомбардировщик I;
- носитель — бомбардировщик I;
 - носитель — бомбардировщик II.
- носитель — бомбардировщик II.
Стратегии противника:
 - атакуется бомбардировщик I;
- атакуется бомбардировщик I;
 - атакуется бомбардировщик II.
- атакуется бомбардировщик II.
Составим матрицу игры, т. е. найдем средний выигрыш при каждой комбинации стратегий.
1.  (носитель
(носитель  , атакуется
, атакуется  ).
).
Носитель не будет поражен, если бомбардировщики собьют истребитель, или не собьют, но он не поразит свою цель:

2.  (носитель II, атакуется I)
(носитель II, атакуется I)

3.  (носитель I, атакуется II)
(носитель I, атакуется II)

4.  (носитель II, атакуется II)
(носитель II, атакуется II)

Матрица игры имеет вид:

Нижняя цена игры 0,82; верхняя цена 1. Матрица не имеет седловой точки; решение ищем в области смешанных стратегий.
Имеем;

Отсюда

Наша оптимальная стратегия есть

т. е. в качестве носителя нужно чаще выбирать  чем II. Цена игры равна
чем II. Цена игры равна

Зная V, определяем  частоты стратегий
частоты стратегий  в оптимальной стратегии противника
в оптимальной стратегии противника  Имеем:
Имеем:

откуда

т. е. оптимальная стратегия противника есть

Пример 4. Сторона А нападает на объект, сторона В — обороняет его. У стороны А — два самолета; у стороны В — три зенитных орудия. Каждый самолет является носителем мощного поражающего средства; для того чтобы объект был поражен, достаточно, чтобы к нему прорвался хотя бы один самолет. Самолеты стороны А могут выбирать для подхода к объекту любое из трех направлений: I, II, III (рис. 4.10).
Противник (сторона В) может разместить любое из своих орудий на любом направлении; при этом каждое орудие простреливает только область пространства, относящуюся к данному направлению, и не простреливает соседних направлений. Каждое орудие может обстрелять только один самолет; обстрелянный самолет поражается с вероятностью 1. Сторона А не знает, где размещены орудия; сторона В не знает, откуда прилетят самолеты. Задача стороны А — поразить объект; задача стороны В — не допустить его поражения. Найти решение игры.
Решение. Игра представляет собой игру 2X3. Выигрыш — вероятность поражения объекта. Наши возможные стратегии:
 - послать по одному самолету на два различных направления.
- послать по одному самолету на два различных направления.
 - послать оба самолета по одному направлению.
- послать оба самолета по одному направлению.
Стратегии противника:
 - поставить по одному орудию на каждое направление;
- поставить по одному орудию на каждое направление;
 - поставить два орудия на одно направление и одно — на другое;
- поставить два орудия на одно направление и одно — на другое;
 - поставить все три орудия на одно направление.
- поставить все три орудия на одно направление.
Составляем матрицу игры.
1.  (самолеты летят по разным направлениям; орудия расставлены по одному).
(самолеты летят по разным направлениям; орудия расставлены по одному).
Очевидно, при этом  один самолет не прорвется к объекту:
один самолет не прорвется к объекту:

2.  (самолеты летяг вместе по одному направлению; орудия расставлены по одному). Очевидно, при этом один самолет пройдет к объекту необстрелянным:
(самолеты летяг вместе по одному направлению; орудия расставлены по одному). Очевидно, при этом один самолет пройдет к объекту необстрелянным:


Рис. 4.10.
3.  (самолеты летят по одному; противник защищает два направления и оставляет незащищенным третье). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности того, что один из них выберет незащищенное направление:
(самолеты летят по одному; противник защищает два направления и оставляет незащищенным третье). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности того, что один из них выберет незащищенное направление:

4.  (самолеты летят вместе по одному направлению; противник защищает одно направление двумя орудиями и одно — одним, т. е. фактически защищает одно направление и оставляет незащищенным два). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности выбора парой самолетов фактически незащищенного направления:
(самолеты летят вместе по одному направлению; противник защищает одно направление двумя орудиями и одно — одним, т. е. фактически защищает одно направление и оставляет незащищенным два). Вероятность того, что хотя бы один самолет прорвется к объекту, равна вероятности выбора парой самолетов фактически незащищенного направления:

5.  (самолеты летят по одному; противник защищает тремя орудиями только одно направление)
(самолеты летят по одному; противник защищает тремя орудиями только одно направление)

6.  (самолеты летят оба вместе; противник защищает тремя орудиями только одно направление). Чтобы объект был поражен, самолеты должны выбрать незащищенное направление:
(самолеты летят оба вместе; противник защищает тремя орудиями только одно направление). Чтобы объект был поражен, самолеты должны выбрать незащищенное направление:

Матрица игры:

Из матрицы видно, что стратегия  является заведомо невыгодной по сравнению с
является заведомо невыгодной по сравнению с  (это можно было решить
(это можно было решить
и заранее). Вычеркиванием стратегии  игра сводится к игре
игра сводится к игре 

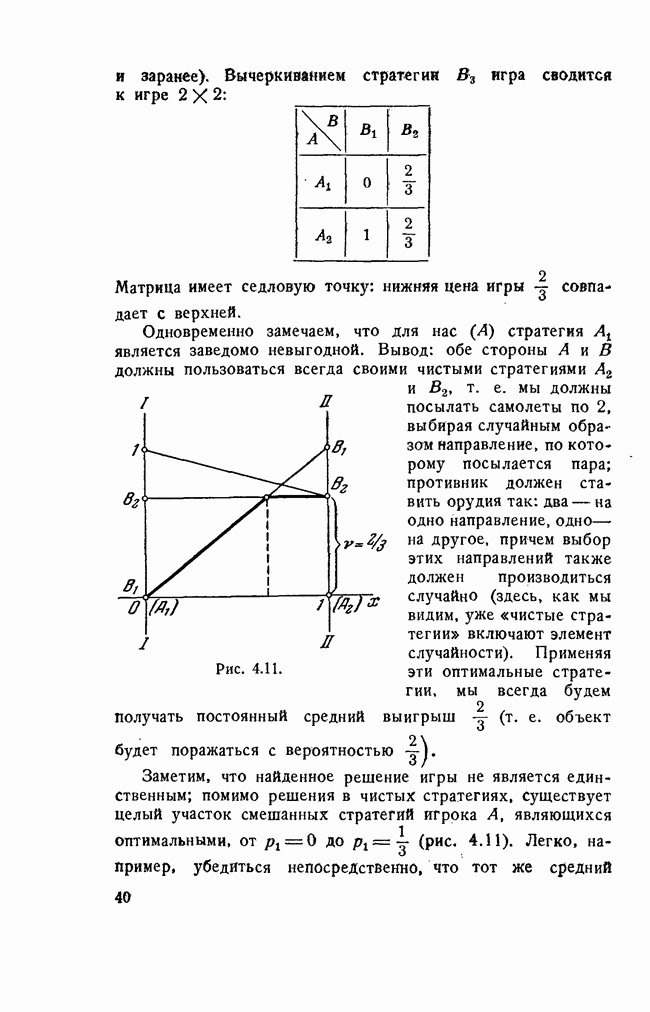
Матрица имеет седловую точку: нижняя цена игры совпадает с верхней.
Одновременно замечаем, что для нас (А) стратегия  является заведомо невыгодной. Вывод: обе стороны А к В должны пользоваться всегда своими чистыми стратегиями
является заведомо невыгодной. Вывод: обе стороны А к В должны пользоваться всегда своими чистыми стратегиями  т. е. мы должны посылать самолеты по 2, выбирая случайным образом направление, по которому посылается пара; противник должен ставить орудия так: два — на одно направление, одно — на другое, причем выбор этих направлений также должен производиться случайно (здесь, как мы видим, уже «чистые стратегии» включают элемент случайности). Применяя эти оптимальные стратегии, мы всегда будем получать постоянный средний выигрыш (т. е. объект будет поражаться с вероятностью
т. е. мы должны посылать самолеты по 2, выбирая случайным образом направление, по которому посылается пара; противник должен ставить орудия так: два — на одно направление, одно — на другое, причем выбор этих направлений также должен производиться случайно (здесь, как мы видим, уже «чистые стратегии» включают элемент случайности). Применяя эти оптимальные стратегии, мы всегда будем получать постоянный средний выигрыш (т. е. объект будет поражаться с вероятностью 
Заметим, что найденное решение игры не является единственным; помимо решения в чистых стратегиях, существует целый участок смешанных стратегий игрока А, являющихся оптимальными, от  до
до  (рис. 4.11). Легко, например, убедиться непосредственно, что тот же средний
(рис. 4.11). Легко, например, убедиться непосредственно, что тот же средний

Рис. 4.11.
выигрыш  получится, если мы будем применять свои стратегии
получится, если мы будем применять свои стратегии  в пропорции
в пропорции  и
и  .
.
Пример 5. Те же условия, что в предыдущем примере, но для нас возможны четыре направления удара, а противник располагает четырьмя орудиями.
Решение. У нас по-прежнему две возможные стратегии:
 - посылать самолеты по одному,
- посылать самолеты по одному,
 - посылать два самолета вместе.
- посылать два самолета вместе.
У противника пять возможных стратегий:
 - ставить по одному орудию на каждое направление;
- ставить по одному орудию на каждое направление;
 - ставить по два орудия на два различных направления;
- ставить по два орудия на два различных направления;
 - ставить два орудия на одно направление и по одному — на два других;
- ставить два орудия на одно направление и по одному — на два других;
 - ставить три орудия на одно направление и одно — на другое;
- ставить три орудия на одно направление и одно — на другое;
 - ставить все четыре орудия на одно направление.
- ставить все четыре орудия на одно направление.
Стратегии  отбросим заранее как заведомо невыгодные. Рассуждая аналогично предыдущему примеру, строим матрицу игры:
отбросим заранее как заведомо невыгодные. Рассуждая аналогично предыдущему примеру, строим матрицу игры:

Нижняя цена игры у, верхняя 
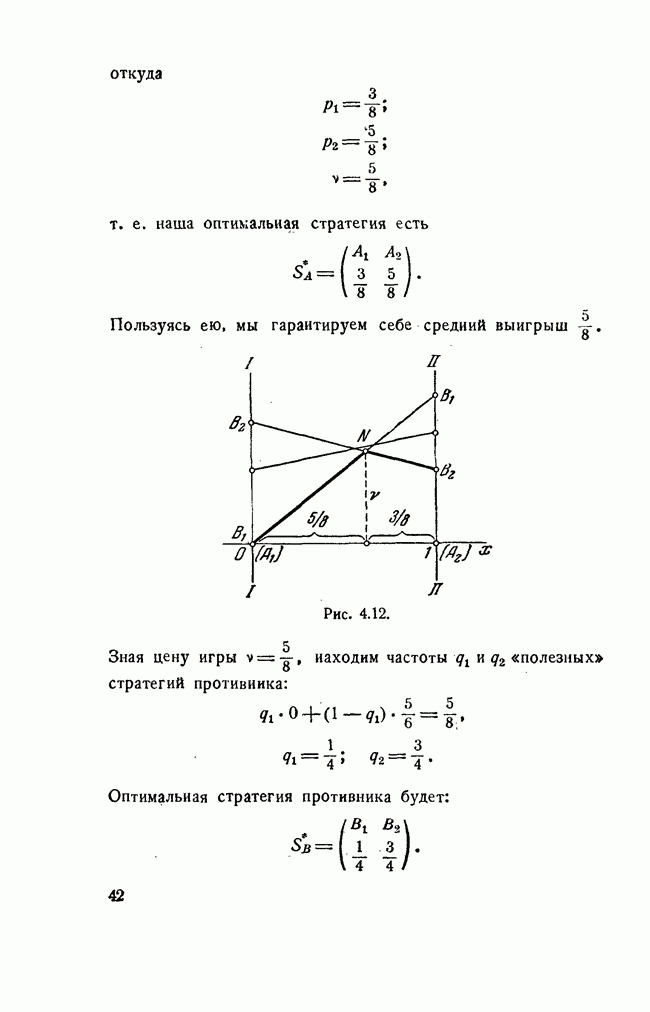
Матрица не имеет седловой точки; решение лежит в области смешанных стратегий. Пользуясь геометрической интерпретацией (рис. 4.12), выделим «полезные» стратегии противника: 
Частоты  определим из уравнений:
определим из уравнений:

откуда

т. е. наша оптимальная стратегия есть

Пользуясь ею, мы гарантируем себе средний выигрыш 

Рис. 4.12.
Зная цену игры  находим частоты
находим частоты  «полезных» стратегий противника:
«полезных» стратегий противника:

Оптимальная стратегия противника будет:

Пример 6. Сторона А располагает двумя стратегиями  сторона В — четырьмя
сторона В — четырьмя  . Матрица игры имеет вид:
. Матрица игры имеет вид:

Найти решение игры.
Решение. Нижняя цена игры 0,3; верхняя 0,4. Геометрическая интерпретация (рис. 4.13) показывает, что полезными стратегиями игрока В являются и  или
или 

Рис. 4.13.
Игрок А имеет бесконечно много оптимальных смешанных стратегий: в оптимальной стратегии  может изменяться от
может изменяться от  до
до  . Цена игры
. Цена игры  . Игрок В имеет чистую оптимальную стратегию
. Игрок В имеет чистую оптимальную стратегию  .
.
| << Предыдущий параграф | Следующий параграф >> |
- § 1. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ
- § 2. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП «МИНИМАКСА»
- § 3. ЧИСТЫЕ И СМЕШАННЫЕ СТРАТЕГИИ. РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ
- § 4. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ ИГР. ИГРЫ 2X2 И 2Xn
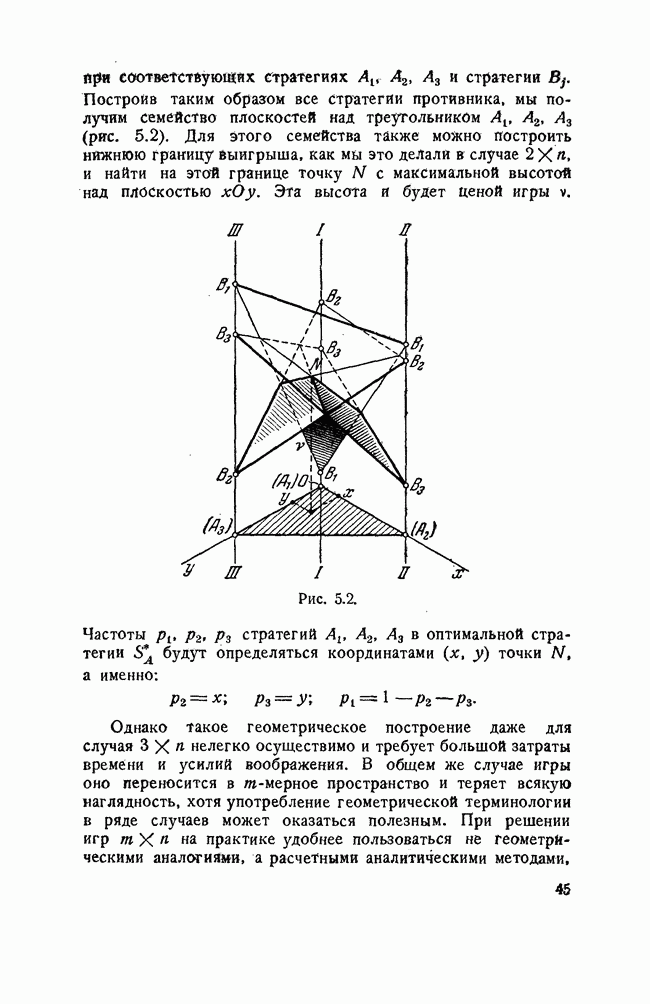
- § 5. ОБЩИЕ МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР
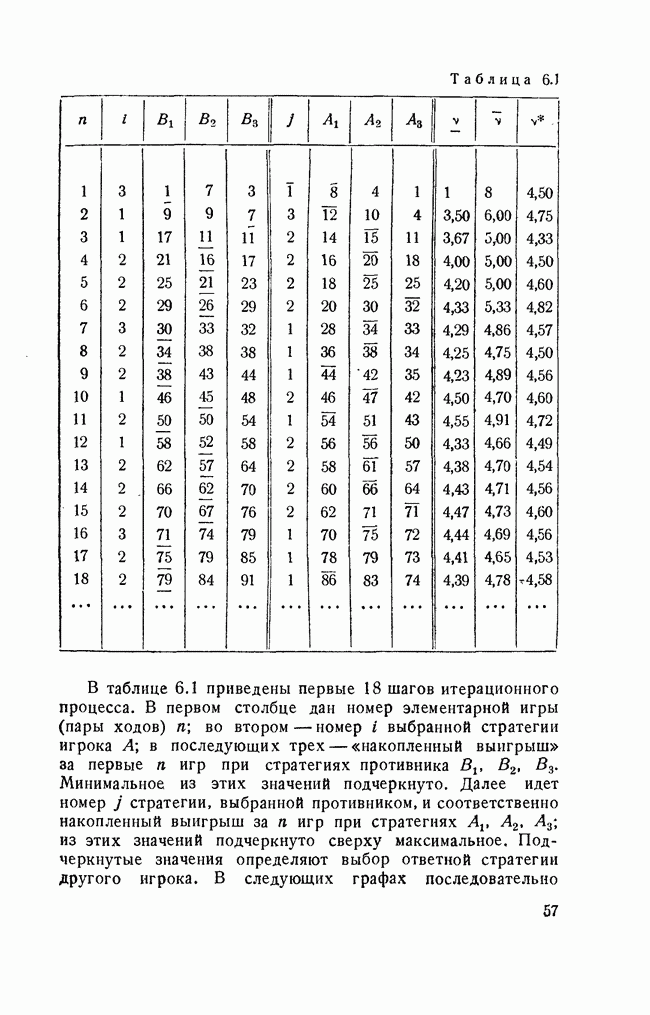
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИГР
- § 7. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР