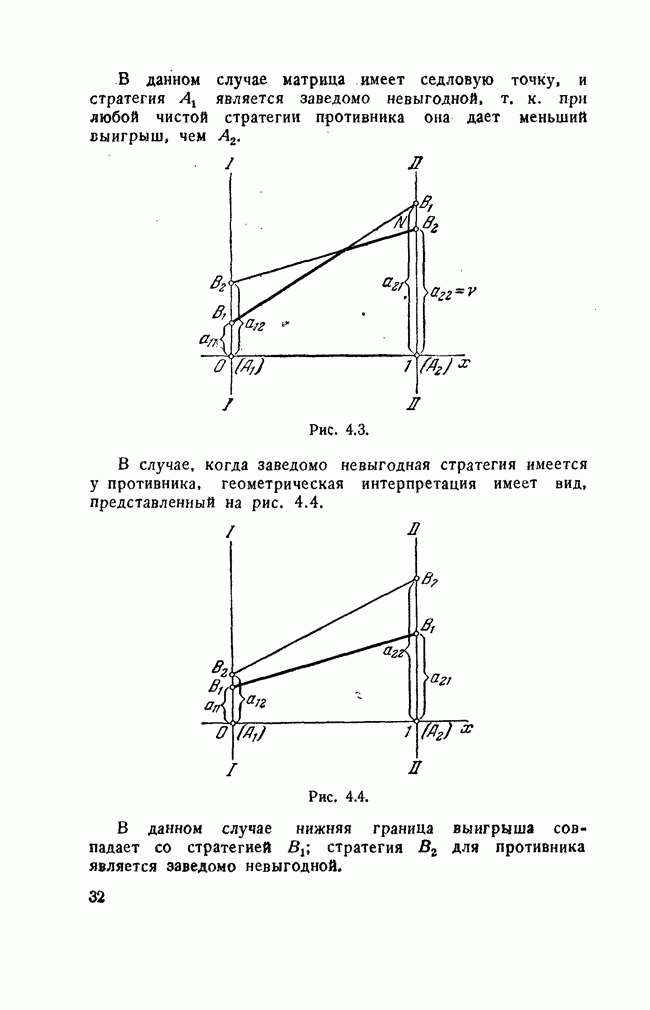
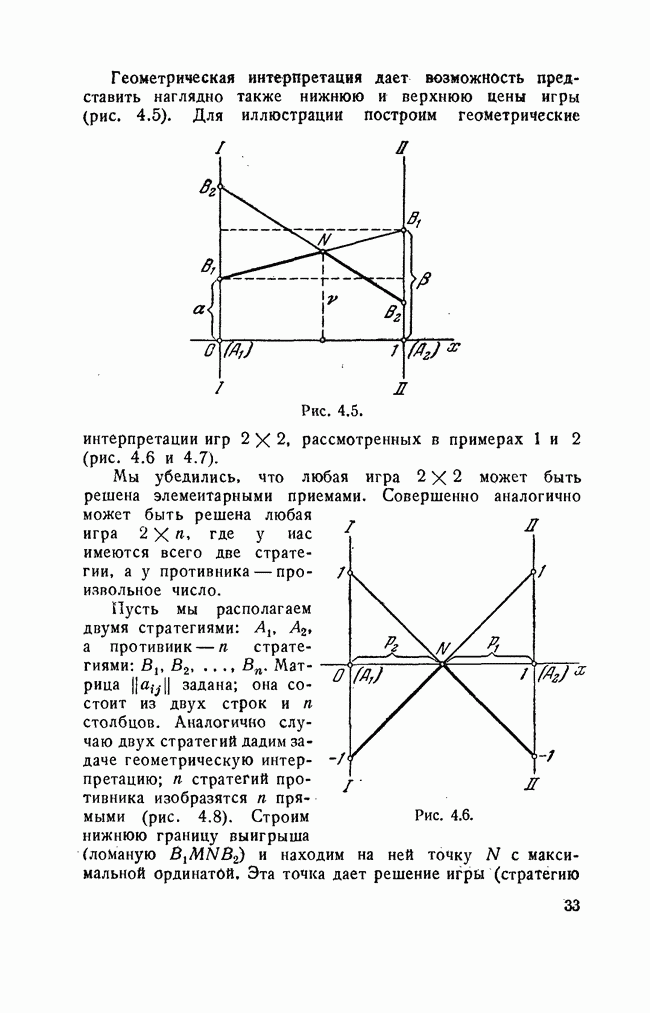
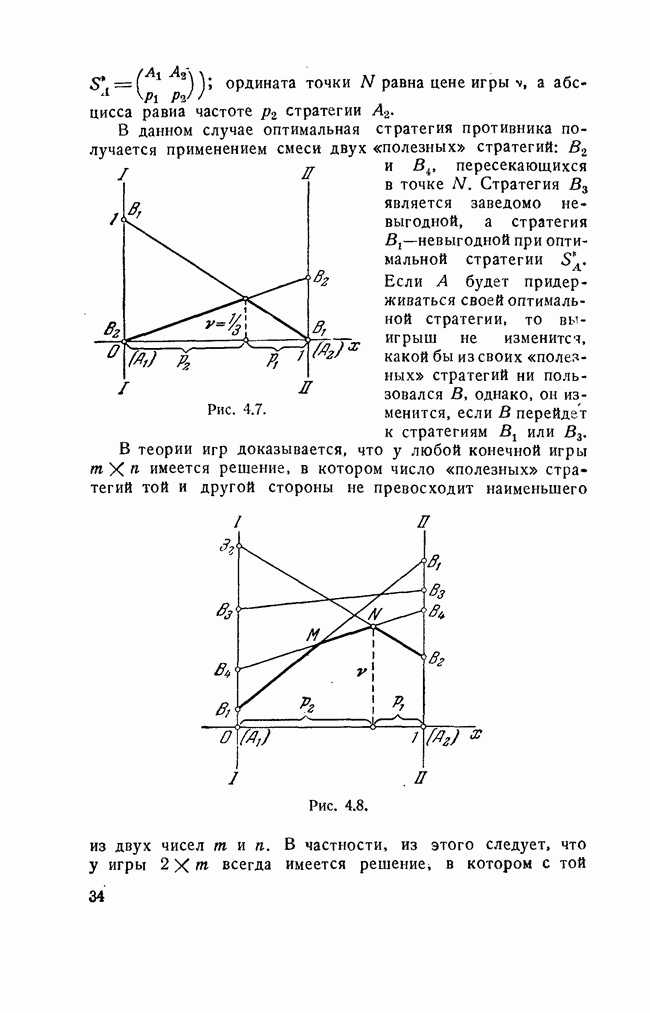
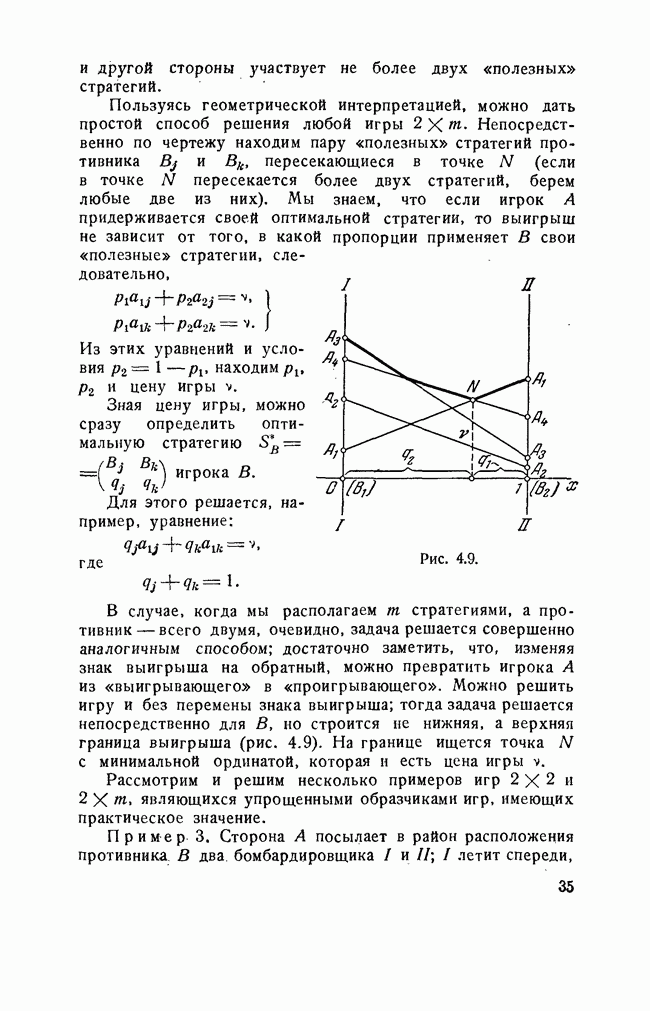
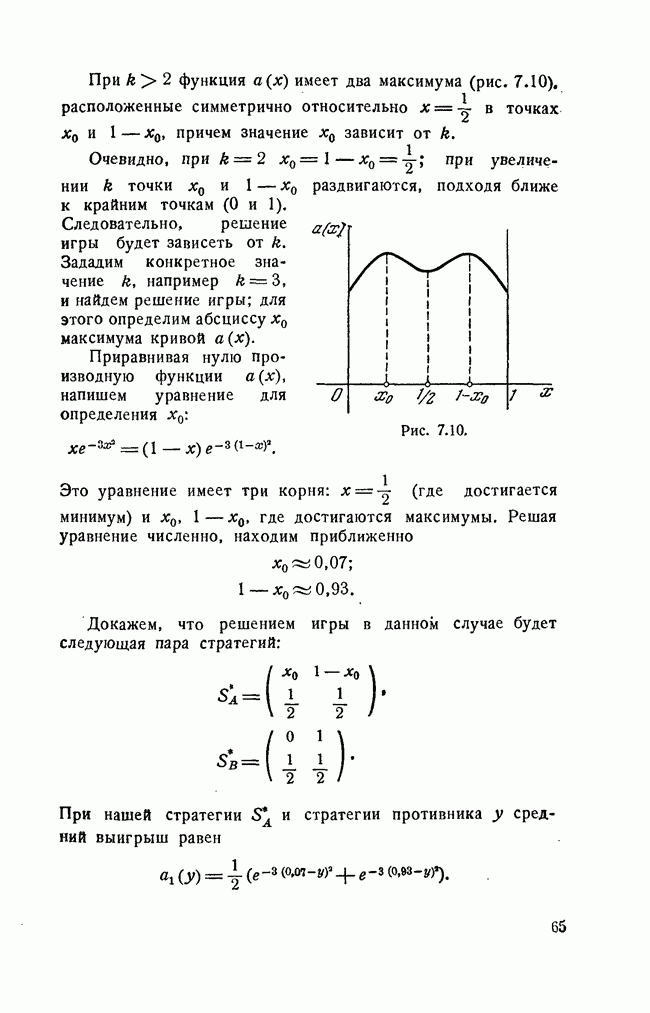
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП «МИНИМАКСА»
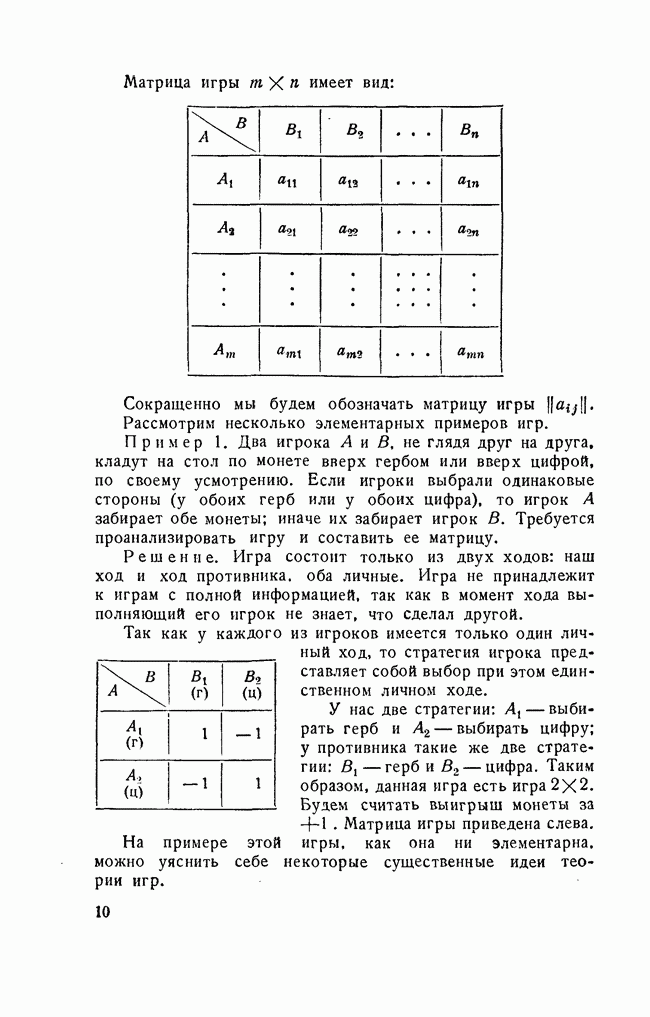
Рассмотрим игру  со следующей матрицей.
со следующей матрицей.
Будем обозначать буквой i номер нашей стратегии; буквой j — номер стратегии противника.

Поставим себе задачу: определить свою оптимальную стратегию. Проанализируем последовательно каждую из наших стратегий, начиная с 
Выбирая стратегию  мы всегда должны рассчитывать на то, что противник ответит на нее той из стратегий
мы всегда должны рассчитывать на то, что противник ответит на нее той из стратегий  для которой наш выигрыш
для которой наш выигрыш  минимален. Определим это значение выигрыша, т. е. минимальное из чисел
минимален. Определим это значение выигрыша, т. е. минимальное из чисел  строке. Обозначим его
строке. Обозначим его 

Здесь знаком  (минимум по j) обозначено минимальное из значений данного параметра при всех возможных
(минимум по j) обозначено минимальное из значений данного параметра при всех возможных 
Выпишем числа  рядом с матрицей справа в виде добавочного столбца:
рядом с матрицей справа в виде добавочного столбца:

Выбирая какую-либо стратегию  мы должны рассчитывать на то, что в результате разумных действий противника мы не выиграем больше чем
мы должны рассчитывать на то, что в результате разумных действий противника мы не выиграем больше чем  Естественно, что, действуя наиболее осторожно и рассчитывая на наиболее разумного противника (т. е. избегая всякого риска), мы должны остановиться на той стратегии для которой число а является максимальным. Обозначим это максимальное значение а:
Естественно, что, действуя наиболее осторожно и рассчитывая на наиболее разумного противника (т. е. избегая всякого риска), мы должны остановиться на той стратегии для которой число а является максимальным. Обозначим это максимальное значение а:

или, принимая во внимание формулу (2.1),

Величина  называется нижней ценой игры, иначе — максиминным выигрышем или просто млксимином.
называется нижней ценой игры, иначе — максиминным выигрышем или просто млксимином.
Число а лежит в определенной строчке матрицы; та стратегия игрока А, которая соответствует этой строчке, называется максиминной стратегией.
Очевидно, если мы будем придерживаться максиминной стратегии, то нам при любом поведении противника  тирован выигрыш, во всяком случае не меньший а. Поэтому величина а и называется «нижней ценой игры». Это — тот гарантированный минимум, который мы можем себе обеспечить, придерживаясь наиболее осторожной («перестраховочной») стратегии.
тирован выигрыш, во всяком случае не меньший а. Поэтому величина а и называется «нижней ценой игры». Это — тот гарантированный минимум, который мы можем себе обеспечить, придерживаясь наиболее осторожной («перестраховочной») стратегии.
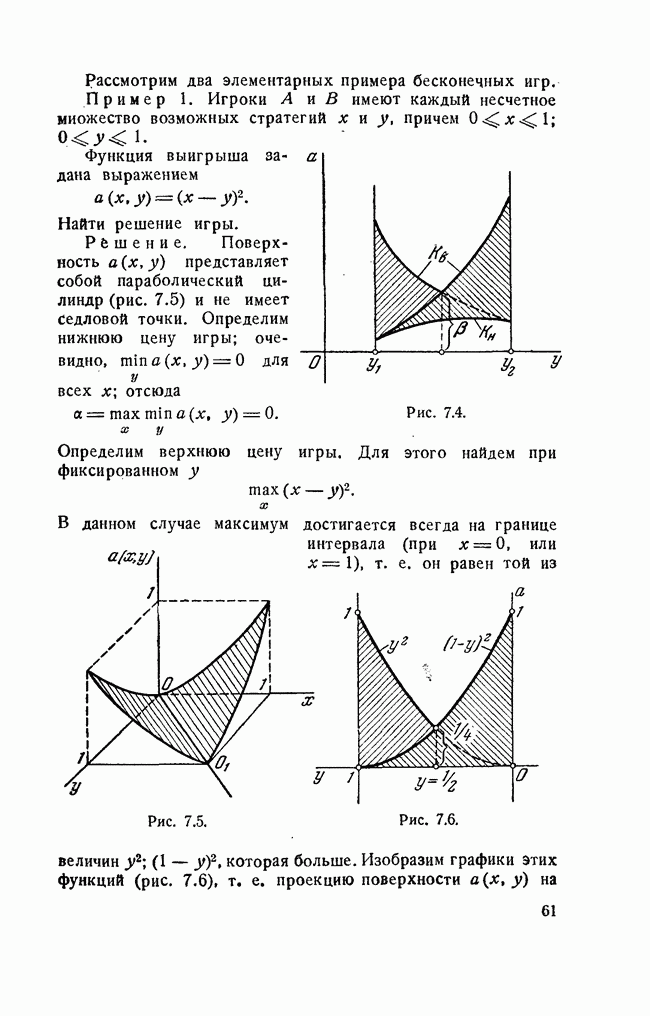
Очевидно, аналогичное рассуждение можно провести и за противника В. Так как противник заинтересован в том, чтобы обратить наш выигрыш в минимум, он должен просмотреть каждую свою стратегию с точки зрения максимального выигрыша при этой стратегии. Поэтому внизу матрицы мы выпишем максимальные значения по каждому столбцу:

и найдем минимальное из 

или

Величина [3 называется верхней ценой игры, иначе — «минимаксом». Соответствующая минимаксному выигрышу стратегия противника называется его «минимаксной стратегией».
Придерживаясь своей наиболее осторожной минимаксной стратегии, противник гарантирует себе следующее: что бы мы ни предприняли против него, он во всяком случае проиграет сумму, не большую чем  .
.
Принцип осторожности, диктующий игрокам выбор соответствующих стратегий (максиминной и минимаксной), в теории игр и ее приложениях часто называют «принципом мини-макса». Наиболее осторожные максиминную и минимаксную стратегии игроков иногда обозначают общим термином «минимаксные стратегии».
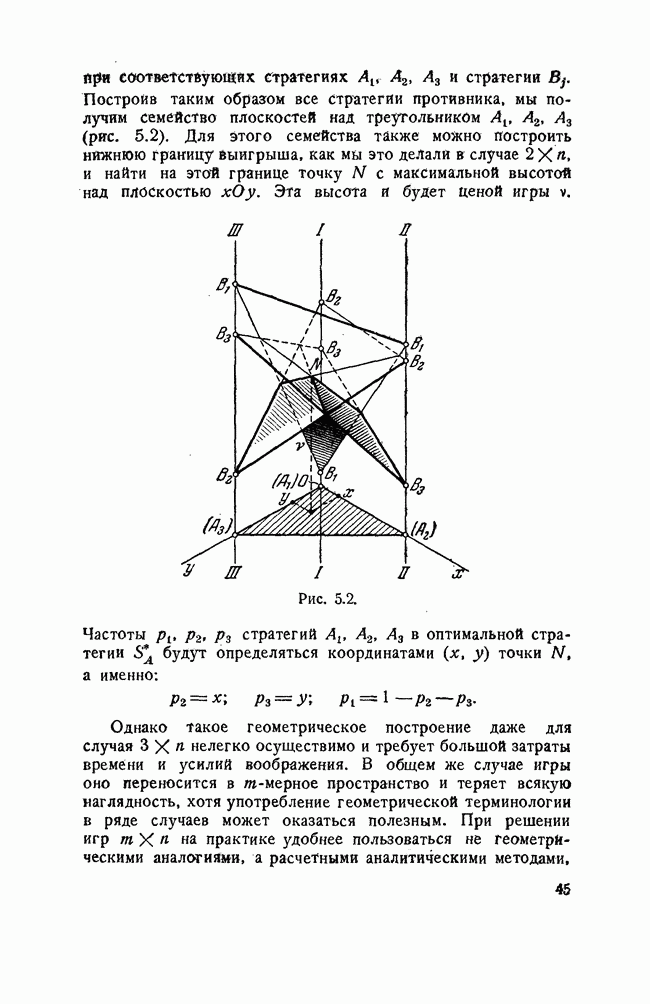
В качестве примеров определим нижнюю и верхнюю цену игры и минимаксные стратегии для примеров 1, 2 и 3 § 1.
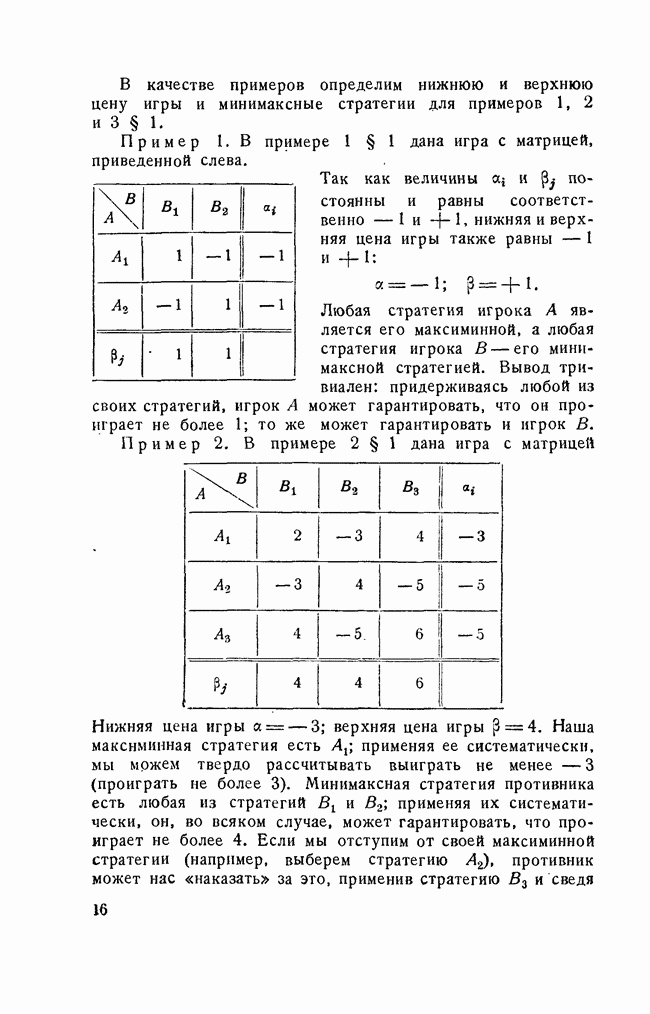
Пример 1. В примере 1 § 1 дана игра с матрицей, приведенной слева.

Так как величины  и постоянны и равны соответственно -1 и +1, нижняя и верхняя цена игры также равны -1 и + 1:
и постоянны и равны соответственно -1 и +1, нижняя и верхняя цена игры также равны -1 и + 1:

Любая стратегия игрока А является его максиминной, а любая стратегия игрока В — его минимаксной стратегией. Вывод тривиален: придерживаясь любой из своих стратегий, игрок А может гарантировать, что он проиграет не более 1; то же может гарантировать и игрок В.
Пример 2. В примере 2 § 1 дана игра с матрицей

Нижняя цена игры  верхняя цена игры
верхняя цена игры  Наша максиминная стратегия есть
Наша максиминная стратегия есть  применяя ее систематически, мы можем твердо рассчитывать выиграть не менее —3 (проиграть не более 3). Минимаксная стратегия противника есть любая из стратегий
применяя ее систематически, мы можем твердо рассчитывать выиграть не менее —3 (проиграть не более 3). Минимаксная стратегия противника есть любая из стратегий  применяя их систематически, он, во всяком случае, может гарантировать, что проиграет не более 4. Если мы отступим от своей максиминной стратегии (например, выберем стратегию
применяя их систематически, он, во всяком случае, может гарантировать, что проиграет не более 4. Если мы отступим от своей максиминной стратегии (например, выберем стратегию  ), противник может нас «наказать» за это, применив стратегию
), противник может нас «наказать» за это, применив стратегию  и сведя
и сведя
наш выигрыш к - 5; равным образом и отступление противника от своей минимаксной стратегии может увеличить его проигрыш до 6.
Пример 3. В примере 3 § 1 дана игра с матрицей

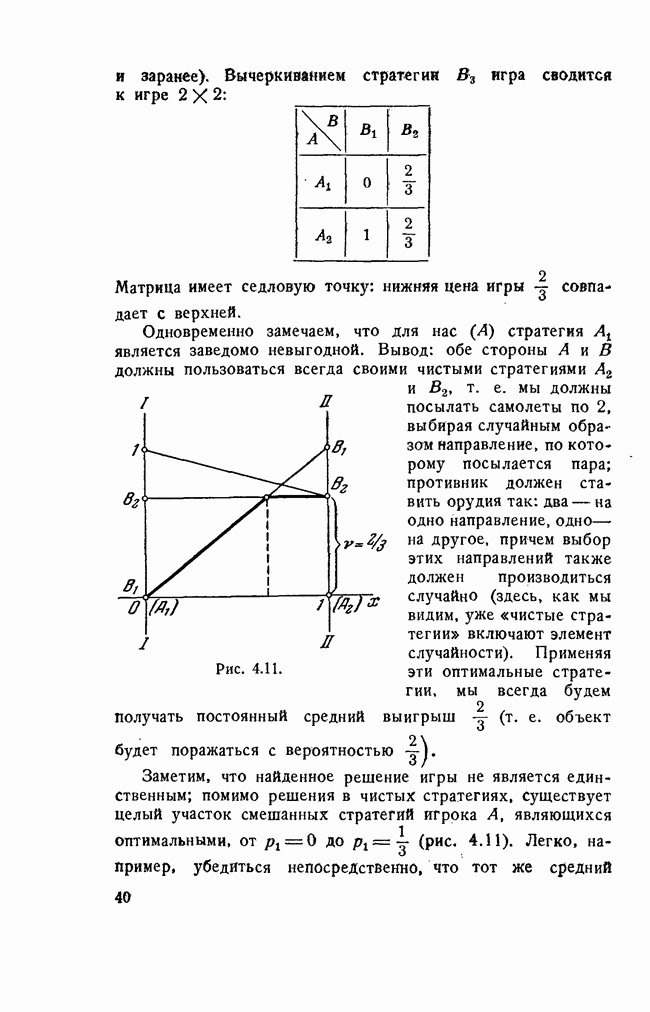
Нижняя цена игры а = 0,3; верхняя ценя игры р = 0,7. Наша наиболее осторожная (максиминная) стратегия есть  ; пользуясь вооружением
; пользуясь вооружением  , мы гарантируем, что будем поражать самолет в среднем не менее чем в 0,3 всех случаев. Наиболее осторожной (минимаксной) стратегией противника является
, мы гарантируем, что будем поражать самолет в среднем не менее чем в 0,3 всех случаев. Наиболее осторожной (минимаксной) стратегией противника является  применяя этот самолет, противник может быть уверен, что он будет поражаться не более чем в 0,7 всех случаев.
применяя этот самолет, противник может быть уверен, что он будет поражаться не более чем в 0,7 всех случаев.
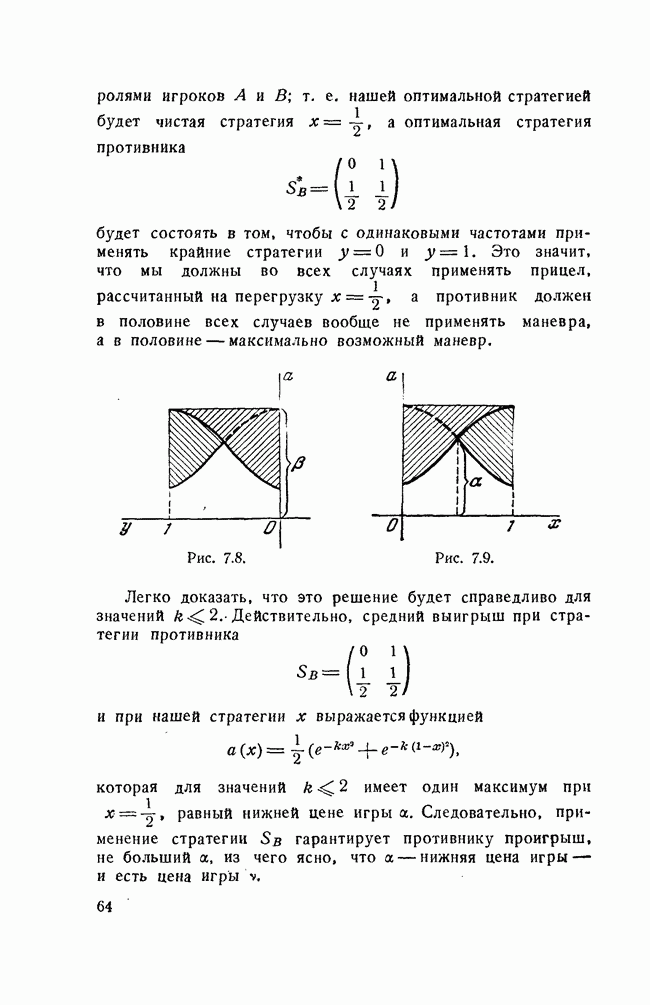
На последнем примере удобно продемонстрировать одно важное свойство минимаксных стратегий — их неустойчивость. Пусть мы применяем свою наиболее осторожную (максиминную) стратегию  , а противник — свою наиболее осторожную (минимаксную) стратегию
, а противник — свою наиболее осторожную (минимаксную) стратегию  . До тех пор, пока оба противника придерживаются этих стратегий, средний выигрыш равен 0,6; он больше нижней, но меньше верхней цены игры. Теперь допустим, что противнику стало известно, что мы применяем стратегию
. До тех пор, пока оба противника придерживаются этих стратегий, средний выигрыш равен 0,6; он больше нижней, но меньше верхней цены игры. Теперь допустим, что противнику стало известно, что мы применяем стратегию  он немедленно ответит на нее стратегией
он немедленно ответит на нее стратегией  и сведет выигрыш к 0,3. В свою очередь, на стратегию
и сведет выигрыш к 0,3. В свою очередь, на стратегию  у нас есть хороший ответ: стратегия
у нас есть хороший ответ: стратегия  дающая нам выигрыш 0,9, и т. д.
дающая нам выигрыш 0,9, и т. д.
Таким образом, положение, при котором оба игрока пользуются своими минимаксными стратегиями, является неустойчивым и может быть нарушено поступившими сведениями о стратегии противной стороны.
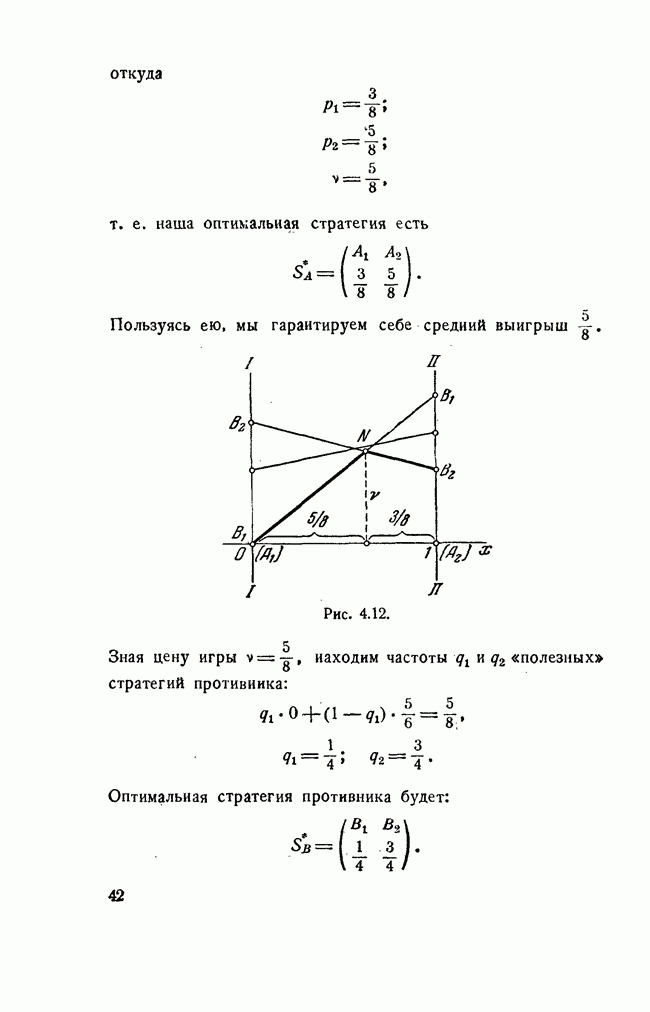
Однако существуют некоторые игры, для которых минимаксные стратегии являются устойчивыми. Это те игры, для которых нижняя цена равна верхней:

Если нижняя цена игры равна верхней, то их общее значение называется частой ценой игры (иногда просто ценой игры), мы его будем обозначать буквой 
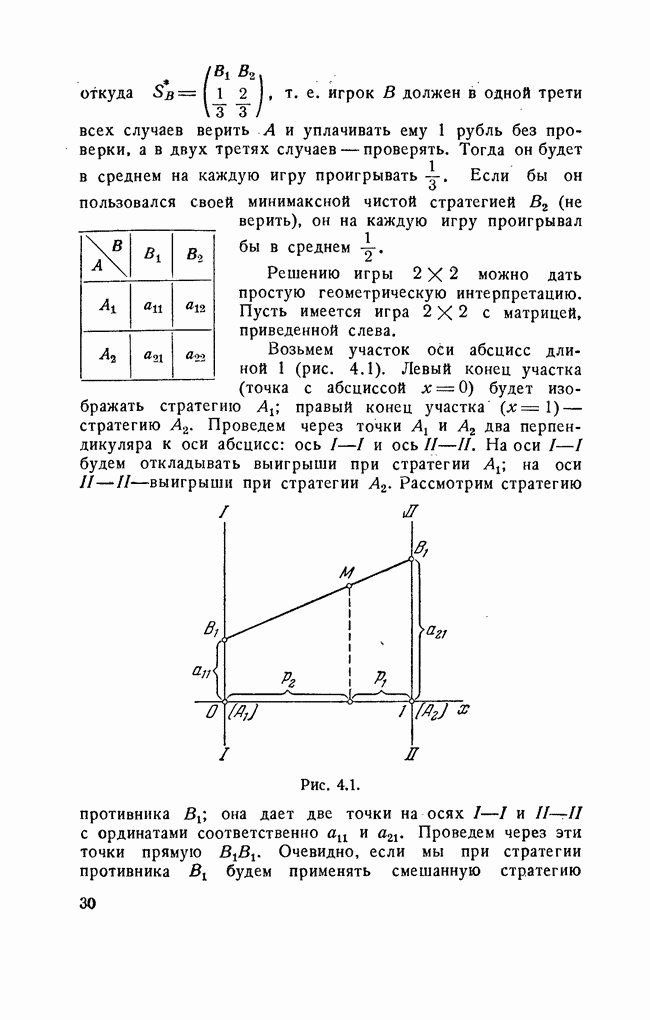
Рассмотрим пример. Пусть игра 4X4 задана матрицей:

Найдем нижнюю цену игры:

Найдем верхнюю цену игры:

Они оказались одинаковыми, следовательно, у игры есть чистая цена, равная 
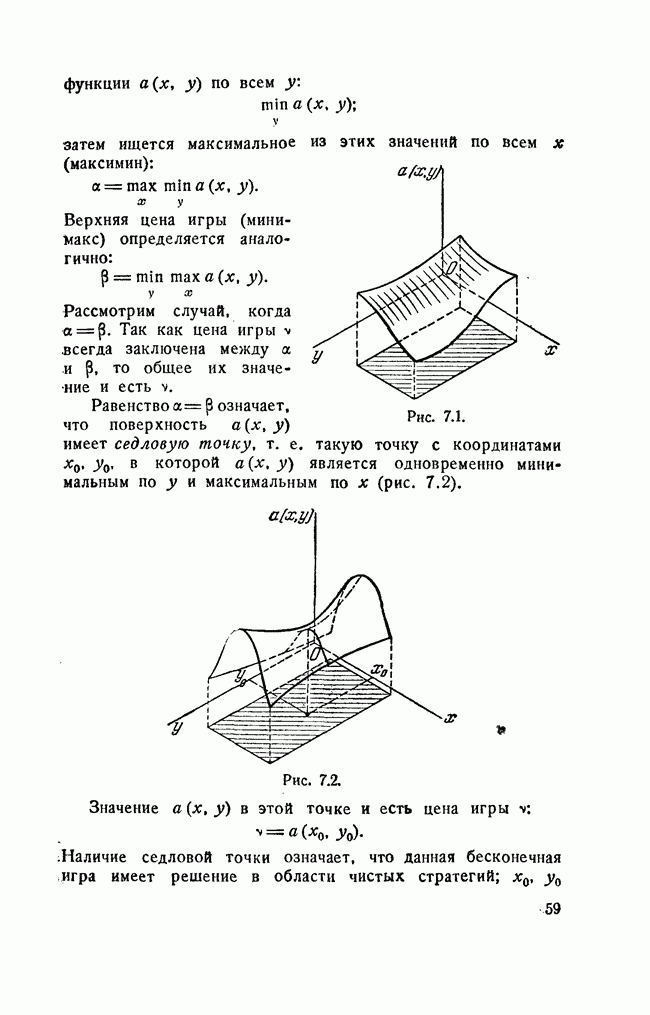
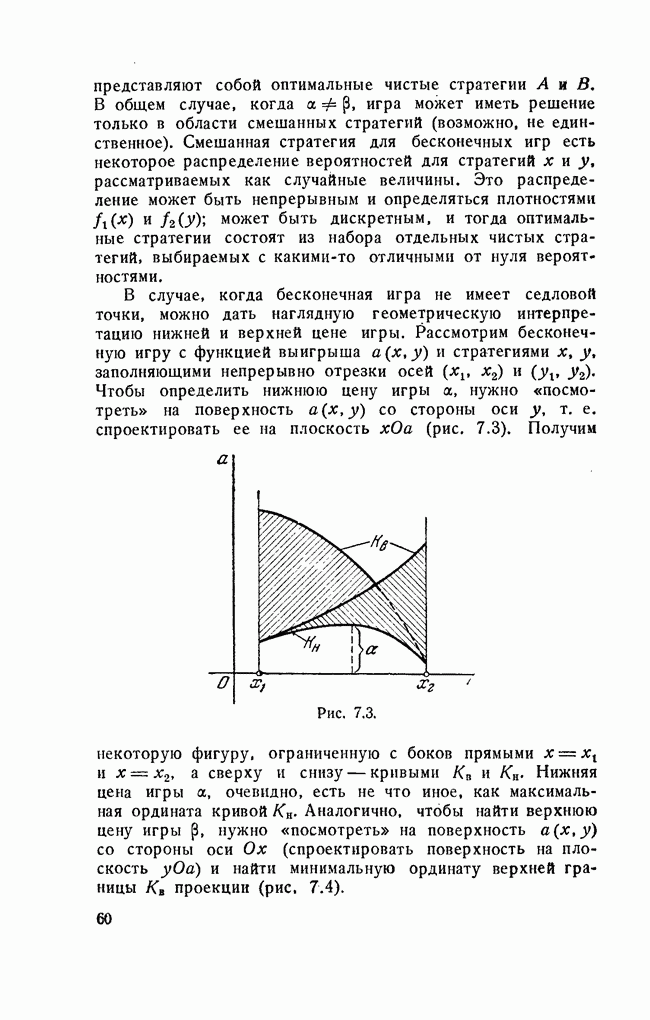
Элемент 0,6, выделенный в платежной матрице, является одновременно минимальным в своей строке и максимальным в своем столбце. В геометрии точку на поверхности, обладающую аналогичным свойством (одновременный минимум по одной координате и максимум по другой), называют седловой точкой, по аналогии этот термин применяется и в теории игр. Элемент матрицы, обладающий этим свойством, называется седловой точкой матрицы, а про игру говорят, что она имеет седловую точку.
Седловой точке соответствует пара минимаксных стратегий (в данном примере  . Эти стратегии называются оптимальными, а их совокупность—решением игры.
. Эти стратегии называются оптимальными, а их совокупность—решением игры.
Решение игры обладает следующим замечательным свойством. Если один из игроков (например А) придерживается своей оптимальной стратегии, а другой игрок (В) будет любым способом отклоняться от своей оптимальной стратегии, то для игрока, допустившего отклонение, это никогда не может оказаться выгодным-, такое отклонение игрока В может в лучшем случае оставить выигрыш неизменным, а в худшем случае — увеличить его.
Наоборот, если В придерживается своей оптимальной стратегии, а А отклоняется от своей, то это ни в коем случае не может быть выгодным для А.
Это утверждение легко проверить на примере рассматриваемой игры с седловой точкой.
Мы видим, что в случае игры с седловой точкой минимаксные стратегии обладают своеобразной «устойчивостью»: если одна сторона придерживается своей минимаксной стратегии, то для другой может быть только невыгодным отклоняться от своей. Заметим, что в этом случае наличие у любого игрока сведений о том, что противник избрал свою оптимальную стратегию, не может изменить собственного поведения игрока: если он не хочет действовать против своих же интересов, он должен придерживаться своей оптимальной стратегии. Пара оптимальных стратегий в игре с седловой точкой является как бы «положением равновесия»: любое отклонение от оптимальной стратегии приводит отклоняющегося игрока к невыгодным последствиям, вынуждающим его вернуться в исходное положение.
Итак, для каждой игры с седловой точкой существует решение, определяющее пару оптимальных стратегий обеих сторон, отличающуюся следующими свойствами.
1) Если обе стороны придерживаются своих оптимальных стратегий, то средний выигрыш равен чистой цене игры v, одновременно являющейся ее нижней и верхней ценой.
2) Если одна из сторон придерживается своей оптимальной стратегии, а другая отклоняется от своей, то от этого отклоняющаяся сторона может только потерять и ни в коем случае не может увеличить свой выигрыш.
Класс игр, имеющих седловую точку, представляет большой интерес как с теоретической, так и с практической точки зрения.
В теории игр доказывается, что, в частности, каждая игра с полной информацией имеет седловую точку, и, следовательно, каждая такая игра имеет решение, т. е. существует пара оптимальных стратегий той и другой стороны, дающая средний выигрыш, равный цене игры. Если игра с полной информацией состоит только из личных ходов, то при применении каждой стороной своей оптимальной стратегии она должна всегда кончаться вполне определенным исходом, а именно, выигрышем, в точности равным цене игры.
В качестве примера игры с полной информацией приведем известную игру с укладыванием монет на круглый стол. Два игрока поочередно кладут одинаковые монеты на круглый стол, выбирая каждый раз произвольное положение центра монеты; взаимное накрывание монет не допускается. Выигрывает тот из игроков, кто положит последнюю монету (когда места для других уже не останется). Очевидно, что исход этой игры всегда предрешен, и существует вполне определенная стратегия, обеспечивающая достоверный выигрыш тому из игроков, который кладет монету первым. А именно, он должен первый раз положить монету в центр стола, а далее на каждый ход противника отвечать симметричным ходом. При этом второй игрок может вести себя как угодно, не изменяя предрешенного результата игры. Поэтому данная игра имеет смысл только для игроков, не знающих оптимальной стратегии. Аналогично дело обстоит с шахматами и другими играми с полной информацией; любая из таких игр обладает седловой точкой и решением, указывающим каждому из игроков его оптимальную стратегию; решение шахматной игры не найдено только потому, что число комбинаций возможных ходов в шахматах слишком велико, чтобы можно было построить платежную матрицу и найти в ней седловую точку.
| << Предыдущий параграф | Следующий параграф >> |
- § 1. ПРЕДМЕТ ТЕОРИИ ИГР. ОСНОВНЫЕ ПОНЯТИЯ
- § 2. НИЖНЯЯ И ВЕРХНЯЯ ЦЕНА ИГРЫ. ПРИНЦИП «МИНИМАКСА»
- § 3. ЧИСТЫЕ И СМЕШАННЫЕ СТРАТЕГИИ. РЕШЕНИЕ ИГРЫ В СМЕШАННЫХ СТРАТЕГИЯХ
- § 4. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ ИГР. ИГРЫ 2X2 И 2Xn
- § 5. ОБЩИЕ МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ИГР
- § 7. МЕТОДЫ РЕШЕНИЯ НЕКОТОРЫХ БЕСКОНЕЧНЫХ ИГР