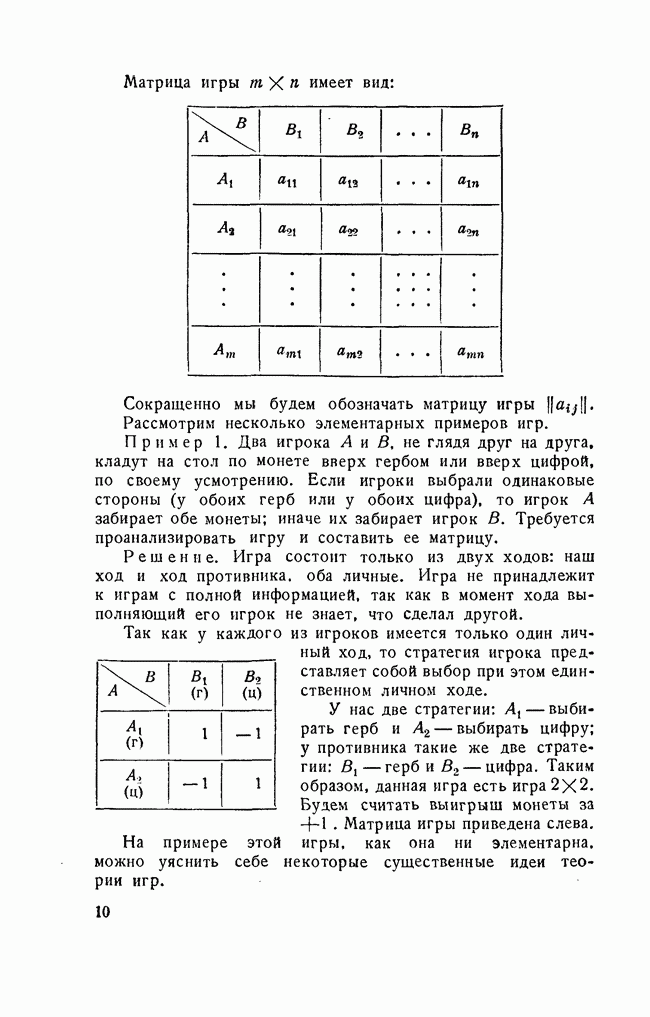
§ 5. ОБЩИЕ МЕТОДЫ РЕШЕНИЯ КОНЕЧНЫХ ИГР

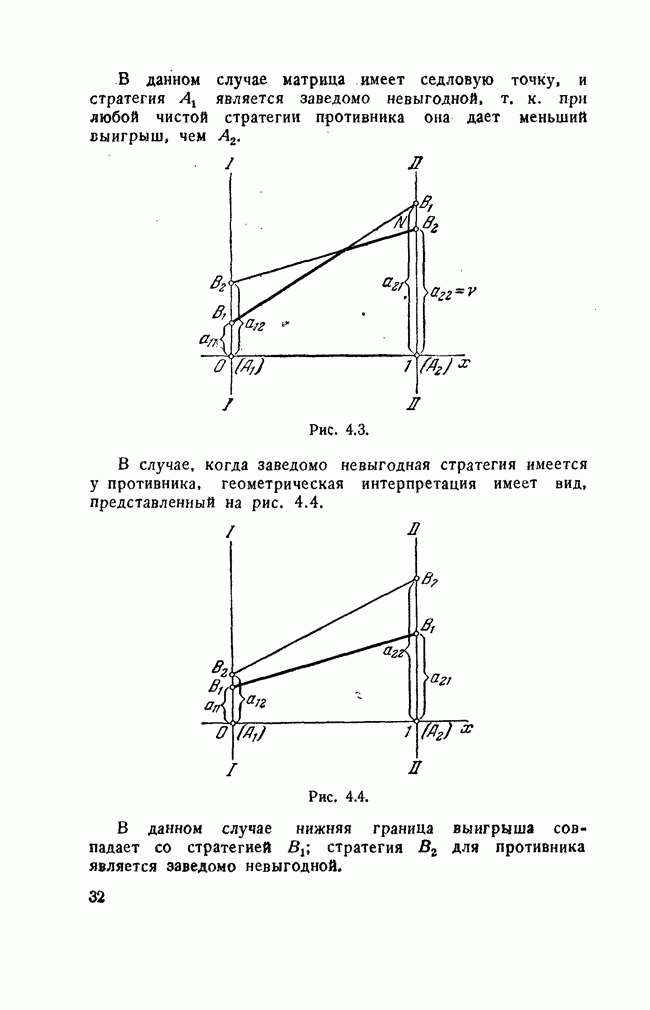
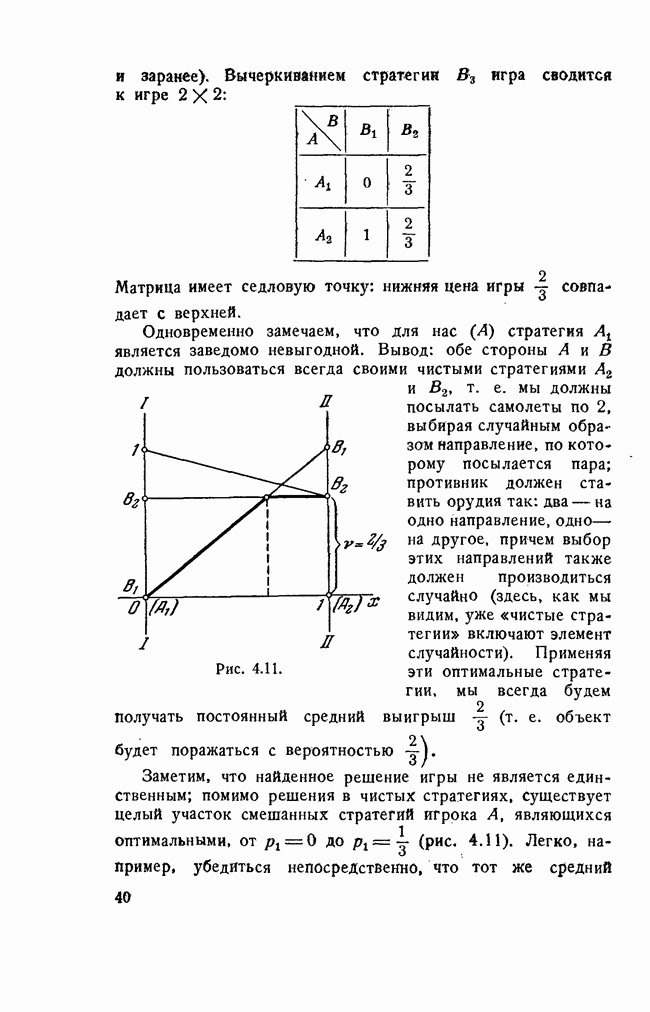
Мы рассматривали до сих пор только самые элементарные игры типа . которые могут быть весьма просто решены и допускают удобную и наглядную геометрическую интерпретацию.

В общем случае решение игры представляет довольно трудную задачу, причем сложность задачи и объем необходимых для решения вычислений резко возрастает с увеличением Однако эти трудности не носят принципиального характера и связаны только с очень большим объемом расчетов, который в ряде случаев может оказаться практически невыполнимым.

Рис. 5.1.

Принципиальная сторона метода отыскания решения остается при любом одной и той же.

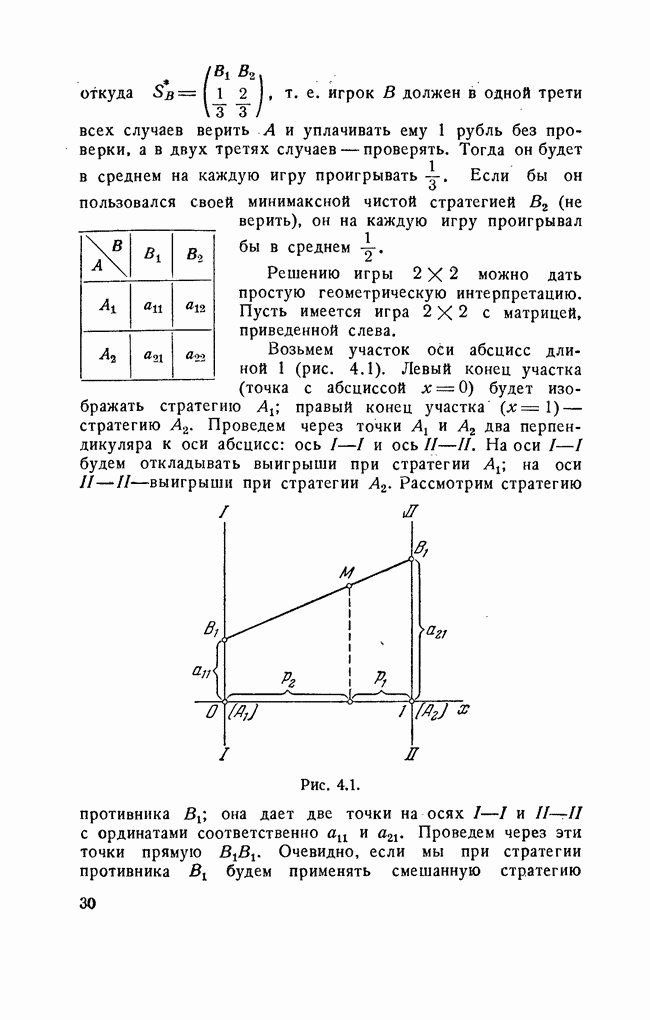
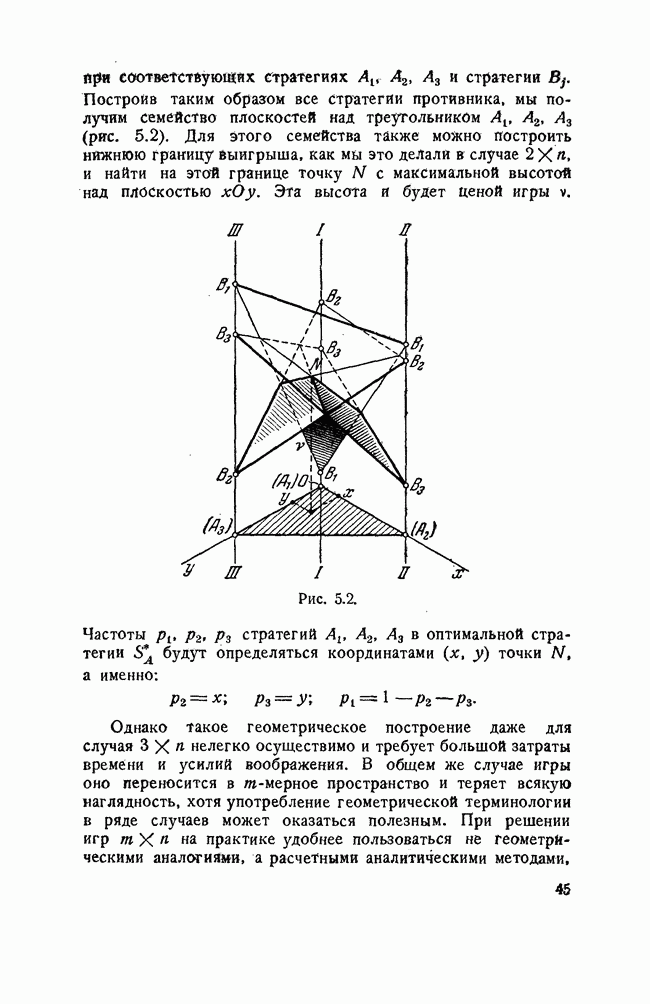
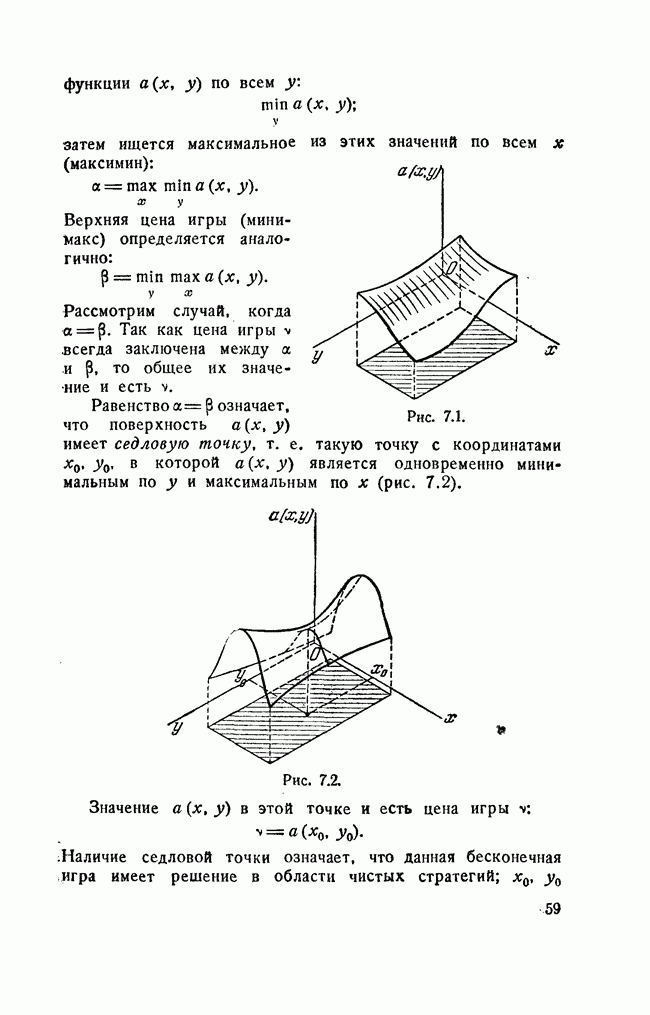
Проиллюстрируем это на примере игры 3 X п. Дадим ей геометрическую интерпретацию — уже пространственную. Три наши стратегии изобразим тремя точками на плоскости первая лежит в начале координат (рис. 5.1), вторая и третья — на осях на расстояниях 1 от начала.

Через точки проводятся оси I-I, II-II и III—III, перпендикулярные к плоскости На оси откладываются выигрыши при стратегии на осях выигрыши при стратегиях Каждая стратегия противника изобразится плоскостью, отсекающей на осях и III—III отрезки, равные выигрышам

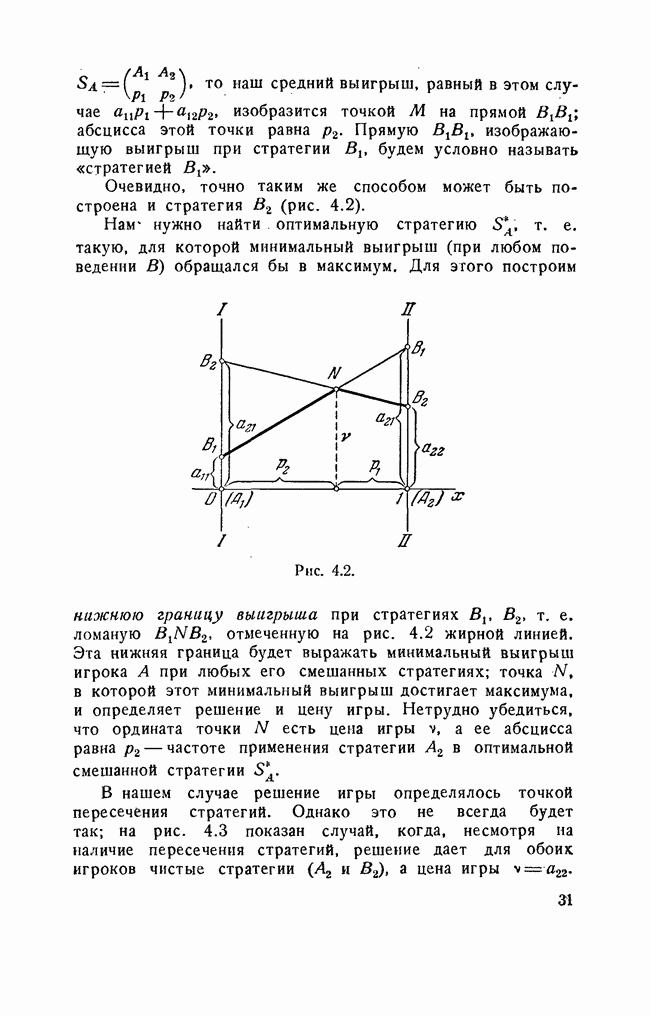
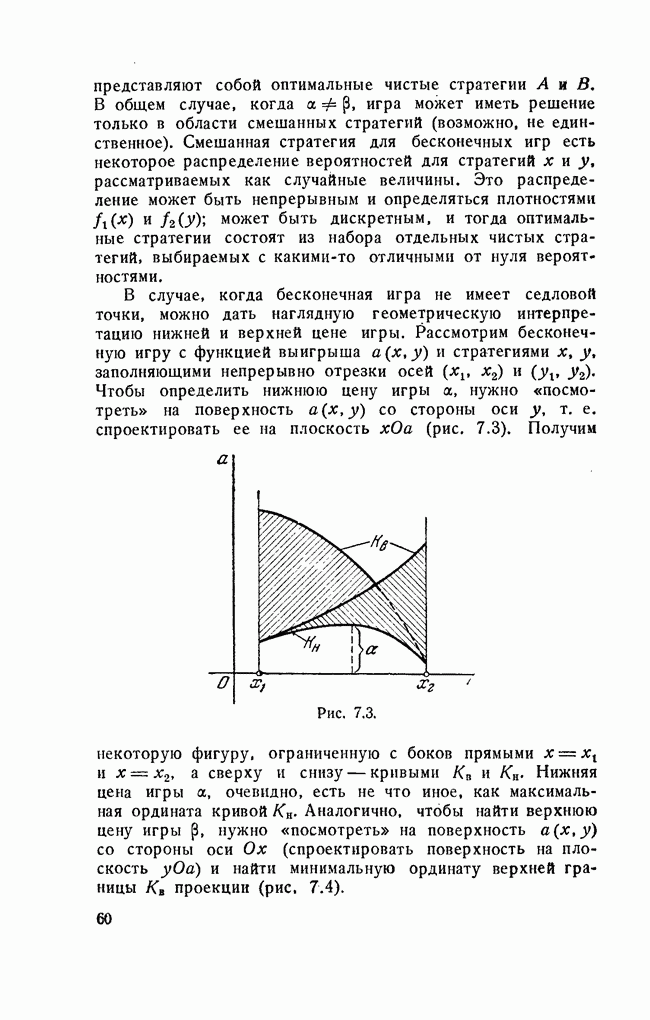
При соответствующих стратегиях и стратегии Построив таким образом все стратегии противника, мы получим семейство плоскостей над треугольником Для Этого семейства также можно построить нижнюю границу выигрыша, как мы это делали в случае и найти на этой границе точку с максимальной высотой над плоскостью Эта высота и будет ценой игры

Рис. 5.2.

Частоты стратегий в оптимальной стратегии 5 будут определяться координатами точки N, а именно:

Однако такое геометрическое построение даже для случая нелегко осуществимо и требует большой затраты времени и усилий воображения. В общем же случае игры оно переносится в -мерное пространство и теряет всякую наглядность, хотя употребление геометрической терминологии в ряде случаев может оказаться полезным. При решении игр на практике удобнее пользоваться не геометрическими аналогиями, а расчетными аналитическими методами,

тем более, что для решения задачи на вычислительных машинах эти методы единственно пригодны.

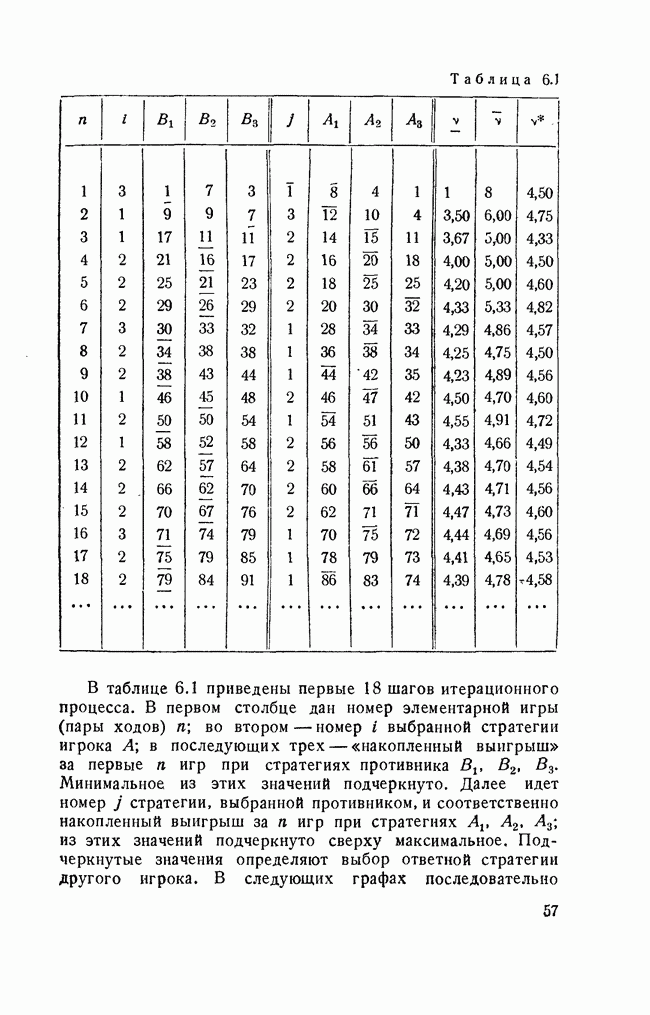
Все эти методы по существу сводятся к решению задачи путем последовательных проб, но упорядочение последовательности проб позволяет построить алгоритм, приводящий к решению наиболее экономичным способом.

Здесь мы вкратце остановимся на одном расчетном методе решения игр на так называемом методе «линейного программирования».

Для этого дадим сначала общую постановку задачи о нахождении решения игры . Пусть дана игра стратегиями игрока стратегиями игрока В и задана платежная матрица

Требуется найти решение игры, т. е. две оптимальные смешанные стратегии игроков А к В

где (некоторые из чисел могут быть равными нулю).

Наша оптимальная стратегия должна обеспечивать нам выигрыш, не меньший v, при любом поведении противника, и выигрыш, равный v, при его оптимальном поведении (стратегия S). Аналогично стратегия SB должна обеспечивать противнику проигрыш, не больший v, при любом нашем поведении и равный v при нашем оптимальном поведении (стратегия

Величина цены игры v в данном случае нам неизвестна; будем считать, что она равна некоторому положительному числу. Полагая так, мы не нарушаем общности рассуждений; для того чтобы было очевидно, достаточно, чтобы все элементы матрицы были неотрицательными. Этого всегда можно добиться, прибавляя к элементам достаточно большую положительную величину L; при этом цена игры увеличится на L, а решение не изменится.

Пусть мы выбрали свою оптимальную стратегию 5. Тогда наш средний выигрыш при стратегии противника будет равен:

Наша оптимальная стратегия обладает тем свойством, что при любом поведении противника обеспечивает выигрыш не меньший, чем v; следовательно, любое из чисел не может быть меньше v. Получаем ряд условий:

Разделим неравенства (5.1) на положительную величину v и обозначим

Тогда условия (5.1) запишутся в виде

где неотрицательные числа. Так как , то величины удовлетворяют условию

Мы хотим сделать свой гарантированный выигрыш максимально возможным; очевидно, при этом правая часть равенства (5.3) принимает минимальное значение.

Таким образом, задача нахождения решения игры сводится к следующей математической задаче: определить неотрицательные величины удовлетворяющие условиям (5.2), так, чтобы их сумма

была минимальной.

Обычно при решении задач, связанных с нахождением экстремальных значений (максимумов и минимумов), функцию дифференцируют и приравнивают производные нулю. Но такой прием в данном случае бесполезен, так как функция Ф, которую нужно обратить в минимум, линейна, и ее производные по всем аргументам равны единице, т. е. нигде

не обращаются в нуль. Следовательно, максимум функции достигается где-то на границе области изменения аргументов, которая определяется требованием неотрицательности аргументов и условиями (5.2). Прием нахождения экстремальных значений при помощи дифференцирования непригоден и в тех случаях, когда для решения игры определяется максимум нижней (или минимум верхней) границы выигрыша, как мы, например, делали при решении игр . Действительно, нижняя граница составлена из участков прямых линий, и максимум достигается не в точке, где производная равна нулю (такой точки вообще нет), а на границе интервала или в точке пересечения прямолинейных участков.

Для решения подобных задач, довольно часто встречающихся на практике, в математике разработан специальный аппарат линейного программирования.

Задача линейного программирования ставится следующим образом.

Дана система линейных уравнений:

Требуется найти неотрицательные значения величин удовлетворяющие условиям (5.4) и вместе с тем обращающие в минимум заданную однородную линейную функцию величин (линейную форму):

Легко убедиться, что поставленная выше задача теории игр является частным случаем задачи линейного программирования При .

С первого взгляда может показаться, что условия (5.2) не эквивалентны условиям (5.4), так как вместо знаков равенства они содержат знаки неравенства. Однако от знаков неравенства легко избавиться, вводя новые фиктивные неотрицательные переменные и записывая условия (5.2) в виде:

Форма Ф, которую нужно обратить в минимум, равна

Аппарат линейного программирования позволяет путем сравнительно небольшого числа последовательных проб подобрать величины удовлетворяющие поставленным требованиям. Для большей ясности мы здесь продемонстрируем применение Этого аппарата прямо на материале решения конкретных игр.

Пример 1. Требуется найти решение игры , данной в примере 2 § 1, с матрицей:

Чтобы сделать все неотрицательными, прибавим ко всем элементам матрицы . Получим матрицу:

При этой цена игры увеличится на 5, а решение не изменится.

Определим оптимальную стратегию . Условия (5.2) имеют вид:

где

Чтобы избавиться от знаков неравенства, введем фиктивные переменные условия (5.6) запишутся в виде:

Линейная форма Ф имеет вид:

и должна быть сделана как можно меньше.

Если все три стратегии В являются «полезными», то все три фиктивные переменные обратятся в нуль (т. е. выигрыш, равный цене игры v, будет достигаться при каждой стратегии ). Но мы пока не имеем оснований утверждать, что все три стратегии являются «полезными». Чтобы проверить это, попытаемся выразить форму Ф через фиктивные переменные и посмотрим, добьемся ли мы, полагая их равными нулю, минимума формы. Для этого разрешим уравнения (5.7) относительно переменных (т. е. выразим через фиктивные переменные ):

Складывая получим:

В выражении (5.9) коэффициенты при всех z положительны; значит, любое увеличение сверх нуля может

привести только к увеличению формы Ф, а мы хотим, чтобы она была минимальна. Следовательно, значениями обращающими форму (5.9) в минимум, являются

Подставляя их в формулу (5.9), находим минимальное значение формы Ф:

откуда цена игры

Подставляя нулевые значения в формулы (5.8), находим:

или, умножая их на

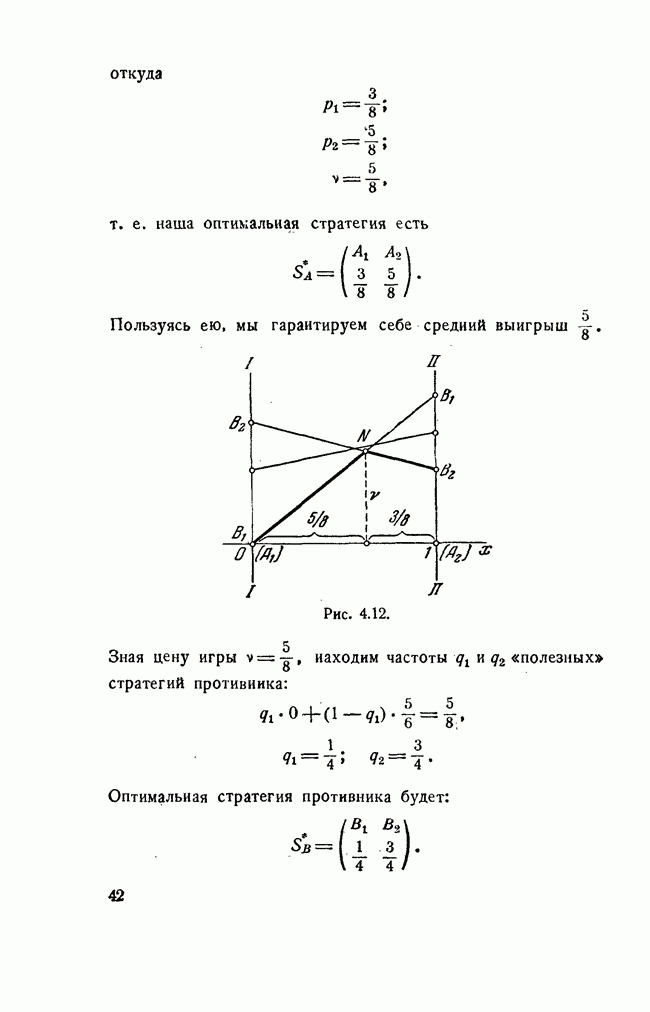
Таким образом, оптимальная стратегия А найдена:

т. е. мы должны в одной четверти всех случаев писать цифру 1, в половине случаев 2 и в остальной четверти случаев 3.

Зная цену игры можно уже известными способами найти оптимальную стратегию противника с

Для этого воспользуемся нашими любыми двумя «полезными» стратегиями (например, ) и напишем уравнения:

откуда Оптимальная стратегия противника будет такой же, как наша:

Теперь вернемся к первоначальной (не преобразованной) игре. Для этого нужно только от цены игры отнять

величину прибавленную к элементам матрицы. Получим цену исходной игры Следовательно, оптимальные стратегии обеих сторон обеспечивают средний выигрыш, равный нулю; игра в одинаковой мере выгодна или невыгодна для обеих сторон.

Пример 2. Спортивный клуб А располагает тремя вариантами состава команды . Клуб В — также тремя вариантами . Подавая заявку для участия в соревновании, ни один из клубов не знает, какой состав изберет противник. Вероятности выигрыша клуба А при различных вариантах составов команд, примерно известные из опыта прошлых встреч, заданы матрицей.

Найти, с какой частотой клубы должны выставлять каждый из составов во встречах друг с другом, чтобы добиться наибольшего в среднем числа побед.

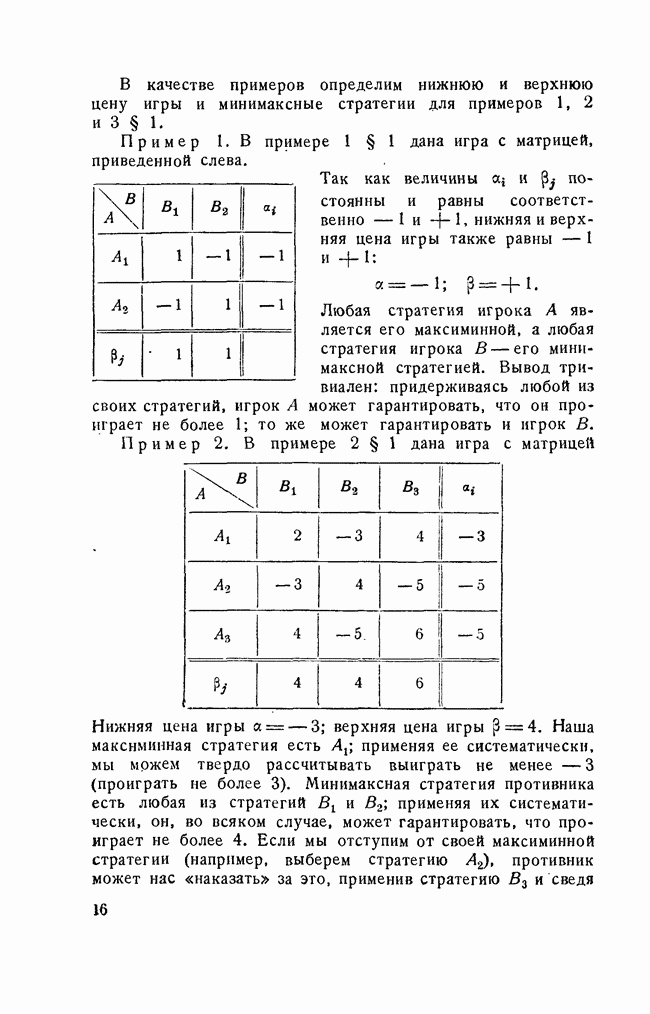
Решение. Нижняя цена игры 0,4; верхняя 0,6; решение ищем в области смешанных стратегий. Чтобы не иметь дела с дробями, умножим все элементы матрицы на 10; при этом цена игры увеличится в 10 раз, а решение не изменится. Получим матрицу:

Условия (5.5) имеют вид:

а условие минимума

Проверяем, все ли три стратегии противника являются «полезными». В качестве гипотезы сначала предполагаем, что фиктивные переменные равны нулю, и для проверки решаем уравнения (5.10) относительно

откуда

Формула (5.12) показывает, что увеличение переменных по сравнению с их предполагаемым значением нуль может только увеличить Ф, тогда как увеличение величины может уменьшить Ф. Однако увеличение надо производить осторожно, чтобы величины зависящие от не стали при этом отрицательными. Поэтому положим в правых частях равенств (5.11) величины равными нулю, а величину будем увеличивать до допустимых пределов (пока какая-нибудь из величин не обратится в нуль). Из второго равенства (5.11) видно, что увеличение «безопасно» для величины она от этого только увеличивается. Что касается величин и то здесь увеличение возможно только до некоторого предела. Величина обращается в нуль при величина обращается в нуль раньше, уже при Следовательно, давая его максимально допустимое значение мы при этом обратим в нуль величину

Чтобы проверить, обращается ли в минимум форма Ф при выразим остальные (не равные

нулю) переменные через предположительно равные нулю

Разрешая уравнения (5.10) относительно получим:

откуда

Из формулы (5.13) видно, что любое увеличение величин сверх их предполагаемых нулевых значений может только увеличить форму Ф. Следовательно, решение игры найдено; оно определяется значениями

откуда

Подставляя в формулу (5.13), находим цену игры v:

Наша оптимальная стратегия;

«Полезные» стратегии (составы ) должны применяться с частотами состав — никогда не применяться.

Чтобы найти оптимальную стратегию противника, в общем случае можно поступать так: изменить знак выигрыша на обратный, прибавить к элементам матрицы постоянную величину L, чтобы сделать их неотрицательными, и решать задачу за противника так же, как мы решали ее за себя. Однако то, что нам уже известна цена игры v, несколько упрощает задачу. К тому же в данном конкретном случае задача дополнительно упрощается тем, что в решении участвуют только две «полезные» стратегии противника так как величина

не равна нулю, и, значит, при стратегии цена игры не достигается. Выбирая любую «полезную» стратегию игрока А, например можно найти частоты Для этого пишем уравнение

откуда

оптимальная стратегия противника будет:

т. е. противник не должен пользоваться составом а составы должны применяться с частотами .

Возвращаясь к первоначальной матрице, определим истинную цену игры

Это значит, что при большом числе встреч число побед клуба А составит 0,457 всех встреч.