| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
11. ЗЕМЛЯ, ЕЕ РАЗМЕР, ФОРМА, МАССА, ДВИЖЕНИЕ
1. Размер и форма Земли.
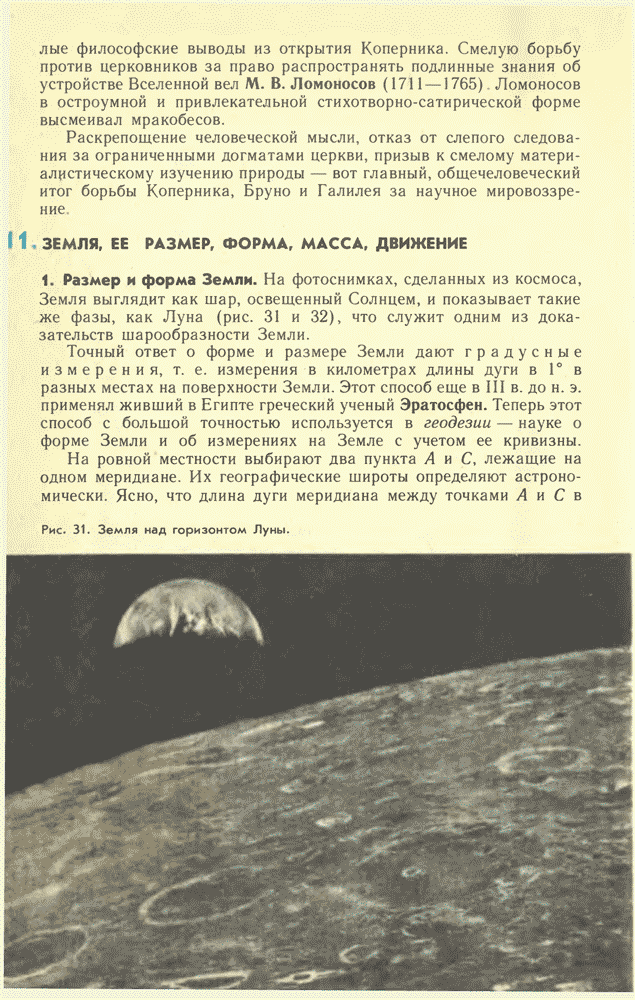
На фотоснимках, сделанных из космоса, Земля выглядит как шар, освещенный Солнцем, и показывает такие же фазы, как Луна (рис. 31 и 32), что служит одним из доказательств шарообразности Земли.
Точный ответ о форме и размере Земли дают градусные измерения, т. е. измерения в километрах длины дуги в 1° в разных местах на поверхности Земли. Этот способ еще в III в. до н. э. применял живший в Египте греческий ученый Эратосфен. Теперь этот способ с большой точностью используется в геодезии — науке о форме Земли и об измерениях на Земле с учетом ее кривизны.
На ровной местности выбирают два пункта А и С, лежащие на одном меридиане. Их географические широты определяют астрономически. Ясно, что длина дуги меридиана между точками А и С в

Рис. 31. Земля над горизонтом Луны.
градусах равна разности географических широт этих точек:  Расстояние от А до С измеряют по поверхности Земли, оно обычно составляет несколько сот километров, а потом вычисляют длину дуги в 1° в километрах.
Расстояние от А до С измеряют по поверхности Земли, оно обычно составляет несколько сот километров, а потом вычисляют длину дуги в 1° в километрах.
Из-за неровностей земной поверхности и отсутствия прямой видимости точки А из точки С (и наоборот) для определения расстояний применяют метод триангуляции (от латинского слова триангулум — треугольник, рис. 33).
Метод триангуляции состоит в том, что пространство между точками А и С покрывается сетью «воздушных» треугольников, вершинами которых служат геодезические сигналы (рис. 34). Вы, вероятно, встречали такие сигналы в виде ажурных пирамид в поле и на горах. С вершины такой пирамиды обязательно видно еще не менее двух других далеких геодезических сигналов. Измеряют углы треугольников, а длину сторон вычисляют, предварительно определив с наибольшей точностью длину одной опорной стороны, прилежащей, например, к точке А. Опорная сторона сети геодезических треугольников называется базисом. (Этот метод вычисления расстояний (длин) путем измерения углов в треугольнике, прилежащих к базису, применяют и для определения расстояний до небесных тел.)
Длину дуги меридиана  определяют как сумму проекций на это направление соответствующих сторон построенных треугольников. Углы, образуемые сторонами треугольников с плоскостью меридиана, должны быть при этом известны.
определяют как сумму проекций на это направление соответствующих сторон построенных треугольников. Углы, образуемые сторонами треугольников с плоскостью меридиана, должны быть при этом известны.
Если длина измеряемой дуги в километрах будет  а в градусах
а в градусах  то при шарообразности Земли одному градусу
то при шарообразности Земли одному градусу  дуги будет соответствовать длина в километрах:
дуги будет соответствовать длина в километрах:  Тогда длина окружности земного меридиана
Тогда длина окружности земного меридиана  Разделив ее на
Разделив ее на  получим радиус Земли.
получим радиус Земли.
Одна из наибольших дуг меридиана от Ледовитого океана до Черного моря была измерена в России и в Скандинавии в середине XIX в. под руководством В. Я. Струве, директора Пулковской обсерватории, Большие геодезические измерения в нашей стране выполнены после Великой Октябрьской социалистической революции.

Рис. 32. Фотография Земли, сделанная из космоса.

Рис. 33. Схема триангуляции.

Рис. 34. Геодезический сигнал.
Градусные измерения показали, что длина Г дуги меридиана в километрах в полярной области наибольшая (111,7 км), а на экваторе наименьшая (110,6 км). Следовательно, на экваторе кривизна поверхности Земли больше, чем у полюсов, а это говорит о том, что Земля не является шаром.
Быстрое вращение вызывает сжатие планет. Величина сжатия  определяется отношением:
определяется отношением:

где а — экваториальный,  полярный радиус планеты
полярный радиус планеты
У Земли сжатие  (у быстро вращающихся Юпитера и Сатурна оно больше, у Сатурна
(у быстро вращающихся Юпитера и Сатурна оно больше, у Сатурна  ). Таким образом, меридиональное сечение Земли является не окружностью, а эллипсом. Землю можно считать эллипсоидом вращения, т. е. фигурой, полученной от вращения эллипса вокруг его малой оси. Экваториальный радиус Земли больше полярного на 21,4 км. Изучение движения искусственных спутников Земли позволило уточнить ее сжатие по возмущениям, которые вносит в их движение несферичность Земли.
). Таким образом, меридиональное сечение Земли является не окружностью, а эллипсом. Землю можно считать эллипсоидом вращения, т. е. фигурой, полученной от вращения эллипса вокруг его малой оси. Экваториальный радиус Земли больше полярного на 21,4 км. Изучение движения искусственных спутников Земли позволило уточнить ее сжатие по возмущениям, которые вносит в их движение несферичность Земли.
Если Землю для простоты принять за шар, равновеликий Земле, то ее радиус можно взять за 6370 км. Экваториальный радиус Земли, по данным советских ученых, равен 6378,2 км.
В последнее время для определения координат различных пунктов на земной поверхности, составления точных карт и изучения формы Земли используются космические методы исследования: искусственные спутники Земли, снабженные специальной аппаратурой.
(см. скан)
2. Масса и плотность Земли.
Массу Земли можно определить многими способами. Воспользуемся тем, что из физики вам известен опыт Кавендиша с крутильными весами, при помощи которых он вычислил силу притяжения между свинцовыми шарами. Это позволило определить коэффициент  в формуле закона всемирного тяготения. А исходя из этого закона ускорение свободного падения
в формуле закона всемирного тяготения. А исходя из этого закона ускорение свободного падения

где М — масса Земли,  ее радиус. Под действием притяжения к центру Земли на уровне моря и на широте 45° ускорение
ее радиус. Под действием притяжения к центру Земли на уровне моря и на широте 45° ускорение  Подставив в формулу известные нам значения
Подставив в формулу известные нам значения  и
и  находим, что масса Земли
находим, что масса Земли  кг.
кг.
Зная массу и объем Земли, молено вычислить  среднюю плотность. Она равна
среднюю плотность. Она равна  плотность Земли с глубиной возрастает, и, по расчетам, близи центра, в ядре Земли, она равна
плотность Земли с глубиной возрастает, и, по расчетам, близи центра, в ядре Земли, она равна  Рост плотности с глубиной происходит за счет увеличения содержания тяжелых элементов, а также за счет увеличения давления.
Рост плотности с глубиной происходит за счет увеличения содержания тяжелых элементов, а также за счет увеличения давления.
(С внутренним строением Земли, изучаемым астрономическими и геофизическими методами, вы знакомились в курсе физической географии.)
(см. скан)
3. Доказательство суточного вращения Земли опытом Фуко.
Классическим доказательством вращения Земли вокруг оси является опыт с маятником по методу французского физика Фуко. Такой маятник длиной  имеется, цапример, в здании Исаакиевского собора в Ленинграде (рис. 35). Опыт основан на свойстве маятника сохранять без изменений плоскость своих колебаний, когда точка подвеса поворачивается. Это свойство можно продемонстрировать,
имеется, цапример, в здании Исаакиевского собора в Ленинграде (рис. 35). Опыт основан на свойстве маятника сохранять без изменений плоскость своих колебаний, когда точка подвеса поворачивается. Это свойство можно продемонстрировать,
подвесив на нитке шарик над центром школьной центробежной машины. Когда она вращает подвес, маятник продолжает качаться в той же плоскости Следовательно, если бы мы подвесили маятник над полюсом Земли, Земля поворачивалась бы под ним на 15° в час. Теория и опыт показывают, что на широте Ф плоскость колебания маятника кажется поворачивающейся за час на  .
.
Следствием вращения Земли вокруг оси является подмывание рекой, текущей на север или на юг, одного берега (скажите, какого?), отклонения воздушных вихрей и ветров в северном полушарии Земли вправо, в южном полушарии влево.
4. Доказательство обращения Земли вокруг Солнца.
Земля движется вокруг Солнца по орбите, которая по форме мало отличается от окружности. Определение скоростей звезд, находящихся вблизи эклиптики, по их спектрам (см. § 13) показывает, что в любой момент мы приближаемся к одним звездам и удаляемся от противоположных им на небе звезд со скоростью 30 км/с. Указанная скорость является скоростью движения Земли по ее орбите. Направление движения Земли непрерывно меняется с периодом в 1 год. Это есть прямое доказательство годичного обращения Земли вокруг Солнца. С другим доказательством годичного обращения Земли вы ознакомитесь позднее, в § 22, 2. Смена времен года является следствием того, что при обращении Земли вокруг Солнца ось ее суточного вращения сохраняет неизменное положение в пространстве и наклонена к плоскости орбиты. Этот наклон составляет 66,5°.
Вследствие небольшой эллиптичности орбиты Земля в январе немного ближе к Солнцу, чем в июле. Различие в расстояниях Земли от Солнца в афелии и в перигелии мало и поэтому оказывает малозаметное влияние на получаемую от Солнца энергию.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- I. ВВЕДЕНИЕ
- 2. АСТРОНОМИЧЕСКИЕ НАБЛЮДЕНИЯ И ТЕЛЕСКОПЫ
- 3. СОЗВЕЗДИЯ. ВИДИМОЕ ДВИЖЕНИЕ ЗВЕЗД
- 4. ЭКЛИПТИКА И «БЛУЖДАЮЩИЕ» СВЕТИЛА — ПЛАНЕТЫ
- 5. ЗВЕЗДНЫЕ КАРТЫ, НЕБЕСНЫЕ КООРДИНАТЫ И ВРЕМЯ
- II. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
- 7. ЗАКОНЫ ДВИЖЕНИЯ ПЛАНЕТ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
- 8. КОНФИГУРАЦИИ И СИНОДИЧЕСКИЕ ПЕРИОДЫ ОБРАЩЕНИЯ ПЛАНЕТ
- 9. ВОЗМУЩЕНИЯ В ДВИЖЕНИИ ПЛАНЕТ. ПОНЯТИЕ О ПРИЛИВАХ. ОПРЕДЕЛЕНИЕ МАСС НЕБЕСНЫХ ТЕЛ
- 10. БОРЬБА ЗА НАУЧНОЕ МИРОВОЗЗРЕНИЕ
- 11. ЗЕМЛЯ, ЕЕ РАЗМЕР, ФОРМА, МАССА, ДВИЖЕНИЕ
- 12. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ И РАЗМЕРОВ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- III. ФИЗИЧЕСКАЯ ПРИРОДА ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ
- 14. ОБЩИЕ ХАРАКТЕРИСТИКИ ПЛАНЕТ ЗЕМНОЙ ГРУППЫ И ЗЕМЛИ
- 15. ФИЗИЧЕСКИЕ УСЛОВИЯ НА ЛУНЕ И ЕЕ РЕЛЬЕФ
- 16. ПЛАНЕТЫ МЕРКУРИЙ, ВЕНЕРА И МАРС
- 17. ПЛАНЕТЫ-ГИГАНТЫ
- 18. ДВИЖЕНИЕ ЛУНЫ И СПУТНИКОВ ПЛАНЕТ. ЗАТМЕНИЯ
- 19. АСТЕРОИДЫ И МЕТЕОРИТЫ
- 20. КОМЕТЫ И МЕТЕОРЫ
- IV. СОЛНЦЕ И ЗВЕЗДЫ
- 1. СОЛНЦЕ — БЛИЖАЙШАЯ ЗВЕЗДА
- 22. СПЕКТРЫ, ТЕМПЕРАТУРЫ, СВЕТИМОСТИ ЗВЕЗД И РАССТОЯНИЯ ДО НИХ
- 23. ДВОЙНЫЕ ЗВЕЗДЫ, МАССЫ ЗВЕЗД
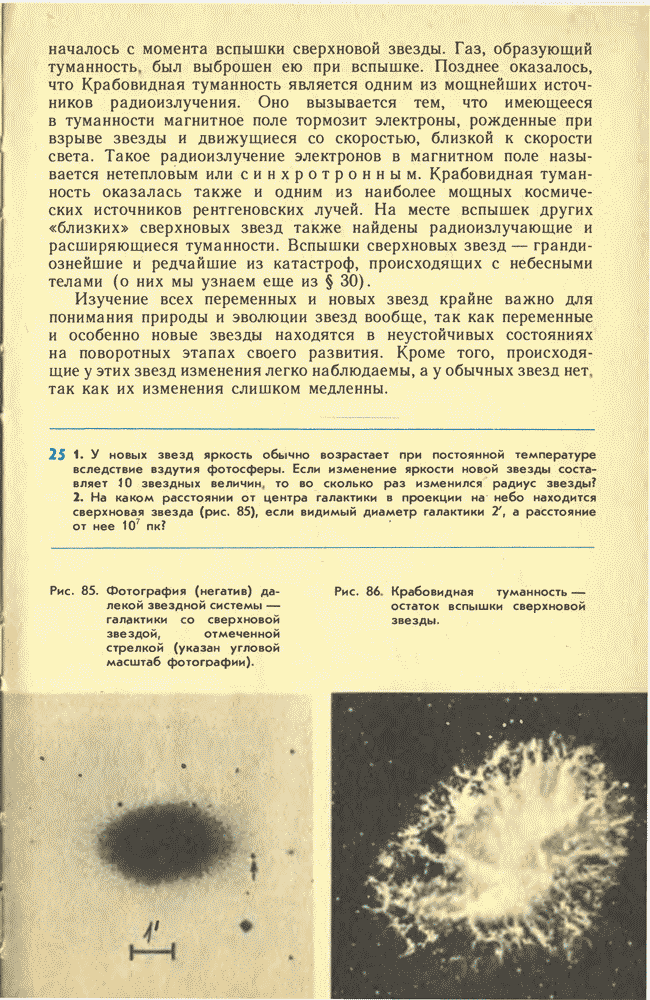
- 24. ПЕРЕМЕННЫЕ И НОВЫЕ ЗВЕЗДЫ
- 25. РАЗНООБРАЗИЕ ЗВЕЗДНЫХ ХАРАКТЕРИСТИК И ИХ ЗАКОНОМЕРНОСТИ
- V. СТРОЕНИЕ И ЭВОЛЮЦИЯ ВСЕЛЕННОЙ
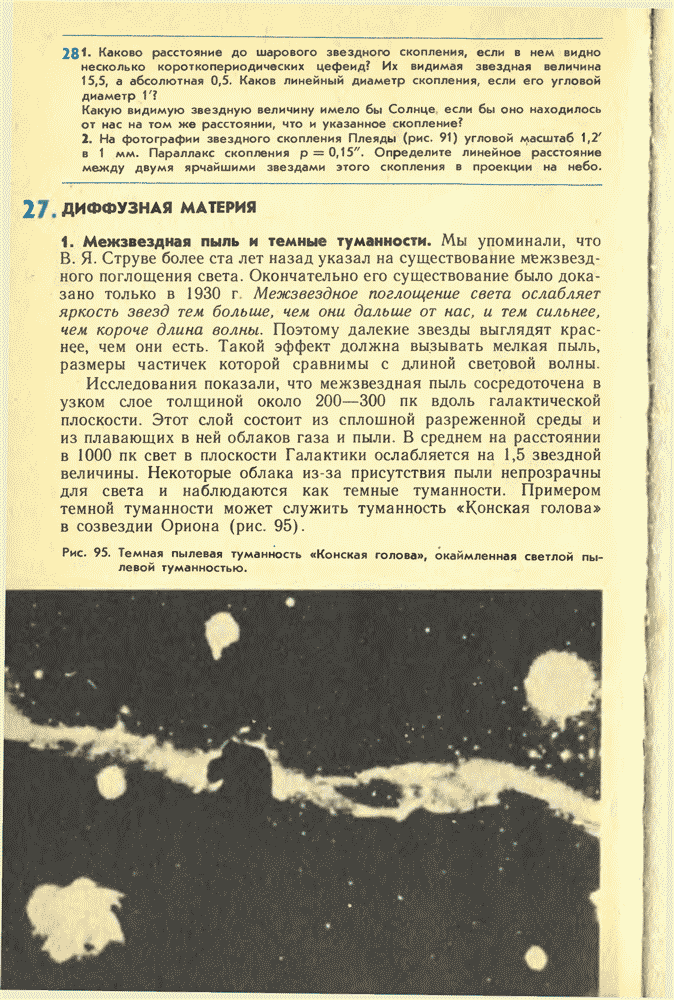
- 27. ДИФФУЗНАЯ МАТЕРИЯ
- 28. ДВИЖЕНИЯ ЗВЕЗД В ГАЛАКТИКЕ
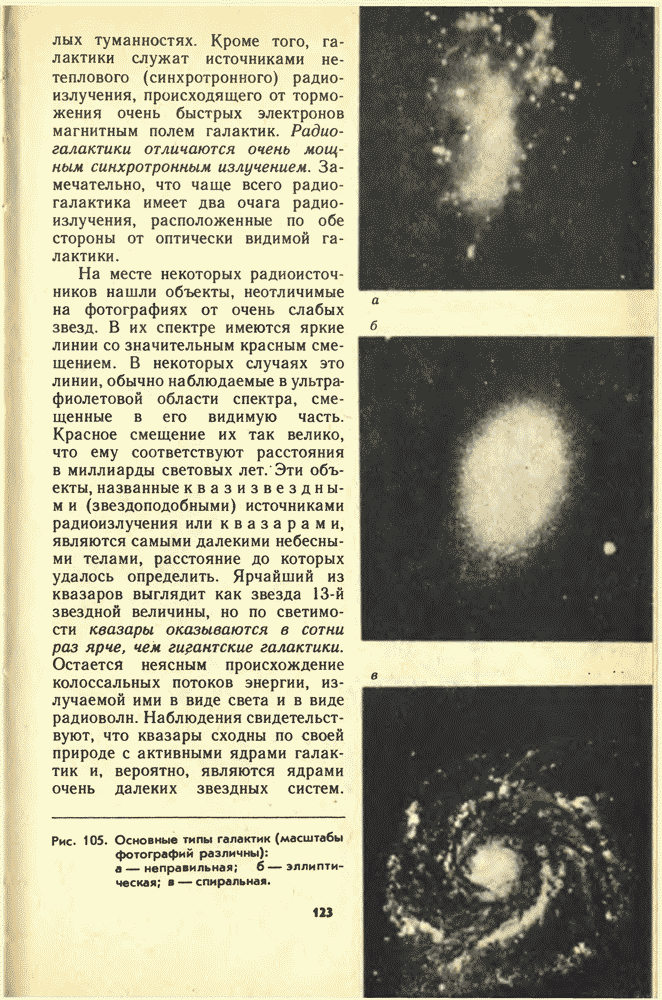
- 29. ЗВЕЗДНЫЕ СИСТЕМЫ — ГАЛАКТИКИ. МЕТАГАЛАКТИКА
- 30. ВОЗРАСТ НЕБЕСНЫХ ТЕЛ. ВОЗНИКНОВЕНИЕ И РАЗВИТИЕ ГАЛАКТИК И ЗВЕЗД
- 31. ВОЗНИКНОВЕНИЕ ПЛАНЕТНЫХ СИСТЕМ И ЗЕМЛИ
- 32. МАТЕРИАЛИСТИЧЕСКАЯ КАРТИНА МИРОЗДАНИЯ. ПРОБЛЕМА ВНЕЗЕМНЫХ ЦИВИЛИЗАЦИЙ
- ПРИЛОЖЕНИЯ
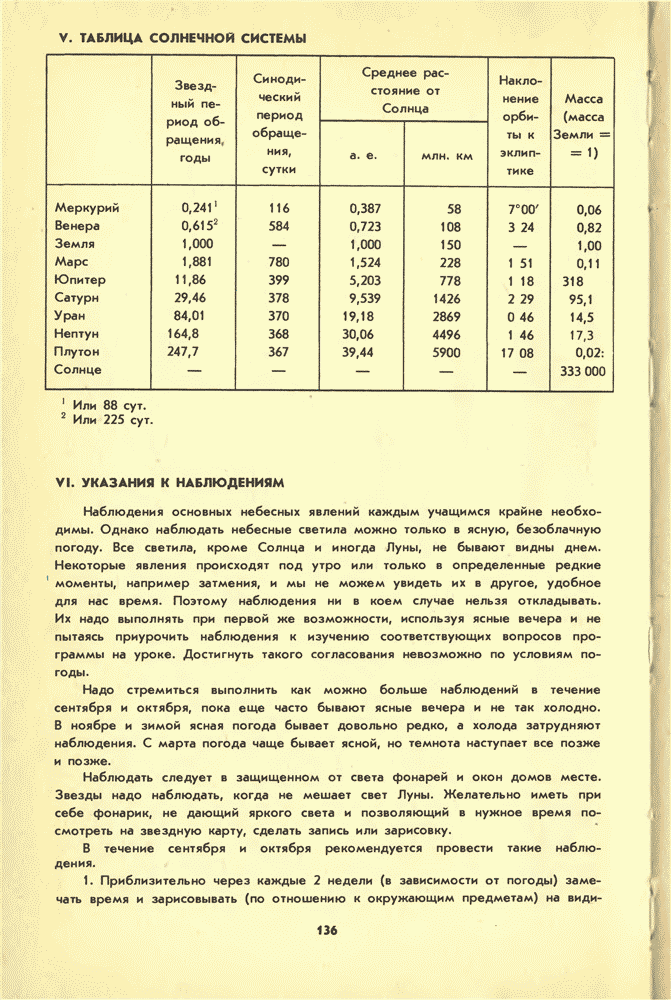
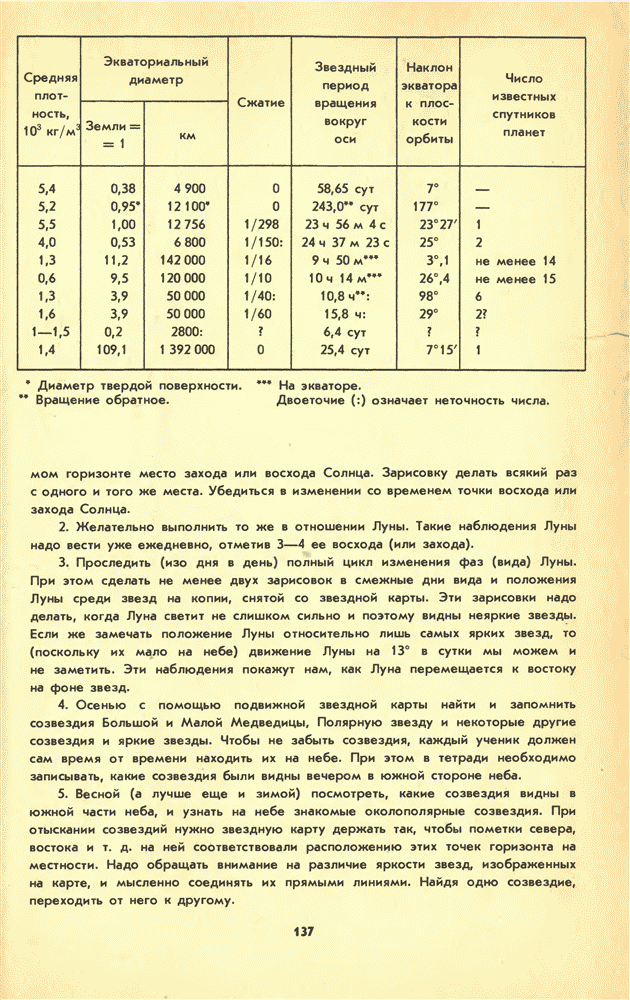
- V. ТАБЛИЦА СОЛНЕЧНОЙ СИСТЕМЫ
- VI. УКАЗАНИЯ К НАБЛЮДЕНИЯМ