| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. ЗАКОНЫ ДВИЖЕНИЯ ПЛАНЕТ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
1. Форма орбиты и скорость движения.
Чем ближе планета к Солнцу, тем, больше ее линейная и угловая скорости и короче период обращения вокруг Солнца. Мы наблюдаем планеты с Земли, которая сама обращается вокруг Солнца. Это движение Земли необходимо учитывать, чтобы узнать периоды обращения планет в невращающейся инерциальной системе отсчета, или, как часто говорят, по отношению к звездам.
Период обращения планет вокруг Солнца по отношению к звездам называется звездным или сидерическим периодом. Наименьший звездный период обращения у планеты Меркурий — 88 сут. У Марса он составляет почти 2 года, а у Юпитера — 12 лет и, все возрастая с удалением от Солнца, у Плутона доходит почти до 250 лет.
Заслуга открытия законов движения планет принадлежит выдающемуся немецкому ученому Иоганну Кеплеру. В начале
XVII в. Кеплер установил три закона движения планет. Они названы законами Кеплера.
Первый закон Кеплера: каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце (рис. 24).
Эллипсом (рис. 24) называется плоская замкнутая кривая, имеющая такое свойство, что сумма расстояний каждой ее точки от двух точек, называемых фокусами, остается постоянной. Эта сумма расстояний равна длине большой оси  эллипса (рис. 24). Точка О — центр эллипса, К и 5 — фокусы. Солнце находится в данном случае в фокусе
эллипса (рис. 24). Точка О — центр эллипса, К и 5 — фокусы. Солнце находится в данном случае в фокусе  — большая полуось эллипса. Большая полуось а является средним расстоянием планеты от Солнца:
— большая полуось эллипса. Большая полуось а является средним расстоянием планеты от Солнца: 
Ближайшая к Солнцу точка орбиты А называется перигелием, а самая далекая от него точка  называется афелием.
называется афелием.
Степень вытянутости эллипса характеризуется его эксцентриситетом
 . Эксцентриситет равен отношению расстояния фокуса от центра
. Эксцентриситет равен отношению расстояния фокуса от центра  к длине большой полуоси а, т. е.
к длине большой полуоси а, т. е.  совпадении фокусов с центром
совпадении фокусов с центром  эллипс превращается в окружность.
эллипс превращается в окружность.
Орбиты планет — эллипсы, мало отличающиеся от окружностей, их эксцентриситеты малы. Например, эксцентриситет орбиты Земли 
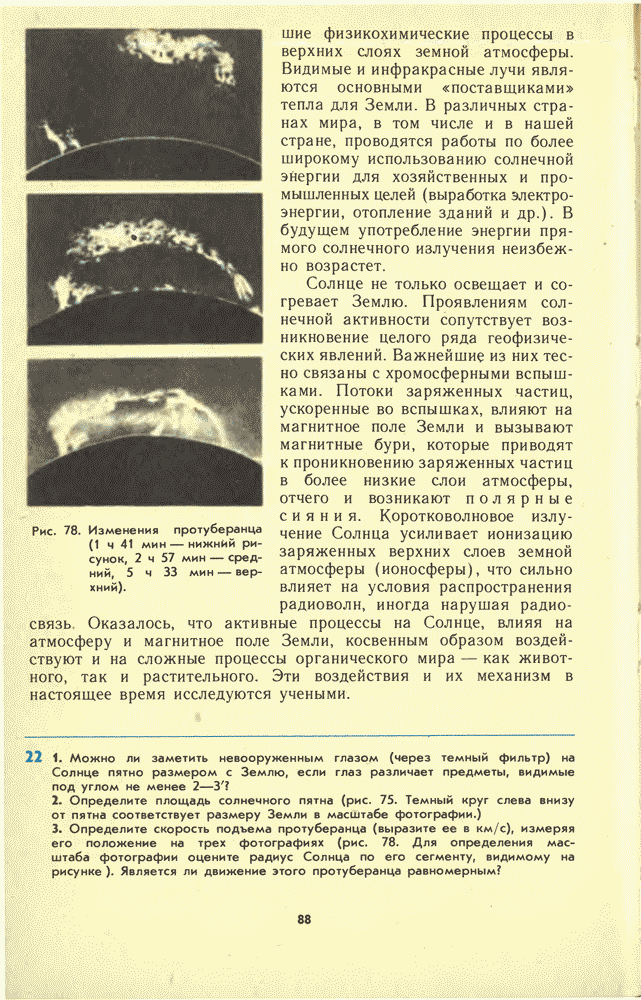
Эксцентриситеты орбит у большинства комет близки к единице. При  второй фокус эллипса удаляется в бесконечность, так что орбита становится разомкнутой кривой (рис. 25), называемой параболой. При
второй фокус эллипса удаляется в бесконечность, так что орбита становится разомкнутой кривой (рис. 25), называемой параболой. При  орбита является гиперболой (рис. 25). Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.
орбита является гиперболой (рис. 25). Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.
Кеплер открыл свои законы, изучая периодическое обращение Марса вокруг Солнца. Ньютон, исходя из наблюдений движения Луны и законов Кеплера, открыл закон всемирного тяготения. При этом он доказал, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу (в частности, по кругу), по параболе и по гиперболе. Ньютон установил, что вид орбиты, которую описывает тело, зависит от его скорости в данном месте орбиты.
При некоторой скорости тело описывает окружность около притягивающего центра. Такую скорость называют первой космической или круговой скоростью, ее сообщают телам, запускаемым в качестве искусственных спутников Земли по круговым орбитам. Вывод формулы для вычисления первой космической скорости известен из курса физики. Первая космическая скорость вблизи поверхности Земли составляет около 
Если телу сообщить скорость, в раза большую круговой  называемую второй космической или параболической скоростью, то тело навсегда удалится от Земли и может стать спутником Солнца. В этом случае движение тела будет происходить по параболе относительно Земли. При еще большей скорости относительно Земли тело полетит по гиперболе.
называемую второй космической или параболической скоростью, то тело навсегда удалится от Земли и может стать спутником Солнца. В этом случае движение тела будет происходить по параболе относительно Земли. При еще большей скорости относительно Земли тело полетит по гиперболе.
Средняя скорость движения Земли по орбите  Орбита Земли близка к окружности, а скорость движения Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость на расстоянии Земли от Солнца равна
Орбита Земли близка к окружности, а скорость движения Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость на расстоянии Земли от Солнца равна  При такой скорости относительно Солнца тело с орбиты Земли покинет Солнечную систему.
При такой скорости относительно Солнца тело с орбиты Земли покинет Солнечную систему.
2. Второй и третий законы Кеплера.
Второй закон Кеплера (закон площадей): радиус-вектор планеты за одинаковые промежутки времени описывает равные площади, т. е. площади  равны (рис. 24), если дуги
равны (рис. 24), если дуги  описаны планетой за одинаковые промежутки времени. Но длины этих дуг, ограничивающих равные площади, различны:
описаны планетой за одинаковые промежутки времени. Но длины этих дуг, ограничивающих равные площади, различны:  Следовательно, линейная скорость движения планеты неодинакова в разных точках ее
Следовательно, линейная скорость движения планеты неодинакова в разных точках ее

Рис. 24. Закон площадей (второй закон Кеплера).

Рис. 25. Формы орбит космических ракет (посланные по стрелке, они не вернутся, если пойдут по параболе или гиперболе, и по прерывистым частям кривых движения не будет).
орбиты. Скорость планеты при движении ее по орбите тем больше, чем ближе она к Солнцу. В перигелии скорость планеты наибольшая, в афелии наименьшая. Таким образом, второй закон Кеплера количественно определяет изменение скорости движения планеты по эллипсу.
Третий закон Кеплера: квадраты звездных периодов обращения планет относятся как кубы больших полуосей их орбит. Если большую полуось орбиты и звездный период обращения одной планеты обозначить через  а другой планеты — через
а другой планеты — через  то формула третьего закона будет такова:
то формула третьего закона будет такова:

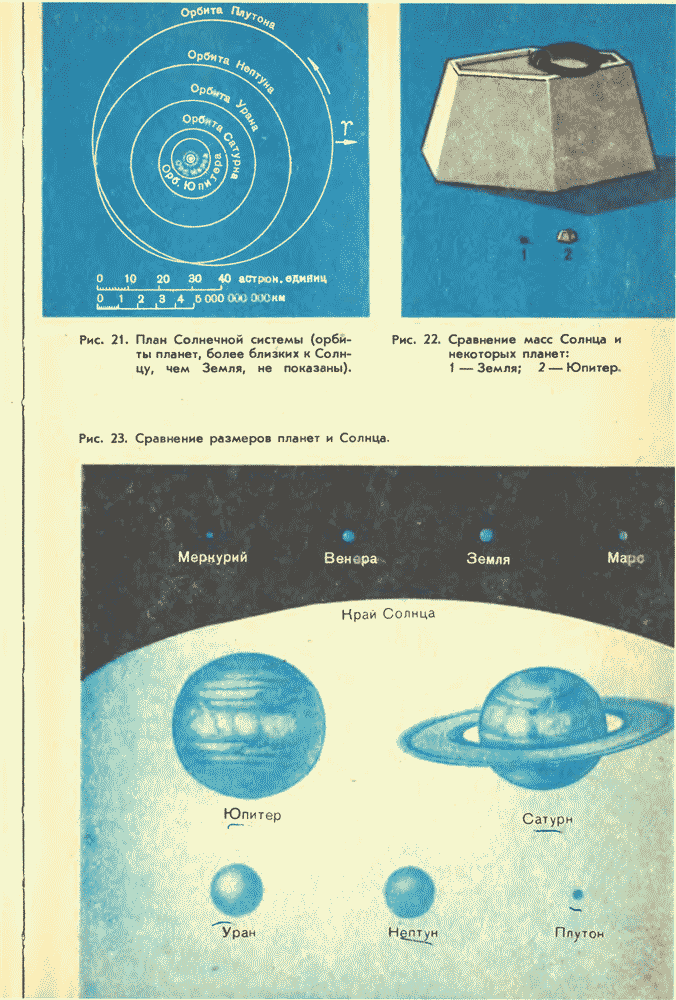
Этот закон Кеплера связывает средние расстояния планет от Солнца с периодами их звездных обращений и позволяет большие полуоси всех планетных орбит выразить в единицах большой полуоси земной орбиты. Большая полуось земной орбиты принята за астрономическую единицу расстояний. В астрономических единицах средние расстояния планет от Солнца были определены раньше, чем узнали длину астрономической единицы в километрах.
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- I. ВВЕДЕНИЕ
- 2. АСТРОНОМИЧЕСКИЕ НАБЛЮДЕНИЯ И ТЕЛЕСКОПЫ
- 3. СОЗВЕЗДИЯ. ВИДИМОЕ ДВИЖЕНИЕ ЗВЕЗД
- 4. ЭКЛИПТИКА И «БЛУЖДАЮЩИЕ» СВЕТИЛА — ПЛАНЕТЫ
- 5. ЗВЕЗДНЫЕ КАРТЫ, НЕБЕСНЫЕ КООРДИНАТЫ И ВРЕМЯ
- II. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ
- 7. ЗАКОНЫ ДВИЖЕНИЯ ПЛАНЕТ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
- 8. КОНФИГУРАЦИИ И СИНОДИЧЕСКИЕ ПЕРИОДЫ ОБРАЩЕНИЯ ПЛАНЕТ
- 9. ВОЗМУЩЕНИЯ В ДВИЖЕНИИ ПЛАНЕТ. ПОНЯТИЕ О ПРИЛИВАХ. ОПРЕДЕЛЕНИЕ МАСС НЕБЕСНЫХ ТЕЛ
- 10. БОРЬБА ЗА НАУЧНОЕ МИРОВОЗЗРЕНИЕ
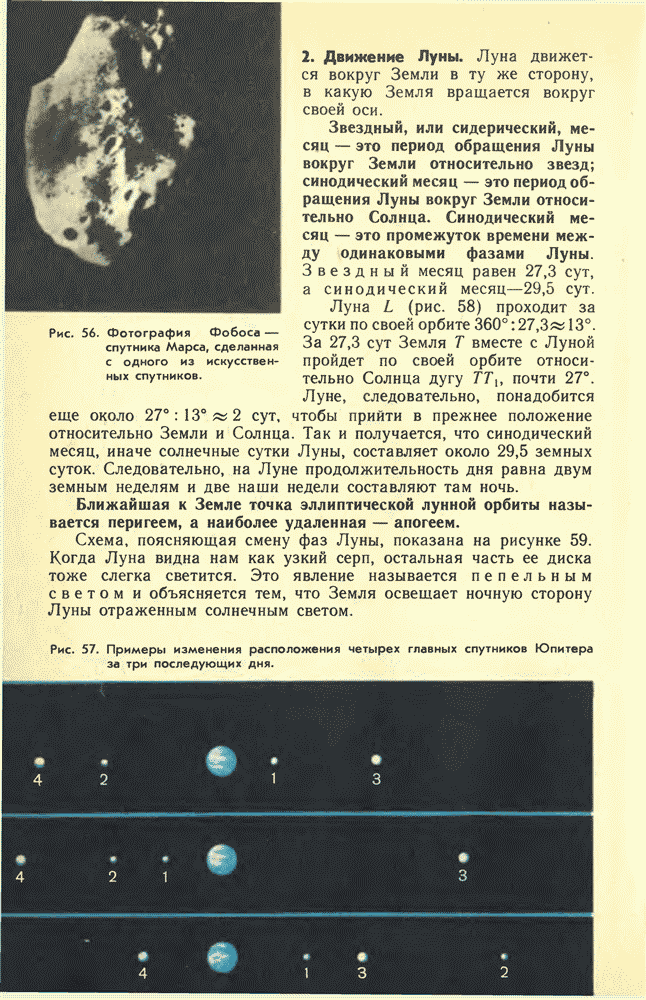
- 11. ЗЕМЛЯ, ЕЕ РАЗМЕР, ФОРМА, МАССА, ДВИЖЕНИЕ
- 12. ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ И РАЗМЕРОВ ТЕЛ В СОЛНЕЧНОЙ СИСТЕМЕ
- III. ФИЗИЧЕСКАЯ ПРИРОДА ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ
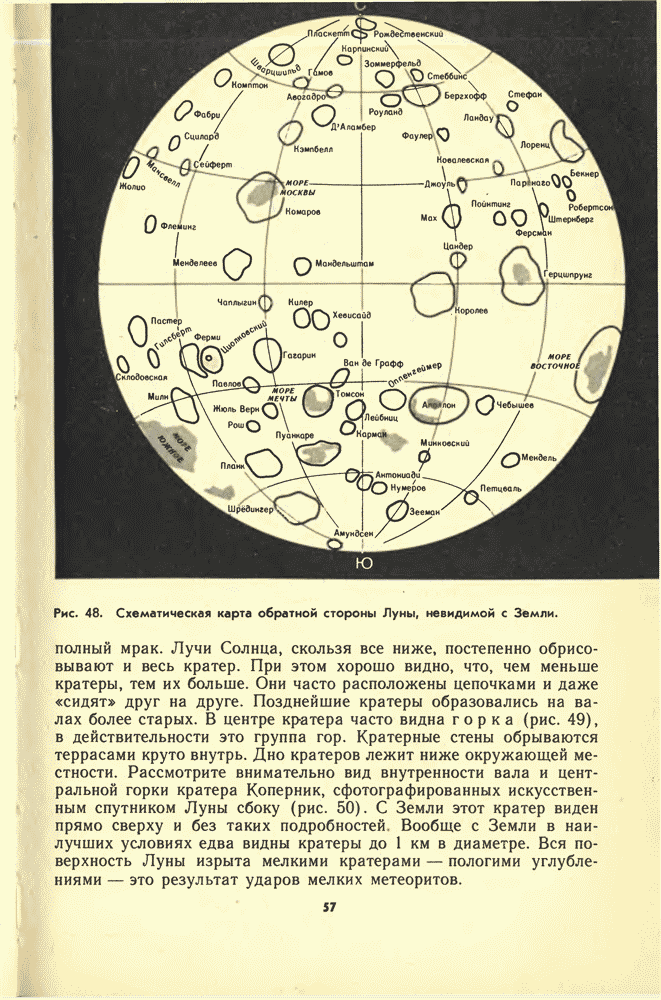
- 14. ОБЩИЕ ХАРАКТЕРИСТИКИ ПЛАНЕТ ЗЕМНОЙ ГРУППЫ И ЗЕМЛИ
- 15. ФИЗИЧЕСКИЕ УСЛОВИЯ НА ЛУНЕ И ЕЕ РЕЛЬЕФ
- 16. ПЛАНЕТЫ МЕРКУРИЙ, ВЕНЕРА И МАРС
- 17. ПЛАНЕТЫ-ГИГАНТЫ
- 18. ДВИЖЕНИЕ ЛУНЫ И СПУТНИКОВ ПЛАНЕТ. ЗАТМЕНИЯ
- 19. АСТЕРОИДЫ И МЕТЕОРИТЫ
- 20. КОМЕТЫ И МЕТЕОРЫ
- IV. СОЛНЦЕ И ЗВЕЗДЫ
- 1. СОЛНЦЕ — БЛИЖАЙШАЯ ЗВЕЗДА
- 22. СПЕКТРЫ, ТЕМПЕРАТУРЫ, СВЕТИМОСТИ ЗВЕЗД И РАССТОЯНИЯ ДО НИХ
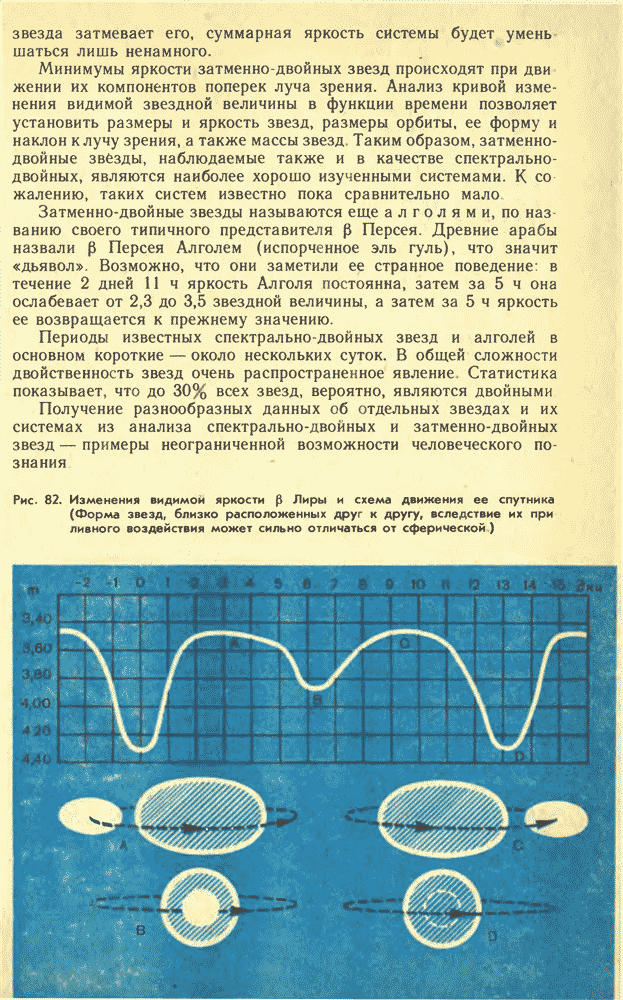
- 23. ДВОЙНЫЕ ЗВЕЗДЫ, МАССЫ ЗВЕЗД
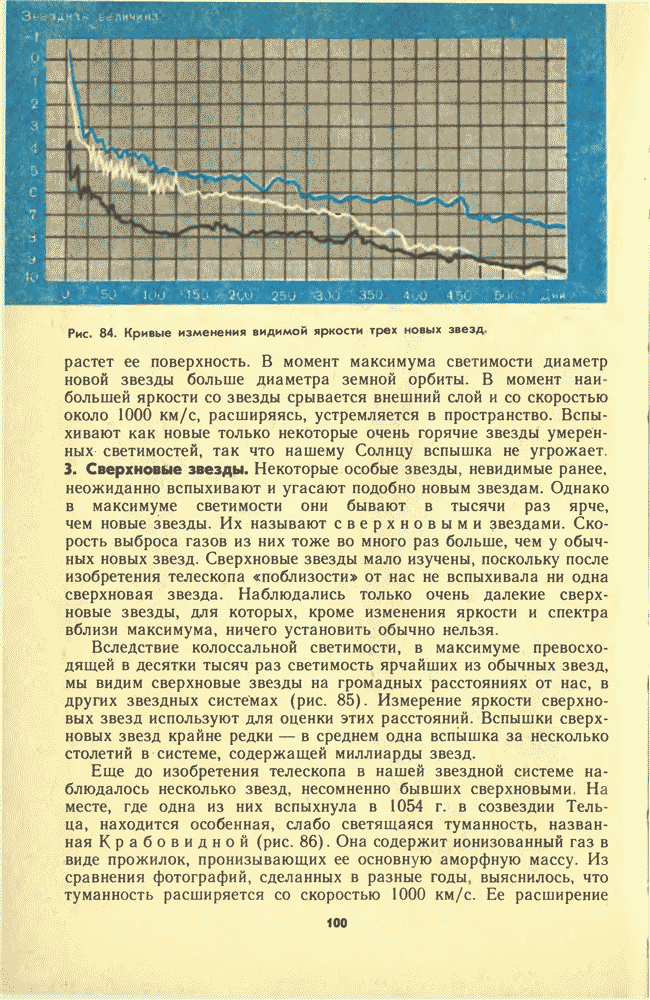
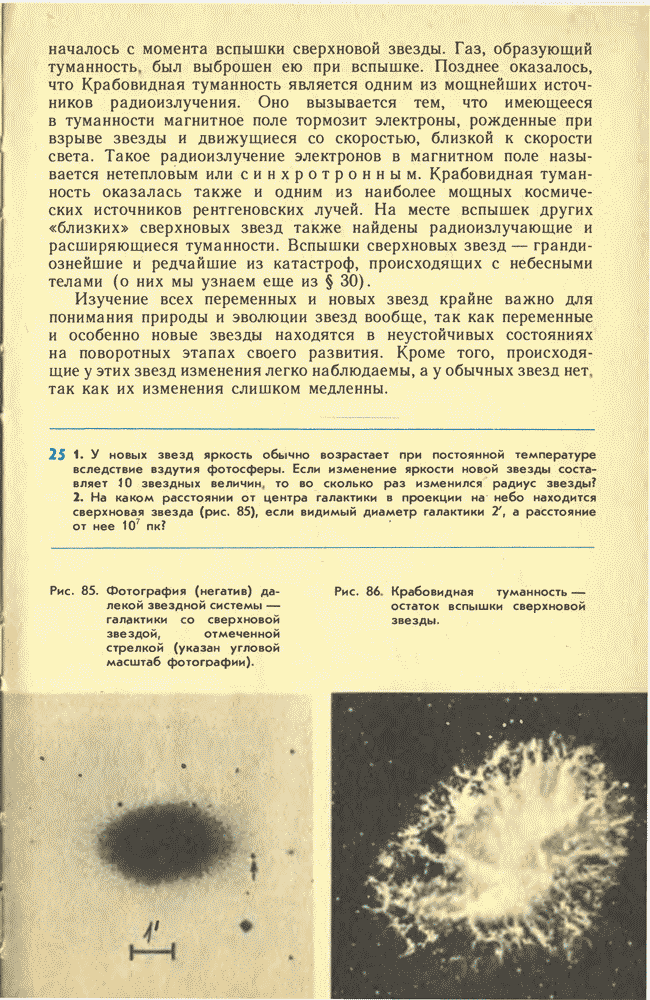
- 24. ПЕРЕМЕННЫЕ И НОВЫЕ ЗВЕЗДЫ
- 25. РАЗНООБРАЗИЕ ЗВЕЗДНЫХ ХАРАКТЕРИСТИК И ИХ ЗАКОНОМЕРНОСТИ
- V. СТРОЕНИЕ И ЭВОЛЮЦИЯ ВСЕЛЕННОЙ
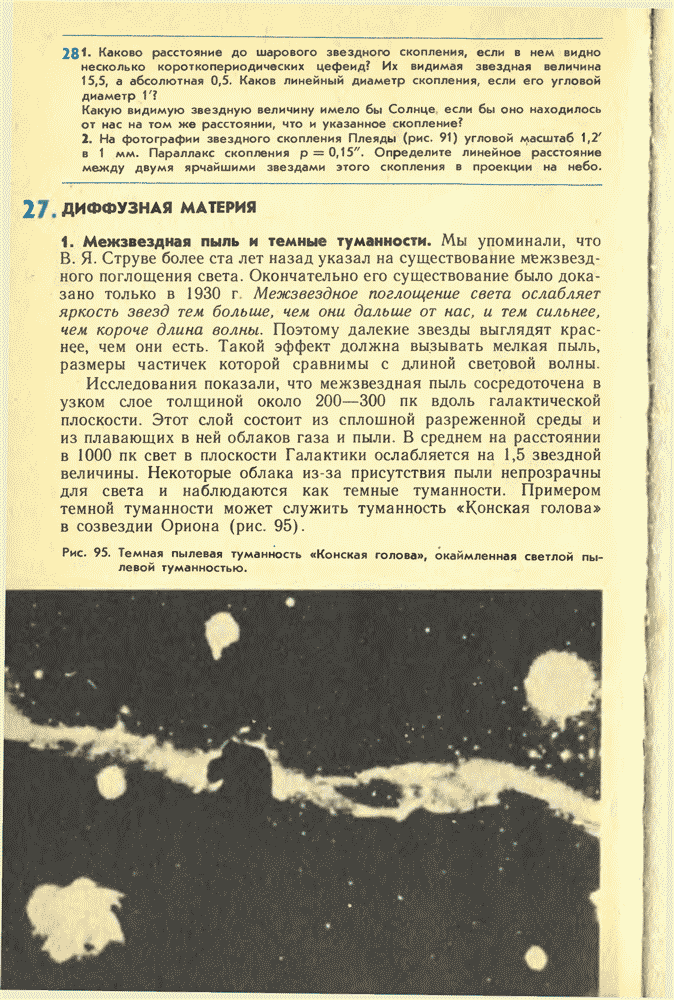
- 27. ДИФФУЗНАЯ МАТЕРИЯ
- 28. ДВИЖЕНИЯ ЗВЕЗД В ГАЛАКТИКЕ
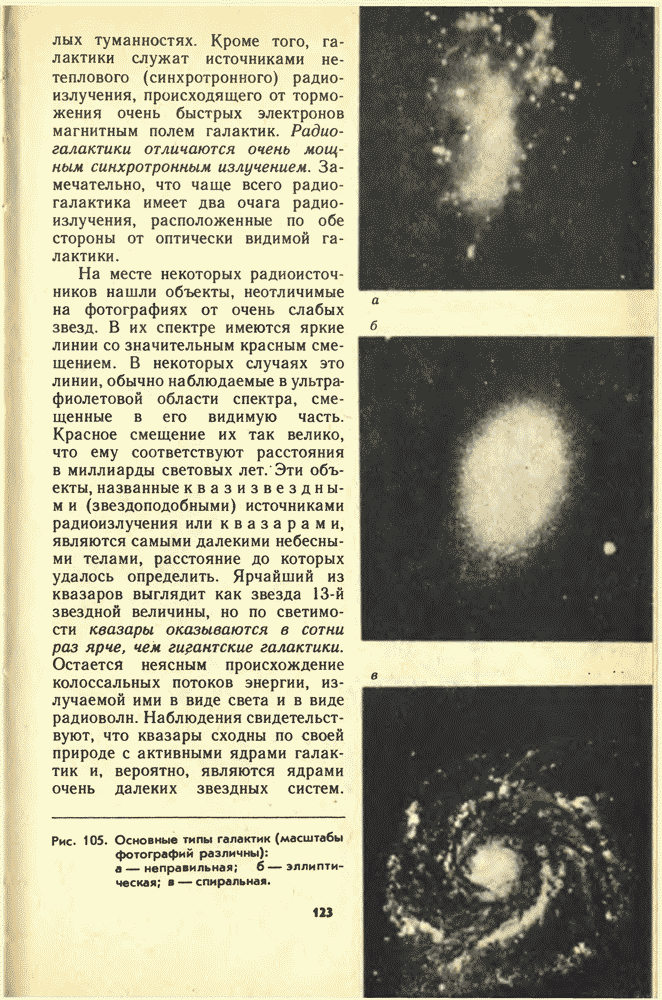
- 29. ЗВЕЗДНЫЕ СИСТЕМЫ — ГАЛАКТИКИ. МЕТАГАЛАКТИКА
- 30. ВОЗРАСТ НЕБЕСНЫХ ТЕЛ. ВОЗНИКНОВЕНИЕ И РАЗВИТИЕ ГАЛАКТИК И ЗВЕЗД
- 31. ВОЗНИКНОВЕНИЕ ПЛАНЕТНЫХ СИСТЕМ И ЗЕМЛИ
- 32. МАТЕРИАЛИСТИЧЕСКАЯ КАРТИНА МИРОЗДАНИЯ. ПРОБЛЕМА ВНЕЗЕМНЫХ ЦИВИЛИЗАЦИЙ
- ПРИЛОЖЕНИЯ
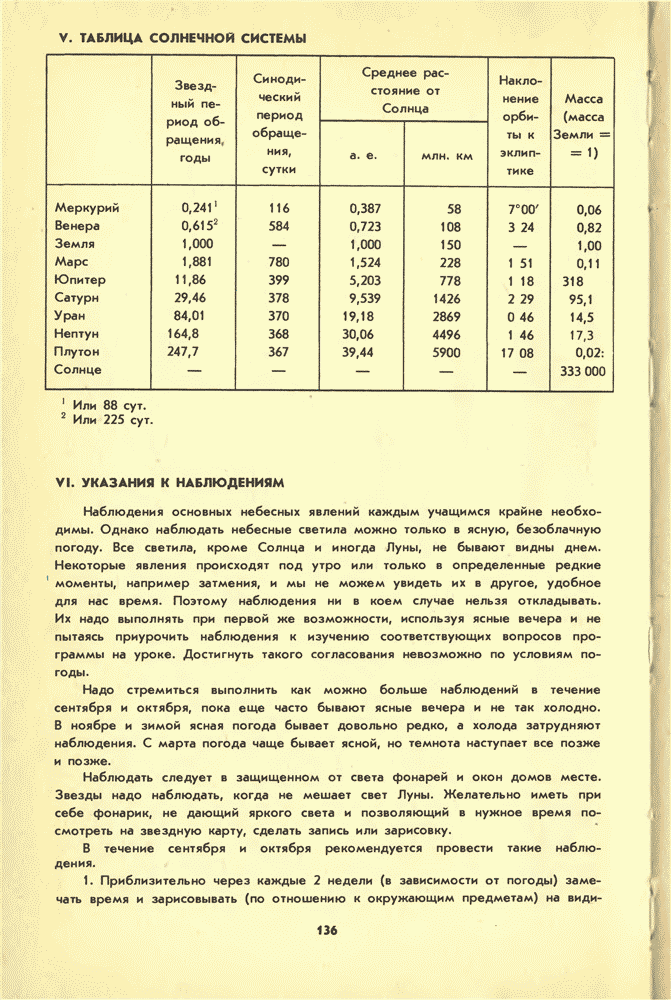
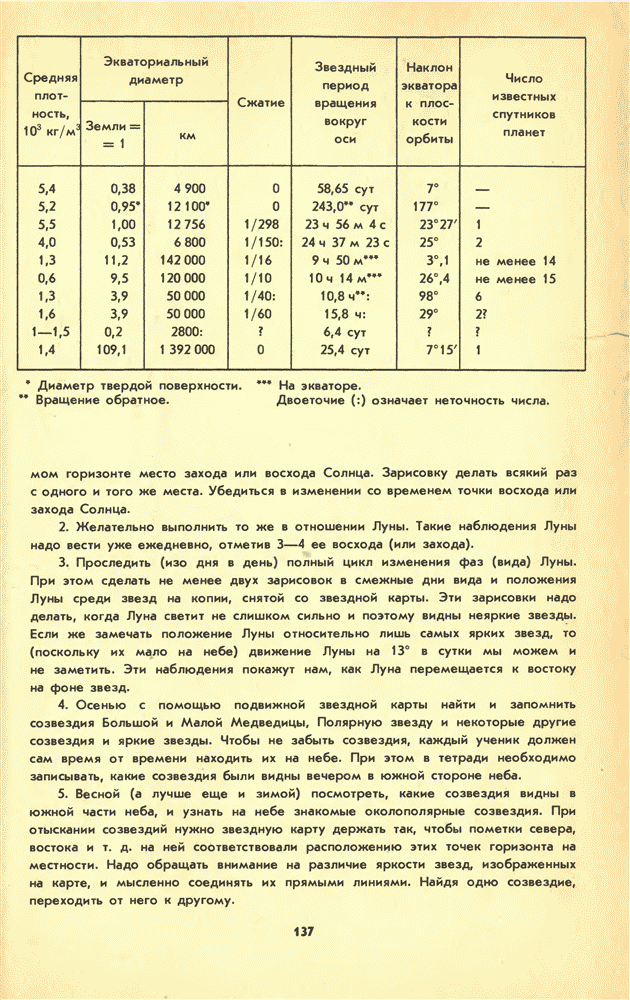
- V. ТАБЛИЦА СОЛНЕЧНОЙ СИСТЕМЫ
- VI. УКАЗАНИЯ К НАБЛЮДЕНИЯМ