| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. МОДЕЛЬ ОБЪЕКТА
3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
Наиболее удобно представлять трехмерные объекты для метода обратного трассирования лучей в виде отдельных строительных блоков, поверхности которых обычно описываются функциями первого и второго порядка. Выбор таких функций обусловлен необходимостью аналитического, а не численного решения уравнений пересечения светового луча с поверхностями. Описание бикубических поверхностей представлено в §3.4.4.
Будем
называть функциональным объемом некоторую часть пространства (необязательно
конечную), которая охватывается поверхностью одной функции. Для того чтобы
однозначно определить, какой участок полупространства относится к телу объекта,
а какой вне его, установим следующее правило: принадлежащим телу объекта
считается подпространство, выделяемое поверхностью ![]() , в любой точке которого
значение скалярного поля
, в любой точке которого
значение скалярного поля ![]() . Назовем такое подпространство
положительным, а смежное с ним и лежащее по другую сторону от поверхности
функции – отрицательным. При соблюдении этой договоренности, автоматически
выполняется условие направленности вектора нормали внутрь тела, т. е. в сторону
положительного подпространства, так как градиент скалярного поля описываемых
классов направлен нормально от поверхности в сторону возрастания значения
. Назовем такое подпространство
положительным, а смежное с ним и лежащее по другую сторону от поверхности
функции – отрицательным. При соблюдении этой договоренности, автоматически
выполняется условие направленности вектора нормали внутрь тела, т. е. в сторону
положительного подпространства, так как градиент скалярного поля описываемых
классов направлен нормально от поверхности в сторону возрастания значения ![]() .
.
Объемными примитивами будем называть конечные участки пространства, ограниченные одной или несколькими функционально описанными поверхностями. Очень часто в качестве примитива используют функциональный объем, ограниченный плоскостями – многогранник. Примитивы, естественно, должны обеспечивать удобство конструирования из них производных тел и обладать относительной математической простотой.
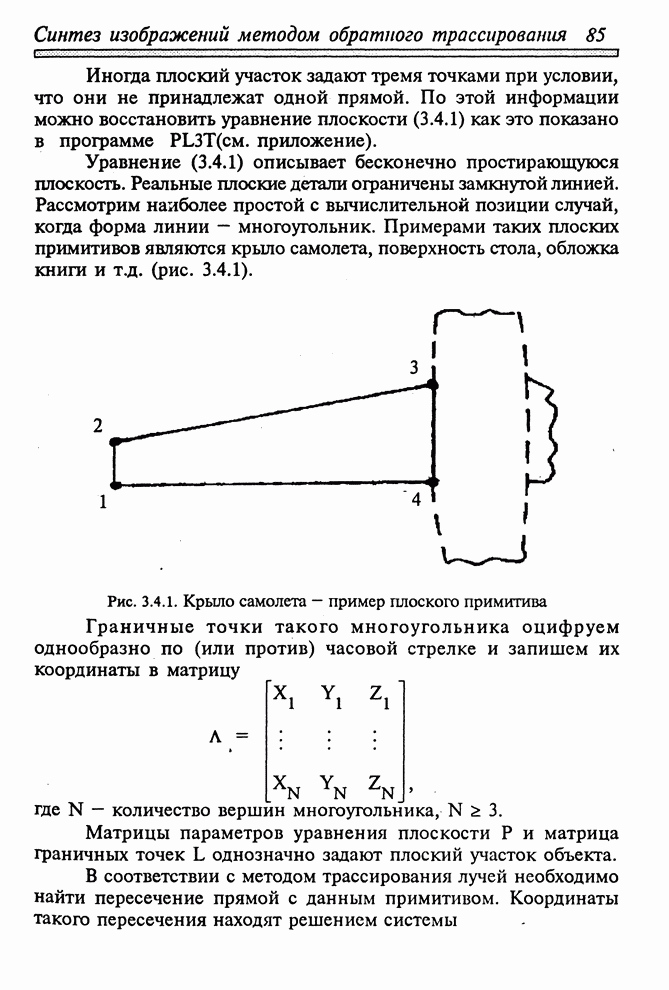
Плоским примитивом будем называть часть плоскости, ограниченную замкнутой линией, состоящей из конечного числа прямолинейных или криволинейных участков.
Для одного и того же примитива характерны неизменное количество ограничивающих его тело поверхностей и стандартный вид функций, описывающих эти поверхности. Параметры функций являются варьируемыми, этим достигается изменение формы примитива (например из эллипсоида в шар), их пространственного положения и ориентации. Наиболее употребительные типы примитивов показаны на рис.3.2.1: а – тетраэдр, б – параллелепипед, в – цилиндр, г – эллипсоид, д – конус, е – часть плоскости.

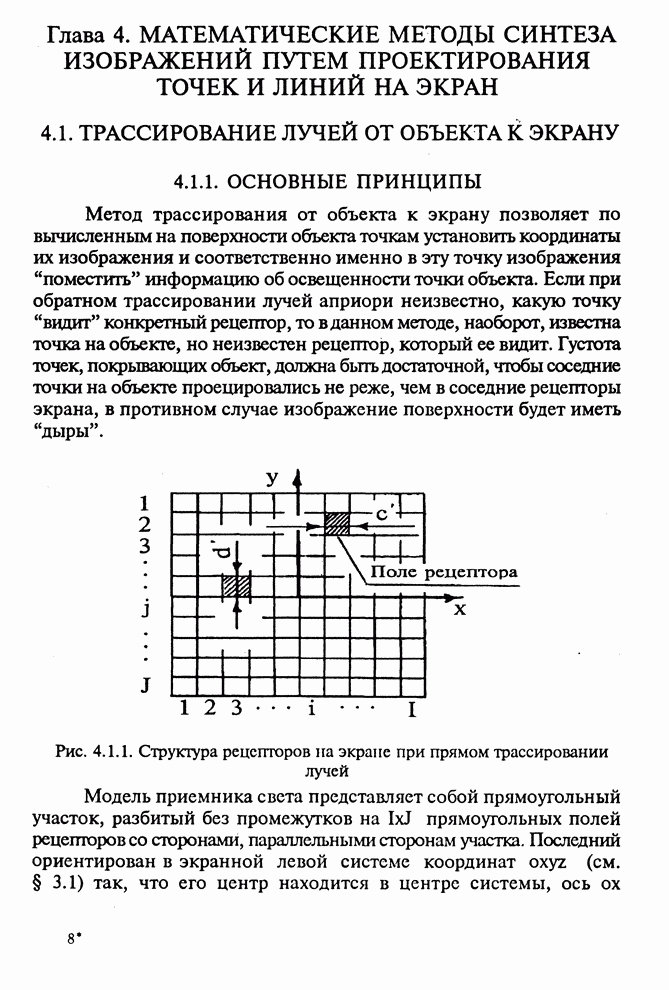
Рис. 3.2.1. Типичные примитивы
Изображения некоторых примитивов, полученные методом машинной графики, показаны на рис.3.2.2 - 3.2.6.

Рис. 3.2.2. Сцена, составленная из эллипсоидов

Рис. 3.2.3. Цилиндр

Рис. 3.2.4. Параллелепипед

Рис. 3.2.5. Конус двухсторонний (а) и односторонний (б)
Приведем пример математического описания цилиндрического примитива в виде кругового цилиндра с плоскими торцами, перпендикулярными оси. Математическая модель примитива состоит из уравнения цилиндра
![]() , (3.2.1)
, (3.2.1)
где
![]() –
координаты любой точки на оси цилиндра;
–
координаты любой точки на оси цилиндра; ![]() – компоненты направляющего вектора
оси цилиндра, и уравнений торцевых поверхностей
– компоненты направляющего вектора
оси цилиндра, и уравнений торцевых поверхностей ![]() ,
, ![]() , где
, где ![]() ,
, ![]() – координаты осевых точек первом и
втором торце соответственно.
– координаты осевых точек первом и
втором торце соответственно.
Для
всех поверхностей примитива сохраним правило размещения положительных
подпространств внутри тела примитива. Так, если в состав примитива входят ![]() уравнений вида
уравнений вида ![]() , где
, где ![]() , то на этапе
конструирования примитива устанавливают состояние:
, то на этапе
конструирования примитива устанавливают состояние:
![]() , (3.2.2)
, (3.2.2)
где
![]() – любая
заведомо внутренняя точка тела примитива. Достижение указанного состояния
осуществляется подбором знака в уравнении
– любая
заведомо внутренняя точка тела примитива. Достижение указанного состояния
осуществляется подбором знака в уравнении ![]() .
.
Формальное
правило преобразования исходно заданной функции ![]() в форму
в форму ![]() , обеспечивающую
положительность подпространства внутри примитива, представляется в виде:
, обеспечивающую
положительность подпространства внутри примитива, представляется в виде: ![]() .
.
Напомним, что положительность значения всех функций внутри тела примитива необходима для локализации примитива в пространстве и однозначного определения положения нормали – внутрь примитива.
На рис. 3.2.6 показан пример изображения истребителя, сконструированного из геометрических примитивов.

Рис. 3.2.6. Истребитель
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
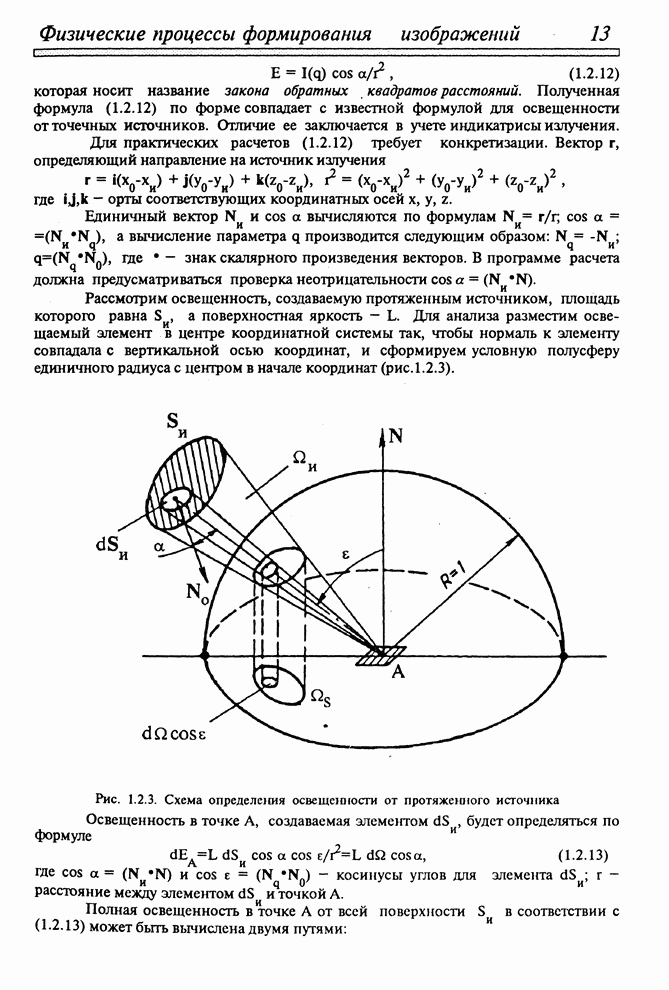
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
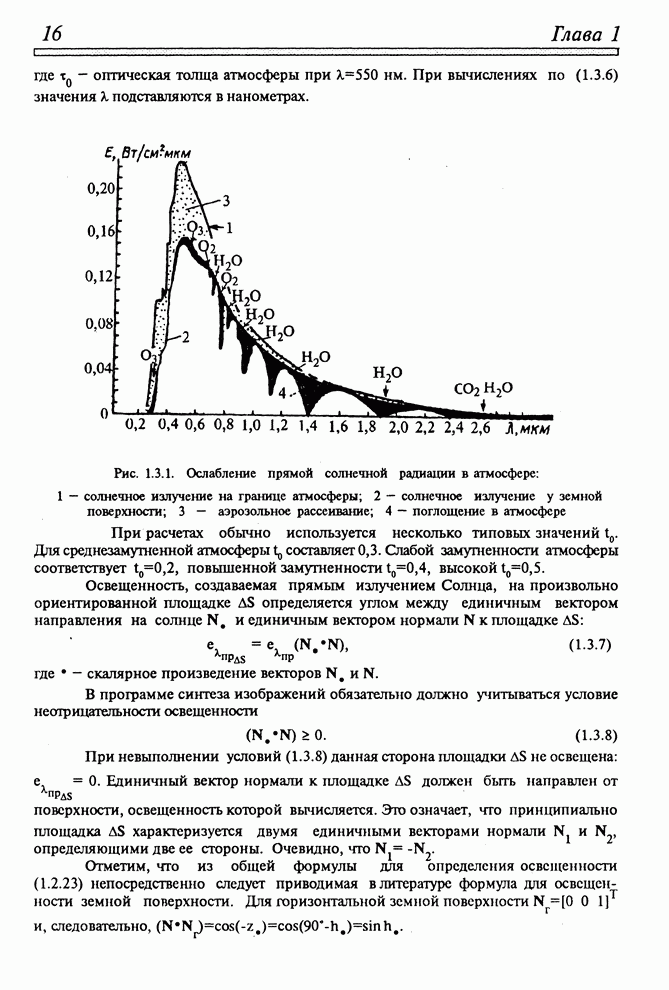
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
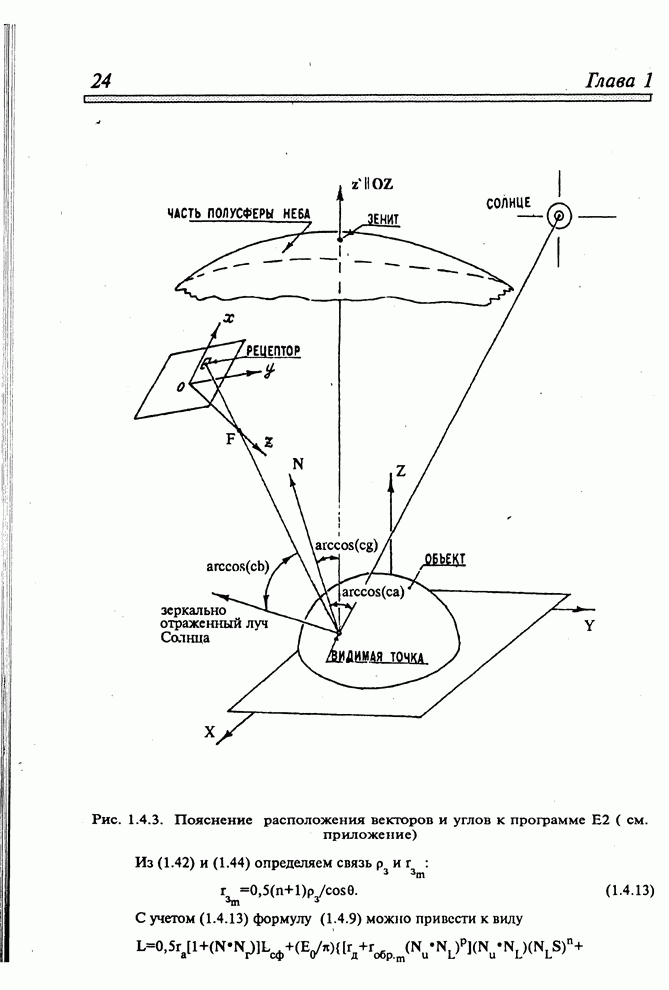
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
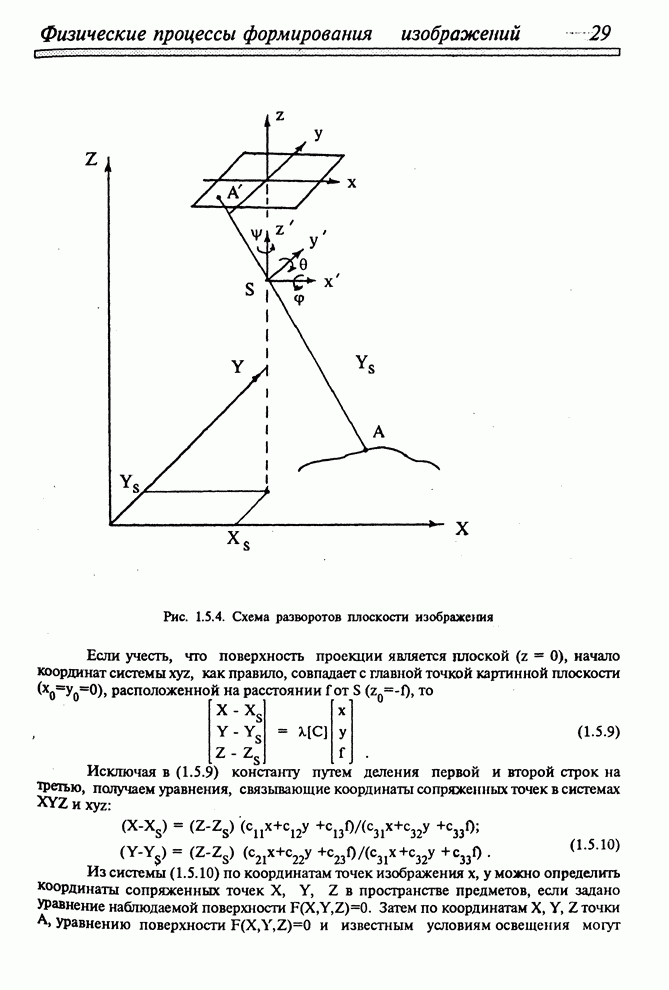
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
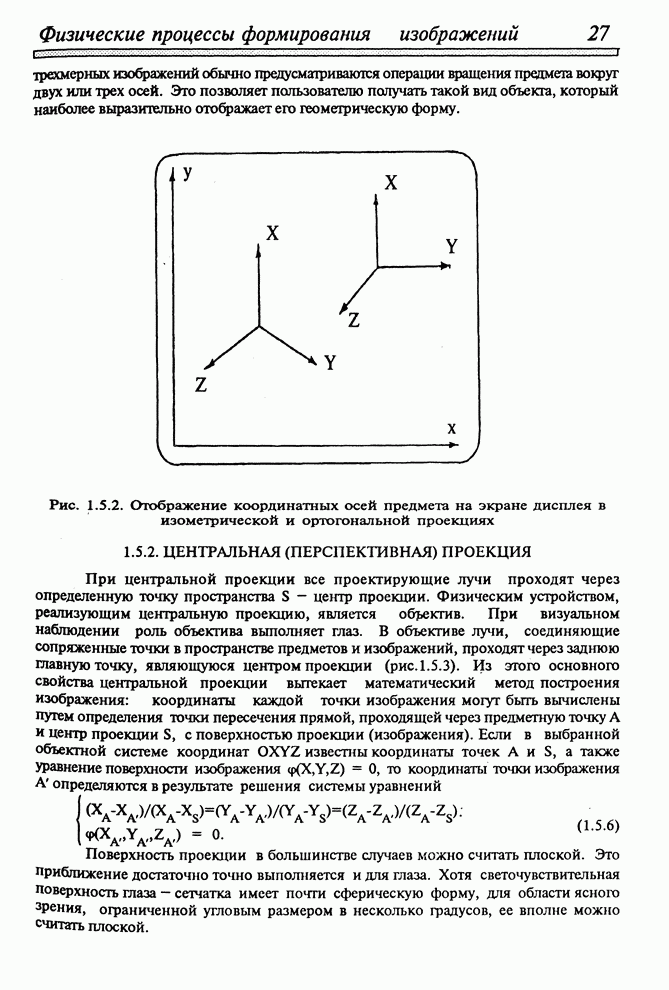
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
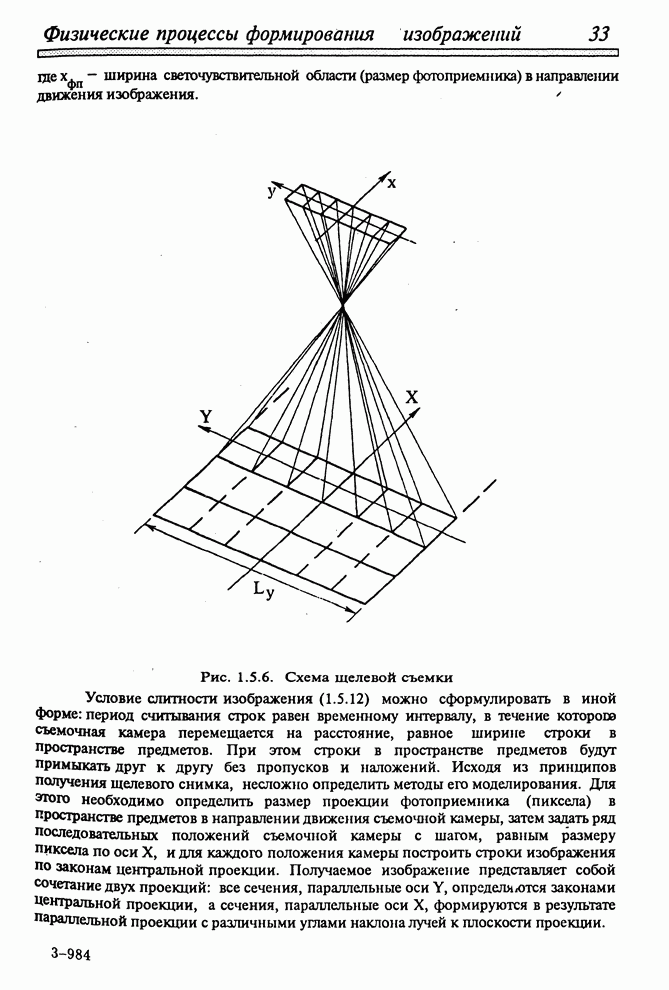
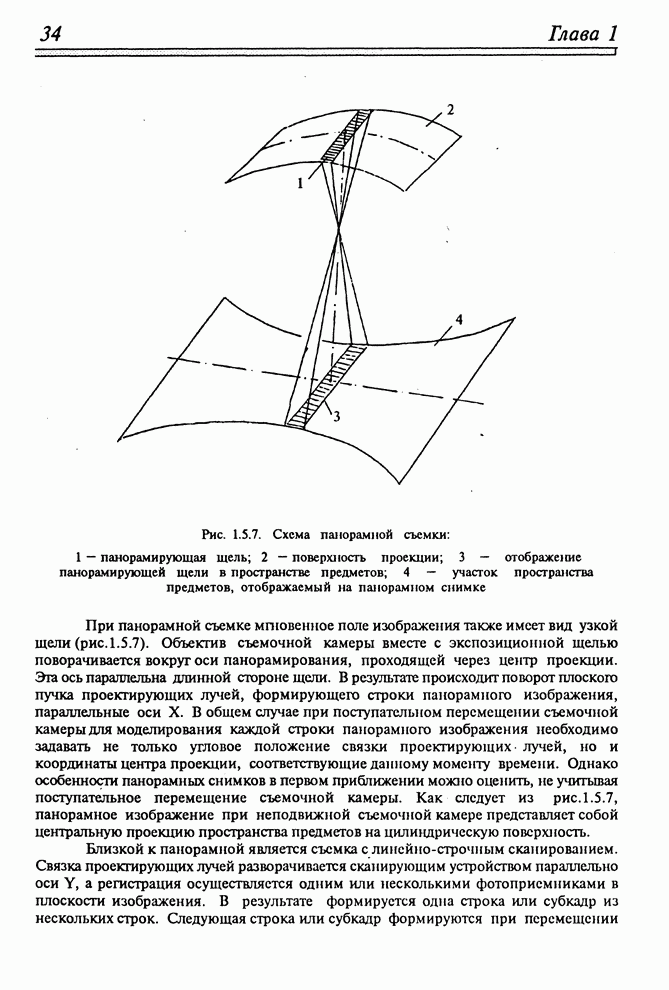
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
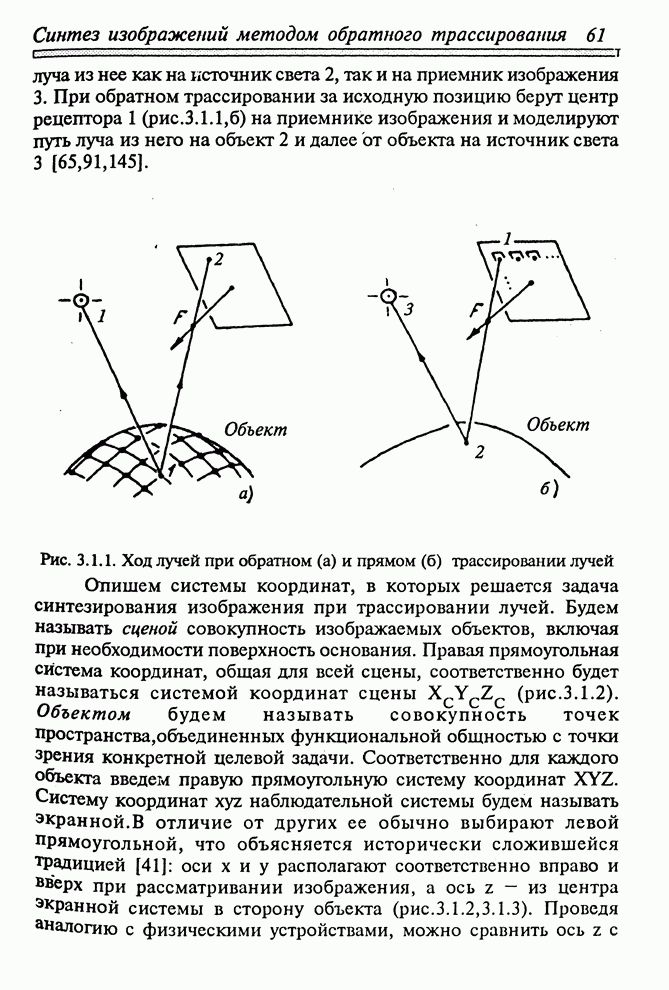
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
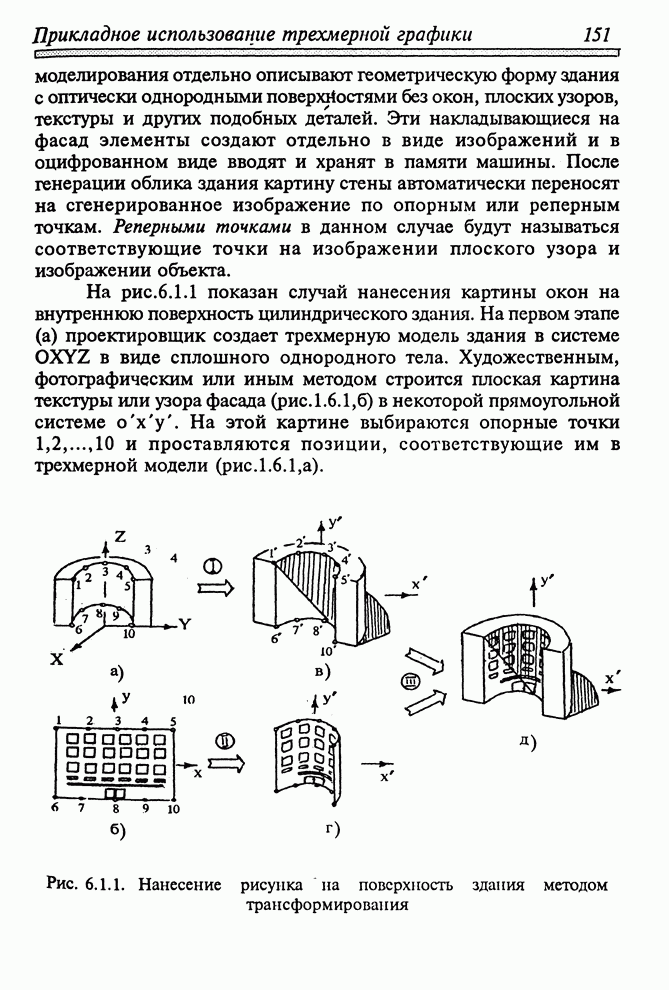
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
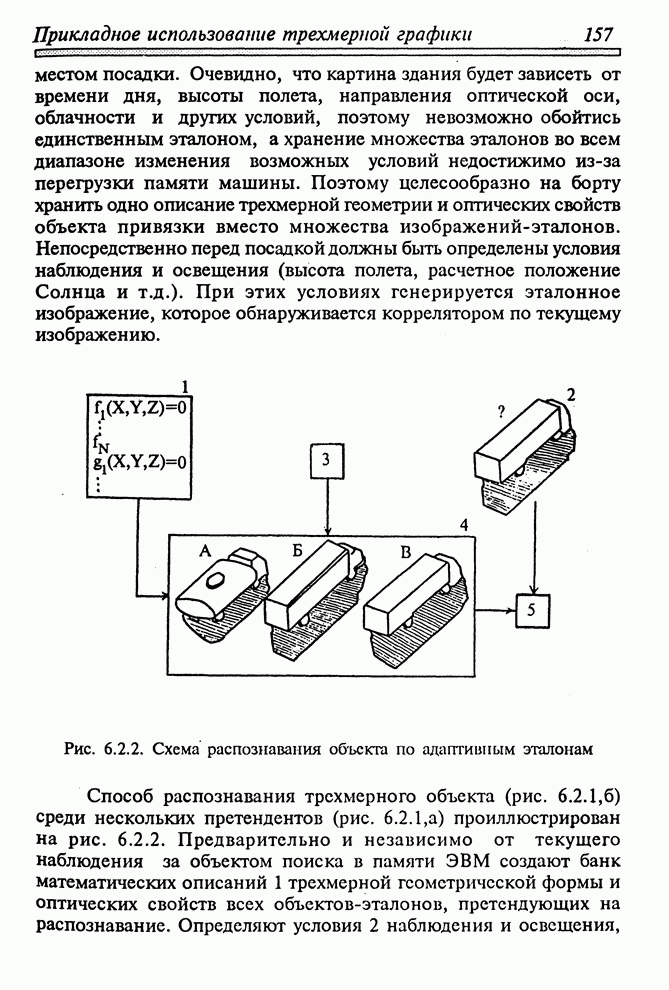
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
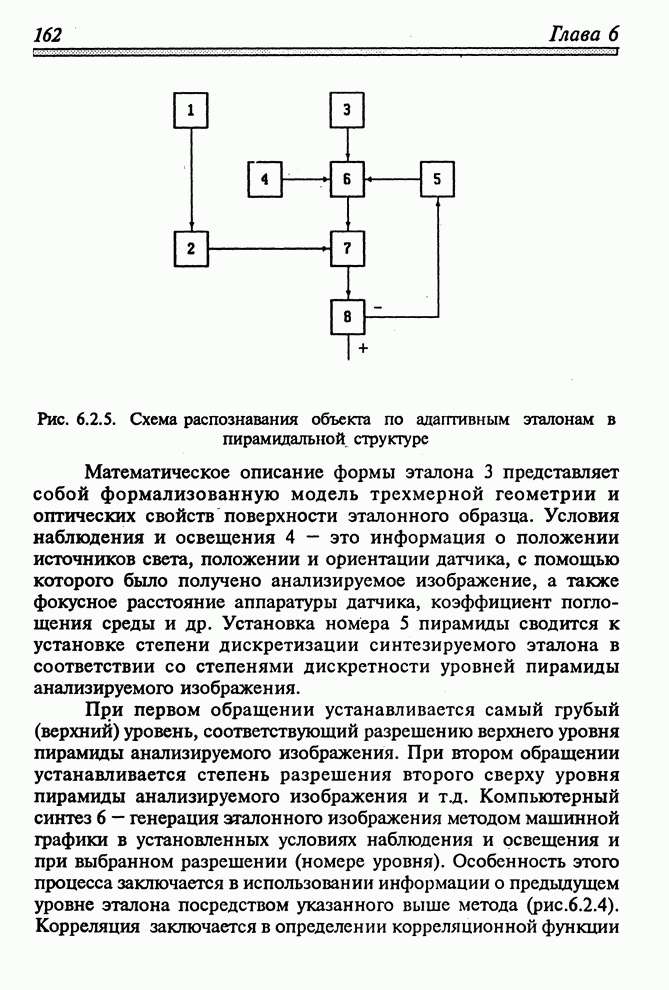
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
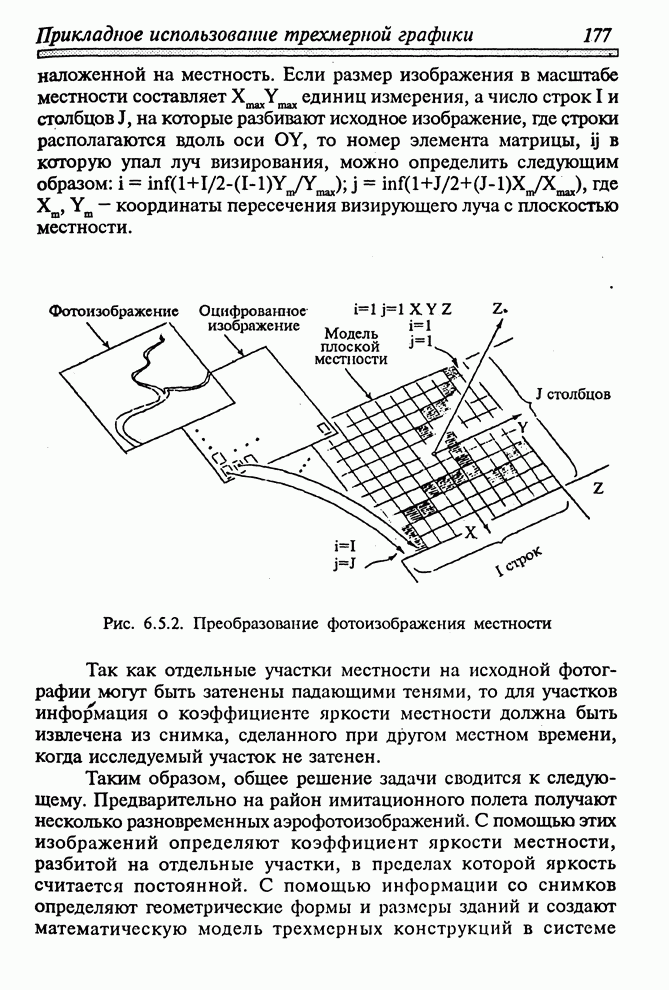
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ