| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
Существует два принципиальных направления сокращения времени синтеза изображений: устранение заведомо лишних вычислений и распараллеливание вычислений. Потребность в ускорении процесса синтеза связана с тем, что высококачественные и сложные изображения формируются на однопроцессорных машинах за десятки минут, что выходит за рамки даже самых скромных потребительских требований.
5.3.1. МЕТОД ОБОЛОЧЕК
Метод оболочек получил широкое распространение в системах трехмерной машинной графики как для однопроцессорных, так и многопроцессорных машин. Свое название он получил от использования простых по конструкции трехмерных выпуклых фигур-оболочек, которые охватывают объект или его составные части и позволяют сравнительно просто выявлять часть пространства, где находится объект. Известно несколько модификаций метода, например в [145] показано его применение на этапе определения видимости.
Оболочки-многоугольники.
Сущность метода, реализующего сокращение времени вычислений изображений с
тенями [21], заключается в следующем. На этапе создания математической
конструкции объекта каждый его отдельный элемент (примитив или система
примитивов) окружается интерактивно или автоматически [64,127] воображаемой
оболочкой – выпуклым многогранником. Число вершин ![]() и ориентация граней выбираются из
соображений надежного охватывания тела элемента оболочкой, минимального объема
оболочки и минимального числа граней. Обозначим одну такую отдельную оболочку
и ориентация граней выбираются из
соображений надежного охватывания тела элемента оболочкой, минимального объема
оболочки и минимального числа граней. Обозначим одну такую отдельную оболочку ![]() и запишем в
матрицу
и запишем в
матрицу ![]() координаты
вершин оболочки
координаты
вершин оболочки ![]() :
:
 ,
,
где
![]() –
координаты
–
координаты ![]() -й
крайней точки выпуклой оболочки
-й
крайней точки выпуклой оболочки ![]() ,
, ![]() ;
; ![]() – число вершин оболочки.
– число вершин оболочки.
При
автоматическом построении выпуклой оболочки в качестве формы последней чаще
всего выбирают параллелепипед [60]. Основная идея определения положения и
размеров параллелепипеда заключается в вычислении максимальных габаритных
размеров охватывающего примитива вдоль осей ![]() . Так как отрезки, определяющие
максимальные габаритные размеры, могут быть не параллельны осям, то часто
построенная оболочка захватывает лишние, не принадлежащие объекту участки
пространства, а это, в свою очередь, снижает эффективность метода. При
"ручном" задании оболочки в виде неправильного многоугольника
достигается более плотное облегание объекта, но зато требуется
неавтоматизированная работа оператора. На практике эта работа сводится к выставлению
в пространстве наименьшего числа точек, лежащих как можно ближе к объекту и
одновременно таких, что выпуклая оболочка, построенная на этих точках, не сечет
своими гранями объекта.
. Так как отрезки, определяющие
максимальные габаритные размеры, могут быть не параллельны осям, то часто
построенная оболочка захватывает лишние, не принадлежащие объекту участки
пространства, а это, в свою очередь, снижает эффективность метода. При
"ручном" задании оболочки в виде неправильного многоугольника
достигается более плотное облегание объекта, но зато требуется
неавтоматизированная работа оператора. На практике эта работа сводится к выставлению
в пространстве наименьшего числа точек, лежащих как можно ближе к объекту и
одновременно таких, что выпуклая оболочка, построенная на этих точках, не сечет
своими гранями объекта.
Координаты
полученных точек и составляют матрицу ![]() , причем порядок следования строк в
ней может быть произвольным. К построенному многограннику
, причем порядок следования строк в
ней может быть произвольным. К построенному многограннику ![]() достраивают второй, так
называемый теневой многогранник (оболочку). Эта теневая оболочка
достраивают второй, так
называемый теневой многогранник (оболочку). Эта теневая оболочка ![]() включает все
вершины оболочки
включает все
вершины оболочки ![]() и дополнительные, которые находят
путем пересечения лучей света, проходящих через вершины многогранника
и дополнительные, которые находят
путем пересечения лучей света, проходящих через вершины многогранника ![]() , с поверхностью,
на которую падают тени. Такой поверхностью в задаче моделирования фотосъемки
здания является основание Земли. Так, если солнечный луч, проходящий через
вершину
, с поверхностью,
на которую падают тени. Такой поверхностью в задаче моделирования фотосъемки
здания является основание Земли. Так, если солнечный луч, проходящий через
вершину ![]() ,
имеет направляющий вектор
,
имеет направляющий вектор ![]() , то координаты точки пересечения
определяются решением системы уравнений
, то координаты точки пересечения
определяются решением системы уравнений

где
![]() –
уравнения поверхности (основания), на которую падают тени.
–
уравнения поверхности (основания), на которую падают тени.
Множество
всех пересечений записывают в матрицу ![]() :
:
 ,
,
где
![]() –
координаты точки пересечения основания с солнечным лучом, проходящим через
–
координаты точки пересечения основания с солнечным лучом, проходящим через ![]() -ю крайнюю точку
оболочки
-ю крайнюю точку
оболочки ![]() ,
и объединяют две матрицы
,
и объединяют две матрицы ![]() и
и ![]() в матрицу
в матрицу ![]() размером
размером ![]() элементов:
элементов: ![]() .
.
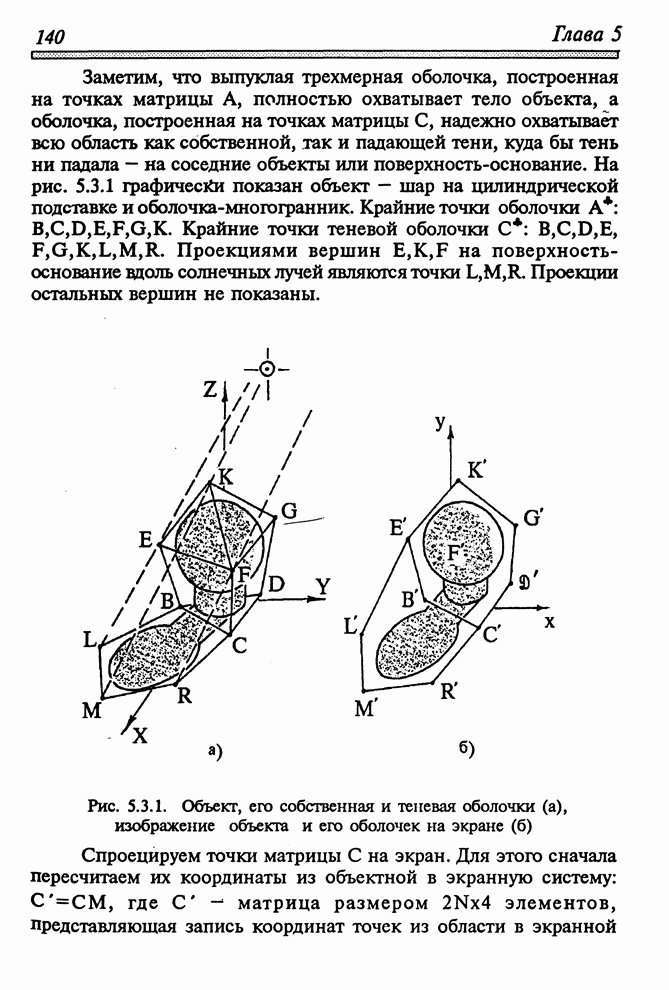
Заметим,
что выпуклая трехмерная оболочка, построенная на точках матрицы ![]() , полностью
охватывает тело объекта, а оболочка, построенная на точках матрицы
, полностью
охватывает тело объекта, а оболочка, построенная на точках матрицы ![]() , надежно
охватывает всю область как собственной, так и падающей тени, куда бы тень ни
падала – на соседние объекты или поверхность-основание. На рис. 5.3.1
графически показан объект – шар на цилиндрической подставке и
оболочка-многогранник. Крайние точки оболочки
, надежно
охватывает всю область как собственной, так и падающей тени, куда бы тень ни
падала – на соседние объекты или поверхность-основание. На рис. 5.3.1
графически показан объект – шар на цилиндрической подставке и
оболочка-многогранник. Крайние точки оболочки ![]() . Крайние точки теневой оболочки
. Крайние точки теневой оболочки ![]() . Проекциями
вершин
. Проекциями
вершин ![]() на
поверхность-основание вдоль солнечных лучей являются точки
на
поверхность-основание вдоль солнечных лучей являются точки ![]() . Проекции остальных вершин
не показаны.
. Проекции остальных вершин
не показаны.

Рис. 5.3.1. Объект, его собственная и теневая оболочки (а), изображение объекта и его оболочек на экране (б)
Спроецируем
точки матрицы ![]() на
экран. Для этого сначала пересчитаем их координаты из объектной в экранную
систему:
на
экран. Для этого сначала пересчитаем их координаты из объектной в экранную
систему: ![]() ,
где
,
где ![]() –
матрица размером
–
матрица размером ![]() элементов, представляющая запись
координат точек из области в экранной системе координат;
элементов, представляющая запись
координат точек из области в экранной системе координат; ![]() – матрица преобразования
размером
– матрица преобразования
размером ![]() элемента
[19,21]. Затем определим перспективные координаты в плоскости экрана для всех
точек из матрицы
элемента
[19,21]. Затем определим перспективные координаты в плоскости экрана для всех
точек из матрицы ![]() :
: ![]() ;
; ![]() , где
, где ![]() – фокусное расстояние наблюдательной
системы;
– фокусное расстояние наблюдательной
системы; ![]() –
координаты изображения
–
координаты изображения ![]() -й точки матрицы
-й точки матрицы ![]() ,
, ![]() . Здесь предполагается, что
центр проекции лежит между экраном и объектом.
. Здесь предполагается, что
центр проекции лежит между экраном и объектом.
Полученные
значения координат изображения точек из матрицы ![]() запишем в виде
запишем в виде
 ,
,
где
![]() включает
координаты изображений точек выпуклой оболочки
включает
координаты изображений точек выпуклой оболочки ![]() ,
, ![]() .
.
Так
как теневая трехмерная оболочка ![]() уверенно охватывает целиком область
тени объекта, то двухмерная выпуклая оболочка
уверенно охватывает целиком область
тени объекта, то двухмерная выпуклая оболочка ![]() , построенная вокруг изображений
, построенная вокруг изображений ![]() крайних точек
оболочки
крайних точек
оболочки ![]() ,
надежно охватывает изображения тени от данного объекта. Аналогично можно
определить область положения на изображении самого тела объекта путем
построения выпуклой двухмерной оболочки
,
надежно охватывает изображения тени от данного объекта. Аналогично можно
определить область положения на изображении самого тела объекта путем
построения выпуклой двухмерной оболочки ![]() вокруг точек множества из
вокруг точек множества из ![]() . На рис. 5.3.1,б
показано изображение объекта и оболочек на экране. Крайние точки двухмерной
оболочки
. На рис. 5.3.1,б
показано изображение объекта и оболочек на экране. Крайние точки двухмерной
оболочки ![]() .
Крайние точки двухмерной оболочки
.
Крайние точки двухмерной оболочки ![]() . Штрихи в обозначениях указывают,
что речь идет о изображении приведенной точки, т. е.
. Штрихи в обозначениях указывают,
что речь идет о изображении приведенной точки, т. е. ![]() есть изображение
есть изображение ![]() . Способ
построения выпуклой оболочки вокруг множества точек на плоскости известен
[17,64,81,126,127]. Так, если
. Способ
построения выпуклой оболочки вокруг множества точек на плоскости известен
[17,64,81,126,127]. Так, если ![]() – оператор, выбирающий из множества
точек на плоскости крайние точки выпуклой оболочки, то
– оператор, выбирающий из множества
точек на плоскости крайние точки выпуклой оболочки, то ![]() ,
, ![]() .
.
На
этапе построения самого изображения, прежде чем производить трассирование луча
из каждого рецептора, последний оценивается на принадлежность внутренней
области оболочек ![]() и
и ![]() .
.
Если
рецептор находится снаружи оболочки ![]() , то он не "видит" тело
объекта, и если рецептор находится снаружи оболочки
, то он не "видит" тело
объекта, и если рецептор находится снаружи оболочки ![]() , то он не принадлежит
области тени отданного объекта. Оценивание пересечения трассирующего луча с
примитивом производится только в случае принадлежности рецептора внутренней
области оболочки
, то он не принадлежит
области тени отданного объекта. Оценивание пересечения трассирующего луча с
примитивом производится только в случае принадлежности рецептора внутренней
области оболочки ![]() , а оценивание затененности точки,
видимой из рецептора, производится только в случае попадания рецептора во
внутреннюю область оболочки
, а оценивание затененности точки,
видимой из рецептора, производится только в случае попадания рецептора во
внутреннюю область оболочки ![]() . В приложении даны описания
подпрограмм AVTOZON, YNZONA, позволяющих оценивать принадлежность текущего
рецептора областям
. В приложении даны описания
подпрограмм AVTOZON, YNZONA, позволяющих оценивать принадлежность текущего
рецептора областям ![]() и
и ![]() .
.
Использование описанного подхода для иерархии примитивов избавляет от слепого поиска и анализа точек пересечения трассирующего луча с заведомо невидимыми примитивами и комбинациями примитивов и сокращает время вычислений в несколько раз. При этом эффект от использования оболочек становится тем ощутимее, чем больше примитивов в составе объекта и сложнее их конструкция.
Заметим,
что при вычислении матрицы ![]() удобно использовать аналитически
полученное значение матрицы
удобно использовать аналитически
полученное значение матрицы ![]() преобразования координат из
объектной системы в экранную:
преобразования координат из
объектной системы в экранную:
 ,
,
где
![]() ;
; ![]() ;
; ![]() .
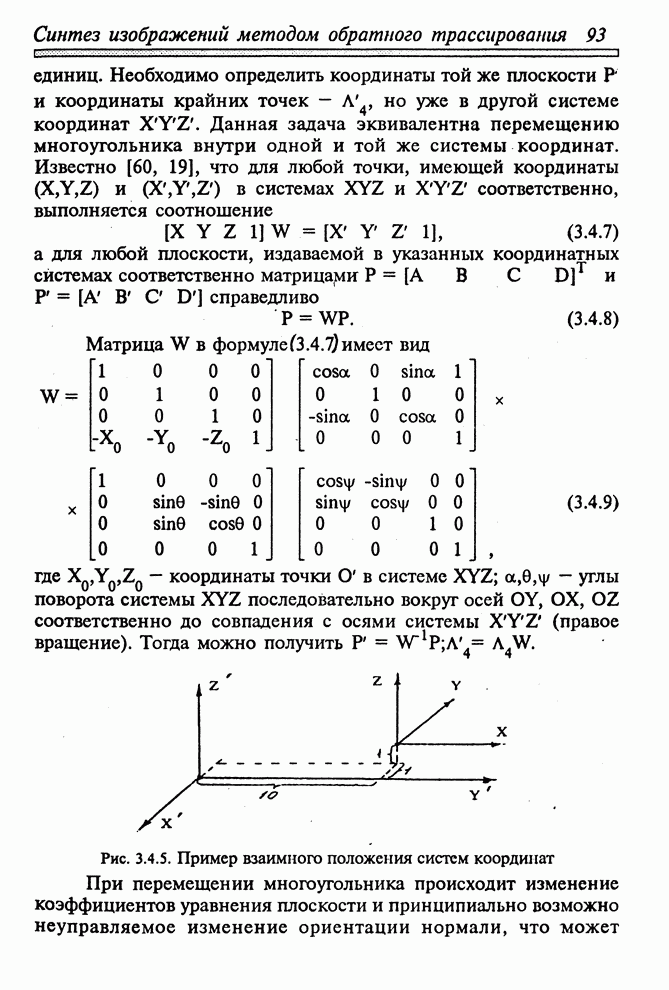
Пространственное расположение систем координат и правила отсчитывания углов
приведены на рис.3.1.4, пояснения к структуре компонент – в § 3.1.
.
Пространственное расположение систем координат и правила отсчитывания углов
приведены на рис.3.1.4, пояснения к структуре компонент – в § 3.1.
Эллиптические оболочки. Кроме многогранников и параллелепипедов в качестве оболочек можно применить эллипсоиды. Замечательным свойством эллипсоида среди всех поверхностей второго порядка является замкнутость поверхности, и поэтому эллипсоид может быть использован как оболочка, охватывающая объект. Изменением размера и ориентации полуосей можно достаточно плотно охватить тело практически любой конфигурации.
Уиттед [149] впервые отметил применимость таких оболочек для сокращения вычислительных затрат при трассировании лучей. Для других методов синтеза эллиптическую форму оболочек применять нецелесообразно из-за необходимости поточечного или полигонального представления эллипсоида, что значительно сложнее, чем описание многогранника.
Основная
идея предлагаемого подхода заключается в следующем. На этапе конструирования
объекта отдельные его части или весь объект окружают воображаемыми оболочками –
эллипсоидами. Определить видимость или затененность от эллипсоида гораздо
быстрее, чем для сложного, композиционного объекта или пространственно
комбинирующихся примитивов. Тогда устанавливают тс рецепторы, которые
"видят" эллипсоид и тень от него и все дальнейшие вычисления по
наблюдению самого объекта ведут только для этих, так называемых рабочих
рецепторов. Отношение общего числа рецепторов к числу рабочих приближенно
показывает, во сколько раз сократились вычислительные затраты. Приближенность
(оценки) связана с неплотностью прилегания оболочки к телу объекта. Рецепторы,
которые "видят" промежуток между оболочкой и объектом, определяют
некоторую часть ненужных вычислений, на которую уменьшается теоретический
коэффициент сокращения ![]() .
.
Пусть
некоторый геометрически сложный объект ![]() расположен над поверхностью падения
теней
расположен над поверхностью падения
теней ![]() (рис.
5.3.2). Окружим объект оболочкой
(рис.
5.3.2). Окружим объект оболочкой ![]() в виде эллипсоида, описываемого
функцией
в виде эллипсоида, описываемого
функцией ![]() .
Определим видимость эллипсоида для каждого
.
Определим видимость эллипсоида для каждого ![]() -гo рецептора экрана
-гo рецептора экрана ![]() . Для этого
необходимо определить факт наличия решений системы следующих четырех уравнений;
. Для этого
необходимо определить факт наличия решений системы следующих четырех уравнений;

где
![]() –
матрица эллипсоида;
–
матрица эллипсоида; ![]() – параметр;
– параметр; ![]() – координаты центра
проекции;
– координаты центра
проекции; ![]() –
направляющие векторы
–
направляющие векторы ![]() -гo светового луча;
-гo светового луча; ![]() ;
; ![]() ;
; ![]() . Первое уравнение
в системе описывает эллипсоид, остальные – прямую, проходящую через
. Первое уравнение
в системе описывает эллипсоид, остальные – прямую, проходящую через ![]() -й рецептор
-й рецептор ![]() и центр проекции.
и центр проекции.
Нетрудно показать из решения квадратного уравнения, к которому сводится данная система, что действительные решения существуют при условии
![]() , (5.3.1)
, (5.3.1)
где
![]() ,
, ![]() .
.
В другой форме это условие можно представить в виде[39]
![]() , (5.3.2)
, (5.3.2)
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() –
коэффициенты матрицы квадратичной поверхности
–
коэффициенты матрицы квадратичной поверхности
 .
.
Заметим,
что с вычислительной точки зрения эффективно провести проверку условия (5.3.2)
в два этапа. Сначала следует вычислить только значение ![]() и проверить его равенство
нулю. Если
и проверить его равенство
нулю. Если ![]() ,
то условие (5.3.2) выполняется автоматически и уже нет потребности вычислять
,
то условие (5.3.2) выполняется автоматически и уже нет потребности вычислять ![]() и
и ![]() . Если же
. Если же ![]() , то процедуру
следует провести полностью, определив
, то процедуру
следует провести полностью, определив ![]() и
и ![]() и результат
и результат ![]() . Состояние
. Состояние ![]() невозможно, так
как это означало бы пересечение оболочкой центра проекции
невозможно, так
как это означало бы пересечение оболочкой центра проекции ![]() , которая находится снаружи
оболочки. Поэтому отдельная проверка
, которая находится снаружи
оболочки. Поэтому отдельная проверка ![]() на равенство нулю не производится.
на равенство нулю не производится.
Проверка условий (5.3.1), (5.3.2) является простой операцией для процессора, что обеспечивает быстрый отбор всех рецепторов, которые "видят" оболочку. Только для этих рецепторов следует вести дальнейшие вычисления по определению видимости самого тела объекта, что чувствительно сокращает вычисления.
Как
и оболочки других форм, эллиптические оболочки могут составлять структуру с
несколькими уровнями вложения. На рис. 5.3.2,а показана башня, оболочкой
которой является ![]() , купол имеет оболочку
, купол имеет оболочку ![]() , основание –
, основание – ![]() . На рис.5.3.2,б
приведено изображение, на которое спроецированы оболочки в соответствующие
двухмерные зоны -
. На рис.5.3.2,б
приведено изображение, на которое спроецированы оболочки в соответствующие
двухмерные зоны - ![]() . Рецепторы, попадающие в зону
. Рецепторы, попадающие в зону ![]() ,
"видят" всю башню, те из них, которые попадают в зону
,
"видят" всю башню, те из них, которые попадают в зону ![]() – только купол, в
– только купол, в
![]() –
только основание, в
–
только основание, в ![]() – либо купол, либо основание. Такое
разбиение площади изображения на области позволяет сокращать объем вычислений в
несколько раз.
– либо купол, либо основание. Такое
разбиение площади изображения на области позволяет сокращать объем вычислений в
несколько раз.

Рис. 5.3.2. Эллиптические оболочки (а) и их изображение (б)
Оболочки-параллелепипеды. Такая оболочка определяет габаритные размеры примитива или семейства примитивов вдоль координатных осей. Каждый примитив представляется как бы погруженным в ящик, стенки которого параллельны координатным плоскостям.
Пусть
примитивы и их оболочки заданы (пересчитаны) в экранной системе координат. Как
и раннее, ось ![]() экранной
системы направим на объект, строки рецепторов разместим вдоль
экранной
системы направим на объект, строки рецепторов разместим вдоль ![]() , столбцы – вдоль
, столбцы – вдоль ![]() . Тогда строка
рецепторов компланарна
. Тогда строка
рецепторов компланарна ![]() , а стенки оболочек компланарны
, а стенки оболочек компланарны ![]() .
.
При
ортографической проекции легко установить (см.[9]) признак необходимости
обработки очередным ![]() -м рецептором
-м рецептором ![]() -го примитива. Обозначим
через
-го примитива. Обозначим
через ![]() максимальные
ординаты и абсциссу
максимальные
ординаты и абсциссу ![]() -й оболочки. Тогда
-й оболочки. Тогда ![]() -й рецептор должен
обрабатывать
-й рецептор должен
обрабатывать ![]() -й
примитив, если
-й
примитив, если ![]() ;
;
![]() . При
невыполнении последнего условия
. При
невыполнении последнего условия ![]() -й примитив надежно не попадает в
поле зрения рецептора (рис.5.3.3).
-й примитив надежно не попадает в
поле зрения рецептора (рис.5.3.3).

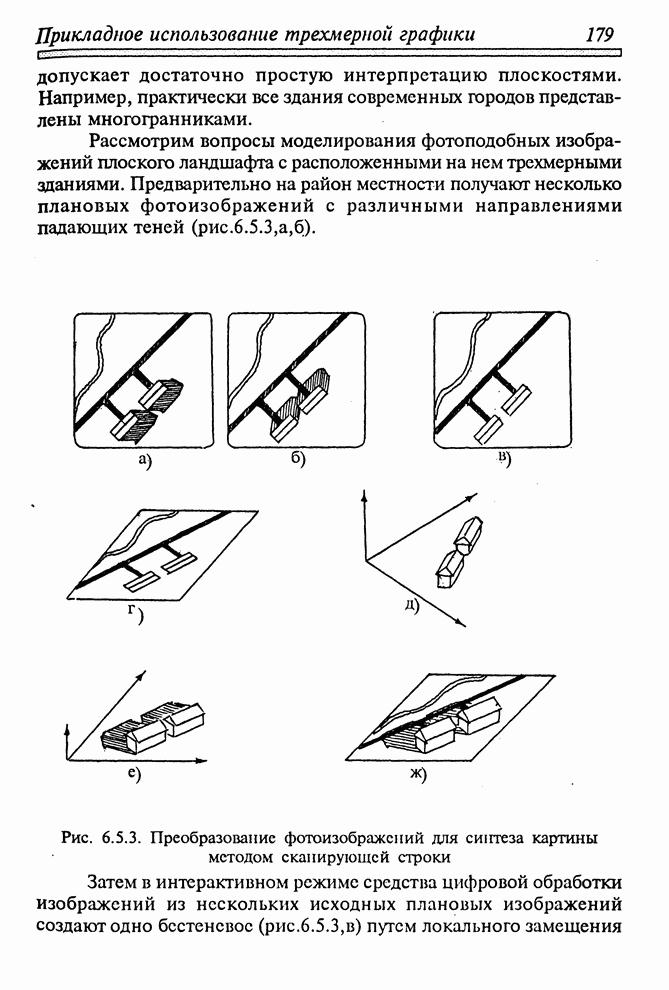
Рис. 5.3.3. Построение оболочек-параллелепипедов
Этот алгоритм может быть легко трансформирован для случая центральной проекции.
Положение
граней параллелепипеда может быть определено аналитически как положение
касательных плоскостей, параллельных ![]() . Это позволяет автоматически строить
оболочки, что значительно повышает эффективность использования системы
машинного зрения.
. Это позволяет автоматически строить
оболочки, что значительно повышает эффективность использования системы
машинного зрения.
Покажем
на примере поверхностей второго порядка правила определения габаритных точек
примитивов. Под габаритными точками будем понимать точки касания поверхности
второго порядка с касательными плоскостями, параллельными ![]() . Габаритные точки являются
точками экстремума функции второго порядка
. Габаритные точки являются
точками экстремума функции второго порядка ![]() в направлениях вдоль
в направлениях вдоль ![]() , и одновременно
они лежат на самой поверхности. Поэтому координаты габаритных точек
определяются решением систем следующих троек уравнений в направлении
, и одновременно
они лежат на самой поверхности. Поэтому координаты габаритных точек
определяются решением систем следующих троек уравнений в направлении ![]()
![]() ,
, ![]() ,
, ![]() ;
; ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() . Значения частных
производных определяются следующим образом в обозначениях § 2.2, 3.4.3,
принятых для поверхности второго порядка:
. Значения частных
производных определяются следующим образом в обозначениях § 2.2, 3.4.3,
принятых для поверхности второго порядка: ![]() ;
; ![]() ;
; ![]() . Решение каждой из приведенных
систем сводится к квадратному уравнению. Если существует два действительных
корня, то они определяют две габаритные точки в соответствующем направлении.
. Решение каждой из приведенных
систем сводится к квадратному уравнению. Если существует два действительных
корня, то они определяют две габаритные точки в соответствующем направлении.
Таким образом обеспечивается автоматическое построение параллелепипедных оболочек вокруг поверхностей второго порядка. В общем случае только эллипсоид имеет две габаритные точки в каждом направлении, поверхности другого вида простираются в бесконечность, поэтому их оболочка может быть представлена как полупространство.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- ГЛАВА 1. ФИЗИЧЕСКИЕ ПРОЦЕССЫ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ И ИХ МОДЕЛИРОВАНИЕ
- 1.1. МОДЕЛИ В МАШИННОЙ ГРАФИКЕ
- 1.2. ИСТОЧНИКИ ОСВЕЩЕНИЯ
- 1.2.1. ИСТОЧНИКИ ИСКУССТВЕННОГО ОСВЕЩЕНИЯ
- 1.2.2. ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИСТОЧНИКОВ ПРОСТОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ
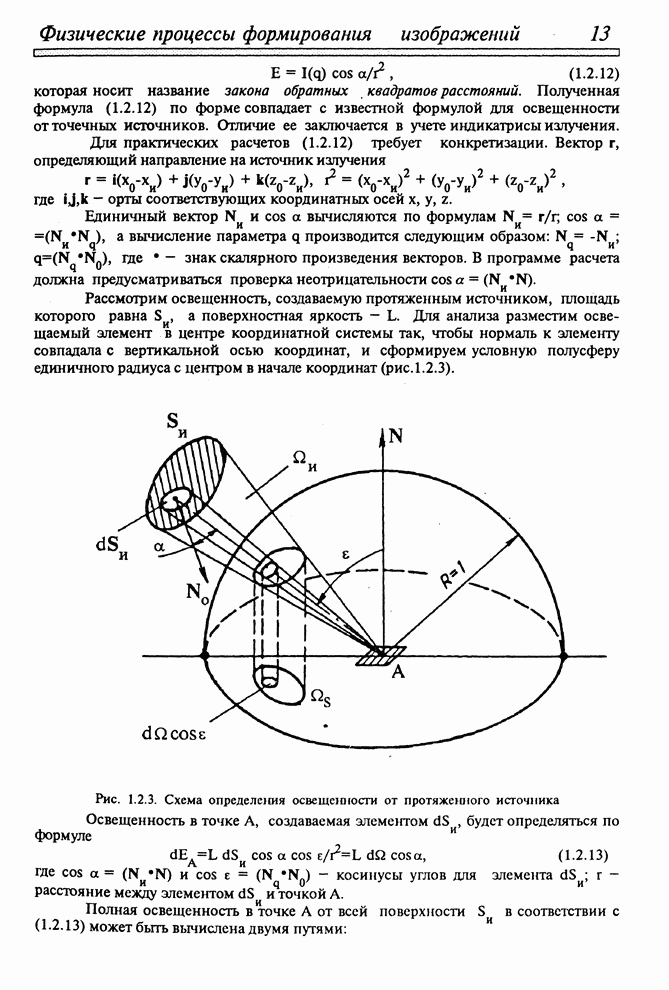
- 1.2.3. ОСВЕЩЕННОСТЬ, СОЗДАВАЕМАЯ ТОЧЕЧНЫМИ И ПРОТЯЖЕННЫМИ ИСТОЧНИКАМИ
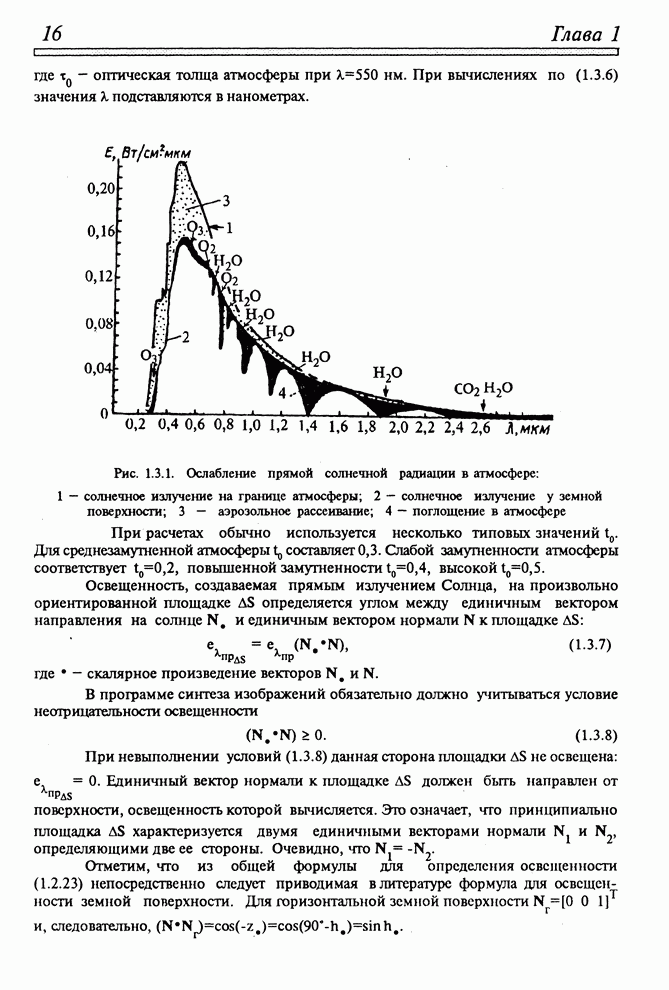
- 1.3. ЕСТЕСТВЕННОЕ ОСВЕЩЕНИЕ
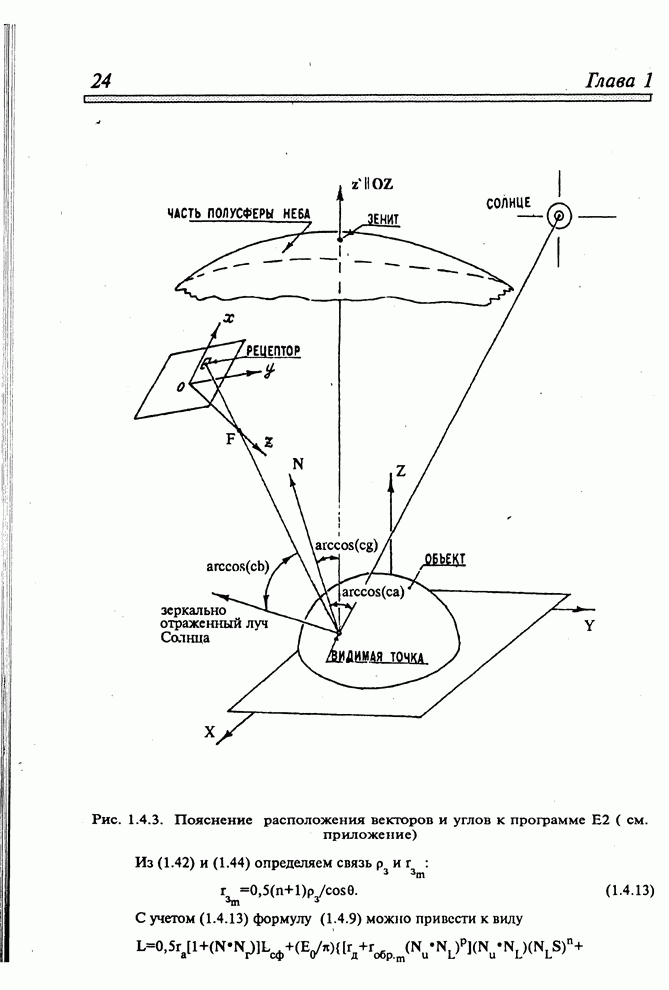
- 1.4. МОДЕЛИРОВАНИЕ ОТРАЖЕННОГО ИЗЛУЧЕНИЯ ОБЪЕКТОВ
- 1.5. ПРОЕКЦИИ В ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКЕ И ИХ МАТЕМАТИЧЕСКИЕ МОДЕЛИ
- 1.5.1. ПАРАЛЛЕЛЬНАЯ ПРОЕКЦИЯ
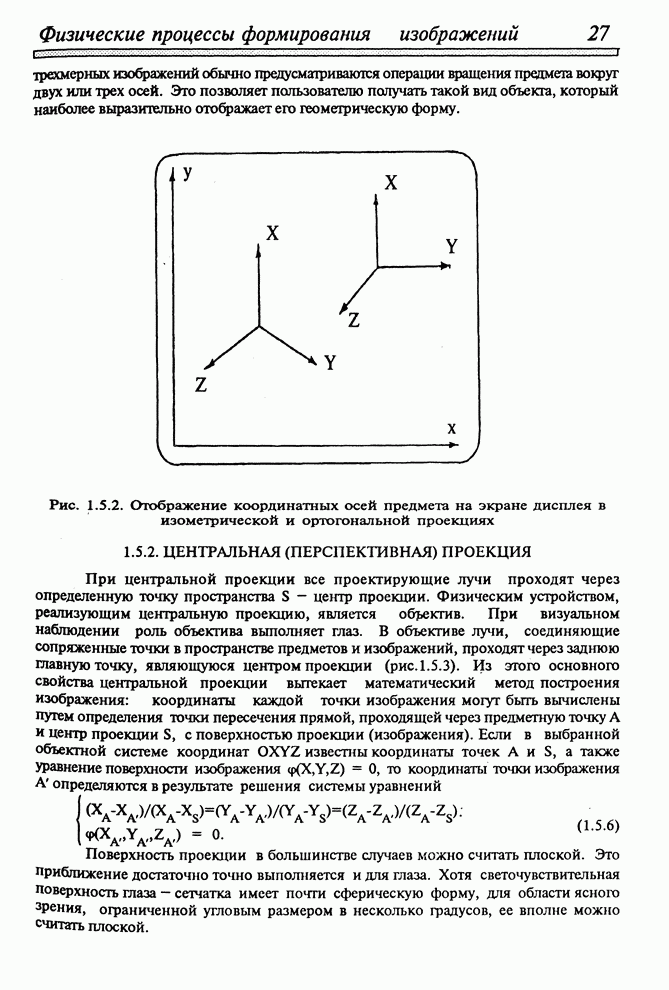
- 1.5.2. ЦЕНТРАЛЬНАЯ (ПЕРСПЕКТИВНАЯ) ПРОЕКЦИЯ
- 1.5.3. ОПИСАНИЕ ПРЕОБРАЗОВАНИЙ С ИСПОЛЬЗОВАНИЕМ ОДНОРОДНЫХ КООРДИНАТ
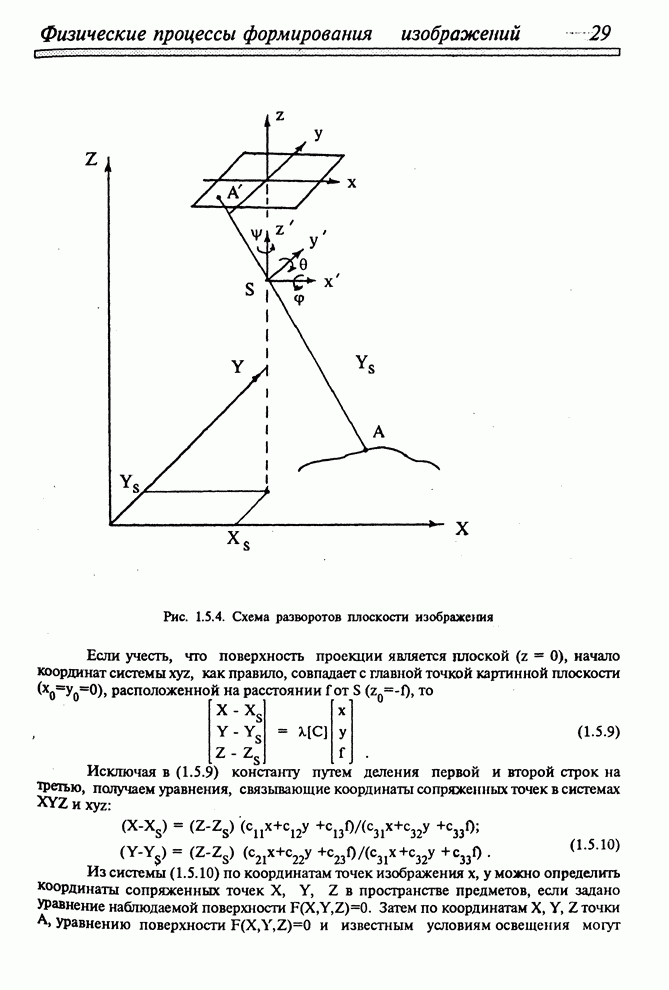
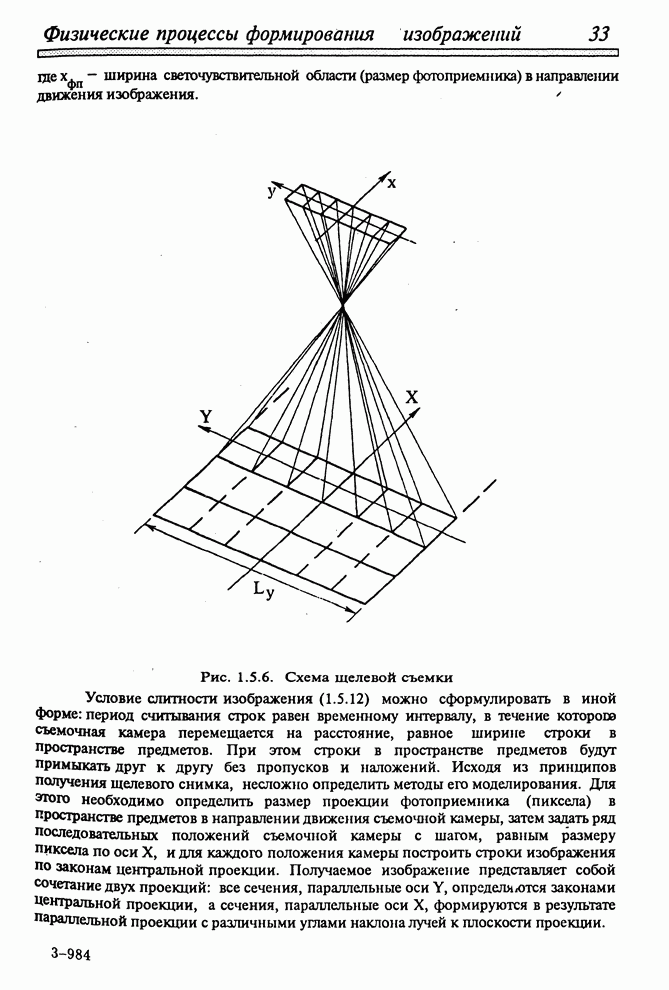
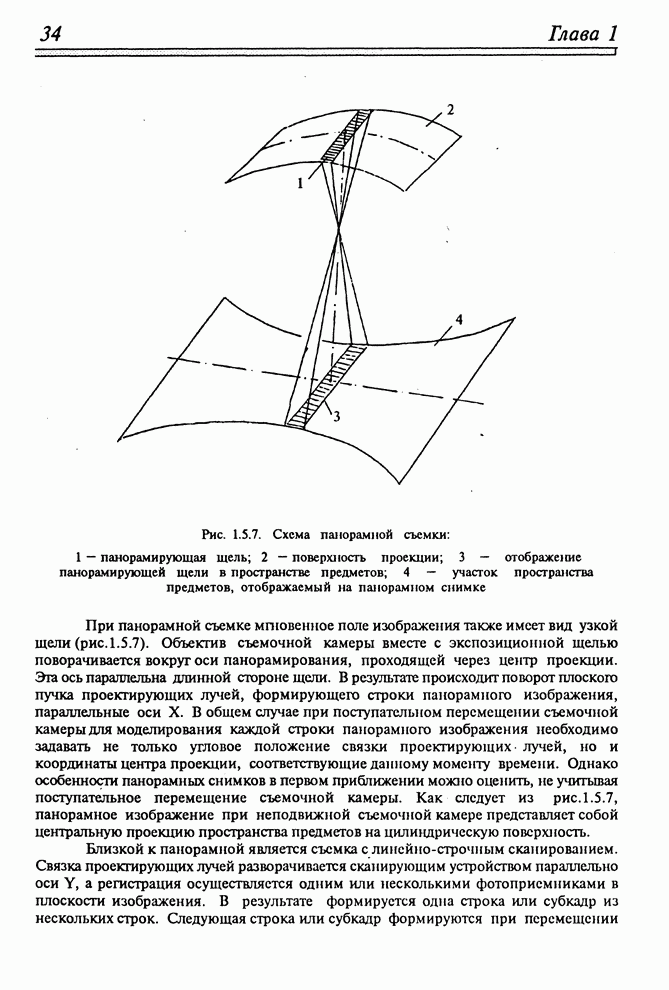
- 1.5.4. ПРОЕКЦИИ ПРИ РАЗЛИЧНЫХ ВИДАХ СЪЕМКИ
- 1.6. ТЕКСТУРА ИЗОБРАЖЕНИЯ
- 1.7. МОДЕЛИРОВАНИЕ ЭНЕРГЕТИЧЕСКИХ ПРЕОБРАЗОВАНИЙ В СИСТЕМАХ ФОРМИРОВАНИЯ ИЗОБРАЖЕНИЙ
- 1.8. СИНТЕЗ ИЗОБРАЖЕНИЙ С УЧЕТОМ СПЕЦИФИКИ ИХ ФОРМИРОВАНИЯ В РЕАЛЬНЫХ УСЛОВИЯХ
- ГЛАВА 2. ОПИСАНИЕ ГЕОМЕТРИЧЕСКИХ ФОРМ
- 2.1. ОПИСАНИЕ ПОВЕРХНОСТЕЙ
- 2.2. ОБЩИЕ ХАРАКТЕРИСТИКИ ОСНОВНЫХ ТИПОВ ПОВЕРХНОСТЕЙ
- 2.3. МОДЕЛИ ОБЪЕКТОВ И ИХ КЛАССИФИКАЦИЯ
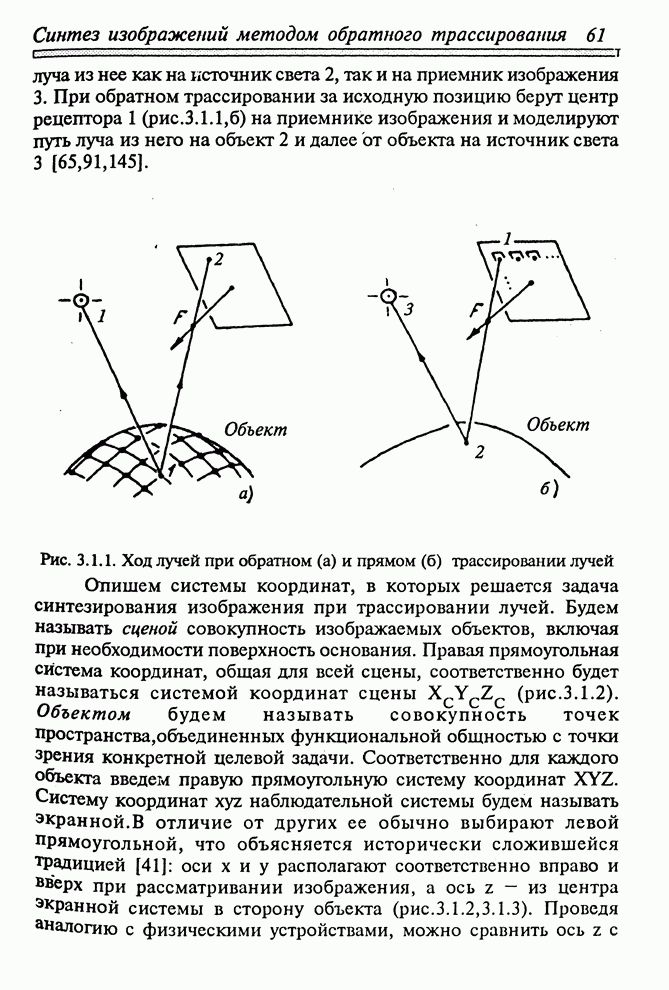
- ГЛАВА 3. СИНТЕЗ ИЗОБРАЖЕНИЙ МЕТОДОМ ОБРАТНОГО ТРАССИРОВАНИЯ ЛУЧЕЙ
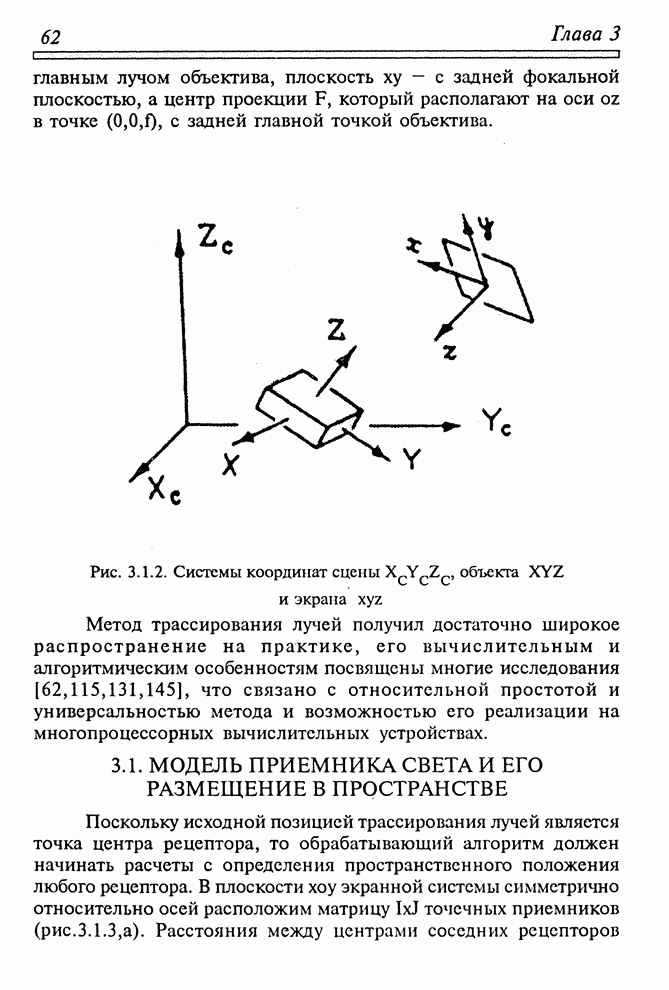
- 3.1. МОДЕЛЬ ПРИЕМНИКА СВЕТА И ЕГО РАЗМЕЩЕНИЕ В ПРОСТРАНСТВЕ
- 3.2. МОДЕЛЬ ОБЪЕКТА
- 3.2.1. ПРИМИТИВЫ – БАЗОВЫЕ СТРОИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ОБЪЕКТА
- 3.2.2. ПРОСТРАНСТВЕННЫЕ КОМБИНАЦИИ ПРИМИТИВОВ
- 3.2.3. ФОРМАЛИЗОВАННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОБЪЕКТА
- 3.2.4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ТОЧКИ И ОБЪЕКТА
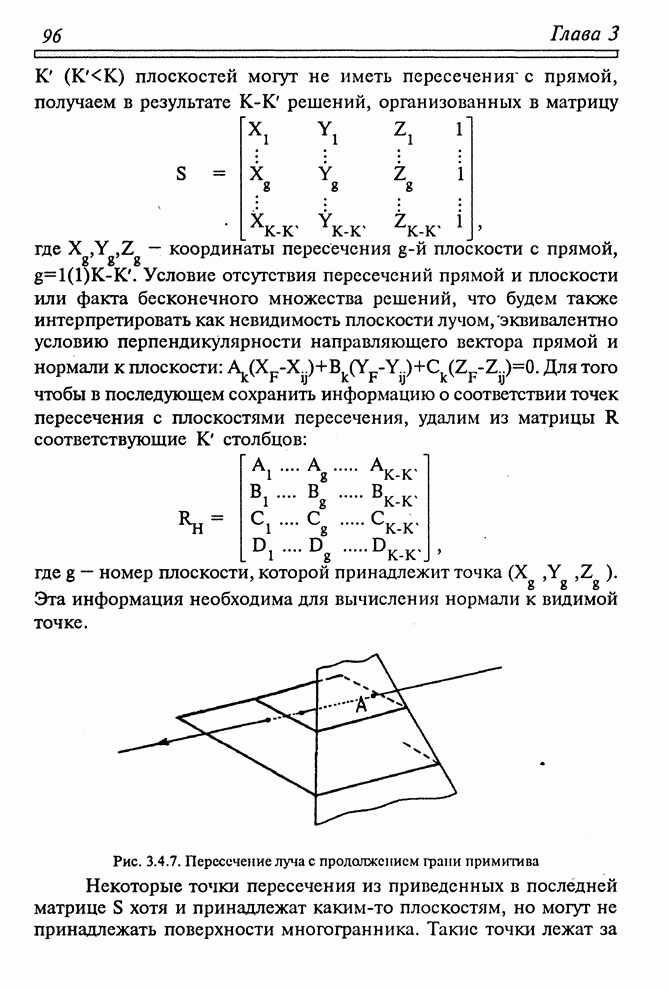
- 3.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ И ЗАТЕНЕННЫХ ТОЧЕК
- 3.3.1. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С ПРИМИТИВОМ
- 3.3.2. ПЕРЕСЕЧЕНИЯ СВЕТОВОГО ЛУЧА С КОМБИНАЦИЕЙ ПРИМИТИВОВ
- 3.3.3. ОПРЕДЕЛЕНИЕ ЗАТЕНЕННЫХ ТОЧЕК
- 3.4. ИЗОБРАЖЕНИЕ ОСНОВНЫХ ПРИМИТИВОВ МЕТОДОМ ТРАССИРОВАНИЯ ЛУЧЕЙ
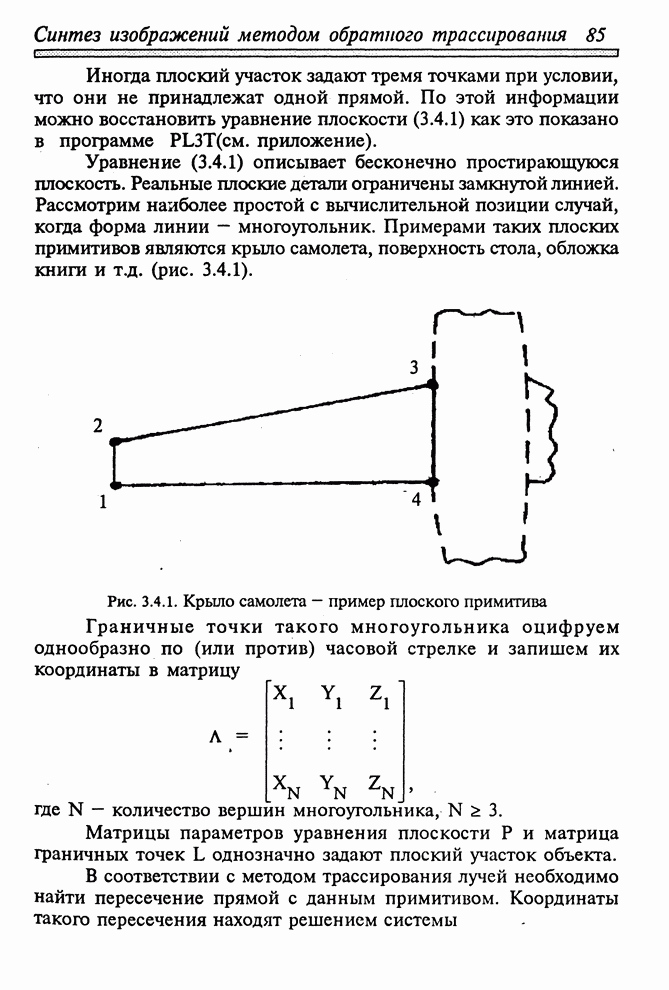
- 3.4.1. ПЛОСКИЕ МНОГОУГОЛЬНИКИ
- 3.4.2. ВЫПУКЛЫЕ МНОГОГРАННИКИ
- 3.4.3. КВАДРАТИЧНЫЕ ПОВЕРХНОСТИ
- 3.4.4. БИКУБИЧЕСКИЕ ПОВЕРХНОСТИ
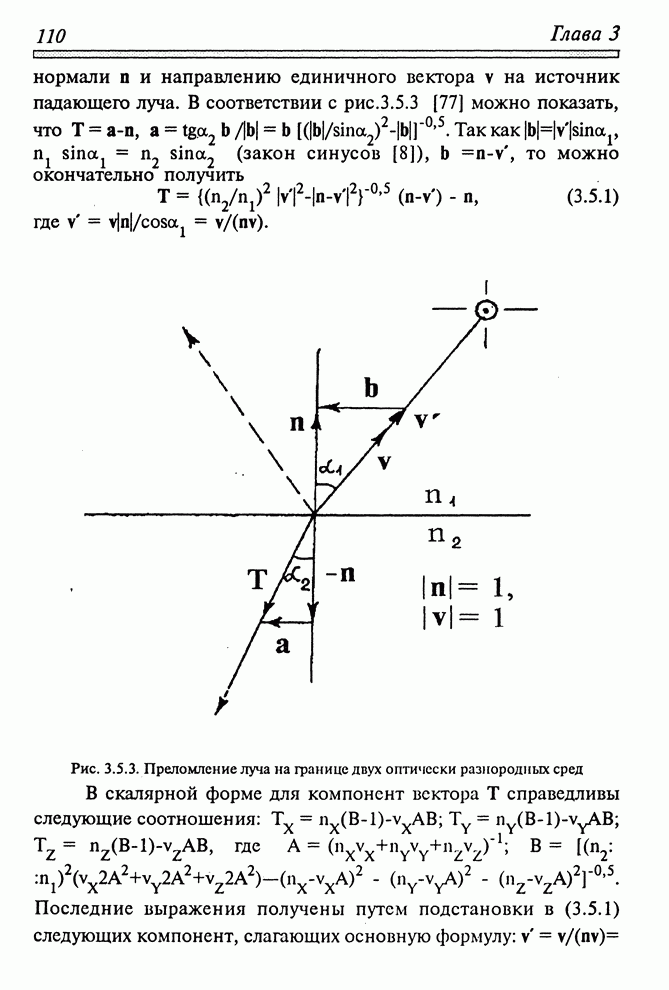
- 3.5. ИЗОБРАЖЕНИЕ ЗЕРКАЛЬНЫХ И ПРЕЛОМЛЯЮЩИХ ПОВЕРХНОСТЕЙ
- 3.6. ОСОБЕННОСТИ ОПРЕДЕЛЕНИЯ ОСВЕЩЕННОСТИ
- ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СИНТЕЗА ИЗОБРАЖЕНИЙ ПУТЕМ ПРОЕКТИРОВАНИЯ ТОЧЕК И ЛИНИЙ НА ЭКРАН
- 4.1. ТРАССИРОВАНИЕ ЛУЧЕЙ ОТ ОБЪЕКТА К ЭКРАНУ
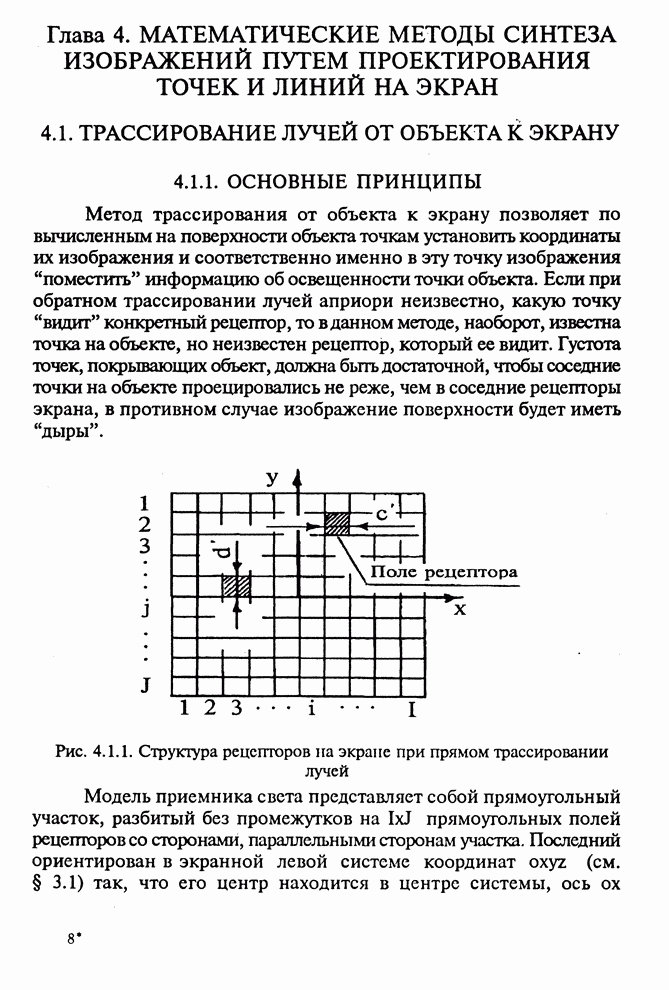
- 4.1.1. ОСНОВНЫЕ ПРИНЦИПЫ
- 4.1.2. МОДЕЛЬ ОБЪЕКТА
- 4.1.3. ОПРЕДЕЛЕНИЕ ВИДИМЫХ ТОЧЕК
- 4.1.4. ОПРЕДЕЛЕНИЕ ОСВЕЩЕННОСТИ
- 4.1.5. ИЗОБРАЖЕНИЕ ПОТОЧЕЧНО ОПИСАННЫХ ОБЪЕКТОВ
- 4.2. МЕТОД СКАНИРУЮЩЕЙ СТРОКИ
- 4.2.1. МОДЕЛЬ ОБЪЕКТА ИЗ МНОГОУГОЛЬНИКОВ
- 4.2.2. МОДЕЛЬ ПРИЕМНИКА
- 4.2.3. ИЗОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ НА ЭКРАНЕ
- 4.2.4. ИЗОБРАЖЕНИЕ КРИВОЛИНЕЙНЫХ ПОВЕРХНОСТЕЙ
- 4.3. АЛГОРИТМ РОБЕРТСА
- 4.3.1. МОДЕЛЬ ОБЪЕКТА
- 4.3.2. СИНТЕЗ ИЗОБРАЖЕНИЯ
- ГЛАВА 5. ОРГАНИЗАЦИЯ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.1. УПРАВЛЕНИЕ ПРОЦЕССОМ СИНТЕЗА
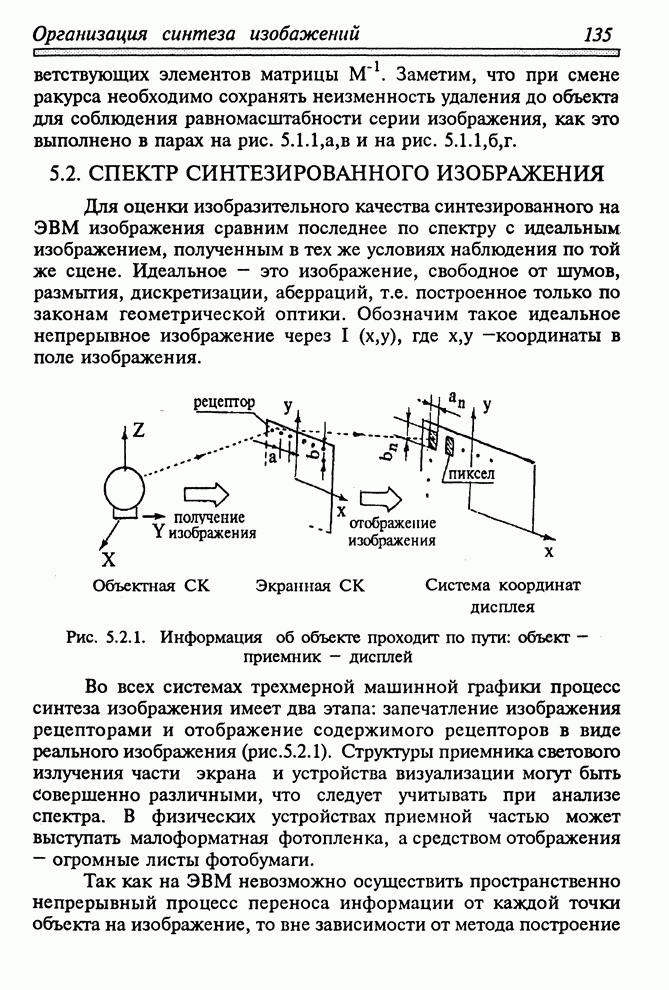
- 5.2. СПЕКТР СИНТЕЗИРОВАННОГО ИЗОБРАЖЕНИЯ
- 5.3. СОКРАЩЕНИЕ ВРЕМЕНИ СИНТЕЗА ИЗОБРАЖЕНИЙ
- 5.3.1. МЕТОД ОБОЛОЧЕК
- 5.3.2. ВОЗМОЖНОСТИ ИСПОЛЬЗОВАНИЯ ТРАНСПЬЮТЕРОВ В МАШИННОЙ ГРАФИКЕ
- ГЛАВА 6. ПРИКЛАДНОЕ ИСПОЛЬЗОВАНИЕ ТРЕХМЕРНОЙ МАШИННОЙ ГРАФИКИ
- 6.1. АРХИТЕКТУРНОЕ ПРОЕКТИРОВАНИЕ
- 6.2. РАСПОЗНАВАНИЕ ВИДЕООБРАЗОВ
- 6.2.1. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИВНЫМ ЭТАЛОНАМ
- 6.2.2. РАСПОЗНАВАНИЕ ОБРАЗОВ В УСЛОВИЯХ НЕИЗВЕСТНОЙ ОРИЕНТАЦИИ ИХ КОРПУСОВ
- 6.2.3. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО АДАПТИРОВАННЫМ ЭТАЛОНАМ В ПИРАМИДАЛЬНОЙ СТРУКТУРЕ
- 6.2.4. РАСПОЗНАВАНИЕ ОБРАЗОВ ПО ЭТАЛОНАМ, АДАПТИРОВАННЫМ ПО УСЛОВИЯМ НАБЛЮДЕНИЯ И КАЧЕСТВУ
- 6.3. АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ В МАШИНОСТРОЕНИИ
- 6.4. ВОССТАНОВЛЕНИЕ ФОРМЫ СКРЫТЫХ ОБЪЕКТОВ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ
- 6.5. ВИДЕОТРЕНАЖЕРЫ И ИМИТАТОРЫ СЛОЖНЫХ СЦЕН
- 6.5.1. ТРЕНАЖЕР ДЛЯ ИМИТАЦИИ ПОЛЕТА НАД РЕАЛЬНОЙ МЕСТНОСТЬЮ
- 6.5.2. КОМПЬЮТЕРНЫЙ ИМИТАТОР ИЗОБРАЖЕНИЙ ОБЛАКОВ
- 6.6. РЕКЛАМА И МУЛЬТИПЛИКАЦИЯ
- ПРИЛОЖЕНИЕ. ОПИСАНИЕ ПРИКЛАДНЫХ ПОДПРОГРАММ
- СПИСОК ЛИТЕРАТУРЫ