| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
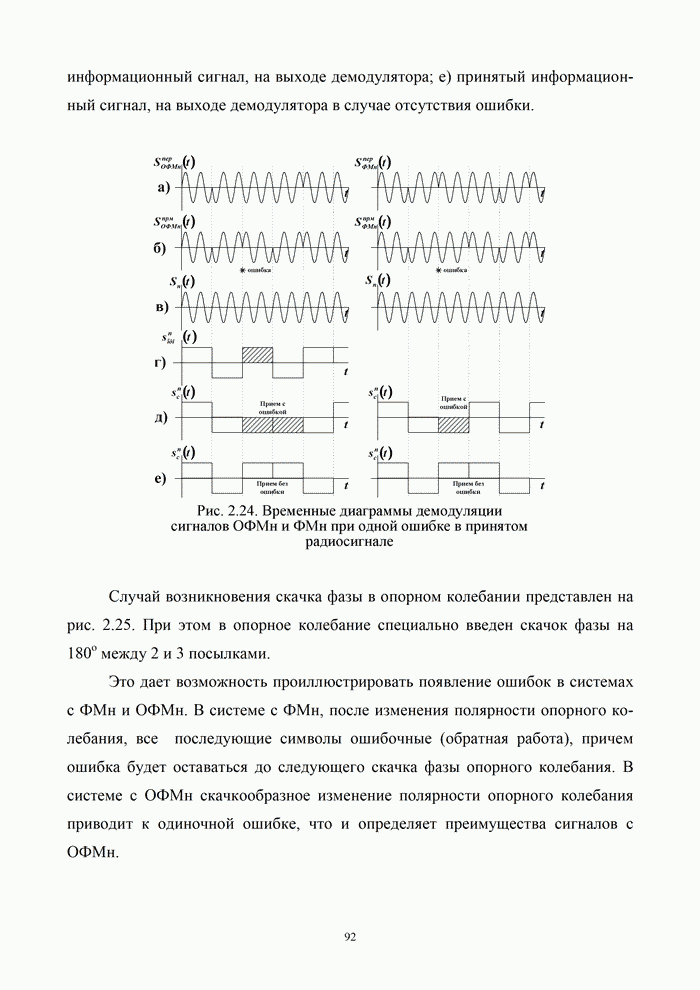
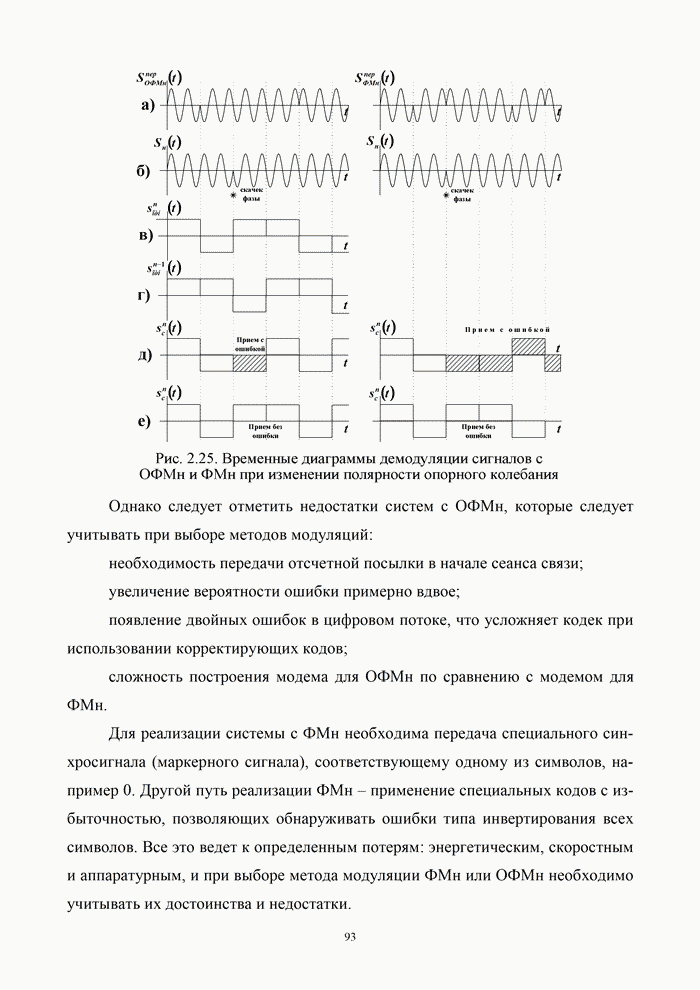
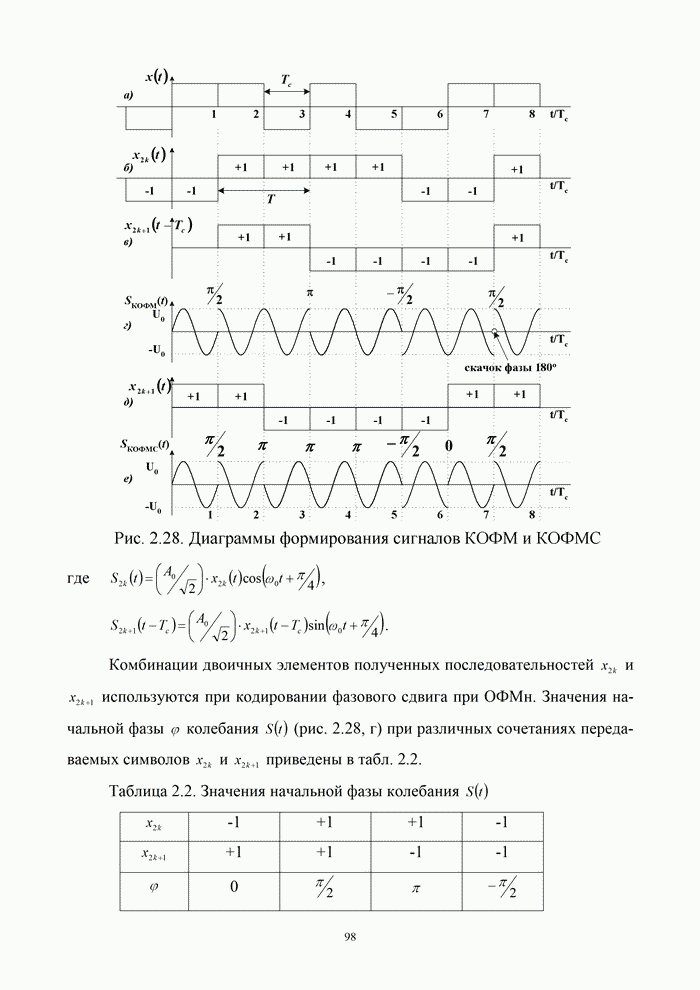
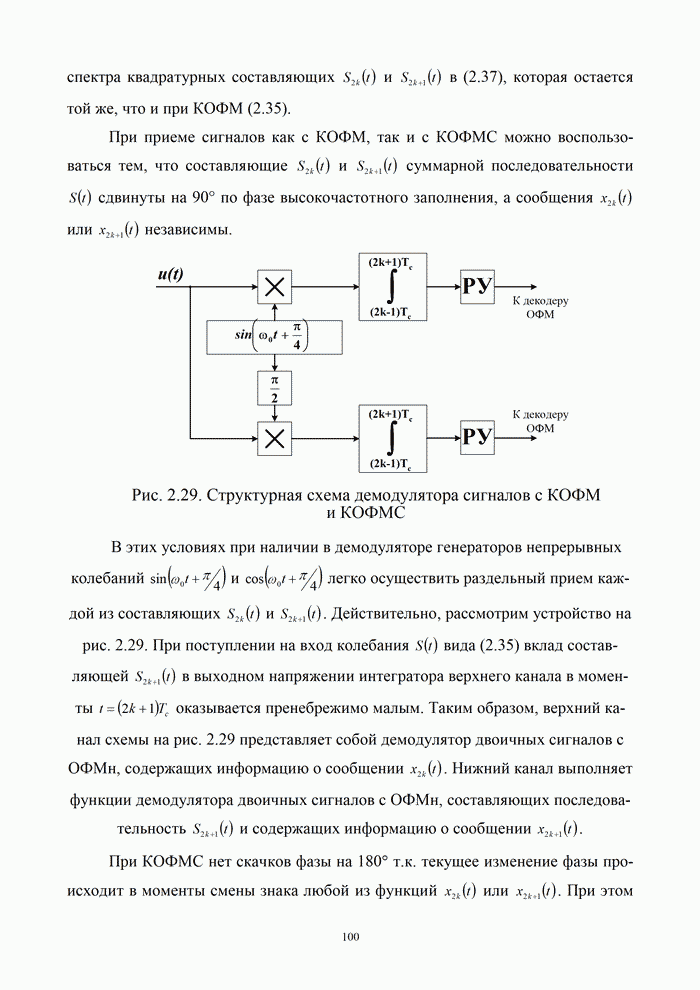
3.3. Помехоустойчивость приема сигналов с известными параметрами
Помехоустойчивость
дискретного канала связи определяется вероятностью ошибочного приема ![]() сигналов. Рассмотрим определение
сигналов. Рассмотрим определение
![]() для двоичного
канала связи m=2, по которому передается один из двух сигналов
для двоичного
канала связи m=2, по которому передается один из двух сигналов ![]() или
или ![]() . Перепишем правило
принятия решения в виде:
. Перепишем правило
принятия решения в виде:
|
Если |
(3.45) |
то
принимается решение в пользу ![]() .
.
Пусть
на вход схемы оптимальной обработки поступает сигнал ![]() . В этом случае правильное
решение принимается, если неравенство выполняется, и ошибочное, если
. В этом случае правильное
решение принимается, если неравенство выполняется, и ошибочное, если
|
|
(3.46) |
Раскроем скобки первого интеграла, и представим энергию первого и второго сигналов, а также взаимную корреляционную функцию соответственно следующим образом:
|
|
|
неравенство (3.46) принимает вид
|
|
(3.47) |
где ![]() суммарная (эквивалентная)
энергия двух сигналов.
суммарная (эквивалентная)
энергия двух сигналов.
Последнее
слагаемое в правой части неравенства (3.47) гауссовская случайная величина с нулевым
математическим ожиданием (средним) и дисперсией ![]() таким образом
таким образом ![]()
 будет
иметь гауссовское распределение со средним
будет
иметь гауссовское распределение со средним ![]() и дисперсией
и дисперсией ![]() (рис. 3.7).
(рис. 3.7).

Вероятность
ошибок (рис. 3.7) для рассматриваемого двоичного канала связи, определяется
площадью, ограниченной ПРВ ![]() и осью абсцисс для всех
и осью абсцисс для всех ![]() .
.
Формула,
характеризующая вероятность ошибочного приема ![]() (т.е. принятия решения о передаче
(т.е. принятия решения о передаче ![]() , когда передавался
, когда передавался ![]() ), будет следующей:
), будет следующей:
|
|
(3.48) |
Из
(3.48) следует, что вероятность ошибочного приема элементов двоичного сообщения
тем меньше, чем больше эквивалентная энергия ![]() и чем меньше спектральная плотность
мощности помех
и чем меньше спектральная плотность
мощности помех ![]() .
.

Оценим
влияние структуры передаваемых сигналов на вероятность их ошибочного приема. Если
сигналы близки по форме ![]() ,то
,то ![]() ,
, ![]() , и вероятность ошибки
максимальна
, и вероятность ошибки
максимальна ![]() .
Такие сигналы разделить невозможно, надо использовать сигналы
.
Такие сигналы разделить невозможно, надо использовать сигналы ![]() и
и ![]() значительно отличающихся друг
от друга. Рассмотрим несколько видов сигналов, применяющихся в системах связи. Поэтому
применение сигналов, близких по форме, нецелесообразно. Наиболее простым
является сигнал с пассивной паузой амплитудно - модулированный:
значительно отличающихся друг
от друга. Рассмотрим несколько видов сигналов, применяющихся в системах связи. Поэтому
применение сигналов, близких по форме, нецелесообразно. Наиболее простым
является сигнал с пассивной паузой амплитудно - модулированный: ![]() ,
, ![]() (рис. 3.8).
(рис. 3.8).
Тогда
энергия первого сигнала равна ![]() :
: ![]() , а энергия второго и взаимная энергия
сигналов равны нулю:
, а энергия второго и взаимная энергия
сигналов равны нулю:![]() ,
тогда
,
тогда ![]() .
.
Вероятность ошибки определяется выражением:
|
|
(3.49) |

Определим
![]() для ортогональных
сигналов
для ортогональных
сигналов ![]() и
и ![]() (рис. 3.9). Пусть
(рис. 3.9). Пусть ![]() . Согласно условию
ортогональности
. Согласно условию
ортогональности ![]() ,
тогда
,
тогда ![]() .
При этом вероятность ошибки:
.
При этом вероятность ошибки:
|
|
(3.50) |
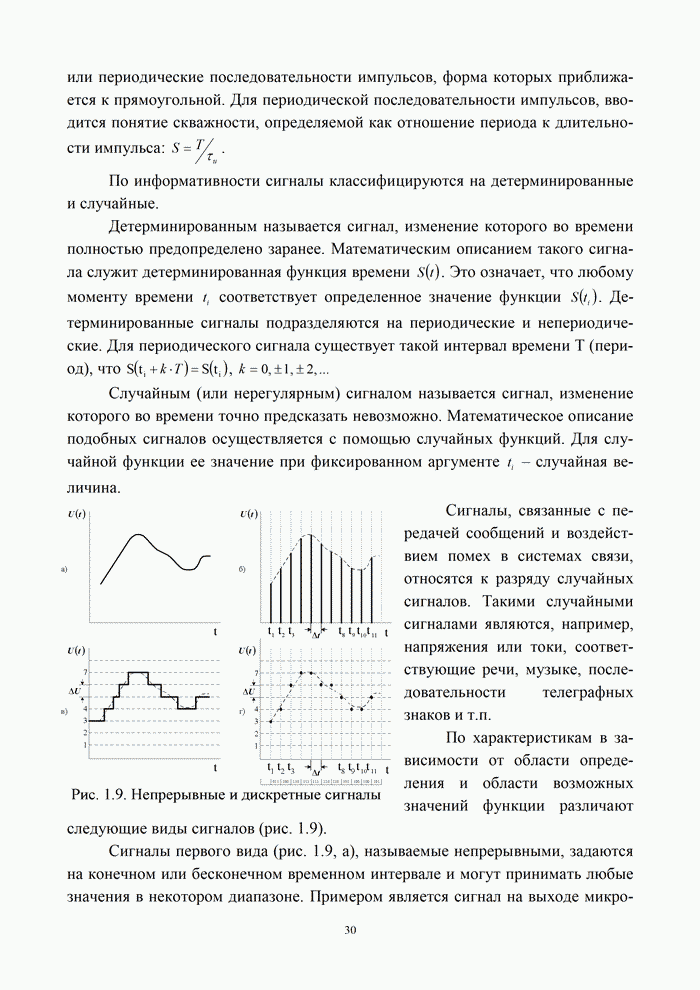
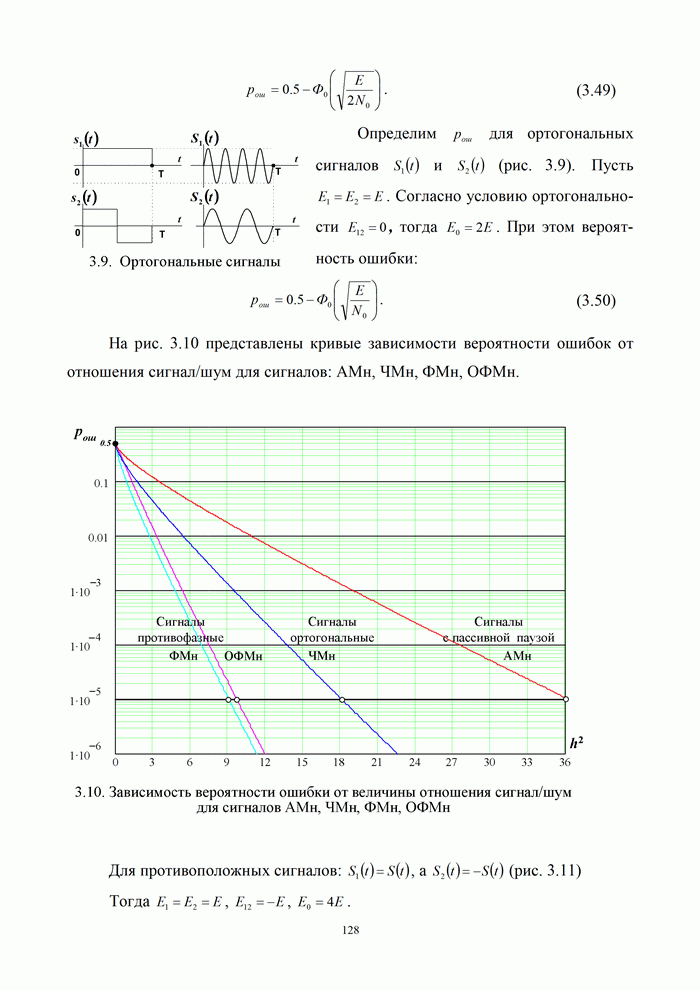
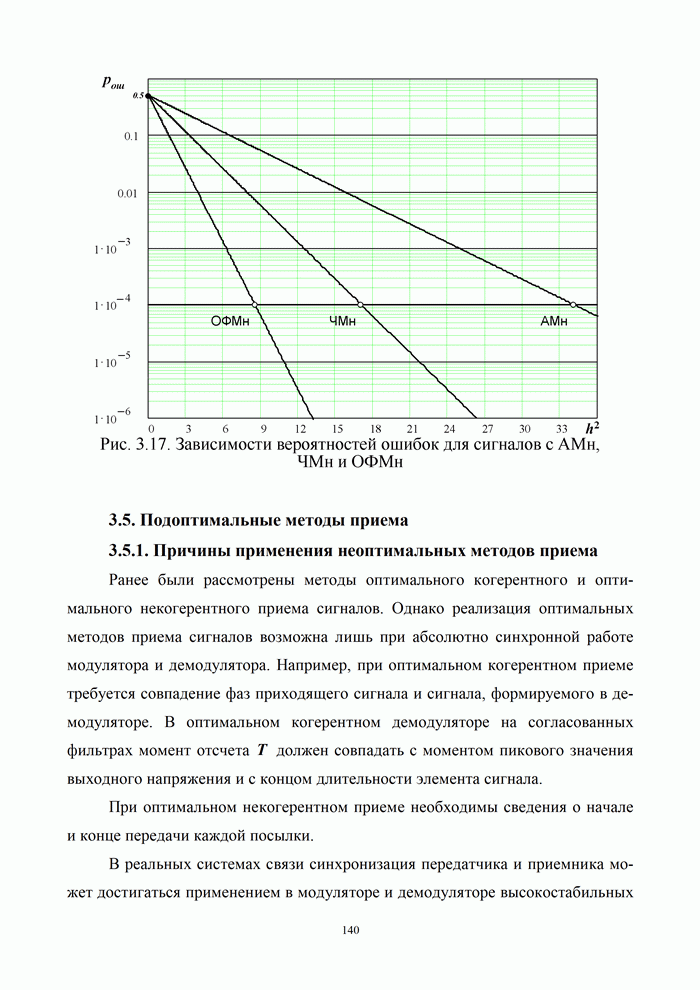
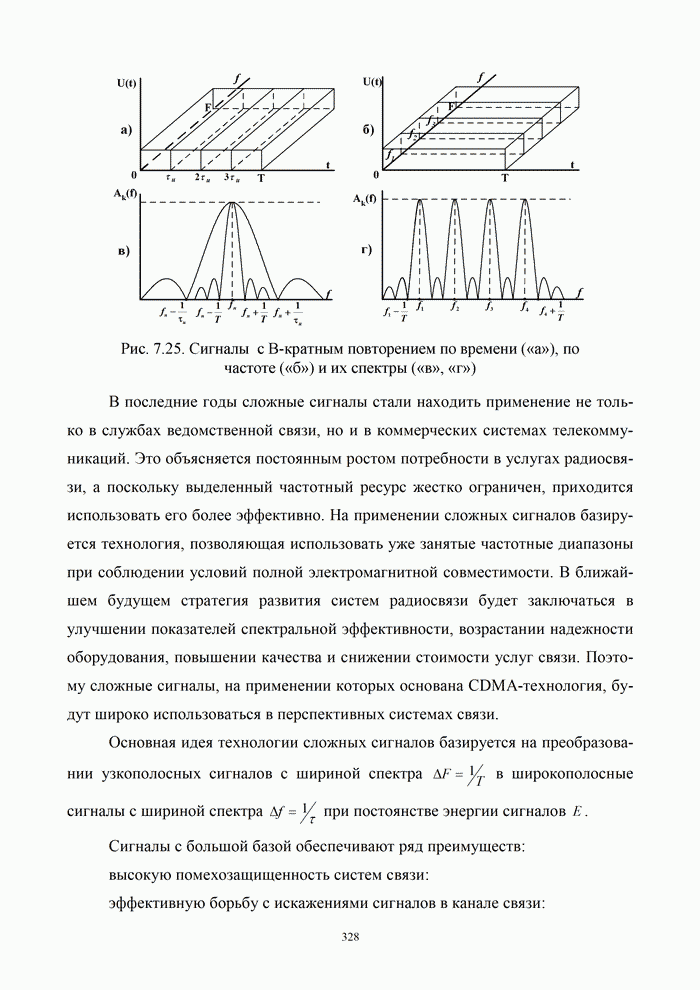
На рис. 3.10 представлены кривые зависимости вероятности ошибок от отношения сигнал/шум для сигналов: АМн, ЧМн, ФМн, ОФМн.

Для
противоположных сигналов: ![]() , а
, а ![]() (рис. 3.11)
(рис. 3.11)
Тогда
![]() ,
, ![]() ,
, ![]() .
.
Вероятность ошибки определяется выражением [21, 32, 39]:
|
|
(3.51) |
В этом случае расчет вероятности ошибки для ОФМн сигналов производится по формуле:
|
|
(3.52) |

Сравнение различных по форме сигналов (рис. 3.9 – 3.11) показывает, что помехоустойчивость противофазных сигналов может быть получена при затратах энергии в 2 раза меньшей, чем при ортогональных сигналах и в 4 раза меньшей, чем при передаче сообщений сигналами с пассивной паузой.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Список сокращений
- Основные обозначения
- ВВЕДЕНИЕ
- Глава 1. Сообщения, сигналы и помехи, их математические модели
- 1.1. Основные понятия и определения
- 1.1.1. Сообщение, сигнал, модуляция
- 1.1.2. Основные параметры сигналов
- 1.2. Системы связи. Каналы связи
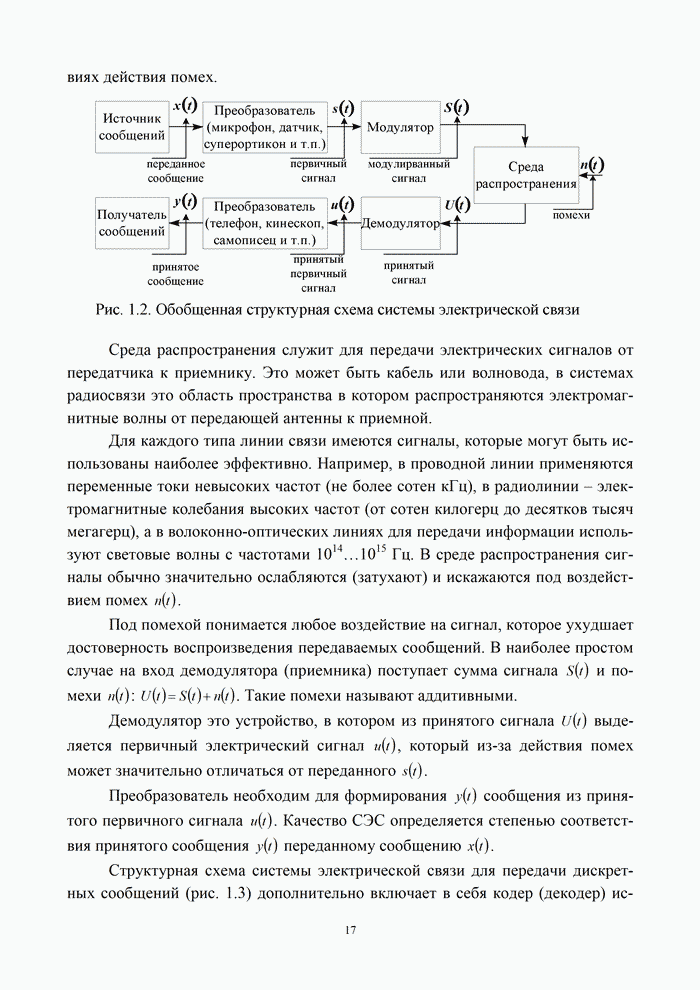
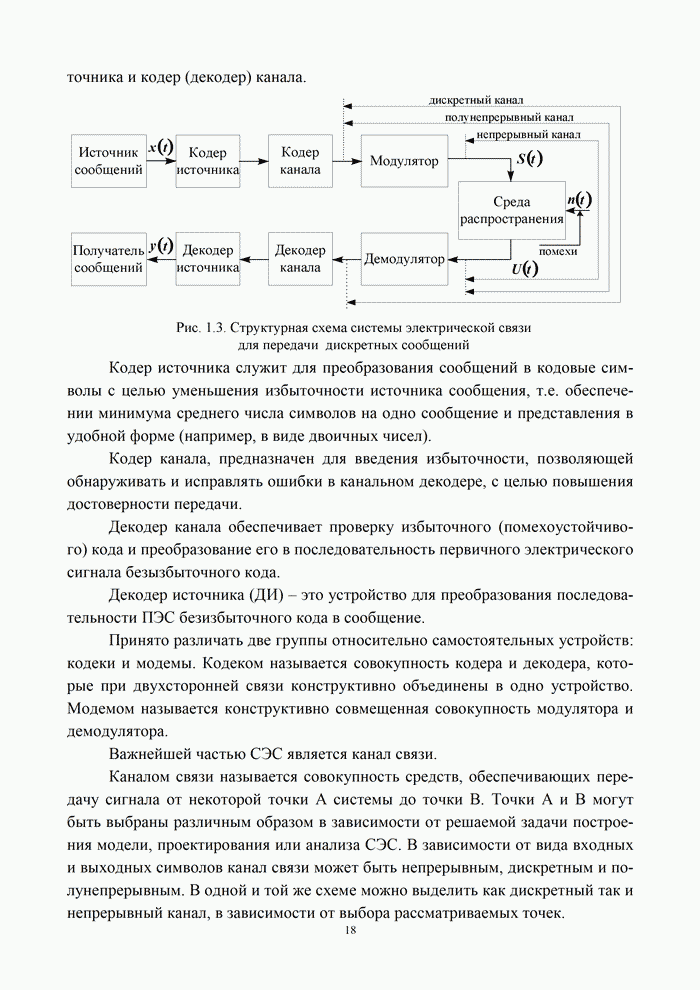
- 1.2.1. Структура канала электросвязи
- 1.2.2. Линия и сеть связи
- 1.2.3. Помехи и искажения в канале
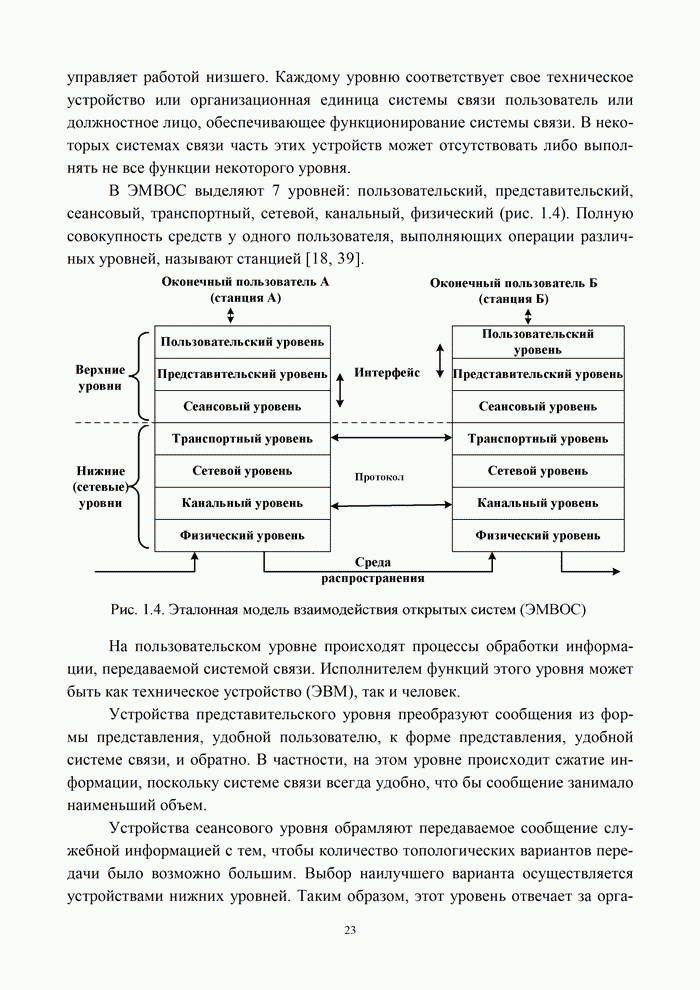
- 1.2.4. Эталонная модель взаимодействия открытых систем
- 1.2.5. Модели каналов связи и их математическое описание
- 1.3. Способы описания сигналов и помех
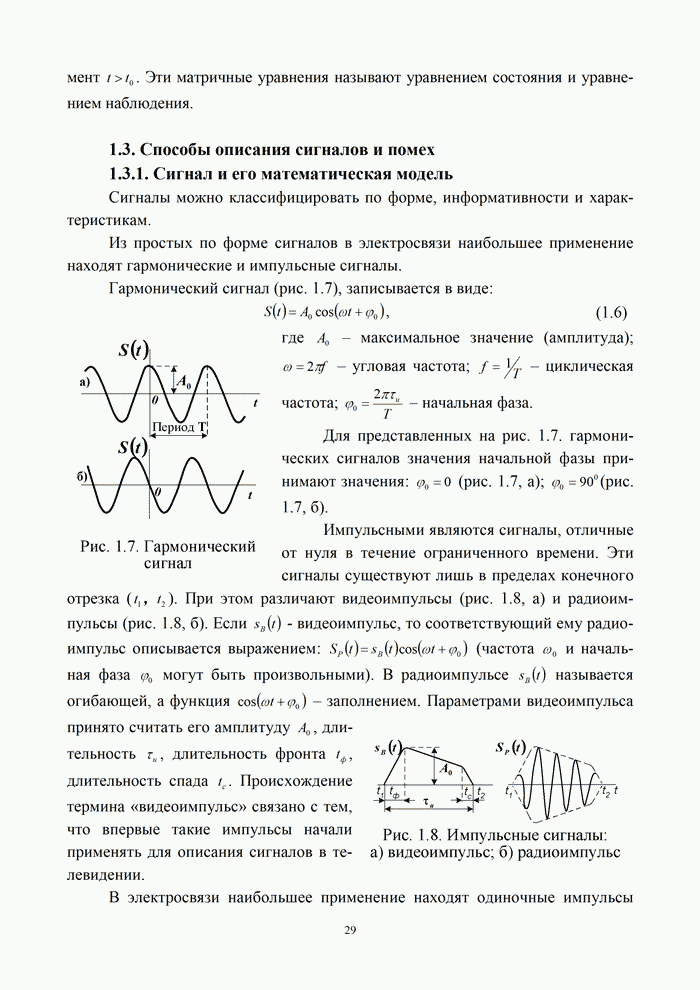
- 1.3.1. Сигнал и его математическая модель
- 1.3.2. Энергетические характеристики детерминированного сигнала
- 1.4.2. Представление сигналов и помех рядом Фурье
- 1.4.3. Применение преобразования Фурье для непериодических сигналов
- 1.5. Теорема Котельникова
- 1.6. Пространство сигналов
- 1.6.1. Линейное пространство
- 1.6.2. Представление сигнала в многомерном пространстве
- 1.7. Сигналы как случайные процессы
- 1.7.1. Характеристики случайного процесса
- 1.7.2. Флуктуационный шум
- 1.8. Комплексное представление сигналов и помех
- 1.8.1. Понятие аналитического сигнала
- 1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
- Контрольные вопросы
- Глава 2. Методы формирования и преобразования сигналов
- 2.1. Модуляция сигналов
- 2.1.1. Амплитудная модуляция гармонической несущей
- 2.1.2. Балансная и однополосная модуляция гармонической несущей
- 2.2. Методы угловой модуляции
- 2.2.1. Принципы частотной и фазовой (угловой) модуляции
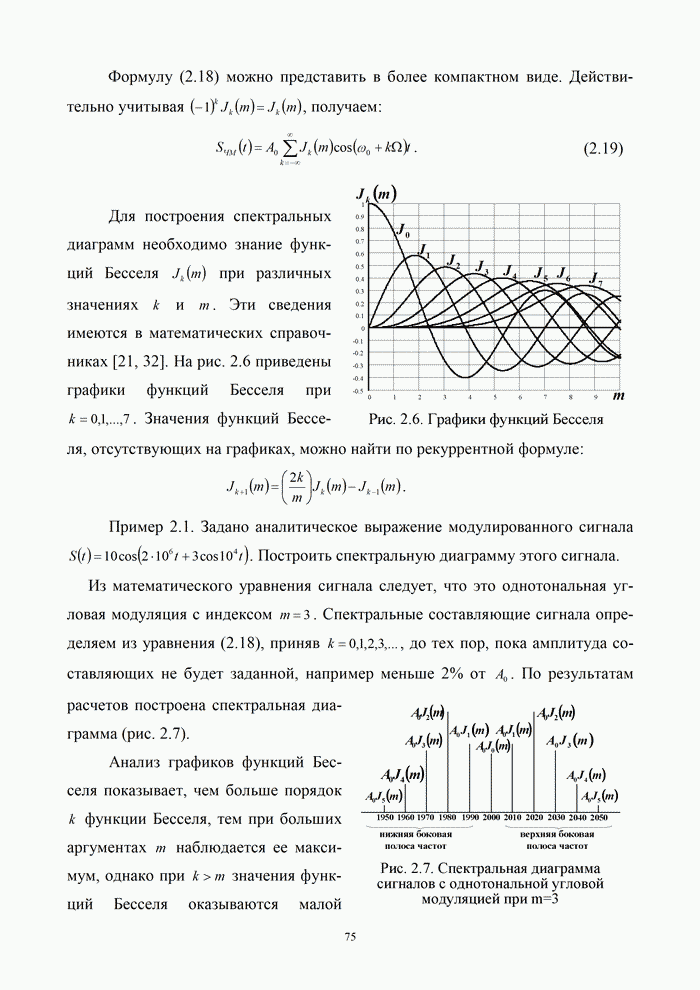
- 2.2.2. Спектр сигналов угловой модуляции
- 2.3. Формирование и детектирование модулированных сигналов
- 2.3.1. Формирование и детектирование сигналов амплитудной и однополосной амплитудной модуляции
- 2.3.2. Формирование и детектирование сигналов угловой модуляции
- 2.4. Манипуляция сигналов
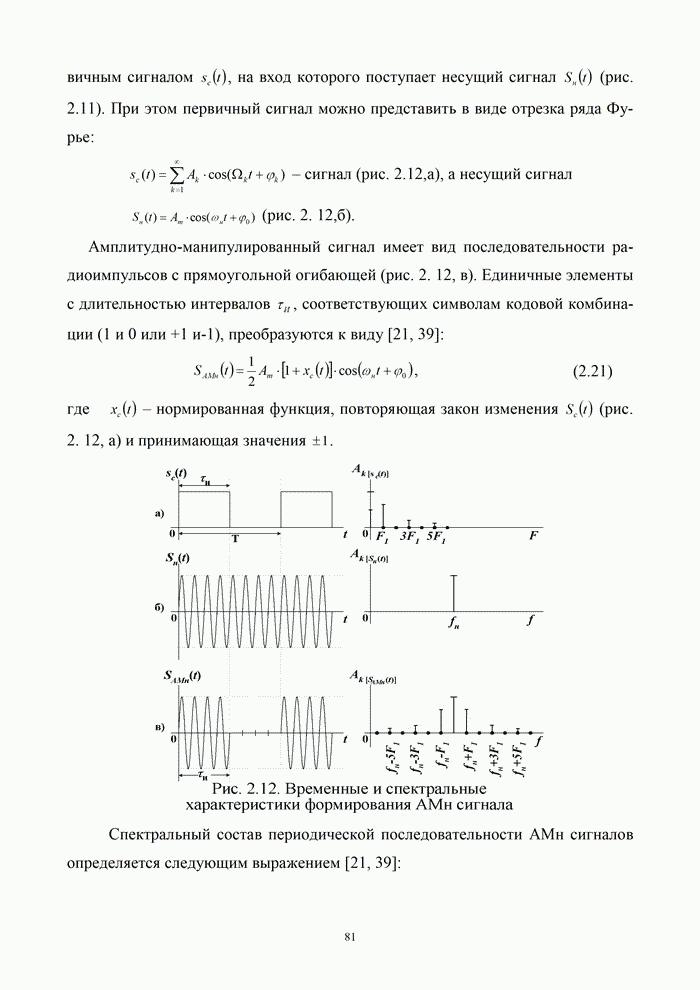
- 2.4.1. Временные и спектральные характеристики амплитудно-манипулированных сигналов
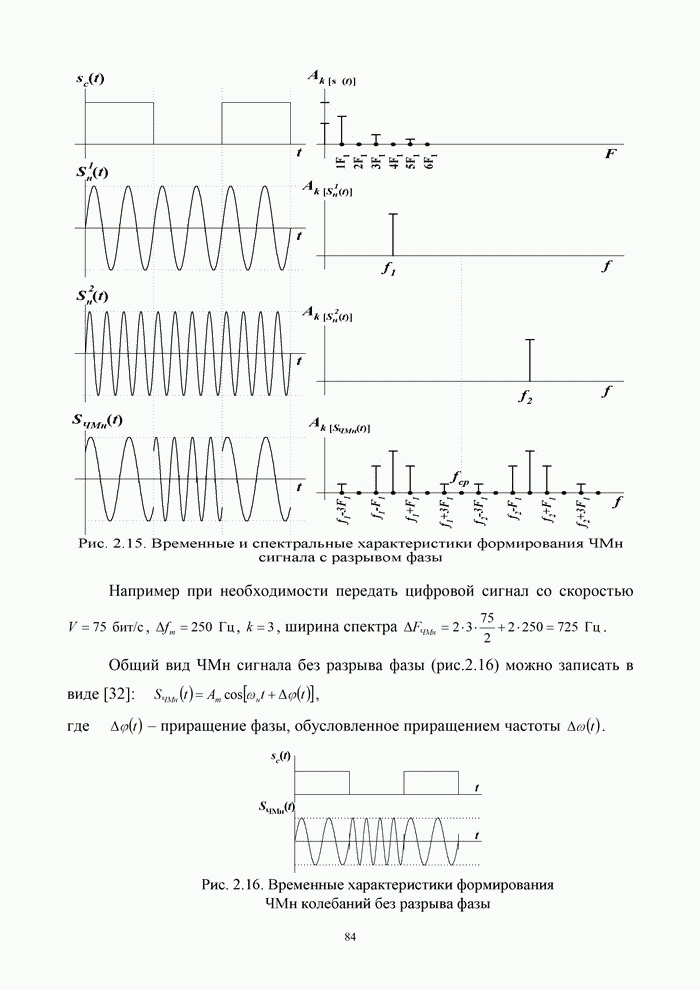
- 2.4.2. Временные и спектральные характеристики частотно-манипулированных сигналов
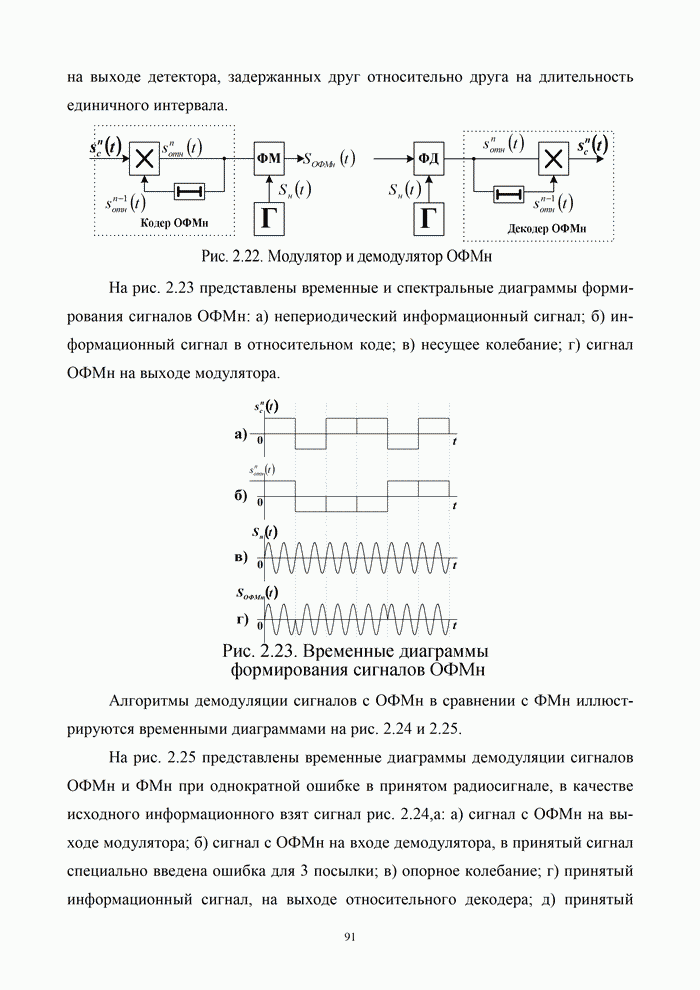
- 2.4.3. Фазовая (относительно-фазовая) манипуляция сигналов
- 2.5. Системы связи с многопозиционной относительной фазовой манипуляцией
- 2.5.1. Принцип формирования сигнала с многократной относительной фазовой манипуляцией
- 2.5.2. Квадратурная относительно-фазовая манипуляция (КОФМ)
- 2.5.3. Принцип частотной модуляции с непрерывной фазой
- Контрольные вопросы
- Глава 3. Помехоустойчивость приема дискретных сообщений
- 3.1. Критерии качества и правила приема дискретных сообщений
- 3.1.1. Понятие о помехоустойчивости систем электрической связи
- 3.1.2. Задача оптимального приема
- 3.1.3. Вычисление вероятностей ошибок
- 3.2. Оптимальная демодуляция при когерентном приеме сигналов
- 3.2.1. Оптимальные алгоритмы приема при полностью известных сигналах
- 3.2.2. Реализация алгоритмов оптимального когерентного приема
- 3.3. Помехоустойчивость приема сигналов с известными параметрами
- 3.4. Прием сигналов с неопределенной фазой
- 3.4.1. Оптимальный некогерентный прием дискретных сигналов
- 3.4.2. Помехоустойчивость оптимального некогерентного приема
- 3.5. Подоптимальные методы приема
- 3.5.1. Причины применения неоптимальных методов приема
- 3.5.2. Квазиоптимальные методы приема
- Контрольные вопросы
- Глава 4. Теория передачи информации
- 4.1. Информационные характеристики источника сообщений
- 4.1.1. Количественное определение информации
- 4.1.2. Энтропия и производительность дискретного источника сообщений
- 4.2. Пропускная способность дискретного канала
- 4.2.1. Количество информации переданной по дискретному каналу
- 4.2.2. Пропускная способность дискретного канала
- 4.2.3. Пропускная способность симметричного дискретного канала без памяти
- 4.3. Методы сжатия дискретных сообщений
- 4.3.1. Условия существования оптимального неравномерного кода
- 4.3.2. Прямая и обратная теоремы кодирования источника неравномерными кодами
- 4.3.3. Показатели эффективности сжатия
- 4.3.4. Кодирование источника дискретных сообщений методом Шеннона-Фано
- 4.3.5. Кодирование источника дискретных сообщений методом Хаффмена
- 4.4. Пропускная способность непрерывного канала
- 4.4.1. Постановка задачи передачи дискретных сообщений в непрерывном канале
- 4.4.2. Количество информации, переданной по непрерывному каналу
- 4.4.3. Пропускная способность непрерывного канала
- Контрольные вопросы
- Глава 5. Теория кодирования сообщений
- 5.1. Помехоустойчивое кодирование: блочные и непрерывные коды
- 5.1.1. Постановка задачи помехоустойчивого кодирования
- 5.1.2. Классификация кодов
- 5.1.3. Основные характеристики и свойства блочных кодов
- 5.2. Эффективность помехоустойчивого кодирования
- 5.2.1. Эффективность кода в режиме исправления ошибок
- 5.2.2. Эффективность кода в режиме обнаружения ошибок
- 5.2.3. Эффективность помехоустойчивых кодов
- 5.3. Математические основы теории помехоустойчивого кодирования
- 5.3.1. Краткие сведения из теории чисел
- 5.3.2. Группы
- 5.3.3. Кольца и поля
- 5.3.4. Векторное пространство
- 5.3.5. Конечные поля
- 5.4. Линейные блочные коды
- 5.4.1. Система передачи дискретных сообщений
- 5.4.2. Параметры линейного кода
- 5.4.3. Полиномиальные циклические коды
- 5.4.4. Циклические коды и корни полиномов
- 5.4.5. Спектральное описание циклических кодов
- 5.4.6. Простейшие блочные линейные коды
- 5.5. Коды Боуза-Чоудхури-Хоквингема
- 5.5.1. Методы задания кодов БЧХ
- 5.5.2. Принципы декодирования кодов БЧХ
- 5.5.3. Методы реализации этапов декодирования кодов БЧХ
- 5.6. Коды Рида-Соломона
- 5.6.1. Основные определения
- 5.6.2. Обнаружение и исправление пакетов ошибок
- 5.7. Коды Рида-Маллера
- 5.7.1. Задание и декодирование кодов Рида-Маллера
- 5.7.2. Симплексные коды и m-последовательности
- 5.7.3. Связь между блочными кодами
- 5.8. Сверточные коды
- 5.8.1. Основные параметры
- 5.8.2. Способы задания сверточного кода
- 5.8.3. Алгоритм декодирования Витерби
- 5.9. Помехоустойчивость систем передачи дискретных сообщений
- 5.9.1. Две процедуры приема сигналов
- 5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
- 5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
- Контрольные вопросы
- Глава 6. Сигналы с импульсной модуляцией
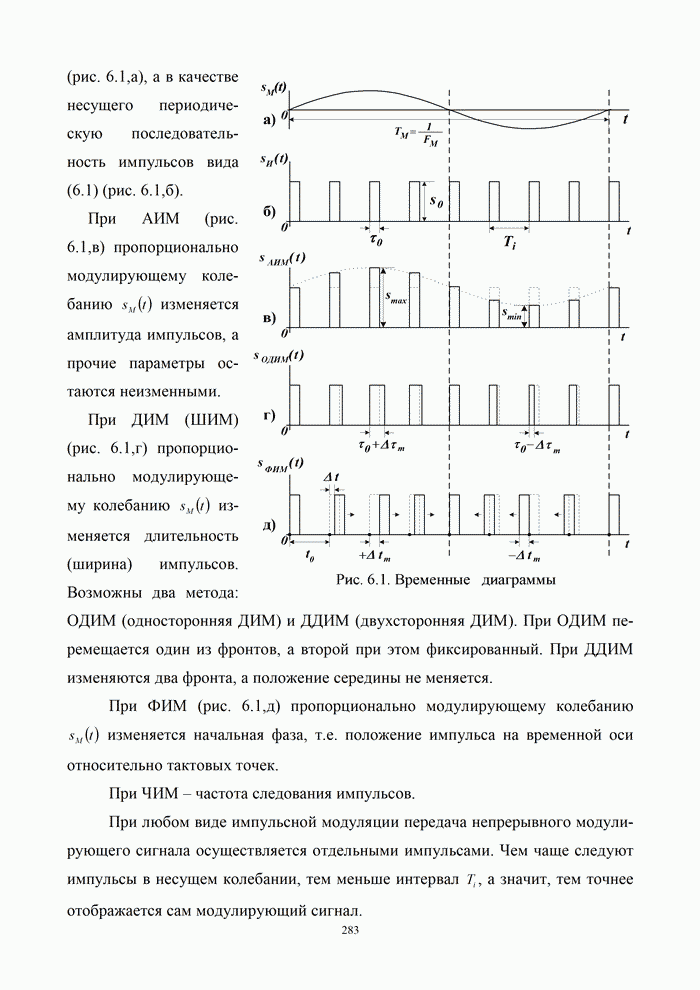
- 6.1. Методы импульсной модуляции
- 6.1.1. Импульсные методы передачи непрерывных сигналов
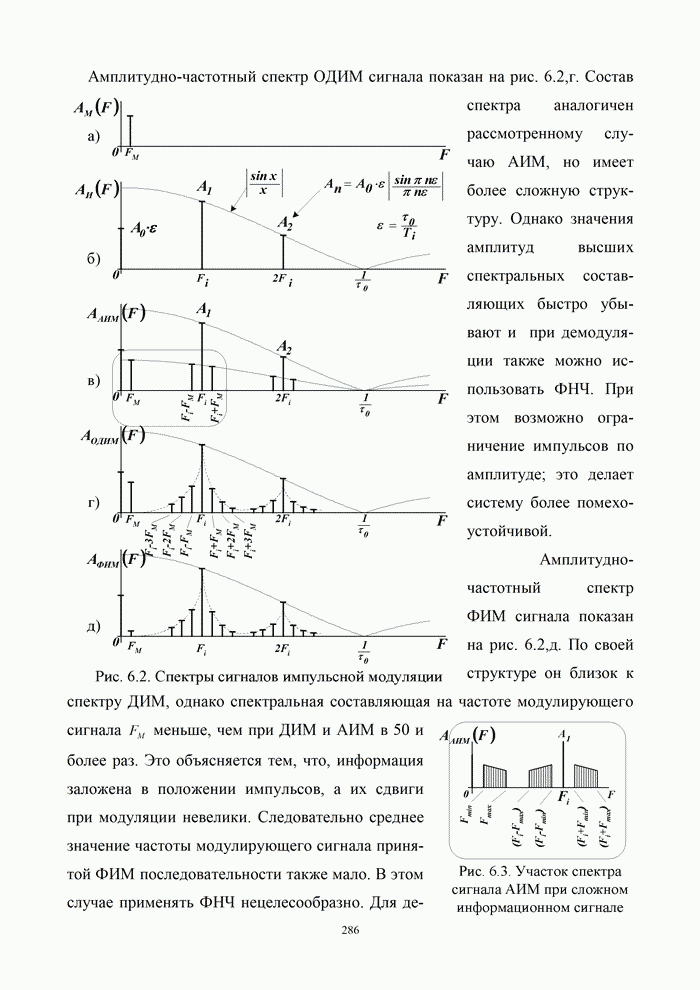
- 6.1.2. Спектральные характеристики импульсных методов модуляции
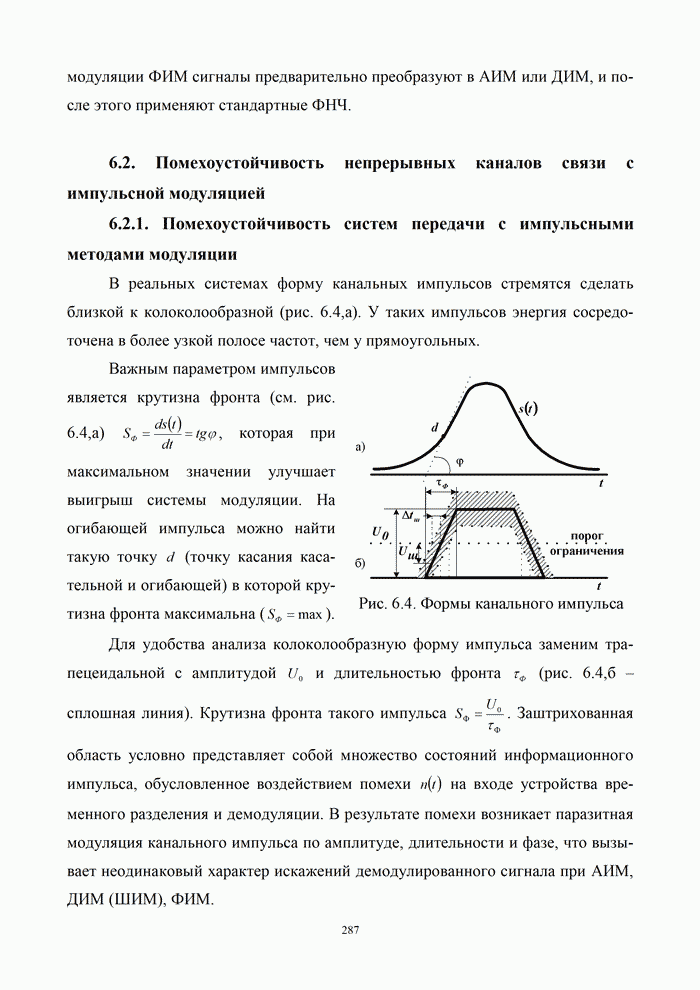
- 6.2. Помехоустойчивость непрерывных каналов связи с импульсной модуляцией
- 6.2.1. Помехоустойчивость систем передачи с импульсными методами модуляции
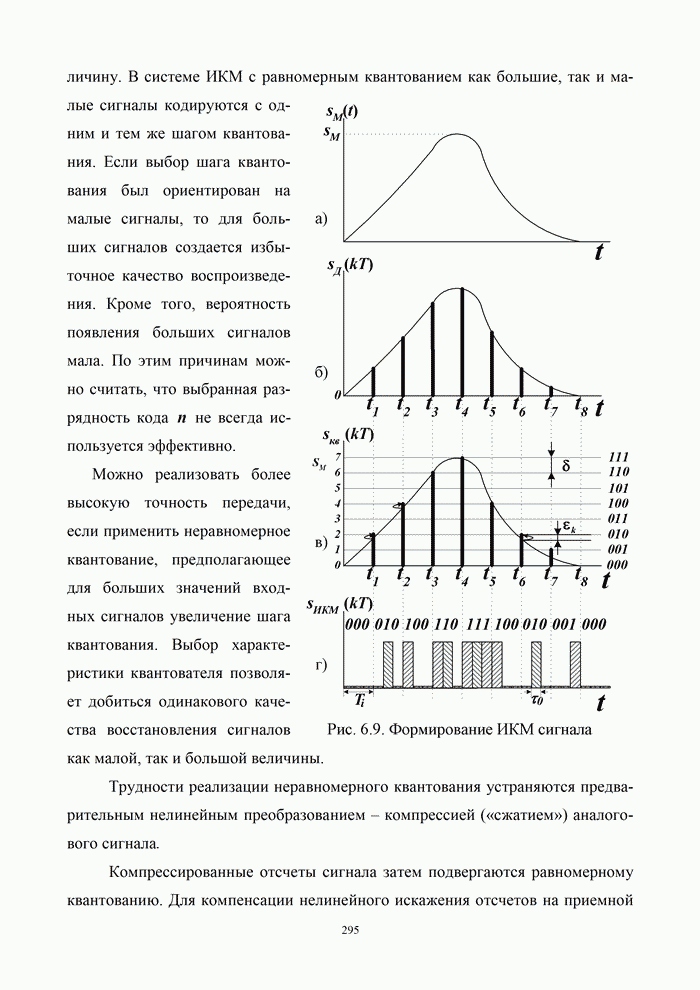
- 6.3. Цифровые методы передачи непрерывных сообщений
- 6.3.1. Передача сигналов с импульсно-кодовой модуляцией
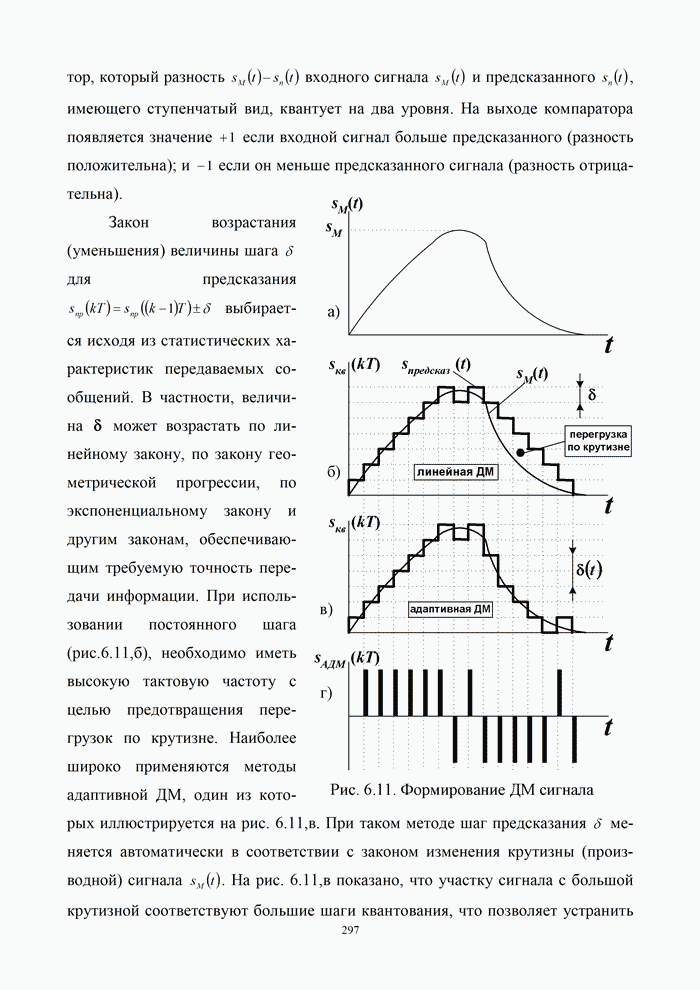
- 6.3.2. Передача сигналов с дельта модуляцией
- 6.3.3. Квантование сигналов в системах с ИКМ и ДМ
- Контрольные вопросы
- Глава 7. Методы приема сигналов в сложных условиях
- 7.1. Прием сигналов в каналах с замираниями
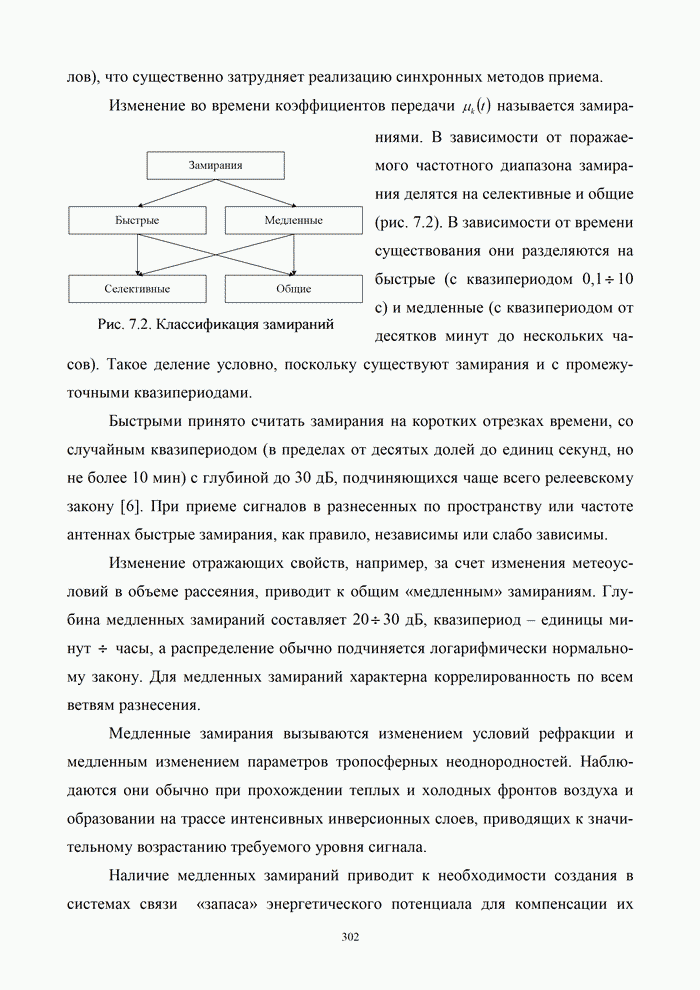
- 7.1.1. Сущность замираний и их классификация
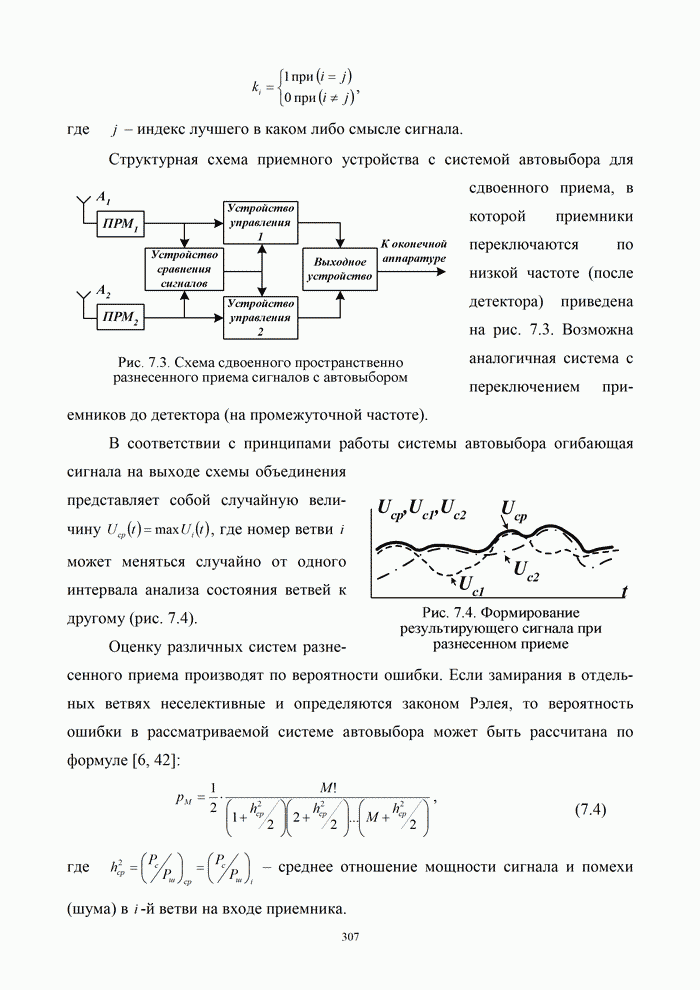
- 7.1.2. Принципы разнесенного приема сигналов
- 7.2. Методы борьбы с замираниями сигналов
- 7.2.1. Методы борьбы с замираниями в аналоговых системах связи
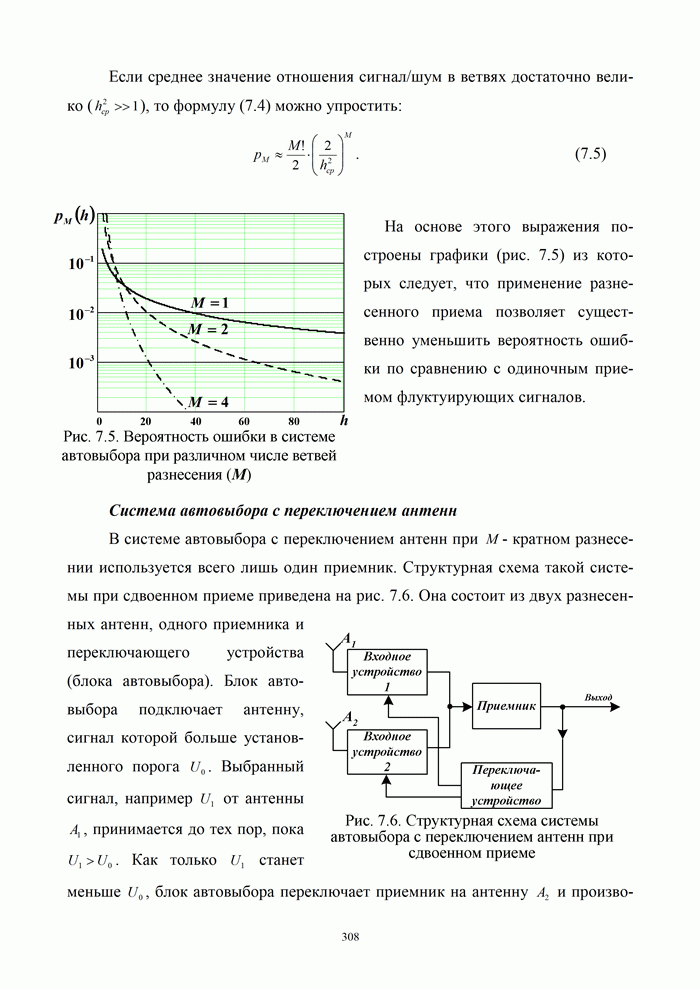
- 7.2.2. Методы борьбы с замираниями в цифровых системах связи
- 7.3. Методы борьбы с межсимвольной интерференцией
- 7.3.1. Причины возникновения и сущность межсимвольной интерференции
- 7.3.2. Обработка сигналов в каналах с межсимвольной интерференцией
- 7.3.3. Помехоустойчивость в каналах с межсимвольной интерференцией
- 7.4. Прием дискретных сообщений в каналах с сосредоточенными по спектру и импульсными помехами
- 7.4.1. Общая характеристика сосредоточенных по спектру и импульсных помех
- 7.4.2. Борьба с сосредоточенными и импульсными помехами
- 7.5. Компенсация помех и искажений в канале
- 7.5.1. Принцип работы радиолинии с ФМ ПСС (ФМ ШПС)
- 7.5.2. Помехоустойчивость радиолинии с ФМ ПСС
- 7.5.3. Принципы работы радиолиний с ППРЧ
- 7.5.4. Помехоустойчивость радиолиний с ППРЧ
- Контрольные вопросы
- Глава 8. Многоканальная связь и распределение информации
- 8.1. Методы распределения ресурса общего канала
- 8.1.1. Классификация систем передачи информации, использующих единый ресурс
- 8.1.2. Постановка задачи объединения и разделения сигналов
- 8.1.3. Энергетическая и спектральная цена уплотнения
- 8.2. Частотное разделение каналов
- 8.2.1. Принцип частотного объединения и разделения каналов
- 8.2.2. Групповой сигнал, его структура и характеристики
- 8.3. Временное разделение каналов
- 8.3.1. Принцип временного разделения каналов
- 8.3.2. Характеристики группового сигнала систем с ВРК
- 8.4. Разделение сигналов по форме
- Контрольные вопросы
- Глава 9. Эффективность систем связи
- 9.1. Оценка эффективности систем связи
- 9.1.1. Подходы к оценке эффективности
- 9.1.2. Критерии эффективности
- 9.1.3. Эффективность аналоговых и цифровых систем
- 9.2. Выбор сигналов и помехоустойчивых кодов
- 9.2.1. Многопозиционные сигналы
- 9.2.2. Корректирующие коды
- 9.3. Оптимизация систем связи
- 9.3.1. Согласование методов модуляции и кодирования
- 9.3.2. Классификация сигнально – кодовых конструкций
- 9.4. Характеристики основных типов СКК
- 9.4.1. Согласование канала кодом Грея
- 9.4.2. Согласование на основе разбиения ансамбля на вложенные подансамбли
- 9.5. Алгоритмы цифровой обработки сигналов
- 9.5.1. Дискретные сигналы и их спектры
- 9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье
- Контрольные вопросы
- Глава 10. Теоретико-информационные основы криптозащиты сообщений в телекоммуникационных системах
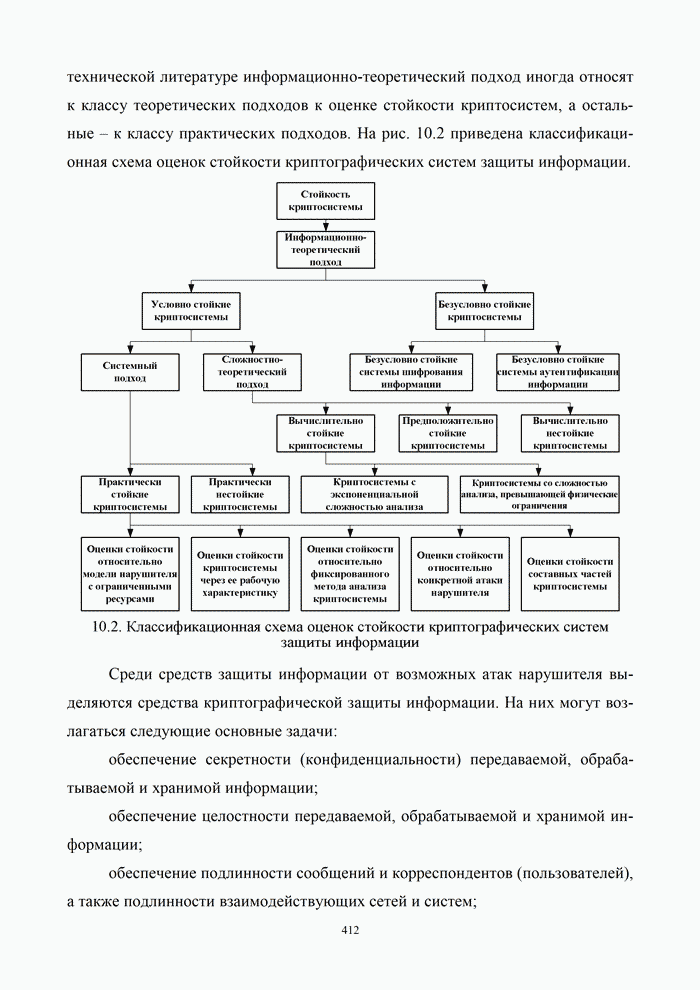
- 10.1. Классификация криптографических систем
- 10.1.2. Классификация криптографических систем защиты информации
- 10.1.3. Оценка стойкости криптосистем
- 10.2. Функции, используемые в криптографических системах
- 10.2.1. Общее описание функций, используемых в криптографических системах
- 10.2.2. Однонаправленные функции
- 10.2.3. Криптографические хэш-функции
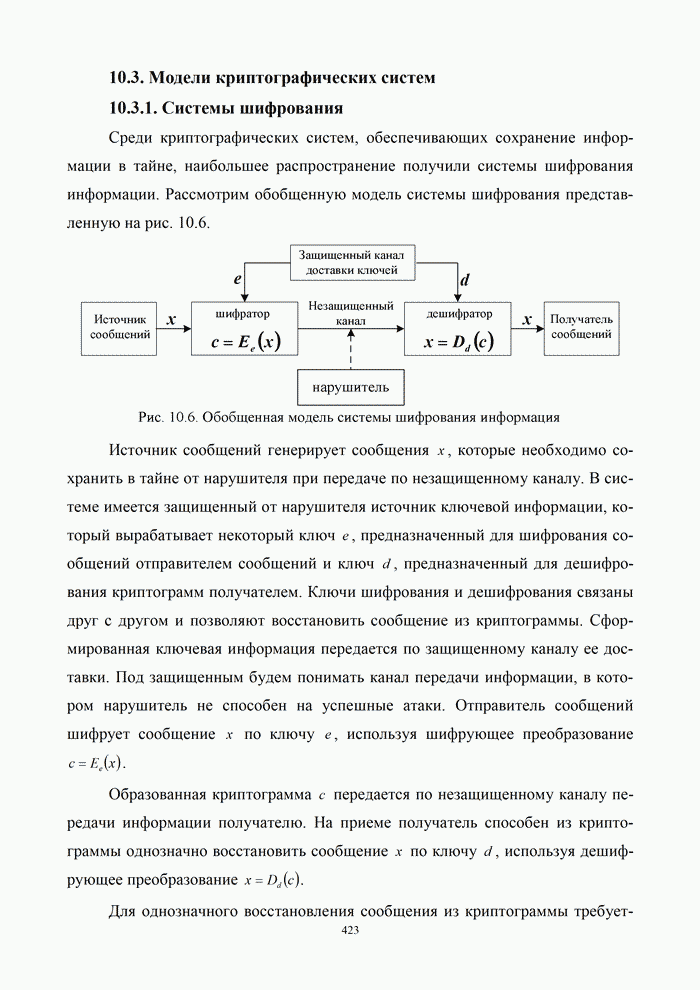
- 10.3. Модели криптографических систем
- 10.3.1. Системы шифрования
- 10.3.2. Традиционные симметричные криптосистемы
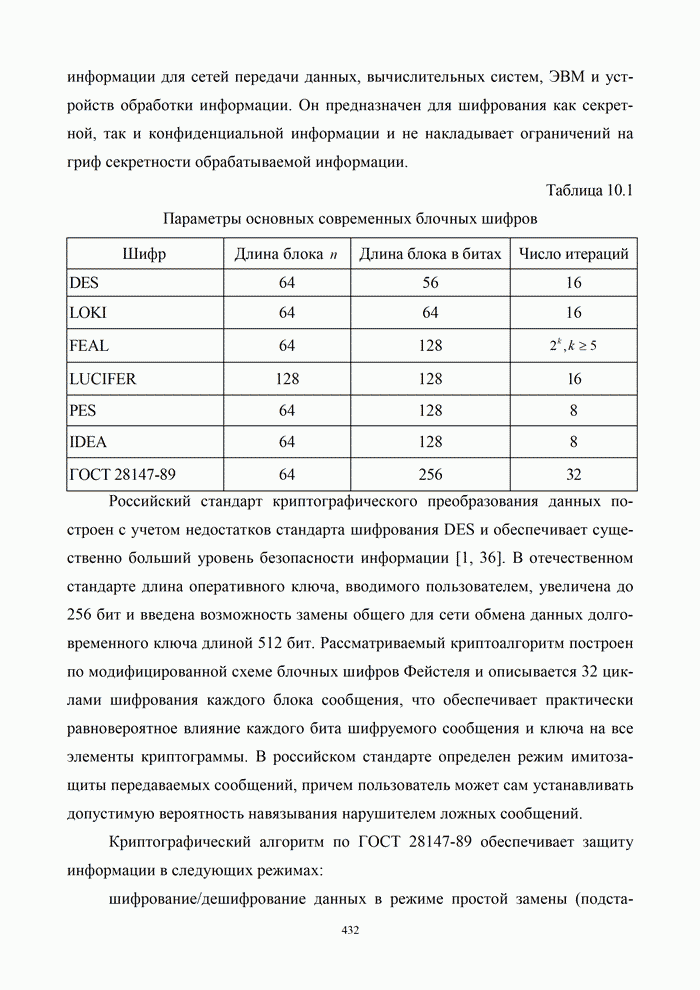
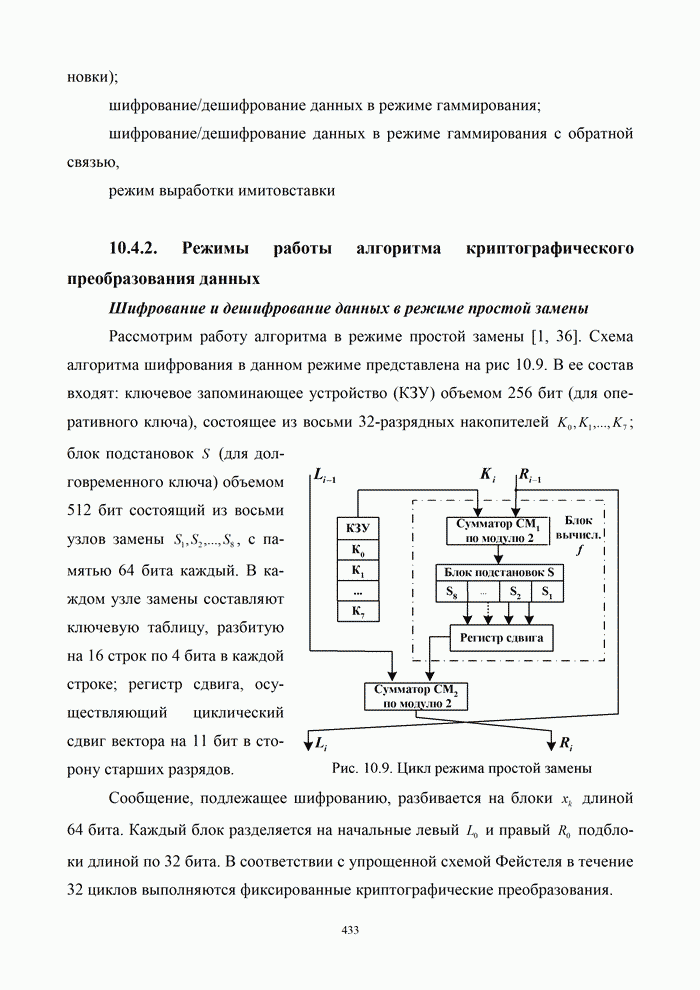
- 10.4. Алгоритмы криптографической защиты
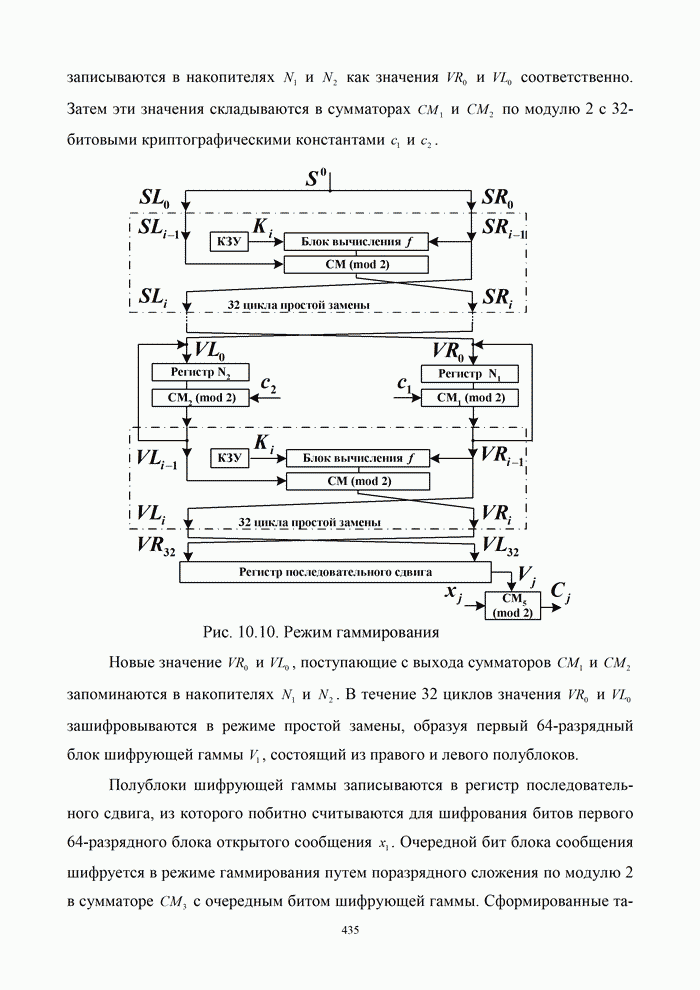
- 10.4.1. Алгоритм криптографической защиты информации согласно ГОСТ 28147-89
- Контрольные вопросы
- Заключение
- Список литературы



















































































































































































































































































































































































 ,
,
 .
.
 ,
,  ,
,  .
.
 .
.
 .
.
 .
.
 .
.
