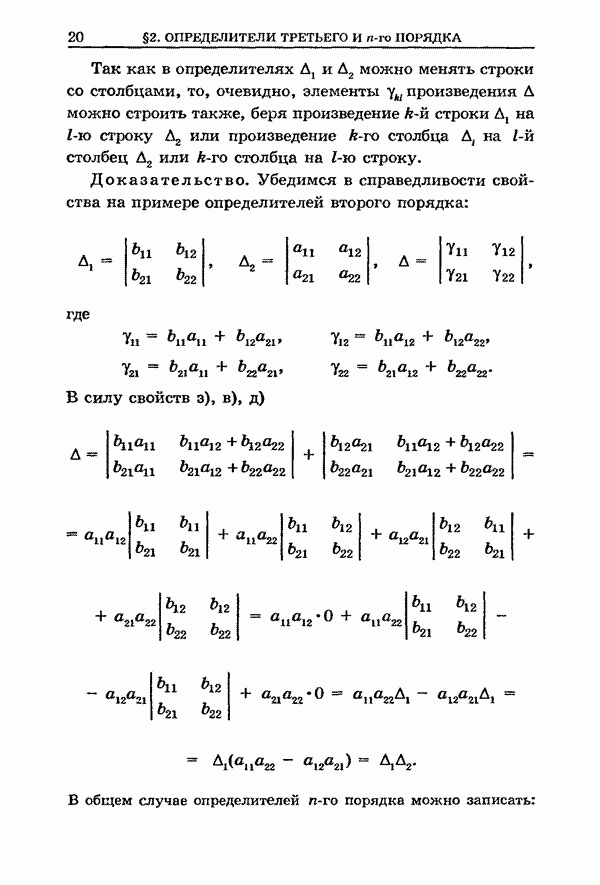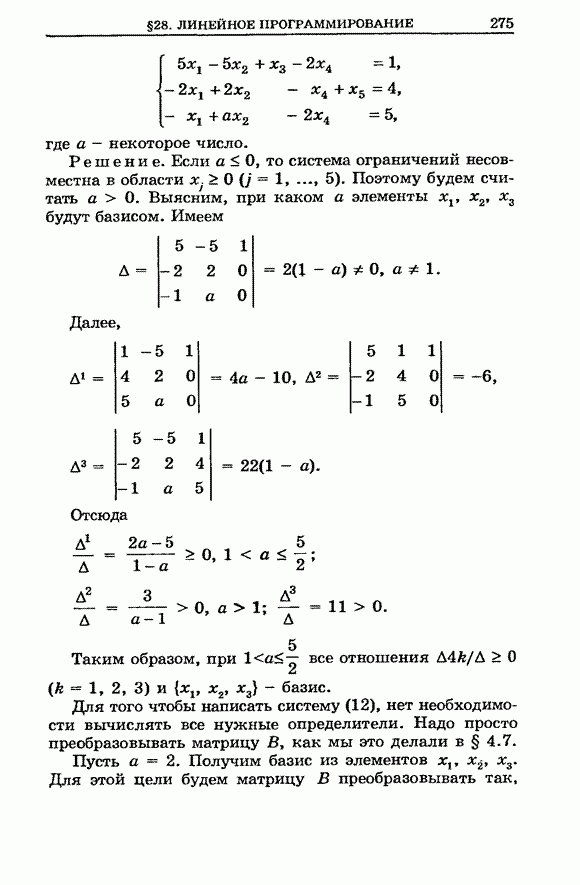| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 16. Базисы в Rn
В пространстве ![]() (действительном или
комплексном) введем
(действительном или
комплексном) введем ![]() векторов:
векторов:
 (1)
(1)
называемых
ортами осей пространства ![]() .
.
Осью ![]() пространств
пространств ![]() называется множество
точек вида
называется множество
точек вида ![]() ,
где
,
где ![]() стоит
на
стоит
на ![]() -м месте
и пробегает все действительные (комплексные) значения, а вектор
-м месте
и пробегает все действительные (комплексные) значения, а вектор ![]() называется ортом оси
называется ортом оси
![]() .
.
Если ![]() есть произвольный
вектор (действительный в действительном
есть произвольный
вектор (действительный в действительном ![]() или комплексный в комплексном
или комплексный в комплексном ![]() ), то его можно,
очевидно, записать в виде линейной комбинации из векторов (1) следующим
образом:
), то его можно,
очевидно, записать в виде линейной комбинации из векторов (1) следующим
образом:
![]() . (2)
. (2)
Так как из
равенства ![]() следует,
что
следует,
что ![]() , то
система
, то
система ![]() линейно
независима.
линейно
независима.
Зададим
произвольную систему из ![]() линейно независимых векторов
линейно независимых векторов
 (3)
(3)
Как мы знаем (см. § 14, теорема 1), система (3) линейно независима, если определитель
 . (4)
. (4)
Если же ![]() , то система (3)
линейно зависима.
, то система (3)
линейно зависима.
Согласно теореме
1 § 14 любые ![]() векторов
в пространстве
векторов
в пространстве ![]() линейно
зависимы, так как ранг матрицы из компонент этих векторов не превышает
линейно
зависимы, так как ранг матрицы из компонент этих векторов не превышает ![]() . Поэтому, если
. Поэтому, если ![]() произвольный вектор
и система векторов (3) линейно независима
произвольный вектор
и система векторов (3) линейно независима ![]() , то система векторов
, то система векторов ![]() линейно зависима, т.
е. существуют числа
линейно зависима, т.
е. существуют числа ![]() , одновременно не равные нулю, такие,
что
, одновременно не равные нулю, такие,
что
![]() ,
,
где ![]() (иначе система (3) была
бы линейно зависимой). Отсюда
(иначе система (3) была
бы линейно зависимой). Отсюда
 , (5)
, (5)
где ![]()
![]() . Выразим сумму (5) через орты
. Выразим сумму (5) через орты
![]() (см.(2)):
(см.(2)):
 .
.
С другой стороны, по (2)
 .
.
В силу линейной
независимости системы ![]() коэффициенты при одинаковых векторах
коэффициенты при одинаковых векторах ![]() должны быть равны
должны быть равны
 . (6)
. (6)
Таким образом,
если компоненты ![]() вектора
вектора
![]() по системе
по системе
![]() известны,
то компоненты
известны,
то компоненты ![]() этого
вектора по системе
этого
вектора по системе ![]() находятся
из (6) и притом единственным образом, так как определитель системы (6) есть
находятся
из (6) и притом единственным образом, так как определитель системы (6) есть ![]() .
.
Мы доказали,
что, какова бы ни была линейно независимая система векторов ![]() , любой вектор
, любой вектор ![]() , можно разложить по
этой системе, т. е. представить в виде суммы (5), где
, можно разложить по
этой системе, т. е. представить в виде суммы (5), где ![]() - некоторые числа,
определяемые из (6) и притом единственным образом.
- некоторые числа,
определяемые из (6) и притом единственным образом.
В этом смысле
систему векторов ![]() называют
базисом в
называют
базисом в ![]() ,
желая этим сказать, что любой вектор
,
желая этим сказать, что любой вектор ![]() можно представить в виде
линейной комбинации (5) из этих векторов и притом единственным образом. Мы
доказали, что произвольная линейно независимая система из
можно представить в виде
линейной комбинации (5) из этих векторов и притом единственным образом. Мы
доказали, что произвольная линейно независимая система из ![]() векторов в
векторов в ![]() есть базис в
есть базис в ![]() .
.
Линейно
независимая система из ![]() векторов
векторов
 ,
,
где ![]() , не есть базис в
, не есть базис в ![]() . В самом деле, ранг
матрицы компонент этих векторов равен
. В самом деле, ранг
матрицы компонент этих векторов равен ![]() . Будем считать, что первые
. Будем считать, что первые ![]() столбцов этой
матрицы образуют определитель, не равный нулю. Расширим эту матрицу, приписав к
ней внизу строку
столбцов этой
матрицы образуют определитель, не равный нулю. Расширим эту матрицу, приписав к
ней внизу строку
![]() ,
,
где 1 стоит на ![]() -м месте. Расширенная
матрица имеет ранг
-м месте. Расширенная
матрица имеет ранг ![]() ,
и, следовательно, система векторов
,
и, следовательно, система векторов ![]() линейно независима. Но тогда вектор
линейно независима. Но тогда вектор ![]() не может быть
линейной комбинацией из векторов системы
не может быть
линейной комбинацией из векторов системы ![]() , и эта система не есть базис в
, и эта система не есть базис в ![]() . Обозначим через
. Обозначим через

матрицу векторов
![]() .
.
Переход от
базиса ![]() к
базису
к
базису ![]() осуществляется
при помощи матрицы
осуществляется
при помощи матрицы ![]() :
:
 , (7)
, (7)
т. е. вектор ![]() выражается через
векторы
выражается через
векторы ![]() с
помощью
с
помощью ![]() -й строки
матрицы
-й строки
матрицы ![]() . Обратный
переход от
. Обратный
переход от ![]() к
к
![]() происходит
при помощи обратной матрицы
происходит
при помощи обратной матрицы ![]() (см. § 15, (9))
(см. § 15, (9))
 , (8)
, (8)
элементы которой
вычисляются по формулам ![]() , где
, где ![]() адъюнкт элемента
адъюнкт элемента ![]() в определителе
в определителе ![]() (обратим внимание,
что элемент
(обратим внимание,
что элемент ![]() принадлежащий
принадлежащий
![]() -й строке и
-й строке и
![]() -му столбцу,
выражается через адъюнкт
-му столбцу,
выражается через адъюнкт ![]() элемента
элемента ![]() , принадлежащего
, принадлежащего ![]() -й строке и
-й строке и ![]() -му столбцу). Отметин
еще, что
-му столбцу). Отметин
еще, что
 ,
,
откуда
 (9)
(9)
т.е. переход от
координат ![]() к
к
![]() происходит
при помощи матрицы (см. §3)
происходит
при помощи матрицы (см. §3)
![]() .
.
Из (9) видно,
что ![]() выражается
через
выражается
через ![]() с
помощью
с
помощью ![]() -го
столбца матрицы
-го
столбца матрицы ![]() или
или
![]() -й строки матрицы
-й строки матрицы ![]() , транспонированной к
, транспонированной к
![]() .
.
Далее по формуле (6)

видно, что
переход от ![]() к
к
![]() совершается
при помощи матрицы
совершается
при помощи матрицы ![]() транспонированной
к
транспонированной
к ![]() , т. е.
, т. е. ![]() , выражается через
, выражается через ![]() с помощью
с помощью ![]() -й строки матрицы
-й строки матрицы ![]() или
или ![]() -го столбца матрицы
-го столбца матрицы ![]() .
.
Замечание. В § 15 было установлено, что произвольная квадратная матрица
 (10)
(10)
Определяет
линейный оператор ![]() ,
задаваемый по формулам
,
задаваемый по формулам
 . (11)
. (11)
Но имеет место и
обратное утверждение: каков бы ни был линейный оператор ![]() , он определяется некоторой
матрицей (10) так, что вектор
, он определяется некоторой
матрицей (10) так, что вектор ![]() вычисляется по вектору
вычисляется по вектору ![]() по формулам (11).
по формулам (11).
В самом деле,
пусть задан произвольный линейный оператор ![]() . Обозначим образы
ортов
. Обозначим образы
ортов ![]() при
его помощи следующим образом:
при
его помощи следующим образом:
 .
.
Тогда в силу
линейности ![]() любой
вектор
любой
вектор

отображается при
помощи ![]() в
вектор
в
вектор ![]() , определяемый
равенствами
, определяемый
равенствами
 ,
,
откуда следует,
что ![]() -я
компонента
-я
компонента ![]() определяется
по формуле (11). Таким образом, оператор
определяется
по формуле (11). Таким образом, оператор ![]() порождает матрицу (10), у которой в
столбцах стоят координаты образов базисных векторов (ортов) при помощи
оператора
порождает матрицу (10), у которой в
столбцах стоят координаты образов базисных векторов (ортов) при помощи
оператора ![]() .
.
Пример 1. Найти
матрицу линейного оператора (преобразования) ![]() , заключающегося в повороте векторов
плоскости
, заключающегося в повороте векторов
плоскости ![]() ,
выходящих из начала, на угол
,
выходящих из начала, на угол ![]() против часовой стрелки.
против часовой стрелки.
Возьмем за базис
векторы ![]() ,
, ![]() . Тогда, очевидно,
что (рис. 34)
. Тогда, очевидно,
что (рис. 34)
![]() ,
,
![]() .
.

Рис. 34
Поэтому матрица нашего оператора имеет вид
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- § 1. Определители второго порядка
- 2.1. Определители третьего порядка.
- 2.2. Определители n-го порядка.
- §3. Матрицы
- 4.1 Система из n линейных уравнений с n неизвестными.
- 4.2. Формула Крамера
- 4.3. Однородная система
- 4.4 Правило решения системы линейных уравнений
- Системы линейных уравнений: 4.5 Примеры приложения правил
- Системы линейных уравнений: 4.6 Обоснование правил
- 4.7. Метод решения системы путем исключения неизвестных
- 4.8. Нахождение ранга матрицы
- 5.1. Понятие вектора
- 5.2. Проекция вектора
- 5.3. Свойства проекций векторов
- 5.4 Скалярное произведение векторов
- 5.5. Прямоугольная система координат
- 6.1. n-мерное пространство
- 6.2 Скалярное произведение в действительном пространстве
- 6.3 Скалярное произведение в комплексном пространстве
- 6.4. Неравенства Буняковского
- 6.5. Неравенство Минковского
- § 7. Отрезок. Деление отрезка в данном отношении
- § 8. Прямая линия
- 9.1. Уравнение плоскости в нормальном виде
- 9.2. Уравнение плоскости в общем виде
- 9.3. Уравнение плоскости в отрезках
- 9.4. Уравнение плоскости, роходящей через точку
- 9.5. Уравнение плоскости, проходящей через три точки
- 9.6 Угол между двумя плоскостями
- 9.7. Расстояние от точки до плоскости
- 10.1 Уравнение прямой в каноническом виде
- 10.2 Расположение двух плоскостей
- 11.1. Двумерная система координат
- 11.2. Трехмерная система координат
- 12.1. Два определения векторного произведения
- 12.2. Геометрический смысл определителя второго порядка
- 12.3. Свойства векторного произведения
- § 13. Смешанное (векторно-скалярное) произведение
- § 14. Линейно независимая система векторов
- § 15. Линейные операторы
- § 16. Базисы в Rn
- § 17. Ортогональные базисы в Rn
- § 18. Инвариантные свойства скалярного и векторного произведений
- § 19. Преобразование прямоугольных координат в плоскости
- § 20. Линейные подпространства в Rn
- § 21. Теоремы фредгольмова типа
- § 22. Самосопряженный оператор. Квадратичная форма
- § 23. Квадратичная форма в двухмерном пространстве
- § 24. Кривая второго порядка
- Эллипс
- Гипербола
- Парабола
- 24.3 Классификация кривых второго порядка
- § 25. Поверхность второго порядка в трехмерном пространстве
- Эллипсоид
- Однополостный гиперболоид
- Двуполостный гиперболоид
- Эллиптический и гиперболический параболоиды
- Конус второго порядка
- Цилиндры второго порядка
- Линейчатые поверхности
- § 26. Общая теория поверхности второго порядка в трехмерном пространстве
- § 27. Плоскость в Rn. Общие положения
- 27.2. Плоскость в Rn
- 27.3. Уравнение плоскости в нормальном виде
- 27.4. Уравнение плоскости в векторной форме
- 27.5. Геометрическая интерпретация уравнений
- 27.6. Уравнение плоскости, проходящей через n точек
- 27.7. Условия ортогональности и параллельности плоскостей
- 27.8. Уравнение плоскости, проходящей через точку
- 27.9. Прямая в пространстве Rn
- 27.10. Расположение (n-1) плоскостей
- 27.11. Расстояние от точки до плоскости
- 27.12. Различные задачи
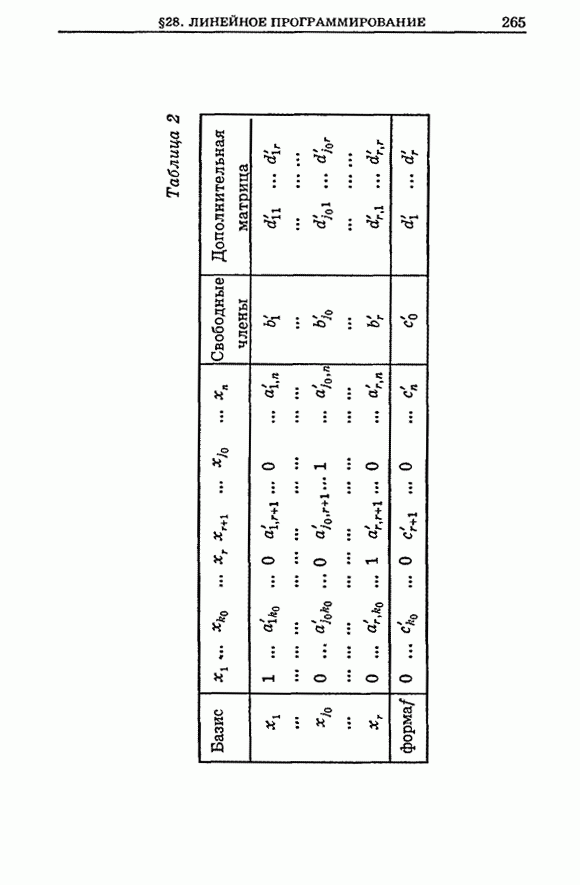
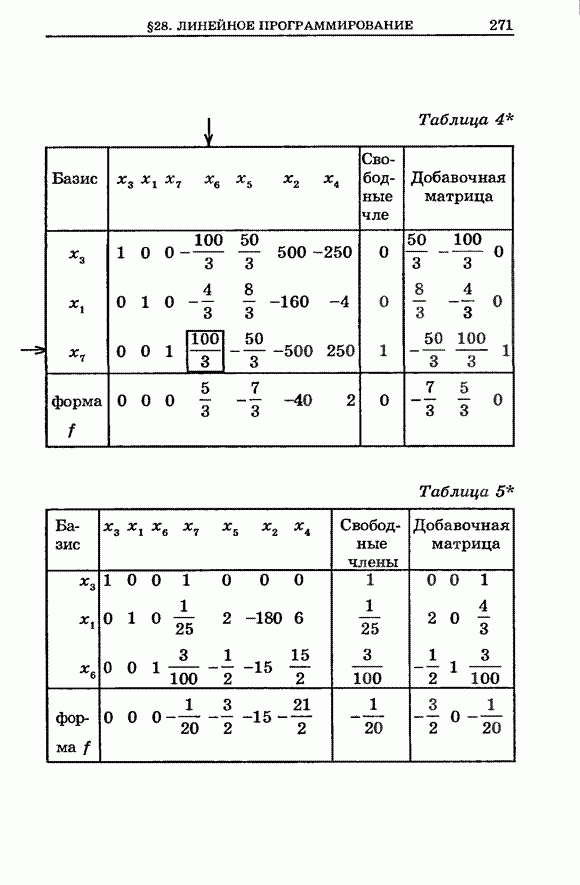
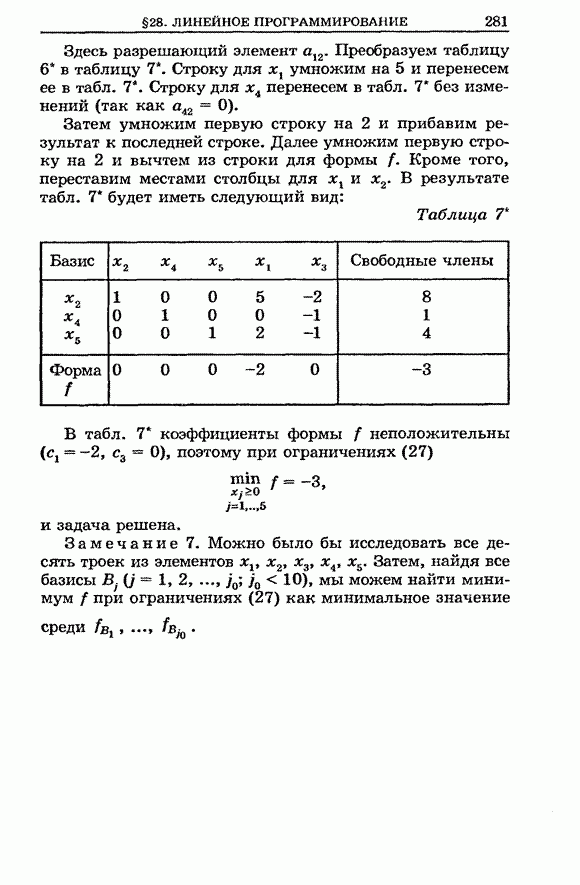
- § 28. Линейное программирование
- 28.2. Транспортная задача
- 28.3.Общая задача линейного программирования
- 28.4. Векторно-матричная форма задачи линейного программирования
- 28.5. Симплекс-метод
- 28.7. Выбор разрешающего элемента
- 28.8. Условия существования базиса