| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1. Система с отказами при простейшем потоке вызовов
Рассмотрим полнодоступную систему с
отказами. Представим ее как физическую систему ![]() с конечным числом состояний
с конечным числом состояний ![]() , где
, где ![]() - число занятых каналов
связи. Данная система в каждый момент времени
- число занятых каналов
связи. Данная система в каждый момент времени ![]() может перейти из состояния
может перейти из состояния ![]() или в состояние
или в состояние ![]() , или в состояние
, или в состояние ![]() , или остаться в прежнем
(рис. 3.1).
, или остаться в прежнем
(рис. 3.1).

Рис. 3.1. Возможные переходы системы
Допустим, что на вход данной системы
поступает простейший поток заявок с интенсивностью ![]() и ПРВ
и ПРВ
![]() ,
, ![]() .
.
Время обслуживания одной заявки показательное с параметром ![]() и ПРВ
и ПРВ
![]() ,
, ![]() .
.
Требуется, на основе этих данных определить вероятности
состояний системы ![]() ,
для любого момента времени
,
для любого момента времени ![]() .
.
Так как оба потока – заявок и
освобождений – простейшие, процесс, протекающий в системе, будет марковским.
Очевидно, для любого момента времени ![]() выполняется условие
выполняется условие
![]() .
.
Зафиксируем момент времени ![]() и найдем вероятности
и найдем вероятности ![]() того, что в момент
времени
того, что в момент
времени ![]() все каналы
связи будут свободны. Это может произойти двумя способами:
все каналы
связи будут свободны. Это может произойти двумя способами:
А – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() не
перешла в состояние
не
перешла в состояние ![]() (не
пришло ни одного вызова);
(не
пришло ни одного вызова);
В – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() освободился
один канал связи.
освободился
один канал связи.
Возможностью «перескока» системы
через состояние за малый промежуток времени ![]() можно пренебречь, как практически
невозможным событием. Тогда по теореме сложения вероятностей двух несовместных
событий получаем
можно пренебречь, как практически
невозможным событием. Тогда по теореме сложения вероятностей двух несовместных
событий получаем
![]() .
.
Найдем вероятность события ![]() . Вероятность того, что
в момент времени
. Вероятность того, что
в момент времени ![]() система
находилась в состоянии
система
находилась в состоянии ![]() равно
равно ![]() , а вероятность того, что за время
, а вероятность того, что за время ![]() не пришло ни одного
вызова определяется выражением
не пришло ни одного
вызова определяется выражением
![]() ,
,
откуда
![]() .
.
Найдем вероятность события ![]() . Вероятность нахождения
системы в состоянии
. Вероятность нахождения
системы в состоянии ![]() в
момент времени
в
момент времени ![]() равно
равно
![]() , а
вероятность освобождения одного канала связи за время
, а
вероятность освобождения одного канала связи за время ![]() определяется формулой
определяется формулой
![]() ,
,
откуда
![]() .
.
Таким образом, вероятность нахождения
системы в момент времени ![]() в состоянии
в состоянии ![]() определяется выражением
определяется выражением
![]() ,
,
или переходя к пределу при ![]() и перенося
и перенося ![]() в левую часть, получим
в левую часть, получим
![]() .
.
Аналогично вычислим вероятности
нахождения системы в состоянии ![]() , при
, при ![]() в момент времени
в момент времени ![]() . Эти вероятности определяются на
основе трех событий:
. Эти вероятности определяются на
основе трех событий:
А – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() не поступило
ни одного вызова;
не поступило
ни одного вызова;
В – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() пришел
один вызов;
пришел
один вызов;
С – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() освободился
один канал связи.
освободился
один канал связи.
Вероятность того, что за время ![]() не придет ни одной
заявки и не освободится ни один из каналов связи, равна
не придет ни одной
заявки и не освободится ни один из каналов связи, равна
![]() ,
,
откуда
![]() .
.
Найдем вероятность события ![]() . Вероятность того, что
за время
. Вероятность того, что
за время ![]() придет
одна заявка, равна
придет
одна заявка, равна
![]() ,
,
откуда
![]() .
.
Определим вероятность ![]() . Вероятность того, что
за время
. Вероятность того, что
за время ![]() освободится
один канал связи, равна
освободится
один канал связи, равна
![]() ,
,
откуда
![]() .
.
Таким образом, искомая вероятность
того, что в момент времени ![]() система будет находиться в состоянии
система будет находиться в состоянии ![]() ,
, ![]() , определяется выражением
, определяется выражением
![]() ,
,
переходя к пределу при ![]() и перенося
и перенося ![]() в левую часть, получим
в левую часть, получим
![]() ,
, ![]() .
.
Найдем теперь вероятность ![]() , того, что в момент
времени
, того, что в момент
времени ![]() система
будет находиться в состоянии
система
будет находиться в состоянии ![]() . Данная вероятность определяется на основе
двух событий:
. Данная вероятность определяется на основе
двух событий:
А – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() не
перешла в состояние
не
перешла в состояние ![]() (не
освободился ни один канал связи);
(не
освободился ни один канал связи);
В – в момент времени ![]() система находилась в
состоянии
система находилась в
состоянии ![]() и
за время
и
за время ![]() пришел
один вызов.
пришел
один вызов.
Очевидно, вероятность ![]() равна
равна
![]() ,
,
а вероятность ![]() определяется как
определяется как
![]() .
.
Искомая вероятность ![]() находится по теореме
сложения вероятностей:
находится по теореме
сложения вероятностей:
![]() ,
,
при переходе к пределу при ![]() , получаем
, получаем
![]() .
.
В результате имеем систему из ![]() дифференциальных
уравнений для вероятностей
дифференциальных
уравнений для вероятностей ![]() состояний системы в момент времени
состояний системы в момент времени ![]() :
:
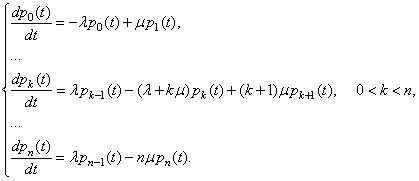
Данные уравнения называются
уравнениями Эрланга. Интегрирование систем дифференциальных уравнений при
начальных условиях ![]() дает
зависимость
дает
зависимость ![]() для
любого
для
любого ![]() .
.
Система дифференциальных уравнений
Эрланга переходит в систему линейных уравнений при установившемся режиме
обслуживания, т.е. при ![]() . В этом случае все вероятности
. В этом случае все вероятности ![]() устремляются к своим
предельным значениям
устремляются к своим
предельным значениям ![]() ,
а их производные к нулю. Таким образом, получаем следующую систему линейных
уравнений:
,
а их производные к нулю. Таким образом, получаем следующую систему линейных
уравнений:
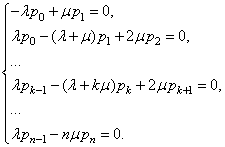
К этим уравнениям необходимо добавить условие
![]() . (3.1)
. (3.1)
Из первого уравнения имеем
![]() , (3.2)
, (3.2)
из второго, с учетом (3.2)
![]()
и в общем случае для любого ![]() вероятности
вероятности
![]() . (3.3)
. (3.3)
Так как параметр ![]() , где
, где ![]() - среднее время обслуживания, то
величина
- среднее время обслуживания, то
величина ![]() равна
входной нагрузки, поступающей на систему связи и выражение (3.3) можно записать
в виде
равна
входной нагрузки, поступающей на систему связи и выражение (3.3) можно записать
в виде
![]()
![]() . (3.4)
. (3.4)
Формула (3.4) выражает все
вероятности через величину ![]() . Чтобы выразить их непосредственно через
входную нагрузку
. Чтобы выразить их непосредственно через
входную нагрузку ![]() ,
воспользуемся условием (3.1):
,
воспользуемся условием (3.1):
![]() ,
,
откуда получаем
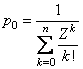
и вероятности ![]() запишутся в виде
запишутся в виде
 ,
, ![]() . (3.5)
. (3.5)
Выражение (3.5) называется формулой Эрланга. Из нее можно получить формулу для вычисления вероятности блокировки поступившей заявки:
![]() ,
,
где ![]() -
вероятность поступления заявки в момент занятости всех
-
вероятность поступления заявки в момент занятости всех ![]() каналов связи. Данную
вероятность можно определить как отношение свободных источников заявок
каналов связи. Данную
вероятность можно определить как отношение свободных источников заявок ![]() к общему числу источников
к общему числу источников
![]() :
:
![]() ,
,
где ![]() -
число обслуживаемых заявок системой связи. Однако, при простейшем входном
потоке
-
число обслуживаемых заявок системой связи. Однако, при простейшем входном
потоке ![]() , а
вероятность
, а
вероятность ![]() .
Следовательно, вероятность блокировки равна
.
Следовательно, вероятность блокировки равна
 . (3.6)
. (3.6)
Данное выражение получило название
первой формулы Эрланга. С помощью данного выражения можно построить кривые
зависимости качества обслуживания ![]() от величины входной нагрузки и числа каналов
связи:
от величины входной нагрузки и числа каналов
связи:
![]() .
.
На основе построенных графиков можно
определять необходимое число линий связи при заданном качестве обслуживания ![]() и величины входной
нагрузки
и величины входной
нагрузки ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Потоки вызовов
- 1.1. Основные понятия потоков вызовов
- 1.2. Простейший поток вызовов
- 1.3. Нестационарный пуассоновский поток
- 1.4. Поток с ограниченным последействием
- 1.5. Примитивный поток
- 1.6. Длительность обслуживания
- 1.7. Поток освобождений
- Контрольные вопросы
- 2. Характеристики качества обслуживания
- 2.1. Нагрузка и ее виды
- 2.2. Измерение интенсивности обслуженной нагрузки
- 2.3. Распределение интенсивности нагрузки по времени и ее измерение
- Контрольные вопросы
- 3. Виды систем передачи информации
- 3.1. Система с отказами при простейшем потоке вызовов
- 3.2. Система с отказами при примитивном потоке вызовов
- 3.3. Система с ожиданием при простейшем потоке вызовов
- 3.4. Система с ожиданием при примитивном потоке вызовов
- 3.5. Система смешанного типа при простейшем потоке вызовов
- Контрольные вопросы
- 4. Анализ коммутационных систем связи
- 4.1. Виды коммутационных систем
- 4.2. Комбинаторный метод Якобеуса для анализа коммутационных схем
- 4.3. Метод расчета потерь для многозвенных схем
- 4.4. Вычисление потерь методом вероятностных графов
- Контрольные вопросы
- 5. Анализ цифровых систем с пакетной коммутацией
- 5.1. Характеристики цифровых сетей
- 5.2. Анализ цифровых сетей с простейшим входным потоком и неограниченным объемом буфера
- 5.3. Анализ цифровых сетей с простейшим входным потоком и ограниченным объемом буфера
- 5.4. Анализ цифровых сетей с примитивным входным потоком
- 5.5. Анализ цифровых сетей с произвольным распределением времени обслуживания
- 5.6. Время доставки пакетов в сети с установлением соединения
- 5.7. Время доставки пакетов в сети без установления соединения
- Контрольные вопросы
- 6. Фрактальные модели трафика
- 6.1. Введение во фракталы
- 6.2. Самоподобные (фрактальные) случайные последовательности
- 6.3. Виды самоподобных случайных последовательностей
- 6.4. Система с самоподобным входным потоком и детерминированным временем обслуживания
- 6.5. Моделирование самоподобных случайных процессов
- 6.6. Анализ систем с самоподобным характером времени обслуживания
- Контрольные вопросы
- 7. Алгоритмы маршрутизации в сетях связи
- 7.1. Таблицы маршрутизации
- 7.2. Методы формирования плана распределения информации
- 7.3. Алгоритмы выбора исходящих линий связи
- 7.4. Определение средней задержки при передаче сообщений в сетях связи с пакетной коммутацией
- Контрольные вопросы
- Список литературы
