6.3. Виды самоподобных случайных последовательностей

Простым примером самоподобных случайных последовательностей может служить случайное движение точки, начиная с некоторого момента времени , когда она находилась в нуле. В каждые последующие моменты времени  ее координата меняется на произвольную случайную добавку . Тогда модель движения можно описать как

,

т.е. текущая координата определяется на основе предыдущей плюс случайное смещение. Если СВ  подчиняется нормальному закону распределения

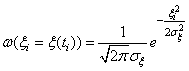
с нулевым математическим ожиданием и дисперсией , то формируемый процесс  будет представлять собой броуновское движение частицы (стохастический винеровский процесс).

Рассмотрим координату частицы  в момент времени . Величина  будет состоять из случайных добавок  в предшествующие моменты времени, т.е.

.

Следовательно, математическое ожидание координаты частицы

,

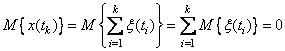а дисперсия

.

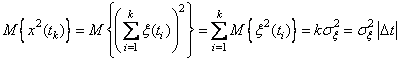Таким образом, при  математическое ожидание СВ  равно нулю, а дисперсия стремится к бесконечности. Кроме того, для любых двух моментов времени  и , дисперсия разности .

Так как процесс  представляет собой суммы гауссовских случайных величин и известную дисперсию для каждого момента времени , то можно записать ПРВ данной величины в виде

,

где  - координата или приращение координаты броуновской частицы (т.к. данный процесс в момент времени  равен нулю);  - интервал времени наблюдения.

Для того чтобы процесс  обладал свойством самоподобности, т.е. являлся фракталом, достаточно значение дисперсии  заменить на , где  - параметр Херста. Такая замена приводит к тому, что отсчеты стохастического броуновского движения становятся коррелированными между собой, т.е. . Следовательно, можно записать, что

.

Корреляция приращений  и  может быть определена как

В дискретном случае, когда величины  и  заменяются на  и  соответственно, получаем следующую корреляционную функцию для приращений фрактального броуновского движения

.

Последовательность случайных приращений с данной корреляционной функцией называется фрактальным гауссовским шумом. Причем коэффициент корреляции , при  и определяет долговременную зависимость между отсчетами случайного процесса. Корреляционная функция  отличается от гауссовских  и экспоненциальных  тем, что предполагает спад в корреляции при увеличении  заметно более медленный, что согласуется с результатами наблюдений интенсивностей в реальных трафиках с пакетной коммутацией. Кроме того, она полностью описывается только двумя параметрами – дисперсией и показателем .

Рассмотрим алгоритм моделирования фрактального броуновского движения (ФБД) на основе RMD-метода.

Шаг 1. Формируются два отсчета  и , причем  (по условию), а  - нормально распределенная случайная величина с нулевым МО и дисперсией  (рис. 6.3).

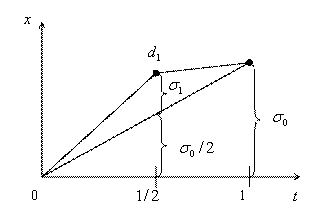
Рис. 6.3. Один шаг генерации ФБД

Шаг 2. На интервале от 0 до 1 берется центральный отсчет , который определяется как

,

где  - гауссовская СВ с нулевым МО и дисперсией выбранной так, чтобы дисперсия сформированного отсчета  была равна

.

Дисперсия линейной аппроксимации  равна , тогда можно записать

.

Шаг 3. Рассматриваются поочередно два интервала (0;1/2) и (1/2;1), в которых выделяются центральные отсчеты  и . Значения этих отсчетов формируются аналогично величине :

; ,

где  и  - гауссовские СВ с нулевым МО и дисперсией выбранной так, чтобы дисперсии сформированных отсчетов  и  удовлетворяли условию

.

Для отсчета  дисперсия линейной аппроксимации  равна , тогда можно записать

.

Аналогичное значение дисперсии сохраняется и для величины .

Шаг 4…. На данных шагах повторяются действия, описанные на 2 и третьем шагах. Причем для значений дисперсий случайных добавок  имеем следующую формулу

,