| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. Нестационарный пуассоновский поток
Если поток событий нестационарный, то
его основной характеристикой является мгновенная плотность ![]() . Мгновенной плотностью потока
называется предел отношения среднего числа событий, приходящихся на
элементарный участок времени
. Мгновенной плотностью потока
называется предел отношения среднего числа событий, приходящихся на
элементарный участок времени ![]() , к длине этого участка, когда последний
стремится к нулю:
, к длине этого участка, когда последний
стремится к нулю:
![]() ,
,
где ![]() -
математическое ожидание числа событий на участке
-
математическое ожидание числа событий на участке ![]() .
.
Рассмотрим поток однородных событий,
одинарный и без последействия, но не стационарный, с переменной плотностью ![]() . Такой поток называется
нестационарным пуассоновским потоком. Это первая ступень обобщения по сравнению
с простейшим потоком.
. Такой поток называется
нестационарным пуассоновским потоком. Это первая ступень обобщения по сравнению
с простейшим потоком.
Для такого потока число событий,
попадающих на участок длины ![]() , начинающийся в точке
, начинающийся в точке ![]() , подчиняется закону Пуассона:
, подчиняется закону Пуассона:
![]() ,
, ![]()
где ![]() -
математическое ожидание числа событий на участке от
-
математическое ожидание числа событий на участке от ![]() до
до ![]() , равное
, равное
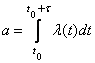 .
.
Анализ данного выражения показывает,
что величина ![]() зависит
не только от длины участка
зависит
не только от длины участка ![]() , но и от его положения на оси
, но и от его положения на оси ![]() .
.
Найдем для этого потока закон
распределения промежутка времени ![]() между соседними событиями. Допустим, что в
момент времени
между соседними событиями. Допустим, что в
момент времени ![]() появилось
событие (точка на числовой оси
появилось
событие (точка на числовой оси ![]() ). Тогда закон распределения времени
). Тогда закон распределения времени ![]() между этим событием и
следующим будет иметь вид
между этим событием и
следующим будет иметь вид
![]() ,
,
где ![]() -
вероятность того, что на участке времени от
-
вероятность того, что на участке времени от ![]() до
до ![]() не появится ни одного события:
не появится ни одного события:
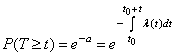 ,
, ![]() ,
,
откуда
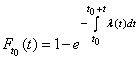 ,
, ![]() .
.
Дифференцируя данное выражение, найдем ПРВ
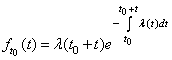 ,
, ![]() .
.
Полученный закон распределения уже не
будет показательным. Вид его зависит от параметра ![]() и вида функции
и вида функции ![]() . Например, при линейном
изменении
. Например, при линейном
изменении ![]() ,
ПРВ будет иметь вид
,
ПРВ будет иметь вид
![]() ,
, ![]() .
.
Несмотря на то, что структура
нестационарного пуассоновского потока несколько сложнее простейшего, он
остается удобным для практических применений: главное свойство простейшего
потока – отсутствие последействия – в нем сохранено. Это значит, что для
произвольной фиксированной точки ![]() закон распределения
закон распределения ![]() времени
времени ![]() не будет зависеть от того, что
происходило на участке времени
не будет зависеть от того, что
происходило на участке времени ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Потоки вызовов
- 1.1. Основные понятия потоков вызовов
- 1.2. Простейший поток вызовов
- 1.3. Нестационарный пуассоновский поток
- 1.4. Поток с ограниченным последействием
- 1.5. Примитивный поток
- 1.6. Длительность обслуживания
- 1.7. Поток освобождений
- Контрольные вопросы
- 2. Характеристики качества обслуживания
- 2.1. Нагрузка и ее виды
- 2.2. Измерение интенсивности обслуженной нагрузки
- 2.3. Распределение интенсивности нагрузки по времени и ее измерение
- Контрольные вопросы
- 3. Виды систем передачи информации
- 3.1. Система с отказами при простейшем потоке вызовов
- 3.2. Система с отказами при примитивном потоке вызовов
- 3.3. Система с ожиданием при простейшем потоке вызовов
- 3.4. Система с ожиданием при примитивном потоке вызовов
- 3.5. Система смешанного типа при простейшем потоке вызовов
- Контрольные вопросы
- 4. Анализ коммутационных систем связи
- 4.1. Виды коммутационных систем
- 4.2. Комбинаторный метод Якобеуса для анализа коммутационных схем
- 4.3. Метод расчета потерь для многозвенных схем
- 4.4. Вычисление потерь методом вероятностных графов
- Контрольные вопросы
- 5. Анализ цифровых систем с пакетной коммутацией
- 5.1. Характеристики цифровых сетей
- 5.2. Анализ цифровых сетей с простейшим входным потоком и неограниченным объемом буфера
- 5.3. Анализ цифровых сетей с простейшим входным потоком и ограниченным объемом буфера
- 5.4. Анализ цифровых сетей с примитивным входным потоком
- 5.5. Анализ цифровых сетей с произвольным распределением времени обслуживания
- 5.6. Время доставки пакетов в сети с установлением соединения
- 5.7. Время доставки пакетов в сети без установления соединения
- Контрольные вопросы
- 6. Фрактальные модели трафика
- 6.1. Введение во фракталы
- 6.2. Самоподобные (фрактальные) случайные последовательности
- 6.3. Виды самоподобных случайных последовательностей
- 6.4. Система с самоподобным входным потоком и детерминированным временем обслуживания
- 6.5. Моделирование самоподобных случайных процессов
- 6.6. Анализ систем с самоподобным характером времени обслуживания
- Контрольные вопросы
- 7. Алгоритмы маршрутизации в сетях связи
- 7.1. Таблицы маршрутизации
- 7.2. Методы формирования плана распределения информации
- 7.3. Алгоритмы выбора исходящих линий связи
- 7.4. Определение средней задержки при передаче сообщений в сетях связи с пакетной коммутацией
- Контрольные вопросы
- Список литературы
