| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4. Вычисление потерь методом вероятностных графов
Рассмотренные выше методы вычисления потерь удается применить для схем с небольшим числом звеньев. Действительно, если схема имеет, например, десять или более звеньев, то не всегда можно уверенно сказать какие типы потоков обслуживаются теми или иными промежуточными линиями. В таких случаях целесообразно применять другой способ вычисления потерь, который называется метод вероятностных графов.
Идея метода заключается в представлении коммутационной системы в виде графа, в котором вершины соответствуют коммутаторам, а ребра – промежуточным линиям. Вероятность занятости одной промежуточной линии полагают равной средней интенсивности заявок, прошедших через эту линию.
Рассмотрим
правила построения графов на примере трехзвенной схемы, представленной на
рис. 4.6. Будем считать, что число входов ![]() равно числу выходов
равно числу выходов ![]() коммутатора первого звена и
величина
коммутатора первого звена и
величина ![]() равна
числу коммутаторов второго звена. Причем каждый из
равна
числу коммутаторов второго звена. Причем каждый из ![]() выходов подключен к отдельному
коммутатору второго звена. Те же условия накладываем на связи между
коммутаторами второго и третьего звеньев.
выходов подключен к отдельному
коммутатору второго звена. Те же условия накладываем на связи между
коммутаторами второго и третьего звеньев.
Допустим, что на
вход ![]() такой
схемы приходит заявка. Она может поступить на один из
такой
схемы приходит заявка. Она может поступить на один из ![]() коммутаторов второго звена с
помощью промежуточной линии, которая обозначена ребром
коммутаторов второго звена с
помощью промежуточной линии, которая обозначена ребром ![]() (рис. 4.7). В случае
линейного искания (т.е. соединение входа с заданным выходом) соответствующий
выход
(рис. 4.7). В случае
линейного искания (т.е. соединение входа с заданным выходом) соответствующий
выход ![]() -го
коммутатора второго звена должен быть соединен с определенным коммутатором
-го
коммутатора второго звена должен быть соединен с определенным коммутатором ![]() третьего звена с
помощью промежуточной линии
третьего звена с
помощью промежуточной линии ![]() . И наконец, вход, на который поступил
вызов, должен быть соединен с заданным выходом
. И наконец, вход, на который поступил
вызов, должен быть соединен с заданным выходом ![]() , что соответствует звену
, что соответствует звену ![]() . Таким образом,
получаем следующий граф трехзвенной схемы для режима линейного искания
(рис. 4.7).
. Таким образом,
получаем следующий граф трехзвенной схемы для режима линейного искания
(рис. 4.7).
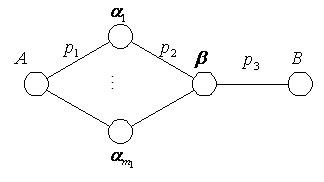
Рис. 4.7. Граф трехзвенной схемы для режима линейного искания
Через ![]() и
и ![]() обозначены вероятности занятости
занятости соответствующих ребер. Заметим, что вероятности
обозначены вероятности занятости
занятости соответствующих ребер. Заметим, что вероятности ![]() ,
, ![]() и
и ![]() соответствуют свободным состояниям
промежуточных линий. Используя данные обозначения, вероятность того, что два
звена
соответствуют свободным состояниям
промежуточных линий. Используя данные обозначения, вероятность того, что два
звена ![]() и
и ![]() будут свободными равна
будут свободными равна ![]() , а вероятность
занятости этих звеньев
, а вероятность
занятости этих звеньев ![]() . Так как в графе число таких звеньев равно
. Так как в графе число таких звеньев равно
![]() , то
вероятность возможности соединения между узлами
, то
вероятность возможности соединения между узлами ![]() и
и ![]() можно выразить с помощью формулы
можно выразить с помощью формулы
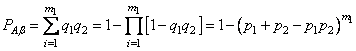 .
.
Соединение между
узлами ![]() и
и ![]() возможно при
одновременном возникновении двух событий: доступен узел
возможно при
одновременном возникновении двух событий: доступен узел ![]() и свободна промежуточная линия
и свободна промежуточная линия ![]() :
:
![]()
и общие потери определяются как
![]() .
.
Так как
вероятности ![]() и
и
![]() равны средним
интенсивностям потока заявок
равны средним
интенсивностям потока заявок ![]() ,
, ![]() и
и ![]() , то потери можно выразить непосредственно
через эти величины:
, то потери можно выразить непосредственно
через эти величины:
![]() .
.
Построим другой
граф данной трехзвенной схемы при тех же условиях, наложенные на связи между
звеньями системы, что и в предыдущем случае. Изменим только режим линейного
икания, при котором вход соединяется с одним из свободных выходов. Очевидно,
что ребра ![]() будут
иметь то же расположение что и ранее, а ребра между выходом
будут
иметь то же расположение что и ранее, а ребра между выходом ![]() -го коммутатора второго звена и
входом
-го коммутатора второго звена и
входом ![]() -го
коммутатора третьего звена будут иметь другую конфигурацию. Действительно,
вызов с выхода коммутатора второго звена, в случае группового искания, может
перейти на вход любого коммутатора третьего звена. Таким образом, получаем
множество вершин графа
-го
коммутатора третьего звена будут иметь другую конфигурацию. Действительно,
вызов с выхода коммутатора второго звена, в случае группового искания, может
перейти на вход любого коммутатора третьего звена. Таким образом, получаем
множество вершин графа ![]() , которые соединены с вершинами
, которые соединены с вершинами ![]() (рис. 4.8). Кроме
того, каждый из входов коммутатора третьего звена может быть соединен с любым
из
(рис. 4.8). Кроме
того, каждый из входов коммутатора третьего звена может быть соединен с любым
из ![]() выходов. В
результате получаем следующую схему графа трехзвенной системы для режима
группового искания (рис. 4.8).
выходов. В
результате получаем следующую схему графа трехзвенной системы для режима
группового искания (рис. 4.8).
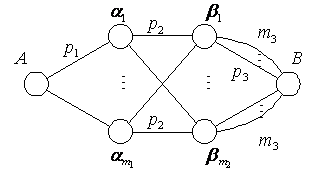
Рис. 4.8. Граф трехзвенной схемы для режима группового искания
Через ![]() и
и ![]() также обозначены вероятности
занятости соответствующих ребер, а дуги показывают возможность соединения входа
с любым из
также обозначены вероятности
занятости соответствующих ребер, а дуги показывают возможность соединения входа
с любым из ![]() выходов
коммутатора третьего звена. Вычислим потери между узлами
выходов
коммутатора третьего звена. Вычислим потери между узлами ![]() и
и ![]() при фиксированном узле
при фиксированном узле ![]() . Соединение между вершиной
. Соединение между вершиной ![]() и вершиной
и вершиной ![]() невозможно, если хотя
бы одно ребро
невозможно, если хотя
бы одно ребро ![]() или
или
![]() окажется
занятым. Учитывая, что вероятности занятия данных ребер
окажется
занятым. Учитывая, что вероятности занятия данных ребер ![]() и
и ![]() , описывающие совместные события, получаем
выражения для потерь между точками
, описывающие совместные события, получаем
выражения для потерь между точками ![]() и
и ![]() :
:
![]() ,
, ![]() .
.
Соответственно, вероятность занятости
одновременно ![]() узлов
узлов
![]() при
фиксированной вершине
при
фиксированной вершине ![]() равна
равна
![]() .
.
Так как число
коммутаторов второго звена равно ![]() , то общие потери между вершиной
, то общие потери между вершиной ![]() и
и ![]() вершинами
вершинами ![]() при разных
при разных ![]() , определяются по формуле
, определяются по формуле
![]() .
.
Потери для всей
системы возникают в случае, когда свободные ![]() входы не могут обеспечить связь с одним из
входы не могут обеспечить связь с одним из
![]() выходов
соответствующих коммутаторов третьего звена. Вероятность занятости всех выходов
одного коммутатора равна
выходов
соответствующих коммутаторов третьего звена. Вероятность занятости всех выходов
одного коммутатора равна ![]() , тогда вероятность занятости ОП
, тогда вероятность занятости ОП ![]() коммутаторов составляет
величину
коммутаторов составляет
величину ![]() .
Используя формулу Бернулли, можно записать вероятность занятости
.
Используя формулу Бернулли, можно записать вероятность занятости ![]() выходов коммутаторов
второго звена:
выходов коммутаторов
второго звена:
![]()
и общие потери выражаются формулой
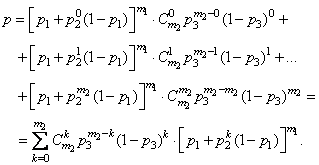
Если
вместо вероятностей ![]() и
и
![]() подставить
величины
подставить
величины ![]() ,
, ![]() и
и ![]() , то потери можно записать в виде
, то потери можно записать в виде
![]() .
.
Аналогично вычисляются потери и для схем с большим числом звеньев, при этом не требуется знания о типах потока заявок поступающего на вход системы, а также внутри нее. Это позволяет значительно упростить анализ схем и расчета вероятностей потерь.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Потоки вызовов
- 1.1. Основные понятия потоков вызовов
- 1.2. Простейший поток вызовов
- 1.3. Нестационарный пуассоновский поток
- 1.4. Поток с ограниченным последействием
- 1.5. Примитивный поток
- 1.6. Длительность обслуживания
- 1.7. Поток освобождений
- Контрольные вопросы
- 2. Характеристики качества обслуживания
- 2.1. Нагрузка и ее виды
- 2.2. Измерение интенсивности обслуженной нагрузки
- 2.3. Распределение интенсивности нагрузки по времени и ее измерение
- Контрольные вопросы
- 3. Виды систем передачи информации
- 3.1. Система с отказами при простейшем потоке вызовов
- 3.2. Система с отказами при примитивном потоке вызовов
- 3.3. Система с ожиданием при простейшем потоке вызовов
- 3.4. Система с ожиданием при примитивном потоке вызовов
- 3.5. Система смешанного типа при простейшем потоке вызовов
- Контрольные вопросы
- 4. Анализ коммутационных систем связи
- 4.1. Виды коммутационных систем
- 4.2. Комбинаторный метод Якобеуса для анализа коммутационных схем
- 4.3. Метод расчета потерь для многозвенных схем
- 4.4. Вычисление потерь методом вероятностных графов
- Контрольные вопросы
- 5. Анализ цифровых систем с пакетной коммутацией
- 5.1. Характеристики цифровых сетей
- 5.2. Анализ цифровых сетей с простейшим входным потоком и неограниченным объемом буфера
- 5.3. Анализ цифровых сетей с простейшим входным потоком и ограниченным объемом буфера
- 5.4. Анализ цифровых сетей с примитивным входным потоком
- 5.5. Анализ цифровых сетей с произвольным распределением времени обслуживания
- 5.6. Время доставки пакетов в сети с установлением соединения
- 5.7. Время доставки пакетов в сети без установления соединения
- Контрольные вопросы
- 6. Фрактальные модели трафика
- 6.1. Введение во фракталы
- 6.2. Самоподобные (фрактальные) случайные последовательности
- 6.3. Виды самоподобных случайных последовательностей
- 6.4. Система с самоподобным входным потоком и детерминированным временем обслуживания
- 6.5. Моделирование самоподобных случайных процессов
- 6.6. Анализ систем с самоподобным характером времени обслуживания
- Контрольные вопросы
- 7. Алгоритмы маршрутизации в сетях связи
- 7.1. Таблицы маршрутизации
- 7.2. Методы формирования плана распределения информации
- 7.3. Алгоритмы выбора исходящих линий связи
- 7.4. Определение средней задержки при передаче сообщений в сетях связи с пакетной коммутацией
- Контрольные вопросы
- Список литературы
