1.4. Поток с ограниченным последействием

Ординарный поток событий называется потоком с ограниченным последействием (потоком Пальма), если промежутки времени между соседними событиями , ,… представляют собой независимые СВ.

Очевидно, простейший поток является частным случаем потока Пальма. Обычно потоки Пальма получаются в виде выходных процессов систем распределения информации.

Основной в теории выходных потоков является теорема Пальма, которая звучит следующим образом. Пусть на систему распределения информации поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ. Если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок является потоком типа Пальма.

В частности, если входной поток заявок будет простейшим, то поток необслуженных, не будучи простейшим, будет все же иметь ограниченное последействие.

Рассмотрим один из типов потоков с ограниченным последействием, потоки Эрланга. Они образуются «просеиванием» простейшего потока. Если, например, из простейшего потока выбросить каждую вторую точку, то оставшиеся точки образуют поток Эрланга 1-го порядка. В то же время этот поток есть поток Пальма: поскольку независимы промежутки между событиями в простейшем потоке, то независимы и величины , ,…, получающиеся суммированием таких промежутков по два.

В общем случае, потоком Эрланга -го порядка называется поток, получаемый из простейшего, если сохранить в нем каждую  точку, а оставшиеся выбросить.

Найдем закон распределения промежутка времени  между соседними событиями в потоке Эрланга -го порядка. Рассмотрим на оси  простейший поток с интервалами , ,… (рис. 1.5).

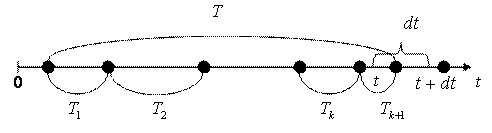
Рис. 1.5. Расположение заявок в простейшем потоке

Величина  представляет собой сумму  независимых СВ:

,

где  - независимая СВ, подчиненная экспоненциальному закону распределения

, .

Обозначим через  ПРВ величины  для потока . Вероятность того, что СВ  попадет в интервал , равна . Это значит, что последняя точка промежутка должна попасть на данный элементарный участок, а предыдущие  точек на участок . Вероятность первого события равна ; вероятность второго

, .

Перемножая данные вероятности, получим следующий закон распределения величины :

, ,

откуда

, .

Математическое ожидание потока  определяется выражением

,

где  - математическое ожидание промежутка между соседними событиями в простейшем потоке. Дисперсия потока Эрланга -го порядка определяется по формуле

; .