| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.4. Определение средней задержки при передаче сообщений в сетях связи с пакетной коммутацией
Рассмотрим
простую сеть связи, в которой имеется несколько УК соединенные между собой
дуплексными соединительными линиями с пропускной способностью ![]() байт/сек. между
байт/сек. между ![]() и
и ![]() узлами (рис. 7.8). Если
линия связи между узлами
узлами (рис. 7.8). Если
линия связи между узлами ![]() и
и ![]() отсутствует, то
отсутствует, то ![]() .
.
Каждый
УК имеет буфер неограниченной емкости. Среднюю длину пакета положим равной ![]() байт. Также для
простоты будем полагать, что поток данных, возникающий в узле
байт. Также для
простоты будем полагать, что поток данных, возникающий в узле ![]() и предназначенный узлу
и предназначенный узлу ![]() , является простейшим со
средней интенсивностью
, является простейшим со
средней интенсивностью ![]() пакетов/сек. Соответственно, полная
средняя интенсивность трафика в сети определяется по формуле
пакетов/сек. Соответственно, полная
средняя интенсивность трафика в сети определяется по формуле
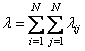 ,
,
где ![]() - общее число УК. Величины
- общее число УК. Величины ![]() считаются известными,
т.к. их можно либо измерить, если сеть находится в режиме эксплуатации, либо
оценить путем моделирования. Действительно, при эксплуатации сети для каждого
узла
считаются известными,
т.к. их можно либо измерить, если сеть находится в режиме эксплуатации, либо
оценить путем моделирования. Действительно, при эксплуатации сети для каждого
узла ![]() можно
подсчитать число переданных сообщений
можно
подсчитать число переданных сообщений ![]() узлу
узлу ![]() за время наблюдения
за время наблюдения ![]() сек. Тогда оценка интенсивности
определяется как
сек. Тогда оценка интенсивности
определяется как ![]() .
.
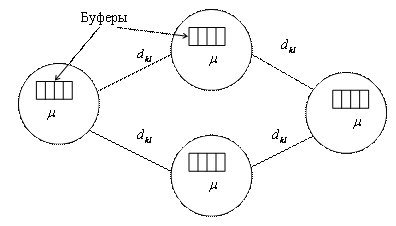
Рис. 7.8. Упрощенная схема сети связи
Так
как пакеты из узла ![]() в
узел
в
узел ![]() могут
передаваться разными маршрутами, то средняя интенсивность использования канала
не равна в точности
могут
передаваться разными маршрутами, то средняя интенсивность использования канала
не равна в точности ![]() .
Однако, зная коэффициенты использования той или иной линии связи, можно
определить данную характеристику по формуле
.
Однако, зная коэффициенты использования той или иной линии связи, можно
определить данную характеристику по формуле
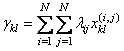 ,
,
где ![]() - доля потока
- доля потока ![]() , проходящая по линии
, проходящая по линии ![]() . Величины
. Величины ![]() подобны весовым
коэффициентам
подобны весовым
коэффициентам ![]() в
игровом методе построения ПРИ и выбора маршрутов. Основное их отличие
заключается в том, что они являются характеристикой потока строго заданного
маршрута между узлами
в
игровом методе построения ПРИ и выбора маршрутов. Основное их отличие
заключается в том, что они являются характеристикой потока строго заданного
маршрута между узлами ![]() и
и
![]() , в то время
как весовые коэффициенты характеризуют распространение потока в целом, не
привязываясь к конкретному маршруту. Поэтому величины
, в то время
как весовые коэффициенты характеризуют распространение потока в целом, не
привязываясь к конкретному маршруту. Поэтому величины ![]() дают более полную информацию о
сети связи и могут быть определены экспериментально подобно коэффициентам
дают более полную информацию о
сети связи и могут быть определены экспериментально подобно коэффициентам ![]() .
.
Важной
характеристикой качества функционирования сети является среднее время ![]() доставки пакета,
которая определяется как математическое ожидание от временных задержек
доставки пакета,
которая определяется как математическое ожидание от временных задержек ![]() доставки пакетов между
узлами
доставки пакетов между
узлами ![]() и
и ![]() :
:
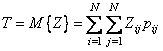 ,
,
где ![]() - вероятность передачи сообщения
от узла
- вероятность передачи сообщения
от узла ![]() к узлу
к узлу
![]() . Данную вероятность
можно выразить через интенсивность потоков
. Данную вероятность
можно выразить через интенсивность потоков ![]() , если предварительно выполнить их
нормировку, т.е.
, если предварительно выполнить их
нормировку, т.е.
![]() .
.
Тогда выражение для средней задержки пакета в сети можно записать в виде
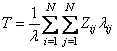 .
.
Применение формулы Литтла к данному выражению приводит к общему, и в то же время чрезвычайно простому результату, впервые полученному Л. Клейнроком [9]:
![]() ,
,
где ![]() - среднее время пребывания
сообщений в линии.
- среднее время пребывания
сообщений в линии.
В
общем случае получить аналитические выражения для ![]() невозможно, однако, учитывая сделанные
предположения о пуассоновском потоке заявок, каждую линию связи можно
рассмотреть как независимую цифровую систему типа M/M/1 и
воспользоваться ранее выведенной формулой для определения среднего времени
нахождения пакета в системе:
невозможно, однако, учитывая сделанные
предположения о пуассоновском потоке заявок, каждую линию связи можно
рассмотреть как независимую цифровую систему типа M/M/1 и
воспользоваться ранее выведенной формулой для определения среднего времени
нахождения пакета в системе:
![]() ,
,
где ![]() - среднее время передачи пакета
по каналу
- среднее время передачи пакета
по каналу ![]() ;
; ![]() - среднее время
пребывания пакета в буфере. Величина нагрузки в данном случае определяется как
- среднее время
пребывания пакета в буфере. Величина нагрузки в данном случае определяется как ![]() . Таким образом,
получаем следующее выражение для среднего времени пребывания пакета в системе:
. Таким образом,
получаем следующее выражение для среднего времени пребывания пакета в системе:
![]()
и приходим к окончательной формуле для вычисления средней задержки передачи пакета в цифровой системе:
![]() .
.
Полученное
выражение для средней задержки пакета в сети связи позволяет поставить обратную
задачу: найти величины ![]() , при которых средняя задержка
, при которых средняя задержка ![]() минимальна. Причем на
основе вычисленных величин
минимальна. Причем на
основе вычисленных величин ![]() можно сформировать матрицы весовых
коэффициентов
можно сформировать матрицы весовых
коэффициентов ![]() ,
используемые в игровом методе при формировании маршрутов движения заявок. К
сожалению, на сегодняшний день отсутствует общее решение данной задачи, но
известны ее частные решения, которые можно найти в работе [10].
,
используемые в игровом методе при формировании маршрутов движения заявок. К
сожалению, на сегодняшний день отсутствует общее решение данной задачи, но
известны ее частные решения, которые можно найти в работе [10].
| << Предыдущий параграф | Следующий параграф >> |
- 1. Потоки вызовов
- 1.1. Основные понятия потоков вызовов
- 1.2. Простейший поток вызовов
- 1.3. Нестационарный пуассоновский поток
- 1.4. Поток с ограниченным последействием
- 1.5. Примитивный поток
- 1.6. Длительность обслуживания
- 1.7. Поток освобождений
- Контрольные вопросы
- 2. Характеристики качества обслуживания
- 2.1. Нагрузка и ее виды
- 2.2. Измерение интенсивности обслуженной нагрузки
- 2.3. Распределение интенсивности нагрузки по времени и ее измерение
- Контрольные вопросы
- 3. Виды систем передачи информации
- 3.1. Система с отказами при простейшем потоке вызовов
- 3.2. Система с отказами при примитивном потоке вызовов
- 3.3. Система с ожиданием при простейшем потоке вызовов
- 3.4. Система с ожиданием при примитивном потоке вызовов
- 3.5. Система смешанного типа при простейшем потоке вызовов
- Контрольные вопросы
- 4. Анализ коммутационных систем связи
- 4.1. Виды коммутационных систем
- 4.2. Комбинаторный метод Якобеуса для анализа коммутационных схем
- 4.3. Метод расчета потерь для многозвенных схем
- 4.4. Вычисление потерь методом вероятностных графов
- Контрольные вопросы
- 5. Анализ цифровых систем с пакетной коммутацией
- 5.1. Характеристики цифровых сетей
- 5.2. Анализ цифровых сетей с простейшим входным потоком и неограниченным объемом буфера
- 5.3. Анализ цифровых сетей с простейшим входным потоком и ограниченным объемом буфера
- 5.4. Анализ цифровых сетей с примитивным входным потоком
- 5.5. Анализ цифровых сетей с произвольным распределением времени обслуживания
- 5.6. Время доставки пакетов в сети с установлением соединения
- 5.7. Время доставки пакетов в сети без установления соединения
- Контрольные вопросы
- 6. Фрактальные модели трафика
- 6.1. Введение во фракталы
- 6.2. Самоподобные (фрактальные) случайные последовательности
- 6.3. Виды самоподобных случайных последовательностей
- 6.4. Система с самоподобным входным потоком и детерминированным временем обслуживания
- 6.5. Моделирование самоподобных случайных процессов
- 6.6. Анализ систем с самоподобным характером времени обслуживания
- Контрольные вопросы
- 7. Алгоритмы маршрутизации в сетях связи
- 7.1. Таблицы маршрутизации
- 7.2. Методы формирования плана распределения информации
- 7.3. Алгоритмы выбора исходящих линий связи
- 7.4. Определение средней задержки при передаче сообщений в сетях связи с пакетной коммутацией
- Контрольные вопросы
- Список литературы
