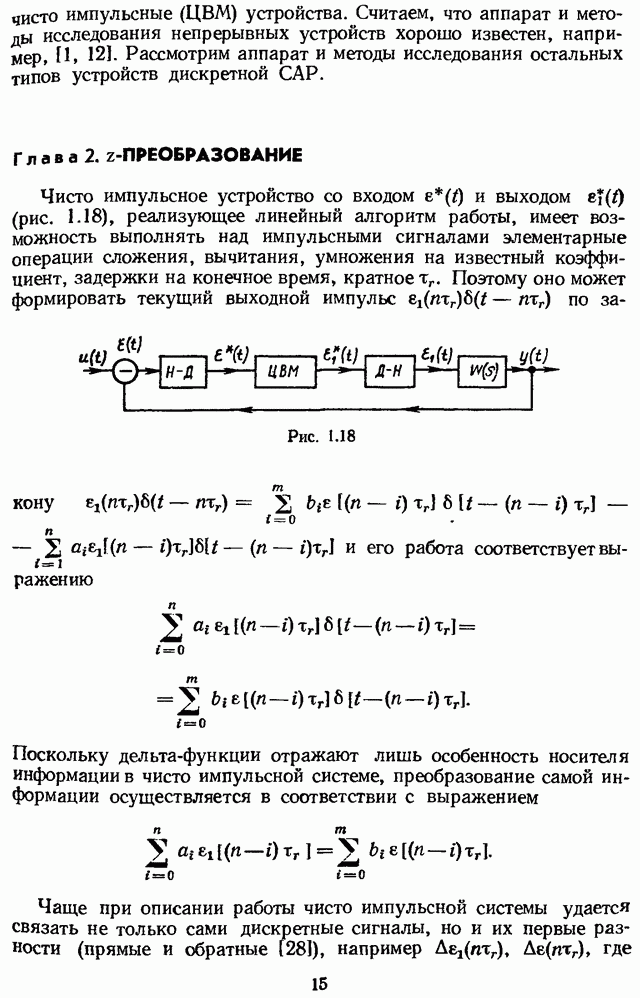
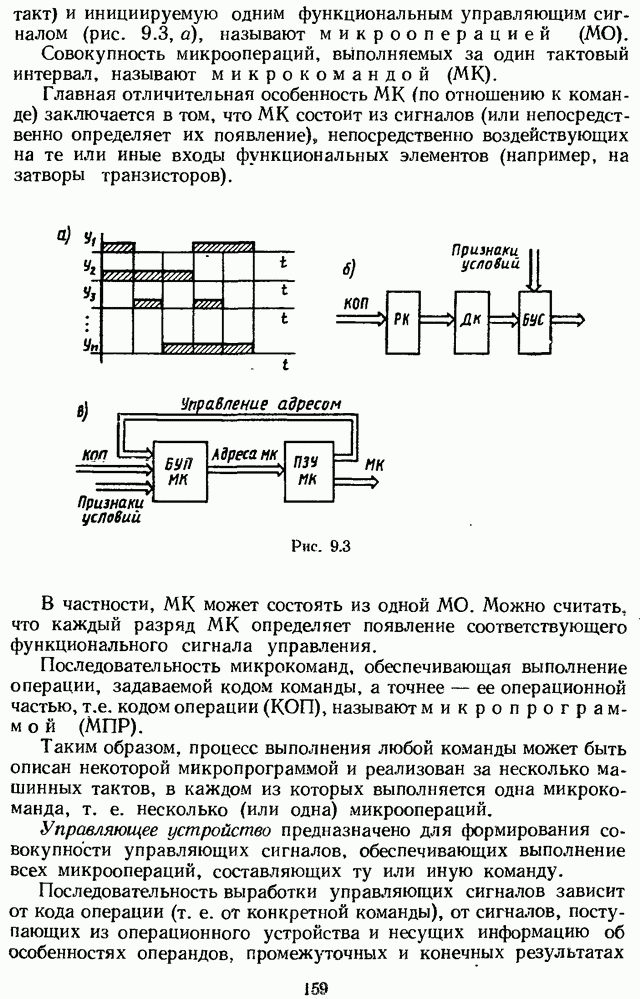
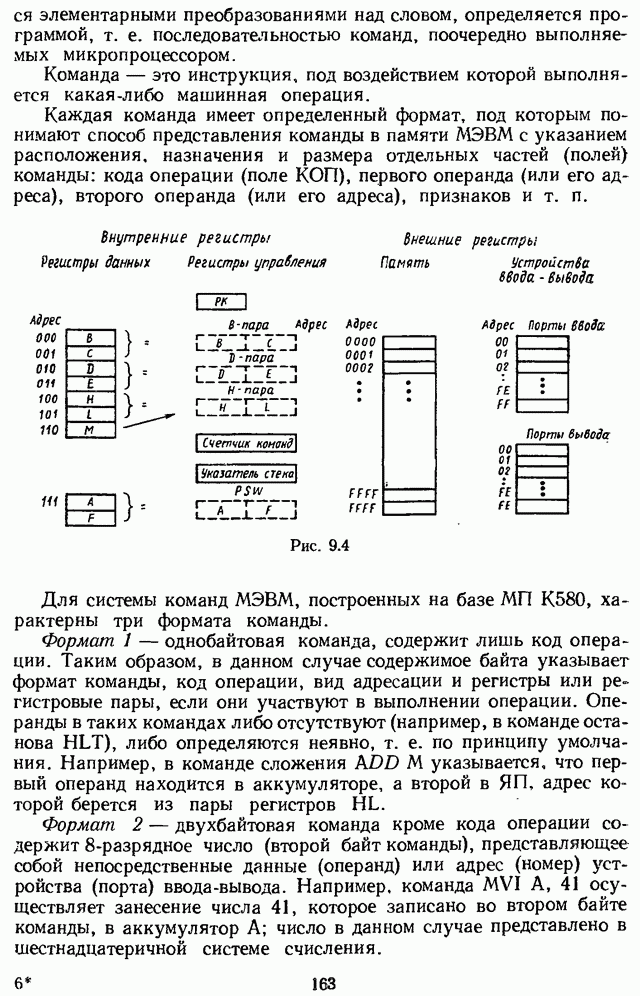
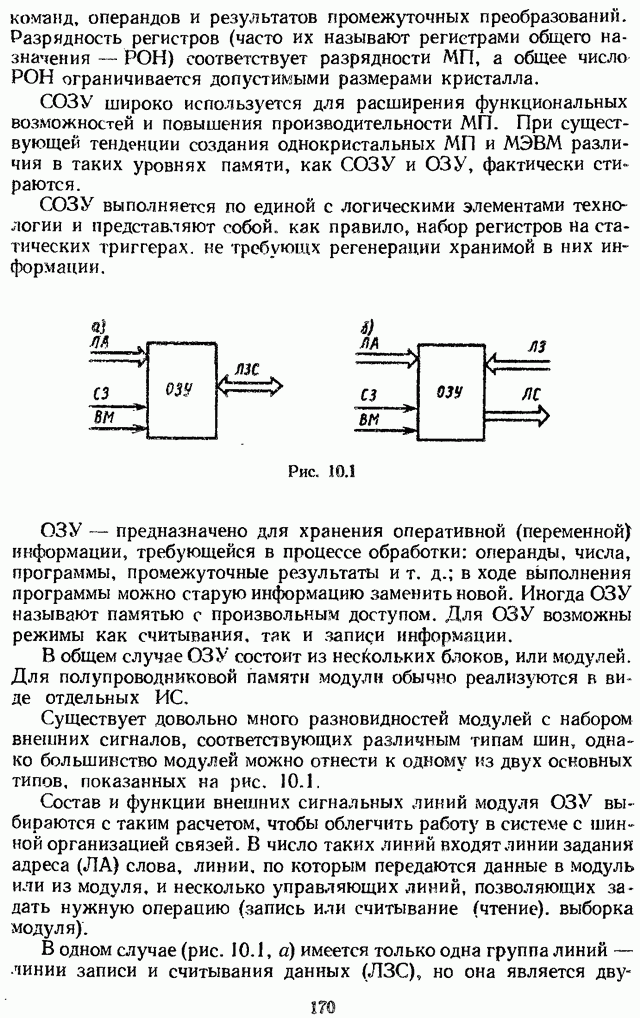
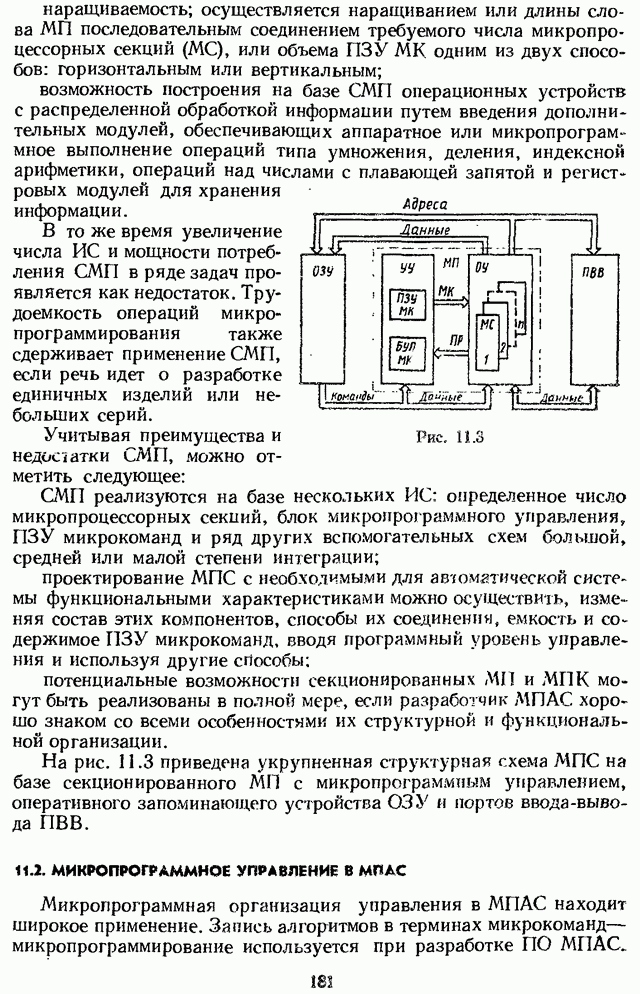
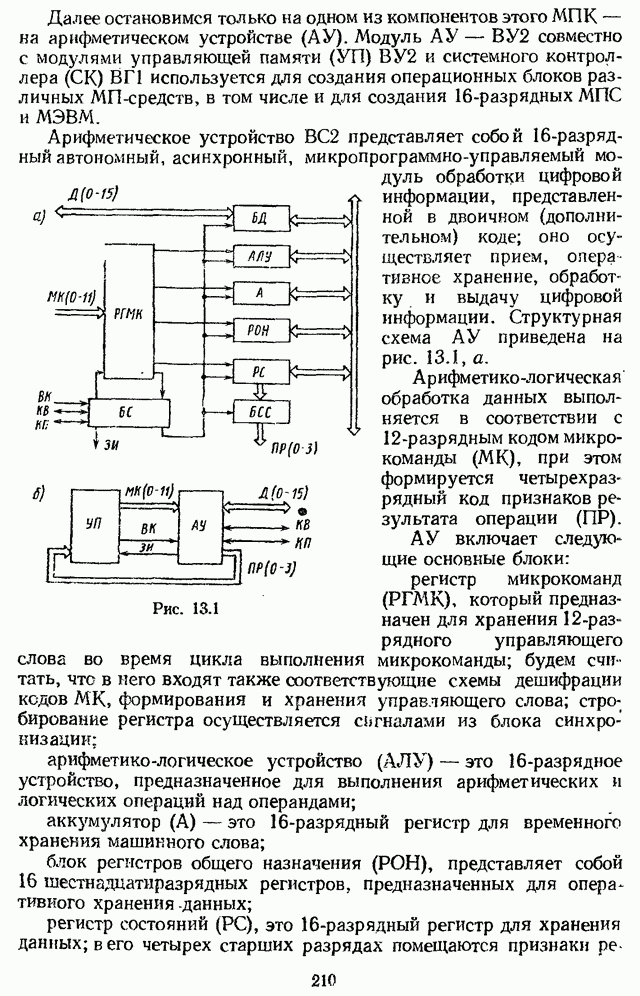
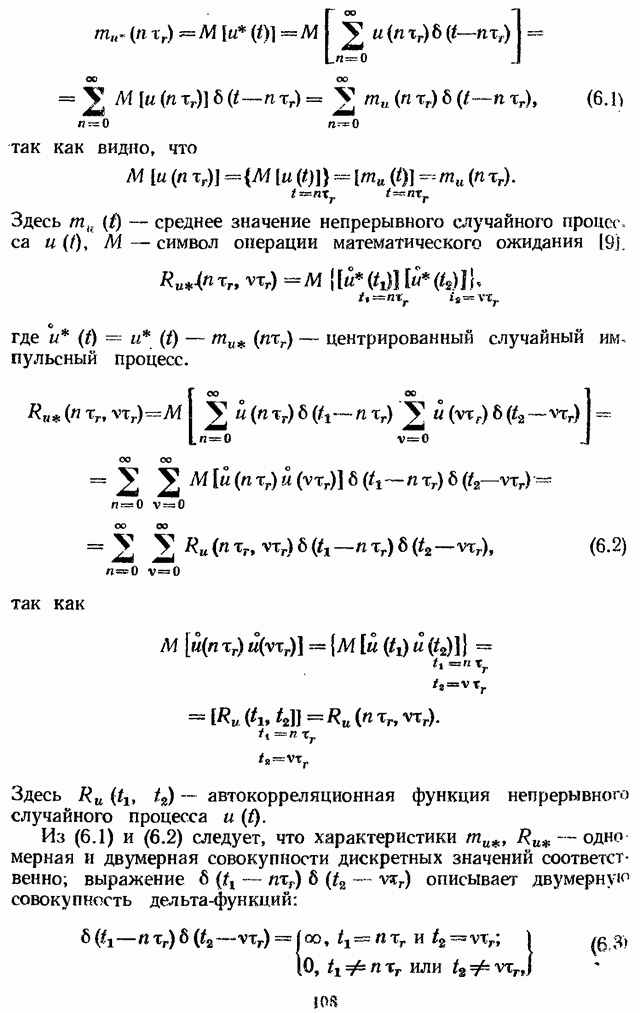| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
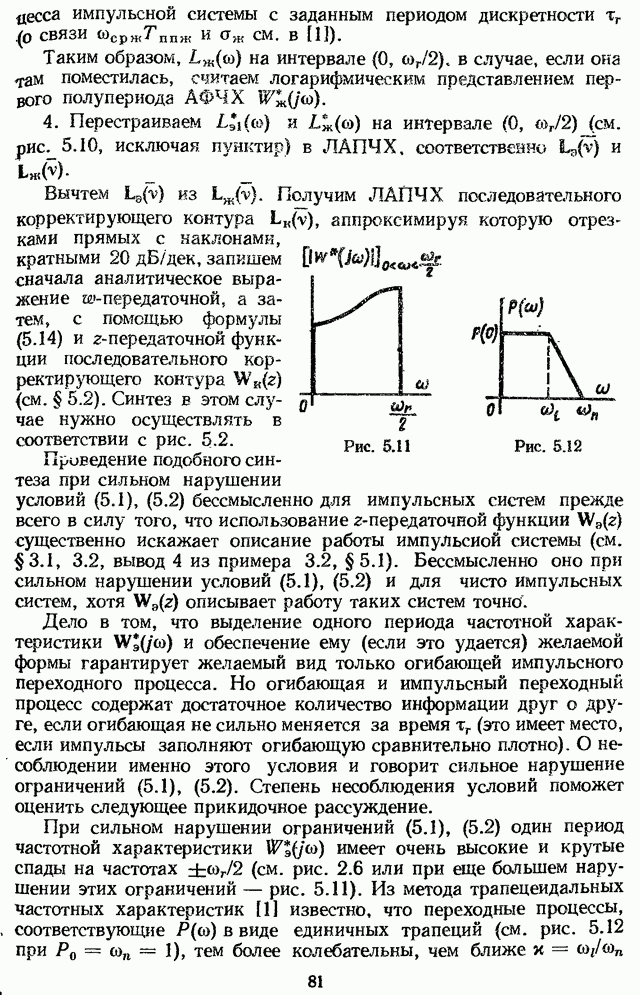
2.2. ВЫЧИСЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА СИГНАЛА ПО ЕГО ОБЫЧНОМУ ПРЕОБРАЗОВАНИЮ ЛАПЛАСА
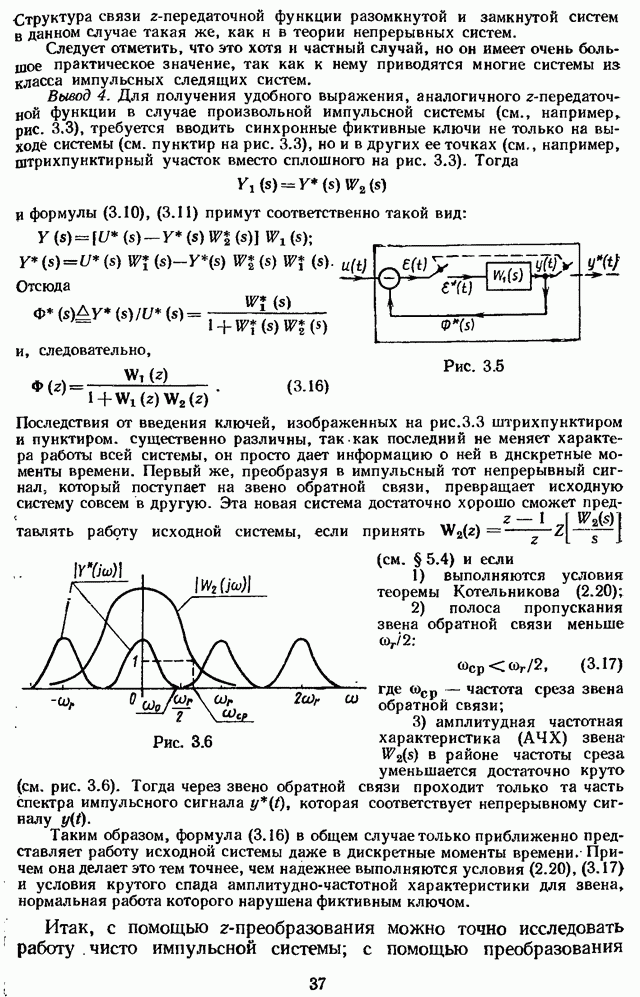
Работу ключа при условии, когда справедлива формула (1.2), рассматривают иногда как работу модулятора М, в котором входной сигнал u(t) модулирует по площади сигнал  , представляющий собой периодическую (с периодом
, представляющий собой периодическую (с периодом  ) последовательность дельта-функций единичной площади (рис. 2.1). (Сигнал
) последовательность дельта-функций единичной площади (рис. 2.1). (Сигнал  ) является опорным сигналом модулятора.) Таким образом,
) является опорным сигналом модулятора.) Таким образом,

Так как r(t) — линейная комбинация смещенных дельта-функций, то ей соответствует преобразование Лапласа  , абсцисса сходимости
, абсцисса сходимости  которой равна нулю:
которой равна нулю:


Рис. 2.1
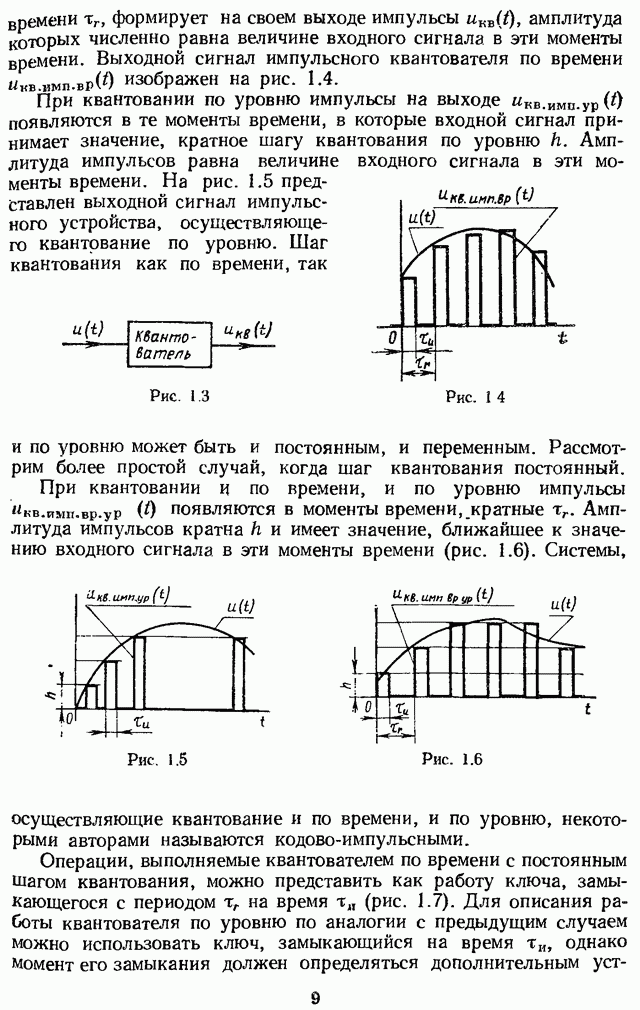
С учетом теоремы запаздывания  получена здесь в незамкнутом математическом виде — в виде суммы бесконечного ряда, но этот ряд является геометрической прогрессией с первым членом
получена здесь в незамкнутом математическом виде — в виде суммы бесконечного ряда, но этот ряд является геометрической прогрессией с первым членом  и знаменателем
и знаменателем  Поэтому
Поэтому  можно представить в замкнутом виде:
можно представить в замкнутом виде:

Выполним над левой и правой частями (2.3) преобразование Лапласа

С учетом (2.1) и теоремы свертки в области комплексной переменной имеем

где

— абсцисса сходимости произведения  — абсциссы сходимости соответственно функций
— абсциссы сходимости соответственно функций  . В (2.6) зафиксировано, что это соотношение справедливо лишь для тех значений s, вещественная часть которых больше
. В (2.6) зафиксировано, что это соотношение справедливо лишь для тех значений s, вещественная часть которых больше

Рис. 2.2
Из (2.6) с учетом того, что  существует [см. (2.5)], следует: дискретное преобразование Лапласа имеет место для всех таких функций
существует [см. (2.5)], следует: дискретное преобразование Лапласа имеет место для всех таких функций  ), для которых существует обычное преобразование Лапласа
), для которых существует обычное преобразование Лапласа 
Замечание 2.2.1. Поскольку нас интересует главным образом исследование процессов в устойчивых системах, считаем, что функция  описывает сходящийся процесс, и поэтому ее абсцисса сходимости
описывает сходящийся процесс, и поэтому ее абсцисса сходимости  .
.
С учетом (2.4), (2.5), (2.7) выражение (2.6) примет вид

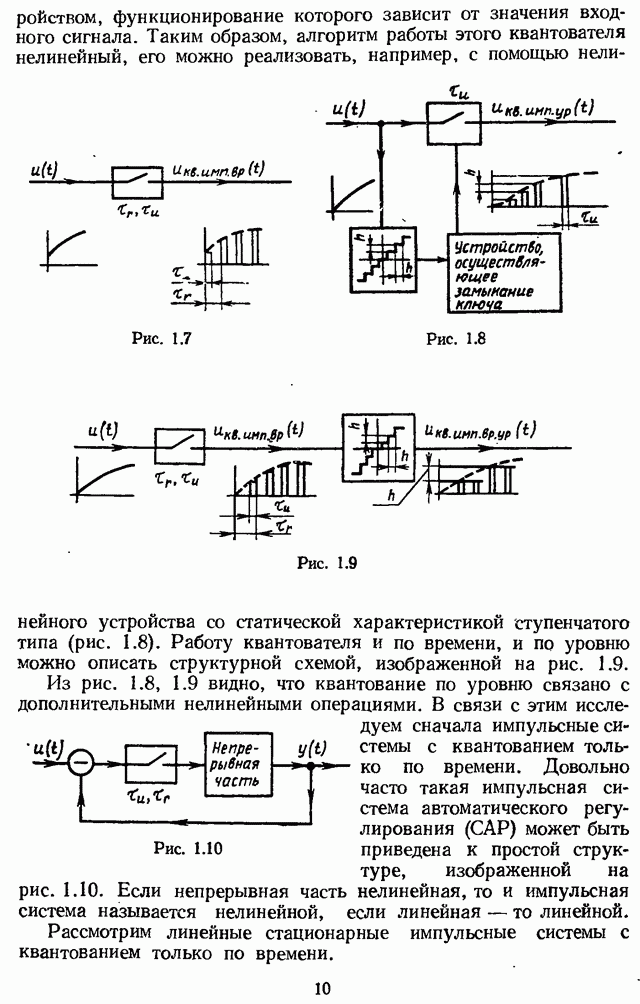
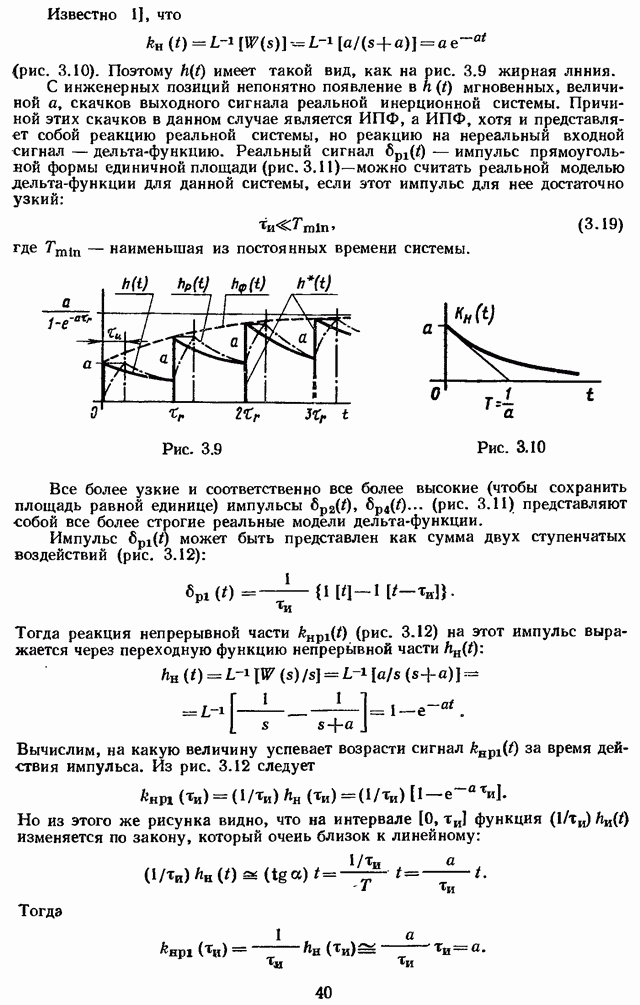
Соотношение (2.8), интегрирование в котором ведется вдоль мнимой оси плоскости независимой комплексной переменной (рис. 2.2), можно выразить либо через интеграл по замкнутому контуру  образованному путем добавления к мнимой оси дуги
образованному путем добавления к мнимой оси дуги  бесконечно большого радиуса, находящейся в левой полуплоскости (см. пунктир на рис. 2.2):
бесконечно большого радиуса, находящейся в левой полуплоскости (см. пунктир на рис. 2.2):

либо через интеграл по замкнутому контуру  , образованному добавлением к мнимой оси дуги
, образованному добавлением к мнимой оси дуги  бесконечно большого радиуса, находящейся в правой полуплоскости (см. штрихпунктир на рис. 2.2):
бесконечно большого радиуса, находящейся в правой полуплоскости (см. штрихпунктир на рис. 2.2):

Замечание 2.2.2. Интеграл по дуге  бесконечно большого радиуса равен нулю, еслн бесконечность представляет собой для подынтегрального выражения ноль, по крайней мере второго порядка [4, с. 207].
бесконечно большого радиуса равен нулю, еслн бесконечность представляет собой для подынтегрального выражения ноль, по крайней мере второго порядка [4, с. 207].
Ниже будет показано, что в нашем случае бесконечность является нулем бесконечного порядка. Поэтому тем более

Представив  через интеграл по замкнутому контуру, имеем возможность вычислить
через интеграл по замкнутому контуру, имеем возможность вычислить  по теореме Коши как сумму вычетов
по теореме Коши как сумму вычетов  подынтегрального выражения в его полюсах, расположенных внутри контура интегрирования, который не должен содержать на себе особенностей подынтегрального выражения. Из (2.9), (2.10) соответственно имеем
подынтегрального выражения в его полюсах, расположенных внутри контура интегрирования, который не должен содержать на себе особенностей подынтегрального выражения. Из (2.9), (2.10) соответственно имеем

где  — полюсы подынтегрального выражения в левой полуплоскости (ЛПП) плоскости
— полюсы подынтегрального выражения в левой полуплоскости (ЛПП) плоскости  — полюсы подынтегрального выражения в правой полуплоскости (ППП) плоскости s, так как контур охватывает всю ЛПП, а контур
— полюсы подынтегрального выражения в правой полуплоскости (ППП) плоскости s, так как контур охватывает всю ЛПП, а контур  — всю ППП плоскости s. Знак минус перед суммой в (2.12) следствие того, что контур
— всю ППП плоскости s. Знак минус перед суммой в (2.12) следствие того, что контур  обходится по часовой стрелке (в отрицательном направлении).
обходится по часовой стрелке (в отрицательном направлении).
Полюсами подынтегрального выражения являются корни уравнения

(нули функции из знаменателя подынтегрального выражения).
Так как единицу на плоскости К представляет вектор  , то уравнение (2.13) приводим к виду
, то уравнение (2.13) приводим к виду 
Следовательно,  откуда корни (2.13) равны:
откуда корни (2.13) равны:

где  — постоянное число, имеющее размерность круговой частоты. Оно играет далее роль шага на оси частот. Этот шагсоответ ствует шагу квантования
— постоянное число, имеющее размерность круговой частоты. Оно играет далее роль шага на оси частот. Этот шагсоответ ствует шагу квантования  по оси времени.
по оси времени.
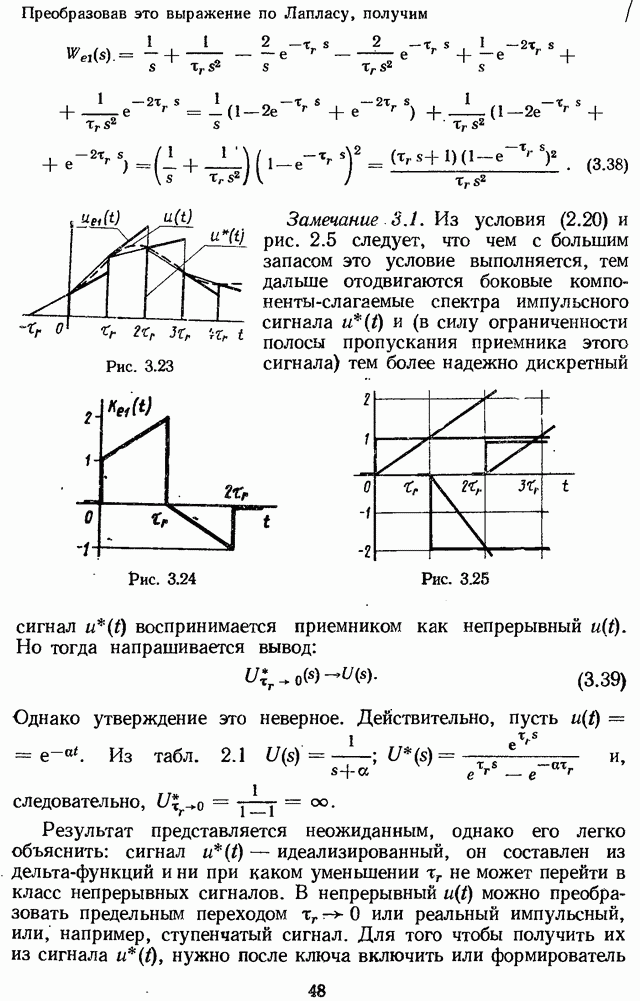
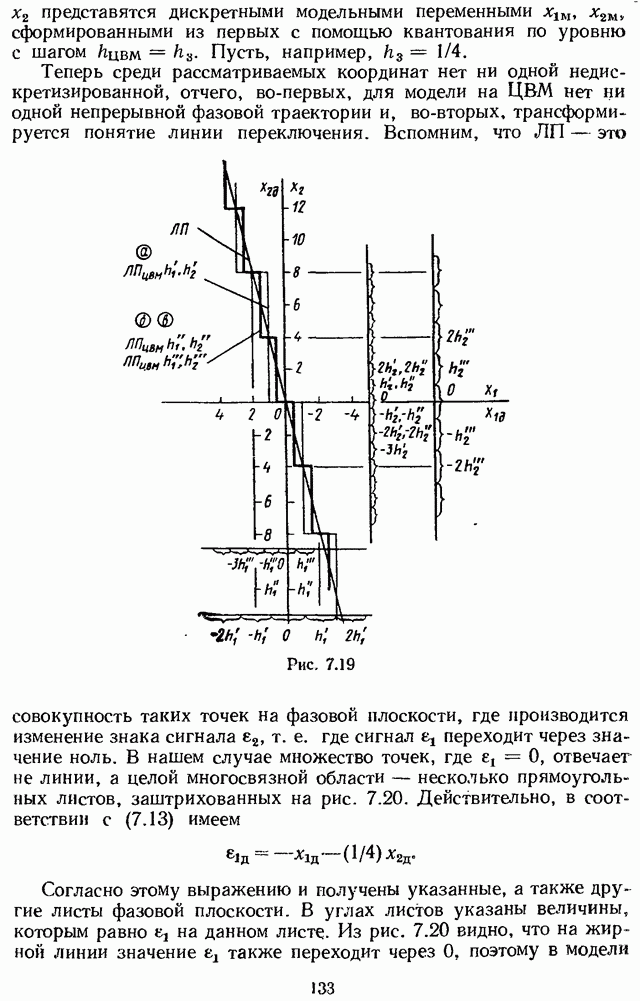
Рассмотрев выражение (2.14), нетрудно заметить следующее.
Следствие 1. Подынтегральное выражение имеет из-за функции в его знаменателе бесконечное число полюсов, и все они простые.
Следствие 2. Если  , то
, то  поскольку s в (2.9)...(2.13) таково, что
поскольку s в (2.9)...(2.13) таково, что  , все полюсы подынтегрального выражения из-за его функции в знаменателе оказываются расположенными только в ППП плоскости s.
, все полюсы подынтегрального выражения из-за его функции в знаменателе оказываются расположенными только в ППП плоскости s.
Следствие 3. Так как  — корнн функции
— корнн функции  , то можно записать:
, то можно записать:

Отсюда видно, что  действительно является для подынтегрального выражения нулем бесконечного порядка, т. е. представление (2.8) в форме (2.9), (2.10) справедливо (см. замечание 2.2).
действительно является для подынтегрального выражения нулем бесконечного порядка, т. е. представление (2.8) в форме (2.9), (2.10) справедливо (см. замечание 2.2).
Функция  как правило, представляет собой дробно-рациональное выражение
как правило, представляет собой дробно-рациональное выражение  , где
, где  — полиномы соответственно порядка
— полиномы соответственно порядка  . Следовательно, полюсами подынтегрального выражения являются еще и полюсы
. Следовательно, полюсами подынтегрального выражения являются еще и полюсы  функции
функции  (нули полинома
(нули полинома  ), которые все расположены в ЛПП плоскости s, поскольку
), которые все расположены в ЛПП плоскости s, поскольку  (см. замечание 2.1).
(см. замечание 2.1).
Используя последнее замечание и следствие 2 из (2.14), можно провести следующие преобразования:
а) выражение (2.11):

где  — полюсы функции
— полюсы функции  так как в ЛПП расположены только полюсы
так как в ЛПП расположены только полюсы  и только они;
и только они;
б) выражение (2.12):

где  — нули функции
— нули функции  так как в ППП расположены полюсы подынтегрального выражения, которые определяются его знаменателем, и только они.
так как в ППП расположены полюсы подынтегрального выражения, которые определяются его знаменателем, и только они.
Из теории функций комплексной переменной 14, с. 2061 известно, что если функция представляет собой дробно-рациональное выражение  с простыми
с простыми  полюсами, то вычеты в ее полюсах вычисляются по формуле
полюсами, то вычеты в ее полюсах вычисляются по формуле

где

Этот факт как раз имеет место для (2.17) [см. следствие 1 из (2.14)], причем здесь

Поэтому

Но с учетом (2.15) имеем  что на плоскости
что на плоскости  изображается точкой
изображается точкой  . Поэтому
. Поэтому  в силу чего с учетом (2.14) выражение (2.17) принимает вид
в силу чего с учетом (2.14) выражение (2.17) принимает вид

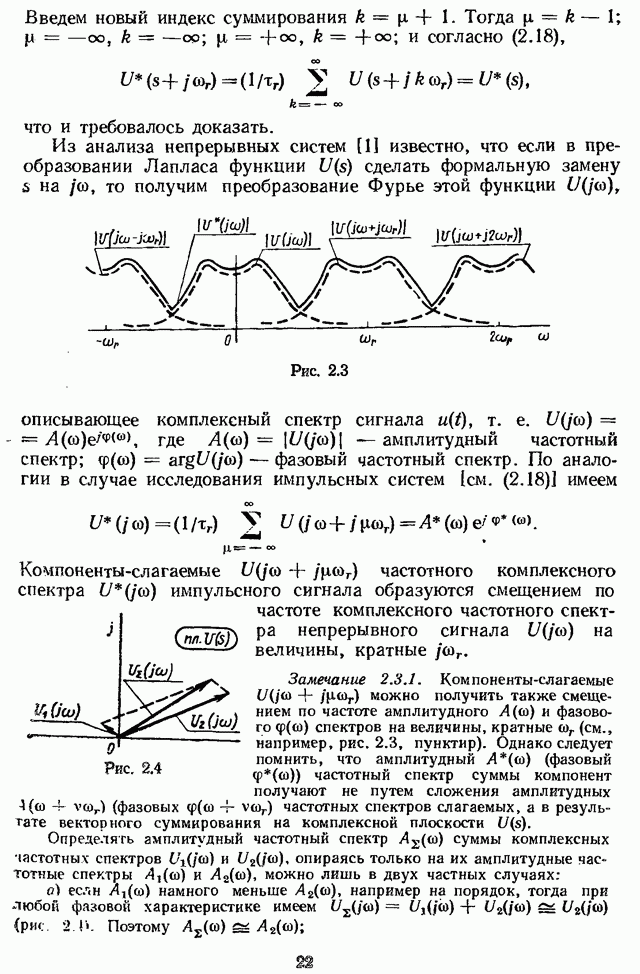
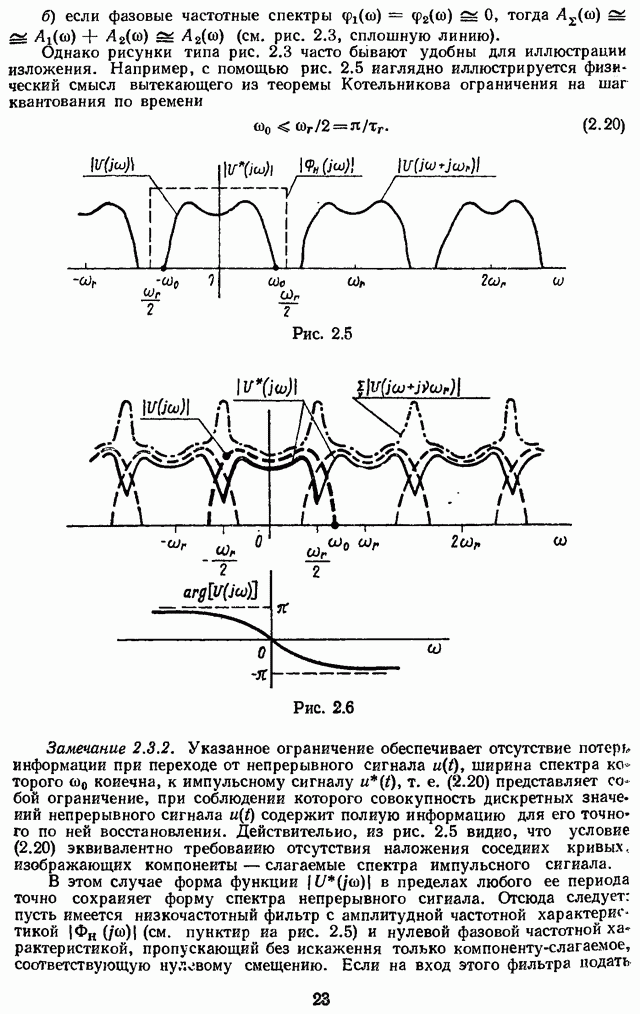
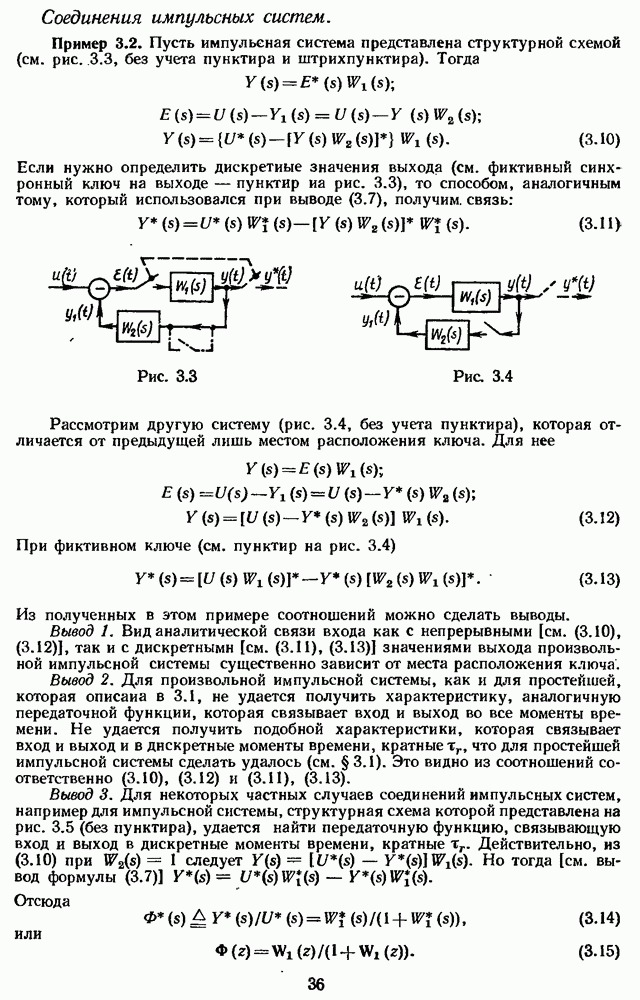
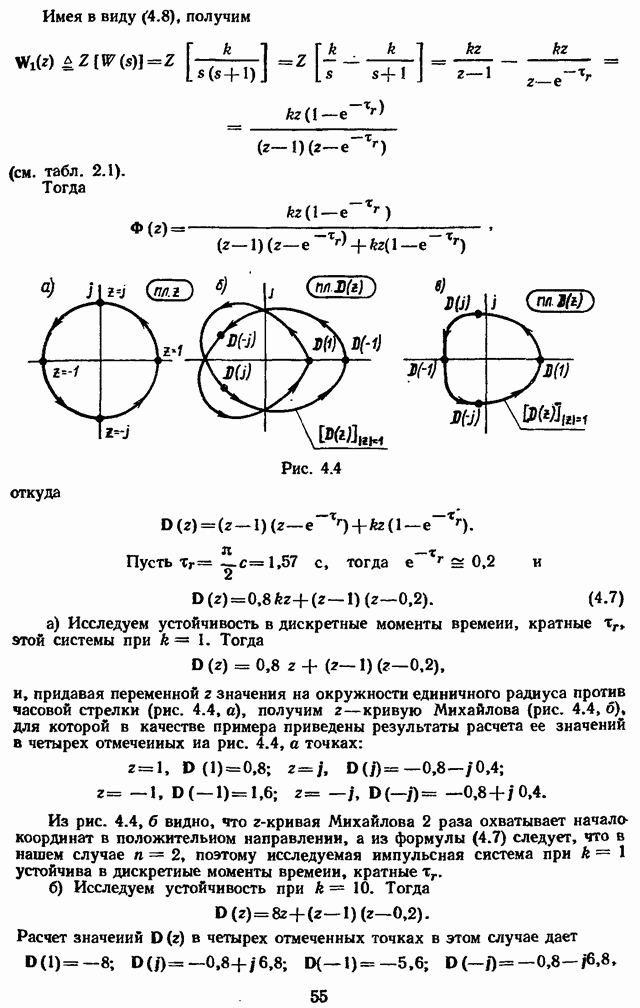
Дискретное преобразование Лапласа функции  можно определить по (2.18) по ее обычному преобразованию Лапласа. Но (2.18), как и (2.2), обладает недостатком — она непосредственно дает результат в незамкнутом математическом виде (см. пример 2.1). Формулу, лишенную этого недостатка, легко получить из (2.16):
можно определить по (2.18) по ее обычному преобразованию Лапласа. Но (2.18), как и (2.2), обладает недостатком — она непосредственно дает результат в незамкнутом математическом виде (см. пример 2.1). Формулу, лишенную этого недостатка, легко получить из (2.16):

Для вычисления дискретного преобразования Лапласа конкретных функций используется (2.19), а (2.2), (2.18) применяются обычно при исследовании свойств дискретного преобразования Лапласа.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ПОНЯТИЕ О ДИСКРЕТНЫХ СИСТЕМАХ
- 1.1. КВАНТОВАНИЕ НЕПРЕРЫВНОГО СИГНАЛА
- 1.2. МОДЕЛЬ ИМПУЛЬСНОГО ЭЛЕМЕНТА
- 1.3. ОСОБЕННОСТИ СИГНАЛОВ И ЭЛЕМЕНТОВ СИСТЕМЫ С МИКРОЭВМ
- Глава 2. z-ПРЕОБРАЗОВАНИЕ
- 2.1. ФОРМУЛА ПРЯМОГО ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
- 2.2. ВЫЧИСЛЕНИЕ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА СИГНАЛА ПО ЕГО ОБЫЧНОМУ ПРЕОБРАЗОВАНИЮ ЛАПЛАСА
- 2.3. СВЯЗЬ СПЕКТРОВ ДИСКРЕТНОГО и НЕПРЕРЫВНОГО СИГНАЛОВ
- 2.4. ОПРЕДЕЛЕНИЕ z-ПРЕОБРАЗОВАНИЯ
- 2.5. СВЯЗЬ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА. ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА И z-ПРЕОБРАЗОВАНИЯ
- Глава 3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ДИСКРЕТНОЙ СИСТЕМЫ
- 3.1. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПРОСТЕЙШЕЙ ПО СТРУКТУРЕ ИМПУЛЬСНОЙ СИСТЕМЫ
- 3.2. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ПРОИЗВОЛЬНОЙ ИМПУЛЬСНОЙ СИСТЕМЫ
- 3.3. ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ЦВМ
- 3.4. ПРЕОБРАЗОВАТЕЛЬ Д-Н
- Глава 4. АНАЛИЗ УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ
- 4.1. z-АНАЛОГ КРИТЕРИЮ УСТОЙЧИВОСТИ МИХАЙЛОВА
- 4.2. z-АНАЛОГ КРИТЕРИЮ УСТОЙЧИВОСТИ НАЙКВИСТА—МИХАЙЛОВА
- 4.3. z-АНАЛОГИ АНАЛИТИЧЕСКИМ КРИТЕРИЯМ УСТОЙЧИВОСТИ
- Главa 5. СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
- 5.1. ПРИБЛИЖЕННЫЙ РАСЧЕТ ПОСЛЕДОВАТЕЛЬНОГО КОРРЕКТИРУЮЩЕГО КОНТУРА С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
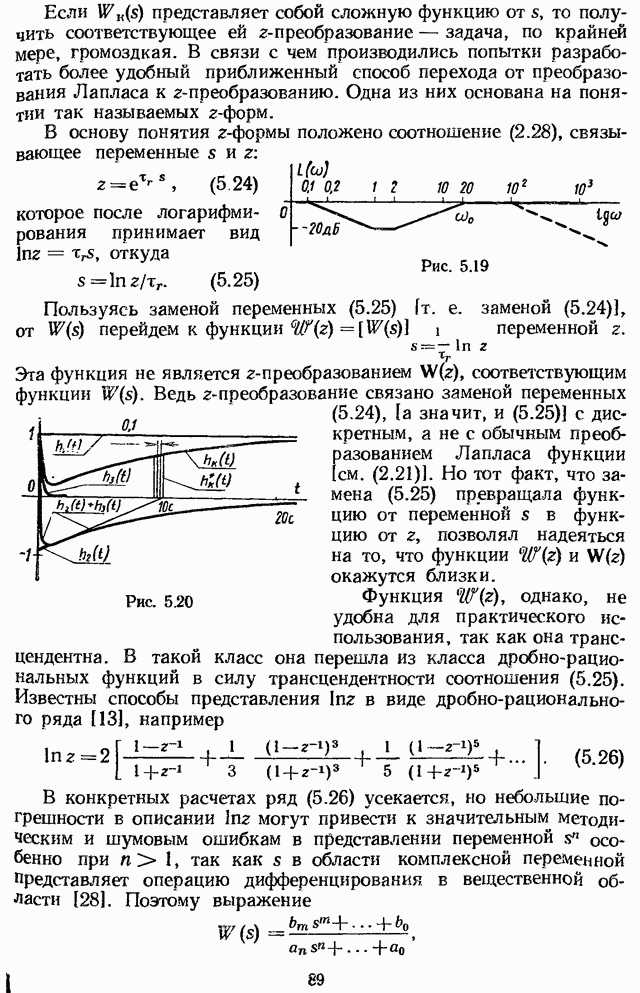
- 5.2. ЛОГАРИФМИЧЕСКАЯ АМПЛИТУДНАЯ И ФАЗОВАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКИ {ЛАХ) ИМПУЛЬСНОЙ СИСТЕМЫ
- 5.3. ПРИБЛИЖЕННЫЙ РАСЧЕТ ПОСЛЕДОВАТЕЛЬНОГО КОРРЕКТИРУЮЩЕГО КОНТУРА С ПОМОЩЬЮ z- и w-ПРЕОБРАЗОВАНИЙ
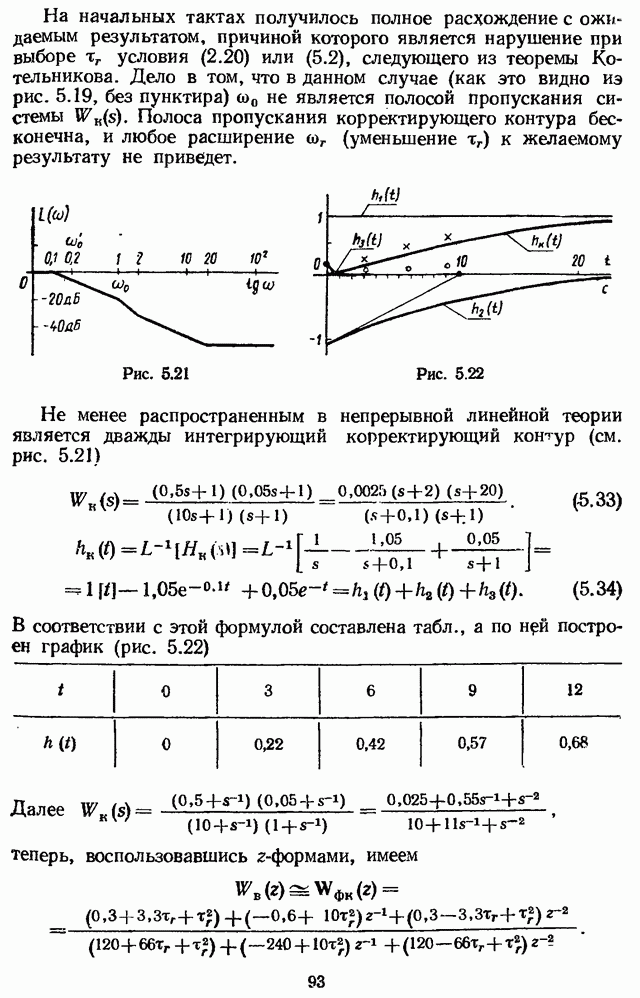
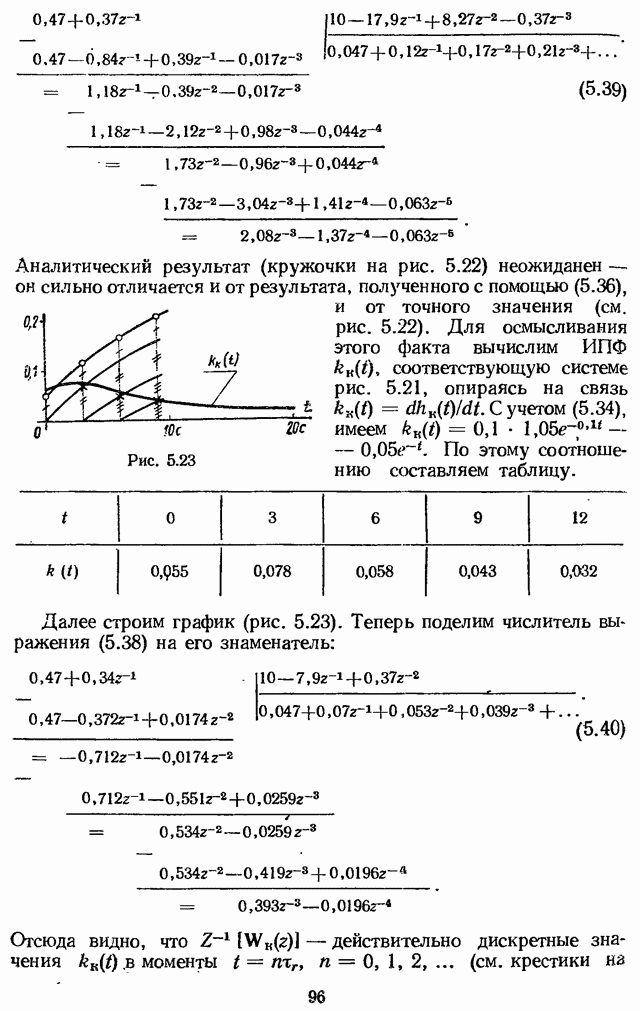
- 5.4. РЕАЛИЗАЦИЯ КОРРЕКТИРУЮЩЕГО КОНТУРА ДИСКРЕТНОЙ СИСТЕМЫ
- 5.5. ДИСКРЕТИЗИРОВАННАЯ МОДЕЛЬ ЛИНЕЙНОЙ НЕПРЕРЫВНОЙ СИСТЕМЫ В ОБЛАСТИ ВРЕМЕНИ
- Глава 6. СЛУЧАЙНЫЕ ПРОЦЕССЫ В ИМПУЛЬСНЫХ СИСТЕМАХ
- 6.1. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИГНАЛОВ
- 6.2. ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ИМПУЛЬСНУЮ СИСТЕМУ, ПРЕДСТАВЛЕННУЮ НА РИС. 6.1
- 6.3. ВЫЧИСЛЕНИЕ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ ИМПУЛЬСНОГО СИГНАЛА ПО ЕГО КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
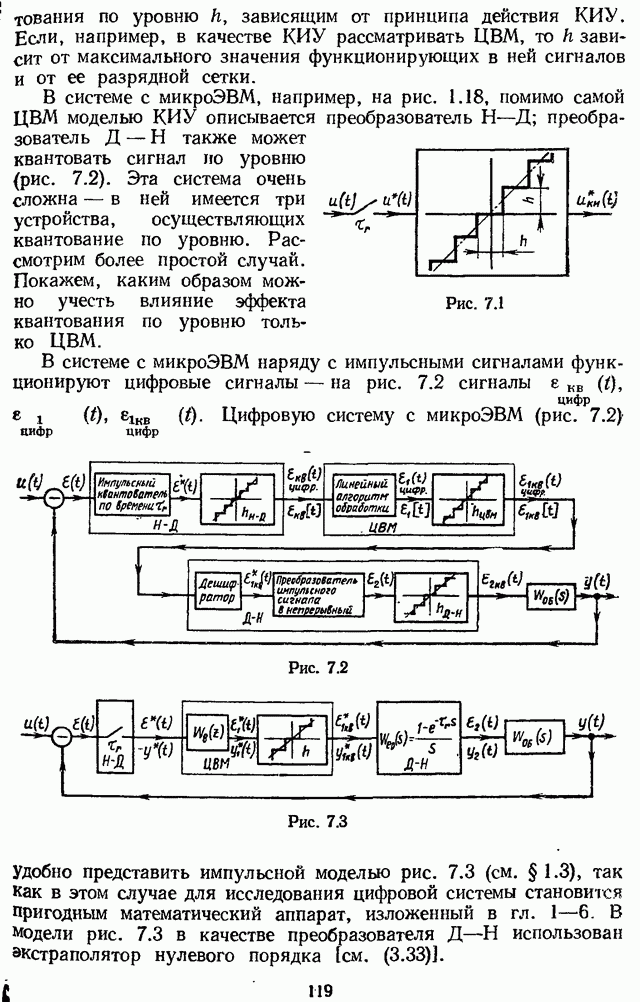
- Глава 7. УЧЕТ ЭФФЕКТА ОТ КВАНТОВАНИЯ ПО УРОВНЮ
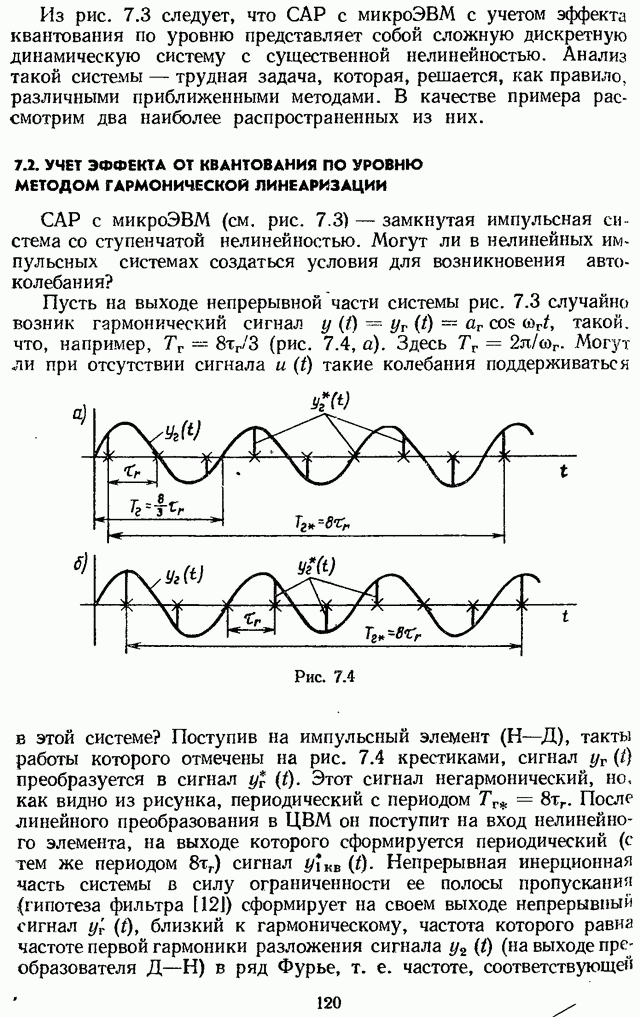
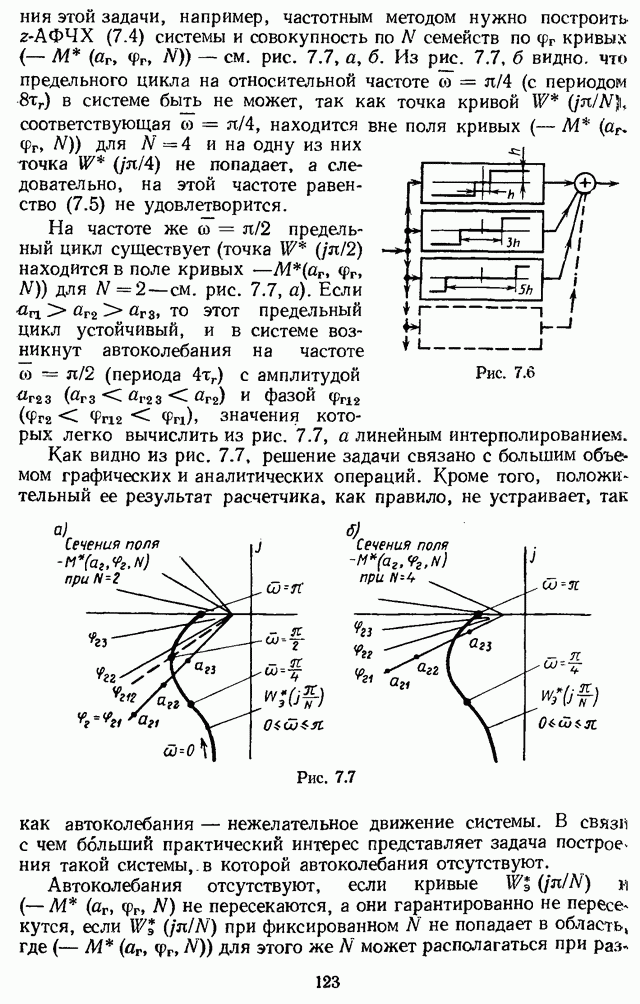
- 7.1. МОДЕЛЬ СИСТЕМЫ С МИКРОЭВМ С УЧЕТОМ КВАНТОВАНИЯ СИГНАЛОВ ПО УРОВНЮ
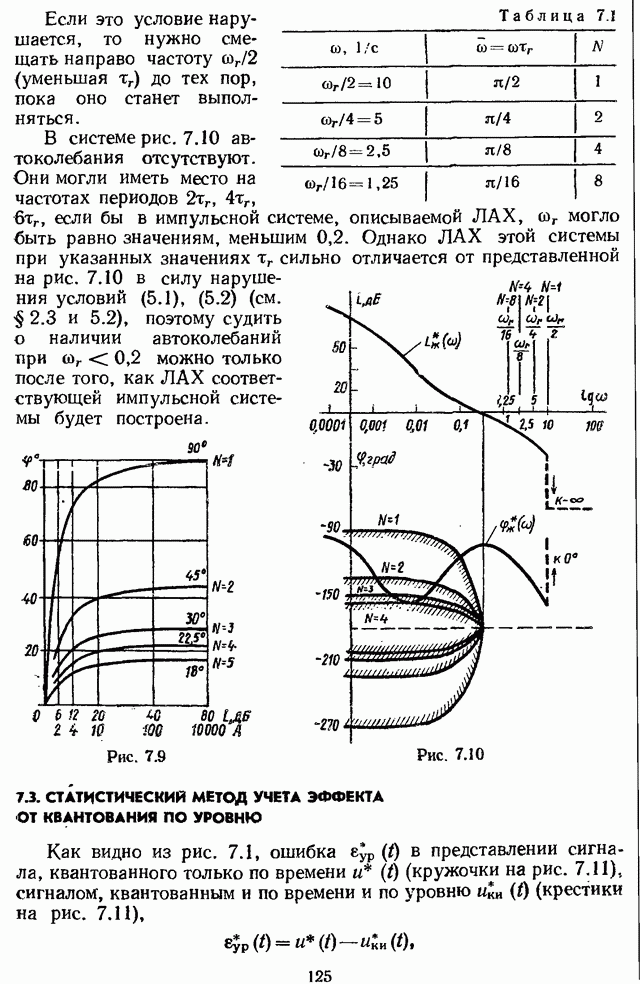
- 7.2. УЧЕТ ЭФФЕКТА ОТ КВАНТОВАНИЯ ПО УРОВНЮ МЕТОДОМ ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
- 7.3. СТАТИСТИЧЕСКИЙ МЕТОД УЧЕТА ЭФФЕКТА ОТ КВАНТОВАНИЯ ПО УРОВНЮ
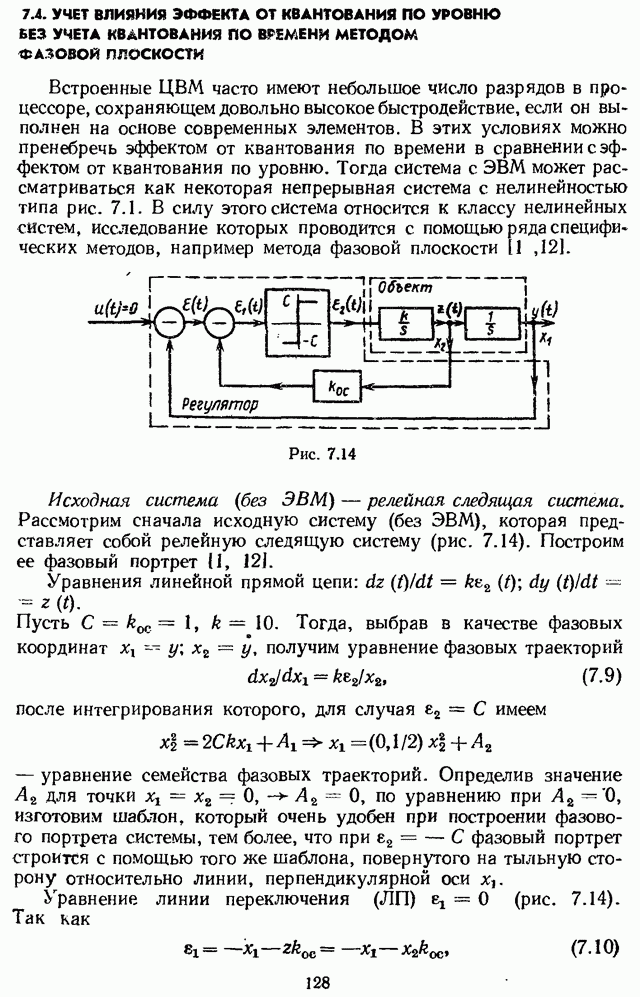
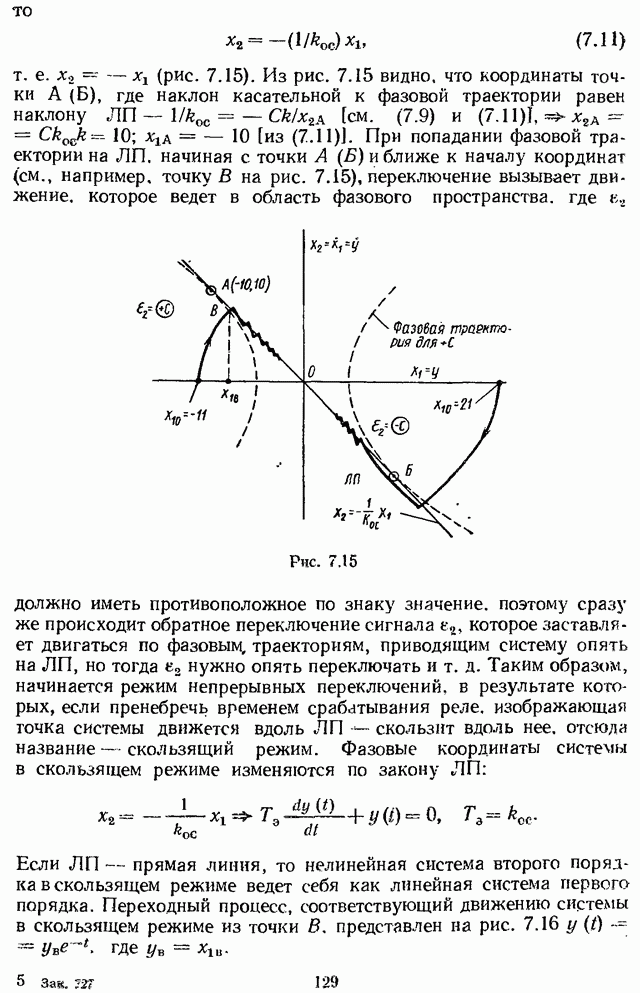
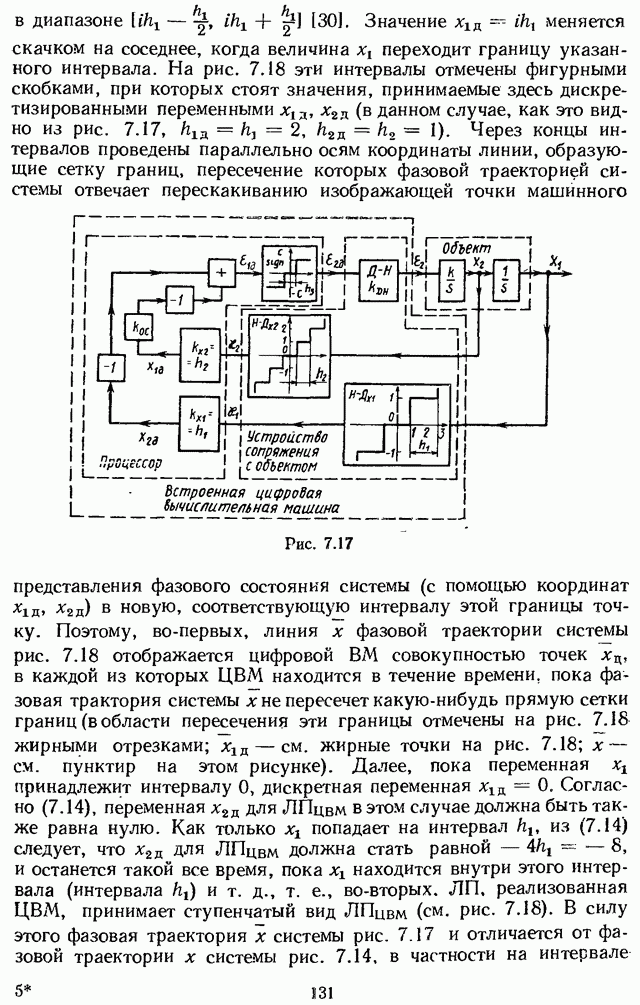
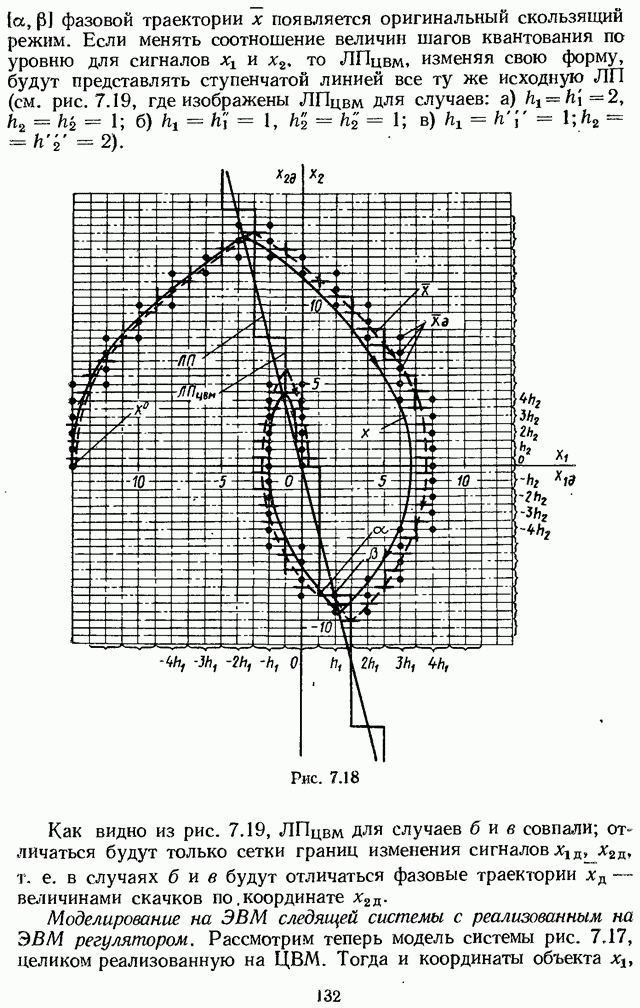
- 7.4. УЧЕТ ВЛИЯНИЯ ЭФФЕКТА ОТ КВАНТОВАНИЯ ПО УРОВНЮ БЕЗ УЧЕТА КВАНТОВАНИЯ ПО ВРЕМЕНИ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- Глава 8. МИКРОПРОЦЕССОРНЫЕ СРЕДСТВА АВТОМАТИКИ, ИХ ВЗАИМОСВЯЗЬ С ЭВМ И ТЕХНОЛОГИЕЙ БИС
- 8.1. МИКРОПРОЦЕССОРЫ И ЭВМ
- 8.2. МИКРОПРОЦЕССОРЫ И ТЕХНОЛОГИЯ БИС
- 8.3. ОБЛАСТИ ПРИМЕНЕНИЯ МИКРОПРОЦЕССОРНЫХ СРЕДСТВ
- 8.4. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ МИКРОПРОЦЕССОРНЫХ СРЕДСТВ [17, 18, 20]
- Глава 9. АРХИТЕКТУРА МИКРОПРОЦЕССОРА
- 9.1. СПОСОБЫ ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ ДЛЯ МП
- 9.2. ТИПОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ И УЗЛЫ МП И МПС
- 9.3. СТРУКТУРНАЯ СХЕМА И УСТРОЙСТВО ОДНОКРИСТАЛЬНОГО МП
- 9.4. УПРАВЛЕНИЕ И СИНХРОНИЗАЦИЯ МП
- 9.5. СИСТЕМА КОМАНД МИКРОПРОЦЕССОРА
- Глава 10. ПАМЯТЬ МИКРОПРОЦЕССОРНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ
- 10.1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И КЛАССИФИКАЦИЯ ЗАПОМИНАЮЩИХ УСТРОЙСТВ
- 10.2. СВЕРХОПЕРАТИВНЫЕ И ОПЕРАТИВНЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 10.3. ПОСТОЯННЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 10.4. ЗАПОМИНАЮЩИЕ УСТРОЙСТВА С ПОСЛЕДОВАТЕЛЬНЫМ ДОСТУПОМ (БУФЕРНЫЕ И СТЕКОВЫЕ ЗУ)
- Глава 11. МНОГОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ И МИКРОПРОГРАММИРОВАНИЕ
- 11.1. СЕКЦИОНИРОВАННЫЕ МП
- 11.2. МИКРОПРОГРАММНОЕ УПРАВЛЕНИЕ В МПАС
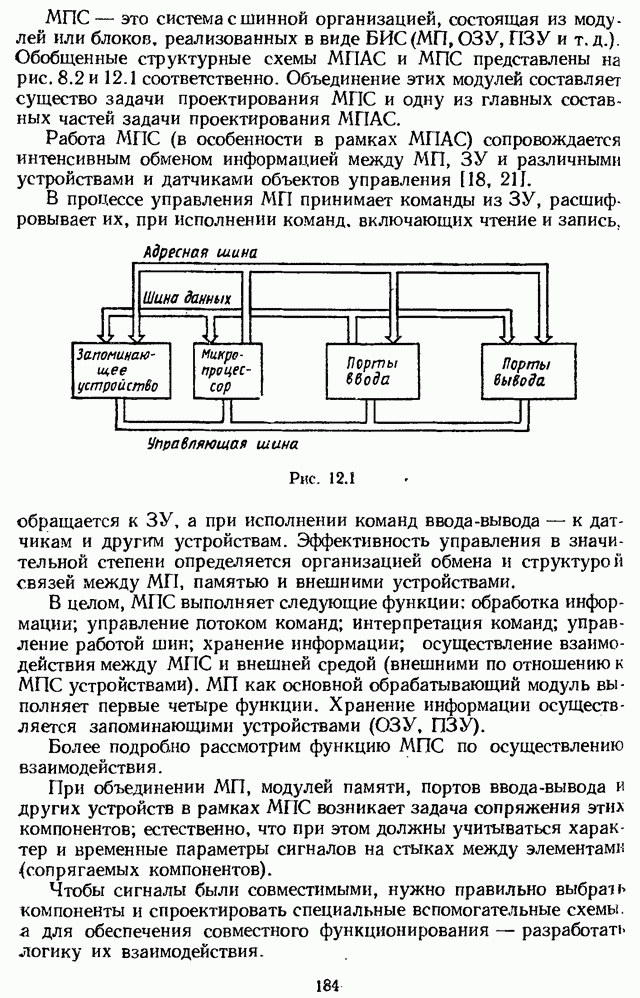
- Глава 12. ОРГАНИЗАЦИЯ ВЗАИМОДЕЙСТВИЯ МИКРОПРОЦЕССОРА (МП) С ВНЕШНЕЙ СРЕДОЙ
- 12.1. ИНТЕРФЕЙС
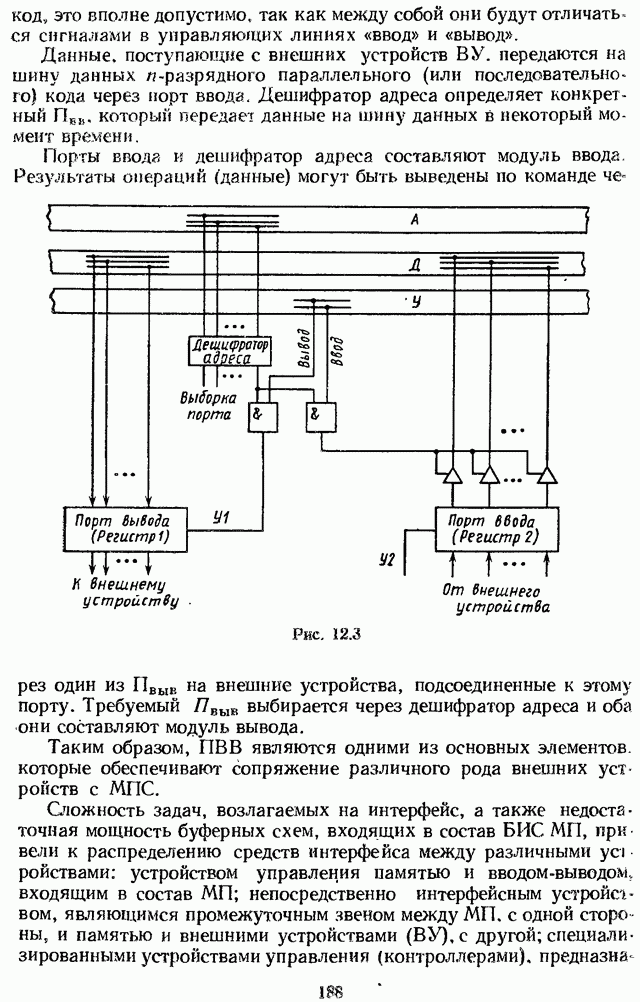
- 12.2. ПОРТЫ ВВОДА-ВЫВОДА
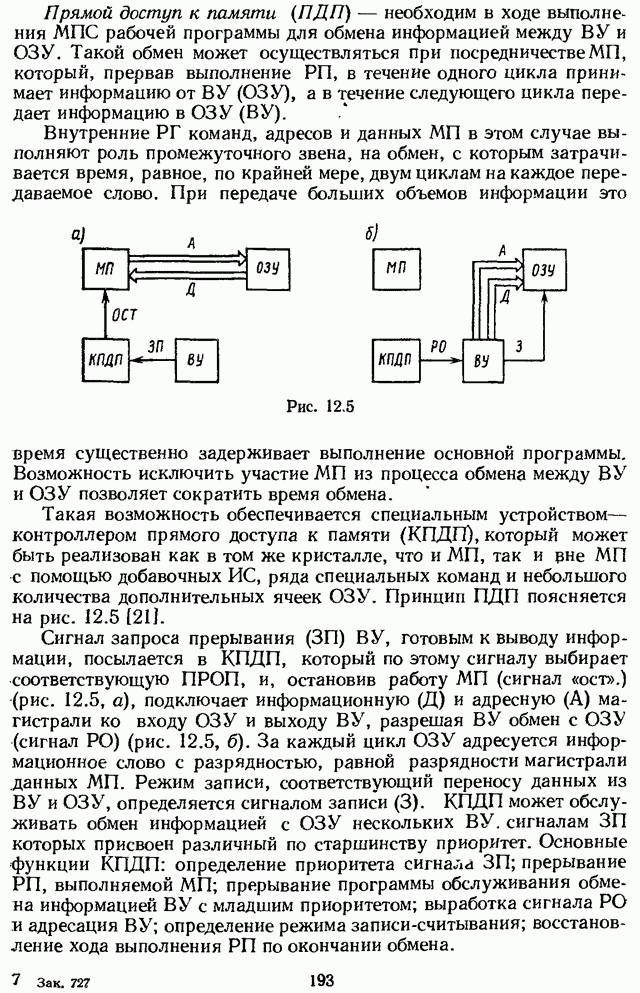
- 12.3. ОБМЕН ИНФОРМАЦИЕЙ МЕЖДУ МИКРОПРОЦЕССОРОМ 44 ВНЕШНЕЙ СРЕДОЙ
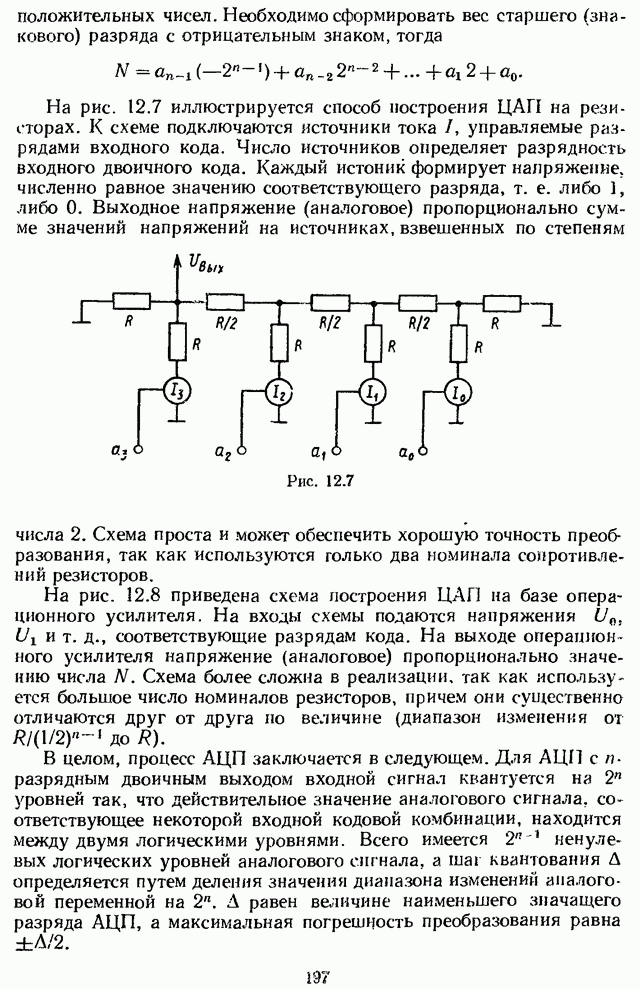
- 12.4. АНАЛОГО-ЦИФРОВЫЕ И ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАНИЯ
- 12.5. АНАЛОГОВЫЙ МИКРОПРОЦЕССОР [17, 24]
- Глава 13. МИКРОПРОЦЕССОРНЫЕ КОМПЛЕКТЫ ИНТЕГРАЛЬНЫХ МИКРОСХЕМ
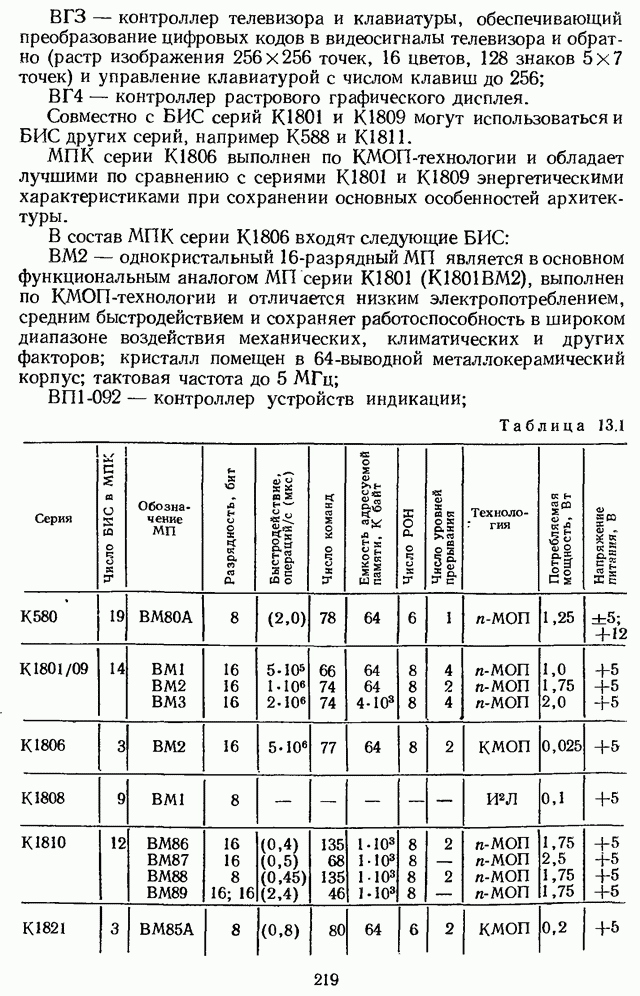
- 13.1. МИКРОПРОЦЕССОРНЫЙ КОМПЛЕКТ СЕРИИ KP580
- 13.2. МИКРОПРОЦЕССОРНЫЙ КОМПЛЕКТ СЕРИИ К588
- 13.3. МИКРОПРОЦЕССОРНЫЕ КОМПЛЕКТЫ ПОВЫШЕННОГО БЫСТРОДЕЙСТВИЯ [СЕРИИ К589, КР1802, КР1804]
- 13.4. ШЕСТНАДЦАТИРАЗРЯДНЫЙ МПК СЕРИЙ К1801/06 09
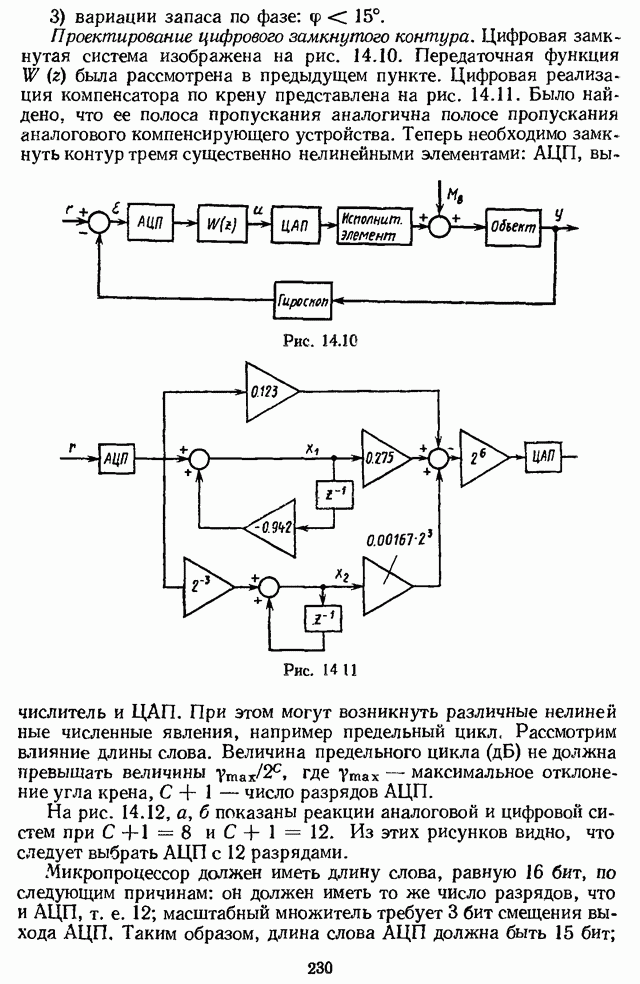
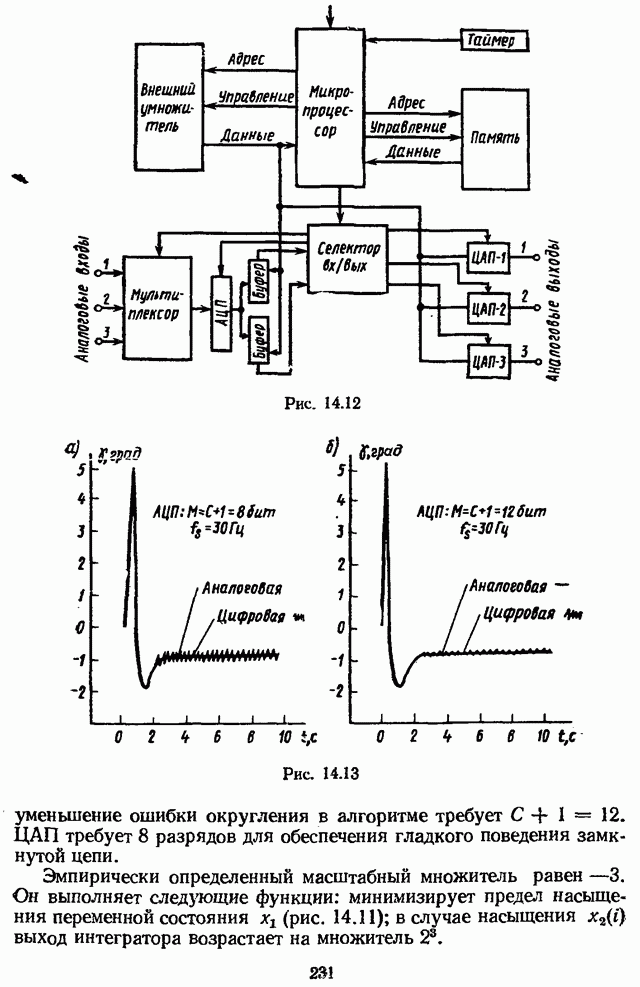
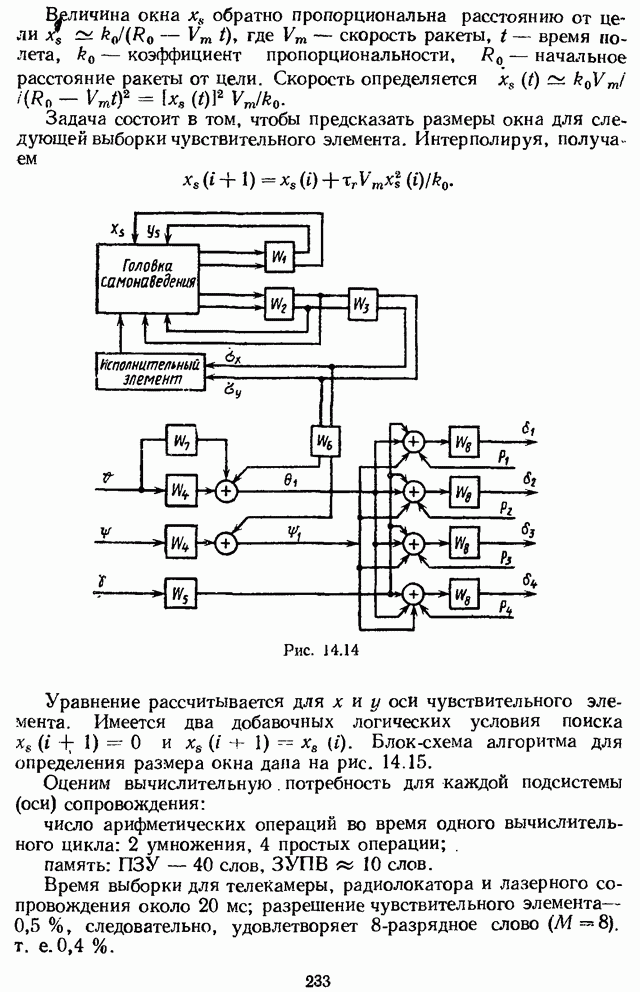
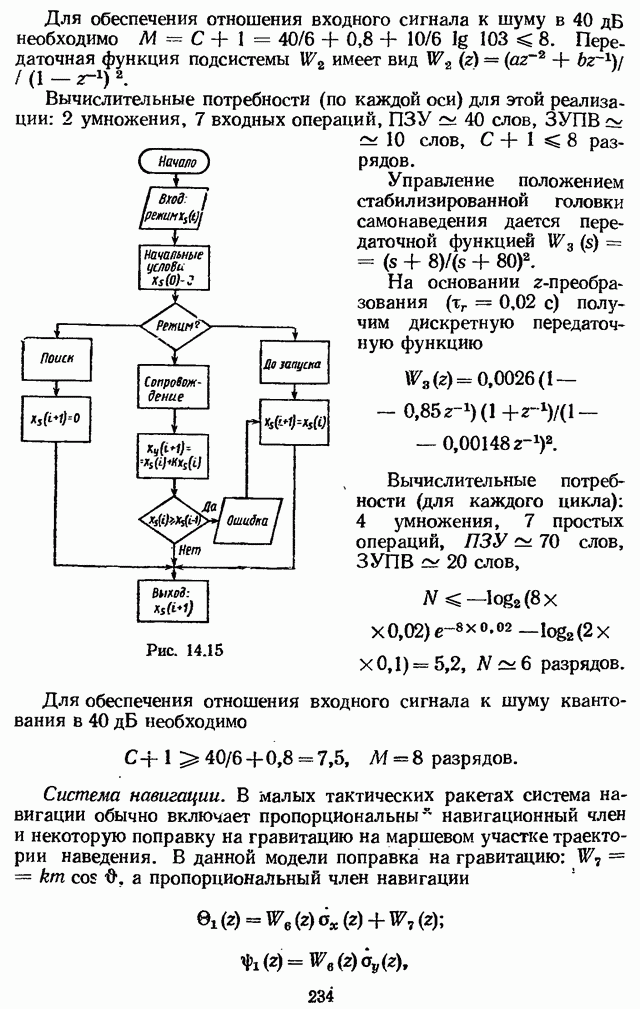
- Глава 14. ПРИМЕНЕНИЕ МИКРОЭВМ В СИСТЕМАХ РЕГУЛИРОВАНИЯ И УПРАВЛЕНИЯ
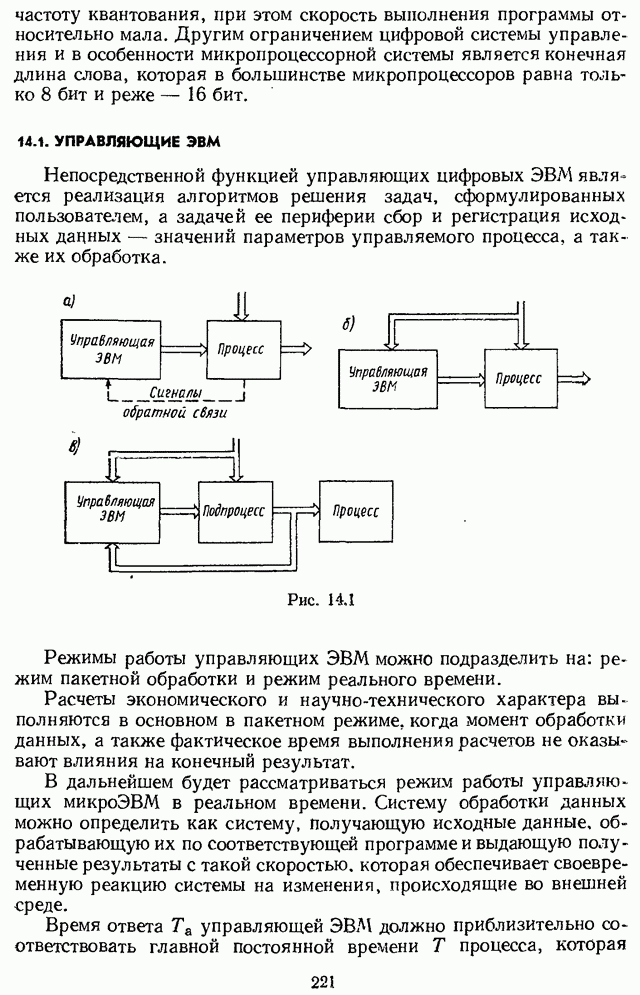
- 14.1. УПРАВЛЯЮЩИЕ ЭВМ
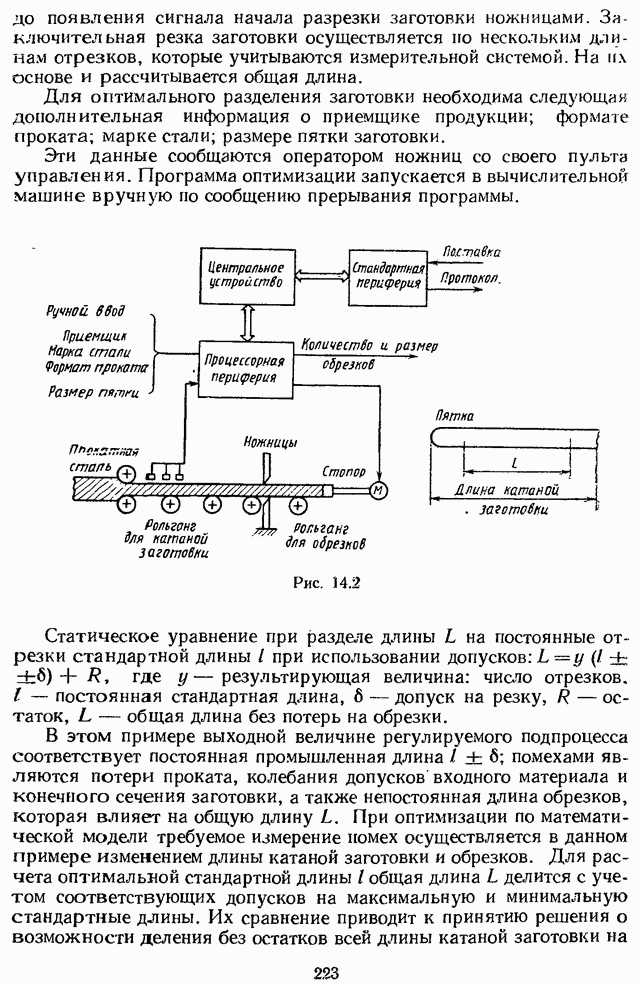
- 14.2. ИСПОЛЬЗОВАНИЕ МИКРОЭВМ ДЛЯ ОПТИМИЗАЦИИ РЕЗКИ КАТАНОЙ ЗАГОТОВКИ НОЖНИЦАМИ [25]
- 14.3. МИКРОКОНТРОЛЛЕР ДЛЯ СТАБИЛИЗАЦИИ АНТЕННЫ
- 14.4. СИСТЕМА УПРАВЛЕНИЯ ПОЛОЖЕНИЕМ ВТОРИЧНОГО ЗЕРКАЛА ТЕЛЕСКОПА [27]
- 14.5. ПРЯМОЕ ЦИФРОВОЕ РЕГУЛИРОВАНИЕ
- 14.6. ПРОЕКТИРОВАНИЕ ЦИФРОВОГО МИКРОПРОЦЕССОРНОГО АВТОПИЛОТА [26]
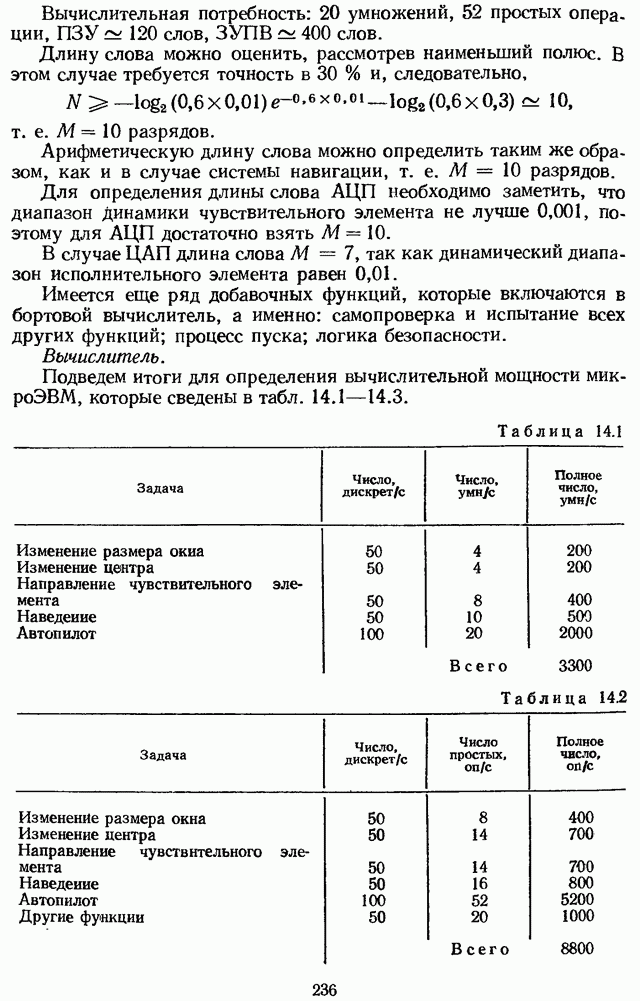
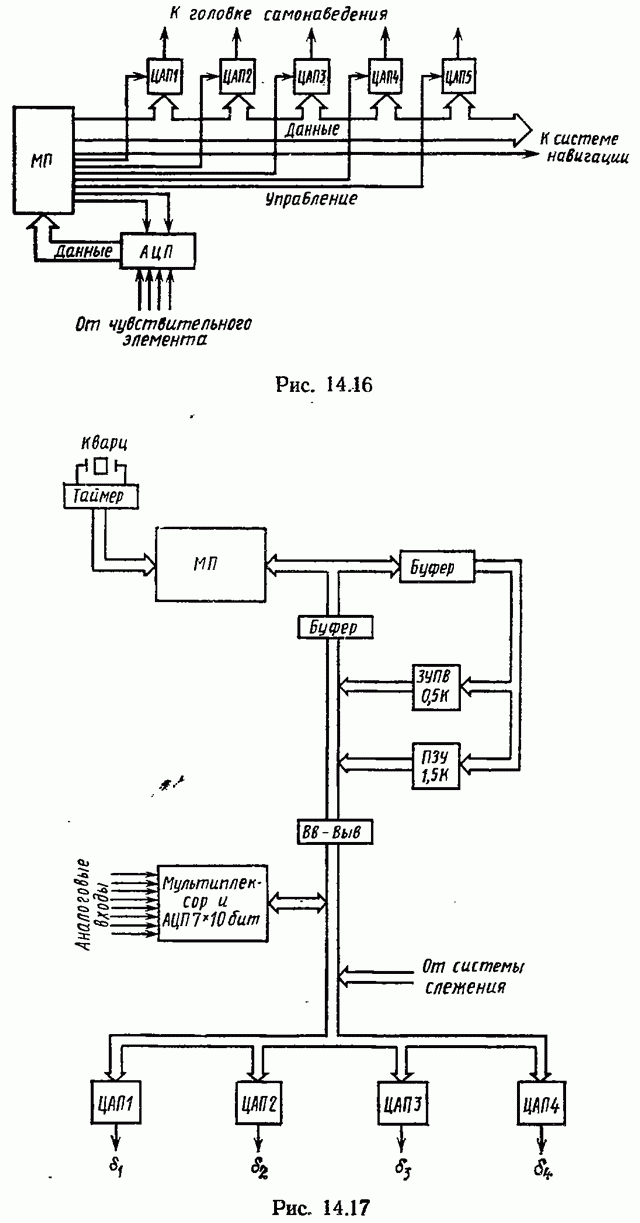
- 14.7. ПРИМЕР РАСЧЕТА МИКРОЭВМ
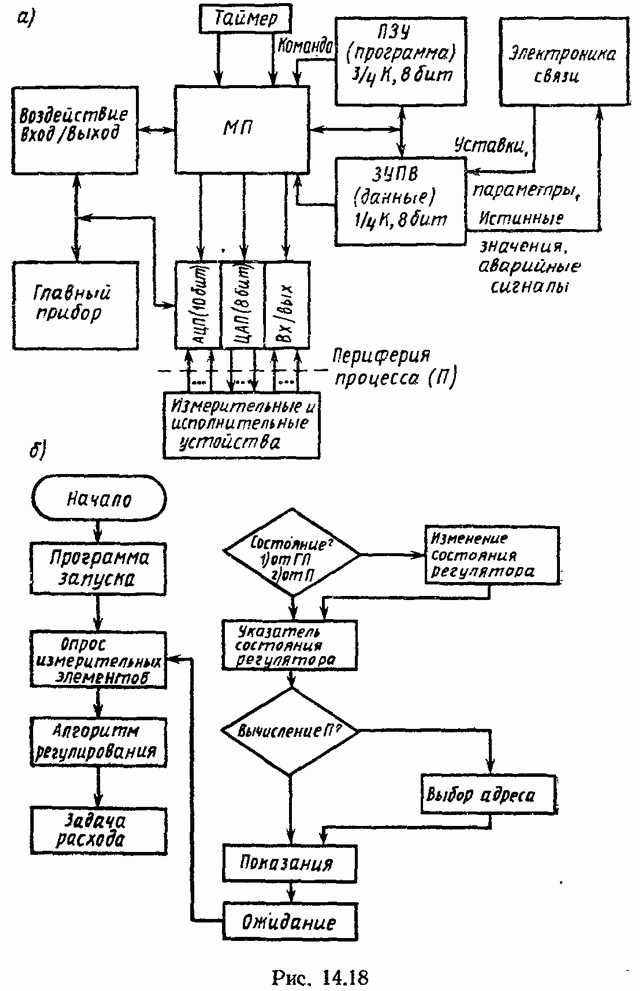
- 14.8. МИКРОПРОЦЕССОР КАК УНИВЕРСАЛЬНЫЙ РЕГУЛЯТОР
- 14.9. МИКРОПРОЦЕССОР КАК ОСНОВА НОВОГО ПОКОЛЕНИЯ СИСТЕМ АВТОМАТИЗАЦИИ
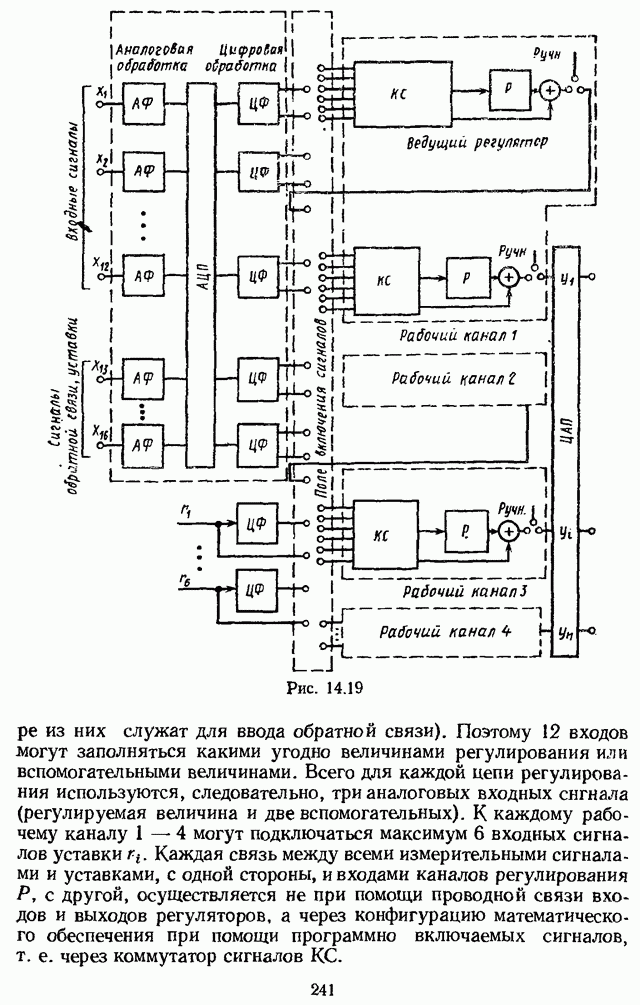
- 14.10. РЕГУЛИРУЮЩИЙ МИКРОПРОЦЕССОРНЫЙ КОНТРОЛЛЕР РЕМИКОНТ Р-100
- СПИСОК ЛИТЕРАТУРЫ