1.2. Каузальные модели изображений

При тензорном представлении СП предполагалось, что для каждого момента t дискретного времени СП  формируется рекуррентно на основе предыдущего значения  и “обновляющего” СП  независимых случайных величин. Несмотря на то, что вычисления во времени осуществляются рекуррентно, при формировании каждого очередного кадра  необходимо выполнять линейное (1.1) или нелинейное (1.7) преобразование всех элементов ,  определенных на n - мерной пространственной сетке J.

Такое преобразование при большом числе m элементов области J даже для простейшей линейной модели (1.6) может потребовать значительного числа m(m+1) операций умножения. Например, для имитации последовательности изменяющихся плоских изображений размером 100х100 элементов  в соответствии (1.6) необходимо около  операций умножения при формировании каждого очередного кадра изображения, т.е.  умножений на один элемент сформированного изображения. Заметим, что решение задач обработки СП, например тензорной фильтрации, потребует еще большего объема вычислений.

Таким образом, тензорные модели дают возможность описать широкий класс негауссовских и неоднородных СП, но приводят к значительным (по современным представлениям) вычислительным затратам при решении задач имитации и обработки СП. В связи с этим возникают вопросы о существовании рекуррентного не только по времени, но и по пространству, представления СП и возможности построения оптимальных и вместе с тем рекуррентных алгоритмов статистического анализа таких СП.

Рассмотрим задачу рекуррентного формирования СП  на n - мерной прямоугольной сетке . При этом предполагается, во-первых, существование некоторой процедуры последовательного перебора точек , т.е. правила линейного упорядочения точек , на основе которого можно сказать, что элемент  предшествует элементу . Во-вторых, должен быть задан алгоритм, определяющий, каким образом очередное значение СП  может быть найдено на основе ранее вычисленных значений , где  - некоторая область индексов , предшествующих очередному элементу . Такую область  конечных размеров обычно называют каузальным окном, каузальной маской, или областью локальных состояний [3, 11, 12]. Наконец, для формирования СП  с определенными вероятностными характеристиками на каждом шаге рекуррентных вычислений функция  должна включать в качестве аргумента совокупность  вспомогательных случайных величин.

         Таким образом, представление СП на основе рекуррентной процедуры должно иметь следующий вид:

 ,                                               (1.8)

,где  – области элементов , на которых уже определены предыдущие значения СП , вообще говоря, нелинейные скалярные или векторные функции двух тензорных аргументов. Наиболее простым частным случаем (1.8) является линейное стохастическое уравнение

,                                              (1.9)

с белым гауссовским СП , соответствующее известному уравнению авторегрессии – скользящего среднего для случайных последовательностей. Однако в отличие от своего одномерного аналога свойства СП , порождаемого (1.9), в настоящее время изучены не полностью даже для моделей с постоянными коэффициентами  и неизменяющимся видом областей  и :

.                                          (1.10)

Важным частным случаем (1.10) являются уравнения многомерной авторегрессии

.                                                (1.11)

         Приведенные уравнения описывают алгоритм формирования СП  в точке . При этом предполагается, что в нашем распоряжении имеются все значения , СП, вычисленные на предыдущих шагах или заданные в качестве начальных условий. Именно такие процедуры будем называть пространственно рекуррентными. Заметим, что при белом поле  и конечных размерах области Y проблем хранения или рекуррентного формирования массива , не возникает. Таким образом, возможности пространственных рекуррентных вычислений зависят от вида области локальных состояний G, порядка последовательного просмотра пространственной сетки J (правила развертки J в последовательность индексов) и соответствующих начальных условий.

         Для иллюстрации рассмотрим двумерное СП  на прямоугольной (MxM) сетке J (рис.2). На этом рисунке показана одна из возможных областей локальных состояний G, допускающих рекуррентные вычисления при последовательном, строка за строкой, формировании массива . Направление перемещения области G вдоль текущей строки указано стрелкой. Очередное значение СП  вычисляется в точке, отмеченной кружком, на основе ранее сформированных чисел  в точках , которые обозначены вертикальными отрезками. Для вычислений вблизи границ должны быть заданы начальные условия, определяющие вероятностные характеристики СП в первом столбце и первой строке области J, а также способ вычисления элементов последнего столбца СП.

         Описанная линейная развертка определяет порядок чередования индексов , если , или и , согласующийся с видом маски G, и обеспечивающий возможность рекуррентных вычислений по формулам (1.8)-(1.11). Заметим, что для приведенной  на рис.2 маски G существуют и другие способы развертки для рекуррентного формирования СП. Одним из них является развертка области J по строкам и диагоналям. В подобных ситуациях появляется возможность сравнения нескольких способов линейного упорядочения элементов и выбора лучшего из этих способов. Вместе с тем, можно привести такие примеры масок G1 и G2, показанных на рис.2, для которых не существует ни одного способа построения развертки сетки J, обеспечивающего рекуррентное формирование СП.

         Таким образом, при построчном сканировании на прямоугольной сетке J все множество масок, допускающих рекуррентные вычисления, может быть сведено к одной несимметричной полуплоскостной области G локальных состояний, представленной на рис.3. Но такую маску, а следовательно и любую каузальную область G, можно отобразить на области G одного квадранта (рис. 4) с помощью преобразования координат  [23]. На рис. 3 такое преобразование можно представить как изменение направления сканирования. Вместо сканирования по строкам и столбцам упорядочение элементов производится по строкам и диагоналям.

         Итак, множество всех областей G, допускающих рекуррентные вычисления, сводится к области одного квадранта (рис.4).

Для того, чтобы уменьшить число слагаемых в (1.10), (1.11) и упростить анализ, введем векторные СП . Выбирая в качестве компонент такого вектора значения СП , можно привести уравнение (1.10) с любой n-мерной маской G одного квадранта  к простейшему виду:

,                                           (1.12)

,где – единичный вектор k-й координатной оси:; Ак и Bk – NxN матрицы. Соответственно уравнение (1.11) пространственной авторегрессии после введения векторных обозначений перепишется следующим образом [11,12]:

                                          (1.13).

         Размерность N вектора , необходимая для преобразования уравнения (1.10) в (1.12), определяется видом области G. В общем случае для перехода от модели (1.10) к минимальной форме (1.12) нужно ввести вектор , компонентами которого являются величины , где  - такое множество индексов, что множества  составляют покрытие множества G. При этом каждый элемент  , будет входить хотя бы в один из векторов . Следовательно, при соответствующем выборе матриц , возможно представление (1.10) в виде (1.12).

         Таким образом, любые стохастические разностные упавнения (1.10) или (1.11), допускающие рекуррентные по развертке вычисления на прямоугольной сетке J, могут быть с помощью преобразования координат и последующего введения векторного СП представлены в форме (1.12) или (1.13) с минимальным числом слагаемых.

         Рассмотренные в п 2.1 стохастические разностные уравнения (1.10), (1.11) и эквивалентные им соотношения (1.12), (1.13) при заданных матричных коэффициентах , дают полное описание линейных многомерных систем, находящихся под воздействием белого СП  При заданных вероятностных характеристиках СП  и начальных условиях формулы (1.12), (1.13) позволяют, в принципе, рассчитать любые вероятностные характеристики СП  или оценить их на основе статистического моделирования даже для случая неоднородных СП с изменяющимися . Однако получить какие-либо общие рекомендации к построению моделей неоднородных СП вида (1.12), (1.13) не удается из-за многообразия возможных видов определения матричных коэффициентов на n-мерной сетке J. В связи с этим ограничимся  частным, но важным для приложений классом однородных СП, для которых можно получить ряд полезных результатов.

         Для однородного СП его КФ  зависит только от разности аргументов . Это позволяет после домножения уравнения (1.13) на справа и определения математического ожидания получить следующее рекуррентное соотношение

,                                   (1.14)

где  - единичный вектор k-й координатной оси. При заданных начальных условиях в виде набора функций  уравнение (1.14) позволяет последовательно рассчитать все другие значения .

         Другой вариант расчета КФ может быть основан на методах спектрального анализа. Для этого выполним n - мерное z - преобразование СП (1.10). При этом нетрудно получить следующую связь

между z - преобразованиями  и  СП  и , причем

                                          (1.15)

передаточная функция линейного фильтра (1.10); . В этом случае спектральная плотность СП  может быть представлена в виде

,                                            (1.16)

где . Наконец, с помощью обратного z-преобразования находим КФ случайного поля :

,

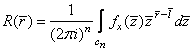где ; cn - единичная полиокружность: .

         Для векторного представления (1.12) модели (1.10) изменится только формула для передаточной функции:

.

         Таким образом, представленные соотношения позволяют найти КФ однородных СП, порожденных рассмотренными стохастическими уравнениями (1.10)(1.13).

         Рассмотрим в качестве примера двумерное СП, заданное одной из наиболее простых моделей . В этом случае передаточная функция фильтра запишется в виде

                                (1.17)

и может быть легко найдена КФ для любых значений коэффициентов. Вместе с тем, для частного случая, когда , анализ СП упрощается. Действительно, передаточная функция (1.17) приводится к виду

,

т.е. может быть представлена в виде произведения  передаточных функций  и , соответствующих одномерным линейным системам. При этом и КФ  также равна произведению  КФ случайных последовательностей. Случайные поля дискретного аргумента, спктральные плотности которых могут быть факторизованы 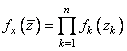, составляют наиболее простой объект для исследований. Двумерное разделимое поле впервые было рассмотрено в работе [34]. В дальнейшем полученные результаты были существенным образом расширены и обобщены на СП произвольной размерности [12, 29]. Весьма важно, что применение этих результатов позволяет решить задачу синтеза модели, т.е. нахождения коэффициентов уравнений (1.10)¸(1.13) по заданным сечениям  КФ  вдоль соответствующих координатных осей . Действительно, предположим, что существуют стохастические разностные уравнения авторегрессии - скользящего среднего

,                                  (1.18)

определяющие случайные последовательности с заданными нормированными КФ. Передаточные функции таких одномерных систем записываются в виде

.

При этом передаточная функция n-мерного фильтра, определяющего СП с КФ , может быть найдена как произведение

.

С другой стороны, передаточная функция пространственного n-мерного фильтра (1.10) определяются соотношением (1.15). Приравнивания коэффициенты  числителей и коэффициенты  знаменателей при одинаковых степенях  в формулах (1.10) и (1.15), получаем набор необходимых коэффициентов , полностью определяющих пространственный фильтр (1.10) по одномерным прототипам. В работах [12, 29] приведены конкретные примеры синтеза и анализа пространственных стохастических разностных уравнений для разделимых СП.

         Существенным недостатком рассмотренного метода построения моделей является значительное сужение класса СП. В частности, с КФ в виде произведения  невозможно описать изотропные СП с КФ . Вместе с тем, при подборе соответствующих одномерных стохастических уравнений удается получить приемлемые для приложений аппроксимации. Как показывает анализ, для получения близких к изотропным СП целесообразно выбирать уравнения (1.18) с кратными корнями соответствующих характеристических уравнений . В качестве примера рассмотрим формирование n-мерного разделимого СП на основе следующих одномерных авторегрессий

,                                  (1.19)

характеристические уравнения  которых имеют корни , кратности 2.

         Известно [12], что нормированные КФ случайных последовательностей (1.19) могут быть записаны в виде

,

где . Перемножая передаточные функции  одномерных систем (1.19), получаем передаточную функцию

,                                                 (1.20)

соответствующую авторегрессионной пространственной модели (1.11). При этом передаточная функция (1.20) дает возможность построить модель вида (1.10), определяющую n-мерное СП с КФ

.

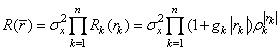Простой анализ полученной КФ на основе разложения в ряд Маклорена по степеням  показывает, что при  сечения нормированной КФ  близкого к единице уровня  могут быть аппроксимированы гиперэллипсоидами

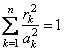
с полуосями . При одинаковых параметрах , , , таким сечением будет гиперсфера . На рис. 5 приведены сечения КФ двумерного СП различных уровней. Как видно из рисунка, при больших уровнях корреляции сечения КФ близки к окружностям. Для иллюстрации на рис.6, а, б представлены две реализации различных двумерных СП в виде полутоновых изображений. При этом на рис.6,а показано изображение, соответствующее СП с КФ , а на рис.6,б – реализация СП, порожденного моделью (1.19), (1.20). Сравнение  этих изображений позволяет сделать вывод о приближении реализаций СП, полученных с помощью каузальных моделей с кратными корнями, к реализациям изотропных СП.