| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.1. Оптимальные алгоритмы обнаружения сигналов
Во многих приложениях возникает задача обнаружения аномалий, которые могут появиться на очередном многомерном кадре последовательности изображений. Такими аномалиями могут быть, например, очаги лесных пожаров, патологические изменения на медицинских изображениях, новые объекты в охраняемой зоне и др. При этом задача обнаружения формализуется следующим образом, Пусть производятся наблюдения
![]() (2.1)
(2.1)
СП ![]() с пространственно-временными
корреляционными связями и СП
с пространственно-временными
корреляционными связями и СП ![]() независимых случайных величин с нулевыми
средними и дисперсиями
независимых случайных величин с нулевыми
средними и дисперсиями ![]() . Вектор параметров
. Вектор параметров ![]() позволяет учесть, например,
возможные взаимные пространственные смещения и повороты соседних кадров
изображения.
позволяет учесть, например,
возможные взаимные пространственные смещения и повороты соседних кадров
изображения.
Появление детерминированного
сигнала приводит к изменению модели (2.1) лишь в области индексов ![]() (рис. 1) последнего из
наблюдаемых кадров:
(рис. 1) последнего из
наблюдаемых кадров:
![]() (2.2)
(2.2)
где ![]() - совокупность отсчетов полезного сигнала.
- совокупность отсчетов полезного сигнала.
В рассмотренных условиях необходимо найти правило проверки гипотезы Н0 об отсутствии аномалии в области G при альтернативном предположении Н1 о справедливости модели (2.2).
При заданных вероятностных
характеристиках компонент моделей (2.1), (2.2) могут быть определены
соответствующие условные плотности распределения вероятностей (ПРВ) наблюдений W(Z|Н0) и W(Z|Н1). Поэтому для решения
задачи обнаружения следует воспользоваться сравнением с пороговым уровнем ![]() отношения правдоподобия
(ОП):
отношения правдоподобия
(ОП):
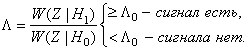 (2.3)
(2.3)
Для упрощения вычислений представим
условные ПРВ в виде произведений: ![]() , где ZG - совокупность наблюдений по области
G; Z0 - совокупность всех наблюдений, не принадлежащих области
предполагаемого сигнала. Поскольку
, где ZG - совокупность наблюдений по области
G; Z0 - совокупность всех наблюдений, не принадлежащих области
предполагаемого сигнала. Поскольку ![]() , ОП (2.3) перепишется в форме:
, ОП (2.3) перепишется в форме:
![]() .
(2.4)
.
(2.4)
Будем аппроксимировать условные ПРВ, входящие в ОП (2.4), гауссовскими распределениями:
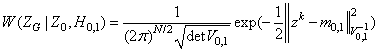 ,
,
где ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() - условные математические ожидания и
пространственные ковариационные матрицы наблюдений ZG при отсутствии и наличии полезного
сигнала соответственно.
- условные математические ожидания и
пространственные ковариационные матрицы наблюдений ZG при отсутствии и наличии полезного
сигнала соответственно.
С учетом моделей наблюдений (2.1),
(2.2) нетрудно получить следующие формулы для условных средних ![]() , где
, где ![]() - оптимальный прогноз
значений СП
- оптимальный прогноз
значений СП ![]() ,
построенный на основе всех имеющихся наблюдений Z0 , не принадлежащих области сигнала. Пространственные матрицы
V0 и V1 оказываются одинаковыми:
,
построенный на основе всех имеющихся наблюдений Z0 , не принадлежащих области сигнала. Пространственные матрицы
V0 и V1 оказываются одинаковыми:![]() , где
, где ![]() - ковариационная
матрица ошибок оптимального прогноза.
- ковариационная
матрица ошибок оптимального прогноза.
После подстановки приведенных соотношений в (2.4), (2.5) и логарифмирования находим следующий алгоритм обнаружения сигнала:
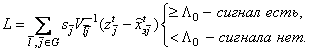 , (2.6)
, (2.6)
где![]() - порог обнаружения. Как следует из формулы
(2.6), процедура обнаружения аномалий включает в себя компенсацию мешающих
изображений с помощью вычитания из наблюдения
- порог обнаружения. Как следует из формулы
(2.6), процедура обнаружения аномалий включает в себя компенсацию мешающих
изображений с помощью вычитания из наблюдения ![]() оптимального прогноза
оптимального прогноза ![]() , найденного на основе всех
наблюдений, не принадлежащих области G. После компенсации мешающих СП осуществляется линейное весовое cуммирование остатков
, найденного на основе всех
наблюдений, не принадлежащих области G. После компенсации мешающих СП осуществляется линейное весовое cуммирование остатков ![]()
Применяя формулу Фробениуса обращения блочных матриц, можно показать, что статистика приводиться к эквивалентному виду:
![]() ,
,
где ![]() ,- оптимальный прогноз значения
,- оптимальный прогноз значения ![]() , построенный на основе
всех имеющихся наблюдений, кроме
, построенный на основе
всех имеющихся наблюдений, кроме ![]() ;
; ![]() . -дисперсия ошибки этого прогноза. В
отличие от
. -дисперсия ошибки этого прогноза. В
отличие от ![]() будем
называть
будем
называть ![]() "прогнозом
в точку". При обнаружении аномалий во всевозможных областях G с большим числом элементов
"прогноз в точку" может быть найден с помощью значительно меньшего
числа вычислительных операций, чем "прогноз в область"
"прогнозом
в точку". При обнаружении аномалий во всевозможных областях G с большим числом элементов
"прогноз в точку" может быть найден с помощью значительно меньшего
числа вычислительных операций, чем "прогноз в область" ![]() .
.
Еще одна форма записи
оптимальной процедуры обнаружения может быть получена в предположении, что
полезный сигнал может занимать все имеющиеся кадры изображения, т.е. область G включает все многомерные сетки ![]() . Тогда наилучший
прогноз
. Тогда наилучший
прогноз ![]() , и
алгоритм (2.6) принимает вид:
, и
алгоритм (2.6) принимает вид:
 ,
(2.8)
,
(2.8)
где ![]() ;
; ![]() - ковариационная матрица мешающего
изображения.
- ковариационная матрица мешающего
изображения.
Непосредственная реализация
процедуры (2.8) затруднительна из-за большого числа вычислительных операций.
Тем не менее, раскладывая пространственную симметрическую матрицу в
произведение двух треугольных ![]() , можно представить (2.8) в форме
, можно представить (2.8) в форме
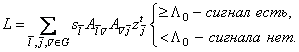 (2.9)
(2.9)
соответствующий предварительному
"выбеливанию" [2,10,24] последовательности изображений ![]() , и последующему
весовому суммированию с весами
, и последующему
весовому суммированию с весами ![]() . Во многих случаях такой подход позволяет
найти приемлемые для практики квазиоптимальные алгоритмы "выбеливания"
[26, 27]. При этом самостоятельное рассмотрение адаптивных рекурсивных
фильтров, близких по свойствам к выбеливающим, является важным направлением
поиска возможностей относительно простой технической или программной реализации
системы обработки последовательностей изображений. Новым качеством, которым
обладают алгоритмы (2.7), (2.8) и (2.9) по отношению к (2.6), является
разделение трудоемкой операции оптимального прогнозирования или выбеливания, не
связанной с формой сигнала, и относительно простого весового суммирования,
учитывающего вид полезного сигнала. Это позволяет достаточно просто решать как
задачи обнаружения аномалий с неизвестными параметрами положения, так и более
сложные проблемы многоальтернативного обнаружения (распознавания) нескольких видов
сигналов [19-21].
. Во многих случаях такой подход позволяет
найти приемлемые для практики квазиоптимальные алгоритмы "выбеливания"
[26, 27]. При этом самостоятельное рассмотрение адаптивных рекурсивных
фильтров, близких по свойствам к выбеливающим, является важным направлением
поиска возможностей относительно простой технической или программной реализации
системы обработки последовательностей изображений. Новым качеством, которым
обладают алгоритмы (2.7), (2.8) и (2.9) по отношению к (2.6), является
разделение трудоемкой операции оптимального прогнозирования или выбеливания, не
связанной с формой сигнала, и относительно простого весового суммирования,
учитывающего вид полезного сигнала. Это позволяет достаточно просто решать как
задачи обнаружения аномалий с неизвестными параметрами положения, так и более
сложные проблемы многоальтернативного обнаружения (распознавания) нескольких видов
сигналов [19-21].
Приведенные результаты
позволяют уточнить условия, при которых справедлива предложенная замена
условных ПРВ нормальными распределениями. Прежде всего, это широкий класс с
гауссовскими моделями (2.1), (2.2). В этих случаях процедуры (2.6), (2.7),
(2.9) строго оптимальны. При негауссовских компонентах моделей (2.1), (2.2)
достаточным условием оптимальности служит возможность аппроксимации
апостериорной ПРВ прогноза ![]() нормальным распределением. Заметим, что
последнее условие выполняется и во многих прикладных задачах обработки СП со
значительными пространственно-временными корреляционными связями и обычно
эквивалентно условию высокой апостериорной точности прогнозирования.
нормальным распределением. Заметим, что
последнее условие выполняется и во многих прикладных задачах обработки СП со
значительными пространственно-временными корреляционными связями и обычно
эквивалентно условию высокой апостериорной точности прогнозирования.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Введение
- 1.1. Тензорные стохастические разностные уравнения
- 1.1. Тензорные стохастические разностные уравнения
- 1.2. Каузальные модели изображений
- 1.2. Каузальные модели изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.2. Эффективность обнаружения аномалий
- 2.2. Эффективность обнаружения аномалий
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.2. Тензорный фильтр Калмана
- 3.2. Тензорный фильтр Калмана
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- Заключение
- Заключение
- Литература
- Литература
