| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
Рассмотрим гауссовское случайное поле (СП)
![]() ,
, ![]() =(
=(![]() ,
,![]() ,…,
,…, ![]() )ÎW, заданное на n-мерной
прямоугольной сетке W={
)ÎW, заданное на n-мерной
прямоугольной сетке W={![]() , k=1,2,…,n}. Математическое
ожидание СП M{
, k=1,2,…,n}. Математическое
ожидание СП M{![]() }=0,
}=0,
![]() , а
корреляционная функция (КФ)
, а
корреляционная функция (КФ) ![]() {
{![]() }=M{
}=M{![]() ×
×![]() } априори неизвестна и
может изменяться в процессе наблюдения. Необходимо построить адаптивное
линейное рекуррентное преобразование
} априори неизвестна и
может изменяться в процессе наблюдения. Необходимо построить адаптивное
линейное рекуррентное преобразование
![]() =L{
=L{![]() },
(2.12)
},
(2.12)
обеспечивающее выполнение условия
![]() {
{![]() }= M{
}= M{![]() ×
×![]() }®0,
}®0, ![]() .
(2.13)
.
(2.13)
Будем предполагать, что на сетке W определено
правило линейного упорядочивания точек ![]() ÎW, на основе
которого можно определить, что элемент
ÎW, на основе
которого можно определить, что элемент ![]() предшествует элементу
предшествует элементу ![]() [6,14]. Такое правило даёт
возможность установить вид развёртки, т.е. вид преобразования массива данных {
[6,14]. Такое правило даёт
возможность установить вид развёртки, т.е. вид преобразования массива данных {![]() } в последовательность
чисел
} в последовательность
чисел ![]() при
рекуррентной обработке многомерного изображения.
при
рекуррентной обработке многомерного изображения.
Для рекуррентной декорреляции СП {![]() } воспользуемся линейным
оператором следующего вида:
} воспользуемся линейным
оператором следующего вида:
![]() =
=![]() -
- 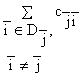 ×
×![]() , (2.14)
, (2.14)
где ![]() =
=![]() (
(![]() ) - весовые коэффициенты;
) - весовые коэффициенты; ![]() – область весового
суммирования (рис.1), перемещающаяся по сетке W в соответствии с
развёрткой изображения.
– область весового
суммирования (рис.1), перемещающаяся по сетке W в соответствии с
развёрткой изображения.
Для однородного СП {![]() } можно подобрать
постоянные коэффициенты
} можно подобрать
постоянные коэффициенты ![]() =
=![]() , обеспечивающие при достаточно большом
размере области D приемлемое качество декорреляции. При изменении
вероятностных свойств СП {
, обеспечивающие при достаточно большом
размере области D приемлемое качество декорреляции. При изменении
вероятностных свойств СП {![]() ,
, ![]() ÎW} необходимо
подстраивать значения
ÎW} необходимо
подстраивать значения ![]() =
=![]() (
(![]() ,
, ![]() Î
Î![]() ) в соответствии с
характеристиками СП. Для этого воспользуемся следующей рекуррентной
псевдоградиентной процедурой [8]:
) в соответствии с
характеристиками СП. Для этого воспользуемся следующей рекуррентной
псевдоградиентной процедурой [8]:
![]() ,
(2.15)
,
(2.15)
где ![]() - реализация градиента функционала качества
алгоритма декорреляции, т.е.
- реализация градиента функционала качества
алгоритма декорреляции, т.е. ![]() =
= ![]() +
+![]() ;
; ![]() - функционал качества;
- функционал качества; ![]() - ошибка наблюдения в точке
- ошибка наблюдения в точке ![]() ;
; ![]() (*) – векторная функция от реализации градиента
функционала качества;
(*) – векторная функция от реализации градиента
функционала качества; ![]() -
скалярные коэффициенты;
-
скалярные коэффициенты; ![]() - следующее после
- следующее после ![]() значение индекса. Для
сходимости процедуры (4) необходимо выполнение условия псевдоградиентности:
значение индекса. Для
сходимости процедуры (4) необходимо выполнение условия псевдоградиентности:
![]() .
.
Это условие означает, что вектор ![]() (
(![]() ) в среднем должен составлять острый угол с
направлением вектора
) в среднем должен составлять острый угол с
направлением вектора ![]() .
.
Функционал ![]() может быть определён несколькими
способами. Известно [6,8], что адаптивные алгоритмы делятся на два класса.
Первый класс включает идентификационные, а второй класс – безыдентификационные
алгоритмы. В алгоритмах первого класса осуществляется предварительное
оценивание неизвестных параметров наблюдений, а затем эти оценки используются
для определения параметров алгоритма обработки. Анализ показывает, что
применение подобных алгоритмов в системах реального времени вызывает большие
трудности. В алгоритмах второго класса параметры алгоритма обработки изменяются
в соответствии с изменением свойств некоторого наблюдаемого функционала. В
рассматриваемой задаче декорреляции таким функционалом может быть, например,
квадратичная форма:
может быть определён несколькими
способами. Известно [6,8], что адаптивные алгоритмы делятся на два класса.
Первый класс включает идентификационные, а второй класс – безыдентификационные
алгоритмы. В алгоритмах первого класса осуществляется предварительное
оценивание неизвестных параметров наблюдений, а затем эти оценки используются
для определения параметров алгоритма обработки. Анализ показывает, что
применение подобных алгоритмов в системах реального времени вызывает большие
трудности. В алгоритмах второго класса параметры алгоритма обработки изменяются
в соответствии с изменением свойств некоторого наблюдаемого функционала. В
рассматриваемой задаче декорреляции таким функционалом может быть, например,
квадратичная форма:
![]() =
=![]() ,
,
где G – n-мерная область декорреляции. Реализация градиента этого функционала имеет вид:
![]() =
= ![]() {
{![]() }=
}= ![]() +
+![]() . (2.16)
. (2.16)
Анализ показывает, что в качестве
функции от ![]() целесообразно
выбрать знаковую функцию
целесообразно
выбрать знаковую функцию ![]() {*}=sign{*}.
{*}=sign{*}.
Отметим, что задача декорреляции
относится к классу некорректно поставленных задач, и для её решения необходимо
использовать методы регуляризации [9]. Для этого входные наблюдения
представляются в виде суммы ![]() =
= ![]() +
+ ![]() , где
, где ![]() - дополнительный гауссовский шум с
дисперсией
- дополнительный гауссовский шум с
дисперсией ![]()
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Введение
- 1.1. Тензорные стохастические разностные уравнения
- 1.1. Тензорные стохастические разностные уравнения
- 1.2. Каузальные модели изображений
- 1.2. Каузальные модели изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.2. Эффективность обнаружения аномалий
- 2.2. Эффективность обнаружения аномалий
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.2. Тензорный фильтр Калмана
- 3.2. Тензорный фильтр Калмана
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- Заключение
- Заключение
- Литература
- Литература
