| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.1. Эффективность оптимальной фильтрации многомерных изображений
Выделение полезной составляющей ![]() на основе наблюдений
(21) является важной задачей, так как дает возможность улучшить многомерное
изображение при наличии помех. Вместе с тем, рассмотрение проблем обнаружения
аномалий также привело к необходимости определения ковариационных матриц
на основе наблюдений
(21) является важной задачей, так как дает возможность улучшить многомерное
изображение при наличии помех. Вместе с тем, рассмотрение проблем обнаружения
аномалий также привело к необходимости определения ковариационных матриц ![]() ошибок фильтрации, если
требуется построить характеристики оптимального обнаружения. Однако, подходы к
решению задач определения потенциальной точности оценивания и построения
алгоритмов фильтрации многомерных СП оказываются совершенно разными. В первом
случае для получения достаточно простых аналитических соотношений целесообразно
обратиться к асимптотическим формулам фильтра Винера. При построении же оценок
многомерных изображений на фоне помех желательно найти структуры оптимальных
или близких к ним алгоритма с небольшими вычислительными затратами. Это удается
сделать с помощью рекуррентных методов оценивания, основанных на рассмотренных
во второй части моделях изображений.
ошибок фильтрации, если
требуется построить характеристики оптимального обнаружения. Однако, подходы к
решению задач определения потенциальной точности оценивания и построения
алгоритмов фильтрации многомерных СП оказываются совершенно разными. В первом
случае для получения достаточно простых аналитических соотношений целесообразно
обратиться к асимптотическим формулам фильтра Винера. При построении же оценок
многомерных изображений на фоне помех желательно найти структуры оптимальных
или близких к ним алгоритма с небольшими вычислительными затратами. Это удается
сделать с помощью рекуррентных методов оценивания, основанных на рассмотренных
во второй части моделях изображений.
Для нахождения дисперсии ошибки ![]() оптимальной фильтрации
рассмотрим однородное информационное СП
оптимальной фильтрации
рассмотрим однородное информационное СП ![]() , заданное на n-мерной сетке J
бесконечных размеров. Пусть на основе наблюдений
, заданное на n-мерной сетке J
бесконечных размеров. Пусть на основе наблюдений ![]() необходимо дать наилучшую (в смысле
минимума дисперсии ошибки) линейную оценку
необходимо дать наилучшую (в смысле
минимума дисперсии ошибки) линейную оценку ![]() элемента
элемента ![]() информационного СП. Условие минимума
информационного СП. Условие минимума ![]() запишется как система
линейных уравнений
запишется как система
линейных уравнений
![]() ,
(3.1)
,
(3.1)
которую можно рассматривать как n-мерный аналог уравнений
Винера-Хопфа: ![]() .
При этом минимально достижимая дисперсия ошибки
.
При этом минимально достижимая дисперсия ошибки ![]() . К сожалению, найти решение (3.1) удается
только для очень узкого класса "разделимых" экспоненциальных
корреляционных функций
. К сожалению, найти решение (3.1) удается
только для очень узкого класса "разделимых" экспоненциальных
корреляционных функций  [12, 28, 29]. Однако, полагая ячейки
пространственной сетки J
малыми по сравнению с интервалом корреляции СП, можно заменить систему (3.1)
одним интегральным уравнением и тогда
[12, 28, 29]. Однако, полагая ячейки
пространственной сетки J
малыми по сравнению с интервалом корреляции СП, можно заменить систему (3.1)
одним интегральным уравнением и тогда
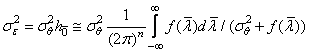 , (3.2)
, (3.2)
где
![]() (3.3)
(3.3)
- спектральная плотность СП ![]() . Итак, для анализа
эффективности фильтрации достаточно найти спектральную плотность (3.3)
информационного СП и произвести вычисления по формуле (3.2). При этом основные
трудности обычно связаны с n-кратным
интегрированием (3.3) и, особенно, (3.2). Эти трудности можно заметно снизить в
случаях, когда СП
. Итак, для анализа
эффективности фильтрации достаточно найти спектральную плотность (3.3)
информационного СП и произвести вычисления по формуле (3.2). При этом основные
трудности обычно связаны с n-кратным
интегрированием (3.3) и, особенно, (3.2). Эти трудности можно заметно снизить в
случаях, когда СП ![]() изотропно
во всем пространстве
изотропно
во всем пространстве ![]() или
на каких-либо подпространствах
или
на каких-либо подпространствах ![]() [12, 28]. Действительно, после введения
сферических координат [30] в
[12, 28]. Действительно, после введения
сферических координат [30] в ![]() формулы (3.3), (3.4) для изотропных СП
преобразуются к виду:
формулы (3.3), (3.4) для изотропных СП
преобразуются к виду:
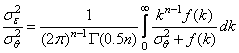 , (3.4)
, (3.4)
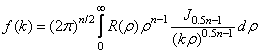 , (3.5)
, (3.5)
где ![]() - функция Бесселя порядка
- функция Бесселя порядка ![]() [31];
[31]; ![]() - полная гамма -
функция [31];
- полная гамма -
функция [31]; ![]() ;
;
![]() .
.
Для изотропных СП на пространствах с нечетным числом измерений функции Бесселя в (3.5) могут быть выражены через элементарные функции. В этих случаях расчеты по формулам (3.4), (3.5) выполняются достаточно просто. Например, для изотропных СП с
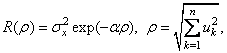
получим
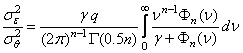 (3.6)
(3.6)
где ![]() - отношение дисперсий информационного и
мешающего СП;
- отношение дисперсий информационного и
мешающего СП; ![]() и
т. д.
и
т. д.
Для изотропных
экспоненциально - коррелированных СП, заданных на пространствах с четным числом
измерений ![]() ,
известно [31] простое выражение для интеграла (3.5):
,
известно [31] простое выражение для интеграла (3.5):
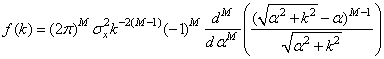 .
.
При этом минимальная
дисперсия ошибки фильтрации также может быть представлена в виде формулы (3.6),
где ![]() и т.д.
и т.д.
К сожалению, для больших
размерностей n однородных СП получаются довольно
громоздкие соотношения и при расчетах по формуле (3.6) целесообразно применять
численные методы. Вместе с тем, как показывает анализ, при увеличении
обобщенного параметра ![]() дисперсия
ошибки оптимальной фильтрации рассмотренных изотропных СП асимптотически
сходится к величине
дисперсия
ошибки оптимальной фильтрации рассмотренных изотропных СП асимптотически
сходится к величине
![]() ,
(3.7)
,
(3.7)
где ![]() .
.
Для иллюстрации скорости сходимости
на рис.8 приведены точные (сплошные линии) и приближенные (пунктир),
зависимости минимальной дисперсии ошибки фильтрации, найденные по формулам
(3.6) и (3.7) соответственно. Как следует из представленных графиков и
детального исследования качества аппроксимации, в области наиболее важных для
приложений малых значений ![]() полученная формула (3.7) дает хорошее
приближение для (3.5), (3.6). Близкие по характеру результаты можно получить
также для анизотропных СП с экспоненциальными корреляционными функциями [28].
полученная формула (3.7) дает хорошее
приближение для (3.5), (3.6). Близкие по характеру результаты можно получить
также для анизотропных СП с экспоненциальными корреляционными функциями [28].
Таким образом, приведенные соотношения дают возможности получения довольно простых оценок потенциальной точности фильтрации СП на фоне помех. Кроме того, полученные граничные значения дисперсии фильтрации позволяют построить характеристики оптимальных алгоритмов обнаружения пространственных аномалий на фоне мешающих многомерных изображений.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- Введение
- 1.1. Тензорные стохастические разностные уравнения
- 1.1. Тензорные стохастические разностные уравнения
- 1.2. Каузальные модели изображений
- 1.2. Каузальные модели изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 1.3. Авторегрессионные модели
- 2. Обнаружение аномалий на фоне мешающих изображений
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.1. Оптимальные алгоритмы обнаружения сигналов
- 2.2. Эффективность обнаружения аномалий
- 2.2. Эффективность обнаружения аномалий
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 2.3. Адаптивные рекуррентные алгоритмы декорреляции случайных полей
- 3. Фильтрация многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.1. Эффективность оптимальной фильтрации многомерных изображений
- 3.2. Тензорный фильтр Калмана
- 3.2. Тензорный фильтр Калмана
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.3. Рекуррентное оценивание многомерных изображений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- 3.4. Алгоритмы оценивания двумерных СП на основе моделей с кратными корнями характеристических уравнений
- Заключение
- Заключение
- Литература
- Литература
