| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. Критерий Байеса
Одним из возможных способов построения критерия
оптимальности может быть байесовский подход, общая методология которого
рассматривалась в предыдущем разделе применительно к задачам оценивания
параметров. Точно так же основой байесовского подхода к проблемам обнаружения
является введение функции потерь, которая приписывает каждой из четырех
возможных ситуаций (рис.3.2) определенную плату. При этом обычно правильным
решениям соответствует нулевой размер штрафа. Ошибке первого рода поставим в
соответствие плату ![]() ,
а ошибке второго рода – плату размером
,
а ошибке второго рода – плату размером ![]() . Тогда средние потери составят величину
. Тогда средние потери составят величину
![]() , (3.4)
, (3.4)
которая и принимается как критерий качества обнаружения. При этом
обнаружитель, для которого средние потери ![]() минимальны, называется оптимальным
байесовским обнаружителем.
минимальны, называется оптимальным
байесовским обнаружителем.
Подставляя выражения (3.1) и (3.2) в формулу (3.4), получим следующую связь средних потерь с видом критической области:
![]()
![]() . (3.5)
. (3.5)
Очевидно, потери минимальны, если интеграл
![]() (3.6)
(3.6)
достигает максимального значения.
Какие же точки пространства ![]() возможных исходов эксперимента следует
включить в область
возможных исходов эксперимента следует
включить в область ![]() для
максимизации выражения (3.6)? Простой анализ показывает, что при наблюдении
для
максимизации выражения (3.6)? Простой анализ показывает, что при наблюдении ![]() следует проверить –
положительным или отрицательным окажется подынтегральное выражение (3.6).
Если
следует проверить –
положительным или отрицательным окажется подынтегральное выражение (3.6).
Если
![]() , (3.7)
, (3.7)
то такую точку ![]() следует отнести к критической области
следует отнести к критической области ![]() . Действительно, после
добавления такой точки вместе с некоторой окрестностью к области
. Действительно, после
добавления такой точки вместе с некоторой окрестностью к области ![]() возрастает интеграл
(3.6) по этой области и, следовательно, уменьшаются средние потери (3.5). Таким
образом, неравенство (3.7) определяет все точки критической области
возрастает интеграл
(3.6) по этой области и, следовательно, уменьшаются средние потери (3.5). Таким
образом, неравенство (3.7) определяет все точки критической области ![]() . Но это, в свою
очередь, означает, что для наблюдений, удовлетворяющих неравенству (3.7),
следует принимать верной гипотезу
. Но это, в свою
очередь, означает, что для наблюдений, удовлетворяющих неравенству (3.7),
следует принимать верной гипотезу ![]() , а для остальных точек – гипотезу
, а для остальных точек – гипотезу ![]() . Переписывая
неравенство (3.7), определяющее критическую область, в форме
. Переписывая
неравенство (3.7), определяющее критическую область, в форме
![]() , (3.8)
, (3.8)
где ![]() –
отношение правдоподобия;
–
отношение правдоподобия; ![]() ; можно заметить, что формула (3.8)
определяет алгоритм обработки входных данных
; можно заметить, что формула (3.8)
определяет алгоритм обработки входных данных ![]() . Действительно, оптимальный обнаружитель
должен формировать на основе наблюдений
. Действительно, оптимальный обнаружитель
должен формировать на основе наблюдений ![]() отношение правдоподобия
отношение правдоподобия ![]() и производить сравнение
этого отношения с пороговым уровнем
и производить сравнение
этого отношения с пороговым уровнем ![]() . Если
. Если ![]() , то выносится решение в пользу
гипотезы
, то выносится решение в пользу
гипотезы ![]() . При
. При
![]() принимается,
что справедлива гипотеза
принимается,
что справедлива гипотеза ![]() . Так же, как и при оценивании
параметров, можно вместо отношения правдоподобия сравнивать с пороговым
уровнем любую монотонную функцию
. Так же, как и при оценивании
параметров, можно вместо отношения правдоподобия сравнивать с пороговым
уровнем любую монотонную функцию![]() , например,
, например, ![]() . При этом достаточно изменить величину
порога обнаружения и положить, что
. При этом достаточно изменить величину
порога обнаружения и положить, что ![]() .
.
Рассмотрим пример решения задачи поcледетекторного
обнаружения радиосигнала по совокупности независимых наблюдений ![]() . При отсутствии
сигнала эти наблюдения подчиняются закону распределения Релея:
. При отсутствии
сигнала эти наблюдения подчиняются закону распределения Релея:
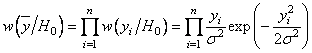 . (3.9)
. (3.9)
Появление полезного сигнала вызывает увеличение параметра ![]() в
в ![]() раз, где
раз, где ![]() – отношение сигнал/шум. При этом
– отношение сигнал/шум. При этом
 . (3.10)
. (3.10)
Для нахождения оптимального алгоритма обнаружения составим отношение правдоподобия
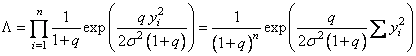
и будем сравнивать его с порогом ![]() , зависящим от априорных вероятностей
наличия
, зависящим от априорных вероятностей
наличия ![]() и
отсутствия
и
отсутствия ![]() полезного
сигнала и стоимостей
полезного
сигнала и стоимостей ![]() и
и
![]() ошибок. После
логарифмирования можно записать оптимальную процедуру обнаружения в виде
сравнения с пороговым значением
ошибок. После
логарифмирования можно записать оптимальную процедуру обнаружения в виде
сравнения с пороговым значением ![]() суммы квадратов наблюдений, т.е.
суммы квадратов наблюдений, т.е.
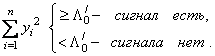 (3.11)
(3.11)
| << Предыдущий параграф | Следующий параграф >> |
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1.2. Случайные величины
- 1.2. Случайные величины
- 1.3. Системы случайных величин
- 1.3. Системы случайных величин
- 1.4. Функции случайных аргументов
- 1.4. Функции случайных аргументов
- 1.5. Марковские последовательности
- 1.5. Марковские последовательности
- 2. Оценивание параметров сигналов
- 2. Оценивание параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.3. Метод моментов
- 2.3. Метод моментов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.5. Скалярный фильтр Калмана
- 2.5. Скалярный фильтр Калмана
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.2. Критерий Байеса
- 3.2. Критерий Байеса
- 3.3. Критерий Неймана-Пирсона
- 3.3. Критерий Неймана-Пирсона
- 3.4. Вычисление вероятностей ошибок
- 3.4. Вычисление вероятностей ошибок
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- Список литературы
- Список литературы
