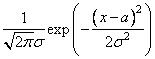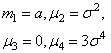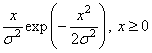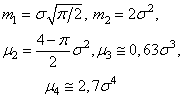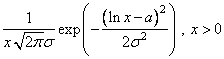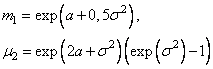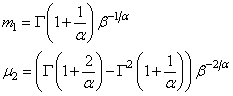1.3. Системы случайных величин

         В тех случаях, когда с каждым исходом  эксперимента связана пара чисел  и , соответствующее отображение  называется двумерной СB или системой двух СВ и обозначается . Например, если случайный сигнал  на выходе радиоприемного устройства наблюдается в два момента времени  и , то упорядоченная пара возможных значений сигнала  и  представляет собой двумерную CB .

         Двумерную СB  можно рассматривать как случайную точку или как случайный вектор на координатной плоскости. При этом каждому конкретному исходу опыта  ставится в соответствие точка плоскости с координатами  и .

                                                                                                                                Таблица 1.1

Функция распределения двумерной СB  определяется как вероятность совместного выполнения двух неравенств

                             ,                              (1.18)

т.е. как вероятность попадания  в квадрант плоскости с вершиной в точке . Отметим свойства функции распределения системы двух СВ, которые легко доказываются на основе (1.18):  . Последнее свойство позволяет найти вероятность попадания системы двух СВ в прямоугольник с вершинами в точках . Вместе с тем определение вероятности попадания системы СВ в произвольную плоскую область  на основе каких-либо алгебраических операций над функцией распределения невозможно. Подобные задачи решаются с помощью плотности распределения вероятностей (ПРВ) системы двух непрерывных СВ:

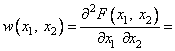
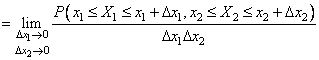                  .                   (1.19)

         Теперь вероятность попадания системы CB в произвольную плоскую область  может быть найдена по формуле

                          .                          (1.20)

Геометрически эта вероятность определяется объемом вертикального цилиндра, построенного на области  как на основании и ограниченного сверху поверхностью .

         Введенная ПРВ обладает следующими основными свойствами:

                    ,                             

,   .

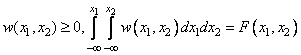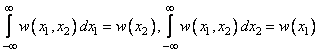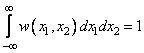         В качестве примера рассмотрим случайный вектор , распределенный  равномерно внутри эллипса с ПРВ:

                   .                            

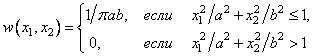Требуется найти ПРВ  и . Заметим, что  и при фиксированном значении  имеем  .

         Таким образом

     .

         Аналогично можно найти и . Заметим, что ПРВ компонентов не являются равномерными, несмотря на равномерное распределение системы СВ. Вместе с тем, если рассмотреть равномерное распределение системы не на эллипсе, а на прямоугольнике, то компоненты оказались бы распределены равномерно. Причины этих свойств СВ оказываются довольно глубокими и связаны с зависимостью или независимостью СВ.

         Для того, чтобы охарактеризовать зависимость между составляющими двумерной СВ вводится понятие условного распределения. Рассмотрим два события  и . Запишем выражение для условной вероятности  в виде

          .          (1.21)

         Условная вероятность (1.21) может рассматриваться как функция распределения СВ , построенная при условии, что СВ  принимает значения на интервале . Переходя в (1.21) к пределу при , введем условную функцию распределения

                   .                    (1.22)

Эту функцию удается выразить через ПРВ системы СВ, если подставить (1.21)  в  (1.22) и вычислить с помощью (1.20):

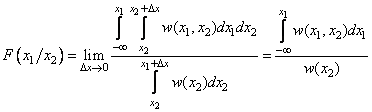             .             (1.23)

         Условная ПРВ определяется как частная производная от условной функции распределения:

                           .                                    

Заметим, что отсюда следует соотношение

                                ,                                (1.24)

которое можно назвать формулой Байеса для непрерывных СВ.

         Если условный закон распределения  не зависит от того, какое значение принимает СВ , т.е. при  СВ  и  называют независимыми. Можно показать, что для того, чтобы СB   и  были независимы, необходимо и достаточно, чтобы функция распределения (или ПРВ) системы  была равна произведению функций распределения  (или ПРВ) составляющих:

                .                (1.25)

         Для системы двух случайных величин , помимо числовых характеристик каждой из составляющих, вводится числовая характеристика их взаимозависимости – смешанный второй центральный момент, или ковариация:

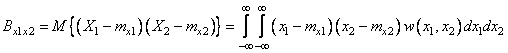.         (1.26)

Если CB  и  независимы, то  и .  В другом крайнем случае, когда , ковариация .

         Используя неравенство Коши-Буняковского , можно показать, что . Поскольку ковариация имеет размерность, равную произведению размерностей СВ  и , то для характеристики зависимости между СВ удобно использовать безразмерный коэффициент корреляции:

                                    .                                     (1.27)

Нетрудно убедиться, что для независимых СВ ; если же , то  ; в общем случае .

         Две СВ, для которых , называются некоррелированными. Следует отметить, что понятие некоррелированности шире понятия независимости, т.е. существуют некоррелированные, но зависимые случайные величины. Например, если , то, очевидно,  и  зависимы. Действительно, при известном значении  , находим . Вместе с тем . Таким образом, СВ  и  зависимы, но некоррелированны.

         Однако существует важнейший класс систем нормальных СВ, для которых понятия независимости и некоррелированности эквивалентны. Двумерная ПРВ нормальных CВ  и  записывается в виде

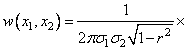
.           (1.28)

         Заметим, что параметры ПРВ (1.28) имеют следующий смысл: . Для некоррелированных нормальных СВ   и в этом случае, , т.е. некоррелированные нормальные СВ независимы.

         Можно компактно записать формулу (1.28), если ввести следующие обозначения: 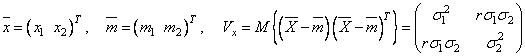. При этом матрица  составлена из вторых центральных моментов системы  и называется ковариационной матрицей случайного вектора . С учетом введенных обозначений

,            (1.29)

где  – обратная матрица; .

         Все приведенные результаты могут быть перенесены на –мерные СВ. Если каждому возможному исходу испытания поставить в соответствие совокупность  чисел, то в результате получаем систему    одномерных СB или –мерный вектор  . Функция распределения системы СВ

                                      (1.30)

и плотность распределения вероятностей

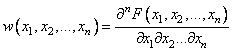                                                        (1.31)

вводятся как прямое обобщение определений этих функций для системы двух СВ. Так же, как и для системы двух СВ, могут быть установлены следующие свойства:

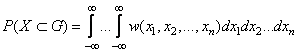,                       (1.32)

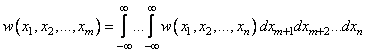              ,              (1.33)

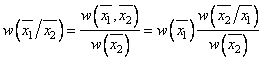                        ,                        (1.34)

где  ;. Для системы независимых СВ:

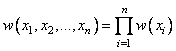                                 .                                 (1.35)

         Числовые характеристики системы  случайных величин объединяются в вектор математического ожидания  и ковариационную матрицу

                 .                         

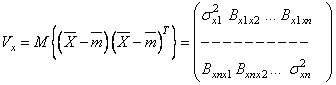C учетом этих обозначений система нормальных СB может быть задана ПРВ (1.29). Заметим, что система произвольного числа некоррелированных нормальных СВ является одновременно и системой независимых СВ. Для таких СВ ковариации  при всех  , и поэтому матрица   является диагональной.