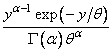| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Метод максимального правдоподобия и метод моментов
Прежде чем перейти к задачам с изменяющимися параметрами,
рассмотрим более подробно оценивание постоянных параметров при равномерном
априорном распределении ![]() . В этом случае оптимальным байесовским
методом нахождения оценок при простой функции потерь является метод
максимального правдоподобия. Этот же метод является основным и в том случае,
когда априорное распределение не задано. Тогда говорят об оценке
неизвестного параметра
. В этом случае оптимальным байесовским
методом нахождения оценок при простой функции потерь является метод
максимального правдоподобия. Этот же метод является основным и в том случае,
когда априорное распределение не задано. Тогда говорят об оценке
неизвестного параметра ![]() по наблюдениям
по наблюдениям ![]() .
.
Качество оценок неизвестных параметров принято определять с помощью следующих основных характеристик.
1. Несмещенность. Оценка ![]() называется несмещенной оценкой параметра
называется несмещенной оценкой параметра ![]() , если математическое
ожидание этой оценки равно оцениваемому параметру, т.е.
, если математическое
ожидание этой оценки равно оцениваемому параметру, т.е. ![]() .
.
2. Состоятельность. Оценка ![]() параметра
параметра ![]() называется состоятельной, если она
сходится по вероятности к оцениваемому параметру при неограниченном увеличении
числа опытов
называется состоятельной, если она
сходится по вероятности к оцениваемому параметру при неограниченном увеличении
числа опытов ![]() ,
т.е. при любом
,
т.е. при любом ![]() выполняется
условие
выполняется
условие 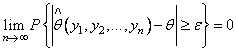 .
С помощью неравенства Чебышева [1-3] можно показать, что достаточным
условием состоятельности несмещенной оценки является уменьшение дисперсии
ошибки до нуля при
.
С помощью неравенства Чебышева [1-3] можно показать, что достаточным
условием состоятельности несмещенной оценки является уменьшение дисперсии
ошибки до нуля при ![]() .
.
3. Эффективность. Оценка ![]() называется эффективной, если средний
квадрат ошибки, вычисленный для
называется эффективной, если средний
квадрат ошибки, вычисленный для ![]() , не больше, чем для любой другой оценки
, не больше, чем для любой другой оценки ![]() этого параметра:
этого параметра:
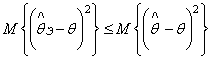 .
.
Для несмещенной оценки средний квадрат ошибки равен
дисперсии. Поэтому эффективная несмещенная оценка определяется из условия
минимума дисперсии ошибки 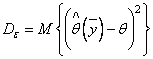 .
.
Существует неравенство [15], с помощью которого можно определить нижнюю границу дисперсии несмещенных оценок. Это позволяет на основе сравнения действительного значения дисперсии ошибки с минимальным дать характеристику качества той или иной оценки.
Предположим, что границы области значений ![]() , где ПРВ
, где ПРВ ![]() отлична от нуля,
не зависят от
отлична от нуля,
не зависят от ![]() .
Пусть
.
Пусть ![]() –несмещенная
оценка параметра
–несмещенная
оценка параметра ![]() ,
т.е.
,
т.е.
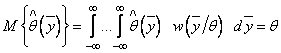 ,
,
где ![]() .
.
Продифференцируем обе части этого равенства по ![]() , используя
предположение о независимости пределов интегрирования от
, используя
предположение о независимости пределов интегрирования от ![]() . В результате
получим:
. В результате
получим:
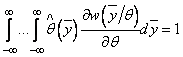
или
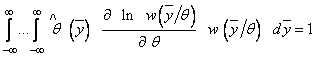 .
.
Последнее выражение с учетом основной теоремы о математическом ожидании можно компактно переписать следующим образом:
![]() . (2.17)
. (2.17)
Кроме того, из очевидного условия
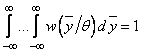
дифференцированием по ![]() находим
находим ![]() . Умножая правую и левую части этого
равенства на
. Умножая правую и левую части этого
равенства на ![]() и
вычитая из (2.17), получим
и
вычитая из (2.17), получим
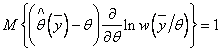 . (2.18)
. (2.18)
Левая часть (2.18) представляет ковариацию ![]() двух СВ
двух СВ ![]() и
и ![]() , имеющих нулевые средние. Как
известно,
, имеющих нулевые средние. Как
известно, ![]() или
или
![]() . После
подстановки выражений для
. После
подстановки выражений для ![]() и
и ![]() в это неравенство получим с учетом
(2.18) следующее соотношение:
в это неравенство получим с учетом
(2.18) следующее соотношение:
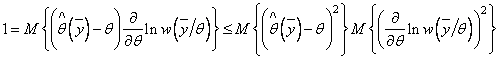 . (2.19)
. (2.19)
При 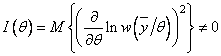 соотношение (2.19) можно переписать в
виде, известном как неравенство Рао-Крамера [15]:
соотношение (2.19) можно переписать в
виде, известном как неравенство Рао-Крамера [15]:
![]() , (2.20)
, (2.20)
где 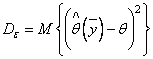 – дисперсия ошибки
оценивания параметра
– дисперсия ошибки
оценивания параметра ![]() .
.
Неотрицательная величина ![]() называется информацией, содержащейся
в выборке (по Р.Фишеру). При независимых наблюдениях
называется информацией, содержащейся
в выборке (по Р.Фишеру). При независимых наблюдениях
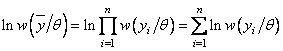
и
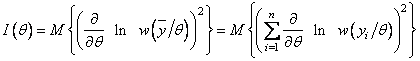 .
.
Так как ![]() , а дисперсия суммы
независимыых СВ равна сумме дисперсий, то количество информации по Фишеру для
независимых
, а дисперсия суммы
независимыых СВ равна сумме дисперсий, то количество информации по Фишеру для
независимых ![]() находится
по формуле:
находится
по формуле:
![]() , (2.21)
, (2.21)
где 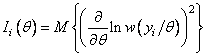 . При независимых наблюдениях с
одним и тем же распределением
. При независимых наблюдениях с
одним и тем же распределением ![]() количество информации
количество информации ![]() пропорционально числу
пропорционально числу ![]() наблюдений. В этом
случае (2.20) запишется в виде:
наблюдений. В этом
случае (2.20) запишется в виде:
![]() . (2.22)
. (2.22)
Правая часть неравенства Рао-Крамера определяет нижнюю
границу ![]() для дисперсии
ошибки оценивания параметра
для дисперсии
ошибки оценивания параметра ![]() при заданной ПРВ
при заданной ПРВ ![]() наблюдений. Если удается найти
несмещенную оценку
наблюдений. Если удается найти
несмещенную оценку ![]() с
дисперсией
с
дисперсией 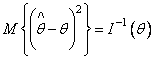 ,
то эта оценка будет эффективной. Однако далеко не всегда минимальная дисперсия
ошибки, т.е. дисперсия
,
то эта оценка будет эффективной. Однако далеко не всегда минимальная дисперсия
ошибки, т.е. дисперсия 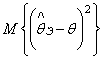 эффективной оценки, совпадает с нижней
границей
эффективной оценки, совпадает с нижней
границей ![]() . Во
многих случаях
. Во
многих случаях 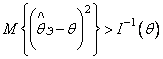 .
.
Рассмотрим два примера нахождения нижних границ дисперсии
ошибки при оценивании параметров нормального и экспоненциального
распределений. Предположим, что производятся независимые наблюдения ![]() с ПРВ
с ПРВ
![]() ,
,
содержащей неизвестный параметр ![]() – математическое ожидание СВ
– математическое ожидание СВ ![]() . Запишем выражение для
. Запишем выражение для ![]() , найдем производную
, найдем производную ![]() и количество
информации
и количество
информации ![]() в
одном наблюдении. Поскольку
в
одном наблюдении. Поскольку ![]() , то для дисперсии любой оценки
, то для дисперсии любой оценки ![]() параметра
параметра ![]() справедливо неравенство
справедливо неравенство
![]() . В
рассмотренной задаче для оценки математического ожидания можно предложить
среднее арифметическое наблюдений
. В
рассмотренной задаче для оценки математического ожидания можно предложить
среднее арифметическое наблюдений ![]() . Дисперсия этой оценки
. Дисперсия этой оценки
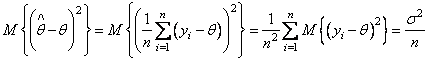
совпадает с нижней границей. Следовательно, предложенная оценка является эффективной.
Другим примером может быть оценка параметра ![]() экспоненциального
распределения
экспоненциального
распределения ![]() .
Нижняя граница дисперсии ошибки равна
.
Нижняя граница дисперсии ошибки равна ![]() , так как
, так как ![]() . Вместе с тем анализ всех возможных оценок
. Вместе с тем анализ всех возможных оценок
![]() показывает,
что нижней границы
показывает,
что нижней границы ![]() достичь
не удается. Минимальную дисперсию
достичь
не удается. Минимальную дисперсию ![]() , но большую чем
, но большую чем ![]() , имеет эффективная несмещенная
оценка
, имеет эффективная несмещенная
оценка ![]() . Изменим
условия этого примера и поставим задачу оценки параметра
. Изменим
условия этого примера и поставим задачу оценки параметра ![]() экспоненциального
распределения:
экспоненциального
распределения:
![]() . Тогда
. Тогда
![]()
![]() , и существует
эффективная оценка
, и существует
эффективная оценка ![]() ,
дисперсия которой
,
дисперсия которой ![]() совпадает
с нижней границей
совпадает
с нижней границей ![]() .
.
В каких же случаях эффективные оценки имеют дисперсию,
совпадающую с нижней границей ![]() ? Для ответа на этот вопрос обратимся к
выводу соотношения (2.19). Точное равенство в (2.19) достигается, когда СВ
? Для ответа на этот вопрос обратимся к
выводу соотношения (2.19). Точное равенство в (2.19) достигается, когда СВ ![]() и
и ![]() при каждом значении
при каждом значении ![]() связаны линейной
зависимостью
связаны линейной
зависимостью
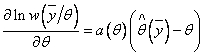 . (2.23)
. (2.23)
Полученное выражение дает описание семейства ПРВ ![]() и соответствующих
оценок
и соответствующих
оценок ![]() ,
обеспечивающих равенство в формулах (2.19), (2.20), т.е. эффективное оценивание
с дисперсией
,
обеспечивающих равенство в формулах (2.19), (2.20), т.е. эффективное оценивание
с дисперсией ![]() .
После интегрирования (2.23) по
.
После интегрирования (2.23) по ![]() семейство таких ПРВ может быть
представлено в виде:
семейство таких ПРВ может быть
представлено в виде:
![]() ,
(2.24)
,
(2.24)
где ![]() и
и
![]() –
дифференцируемые функции
–
дифференцируемые функции ![]() ;
; ![]() – произвольная функция
– произвольная функция ![]() . При этом
. При этом ![]() служит эффективной оценкой
параметра
служит эффективной оценкой
параметра ![]() с
дисперсией
с
дисперсией ![]() .
Для конкретных ПРВ запись в форме (2.24) обычно содержит функции
.
Для конкретных ПРВ запись в форме (2.24) обычно содержит функции ![]() и
и ![]() от собственных параметров
соответствующих распределений, например,
от собственных параметров
соответствующих распределений, например, ![]() и
и ![]() – для экспоненциального или
– для экспоненциального или ![]() и
и ![]() – для нормального распределения.
В этом случае параметр
– для нормального распределения.
В этом случае параметр ![]() может быть найден как функция
может быть найден как функция ![]() с помощью соотношения
с помощью соотношения ![]() . Например, для
. Например, для ![]() , совместная ПРВ
запишется в виде:
, совместная ПРВ
запишется в виде: ![]() ,
где
,
где ![]() ;
; ![]() ;
; ![]() . После дифференцирования находим
параметр
. После дифференцирования находим
параметр ![]() ,
для которого
,
для которого ![]() является
оптимальной оценкой.
является
оптимальной оценкой.
Таким образом, эффективные оценки ![]() с дисперсией, в точности равной
нижней границе
с дисперсией, в точности равной
нижней границе ![]() могут
быть получены только для ПРВ
могут
быть получены только для ПРВ ![]() , входящих в экспоненциальное семейство
(2.24). К этому семейству относятся часто встречающиеся в задачах обработки
сигналов нормальное, биномиальное, пуассоновское и
гамма-распределение. Для каждого из этих распределений
существует определенная условиями (2.24) форма записи и соответствующая
оценка
, входящих в экспоненциальное семейство
(2.24). К этому семейству относятся часто встречающиеся в задачах обработки
сигналов нормальное, биномиальное, пуассоновское и
гамма-распределение. Для каждого из этих распределений
существует определенная условиями (2.24) форма записи и соответствующая
оценка ![]() параметра
(табл.2.1).
параметра
(табл.2.1).
Таблица 2.1
|
Тип распределения |
ПРВ |
|
|
|
1 |
2 |
3 |
4 |
|
Нормальное |
|
|
|
|
Нормальное |
|
|
|
|
Гамма |
|
|
|
|
Биномиальное |
|
|
|
|
Пуассоновское |
|
|
|
Рассмотрим, например, нормальное распределение ![]()
![]() с
неизвестным параметром
с
неизвестным параметром ![]() . Запишем в экспоненциальном виде
совместную ПРВ:
. Запишем в экспоненциальном виде
совместную ПРВ:
 ,
,
где ![]() ;
;![]() ;
;![]() . При этом
. При этом ![]() является эффективной оценкой
параметра
является эффективной оценкой
параметра ![]() .
.
Полученные результаты позволяют определить нижнюю границу ![]() дисперсии ошибки
(2.20), (2.21) и указать эффективные оценки с дисперсией
дисперсии ошибки
(2.20), (2.21) и указать эффективные оценки с дисперсией ![]() определенных параметров ПРВ из
экспоненциального семейства (2.24). В общем случае основным методом поиска
эффективных оценок параметров служит метод максимального правдоподобия
[1,11-16,26]. Наилучшей считается оценка
определенных параметров ПРВ из
экспоненциального семейства (2.24). В общем случае основным методом поиска
эффективных оценок параметров служит метод максимального правдоподобия
[1,11-16,26]. Наилучшей считается оценка ![]() , для которой функция правдоподобия
, для которой функция правдоподобия ![]() или
или ![]() достигает максимума,
т.е.
достигает максимума,
т.е. ![]() . Если
. Если ![]() дифференцируема и
максимум
дифференцируема и
максимум ![]() находится
во внутренней точке области возможных значений параметра
находится
во внутренней точке области возможных значений параметра ![]() , то оценка может быть
определена из уравнений
, то оценка может быть
определена из уравнений ![]() или
или ![]() . Оценки
. Оценки ![]() совокупности
совокупности ![]() параметров
параметров ![]() ПРВ
ПРВ ![]() находятся с помощью решения системы
уравнений правдоподобия:
находятся с помощью решения системы
уравнений правдоподобия:
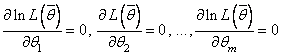 , (2.25)
, (2.25)
где ![]() –
функция правдоподобия. Напомним, что по определению
–
функция правдоподобия. Напомним, что по определению ![]() получается после подстановки
результатов наблюдений
получается после подстановки
результатов наблюдений ![]() в ПРВ
в ПРВ ![]() . Метод максимального правдоподобия
позволяет найти эффективные оценки параметров, если такие оценки существуют.
Поэтому оценки
. Метод максимального правдоподобия
позволяет найти эффективные оценки параметров, если такие оценки существуют.
Поэтому оценки ![]() ,
представленные в табл. 2.1, могут быть получены и с помощью решения
уравнений правдоподобия. Например, для нормального распределения
,
представленные в табл. 2.1, могут быть получены и с помощью решения
уравнений правдоподобия. Например, для нормального распределения ![]()
![]() , логарифм функции правдоподобия
запишется в виде:
, логарифм функции правдоподобия
запишется в виде: ![]() .
Из уравнения
.
Из уравнения ![]() находим
эффективную оценку
находим
эффективную оценку ![]() .
.
Рассмотрим более сложный пример оценки неизвестного
параметра ![]() равномерного
распределения с ПРВ:
равномерного
распределения с ПРВ:
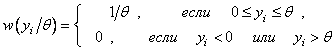 . (2.26)
. (2.26)
Функция правдоподобия 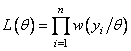 находится после подстановки
экспериментальных данных
находится после подстановки
экспериментальных данных ![]() в (2.26). Если переменное значение
в (2.26). Если переменное значение ![]() удовлетворяет
неравенствам
удовлетворяет
неравенствам ![]() ,
т.е.
,
т.е. ![]() , то
, то![]() . При
. При ![]() функция правдоподобия
функция правдоподобия ![]() , поскольку в этом
случае хотя бы один из сомножителей
, поскольку в этом
случае хотя бы один из сомножителей ![]() обращается в ноль.
обращается в ноль.
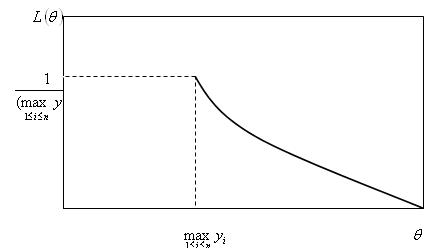
Рис. 2.1. Функция правдоподобия при оценке параметра равномерного распределения
Анализ зависимости ![]() , представленной на рис.2.1, показывает,
что наибольшее значение функции правдоподобия находится в точке
, представленной на рис.2.1, показывает,
что наибольшее значение функции правдоподобия находится в точке ![]() .
.
Следовательно, ![]() – оценка максимального правдоподобия
(ОМП). Заметим, что эта оценка не может быть получена с помощью решения
уравнения правдоподобия, так как в точке
– оценка максимального правдоподобия
(ОМП). Заметим, что эта оценка не может быть получена с помощью решения
уравнения правдоподобия, так как в точке ![]() функция
функция ![]() имеет разрыв, и производная
имеет разрыв, и производная ![]() не существует.
не существует.
Определим математическое ожидание и дисперсию полученной оценки
![]() . Для
наибольшего значения
. Для
наибольшего значения ![]() совокупности
совокупности
![]() случайных
величин вначале найдем функцию распределения
случайных
величин вначале найдем функцию распределения
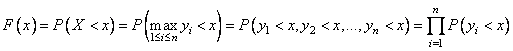 .
При равномерном законе распределения
.
При равномерном законе распределения ![]() , если
, если ![]() . Поэтому
. Поэтому ![]() , а
, а ![]() . Теперь уже нетрудно вычислить
математическое ожидание оценки
. Теперь уже нетрудно вычислить
математическое ожидание оценки 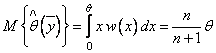 . Как следует из этой формулы, ОМП
. Как следует из этой формулы, ОМП ![]() оказывается смещенной,
но смещение можно устранить, если использовать оценку
оказывается смещенной,
но смещение можно устранить, если использовать оценку ![]() . Точность скорректированной
оценки характеризуется дисперсией
. Точность скорректированной
оценки характеризуется дисперсией
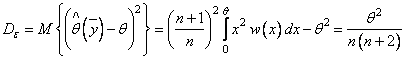 . (2.27)
. (2.27)
Интересно, что дисперсия оценки параметра ![]() равномерного
распределения при увеличении числа
равномерного
распределения при увеличении числа ![]() наблюдений убывает как
наблюдений убывает как ![]() . Это исключение из
правила (2.20), (2.21), согласно которому, для всех «гладких» ПРВ
. Это исключение из
правила (2.20), (2.21), согласно которому, для всех «гладких» ПРВ ![]() при независимых
наблюдениях
при независимых
наблюдениях ![]() .
.
Примером задачи оценивания векторного параметра ![]() может служить
нормальное распределение с ПРВ
может служить
нормальное распределение с ПРВ
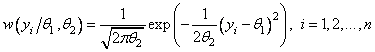 .
.
В этом случае ОМП находится из решения следующих уравнений правдоподобия:
![]() ,
,
![]() .
.
В результате получаем совместные ОМП математического ожидания и дисперсии:
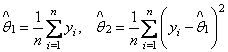 . (2.28)
. (2.28)
Важным свойством ОМП является инвариантность относительно
взаимно однозначных преобразований ![]() параметра
параметра ![]() . Это означает, что при известных ОМП
. Это означает, что при известных ОМП ![]() и функции
и функции ![]() может быть легко
найдена ОМП
может быть легко
найдена ОМП ![]() .
Действительно, так как существует обратная функция
.
Действительно, так как существует обратная функция ![]() , то
, то ![]() .
.
Принцип инвариантности позволяет в каждой конкретной задаче
выбирать наиболее удобную параметризацию, а ОМП получать затем с помощью
соответствующих преобразований. Пусть в условиях нормальной модели с двумя
неизвестными параметрами требуется оценить параметрическую функцию 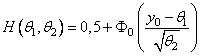 , представляющую собой
вероятность
, представляющую собой
вероятность ![]() .
В этом случае можно положить, например,
.
В этом случае можно положить, например, ![]() и, согласно принципу инвариантности, ОМП
и, согласно принципу инвариантности, ОМП 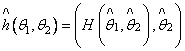 . Учитывая (2.28),
находим
. Учитывая (2.28),
находим
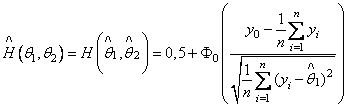 .
.
Метод максимального правдоподобия не всегда приводит к
несмещенным оценкам. Так, при оценке (2.27) двух параметров нормального
распределения ОМП ![]() имеет
смещение
имеет
смещение ![]() ,
убывающее до нуля при
,
убывающее до нуля при ![]() .
Доказано [15], что для широкого класса ПРВ
.
Доказано [15], что для широкого класса ПРВ ![]() оценки максимального правдоподобия
асимптотически (при
оценки максимального правдоподобия
асимптотически (при ![]() )
несмещенные и асимптотически нормальные с дисперсией ошибки, совпадающей
при
)
несмещенные и асимптотически нормальные с дисперсией ошибки, совпадающей
при ![]() с нижней
границей
с нижней
границей ![]() в неравенстве
Рао-Крамера (2.20). Описанные свойства обусловили широкое применение метода
максимального правдоподобия в разнообразных приложениях.
в неравенстве
Рао-Крамера (2.20). Описанные свойства обусловили широкое применение метода
максимального правдоподобия в разнообразных приложениях.
Рассмотрим пример нахождения ОМП углового положения цели в
условиях работы импульсной радиолокационной станции (РЛС) кругового обзора.
Отраженные от цели полезные сигналы на выходе приемника РЛС представим в виде: ![]() , где
, где ![]() – максимальное значение
сигнала в момент равенства углового положения
– максимальное значение
сигнала в момент равенства углового положения ![]() антенны РЛС и углового положения
антенны РЛС и углового положения ![]() цели. Функция
цели. Функция ![]() описывает изменение
уровня сигнала (рис.2.2.а) в дискретном времени при вращении антенны. Прием
отраженных сигналов обычно сопровождается помехами. Поэтому наблюдения
описывает изменение
уровня сигнала (рис.2.2.а) в дискретном времени при вращении антенны. Прием
отраженных сигналов обычно сопровождается помехами. Поэтому наблюдения ![]() , включают независимые
гауссовские СВ
, включают независимые
гауссовские СВ ![]() с
нулевыми средними и дисперсиями
с
нулевыми средними и дисперсиями ![]() . На основе анализа наблюдений необходимо
дать оценку
. На основе анализа наблюдений необходимо
дать оценку ![]() углового
положения цели.
углового
положения цели.
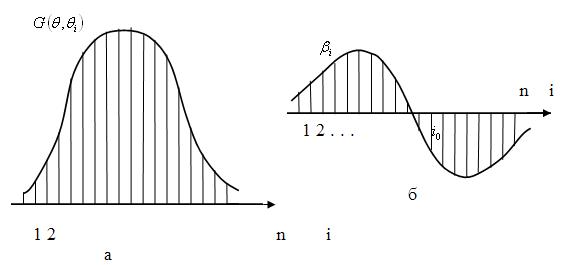
Рис. 2.2. Огибающая пакета отраженных сигналов (а) и ее производная (б)
Для решения поставленной задачи найдем функцию правдоподобия
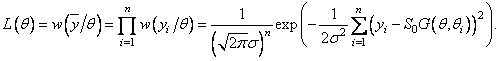
После логарифмирования ![]() и дифференцирования по параметру
и дифференцирования по параметру ![]() получим следующее
уравнение правдоподобия:
получим следующее
уравнение правдоподобия:
![]() .
.
При
симметричной диаграмме направленности антенны РЛС ![]() и уравнение правдоподобия
принимает следующий вид:
и уравнение правдоподобия
принимает следующий вид:
![]() , (2.29)
, (2.29)
где ![]() – весовые коэффициенты
(рис. 2.2, б).
– весовые коэффициенты
(рис. 2.2, б).
Выражение (2.29) определяет необходимые операции над
наблюдениями ![]() при
оценивании углового положения цели. Основными из них являются следующие:
при
оценивании углового положения цели. Основными из них являются следующие:
– прием и запоминание амплитуд ![]() суммы сигнала и помех;
суммы сигнала и помех;
– умножение этих амплитуд на весовые коэффициенты ![]() ;
;
– образование полусумм ![]() и
и 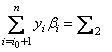 , где
, где ![]() – точка, в которой весовая функция
обращается в ноль;
– точка, в которой весовая функция
обращается в ноль;
– сравнение накопленных полусумм по величине;
– фиксация равенства полусумм и формирование оценки ![]() .
.
Расчет дисперсии найденной оценки углового положения цели
вызывает трудности, поскольку решить уравнение (2.29) относительно ![]() не удается. В подобных
случаях вместо точного значения дисперсии часто используют нижнюю границу
не удается. В подобных
случаях вместо точного значения дисперсии часто используют нижнюю границу ![]() , определяемую
неравенством Рао-Крамера (2.20). Рассмотренные свойства ОМП гарантируют, что
при большом числе наблюдений
, определяемую
неравенством Рао-Крамера (2.20). Рассмотренные свойства ОМП гарантируют, что
при большом числе наблюдений ![]() такой подход не приведет к
значительным ошибкам. Вместе с тем расчет по формулам (2.20), (2.21)
оказывается довольно простым. Учитывая независимость наблюдений, находим
количество информации
такой подход не приведет к
значительным ошибкам. Вместе с тем расчет по формулам (2.20), (2.21)
оказывается довольно простым. Учитывая независимость наблюдений, находим
количество информации
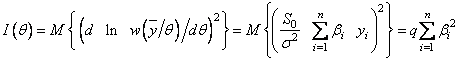 ,
,
где ![]() –
отношение сигнал/шум. Таким образом, нижняя граница дисперсии оценки
–
отношение сигнал/шум. Таким образом, нижняя граница дисперсии оценки ![]() легко вычисляется при
заданной огибающей
легко вычисляется при
заданной огибающей ![]() пакета
отраженных сигналов. Заметим, что для малых объемов выборки действительные
значения дисперсии оценки (2.29) могут оказаться больше, чем
пакета
отраженных сигналов. Заметим, что для малых объемов выборки действительные
значения дисперсии оценки (2.29) могут оказаться больше, чем ![]() . Поэтому возможность
применения приближенных соотношений должна контролироваться с помощью
методов статистического моделирования [30].
. Поэтому возможность
применения приближенных соотношений должна контролироваться с помощью
методов статистического моделирования [30].
Несмотря на отмеченные достоинства метода максимального
правдоподобия, существует ряд задач оценивания, в которых его применение
сталкивается со значительными математическими или вычислительными
трудностями нахождения максимума ![]() . В таких случаях часто используется метод
моментов [15,26], не обладающий свойствами асимптотической оптимальности,
но часто приводящий к сравнительно простым вычислениям.
. В таких случаях часто используется метод
моментов [15,26], не обладающий свойствами асимптотической оптимальности,
но часто приводящий к сравнительно простым вычислениям.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1. Элементы теории вероятностей
- 1.1. Вероятности случайных событий
- 1.2. Случайные величины
- 1.2. Случайные величины
- 1.3. Системы случайных величин
- 1.3. Системы случайных величин
- 1.4. Функции случайных аргументов
- 1.4. Функции случайных аргументов
- 1.5. Марковские последовательности
- 1.5. Марковские последовательности
- 2. Оценивание параметров сигналов
- 2. Оценивание параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.1. Оптимальное оценивание постоянных параметров сигналов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.2. Метод максимального правдоподобия и метод моментов
- 2.3. Метод моментов
- 2.3. Метод моментов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.4. Рекуррентное оценивание изменяющихся параметров сигналов
- 2.5. Скалярный фильтр Калмана
- 2.5. Скалярный фильтр Калмана
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 2.6. Векторный фильтр Калмана
- 3. Обнаружение сигналов
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.1. Обнаружение сигналов при известных параметрах помех
- 3.2. Критерий Байеса
- 3.2. Критерий Байеса
- 3.3. Критерий Неймана-Пирсона
- 3.3. Критерий Неймана-Пирсона
- 3.4. Вычисление вероятностей ошибок
- 3.4. Вычисление вероятностей ошибок
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- 3.5. Обнаружение сигналов при неизвестных параметрах помех
- Список литературы
- Список литературы