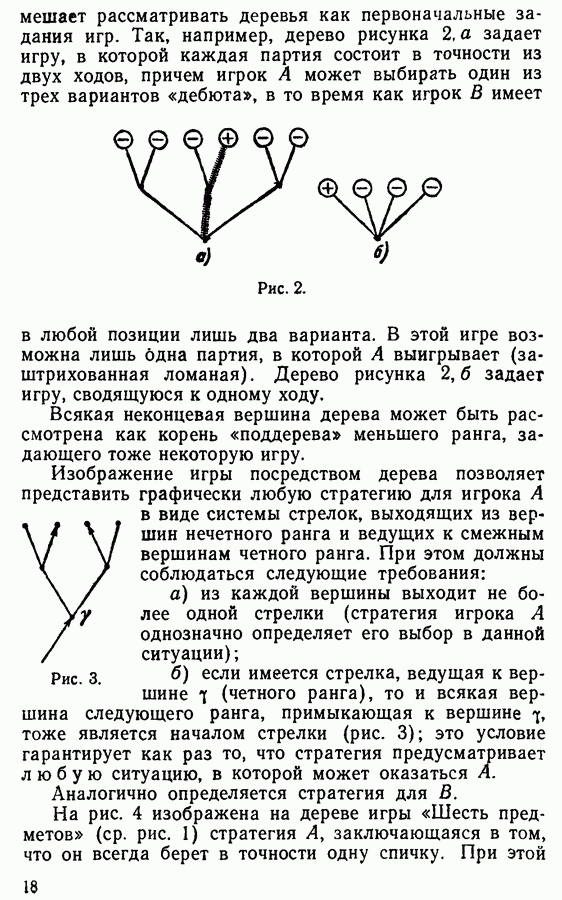
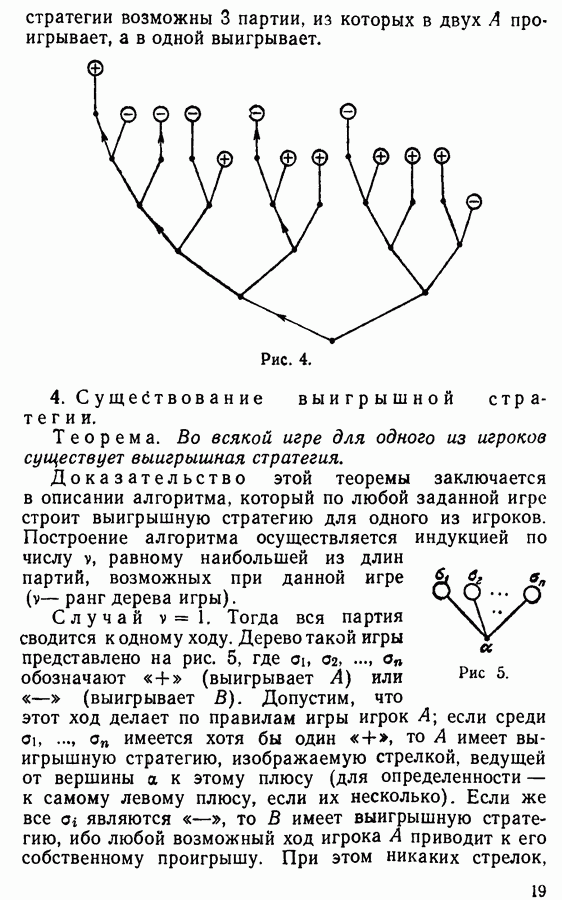
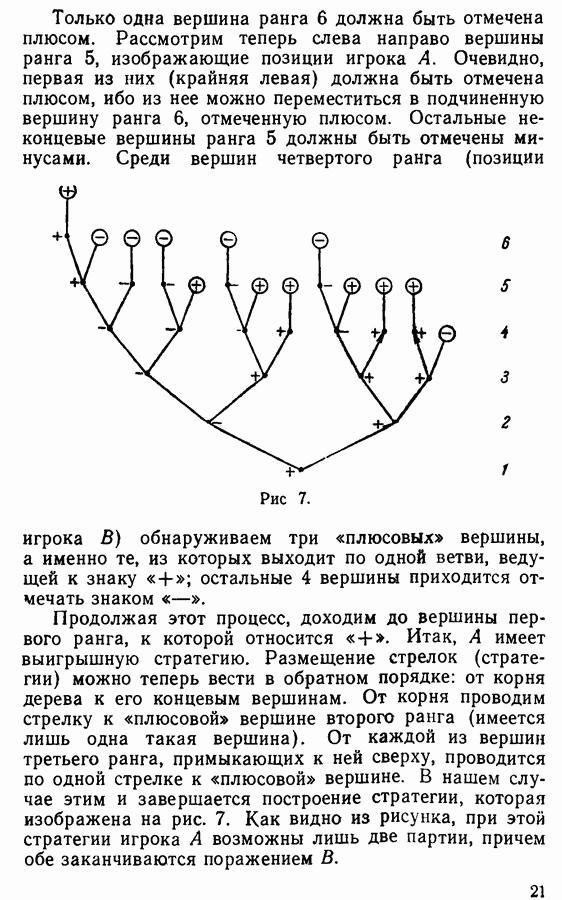
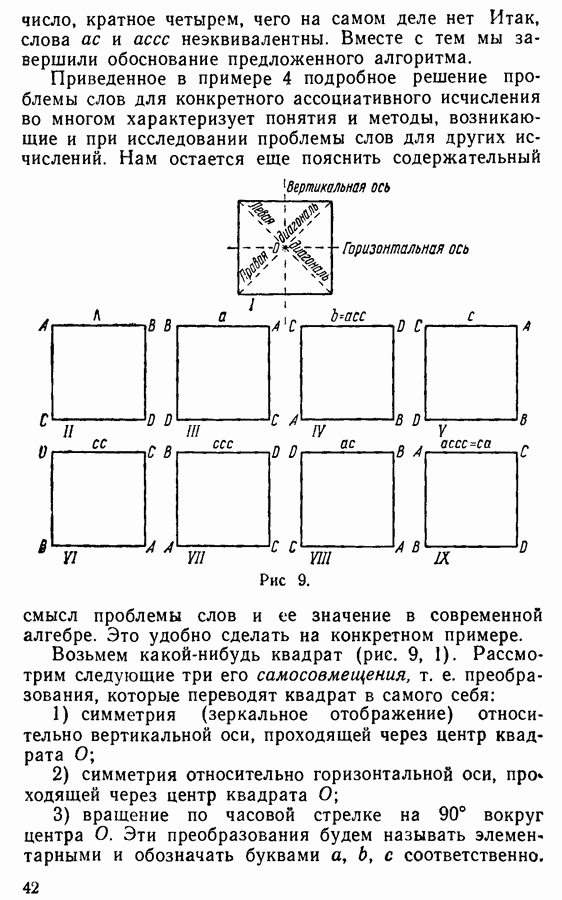
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. МАШИНА ТЬЮРИНГА
Отличительные особенности машины Тьюринга по сравнению с электронными машинами, описанными в §§ 5, 6, заключаются в следующем:
1. В машине Тьюринга расчленение процесса на простые элементарные операции доведено в известном смысле до предельной возможности. Так, например, операция сложения, фигурирующая в электронной машине как единичная элементарная операция, здесь сама расчленяется на цепочку еще более простых операций.
Разумеется, это значительно удлиняет процесс, реализуемый в машине Тьюринга, но вместе с тем логическая структура процесса сильно упрощается и приобретает весьма удобный для теоретических исследований стандартный вид.
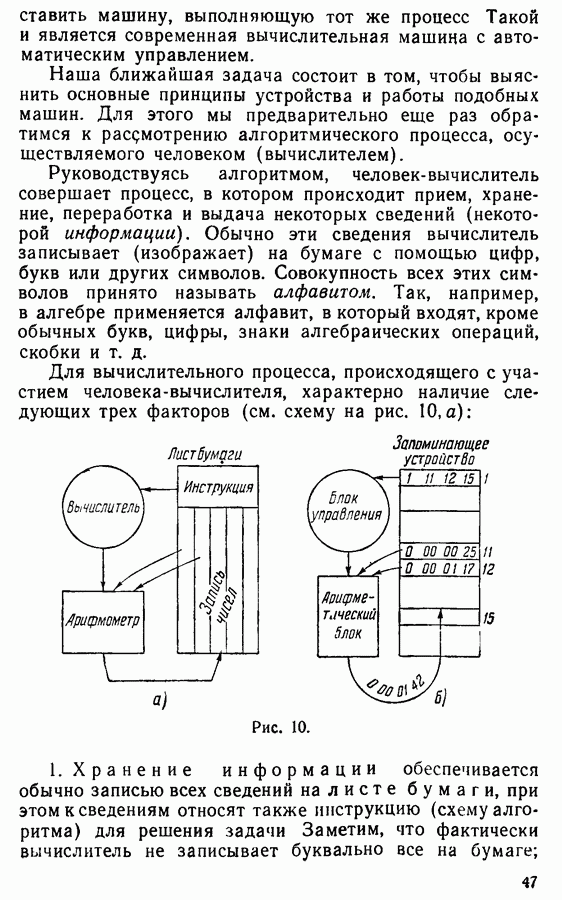
2. В машине Тьюринга часть памяти изображается в виде неограниченной с обеих сторон ленты, разбитой на ячейки.
Очевидно, ни в одной реально осуществимой машине не может быть бесконечной памяти (бесконечной ленты), и в этом смысле машина Тьюринга представляет собою лишь идеализированную схему, отображающую потенциальную возможность увеличения объема памяти.
Такая идеализация оправдывается ранее уже отмечавшейся связью между понятием алгоритма и понятием машины с потенциально неограниченной памятью.
Перейдем теперь к подробному описанию машины Тьюринга.
1. Машина располагает конечным числом знаков (символов)

образующих так называемый внешний алфавит, в котором кодируются сведения, подаваемые в машину, а также те, которые вырабатываются в ней. Для общности последующих рассмотрений удобно принять, что среди знаков внешнего алфавита имеется пустой знак (пусть это будет для определенности  посылка которого (вписывание которого) в какую-либо ячейку ленты (памяти) гасит (стирает) тот знак, который в ней раньше хранился и оставляет ее пустой. О пустой ячейке будем говорить, что она хранит пустой знак.
посылка которого (вписывание которого) в какую-либо ячейку ленты (памяти) гасит (стирает) тот знак, который в ней раньше хранился и оставляет ее пустой. О пустой ячейке будем говорить, что она хранит пустой знак.
На любой стадии работы машины в каждой ячейке может храниться не более одного знака. Каждое сведение, хранящееся на ленте, изображается конечным набором знаков внешнего алфавита, отличных от пустого знака и хранящихся по одному в некоторых ячейках ленты. К началу работы машины на ленту подается начальное сведение (начальная информация); работа машины складывается из следующих один за другим тактов, по ходу которых происходит преобразование
начальной информации в промежуточные информации (к концу каждого такта совокупность знаков, хранящихся на ленте, образует соответствующую промежуточную информацию). В качестве начальной информации на ленту можно подать любую конечную систему знаков внешнего алфавита (любое слово в этом алфавите), расставленную произвольным образом по ячейкам. Однако в зависимости от того, какая была подана начальная информация  возможны два случая:
возможны два случая:
а) после конечного числа тактов машина останавливается, подавая сигнал об остановке; при этом на ленте оказывается изображенной некоторая информация 8. В таком случае говорят, что машина применима к начальной информации  и перерабатывает ее в результирующую информацию
и перерабатывает ее в результирующую информацию
б) остановка и сигнал об остановке никогда не наступают. В таком случае говорят, что машина не применима к начальной информации
Говорят, что машина решает некоторый класс задач, если машина применима всегда к информации, изображающей в определенном коде условия любой отдельной задачи этого типа и перерабатывает ее в информацию, изображающую в том же коде решение этой задачи.
2. Система трехадресных приказов, принятая во многих из действующих электронных машин, обусловлена наличием элементарных операций, в которых участвует сразу содержание трех ячеек памяти.
Однако в некоторых электронных машинах использована система одноадресных приказов, связанная с тем, что в каждом такте участвует лишь одна ячейка памяти. (Эту ячейку будем называть обозреваемой ячейкой на данном этапе.) Так, например, трехадресный приказ о сложении чисел из ячеек  с отправкой результата в ячейку 5 может быть заменен при надлежащих условиях тремя последовательными приказами:
с отправкой результата в ячейку 5 может быть заменен при надлежащих условиях тремя последовательными приказами:
а) вызов (в сумматор) числа из ячейки (3,
б) вызов числа из ячейки 7,
в) отправка результата в ячейку 8.
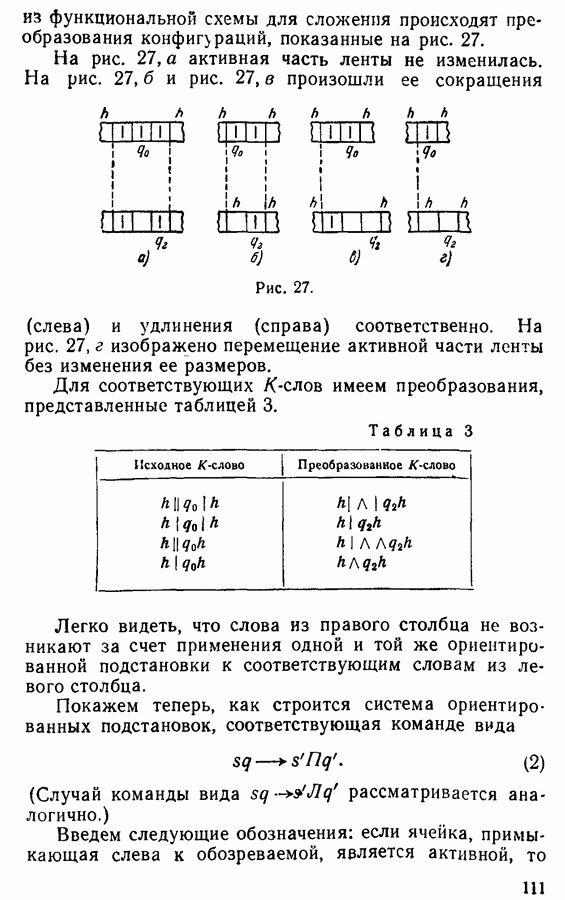
В машине Тьюринга система элементарных операций и вместе с нею система одноадресных приказов еще больше упрощены: на каждом отдельном такте приказ предписывает лишь замену единственного знака  хранящегося в обозреваемой ячейке, каким-либо другим
хранящегося в обозреваемой ячейке, каким-либо другим
знаком  При
При  это означает, что содержание обозреваемой ячейки не изменяется; при
это означает, что содержание обозреваемой ячейки не изменяется; при  это означает, что если в обозреваемой ячейке хранился какой-либо знак, то он гасится. Дальнейшее упрощение заключается в том, что при переходе машины от одного такта к непосредственно следующему такту адрес обозреваемой ячейки может изменяться не более, чем на одну единицу, т. е. обозревается соседняя слева или соседняя справа ячейка, или же обозревается та же ячейка, что и в предыдущем такте.
это означает, что если в обозреваемой ячейке хранился какой-либо знак, то он гасится. Дальнейшее упрощение заключается в том, что при переходе машины от одного такта к непосредственно следующему такту адрес обозреваемой ячейки может изменяться не более, чем на одну единицу, т. е. обозревается соседняя слева или соседняя справа ячейка, или же обозревается та же ячейка, что и в предыдущем такте.
Идея этого упрощения заключается в том, что необходимое для процесса содержание какой-либо отдельной ячейки отыскивается путем постепенной проверки всех ячеек подряд до тех пор, пока не будет обнаружена нужная ячейка. Разумеется, это очень удлиняет процесс, но вместе с тем возникает следующее удобство: в командах программы вместо произвольных адресов обозреваемых ячеек можно ограничиваться применением всего лишь трех стандартных адресов, которые изображаются специальными знаками:
 — обозревать соседнюю справа ячейку,
— обозревать соседнюю справа ячейку,
 обозревать соседнюю слева ячейку,
обозревать соседнюю слева ячейку,
 продолжать обозревать ту же ячейку
продолжать обозревать ту же ячейку
3. Для обработки числовой информации, хранящейся в памяти, электронная машина, описанная в §§ 5, 6, имеет арифметический блок  который может пребывать в одном из конечного числа состояний: складывающее, вычитающее и т. д.
который может пребывать в одном из конечного числа состояний: складывающее, вычитающее и т. д.
Для осуществления какой-либо операции в блок подаются по определенным каналам не только числа, над которыми операции совершаются, но также сигналы, настраивающие блок на соответствующую операцию, т. е. на соответствующее состояние (см. рис. 10, б) В машине Тьюринга обработка информации происходит в логическом блоке, который также может пребывать в одном из конечного числа состояний; пусть

— специальные знаки, введенные для обозначения этих состояний. Блок имеет два входных канала; по одному из них на каждой стадии работы машины (в каждом такте) поступает знак из обозреваемой ячейки, по
другому — знак  того состояния, которое предписывается блоку на данный такт; по выходному же каналу блок посылает в обозреваемую ячейку соответствующий, «переработанный» знак
того состояния, которое предписывается блоку на данный такт; по выходному же каналу блок посылает в обозреваемую ячейку соответствующий, «переработанный» знак  являющийся однозначной функцией от сигналов
являющийся однозначной функцией от сигналов  поданных на вход. Команды, обусловливающие срабатывание машины на каждом отдельном такте, имеют вид:
поданных на вход. Команды, обусловливающие срабатывание машины на каждом отдельном такте, имеют вид:

где первый знак заменяет адрес обозреваемой ячейки (см выше), а второй предписывает логическому блоку надлежащее состояние. Знаки  образуют внутренний алфавит машины.
образуют внутренний алфавит машины.

Рис. 11.
Специфической особенностью машины Тьюринга является то, что на логический блок возлагается также и выработка на каждом данном такте той команды, которая будет подаваться в блок управления к началу следующего такта. Таким образом, логический блок имеет, кроме канала для выдачи знака  еще два канала для выдачи двух знаков очередной команды. Соответствующая схема дана на рис. 11. При этом существенным является то, что выходная тройка знаков
еще два канала для выдачи двух знаков очередной команды. Соответствующая схема дана на рис. 11. При этом существенным является то, что выходная тройка знаков  зависит исключительно от того, какая входная пара знаков
зависит исключительно от того, какая входная пара знаков  была подана в том же такте на входы блока. Это означает, что логический блок реализует функцию, сопоставляющую каждой паре знаков
была подана в том же такте на входы блока. Это означает, что логический блок реализует функцию, сопоставляющую каждой паре знаков  (всего таких пар
(всего таких пар  тройку знаков
тройку знаков  Эту функцию, которую мы будем называть логической функцией машины, удобно изобразить в виде прямоугольной таблицы, столбцы которой занумерованы знаками состояний, а строки — знаками внешнего алфавита; в каждой же ячейке таблицы записана соответствующая выходная тройка знаков. Эту таблицу будем называть функциональной схемой машины; на рис. 12 приводится пример такой схемы.
Эту функцию, которую мы будем называть логической функцией машины, удобно изобразить в виде прямоугольной таблицы, столбцы которой занумерованы знаками состояний, а строки — знаками внешнего алфавита; в каждой же ячейке таблицы записана соответствующая выходная тройка знаков. Эту таблицу будем называть функциональной схемой машины; на рис. 12 приводится пример такой схемы.
Из приведенного описания ясно, что работа машины Тьюринга вполне определяется той логической
функцией, которую реализует логический блок. Иными словами, две машины Тьюринга с общей функциональной схемой неразличимы, коль скоро мы интересуемся лишь тем, как они работают. С другой стороны, структура машины, состав отдельных ее органов и их взаимодействие можно задать в виде структурной схемы, общей для всех машин Тьюринга (см. рис. 13).
В этой схеме отражено разделение памяти на внешнюю и внутреннюю. Внешняя память изображена ячейками бесконечной ленты, предназначенными для хранения информации, закодированной в символах внешнего алфавита; внутренняя память — двумя ячейками для хранения очередной команды:  -ячейка хранит знак состояния и
-ячейка хранит знак состояния и  -ячейка — знак сдвига.
-ячейка — знак сдвига.

Рис. 12

Рис. 13.
В этих двух ячейках происходит задержка знаков  полученных на выходе логического блока в данном такте работы, до начала следующего такта, когда они поступают в блок управления. Функции блока управления теперь уже чрезвычайно упрощены и заключаются по существу лишь в обеспечении сдвига ленты не более, чем на одну ячейку, в соответствии с поступившим
полученных на выходе логического блока в данном такте работы, до начала следующего такта, когда они поступают в блок управления. Функции блока управления теперь уже чрезвычайно упрощены и заключаются по существу лишь в обеспечении сдвига ленты не более, чем на одну ячейку, в соответствии с поступившим  -знаком. Знак состояния можно было бы фактически подавать из
-знаком. Знак состояния можно было бы фактически подавать из  -ячейки прямо в
-ячейки прямо в  образуя так называемую линию обратной связи, по которой в блок
образуя так называемую линию обратной связи, по которой в блок  поступает знак
поступает знак  выработанный в нем же в предыдущем такте.
выработанный в нем же в предыдущем такте.
Работа машины Тьюринга протекает следующим образом. Перед ее запуском на ленту заносится начальная информация (на нашем рис. 13 последовательность из пяти палочек) и в «поле зрения» машины устанавливается определенная начальная ячейка (на чертеже — ячейка, содержащая четвертую справа палочку), а в ячейки  вводятся знаки начального состояния и
вводятся знаки начального состояния и
начального сдвига (предположим q и  ). Дальнеишии процесс протекает уже автоматически и однозначным образом определяется функциональной схемой машины. Посмотрим, например, что произойдет в том случае, когда задана функциональная схема рис. 12.
). Дальнеишии процесс протекает уже автоматически и однозначным образом определяется функциональной схемой машины. Посмотрим, например, что произойдет в том случае, когда задана функциональная схема рис. 12.
Первый такт. Обозревается знак  (палочка) из начальной ячейки (сдвиг
(палочка) из начальной ячейки (сдвиг  при состоянии
при состоянии  Результат: выходная тройка знаков
Результат: выходная тройка знаков  т. е. знак
т. е. знак  заменен знаком а, а в ячейки
заменен знаком а, а в ячейки  послана на хранение до следующего такта очередная команда
послана на хранение до следующего такта очередная команда 
Второй такт. Обозревается знак а из той же ячейки (сдвиг  при состоянии
при состоянии  Выходная тройка:
Выходная тройка:  т. е. знак а оставляется без изменения с переходом к команде
т. е. знак а оставляется без изменения с переходом к команде 
Третий такт. Обозревается палочка из соседней справа ячейки (сдвиг  при состоянии
при состоянии  Результат: знак
Результат: знак  заменен знаком
заменен знаком  с переходом к команде
с переходом к команде 
Как видно из последнего столбца функциональной схемы рис. 12, остановка машины произойдет лишь при условии, что на некоторой стадии процесса возникнет состояние  Действительно, каков бы ни был обозреваемый знак, он не будет заменен никаким другим, и машина будет продолжать обозревать его (сдвиг
Действительно, каков бы ни был обозреваемый знак, он не будет заменен никаким другим, и машина будет продолжать обозревать его (сдвиг  при том же состоянии
при том же состоянии  Это и есть стоп-состояние, сигнализирующее о результативном завершении процесса в том случае, когда машина применима к информации, поданной в нее до запуска.
Это и есть стоп-состояние, сигнализирующее о результативном завершении процесса в том случае, когда машина применима к информации, поданной в нее до запуска.
По существу функциональной схемой может пользоваться и человек-вычислитель; она представляет для него некоторый стандартный способ задания алгоритма преобразования исходных данных, записанных во внешнем алфавите, в соответствующий результат, записанный в том же алфавите. Фактически мы так и поступили только что с функциональной схемой рис. 6 при переработке слова из пяти палочек, сознавая при этом, что машина Тьюринга сделала бы то же самое. Впредь в подобных случаях мы для большей наглядности будем пользоваться так называемыми конфигурациями. Под конфигурацией мы будем понимать изображение ленты машины с информацией, сложившейся на ней к началу  такта, причем под обозреваемой ячейкой записан знак того состояния, которое подается в логический блок
такта, причем под обозреваемой ячейкой записан знак того состояния, которое подается в логический блок  началу этого же такта. Таким образом
началу этого же такта. Таким образом
в  конфигурации явно указана входная пара знаков, а, следовательно, можно, обращаясь к функциональной схеме, определить соответствующую выходную тройку, а тем самым и
конфигурации явно указана входная пара знаков, а, следовательно, можно, обращаясь к функциональной схеме, определить соответствующую выходную тройку, а тем самым и  конфигурацию.
конфигурацию.
В разобранном выше примере первая и вторая конфигурации таковы:

со входными парами  соответственно. Переход от первой конфигурации ко второй обусловливается выходной тройкой
соответственно. Переход от первой конфигурации ко второй обусловливается выходной тройкой  соответствующей в схеме рис. 6 входной nape
соответствующей в схеме рис. 6 входной nape  .
.

Рис. 14.
Условимся еще в следующей упрощенной записи функциональных схем, которая делает схему более обозримой и удобной при выписывании конфигураций. Именно, мы откажемся от полной записи выходной тройки  опуская знаки
опуская знаки  если они не отличаются от соответствующих входных знаков, а также знак
если они не отличаются от соответствующих входных знаков, а также знак  указывающий на отсутствие сдвига. В частности, это позволяет полностью опустить столбец, соответствующий стоп-состоянию. Упрощенная запись для схемы рис. 12 приведена на рис.
указывающий на отсутствие сдвига. В частности, это позволяет полностью опустить столбец, соответствующий стоп-состоянию. Упрощенная запись для схемы рис. 12 приведена на рис.  котором стоп-состояние обозначено знаком
котором стоп-состояние обозначено знаком  Из столбца
Из столбца  схемы рис. 14 проще усматривается, чем из рис. 12, что, оказавшись в состоянии
схемы рис. 14 проще усматривается, чем из рис. 12, что, оказавшись в состоянии  при обозреваемом знаке а, машина начинает серию сдвигов влево сквозь все рядом стоящие знаки
при обозреваемом знаке а, машина начинает серию сдвигов влево сквозь все рядом стоящие знаки  продолжая оставаться в состоянии
продолжая оставаться в состоянии  и не изменяя содержания обозреваемых ячеек, до тех пор, пока в ее поле зрения попадет впервые палочка или пустая клетка; только при этих условиях машина выйдет из состояния
и не изменяя содержания обозреваемых ячеек, до тех пор, пока в ее поле зрения попадет впервые палочка или пустая клетка; только при этих условиях машина выйдет из состояния 
Впредь знак  будет всюду применяться для обозначения стоп-состояния.
будет всюду применяться для обозначения стоп-состояния.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- § 1. ЧИСЛЕННЫЕ АЛГОРИТМЫ
- § 2. АЛГОРИТМЫ ИГР
- § 3. АЛГОРИТМЫ ПОИСКА ПУТИ В ЛАБИРИНТЕ
- § 4. ПРОБЛЕМА СЛОВ
- § 5. ВЫЧИСЛИТЕЛЬНАЯ МАШИНА С АВТОМАТИЧЕСКИМ УПРАВЛЕНИЕМ
- § 6. ПРОГРАММА (машинный алгоритм)
- § 7. НЕОБХОДИМОСТЬ УТОЧНЕНИЯ ПОНЯТИЯ АЛГОРИТМА
- § 8. МАШИНА ТЬЮРИНГА
- § 9. РЕАЛИЗАЦИЯ АЛГОРИТМА В МАШИНЕ ТЬЮРИНГА
- § 10. ОСНОВНАЯ ГИПОТЕЗА ТЕОРИИ АЛГОРИТМОВ
- § 11. УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА
- § 12. АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
- § 13. НЕВОЗМОЖНОСТЬ АЛГОРИТМА ДЛЯ ПРОБЛЕМЫ ЭКВИВАЛЕНТНОСТИ СЛОВ
- ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ