§ 9. РЕАЛИЗАЦИЯ АЛГОРИТМА В МАШИНЕ ТЬЮРИНГА

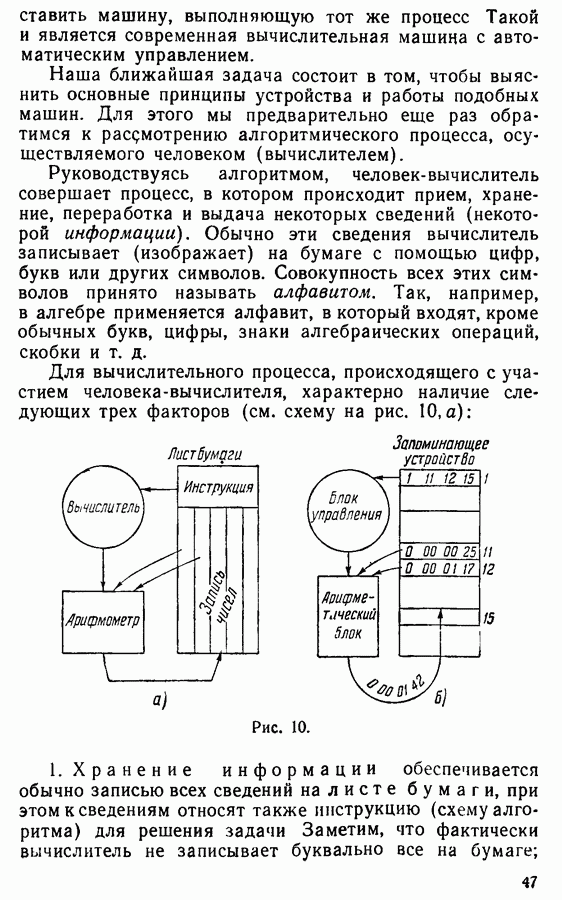
В этом параграфе на ряде примеров мы покажем, как строятся тьюринговы машины, реализующие некоторые простые арифметические алгоритмы, и как происходит в машине процесс реализации этих алгоритмов; в соответствии с содержанием предыдущего параграфа под построением машины мы будем понимать построение функциональной схемы ее логического блока, которая и представляет собою некоторую стандартную форму записи алгоритма. Кроме того, будут изложены и некоторые более общие соображения о методике построения тьюринговых машин (функциональных схем).

1. Алгоритм перехода от в десятичной системе счисления. Решается задача следующего типа:

Дана десятичная запись числа (т. е. представление натурального числа в десятичной системе счисления); требуется указать десятичную запись числа

Рис. 15.

Для этого берется внешний алфавит, состоящий из десяти цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и пустого знака Машина может пребывать лишь в двух состояниях: (рабочее состояние) и ! (остановка). Заданное число а также результирующее число будут записаны в десятичной системе, причем цифры будут помещаться по одной в ячейке (ячейки следуют подряд одна за другой без пропусков). Соответствующая функциональная схема дана на рис. 15 в виде той части указанной на нем таблицы, которая получится, если не учитывать в ней последнюю строку и последний столбец (смысл расширенной таблицы будет пояснен несколько позже). Пусть к началу работы в поле зрения установлена цифра разряда единиц числа а машина настроена в состояние если эта цифра отлична от 9, то машина остановится уже после первого такта работы, в котором происходит замена этой цифры другой цифрой в соответствии со схемой. Если же последняя цифра 9, то

машина заменяет ее нулем и производит сдвиг влево (к соседнему, более высокому разряду) и продолжает пребывать в рабочем состоянии (таким образом обеспечивается перенос единицы в более высокие разряды). Если число оканчивается девятками, то машина закончит работу в точности после такта. На рис. 16 выписаны соответствующие конфигурации при

Рис. 16.

Поясним теперь смысл расширенной таблицы, помещенной на рис. 15. Она задает функциональную схему машины, в которой имеется еще одно состояние — кроме того, во внешнем алфавите имеется еще один знак, а именно «палочка». Если к началу работы машина настроена в состоянии а на ленте нет ни одной палочки, то работа будет протекать в точности так же, как если бы мы имели дело с машиной из предыдущего примера. Это непосредственно очевидно из того, что при указанных условиях последняя строка и последний столбец таблицы не принимают никакого участия в описании работы. В частности, это означает, что данная машина может также быть использована для реализации предыдущего алгоритма. Однако данная машина способна делать еще кое-что и ради этого мы как раз и стали ее рассматривать.

Пусть на ленте задана десятичная запись числа а в нескольких ячейках, подряд расположенных правее этой записи, записаны палочки, по одной в ячейке. Посмотрим, как будет работать машина с этой функциональной схемой, если к началу работы в поле зрения установлена самая правая палочка, а сама машина настроена в состоянии . В первом такте (входная пара ) стирается эта палочка, а также происходит сдвиг налево и переход в состояние (выходная тройка ). В последующих тактах машина продолжает сдвиг налево при состоянии сквозь все палочки до первой цифры разряда единиц. Начиная с этого момента все протекает уже как и в предыдущем алгоритме, т. е. происходит переработка записи числа в запись числа и процесс завершается.

Короче, машина уменьшает на единицу число палочек и осуществляет в десятичной записи переход от

числа к числу Условимся этот процесс называть контролируемым переходом от десятичной записи к десятичной записи

На рис. 17 выписаны конфигурации для набора из пяти палочек и для

Рис. 17.

Рис. 18.

2. Алгоритм перевода в десятичную систему счисления. Построим функциональную схему машины (алгоритма), решающей задачу следующего типа:

Дана конечная совокупность палочек, вписанных в ячейки, взятые подряд без пропусков (такие совокупности будем называть наборами палочек), требуется записать в десятичной системе число этих палочек.

Короче: пересчитать набор палочек.

Такая схема задана на рис. 18. Для того, чтобы убедиться в том, что эта схема действительно описывает нужную машину (алгоритм), полезно сравнить ее со схемой расширенной таблицы рис. 15. Столбец в схеме рис. 18 отличается от столбца в схеме рис. 15 лишь тем, что вместо состояния в нем всюду фигурирует новое состояние различие столбцов не имеет существенного значения в работе схемы рис. 15. Поэтому, если на ленте задана десятичная запись числа , а правее ее — набор палочек, если, далее, в поле зрения машины, как и прежде, установлена самая правая палочка,

а сама машина настроена в состоянии то в машине будет вначале протекать такой же процесс, как и при схеме рис. 15; именно палочка набора будет стерта, а запись числа будет заменена записью числа Однако в то время как согласно схеме рис. 15 на этой стадии процесса появится состояние !, т. е. процесс прекращается, согласно схеме рис. 18 появляется состояние и процесс продолжается. В частности, если первая конфигурация взята как на рис. 17, то восьмая конфигурация получится уже такой, как на рис. 19. Как процесс будет продолжаться, видно из столбца состояния начнется серия сдвигов вправо сквозь все цифры и все палочки, пока будет достигнута первая пустая ячейка при входной паре конфигурацию 14 рис. 19), тогда последует сдвиг налево с одновременным переходом в состояние (конфигурация 15 рис. 19). Таким образом, в поле зрения машины окажется опять самая правая палочка набора при состоянии тем самым кончается один цикл работы и начинается второй цикл работы, аналогичный первому. В результате второго цикла будет стерта еще одна палочка, а запись числа будет заменена записью числа Если первоначально в наборе было палочек, то после циклов работы все они будут стерты, а вместо первоначальной записи числа появится запись числа По окончании цикла машина опять окажется в состоянии но в ее поле зрения уже будет не палочка (палочки все уже стерты), а самая первая цифра (т. е. цифра единиц) в записи числа (предпоследняя конфигурация на рис. 19). Как видно из схемы рис. 18, в этом случае произойдет остановка (последняя конфигурация на рис. 19).

Рис. 19.

Из всего сказанного вытекает, что если к началу работы машины на ленте будут записаны цифра и набор из палочек, то машина сотрет все эти палочки, а вместо нуля появится десятичная запись числа т. е. На самом же деле к началу работы можно обойтись

и без нуля, так как если вместо нуля фигурирует знак то при состояниях машина ведет себя так же, как если бы это был нуль (см. схему рис. 18). Итак, предложенная схема рис. 18 действительно описывает алгоритм перевода набора палочек в десятичную запись их числа.

Упражнение. Составить по аналогии с п. 1 функциональную схему машины (алгоритма), реализующей переход от десятичной записи числа к десятичной записи числа Далее, по аналогии с п. 2 составить функциональную схему машины для перевода с десятичной системы счисления, т. е. для замены десятичной записи какого-либо числа набором из палочек.

Мы рассмотрим еще некоторые примеры Тьюринговых машин для решения арифметических задач. В этих задачах как исходные данные (условия задачи), так и результат являются натуральными числами. Мы условимся считать, что в машине каждое натуральное число задано в виде набора из такого же числа палочек; если же в задаче фигурируют несколько натуральных чисел, то изображающие их наборы палочек будем отделять каким-нибудь специальным знаком, например звездочкой Этот знак тоже входит во внешний алфавит машины.

3. Алгоритм сложения. На ленту подается пара чисел, например,

В результате должна получиться их сумма, в данном случае

Заметим, что работу машины нельзя свести просто к стиранию звездочки, ибо тогда возникает пустая ячейка между палочками, а, следовательно, совокупность оставшихся палочек нельзя будет рассматривать как изображение одного натурального числа. Согласно предлагаемой функциональной схеме (см. рис. 20) работа машины будет протекать так.

Начальные условия: в поле зрения установлена самая левая палочка и машина настроена в состоянии (конфигурация 1 на рис. 21).

Первый такт. Обозреваемая палочка стирается, сдвиг вправо (в поле зрения устанавливается следующая палочка) и переход к состоянию (конфигурация 2).

Последующие такты, как видно из столбца сводятся к сдвигам направо сквозь все палочки и звездочку до тех пор, пока не будет достигнута первая пустая ячейка (конфигурация 12); тогда (входная пара в эту пустую ячейку вписывается палочка и машина переходит в состояние (конфигурация 13).

Рис. 20.

Рис. 21.

При состоянии происходят сдвиги влево сквозь все палочки и звездочку до первой пустой ячейки слева (конфигурация 24), тогда (входная пара происходит сдвиг вправо, в поле зрения устанавливается первая из оставшихся палочек левее звездочки, и машина переходит в состояние (конфигурация 25). В результате этого цикла одна палочка левого слагаемого оказалась перенесенной в правое слагаемое. Если левее звездочки было первоначально палочек, то через циклов все будут перенесены правее звездочки. При заходе

вправо, в поле зрения машины при состоянии попадает уже не палочка (их нет уже левее звездочки), а сама звездочка (предпоследняя конфигурация). Тогда (входная пара ) звездочка вычеркивается, и машина останавливается (последняя конфигурация). Вместе с тем получена уже и нужная сумма.

4. Алгоритмы повторного суммирования и умножения. Посмотрим, как нужно изменить схему рис. 20 для того, чтобы при первоначальной подаче на ленту пары чисел например

машина впадала бы в бесконечный процесс, заключающийся в том, что левое число прибавляется к правому и потом оно прибавляется к полученной сумме потом к сумме без конца. Для этого нужно, очевидно, чтобы левое слагаемое не исчезло бесследно после первого сложения, а, наоборот, чтобы его можно было восстановить после каждого сложения и снова прибавить к числу, изображенному правее звездочки. Этого можно добиться, например, тем, что палочки левого набора не стираются, а временно заменяются какими-то знаками или пометками. На рис. 22 изображена схема, в которой роль такой пометки играет буква а. В соответствии с этим, вхождение пустого знака в первой строке схемы 14 отвечает вхождению знака а в первой строке схемы 16 и, кроме того, в схеме рис. 22 имеется еще четвертая строка для буквы а; в этой строке первые три клетки такие же, как в строке для на рис. 20.

Рис. 22.

Далее, для того чтобы процесс не прекратился после первого сложения, необходимо, чтобы в схеме рис. 22 вместо знака который в схеме рис. 20 появляется при входной входил знак другого состояния, обеспечивающего продолжение процесса; в нашем случае таким будет дополнительно введенное состояние Для этого знака нужно ввести и соответствующий ему столбец.

В схеме рис. 22 нет знака «!» (остановки), поэтому процесс, описываемый ею, не имеет конца. Читатель теперь без особого труда проверит, что соответствующая машина реализует как раз неограниченное прибавление числа, изображенного левее звездочки, к числу, изображенному правее ее. Если правее звездочки к началу работы нет палочек (т. е. второе число нуль), то правее звездочки появятся палочек, потом потом без конца.

Упражнение. Составить функциональную схему для алгоритма умножения.

Указание. Взять за основу предыдущую схему и изменить ее так, чтобы процесс повторного суммирования не продолжался неограниченно, а выполнялся столько раз, сколько единиц во множителе (после каждого цикла сложения стирается одна палочка из набора, изображающего множитель).

5. Алгоритм Евклида. Рассмотрим теперь, как выглядит в машине Тьюринга алгоритм Евклида для нахождения общего наибольшего делителя чисел Этот алгоритм был уже ранее описан нами дважды: первый раз в виде словесного предписания, а второй раз в виде программы для электронной машины с автоматическим управлением. На этот раз алгоритм мы зададим в виде функциональной схемы Тьюринговой машины и проследим процесс вычисления в машине. Этот процесс складывается из чередующихся попеременно циклов сравнения и циклов вычитания, соответствующих элементарным операциям сравнения и вычитания в электронной машине Соответствующая функциональная схема изображена на рис. 8; ее внешний алфавит состоит из четырех знаков:

Натуральные числа будут по-прежнему изображаться соответствующими наборами палочек. Во избежание таких деталей, которые не связаны с существом дела и способны лишь усложнить наши рассмотрения, условимся наборы палочек, изображающие заданные два числа, располагать на ленте один за другим без пропусков и не отделяя их звездочкой, причем в начале процесса в поле зрения машины установлена самая правая палочка в наборе первого числа. После подробного

разбора, который будет приведен ниже, читатель в качестве упражнения, без особого труда, сумеет изменить предложенную функциональную схему так, чтобы она обеспечивала правильную работу машины и при другом способе задания условий задачи (например, если наборы отделены звездочкой, а в поле зрения машины установлена какая-нибудь пустая ячейка). Отметим еще, что буквы будут играть роль временных пометок, которые вычислитель делает (обычно в виде штрихов или галочек) для запоминания некоторых обстоятельств, возникающих по ходу процесса.

Дальнейшее описание будем сопровождать наглядной иллюстрацией применительно к случаю посредством конфигурации. Первая конфигурация выглядит так:

В цикле сравнения участвуют лишь состояния в цикле вычитания участвуют же

Рис. 23.

Проследим теперь процесс подробней. Вначале машина сравнивает числа, изображенные на ленте для того, чтобы установить, какое из них больше. При этом она поступает так же, как стал бы делать человек, сравнивающий две длинные последовательности из единиц, которые трудно сразу полностью обозреть. Именно, человек отмечает каким-либо способом поочередно по одной единице в обеих последовательностях (например, снабжая их штрихами), с исчерпанием одной последовательности выяснится, которая из них состоит из большего числа единиц.

Машина же заменяет палочку первого числа символом а, потом заменяет палочку второго числа символом потом опять возвращается к палочкам первого числа и заменяет еще одну из них символом а, потом заменяет еще одну палочку второго числа символом и т. д.

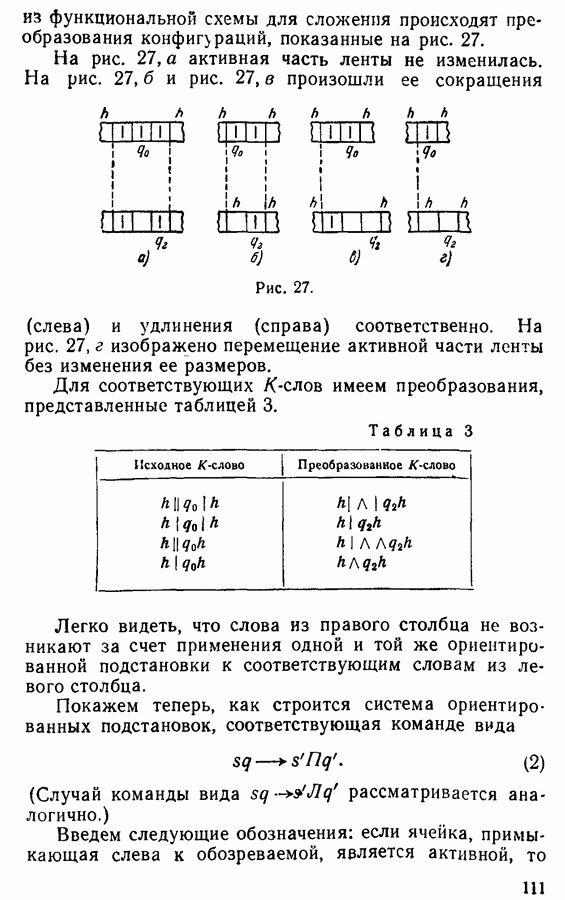
В первых четырех тактах на ленте складываются конфигурации, представленные на рис. 23, т. е. к концу четвертого такта машина успела отметить уже по одной

палочке каждого числа и теперь начинает сдвиг налево в поиске ближайшей, еще не отмеченной палочки левого числа. После еще нескольких тактов на ленте возникает конфигурация I рис. 24, т. е. первое число уже исчерпано, а второе еще нет. Поиски палочки слева не обнаружат таковой, а приведут к конфигурации II, и цикл сравнения уже осуществлен при участии одних лишь состояний

Рис. 24

Следующий такт дает уже конфигурацию III.

Как видно из столбца состояния в схеме, представленной на рис. 14, теперь начинается сдвиг направо с заменой всех а пустыми знаками (т. е. с вычеркиванием всех а) и заменой всех палочками. После того как последняя справа уже заменена палочкой, на ленте возникает конфигурация IV рис. 24, а вслед за тем конфигурация Таким образом, после цикла сравнения произошел цикл вычитания первого числа из второго, в результате которого меньшее число а стерто, а большее число разбито на а; при этом обозревается последняя палочка первого из этих чисел, а машина опять приходит в состояние Это означает, что первоначальная задача для чисел сведена к такой же задаче для чисел а Как раз на этом и основан, как мы уже знаем, алгоритм Евклида.

Дальше, разумеется, пойдет опять цикл сравнения. Теперь, однако, он заканчивается уже исчерпанием второго числа (справа), которое оказывается на этот раз меньшим. Последнее обнаруживается после того, как машина, заменив три палочки первого числа, не находит

уже больше палочек во втором числе, т. е. возникает конфигурация VI.

Последующий такт порождает конфигурацию VII и с ним начинается цикл вычитания второго числа из первого, т. е. стирание всех и замена всех а палочками. После замены последней слева а палочкой появляется на ленте конфигурация VIII, а затем и IX и тем самым цикл вычитания закончен и начинается следующий цикл сравнения и т. д. Этот процесс продолжается до тех пор, пока задача не будет сведена к случаю двух равных между собою чисел (в нашем примере это уже достигнуто). Тогда начинается последний цикл сравнения, который должен привести к результативному завершению процесса. Действительно, после того как получена конфигурация X, вычитание порождает конфигурацию XI и, наконец, результативную конфигурацию XII.

6. Сочетание алгоритмов. При построении новых функциональных схем бывает удобным использовать ранее построенные схемы; это возможно в тех случаях, когда рассматривается алгоритм, являющийся в определенном смысле сочетанием алгоритмов, ранее уже изученных. Поясним на примере. Пусть требуется построить функциональную схему алгоритма, перерабатывающего пару чисел заданных соответствующими наборами палочек, в их общий наибольший делитель, записанный в десятичной системе счисления. Поскольку этот алгоритм может быть получен в результате композиции, т. е. последовательного применения двух ранее рассмотренных алгоритмов — в п. 5 и в п. 2, — его функциональная схема, изображенная на рис. 25, может быть также получена посредством надлежащего сочетания схем рис. 14 и рис. 18. Для этого сперва переименуем состояния схемы рис. 18 в с тем, чтобы отличить их от состояний схемы рис. 14, а в схеме рис. 14 знак остановки заменим на Далее объединим эти измененные схемы в одну схему так, как это показано на рис. 25. (Клетки, оставленные незаполненными, соответствуют таким входным парам, которые в интересующем нас процессе не будут участвовать; в эти клетки можно вписать любые выходные тройки.) Теперь нетрудно проверить, что в соответствии со схемой рис. 25 сперва будет протекать процесс переработки двух заданных наборов палочек до тех пор, пока на ленте

появится набор, изображающий общий наибольший делитель; однако вместо остановки «!» (см., например, конф. XII рис. 24) теперь появится состояние и процесс будет продолжаться, обеспечивая дальнейшую переработку этого набора в десятичную запись числа.

Легко понять, что этот метод можно распространить на случай композиции любого конечного числа алгоритмов.

Рис. 25.

Отсюда, в частности, вытекает, что при рассмотрении численных алгоритмов можно считать, что натуральные числа заданы наборами палочек, ибо, составив в таком предположении надлежащую схему 21, можно от нее легко перейти к схеме 23 применительно к десятичной системе счисления. Для этого достаточно построить схему 23 по указанному выше методу путем композиции схем трех алгоритмов: алгоритма перевода из десятичной системы, алгоритма 21 и алгоритма перевода в десятичную систему.

Другим способом сочетания алгоритмов является многократное повторное применение одного и того же

алгоритма до тех пор, пока не выполнено некоторое заранее указанное условие. Так, например, алгоритм перевода в десятичную систему сводится к повторному применению алгоритма контролируемого перехода от до тех пор, пока не будут стерты все палочки. По функциональной схеме данного алгоритма (если такая уже имеется) и по предъявляемому условию можно строить схему для повторного алгоритма; однако этот метод сложнее, чем в случае композиции, и мы его не будем здесь подробно рассматривать.

Из разобранных примеров становится достаточно ясным, как составлять функциональные схемы и для других алгоритмов, в частности не численных. Укажем общий план составления функциональной схемы для алгоритма приведения слов (см. пример 4 § 4). Сперва составляются схемы которые реализуют ориентированные подстановки:

соответственно. Так, например, машина со схемой перерабатывает любое слово в алфавите записанное на ленте, в слово, получаемое путем вычеркивания самой левой четверки рядом стоящих букв с; если же таких четверок нет, то слово оставляется неизменным. Далее строятся схемы Для повторения алгоритмов 213, соответственно. Так, например, машина со схемой вычеркивает одну четверку букв с, потом другую и т. д. до тех пор, пока не выполнено условие: получено слово, в котором нет ни одной четверки рядом записанных с. Наконец, искомая схема для алгоритма приведения представляет собою композицию схем