§ 2. АЛГОРИТМЫ ИГР

Примеры, рассмотренные в предыдущем параграфе, были взяты из арифметики, алгебры, теории чисел. Они являются достаточно типичными для проблематики этих областей математики и носят, так сказать, традиционный математический характер. В этом и последующих параграфах мы разберем два класса задач, которые имеют несколько иной характер: их можно было бы скорее назвать логическими, чем математическими, хотя и весьма затруднительно предложить достаточно четкий критерий для различения подобных логических задач от обычных математических задач. Не вдаваясь в дальнейшее обсуждение терминологии, заметим лишь, что по-прежнему речь идет о нахождении алгоритма, позволяющего единым методом решать любую задачу из рассматриваемого класса однотипных задач; однако в рассматриваемых случаях эти алгоритмы уже не являются численными.

1. Одиннадцать предметов. В книге Б. А. Кордемского «Математическая смекалка» разбирается ряд игр, успешное проведение которых зависит не от случайного стечения благоприятных обстоятельств,

а от смекалки игроков и предварительного расчета. Следуя этой книге, начнем с рассмотрения игры «Одиннадцать предметов».

На столе — одиннадцать предметов, например, спичек. Первый играющий берет себе из этого количества по своему усмотрению 1, 2 или 3 спички. Затем второй играющий берет себе из числа оставшихся спичек также по своему усмотрению 1, 2 или 3. Потом опять берет первый и т. д. Так поочередно оба играющих берут каждый раз не более чем по три спички. Проигрывает тот, которому приходится взять последнюю спичку. Может ли игрок А, начинающий игру, поставить своего партнера В перед необходимостью взять последнюю спичку?

Анализ игры показывает, что игрок А может вынудить игрока В взять последним спичку, если он будет руководствоваться следующей системой указаний:

1. Первыйход. А берет 2 спички.

2. Очередной ход. Если В при своем очередном ходе взял I спичек причем еще остались неотобранные спички, то А берет спичек.

Можно показать, что эта система указаний является полной в следующем смысле: она предусматривает для игрока А любые возможные положения, в которых ему придется делать ход и определяет для каждого хода тот выбор, который должен быть сделан.

Такая полная система указаний в теории игр называется стратегией. Стратегия игрока А называется выигрышной, если любая партия, сыгранная в соответствии с нею, заканчивается для А выигрышем.

Предложенная стратегия для А действительно является выигрышной, ибо она обеспечивает А выигрыш независимо от того, как будет играть В. Проиллюстрируем это на примере следующих двух партий:

Вместе с тем можно показать, что если первым ходом А берет одну или три спички, то В может вести игру так, чтобы наверняка ее выиграть.

2. Побеждает чет. Рассмотрим теперь игру «Побеждает чет» из книги Б. А. Кордемского.

Из 27 спичек двое играющих поочередно берут не менее одной и не более четырех. Выигрывает тот, у кого по окончании игры окажется четное число спичек.

Оказывается, что для игрока А, делающего первый ход в игре, существует выигрышная стратегия, заключающаяся в следующем:

1. Первый ход. А берет 2 спички.

2. Очередной ход А, если В имеет четное число спичек. Оставить противнику число спичек, которое на 1 больше кратного шести (19, 13, 7). Если это невозможно, то при наличии 5 или 3 еще неотобранных спичек взять 4 или 2 соответственно.

3. Очередной ход А, если В имеет нечетное число спичек. Оставить противнику количество спичек, которое на 1 меньше кратного шести (23, 17, 11,. 5). Если это невозможно, то оставить число спичек кратное шести; если и это невозможно, то при наличии неотобранных еще 3 спичек или 1 спички следует брать 3 или 1 соответственно.

Приведем пример партии, разыгранной в соответствии с этой стратегией игрока А:

Как и в случае предыдущей игры, мы опускаем здесь изложение расчетов, позволивших обнаружить существование выигрышной стратегии для игрока А и описать ее. Подобные расчеты применительно к рассмотренным двум играм, а также к некоторым другим, приведены в книге Б. А. Кордемского. При этом, в зависимости от той или иной конкретной игры, привлекаются различные соображения, учитывающие каждый раз специфику игры и требующие большой смекалки и находчивости.

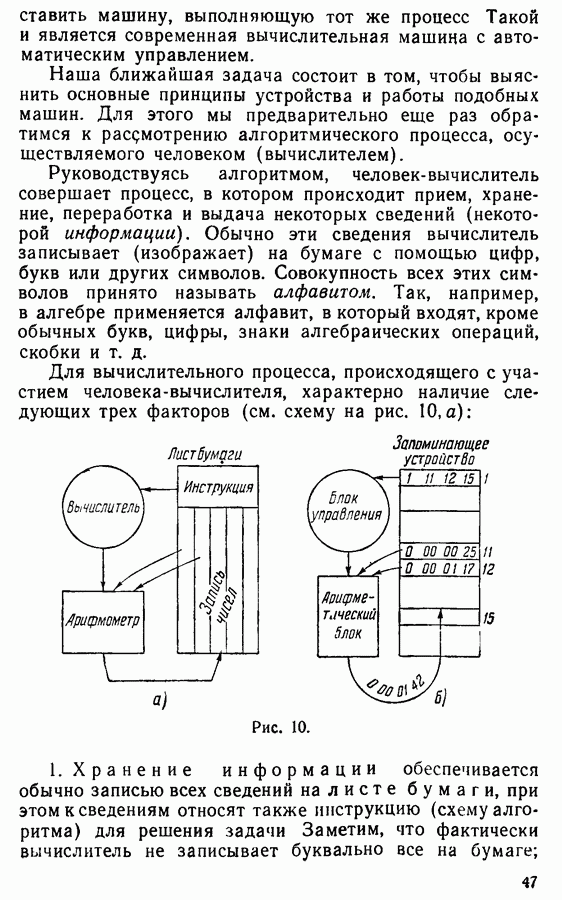
3. Дерево игры. Наша ближайшая цель заключается в описании алгоритма, применимого к любой игре из некоторого весьма обширного класса игр, который устанавливает для каждого игрока «наилучшую» из возможных для него стратегий. Во избежание чрезмерной формализации, вместо точных определений употребляемых понятий будем иногда ограничиваться лишь разъяснением их содержания с иллюстрацией на примерах.

Отметим сначала следующие особенности, присущие двум изложенным выше играм:

1. В игре участвуют два игрока, ходы которых строго чередуются.

2. Для каждой партии возможен лишь один из двух исходов:

а) выигрыш игрока А, начинающего игру (обозначаемый в дальнейшем знаком «+»);

б) выигрыш игрока В (обозначение «-»).

3. Каждый ход представляет собой выбор игроком одного из допустимого множества вариантов без всякого участия какого-либо механизма случайного выбора (например, бросания игральной кости).

4. При каждом ходе игрок знает выборы и исходы всех предыдущих ходов в данной партии.

Ниже, при отсутствии особых оговорок, под игрой подразумевается такая игра, которая обладает перечисленными свойствами 1—4.

То, что оба партнера по игре не могут иметь одновременно выигрышных стратегий, является совершенно очевидным и тривиальным фактом. Более содержательным является утверждение, что во всякой игре один из игроков имеет выигрышную стратегию. Прежде чем перейти к доказательству этого утверждения, укажем один удобный способ графического изображения игр посредством деревьев.

На рисунке 1 для определенности изображено дерево следующей игры (видоизменение игры «Одиннадцать предметов»):

Двое берут поочередно спички со стола. Первоначально на столе лежит 6 спичек, а за один раз разрешается брать не более двух. Проигрывает тот, кто берет последнюю спичку.

Вершины дерева представляют различные положения, которые могут возникнуть в партиях, разыгрываемых в соответствии с правилами игры. Ветви, выходящие из одной вершины, изображают возможные варианты в очередном ходе.

В нашем примере в любом ходе (кроме последнего) возможны два варианта. Для определенности примем, что левая ветвь, выходящая из любой вершины, соответствует изъятию одной спички, а правая — двух. Партия изображается ломаной, которая начинается с самой

нижней вершины а дерева (корень дерева), причем каждый ход изображается перемещением из данной вершины в какую-нибудь из примыкающих верхних вершин. Партия закончена тогда, когда достигнута какая-нибудь вершина, из которой не выходят ветви (концевая вершина). При каждой концевой вершине в кружке указан исход партии.

Рис. 1.

На рисунке 1 для каждой ветви указано общее число спичек, изъятых на данной стадии разыгрывания партии. Заштрихованная ломаная изображает партию

в которой А выигрывает.

Вершинам (неконцевым) дерева отнесем ранги (см. рис. 1). Наивысший из этих рангов будем называть рангом дерева; он определяет максимальную длину партий, возможных в данной игре. Вершины нечетного ранга изображают позиции, в которых ход делает игрок А, начинающий игру, а вершины четного ранга — позиции, где очередь хода за игроком В.

До сих пор дерево рассматривалось лишь как некая графическая иллюстрация игры, правила которой первоначально были заданы другим образом. Но ничто не

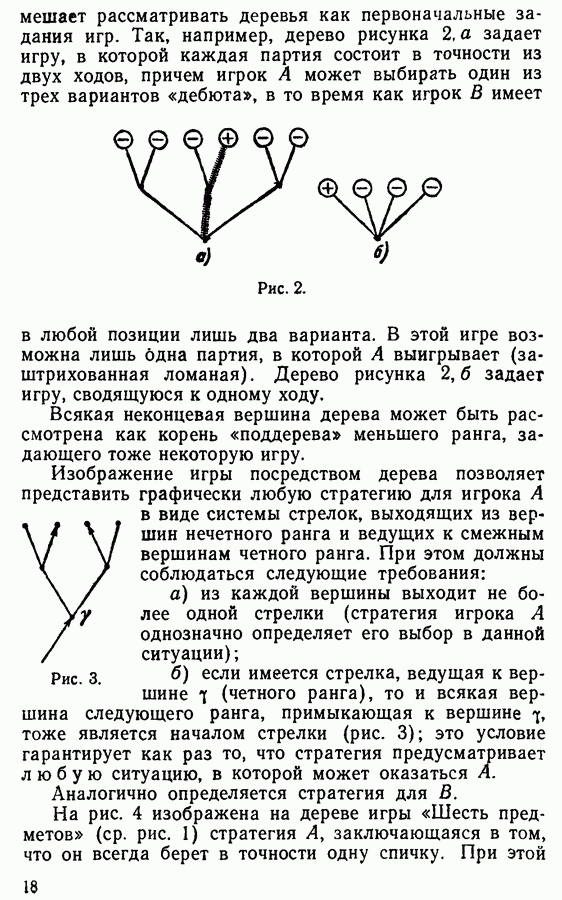
мешает рассматривать деревья как первоначальные задания игр. Так, например, дерево рисунка 2, а задает игру, в которой каждая партия состоит в точности из двух ходов, причем игрок может выбирать один из трех вариантов «дебюта», в то время как игрок В имеет в любой позиции лишь два варианта.

Рис. 2.

В этой игре возможна лишь одна партия, в которой выигрывает (заштрихованная ломаная). Дерево рисунка 2,6 задает игру, сводящуюся к одному ходу.

Всякая неконцевая вершина дерева может быть рассмотрена как корень «поддерева» меньшего ранга, задающего тоже некоторую игру.

Рис. 3.

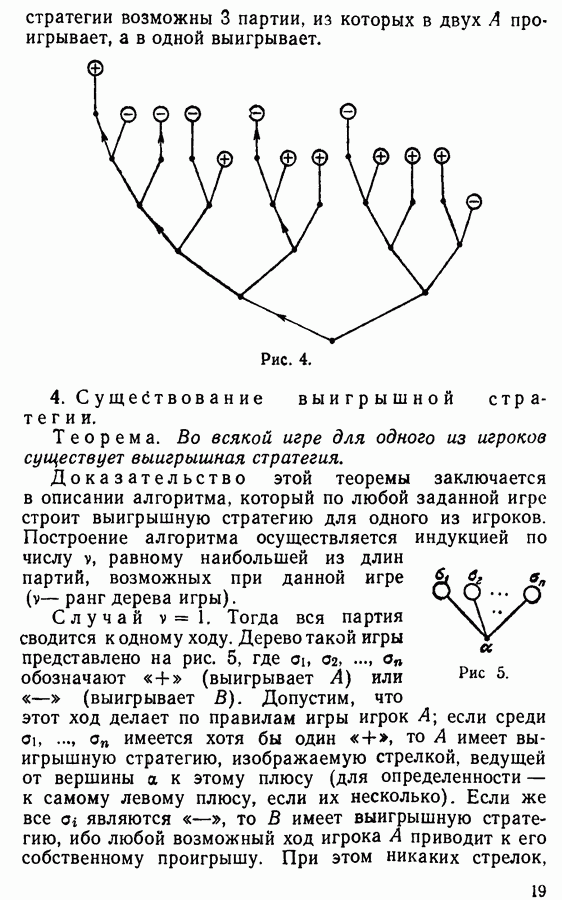
Изображение игры посредством дерева позволяет представить графически любую стратегию для игрока в виде системы стрелок, выходящих из вершин нечетного ранга и ведущих к смежным вершинам четного ранга. При этом должны соблюдаться следующие требования:

а) из каждой вершины выходит не более одной стрелки (стратегия игрока А однозначно определяет его выбор в данной ситуации);

б) если имеется стрелка, ведущая к вершине к (четного ранга), то и всякая вершина следующего ранга, примыкающая к вершине тоже является началом стрелки (рис. 3); это условие гарантирует как раз то, что стратегия предусматривает любую ситуацию, в которой может оказаться

Аналогично определяется стратегия для В.

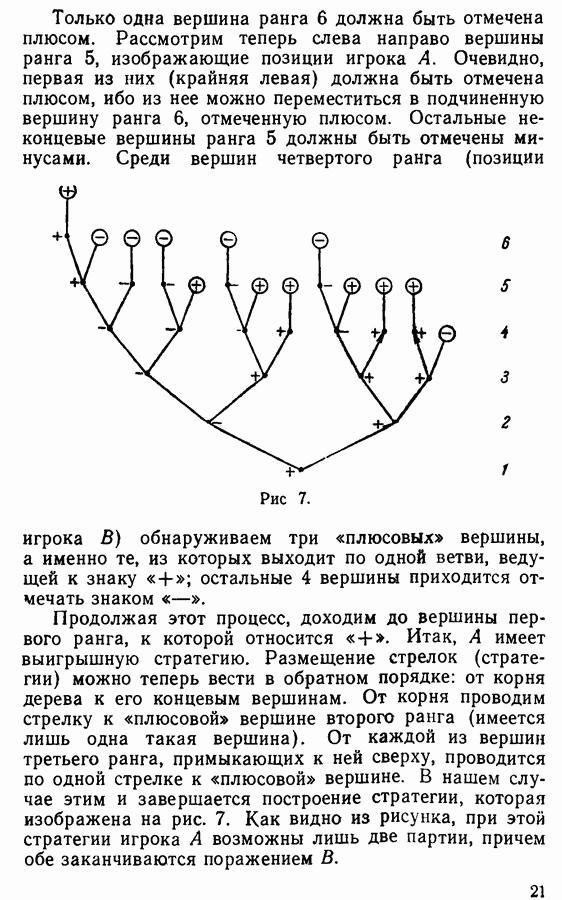
На рис. 4 изображена на дереве игры «Шесть предметов» (ср. рис. 1) стратегия А, заключающаяся в том, что он всегда берет в точности одну спичку. При этой

стратегии возможны 3 партии, из которых в двух А проигрывает, а в одной выигрывает.

Рис. 4.

4. Существование выигрышной стратегии.

Теорема. Во всякой игре для одного из игроков существует выигрышная стратегия.

Доказательство этой теоремы заключается в описании алгоритма, который по любой заданной игре строит выигрышную стратегию для одного из игроков. Построение алгоритма осуществляется индукцией по числу равному наибольшей из длин партий, возможных при данной игре ранг дерева игры).

Рис. 5

Случай . Тогда вся партия сводится к одному ходу. Дерево такой игры представлено на рис. 5, где обозначают (выигрывает А) или (выигрывает В). Допустим, что этот ход делает по правилам игры игрок если среди имеется хотя бы один то А имеет выигрышную стратегию, изображаемую стрелкой, ведущей от вершины а к этому плюсу (для определенности — к самому левому плюсу, если их несколько). Если же все являются то В имеет выигрышную стратегию, ибо любой возможный ход игрока А приводит к его собственному проигрышу. При этом никаких стрелок,

указывающих выборы игрока В, расставлять не приходится, поскольку в данной игре В вовсе не ходит.

Совершенно аналогично рассматривается случай, когда а изображает позицию, в которой ходит В. Именно, если среди имеется хотя бы один минус, то В имеет выигрышную стратегию; в противном же случае А имеет выигрышную стратегию.

Переход от Пусть теорема уже установлена для всех рангов докажем ее для В этом случае дерево игры имеет вид, представленный на рис. 6, где треугольниками изображены поддеревья, корнями которых являются вершины примыкающие к корню а всего дерева. Пусть для определенности а изображает позицию игрока А. Тогда поддеревья изображают игры, в которых первый ход делает В, причем в каждой из них наибольшая длина партии не превосходит По предположению индукции для каждой из них теорема справедлива. Допустим, что хотя бы в одной из этих подыгр А имеет выигрышную стратегию (для определенности — самое левое дерево). Тогда и во всей игре А имеет выигрышную стратегию. Для того чтобы ее построить, достаточно сохранить в поддереве Д] выигрышную стратегию и добавить стрелку, ведущую из корня а к корню «благоприятного» поддерева. Если же в каждой из подыгр игрок В имеет выигрышную стратегию, то и во всей игре В имеет выигрышную стратегию, изображаемую объединением его выигрышных стратегий во всех подыграх.

Рис. 6.

Совершенно аналогично рассматривается случай, когда а изображает позицию игрока В.

Тем самым теорема доказана и описан процесс построения алгоритма. Проиллюстрируем этот процесс на примере дерева игры «Шесть предметов» (рис. 7). Сперва, идя от конца, т. е. от вершин высшего ранга к вершинам низшего ранга, мы размещаем в вершинах дерева знак или в зависимости от того, имеет А или В выигрышную стратегию в соответствующей подыгре.

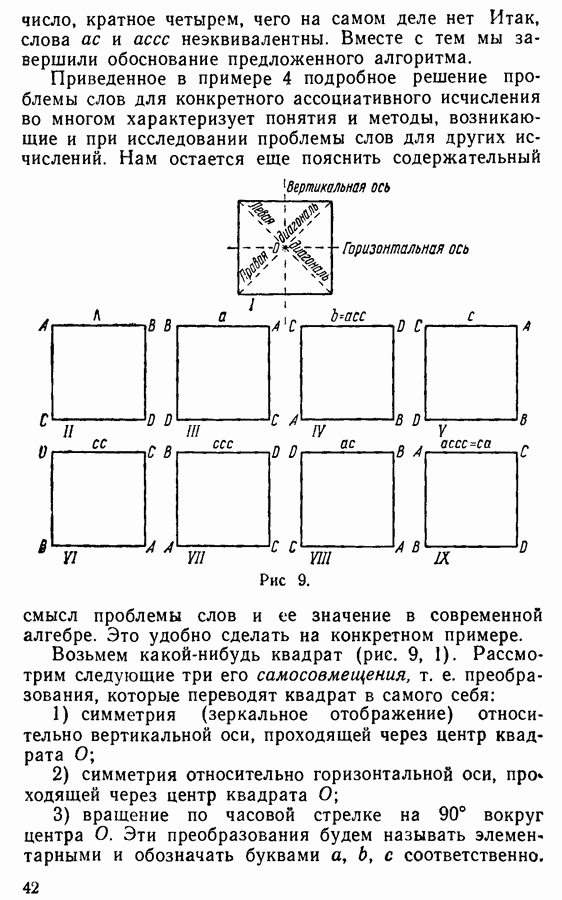
Только одна вершина ранга должна быть отмечена плюсом. Рассмотрим теперь слева направо вершины ранга 5, изображающие позиции игрока А. Очевидно, первая из них (крайняя левая) должна быть отмечена плюсом, ибо из нее можно переместиться в подчиненную вершину ранга 6, отмеченную плюсом. Остальные неконцевые вершины ранга 5 должны быть отмечены минусами.

Рис. 7.

Среди вершин четвертого ранга (позицииигрока В) обнаруживаем три «плюсовых» вершины, а именно те, из которых выходит по одной ветви, ведущей к знаку «+»; остальные 4 вершины приходится отмечать знаком «-».

Продолжая этот процесс, доходим до вершины первого ранга, к которой относится «+». Итак, А имеет выигрышную стратегию. Размещение стрелок (стратегии) можно теперь вести в обратном порядке: от корня дерева к его концевым вершинам. От корня проводим стрелку к «плюсовой» вершине второго ранга (имеется лишь одна такая вершина). От каждой из вершин третьего ранга, примыкающих к ней сверху, проводится по одной стрелке к «плюсовой» вершине. В нашем случае этим и завершается построение стратегии, которая изображена на рис. 7. Как видно из рисунка, при этой стратегии игрока А возможны лишь две партии, причем обе заканчиваются поражением В.

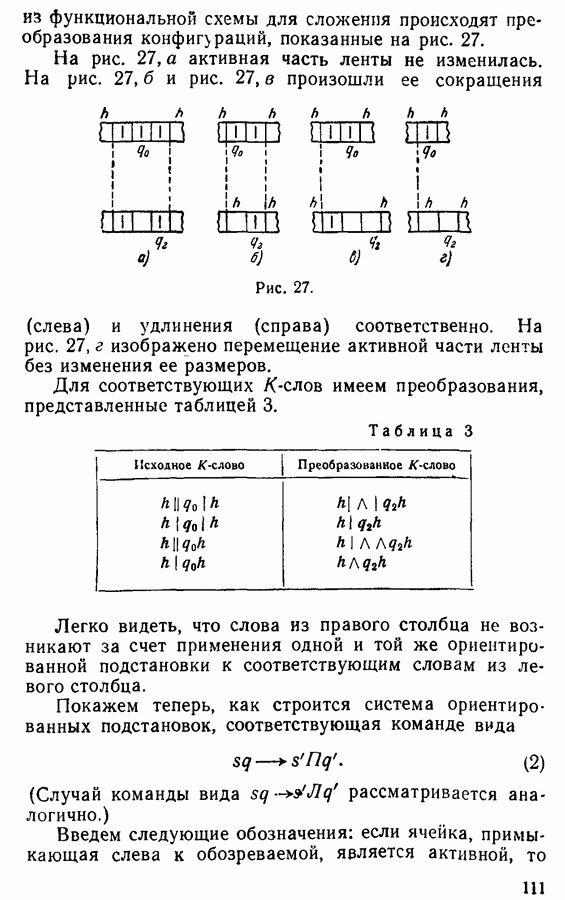
Заметим теперь, что теорема этого параграфа и лежащий в ее основе алгоритм легко обобщаются и на такие игры, для которых условия 1 и 2 пункта 3 не соблюдены, лишь бы выполнялись условия 3 и 4, которые и являются существенными. Можно, например, рассматривать игры двух партнеров в которых, кроме выигрыша А или В, возможна и ничья. Здесь может оказаться, что ни один из игроков не имеет выигрышной стратегии, но тогда алгоритм строит для каждого игрока стратегию, гарантирующую ему по крайней мере ничью (а при неразумной игре противника, быть может, и выигрыш).

Поскольку шахматы относятся к играм такого типа, то наш алгоритм устанавливает для них, какая именно ситуация имеет место и какова лучшая стратегия для белых. Для этого достаточно построить дерево шахматной игры и восстановить по нему лучшие стратегии для игроков. Если при этом окажется, что белые (игрок А) имеют выигрышную стратегию, то исход игры предрешен в пользу белых, если они только будут строго следовать этой стратегии. Точно так же исход игры будет предрешенным, если выяснится, что черные имеют выигрышную стратегию или что оба партнера имеют ничейные стратегии.

Таким образом применение рассмотренного выше алгоритма к шахматам должно привести к полному рассекречиванию этой игры в том смысле, как это удалось сделать для игры со спичками. Почему же при наличии указанного алгоритма такая ситуация до сих пор еще не возникла, а шахматы по-прежнему относятся к играм, требующим большого мастерства и смекалки?

Здесь мы очевидным образом сталкиваемся с практической неосуществимостью процесса, предписанного алгоритмом. Ведь из корня шахматного дерева выходят 20 ветвей, изображающих всевозможные дебюты белых. Из каждой вершины второго ранга тоже выходит по много ветвей и т. д., причем ранг этого дерева очень велик. В нашем распоряжении нет ни времени, ни места, ни материалов, достаточных для реализации такого замысла. Тем не менее, на вопрос, обладаем ли мы точным предписанием, позволяющим единым методом в результате конечного числа шагов находить лучшие стратегии в любой игре рассматриваемого типа, мы должны

дать утвердительный ответ. При этом мы имеем в виду, что процесс, определяемый этим предписанием, является потенциально осуществимым, т. е. что он осуществим в результате конечного (хотя, быть может, и очень большого) числа элементарных операций.

Разумеется, мы заинтересованы, главным образом, в практически осуществимых процессах. Однако выдвинуть формальный математический критерий, позволяющий раз навсегда различить практически осуществимый процесс от практически неосуществимого, мы не можем. Дело в том, что практическая осуществимость зависит от имеющихся в распоряжении вычислителя средств, которые могут меняться, например, в связи с развитием техники. Так, в связи с появлением быстродействующих электронных машин стали практически осуществимыми и такие процессы, которые ранее были только потенциально осуществимыми.

При всей громоздкости рассмотренного выше алгоритма его существование является важным обстоятельством. Ведь для проблемы Гильберта о диофантовых уравнениях не удалось обнаружить никакого алгоритма! А между тем обнаружение алгоритма, пусть и громоздкого, может подать надежду на его улучшение или создание более удобных алгоритмов.

В силу соображений, изложенных выше, говоря о вычислительном процессе или вообще о процессе, предписанном каким-то алгоритмом, будем всегда подразумевать потенциально осуществимый процесс.